The significance of the metal cation in guanine-quartet – metalloporphyrin complexes
Ana
Stanojević
 a,
Branislav
Milovanović
a,
Branislav
Milovanović
 a,
Ivana
Stanković
b,
Mihajlo
Etinski
a,
Ivana
Stanković
b,
Mihajlo
Etinski
 a and
Milena
Petković
a and
Milena
Petković
 *a
*a
aUniversity of Belgrade – Faculty of Physical Chemistry, Studentski trg 12-16, 11 158 Belgrade, Serbia. E-mail: milena@ffh.bg.ac.rs
bInstitute of Chemistry, Technology and Metallurgy, Njegoševa 12, 11 000 Belgrade, Serbia
First published on 8th December 2020
Abstract
The planarity and the appropriate size of the porphyrin ring make porphyrin derivatives ideal ligands for stacking to guanine quartets and they could thus be used as anti-cancer drugs. In this contribution we analyzed complexes of a guanine quartet with a porphyrin molecule, magnesium porphyrin and calcium porphyrin. As magnesium and calcium ions are located in the center and above the porphyrin ring, respectively, the two metalloporphyrins are expected to have different impacts on the target. The optimized structures of the three systems revealed geometrical changes in the guanine quartet upon complexation: while stacking of porphyrin and magnesium porphyrin does not induce significant changes, calcium porphyrin considerably distorts the quartet's structure, which has significant implications for the binding properties among guanine molecules. Ab initio molecular dynamics simulations revealed that the systems perform small fluctuations around the equilibrium structures. The largest atom displacements are performed by the calcium ion. The interacting quantum atoms methodology enabled analysis of the binding properties in the studied complexes. Interestingly, although the proximity of the calcium ion is responsible for the quartet's pronounced deformation and weakening of guanine–guanine binding, it also enables stronger binding of the metal ion to the quartet, resulting in a more stable complex. These results imply that metalloporphyrin-like ligands with out-of-plane central ions might represent promising drug candidates in anti-tumor treatment.
1 Introduction
More than three decades ago, Sena and Gilbert1 suggested that guanine molecules in guanine rich telomeres are prone to self-organization into larger assemblies than Watson–Crick base pairing. The ability to form quartets (composed of four guanine molecules) and quadruplexes (two or more stacked quartets) was soon recognized as a convenient property for these species to serve as anti-cancer pharmaceutical targets2 as binding of the drug to the quartet would prevent the DNA chain from unfolding. The quartet's flat structure implied that planar ligands might represent suitable drug candidates as they could be stacked to the target.3–15 Porphyrin-like compounds possess necessary properties that enable their successful stacking to a guanine quartet: the ring is flat, it is of comparable size to the quartet, and the presence of carefully selected substituents might enhance its interaction with the target. In a series of experiments, porphyrin's methyne hydrogen atoms were substituted with anionic4,16 or more often with cationic groups,5,17–24 while the central hydrogen atoms (the two protons) were replaced with metal ions.23,25–31 The porphyrin ring and the central metal ion interact with the guanine molecules themselves, whereas lateral substituent groups communicate with the DNA backbone. So far, four guanine quartet–porphyrin derivative binding modes have been identified: (i) end stacking,19,21–25,28,31 (ii) intercalation,5,19,22,23,25,28,31 (iii) sandwich formation,5,32 and (iv) external binding.18,21,28In this work, only the end stacking binding mode is considered: we focused on the nature and the strength of the guanine quartet (G4) – porphyrin derivative (PM) interaction, as well as on the role of the porphyrin ring and the metal ion in metalloporphyrins in the hydrogen bond properties in the quartet. Three drug models were studied: the porphyrin molecule (PH2), magnesium porphyrin (PMg) and calcium porphyrin (PCa). We recently analyzed the influence of alkaline earth cations on hydrogen bond cooperativity in guanine quartets33 and demonstrated that the metal cation considerably deforms the guanine quartet, which results in its large deformation energy, but at the same time enhances the interaction among guanine molecules. Herein, we extend that analysis to the impact of porphyrin stacking, along with the synergetic effect of the porphyrin ring and the alkaline earth cation on the quartet's hydrogen bond strength.
Since life, as we know it, could not exist without magnesium porphyrins, these species have been thoroughly investigated both experimentally and theoretically.34–46 In addition to naturally occurring products, synthetic analogues have also attracted attention.47,48 On the other hand, publications involving calcium porphyrins are scarce.49–52 While substitution of the central protons with a magnesium cation results in a planar porphyrin derivative, the calcium ion is located above the porphyrin plane. When calcium porphyrin is stacked to another planar ligand, Ca2+ is found between the two planes, forming a so-called double-decker structure (see ref. 50 and references therein). Since both cations are doubly charged, their distinct positions in the two metalloporphyrins enabled us to access the influence of the ion's radius on the quartet–metalloporphyrin interaction. The conclusions are drawn from results obtained by employing the interacting quantum atoms approach, which has so far been used for analysis of numerous different systems, unraveling the nature and the strength of various inter- and intramolecular interactions.33,53–68 The energy decomposition investigation presented in this work was performed in vacuo.
The manuscript is organized as follows. First, the computational details are presented. In the following section, the structural parameters of the three complexes are analyzed. Subsequently, a detailed investigation of interaction energies among different fragments is presented and the corresponding binding energies are analyzed. The results are summarized in the final section.
2 Computational details
Quantum-chemical calculations were performed with the Gaussian software69 by employing the M06-2X functional70 in conjunction with the 6-31+G(d) and 6-311+G(d) basis sets71–75 and an ultrafine integration grid. It is well known that the M06-2X functional is able to provide a reliable description of non-covalent interactions,33,64,76–83 while diffuse and polarization functions on carbon, nitrogen and oxygen atoms are expected to adequately model stacking interactions. The importance of including solvent effects was tested with the Polarizable Continuum Model (PCM) as implemented in the Gaussian software.84 All optimized complexes have only real frequencies and thus represent stable species. We considered Bader charges, which were computed with the AIMAll software.85Density functional based molecular dynamics simulations of the three complexes (PH2, PMg and PCa) were performed with the CP2K program package.86 We employed the GGA BLYP functional87,88 corrected with the D3 scheme for dispersion interactions.89 The mixed Gaussian and plane wave (GPW) method90 was used to describe the system's electron density. We used the DZVP basis set for localized functions and plane waves for delocalized functions (with the cutoff and the relative cutoff set to 350 Ry and 50 Ry, respectively) to describe valence electrons, while core electrons were described with GTH type pseudopotentials.91 The SCF convergence threshold was set to 5.0 × 10−7 a.u. All systems were equlibrated during a 2 ps long run with a timestep of 0.5 fs for integrating the classical equations of motion within a nonperiodic cubic box of a 25 Å cell constant and under the NVT ensemble. We employed the CSVR thermostat92 to equlibrate the systems at 300 K. Production runs lasted 10 ps under the same conditions after equlibration. The power spectra of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration were computed from 10 ps long NVE trajectories initiated from the last NVT configurations. The power spectra were determined by the TRAVIS program.93,94 We also computed those spectra for G4–G4, G4–Mg–G4 and G4–Ca–G4 quadruplexes by using the same computational procedures as for the porphyrin complexes. The NVE trajectories were initiated from the NVT trajectories examined in our previous work.95
O stretching vibration were computed from 10 ps long NVE trajectories initiated from the last NVT configurations. The power spectra were determined by the TRAVIS program.93,94 We also computed those spectra for G4–G4, G4–Mg–G4 and G4–Ca–G4 quadruplexes by using the same computational procedures as for the porphyrin complexes. The NVE trajectories were initiated from the NVT trajectories examined in our previous work.95
2.1 Interacting quantum atoms
The energy partitioning methodology known as Interacting Quantum Atoms53,54 (IQA) is based on Bader's quantum theory of atoms in molecules,96,97 according to which a molecule can be divided into atomic subspaces. Selected atoms form fragments![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ; the interaction energy between fragments
; the interaction energy between fragments ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) i and
i and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) j,
j, 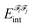 , is an additive property composed of the interaction energies among each pair of atoms I (that belongs to
, is an additive property composed of the interaction energies among each pair of atoms I (that belongs to ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) i) and J (that belongs to
i) and J (that belongs to ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) j):
j):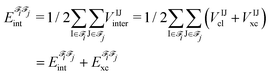 | (1) |
In the above equation, the interaction energy among each pair of atoms VIJinter is written as a sum of its classical VIJcl and its non-classical VIJxc contribution, which constitute analogue energy components that describe the fragment–fragment interaction (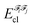 and
and 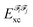 ).
).
A fragment's deformation energy 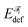 is defined with respect to its reference state, which is an isolated fragment with the geometry it adopts in the complex. The sum of the interaction and deformation energies defines the IQA binding energy:
is defined with respect to its reference state, which is an isolated fragment with the geometry it adopts in the complex. The sum of the interaction and deformation energies defines the IQA binding energy:
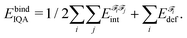 | (2) |
The number of fragments depends on the phenomenon of interest. In the current manuscript we employed several fragmentation schemes for the guanine quartet – metalloporphyrin complex, and they are based on: (i) two fragments (G4 and PH2/PMg/PCa), (ii) three fragments (G4, P and H2/Mg/Ca) and (iii) five fragments (four guanine molecules and PH2/PMg/PCa). IQA analysis was performed with the AIMAll program85 by employing the promega5 basin integration method. The precision of this approach, when applied on the system of interest, can be accessed by comparing the IQA binding energy EbindIQA to the SCF binding energy EbindSCF:
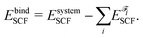 | (3) |
Let us consider, for example, G4–PCa composed of six fragments: four guanine molecules, the porphyrin ring and the calcium ion. The IQA and SCF binding energies amount to −1336 and −1310 kJ mol−1, respectively. Such a deviation is a consequence of numerical integrations: this system contains 101 atoms, therefore 101 × (101 − 1)/2 = 5050 pair interactions are considered. Although the absolute value of the deviation equals 26 kJ mol−1, it represents only 2% of the SCF binding energy. We can also analyze those results from another perspective: if we consider just the quartet, the difference between the IQA and SCF binding energies equals 11 kJ mol−1. Since the quartet is composed of four identical units, there are six pairs of guanine molecules (four neighboring and two diagonal pairs). If we neglect interactions among diagonal molecules and only consider neighbors, the average deviation of the binding energy per guanine–guanine pair is below 3 kJ mol−1, which is acceptable for the current analysis.
3 Results and discussion
We start the analysis by inspecting the optimized geometries of the three complexes, which paves the way to the study of the interactions among different fragments.3.1 Basis set convergence and solvent effect
Let us first analyze the quality of the employed level of theory. We will use the term complexation energy Ecomplex for the energy difference between the optimized structure of the complex and the optimized structures of the target and the ligand (note that the term binding energy refers to the value computed by taking the geometries of the target and the ligand that they adopt in the complex). Complexation energies computed at different levels of theory are summarized in Table 1. The M06-2X functional was employed in all cases. First, we will consider the results obtained by optimizing the structures with different basis sets, which are presented in the upper part of the table. Taking the 6-31+G(d) basis set and performing calculations in vacuo gives for G4–PH2, G4–PMg, and G4–PCa complexation energies of −128, −137, and −332 kJ mol−1, respectively. Employment of the 6-311+G(d) basis set results in values that are larger (i.e. more negative) by 10 and 7 kJ mol−1 for G4–PH2 and G4–PMg, and weaker (less negative) by 23 kJ mol−1 for G4–PCa. Almost identical Ecomplex values are obtained at the 6-311+G(d)//6-31+G(d) level, which confirms that the double-zeta basis provides reliable geometries of the ligand, the target and the complex. Finally, let us consider solvent effects by taking the double-zeta geometries and performing triple-zeta single point energy calculations in the presence of the solvent included through the Polarizable Continuum Model (PCM) as implemented in the Gaussian software.84 The complexation energy is only 3 and 9 kJ mol−1 lower for G4–PH2 and G4–PMg compared to the 6-31+G(d) in vacuo values, but it is as much as 82 kJ mol−1 lower for G4–PCa. The presented results indicate less significant importance of solvent inclusion in the absence of metal ions and in the case when the metal ion is shielded by the porphyrin ring, as well as its significance if the metal ion does not lie in the plane of the porphyrin ring. However, the Ecomplex values computed at each level of theory presented in Table 1 are significantly larger in G4–PCa with respect to the other two complexes. These results demonstrate that neglection of the solvent does not alter the qualitative picture and that the IQA procedure (in which solvent effects have not been implemented yet) offers a reliable description of the studied systems. Additionally, since the 6-311+G(d) basis set only slightly alters the 6-31+G(d) geometries and complexation energy values, IQA analysis was performed with the double-zeta basis set.| Basis set & vacuum or solvent | E complex | ||
|---|---|---|---|
| G4–PH2 | G4–PMg | G4–PCa | |
| 6-31+G(d) | −128 | −137 | −332 |
| 6-311+G(d) | −138 | −144 | −309 |
| 6-311+G(d)//6-31+G(d) | −138 | −144 | −310 |
| 6-311+G(d)(PCM)//6-31+G(d) | −125 | −128 | −250 |
| d(GCOM4–PCOM) | d(GCOM4–Mg/Ca) | d(Mg/Ca–PCOM) | |
|---|---|---|---|
| G4–PH2 | 3.280 ± 0.101 | ||
| G4–PMg | 3.233 ± 0.107 | 2.832 ± 0.036 | 0.405 ± 0.072 |
| G4–PCa | 3.248 ± 0.145 | 1.571 ± 0.187 | 1.676 ± 0.115 |
| d(GCOM4–GCOM4) | d(GCOM4–Mg/Ca) | d(Mg/Ca–GCOM4) | |
|---|---|---|---|
| G4–G4 | 4.110 ± 0.355 | ||
| G4–Mg–G4 | 3.809 ± 0.109 | 1.751 ± 0.056 | 2.068 ± 0.054 |
| G4–Ca–G4 | 3.404 ± 0.120 | 1.684 ± 0.142 | 1.727 ± 0.162 |
3.2 Geometric considerations
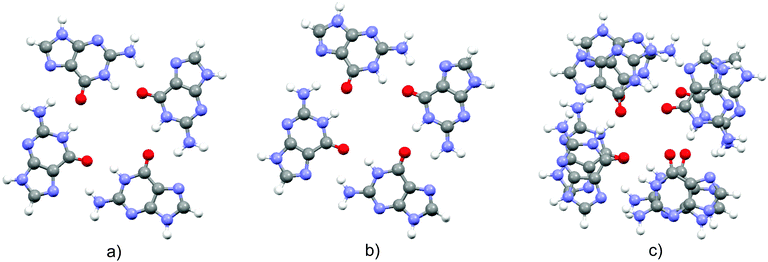
Optimized structures of the three complexes are presented in Fig. 1. The area of the porphyrin ring is slightly smaller than the one of the quartet. Both species are essentially planar, which enables effective stacking. The small size of the magnesium cation allows its settlement in the center of the porphyrin ring. Consequently, substitution of the two central porphyrin protons with Mg2+ does not significantly alter the quartet–porphyrin complex geometry. However, the larger radius of the calcium cation compared to its analogue with fewer electrons disables its residence in the center of the porphyrin ring and is responsible for the ion's location between G4 and P. Such a structure enables simultaneous compensation of the negative charge located in the porphyrin ring and on guanine oxygen atoms.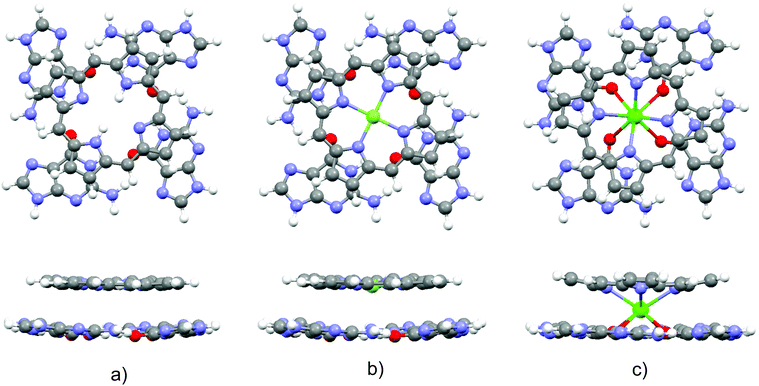 | ||
| Fig. 1 Optimized structures of the complexes (top and side view) formed by G4 and (a) PH2, (b) PMg and (c) PCa. | ||
The fact that smaller cations fit in a certain cavity while larger ones are not able to do so is a well-known fact for metal ion complexes with guanine quartets: while Na+ is able to accommodate itself between the oxygen atoms of the four guanine molecules, K+ is located above the quartet.33,98–102 Marek and coworkers102 demonstrated that stacking G4–Na to another guanine quartet pulls the metal ion into the cavity between the quartets, enabling it to stabilize the structure through the compensation of the negative charge of all eight oxygen atoms in the quadruplex. While in G4–K–G4 the cation is positioned at the midpoint between the quartets, the sodium ion in G4–Na–G4 can be found at two equivalent positions closer to either of the two G4 systems, as analyzed by van Mourik and Dingley.101 This is to be contrasted with the situation in magnesium porphyrin, as its stacking to G4 does not withdraw Mg2+ from the porphyrin ring: since the ring is charged, unlike the quartet, it does not allow significant displacement of the cation.
In order to obtain evidence of whether the structure of the guanine quartet is deformed upon complex formation, the geometry of the free quartet is overlapped with its analogues from each of the three complexes, Fig. 2. Oxygen atoms were used to orient the quartets. Let us label them O1, O2, O3 and O4 in the monomers down-left, down-right, up-right and up-left, respectively. O1 is set as the origin of the coordinate system, and the x-axis is formed by O1 and O2, whereas O1, O2 and O3 define the xy-plane. While PH2 and PMg do not generate significant distortion in G4, calcium's proximity causes electron redistribution in the quartet, which is reflected in the decrease of the oxygen–oxygen distance from 4.165 Å in unbound G4, 4.168 Å in G4–PH2 (average value) and 4.104 Å in G4–PMg, to only 3.111 Å in G4–PCa. This simple analysis implies that metal–porphyrin complexes do not significantly perturb the quartet, provided that the size of the divalent metal cation is small enough to fit in the center of the porphyrin ring.
 | ||
| Fig. 2 Overlapped structures of a guanine quartet in free G4 with the quartet structures in its complexes with (a) PH2, (b) PMg and (c) PCa (see the text for details). | ||
As can be seen in Fig. 2, each oxygen atom might form hydrogen bonds with hydrogen atoms of both amino and imino groups of the neighbor. The question of whether bifurcated hydrogen bonds exist in G4 was analyzed by various authors103,104 (see the discussion in ref. 33). The M06-2X functional in free G4 favors the structure with bifurcated hydrogen bonds. The average O⋯Hamino distance in G4, G4–PH2, G4–PMg, and G4–PCa equals 2.037, 2.010, 2.044 and 3.445 Å, respectively, while the average electron density at the O⋯Hamino bond critical points in G4, G4–PH2, and G4–PMg amounts to 0.023, 0.024, and 0.021 a.u., respectively, suggesting the existence of bifurcated hydrogen bonds in these three complexes and comparable O⋯Hamino hydrogen bond strength. On the other hand, the O⋯Hamino bond critical point in G4–PCa does not exist. Thus, the calcium ion causes vanishing of bifurcated hydrogen bonds in the guanine quartet.
3.3 Are thermal fluctuations in G4–PM complexes significant?
Insight into the system's flexibility can be gained from ab initio molecular dynamics simulations. The changes of the GCOM4–PCOM, GCOM4–Mg/Ca and Mg/Ca–PCOM distances (the abbreviation COM is used for a center of mass) in the three systems are displayed in Fig. 3, while their average values are shown in Table 2. The metal cation does not significantly alter the average GCOM4–PCOM distance. Its most pronounced fluctuations are observed in G4–PCa. As expected, the GCOM4–Mg separation is significantly larger compared to d(GCOM4–Ca), but it is characterized by considerably smaller variations. Finally, the average Mg–PCOM distance is almost four times smaller compared to the calcium analogue. Interestingly, the curves that correspond to the GCOM4–Ca and Ca–PCOM distances are out of phase, which indicates calcium's oscillation between two negatively charged regions. The time evolution of selected distances in the analyzed complexes implies small geometry changes due to the thermal motion.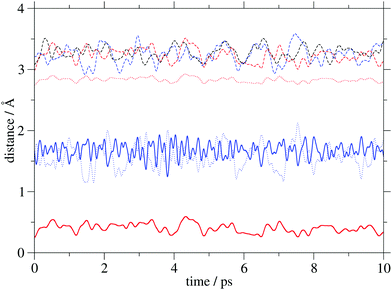 | ||
| Fig. 3 Distances (COM stands for a center of mass) between GCOM4 and PCOM (dashed lines), GCOM4 and Mg/Ca (dotted lines), and Mg/Ca and PCOM (full lines) in PH2 (black), PMg (red) and PCa (blue). | ||
3.4 Intermolecular interactions and binding energies
Let us now turn to intermolecular interactions. We will analyze the following: (i) the impact of the ligand on the guanine–guanine interaction, (ii) the porphyrin ring – metal cation interaction, (iii) the ligand – target interaction, and finally (iv) the deformation and binding energies.![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) are compiled in Table 3. In the absence of the ligand, Eint amounts to −253 and −20 kJ mol−1 between neighboring and diagonal molecules, respectively. Around 40% of the interaction energy among the neighbors is due to Coulomb interactions, whereas the interaction between diagonal guanines is entirely classical. Stacking of the porphyrin molecule PH2 does not significantly perturb the guanine–guanine interaction, which is also the case with magnesium porphyrin. A similar situation was encountered in guanine quadruplexes as it was demonstrated that the energies of N–H⋯O and N–H⋯N hydrogen bonds do not significantly change upon stacking of two guanine quartets.102 While sole alkaline earth cations weaken the guanine–guanine interaction,33 PMg has a negligible influence on the quartet's building blocks due to Mg's position in the center of the porphyrin ring, which keeps it distanced from G4 (Fig. 3 and Table 2). This is not the case with PCa and the proximity of the calcium ion is reflected in slight strengthening of the
are compiled in Table 3. In the absence of the ligand, Eint amounts to −253 and −20 kJ mol−1 between neighboring and diagonal molecules, respectively. Around 40% of the interaction energy among the neighbors is due to Coulomb interactions, whereas the interaction between diagonal guanines is entirely classical. Stacking of the porphyrin molecule PH2 does not significantly perturb the guanine–guanine interaction, which is also the case with magnesium porphyrin. A similar situation was encountered in guanine quadruplexes as it was demonstrated that the energies of N–H⋯O and N–H⋯N hydrogen bonds do not significantly change upon stacking of two guanine quartets.102 While sole alkaline earth cations weaken the guanine–guanine interaction,33 PMg has a negligible influence on the quartet's building blocks due to Mg's position in the center of the porphyrin ring, which keeps it distanced from G4 (Fig. 3 and Table 2). This is not the case with PCa and the proximity of the calcium ion is reflected in slight strengthening of the ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) interaction. Interestingly, Ca2+ decreases the classical component and increases the exchange–correlation term between the neighbors. On the other hand, the interaction among diagonal terms remains completely electrostatic and is basically negligible. This behavior differs from the one in Na+ and K+ sandwiched between two quartets102 – while the sodium ion does not significantly affect the guanine–guanine interaction due to the more pronounced G4 planarity in the presence of the cation, the potassium ion weakens the hydrogen bonds in G4 as a result of the stronger oxygen–cation interaction. The opposite influence of K+ and Ca2+ is most likely due to different charges, as the calcium ion causes pronounced quartet distortion, which results in the decrease of the guanine–guanine distance, Fig. 2, and consequently stronger intermolecular interactions in G4. This finding is in accord with the results presented by van Mourik and Dingley101 who analyzed complexes of guanine quartets and alkali cations, and demonstrated that the cation decreases the distance between the oxygen atoms. The decrease in the O–O distance is even more pronounced in the presence of alkaline earth cations.
interaction. Interestingly, Ca2+ decreases the classical component and increases the exchange–correlation term between the neighbors. On the other hand, the interaction among diagonal terms remains completely electrostatic and is basically negligible. This behavior differs from the one in Na+ and K+ sandwiched between two quartets102 – while the sodium ion does not significantly affect the guanine–guanine interaction due to the more pronounced G4 planarity in the presence of the cation, the potassium ion weakens the hydrogen bonds in G4 as a result of the stronger oxygen–cation interaction. The opposite influence of K+ and Ca2+ is most likely due to different charges, as the calcium ion causes pronounced quartet distortion, which results in the decrease of the guanine–guanine distance, Fig. 2, and consequently stronger intermolecular interactions in G4. This finding is in accord with the results presented by van Mourik and Dingley101 who analyzed complexes of guanine quartets and alkali cations, and demonstrated that the cation decreases the distance between the oxygen atoms. The decrease in the O–O distance is even more pronounced in the presence of alkaline earth cations.
| Fragments | Neighboring | Diagonal | ||||
|---|---|---|---|---|---|---|
| E int | E cl | E xc | E int | E cl | E xc | |
| G4 | −253 | −107 | −146 | −20 | −20 | 0 |
| G4–PH2 | −258 | −108 | −150 | −20 | −20 | 0 |
| G4–PMg | −258 | −108 | −150 | −20 | −20 | 0 |
| G4–PCa | −278 | −88 | −190 | −8 | −8 | 0 |
The carbonyl group stretching vibration is a sensitive probe for non-covalent interactions in quadruplexes. This mode exhibits in a quadruplex a significant spectral red-shift with respect to a single strand structure due to the hydrogen bonding with other guanine bases, as well as the interaction with a cation located between the quartets.105 In order to understand to what extent thermal motion alters the conclusions from the static calculations, we computed the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching power spectra for the examined systems, Fig. 4. The most intense peak in each spectrum is due to the C
O stretching power spectra for the examined systems, Fig. 4. The most intense peak in each spectrum is due to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, whereas the two peaks on the red side of the spectra arise from vibrational couplings to other modes. The substitution of two porphyrin protons with Mg2+ results in the C
O stretching, whereas the two peaks on the red side of the spectra arise from vibrational couplings to other modes. The substitution of two porphyrin protons with Mg2+ results in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode's small red-shift of 11 cm−1. This is in accordance with our analysis of the optimized geometries of the G4–PH2 and G4–PMg complexes in which we demonstrated that the magnesium ion has a negligible influence on the guanine–guanine interaction. On the other hand, Ca2+ strengthens the
O stretching mode's small red-shift of 11 cm−1. This is in accordance with our analysis of the optimized geometries of the G4–PH2 and G4–PMg complexes in which we demonstrated that the magnesium ion has a negligible influence on the guanine–guanine interaction. On the other hand, Ca2+ strengthens the ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) interaction, which is reflected in the red-shift of the C
interaction, which is reflected in the red-shift of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequency by 56 cm−1 relative to G4–PH2. Therefore, thermal fluctuations do not modify the conclusions drawn from the analysis performed at the optimized geometries.
O stretching frequency by 56 cm−1 relative to G4–PH2. Therefore, thermal fluctuations do not modify the conclusions drawn from the analysis performed at the optimized geometries.
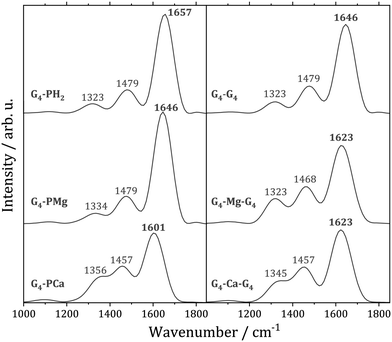 | ||
Fig. 4 Power spectra of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration. Left: G4–PM complexes (M = H2, Mg, Ca). Right: Guanine quadruplex G8 and its sandwiches with Mg and Ca ions. O stretching vibration. Left: G4–PM complexes (M = H2, Mg, Ca). Right: Guanine quadruplex G8 and its sandwiches with Mg and Ca ions. | ||
The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching power spectra of a stacked guanine quartet G4–G4 and its two analogues with sandwiched magnesium and calcium ions are also displayed in Fig. 4. The average distances of the two quartets in the quadruplexes are larger than the average distances between the quartet and the porphyrin ligands, Table 2. Unlike G4–PM complexes in which Mg2+ is located within the ligand, whereas Ca2+ is not, both cations are located between the quartets in both quadruplexes, analogously to quadruplexes with Na+ and K+.102 Note that the Mg2+ cation is closer to one of the quartets, Table 2, similarly to Na+.101 The fact that Ca2+ is closer to the quartet in G4–PCa compared to G4–Ca–G4 is reflected in a more pronounced red shift of the C
O stretching power spectra of a stacked guanine quartet G4–G4 and its two analogues with sandwiched magnesium and calcium ions are also displayed in Fig. 4. The average distances of the two quartets in the quadruplexes are larger than the average distances between the quartet and the porphyrin ligands, Table 2. Unlike G4–PM complexes in which Mg2+ is located within the ligand, whereas Ca2+ is not, both cations are located between the quartets in both quadruplexes, analogously to quadruplexes with Na+ and K+.102 Note that the Mg2+ cation is closer to one of the quartets, Table 2, similarly to Na+.101 The fact that Ca2+ is closer to the quartet in G4–PCa compared to G4–Ca–G4 is reflected in a more pronounced red shift of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode in the complex with calcium porphyrin.
O stretching mode in the complex with calcium porphyrin.
Marek and coworkers106 studied Na+ and K+ ions stacked in artificial DNA quadruplexes (8-halo-9-dezaxanthines) and demonstrated that the metal ions are responsible for the electron density redistribution in both quartets, with the smaller ion causing significant electron polarization towards the cation, while the larger ion shows a tendency of electron sharing with the quartet. The delocalization indices for O–Mg bonds in G4–PMg and O–Ca bonds in G4–PCa amount to 4 × 10−4 and 0.077 a.u., respectively. The significantly more pronounced electron sharing with the heavier cation can in the case of the porphyrin ligands be ascribed to the nature of the metal ion, as its larger radius is responsible for its proximity to the quartet, which results in larger delocalization indices.
| Fragments | P & M in PM | P & M in G4–PM | ||||
|---|---|---|---|---|---|---|
| E int | E cl | E xc | E int | E cl | E xc | |
| PMg | −3107 | −2710 | −396 | −3051 | −2660 | −391 |
| PCa | −2664 | −2202 | −462 | −2155 | −1857 | −298 |
 , the corresponding term in a solvent is also expected to be significantly larger for calcium porphyrin.
, the corresponding term in a solvent is also expected to be significantly larger for calcium porphyrin.
| Fragments | G4 & PM | G4 & M | G4 & P | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E int | E cl | E xc | E int | E cl | E xc | E int | E cl | E xc | |
| G4–PH2 | −697 | −16 | −681 | −57 | −57 | 0 | −640 | 41 | −681 |
| G4–PMg | −714 | −19 | −695 | −128 | −127 | −1 | −586 | 108 | −694 |
| G4–PCa | −1357 | −412 | −945 | −908 | −741 | −167 | −449 | 329 | −778 |
Concerning the interaction between the quartet and the porphyrin ring, it weakens in the order PH2, PMg, PCa. This behavior is a consequence of the accumulation of the negative charge in the porphyrin ring (−0.971 e, −1.638 e and −1.629 e, respectively), whereas the charges of the quartet change in the order −0.072 e, −0.083 e and −0.114 e. Consequently, the electrostatic repulsion is significantly increased on going from PH2 to PCa, despite the system's stabilization through non-classical interactions. The charges of the two central protons, the magnesium ion and the calcium ion equal +1.051 e, +1.728 e and +1.749 e, respectively, which is reflected in the corresponding Ecl term.
| Fragments | E def | E IQAbind | ||||
|---|---|---|---|---|---|---|
| G4 | PM | P | M | G4 & PM | G4 & P & M | |
| G4–PH2 | 291 | 298 | 585 | −2203 | −108 | −4119 |
| G4–PMg | 295 | 302 | 788 | −339 | −117 | −3021 |
| G4–PCa | 472 | 465 | 454 | −148 | −420 | −2734 |
First, consider a two-fragment ligand–target complex. The small adjustment of the ligand's structure upon complexation is the reason behind the comparable deformation energies of PH2 and PMg. 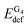 and EIQAbind in G4–PH2 and G4–PMg are essentially the same, which is not surprising as the geometry of the quartet and the interaction energies between G4 and PM are quite similar in the two complexes. On the other hand, the considerable distortion of the target and the ligand in G4–PCa is reflected in significantly larger deformation energies of both fragments. The strong interaction between the quartet and calcium porphyrin is, however, responsible for the significantly stronger binding between this ligand and the target compared to the other two analogues.
and EIQAbind in G4–PH2 and G4–PMg are essentially the same, which is not surprising as the geometry of the quartet and the interaction energies between G4 and PM are quite similar in the two complexes. On the other hand, the considerable distortion of the target and the ligand in G4–PCa is reflected in significantly larger deformation energies of both fragments. The strong interaction between the quartet and calcium porphyrin is, however, responsible for the significantly stronger binding between this ligand and the target compared to the other two analogues.
In order to get a closer look at the importance of the size of the metal ions, we will artificially separate the cation from the porphyrin ring. We want to compare the roles of the magnesium and the calcium ion, while the results for PH2 are presented for consistency (in this case M stands for the two hydrogens). Since the Mg–P interaction is almost 50% stronger than the Ca–P interaction in the corresponding complexes, Table 4, the deformation energy of the porphyrin skeleton and the metal ion is much larger in PMg. Note that the porphyrin ring has a stabilizing effect on the cation, which results in the ion's negative deformation energy. Taking into account the deformation and interaction energies between the three particles leads to larger binding energy in G4–P–Mg with respect to G4–P–Ca by almost 300 kJ mol−1.
Finally, let us address the following questions: how does the ligand affect the binding among guanine molecules and what is the overall binding energy between the five molecules that constitute the complex (four guanine molecules and the metalloporphyrin)? We analyzed the ligand's influence on the guanine–guanine interaction energy but so far we did not consider the ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) deformation energies. The deformation energies of a single guanine molecule in G4, G4–PH2, G4–PMg and G4–PCa amount to 170, 247, 247 and 332 kJ mol−1, respectively. It should be emphasized that the deformation energy of a guanine molecule is not equal to a quarter of the quartet's deformation energy due to different fragment partitioning (i.e. four isolated guanine molecules as compared to a quartet). Note the significantly larger
deformation energies. The deformation energies of a single guanine molecule in G4, G4–PH2, G4–PMg and G4–PCa amount to 170, 247, 247 and 332 kJ mol−1, respectively. It should be emphasized that the deformation energy of a guanine molecule is not equal to a quarter of the quartet's deformation energy due to different fragment partitioning (i.e. four isolated guanine molecules as compared to a quartet). Note the significantly larger ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) deformation energy in G4–PCa with respect to its two counterparts, while all of them notably exceed
deformation energy in G4–PCa with respect to its two counterparts, while all of them notably exceed 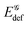 in a non-stacked quartet. The binding energies between guanine molecules in G4 and in the three complexes equal −372, −84, −84 and +152 kJ mol−1, respectively. These results signify that all three ligands weaken the binding among
in a non-stacked quartet. The binding energies between guanine molecules in G4 and in the three complexes equal −372, −84, −84 and +152 kJ mol−1, respectively. These results signify that all three ligands weaken the binding among ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) 's: G4–PH2 and G4–PMg have basically identical impact, while complexation to PCa leads to a positive binding energy among the quartet's constituents. Further, we will estimate the binding energies in a five-particle quartet–metalloporphyrin system, treating the complex G4–PM as being composed of four guanine molecules and a metalloporphyrin ligand. The values for G4–PMg and G4–PCa amount to −495 and −741 kJ mol−1, respectively. Hence, although the calcium ion distorts the quartet and is responsible for the guanines' large deformation energy, it slightly enhances the
's: G4–PH2 and G4–PMg have basically identical impact, while complexation to PCa leads to a positive binding energy among the quartet's constituents. Further, we will estimate the binding energies in a five-particle quartet–metalloporphyrin system, treating the complex G4–PM as being composed of four guanine molecules and a metalloporphyrin ligand. The values for G4–PMg and G4–PCa amount to −495 and −741 kJ mol−1, respectively. Hence, although the calcium ion distorts the quartet and is responsible for the guanines' large deformation energy, it slightly enhances the ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) interaction, Table 3, and as the
interaction, Table 3, and as the ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –Ca interaction is substantial, the result is strong binding between the five fragments (particles).
–Ca interaction is substantial, the result is strong binding between the five fragments (particles).
The binding energies presented in Table 6 are estimated by considering the geometries the fragments adopt in the complexes. On the other hand, the complexation energy for G4–PH2 (computed by considering two optimized species, G4 and PH2) equals −128 kJ mol−1, Table 1, which represents approximately 13 kJ mol−1 weaker binding compared to two stacked quartets.102 In other words, two planar aromatic ligands of similar size bind with comparable strength to the guanine quartet. These results imply that fine tuning of the interaction between a specific planar ligand (with similar shape and dimensions to G4) and the guanine quartet can be achieved by a careful choice of the metal cation. This conclusion is in agreement with the results of Meyer et al.107 who showed that the most significant interaction in G4–M–G4 complexes (M = Na+, K+) is the one between the quartet and the metal ion. Pratviel and coworkers26 performed experimental analysis of binding metalloporphyrins to G4 and concluded that the ligand's metal does not significantly affect the binding energy. They employed four metal ions: Ni2+, Mn3+, Co3+, and Au3+. Their ionic radii amount to 0.69, 0.64/0.58 (high/low spin), 0.61/0.54 (high/low spin), and 0.85 Å, respectively, whereas the corresponding values for Mg2+ and Ca2+ equal 0.72 and 1.00 Å (in all cases six-coordinated ions were considered).108 Due to their small size, all four metal ions considered in the experiments are located in the center of the porphyrin ring, as is the case with the magnesium analogue. In accordance with our results, their impact on the ligand's binding energy is expected to be small.
4 Conclusions
In this contribution we analyzed stacking of porphyrin (PH2), magnesium porphyrin (PMg) and calcium porphyrin (PCa) to a guanine quartet (G4) in the gas phase from the viewpoint of interacting quantum atoms. The guanine quartet is regarded as an anti-cancer pharmaceutical target that can be aimed at with a porphyrin-like (PM) ligand. While the magnesium ion is located in the center of the porphyrin ring, the calcium ion is sandwiched between G4 and PM. The reason for choosing Mg2+ and Ca2+ is twofold: (i) since the impact of these two ions on the quartet had already been established,33 G4–PM study made it possible to assess the cooperative effect of these metal cations and the porphyrin ring on the properties of the quartet; and (ii) due to the distinct position of the divalent metal ion with respect to the porphyrin ring, this investigation enabled us to evaluate the significance of the ion's radius (which dictates the cation's position) to the ligand's binding affinity to the target.Complexation of G4 with PH2 and PMg does not significantly alter the quartet's geometry, which results in a negligible change of the guanine–guanine (![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ) interaction. This is to be contrasted with the G4–PCa formation, which intensifies the interaction among guanine monomers. Namely, the small radius of Mg2+ is responsible for the planar PMg structure with a strong P–Mg interaction where the ring acts as a shield, preventing the cation from engaging in significant interactions with the target. On the other hand, the large radius of the Ca2+ ion forbids its settlement within the porphyrin ring, which results in a smaller G4–Ca2+ distance in G4–PCa. Consequently, the guanine–guanine interaction is stronger in the complex with calcium porphyrin, as is the quartet–ion interaction.
) interaction. This is to be contrasted with the G4–PCa formation, which intensifies the interaction among guanine monomers. Namely, the small radius of Mg2+ is responsible for the planar PMg structure with a strong P–Mg interaction where the ring acts as a shield, preventing the cation from engaging in significant interactions with the target. On the other hand, the large radius of the Ca2+ ion forbids its settlement within the porphyrin ring, which results in a smaller G4–Ca2+ distance in G4–PCa. Consequently, the guanine–guanine interaction is stronger in the complex with calcium porphyrin, as is the quartet–ion interaction.
In order to access the complex stability, we computed binding energies EIQAbind according to three fragmentation schemes. First, the fragments were chosen to be G4 and PM, in which case EIQAbind of G4–PCa is more than three times larger than the one for G4–PMg. According to the second scheme, the fragments are the quartet, the porphyrin ring and the metal cation. Due to the large P–Mg interaction, the binding energy with the magnesium ion is almost 10% larger compared to the calcium analogue. Finally, we used a five fragment system composed of four guanine molecules and PM (M = Mg, Ca). This fragmentation strategy takes into account the fact that guanine molecules are held through non-covalent interactions. In this case, the binding energy is around 50% larger for the complex that contains the calcium ion. Although Ca2+ is responsible for the larger deformation energy of the guanine molecules, it strengthens their mutual interaction, while its proximity to the quartet results in a strong guanine–Ca2+ interaction. Consequently, the binding in the (![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) –
–![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) )–PCa system is significantly more pronounced compared to the Mg counterpart.
)–PCa system is significantly more pronounced compared to the Mg counterpart.
The computed complexation energies are considerably larger for the complex with calcium porphyrin compared to the one with magnesium porphyrin, both in a vacuum and in water. In this case the solvent does not alter the qualitative picture, and the energy decomposition analysis was performed in a vacuum. Moreover, the presence of the DNA backbone and the closest bases was not taken into account as the model would be far too large for quantum chemical calculations. On the other hand, ab initio molecular dynamics simulations demonstrated that the system does not undergo large amplitude motion during a 10 ps run, which confirms that results from static calculations represent a reliable description of the phenomenon we are interested in, i.e. binding of the ligand to the target. The presented results imply that metalloporphyrins with larger metal ions, which are not coplanar with the porphyrin ring, are liable to form more strongly bound complexes compared to the planar analogues and thus might represent superior candidates for anti-cancer drugs. As the number of metal ions that fulfill this condition is limited, further research might be aimed at the synthesis of a porphyrin-like substrate with an out-of-plane central metal cation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia within the framework of contract number: 451-03-68/2020-14/200146. Numerical simulations were run on the PARADOX cluster at the Scientific Computing Laboratory of the Institute of Physics, Belgrade, supported in part by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. The research leading to these results has been co-funded by the European Commission under the H2020 Research Infrastructures contract no. 675121 (project VI-SEEM).References
- D. Sen and W. Gilbert, Nature, 1988, 334, 364–366 CrossRef CAS PubMed.
- S. Neidle and M. A. Read, Biopolymers, 2001, 56, 195–208 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- Y. Li, C. R. Geyer and D. Sen, Biochemistry, 1996, 35, 6911–6922 CrossRef CAS PubMed.
- N. V. Anantha, M. Azam and R. D. Sheardy, Biochemistry, 1989, 37, 2709–2714 CrossRef PubMed.
- F. J. M. Hoeben, P. Jonkheijm, E. W. Meijer and A. P. H. J. Schenning, Chem. Rev., 2005, 105, 1491–1546 CrossRef CAS PubMed.
- Y. Qi and L. G. Hector Jr., Appl. Phys. Lett., 2007, 90, 081922 CrossRef.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2008, 10, 2722–2729 RSC.
- R. Podeszwa and K. Szalewicz, Phys. Chem. Chem. Phys., 2008, 10, 2735–2746 RSC.
- M. Birowska, K. Milowska and J. A. Majewski, Acta Phys. Pol., 2011, 120, 845–848 CrossRef CAS.
- G. V. Janjić, P. V. Petrović, D. B. Ninković and S. D. Zarić, J. Mol. Model., 2011, 17, 2083–2092 CrossRef PubMed.
- X. Qian, Y. Wang, W. Li, J. Lu and J. Li, 2D Mater., 2015, 2, 032003 CrossRef.
- R. Nozawa, H. Tanaka, W. Cha, Y. Hong, I. Hisaki, S. Shimizu, J.-Y. Shin, T. Kowalczyk, S. Irle, D. Kim and H. Shinokubo, Nat. Commun., 2016, 7, 13620 CrossRef CAS PubMed.
- D. N. Sredojević, P. V. Petrović, G. V. Janjić, E. N. Brothers, M. B. Hall and S. D. Zarić, J. Mol. Model., 2014, 22, 30 CrossRef PubMed.
- M. Durec, F. Zaccaria, C. Foncesca Guerra and R. Marek, Chem. – Eur. J., 2016, 22, 10912–10922 CrossRef CAS PubMed.
- H. Yaku, T. M. D. Miyoshi and N. Sugimoto, Molecules, 2012, 17, 10586–10613 CrossRef CAS PubMed.
- F. X. Han, R. T. Wheelhouse and L. H. Harley, J. Am. Chem. Soc., 1999, 121, 3561–3570 CrossRef CAS.
- T. Yamashita, T. Uno and Y. Ishikawa, Bioorg. Med. Chem., 2005, 13, 2423–2430 CrossRef CAS PubMed.
- C. Wei, G. Jia, J. Yuan, Z. Feng and C. Li, Biochemistry, 2006, 45, 6681–6691 CrossRef CAS PubMed.
- P. Zhao, L.-C. Xu, J.-W. Huang, B. Fu, H.-C. Yu and L.-N. Ji, Dyes Pigm., 2009, 83, 81–87 CrossRef CAS.
- C. Wei, L. Wang, G. Jia, J. Zhou, G. Han and C. Li, Biophys. Chem., 2009, 143, 79–84 CrossRef CAS PubMed.
- V. H. Le, N. Nagesh and E. A. Lewis, PLoS One, 2013, 8, e72462 CrossRef CAS PubMed.
- E. Boschi, S. Davis, S. Taylor, A. Butterworth, L. A. Chirayath, V. Purohit, L. K. Siegel, J. Buenaventura, A. H. Sheriff, R. Jin, R. Sheardy, L. A. Yatsunyk and M. Azam, J. Phys. Chem. B, 2016, 120, 12807–12819 CrossRef CAS PubMed.
- T. L. Ruan, S. J. Davis, B. M. Powell, C. P. Harbeck, J. Habdas, P. Habdas and L. A. Yatsunyk, Biochemie, 2017, 132, 121–130 CrossRef CAS PubMed.
- L. R. Keating and V. A. Szalai, Biochemistry, 2004, 43, 15891–15900 CrossRef CAS PubMed.
- C. Romera, O. Bombarde, R. Bonnet, D. Gomez, P. Dumy, P. Calsou, J.-F. Gwan, J.-H. Lin, E. Defrancq and G. Pratviel, Biochemie, 2011, 93, 1310–1317 CrossRef CAS PubMed.
- J. K. Choi, A. D'Urso and M. Balaz, J. Inorg. Biochem., 2013, 127, 1–6 CrossRef CAS PubMed.
- P. Zhao, J.-Z. Lu, F.-Y. Hong, B.-H. Ou, F.-D. Zhang, L.-N. Ma and H.-M. Guo, Spectrochim. Acta, Part A, 2013, 108, 1–7 CrossRef CAS PubMed.
- Y.-H. Kim, C. Lee, S. K. Kim and S. C. Jeoung, Biophys. Chem., 2014, 190–191, 17–24 CrossRef CAS PubMed.
- J. Dejeu, T. Lavergne, J. D. Nora, E. Defrancq and G. Pratviel, Inorg. Chim. Acta, 2016, 452, 98–103 CrossRef CAS.
- X. Yao, D. Song, T. Qin, C. Yang, Z. Ye, X. Li, K. Liu and H. Su, Sci. Rep., 2017, 7, 10951 CrossRef PubMed.
- D. Song, W. Yang, T. Qin, L. Wu, K. Liu and H. Su, J. Phys. Chem. Lett., 2014, 5, 2259–2266 CrossRef CAS PubMed.
- B. Milovanović, A. Stanojević, M. Etinski and M. Petković, J. Phys. Chem. B, 2020, 124, 3002–3014 CrossRef PubMed.
- S. J. Baum, B. F. Burnham and R. A. Plane, Proc. Natl. Acad. Sci. U. S. A., 1964, 52, 1439–1442 CrossRef CAS PubMed.
- J. Barrett, Nature, 1967, 215, 733–735 CrossRef CAS.
- M. E. Druyan, J. R. Norris and J. J. Katz, J. Am. Chem. Soc., 1973, 95, 1682–1683 CrossRef CAS PubMed.
- S. G. Boxer, G. L. Closs and J. J. Katz, J. Am. Chem. Soc., 1974, 96, 7058–7066 CrossRef CAS.
- S. Lesage, H. Xu and L. Durham, Hydrol. Sci. J., 1993, 38, 343–354 CrossRef CAS.
- M. Rubio and B. O. Roos, J. Chem. Phys., 1999, 110, 7202 CrossRef CAS.
- A. R. Battersby, Nat. Prod. Rep., 2000, 17, 507–526 RSC.
- J. Jusélius and D. Sundholm, J. Org. Chem., 2000, 65, 5233–5237 CrossRef PubMed.
- A. Wong, R. Ida, X. Mo, Z. Gan, J. Poh and G. Wu, J. Phys. Chem. A, 2006, 110, 10084–10090 CrossRef CAS PubMed.
- J. R. Black, Q. Yin, J. R. Rustad and W. H. Casey, J. Am. Chem. Soc., 2017, 129, 8690–8691 CrossRef PubMed.
- M. Etinski, M. Petković and M. M. Ristić, J. Serb. Chem. Soc., 2013, 78, 1775–1787 CrossRef CAS.
- M. Etinski, M. Petković, M. M. Ristić and C. M. Marian, J. Phys. Chem. B, 2015, 119, 10156–10169 CrossRef CAS PubMed.
- X. Jiang, Y. Gao, R. Lal, J. Hu and B. Song, Mol. Phys., 2018, 116, 1697–1705 CrossRef CAS.
- J. S. Lindsey and J. N. Woodford, Inorg. Chem., 1995, 34, 1063–1069 CrossRef CAS.
- K. D. Borah and J. Bhuyan, Dalton Trans., 2017, 46, 6497–6509 RSC.
- J. B. Allison and R. S. Becker, J. Phys. Chem., 1963, 67, 2675–2679 CrossRef CAS.
- L. Bonomo, M.-L. Lehaire, E. Solari, R. Scopelliti and C. Floriani, Angew. Chem., Int. Ed., 2001, 40, 771–774 CrossRef CAS PubMed.
- I. Alkorta, J. Elguero, A. M. S. Silva and A. C. Tomé, J. Porphyrins Phthalocyanines, 2010, 14, 631–638 CrossRef.
- F. Feixas, J. Poater, E. Matito and M. Solá, Aromaticity of Organic and Inorganic Heterocycles, Springer, Berlin, Heidelberg, 2014, pp. 129–160 Search PubMed.
- M. A. Blanco, A. M. Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- A. M. Pendás, M. A. Blanco and E. Francisco, J. Comput. Chem., 2007, 28, 161–184 CrossRef PubMed.
- D. Tiana, E. Francisco, M. A. Blanco, P. Macchi, A. Sironi and A. M. Pendás, J. Chem. Theory Comput., 2010, 6, 1064–1074 CrossRef CAS.
- P. Dem'yanov and P. M. Polestshuk, Chem. – Eur. J., 2013, 19, 10945–10957 CrossRef PubMed.
- Z. Badri, C. Foroutan-Nejad, J. Kozelka and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 26183–26190 RSC.
- C. Foroutan-Nejad, Z. Badri and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 30670–30679 RSC.
- Z. Badri and C. Foroutan-Nejad, Phys. Chem. Chem. Phys., 2016, 18, 11693–11699 RSC.
- I. Alkorta, J. C. R. Thacker and P. L. A. Popelier, J. Comput. Chem., 2018, 39, 546–556 CrossRef CAS PubMed.
- J. L. Casalz-Sainz, J. Manuel-Vela, E. Francisco, T. Rocha-Rinza and A. M. Pendás, ChemPhysChem, 2017, 18, 3553–3561 CrossRef CAS PubMed.
- N. Javadi, M. Najafi and S. Yourdkhani, Int. J. Quantum Chem., 2017, 117, e25379 CrossRef.
- M. Petković, Đ. Nakarada and M. Etinski, J. Comput. Chem., 2018, 39, 1868–1877 CrossRef PubMed.
- I. Petrović, B. Milovanović, M. Etinski and M. Petković, Int. J. Quantum Chem., 2019, 119, e25918 CrossRef.
- J. C. R. Thacker and P. L. A. Popelier, J. Phys. Chem. A, 2018, 122, 1439–1450 CrossRef CAS.
- J. C. R. Thacker, M. A. Vincent and P. L. A. Popelier, Chem. – Eur. J., 2018, 24, 11200–11210 CrossRef CAS.
- N. Orangi, K. Eskandari, J. C. R. Thacker and P. L. A. Popelier, ChemPhysChem, 2019, 20, 1922–1930 CrossRef CAS PubMed.
- J. L. Casalz-Sainz, J. Manuel-Vela, E. Francisco, T. Rocha-Rinza and A. M. Pendás, J. Comput. Chem., 2020, 41, 1234–1241 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- J. Blaudeau, J. Chem. Phys., 1997, 107, 5016–5021 CrossRef CAS.
- A. Ruiz, H. Perez, C. Morera-Boado, L. Almagro, C. C. P. da Silva, J. Ellena, J. M. G. de la Vega, R. Martinez-Alvarez, M. Suarez and N. Martin, CrystEngComm, 2014, 16, 7802–7814 RSC.
- S. E. Kochanek, T. M. Clymer, V. S. Pakkala, S. P. Hebert, K. Reeping, S. M. Firestine and J. D. Evanseck, J. Phys. Chem. B, 2015, 119, 1184–1191 CrossRef CAS PubMed.
- S. W. L. Hogan and T. van Mourik, J. Comput. Chem., 2016, 37, 763–770 CrossRef CAS PubMed.
- A. Motahari and A. Fattahi, New J. Chem., 2017, 41, 15110–15119 RSC.
- A. Mortazavifat, H. Raissi and M. Shahabi, J. Biomol. Struct. Dyn., 2019, 37, 4852–4862 CrossRef PubMed.
- I. Iribarren, M. M. Montero-Campillo, I. Alkorta, J. Elguero and D. Quiñonero, Phys. Chem. Chem. Phys., 2019, 21, 5796–5802 RSC.
- Y. Itoh, Y. Nakashima, S. Tsukamoto, T. Kurohara, M. Suzuki, Y. Sakae, M. Oda, Y. Okamoto and T. Suzuki, Sci. Rep., 2019, 9, 767 CrossRef PubMed.
- G. Lv, X. Sun, C. Zhang and M. Li, Atmos. Chem. Phys., 2019, 19, 2833–2844 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 19.10.12, Professional), TK Gristmill Software, Overland Park KS, USA, 2019 (http://aim.tkgristmill.com) Search PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- M. Thomas, M. Brehm, R. Fligg, P. Voehringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622 RSC.
- B. Milovanović, I. Stanković, M. Petković and M. Etinski, J. Phys. Chem. A, 2020, 124, 8101–8111 CrossRef PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990 Search PubMed.
- The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, 2007 Search PubMed.
- M. Meyer, T. Steinke, M. Brandl and J. Sühnel, J. Comput. Chem., 2001, 22, 109–124 CrossRef CAS.
- G. Louit, A. Hocquet, M. Ghomi, M. Meyer and J. Sühnel, PhysChemComm, 2003, 6, 1–5 RSC.
- M. Meyer and J. Sühnel, J. Biomol. Struct. Dyn., 2003, 20, 507–517 CrossRef CAS PubMed.
- T. van Mourik and A. J. Dingley, Chem. – Eur. J., 2005, 11, 6064–6079 CrossRef CAS PubMed.
- Y. P. Yurenko, J. Novotný, V. Sklenář and R. Marek, Phys. Chem. Chem. Phys., 2014, 16, 2072–2084 RSC.
- M. Meyer, M. Brandl and J. Sühnel, J. Phys. Chem. A, 2001, 105, 8223–8225 CrossRef CAS.
- A. K. Jissy, U. P. M. Ashik and A. Datta, J. Phys. Chem. C, 2011, 115, 12530–12546 CrossRef CAS.
- V. Gabelica, F. Rosu, E. D. Pauw, J. Lemaire, J.-C. Gillet, J.-C. Poully, F. Lecomte, G. Grégoire, J.-P. Schermann and C. Desfrançois, J. Am. Chem. Soc., 2008, 130, 1810–1811 CrossRef CAS PubMed.
- Y. P. Yurenko, J. Novotný, M. P. Mitoraj, V. Sklenář, A. Michalak and R. Marek, J. Chem. Theory Comput., 2014, 10, 5353–5365 CrossRef CAS PubMed.
- M. Meyer, A. Hocquet and J. Sühnel, J. Comput. Chem., 2005, 26, 352–364 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
| This journal is © the Owner Societies 2021 |
