Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-adiabatic quantum interference in the ultracold Li + LiNa → Li2 + Na reaction
Brian K.
Kendrick
 *a,
Hui
Li
*a,
Hui
Li
 b,
Ming
Li
b,
Svetlana
Kotochigova
b,
Ming
Li
b,
Svetlana
Kotochigova
 b,
James F. E.
Croft
b,
James F. E.
Croft
 cd and
Naduvalath
Balakrishnan
cd and
Naduvalath
Balakrishnan
 e
e
aTheoretical Division (T-1, MS B221), Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: bkendric@lanl.gov
bDepartment of Physics, Temple University, Philadelphia, PA 19122, USA
cDodd-Walls Centre for Photonic and Quantum Technologies, Dunedin 9054, New Zealand
dDepartment of Physics, University of Otago, Dunedin 9054, New Zealand
eDepartment of Chemistry and Biochemistry, University of Nevada, Las Vegas, NV 89154, USA
First published on 12th February 2021
Abstract
Electronically non-adiabatic effects play an important role in many chemical reactions. However, how these effects manifest in cold and ultracold chemistry remains largely unexplored. Here for the first time we present from first principles the non-adiabatic quantum dynamics of the reactive scattering between ultracold alkali-metal LiNa molecules and Li atoms. We show that non-adiabatic dynamics induces quantum interference effects that dramatically alter the ultracold rotationally resolved reaction rate coefficients. The interference effect arises from the conical intersection between the ground and an excited electronic state that is energetically accessible even for ultracold collisions. These unique interference effects might be exploited for quantum control applications such as a quantum molecular switch. The non-adiabatic dynamics are based on full-dimensional ab initio potential energy surfaces for the two electronic states that includes the non-adiabatic couplings and an accurate treatment of the long-range interactions. A statistical analysis of rotational populations of the Li2 product reveals a Poisson distribution implying the underlying classical dynamics are chaotic. The Poisson distribution is robust and amenable to experimental verification and appears to be a universal property of ultracold reactions involving alkali metal dimers.
1 Introduction
Ultracold molecules and in particular ultracold polar molecules are at the forefront of precision spectroscopy, sensing, controlled studies of chemical reactions, quantum many-body physics, and quantum computing.1–10 Polar molecules comprised of heteronuclear alkali metal dimers such as KRb, NaK, NaRb and LiNa have attracted considerable attention in recent years in controlled studies of chemical reactions.2,5,6,9,10 Electronically non-adiabatic effects are expected to play an important role in atom-dimer reactions involving these molecules. The reactions proceed along a barrierless reaction pathway into a deep attractive potential well. A conical intersection (CI) occurs between the ground electronic state and the first excited doublet electronic state within the attractive well region and this CI is energetically accessible even for collision energies in the ultracold limit for ground state reactants. Thus, a non-adiabatic quantum mechanical treatment is required that includes both electronic states. Explicit quantum calculations for these reactions remain a formidable challenge even for dynamics on a single Born–Oppenheimer adiabatic electronic potential energy surface (PES).11–13 However, calculations on a single adiabatic PES are not accurate for these systems even if a generalized vector potential based approach14,15 is used to include the geometric phase (GP)14,16 associated with the CI. Fortunately, we have recently developed a new non-adiabatic quantum reactive scattering methodology that has made it possible to rigorously treat ultracold reactions occurring on two coupled electronic states for the first time.17 This work presents the first rigorous treatment of non-adiabatic chemistry in the ultracold regime for systems of current experimental interest, advancing the state-of-the-art in the theoretical treatment of ultracold chemistry to new frontiers.Non-adiabatic dynamics is most often associated with collisions at high (thermal) energies where excited electronic states are typically more accessible. At these high energies quantum effects are much less pronounced and the dynamics of heavy nuclei is often treated classically. In contrast, at ultracold collision energies a fully quantum mechanical treatment is required even for heavy nuclei and fundamentally new reaction mechanisms can also come into play. The unique properties of ultracold collisions therefore provide a novel testing ground for exploring and understanding non-adiabatic quantum dynamics. Quantum phenomena (interference, Fermi–Bose statistics, phase shift quantization, etc.) are dramatically enhanced at ultracold temperatures and the delicate interplay between them can lead to unprecedented sensitivity and control of the collision outcome. Alkali metal systems in particular provide an ideal test bed for ultracold experimental and theoretical studies of non-adiabatic effects and their possible technological applications.
In this work, we present a first principles full-dimensional quantum dynamics study of non-adiabatic effects in the Li + LiNa(v = 0, j = 0) → Li2(v′, j′) + Na reaction. The methodology also includes a rigorous treatment of the identical particle exchange symmetry between the two 6Li nuclei. The rotationally resolved rate coefficients are computed as a function of collision energy from 1 nK to 10 K using a coupled two-state diabatic electronic representation.17–19 The non-adiabatic results are compared to a conventional Born–Oppenheimer calculation based on a single adiabatic electronic PES. Both of these calculations are also compared to a universal model which is based on a simple one-dimensional reaction path consisting of a long-range van der Waals (C6) potential.20 Quantum interference between the two reaction pathways which encircle the CI is shown to significantly enhance or suppress the rate coefficients at ultracold collision energies (Ec < 1 mK). The GP which is included in the non-adiabatic calculations reverses the nature of the quantum interference from constructive to destructive and vice versa.21–23 Thus, the non-adiabatic ultracold rate coefficients are significantly enhanced or suppressed relative to the conventional Born–Oppenheimer rate coefficients when quantum interference effects are significant. The quantum interference effects lead to strong fluctuations in the rotationally resolved rate coefficient distributions. A statistical analysis of these fluctuations reveals that they are Poissonian which is consistent with an underlying classically chaotic dynamics.12,13 The Poisson distributions are shown to be robust with respect to variations in the PES and chemical system and therefore appear to be a universal property of these types of reactions that proceed through a potential well. The quantum dynamics calculations are based on full-dimensional accurate ab initio electronic PESs which are computed for both the ground and first excited states for the first time. A state-of-the-art electronic structure code (MOLPRO) is used to compute the electronic PESs and the non-adiabatic coupling elements.24 Also included in the PESs is an accurate experimentally based treatment of the long range (van der Waals) interactions and diatomic potentials.
The paper is organized as follows: in Section 2 the non-adiabatic quantum dynamics methodology is reviewed. Section 3.1 presents the Born–Oppenheimer electronic PESs for the ground and first excited electronic states that include the prominent energetically accessible CI. The energetics and reaction path are discussed for the reaction as it proceeds from reactants Li + LiNa to products Li2 + Na, and notable features of the PESs are also emphasized. The rotationally resolved rate coefficients are then presented in Section 3.2 and the underlying quantum interference mechanisms are discussed in detail. Finally, in Section 3.3 a statistical analysis of the rotational distributions is discussed and the resulting Poisson distributions are presented. The conclusions are presented in Section 4 and additional analysis, figures, and the PES scaling sensitivity studies are included in the Appendix.
2 First principles non-adiabatic quantum dynamics
First principles non-adiabatic quantum dynamics calculations require solving a generalized Born–Oppenheimer equation for the nuclear motion which includes both the ground and first excited electronic states. That is, the total molecular wavefunction |Ψ〉 is expanded as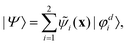 where |φdi〉 denotes the diabatic electronic basis functions and the expansion coefficients
where |φdi〉 denotes the diabatic electronic basis functions and the expansion coefficients ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) i are the nuclear motion wave functions. The nuclear coordinates relative to the center-of-mass of the molecule are collectively denoted by the six-dimensional vector x which includes the three interatomic degrees of freedom and three rotational (Euler) angles. Different choices for the nuclear coordinates can be used as will be discussed in detail below. For numerical reasons it is advantageous to use a diabatic electronic representation for which the PESs are well-behaved smooth functions of the nuclear coordinates. In addition, the coupling between the two electronic states appears simply as an off-diagonal element in the potential energy matrix (PEM) (i.e., there are no derivative coupling terms in the kinetic energy operator).17 The relevant diabatic Schrödinger equation for the nuclear motion is given by
i are the nuclear motion wave functions. The nuclear coordinates relative to the center-of-mass of the molecule are collectively denoted by the six-dimensional vector x which includes the three interatomic degrees of freedom and three rotational (Euler) angles. Different choices for the nuclear coordinates can be used as will be discussed in detail below. For numerical reasons it is advantageous to use a diabatic electronic representation for which the PESs are well-behaved smooth functions of the nuclear coordinates. In addition, the coupling between the two electronic states appears simply as an off-diagonal element in the potential energy matrix (PEM) (i.e., there are no derivative coupling terms in the kinetic energy operator).17 The relevant diabatic Schrödinger equation for the nuclear motion is given by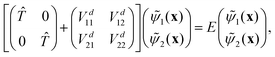 | (1) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) = −ħ2∇2/(2μ),
= −ħ2∇2/(2μ), 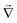 denotes derivatives with respect to x and μ is three-body reduced mass. The second term is the PEM which couples the two diabatic electronic states and is a function of only the three interatomic degrees of freedom (x). That is, each matrix element (i.e., the Vd11, Vd22 and Vd12 = Vd21) of the PEM is a three-dimensional PES. We note that in contrast to the 2 × 2 diabatic Schrödinger equation given in eqn (1), a conventional Born–Oppenheimer quantum dynamics calculation solves the adiabatic single surface Schrödinger equation
denotes derivatives with respect to x and μ is three-body reduced mass. The second term is the PEM which couples the two diabatic electronic states and is a function of only the three interatomic degrees of freedom (x). That is, each matrix element (i.e., the Vd11, Vd22 and Vd12 = Vd21) of the PEM is a three-dimensional PES. We note that in contrast to the 2 × 2 diabatic Schrödinger equation given in eqn (1), a conventional Born–Oppenheimer quantum dynamics calculation solves the adiabatic single surface Schrödinger equation[![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + Va1(x)]ψ1(x) = Eψ1(x). + Va1(x)]ψ1(x) = Eψ1(x). | (2) |
A first-principles solution of eqn (1) requires two primary steps: (1) a quantum mechanical ab initio calculation of the diabatic PEM, and (2) a numerically exact quantum mechanical solution of the six-dimensional diabatic Schrödinger equation for the nuclear motion. Each of these steps are highly non-trivial and require extensive calculations as discussed in the following Sections 2.1 and 2.2, respectively.
2.1 Ab initio potential energy surface calculations
The PESs of the LiNaLi collisional complex were not available from the literature and their computation required substantial effort due to the complexity of the multi-electron open-shell systems. We have computed the two energetically-lowest non-relativistic doublet adiabatic potentials, 2A′ and 2B′, with the MOLPRO electronic structure package.24 The core electron shells of Li and Na are described by the Stuttgart/Cologne energy-consistent, single-valence electron, relativistic pseudo-potentials ECP2SDF and ECP10SDF25 leaving only three valence electrons in the active space for explicit treatment. The polarization of the effective cores and residual core–valence correlations are modeled via the l-independent core polarization potential (CPP) with Müller–Meyer damping functions.26 The CPP parameters, i.e. static dipole polarizabilities of the atomic cores are taken from ref. 27. Cutoff functions with exponents 0.95 a.u. and 0.82 a.u. are employed for Li and Na, respectively (here a.u. stands for atomic unit). Basis sets from ref. 28 describe the three valence electrons, specifically, uncontracted sp basis sets augmented by additional s, p, d and f polarization functions are used for both Li and Na. The multi-configurational self-consistent field (MCSCF) method29,30 is first used to obtain configuration state functions (CSFs). A multi-reference configuration interaction (MRCI) calculation31,32 is then performed using a large active space constructed from the CSFs, giving the three-dimensional adiabatic surfaces of the two lowest energy states for LiNaLi, Va1 and Va2. The adiabatic PESs are computed as functions of the separation between Na and first Li atom, R1, the separation between Na and second Li atom, R2, as well as the angle θ between R1 and R2. We have computed the potentials on the ten angular grid points θ = 10°, 20°, 40°, 60°, 80°, 100°, 120°, 140°, 160°, 178°, and radial R1 and R2 grids from Rmin = 3.2a0 to 10a0 in steps of 0.2a0 and from 10a0 to Rmax = 19a0 in steps of 0.3a0 with the constraint that the separation between the two Li atoms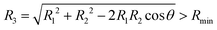 (a0 = 0.0529177 nm is the Bohr radius). In total, more than 40
(a0 = 0.0529177 nm is the Bohr radius). In total, more than 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points were calculated.
000 points were calculated.
The accuracy of the LiNaLi trimer potentials has been determined from a comparison of the singlet X1Σ+ and triplet a3Σ+ potentials of LiNa and Li2 determined with MOLPRO using the same basis sets as for the trimer calculations and the spectroscopically-accurate potentials from ref. 33–35. For example, our computed well depths were smaller by no more than hc × 25 cm−1 for both the singlet and triplet dimer potentials corresponding to 0.3% and 9% of their well depths, respectively. Here, h is the Planck constant and c is the speed of light in vacuum.
In order to study the reaction dynamics we need to diabatize the two adiabatic potentials Va1,2(R1,R2,θ) of LiNaLi, as they have a conical intersection for a single geometry with C2v symmetry. In the adiabatic representation, the electronic eigenstates |φa1,2〉 are coupled by non-adiabatic first-derivative couplings 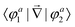 with respect to the nuclear coordinates. The nonadiabatic coupling matrix element was computed for all of the grid points using MRCI theory and a finite difference method for the derivatives (the DDR procedure). These non-adiabatic derivative couplings are problematic at the CI where they become singular. Fortunately, the singular part of these couplings are removable. That is, the non-adiabatic coupling matrix elements are vector quantities and can be decomposed into longitudinal (removable) and transverse (non-removable or residual coupling) components.36,37 By an appropriate unitary transformation from the adiabatic to diabatic electronic representation, the problematic singular (longitudinal) part of the derivative coupling at the CI can be removed. For two electronic states this can be achieved with the transformation
with respect to the nuclear coordinates. The nonadiabatic coupling matrix element was computed for all of the grid points using MRCI theory and a finite difference method for the derivatives (the DDR procedure). These non-adiabatic derivative couplings are problematic at the CI where they become singular. Fortunately, the singular part of these couplings are removable. That is, the non-adiabatic coupling matrix elements are vector quantities and can be decomposed into longitudinal (removable) and transverse (non-removable or residual coupling) components.36,37 By an appropriate unitary transformation from the adiabatic to diabatic electronic representation, the problematic singular (longitudinal) part of the derivative coupling at the CI can be removed. For two electronic states this can be achieved with the transformation
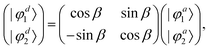 | (3) |
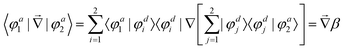 | (4) |
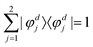 twice. The mixing angle β is then found assuming that β = 0 for all geometries with C2v symmetry, i.e. R1 = R2, and spatial integration of eqn (4).38 The signs of
twice. The mixing angle β is then found assuming that β = 0 for all geometries with C2v symmetry, i.e. R1 = R2, and spatial integration of eqn (4).38 The signs of 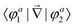 as computed within MOLPRO are arbitrary from geometry to geometry. We chose the convention that leads to a smooth β. The electronic potential matrix in the diabatic basis is the 2 × 2 matrix
as computed within MOLPRO are arbitrary from geometry to geometry. We chose the convention that leads to a smooth β. The electronic potential matrix in the diabatic basis is the 2 × 2 matrix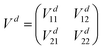 | (5) |
Vd11 = Va1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β + Va2 β + Va2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, β, | (6) |
Vd22 = Va2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β + Va1 β + Va1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, β, | (7) |
Vd12 = Vd21 = (Va2 − Va1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, β, | (8) |
Finally, we fit and interpolate the diabatic PESs Vdij(R1,R2,θ) for i, j = 1, 2 with a two step procedure. Using the dimer-in-molecule theory,39 we separate the diabatic PESs into a pairwise and a three-body component with
| Vdij(R1,R2,θ) = Vpwij(R1,R2,θ) + s(R1,R2,θ)V3Bij(R1,R2,θ). | (9) |
The pairwise components Vpwij(R1,R2,θ) are weighted sums of the spectroscopically-accurate X1Σ+ and a3Σ+ potentials of NaLi and Li2.33–35 The weights follow from the realization that the electron angular momenta of the individual Li and Na atoms in their electronic ground state are ħ/2 (or spin-1/2) and that the two diabatic trimer electron basis functions have a total electron angular momentum equal to ħ/2 for doublet states, after coupling the three spin-1/2 atomic electron angular momenta (ħ is the reduced Planck constant).
The three-body component V3Bij(R1,R2,θ) is fit using the reproducing kernel Hilbert space (RKHS) technique40–42 and relies on an expansion in terms of Legendre polynomials Pλ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as functions of cos
θ) as functions of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. That is,
θ. That is,
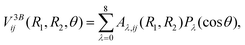 | (10) |
In order to extrapolate the three-body component V3Bij(R1,R2,θ) for geometries where one or both separations R1 or R2 are larger than Rmax, we combine two strategies. First, we use the fact that the three-body component of the adiabatic potentials Vai fall off as43
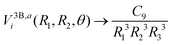 | (11) |
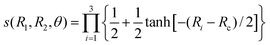 | (12) |
2.2 Non-adiabatic quantum dynamics
The numerically exact quantum mechanical solution of the 2 × 2 diabatic Schrödinger eqn (1) is based on a time-independent coupled-channel (CC) approach.17,44,45 Adiabatically adjusting Principal axis Hyperspherical (APH) coordinates are used in the interaction region and Delves hyperspherical coordinates are used in the long-range asymptotic region.17,44–46 The hyperradius ρ is common to both coordinate systems which facilitates the coordinate transformation from the APH to Delves at an intermediate value of ρ = ρm (determined by numerical convergence studies, see below). Furthermore, hyperspherical coordinates have the advantage of treating all reactant and product channels simultaneously and allow for a natural numerical separation of the problem into radial and angular parts. We choose the body frame (BF) z-axis perpendicular to the plane of the triatomic molecule and the BF x and y axis are chosen to lie along the instantaneous principal axes of inertia (i.e., the Q and q vectors of Pack and Parker, respectively).44 The collective set of six nuclear coordinates are denoted by x = (x,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) where the three internal coordinates are x = (ρ,θ,ϕ) and
) where the three internal coordinates are x = (ρ,θ,ϕ) and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = (α,β,γ) (the three Euler angles which specify the orientation of the BF relative to the space fixed frame). The hyperradial coordinate ρ and hyperangles θ and ϕ correspond to a symmetric stretch, bending, and pseudorotational motion, respectively.47 These three coordinates can be expressed explicitly in terms of the three internuclear distances (see ref. 44 for details).
= (α,β,γ) (the three Euler angles which specify the orientation of the BF relative to the space fixed frame). The hyperradial coordinate ρ and hyperangles θ and ϕ correspond to a symmetric stretch, bending, and pseudorotational motion, respectively.47 These three coordinates can be expressed explicitly in terms of the three internuclear distances (see ref. 44 for details).
The kinetic energy operator in hyperspherical coordinates can be expressed as
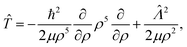 | (13) |
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) is the grand angular momentum operator, and the angular part of eqn (13) is given by
is the grand angular momentum operator, and the angular part of eqn (13) is given by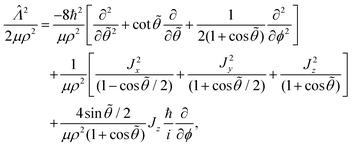 | (14) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) = π − 2θ, and Jx, Jy, Jz denote the BF components of the total angular momentum operator J. For ultracold collision energies we only need to consider the single orbital angular momentum l = 0 (i.e., s-wave scattering). Since the reactant LiNa is in its ground rotational state j = 0, this corresponds to total angular momentum J = l + j = 0.
= π − 2θ, and Jx, Jy, Jz denote the BF components of the total angular momentum operator J. For ultracold collision energies we only need to consider the single orbital angular momentum l = 0 (i.e., s-wave scattering). Since the reactant LiNa is in its ground rotational state j = 0, this corresponds to total angular momentum J = l + j = 0.
The potential matrix strongly couples the radial (ρ) and angular (![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0a8.gif) , ϕ) coordinates so that eqn (1) and (2) are nonseparable. However, we can perform a numerical separation by dividing the hyperradius ρ into many “sectors” and solving the angular part of the problem with ρ fixed at the center of each sector. The angular solutions within each sector provide an optimal localized fixed basis for solving the CC radial equations within that sector. The global radial solution is obtained by propagating a set of CC equations from small to large ρ across each sector. At the boundaries of each sector, the radial solutions are transformed from one sector basis to the next using the overlap matrix between the angular functions computed at the two sectors. Specifically, we expand the total diabatic nuclear motion wave function
, ϕ) coordinates so that eqn (1) and (2) are nonseparable. However, we can perform a numerical separation by dividing the hyperradius ρ into many “sectors” and solving the angular part of the problem with ρ fixed at the center of each sector. The angular solutions within each sector provide an optimal localized fixed basis for solving the CC radial equations within that sector. The global radial solution is obtained by propagating a set of CC equations from small to large ρ across each sector. At the boundaries of each sector, the radial solutions are transformed from one sector basis to the next using the overlap matrix between the angular functions computed at the two sectors. Specifically, we expand the total diabatic nuclear motion wave function 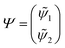 in eqn (1) in terms of the angular functions (Φ) for a given sector ρ = ρξ as
in eqn (1) in terms of the angular functions (Φ) for a given sector ρ = ρξ as
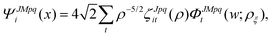 | (15) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ,ϕ,α,β,γ) denotes the angular coordinates of the 5D hypersphere. The radial coefficients ζJpqit are computed numerically from the propagation of the CC radial equations
,ϕ,α,β,γ) denotes the angular coordinates of the 5D hypersphere. The radial coefficients ζJpqit are computed numerically from the propagation of the CC radial equations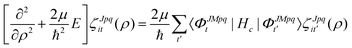 | (16) |
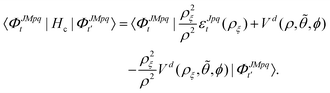 | (17) |
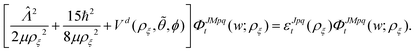 | (18) |
The Vd in eqn (17) and (18) is the 2 × 2 diabatic PEM given in eqn (5)–(8). Once the angular solutions to eqn (18) are computed, they can be used to compute the overlap matrices Ott′ = 〈ΦJMpqt(w;ρξ)|ΦJMpqt(w;ρξ+1)〉 and potential coupling matrices defined in eqn (17) at each sector. These are then used to solve the CC radial eqn (16) using Johnson's log-derivative propagator.48,49 At the matching radius ρ = ρm, the radial solution is transformed into the Delves basis using the overlap matrix between the APH and Delves functions computed at ρ = ρm. The radial propagation in ρ is then continued to the final asymptotic value of ρ = ρf using an equivalent set of Delves CC radial equations (see ref. 46 for the Delves equations). The Delves basis functions at each sector are computed separately for each diatomic arrangement channel (i.e., for ρ > ρm the channels are decoupled). They consist of ro-vibrational wave functions computed numerically using a one-dimensional Numerov propagator for the vibrational motion and a set of analytic spherical harmonics for the rotational part. The Delves basis functions are used to compute the potential coupling matrices and overlap matrices between each sector analogous to the APH propagation. Finally, at the last asymptotic value of ρ = ρf (determined from convergence studies, see below), the Delves radial solution is projected onto the analytic asymptotic radial solution in Jacobi coordinates. From this projection, the full state-to-state scattering (S) matrix is computed for all open reactant and product channels for total energy E. Once the S matrix is computed, cross sections σfi and rate coefficients Kfi = vσfi (where v is the relative collision velocity) can be computed using standard expressions.44 We note that the f,i denote the collective final and initial quantum numbers of the diatomic products and reactants (i.e., f = (τ′,v′,j′) and i = (τ,v,j) where τ′ and τ denote the diatomic arrangement channel Li2 or LiNa), respectively.
In the interaction region (ρ < ρm), the (5D) surface function Hamiltonian matrix in eqn (18) is diagonalized on a discrete grid in ρ at 144 logarithmically spaced points between (ρi = 6.0a0 and ρm = 33.03a0). The 5D basis functions consist of a hybrid FBR (Finite Basis Representation) in ϕ, a DVR (Discrete Variable Representation) in θ, and symmetrized Wigner D functions in α,β,γ.17,45,50 The size of the DVR and FBR basis is specified by the values of the integers łmax and mmax, respectively.17,45 The basis size increases with ρ and is determined from numerical convergence studies. In this study, four regions in ρ were used: 6.0 ≤ ρ ≤ 11.02a0, 11.02 < ρ ≤ 19.54a0, 19.54 < ρ ≤ 23.37a0, and 23.37 < ρ ≤ 33.03a0. The corresponding sets of lmax and mmax are: lmax = 99, 119, 127, and 127; and mmax = 220, 240, 260 and 280, respectively. For total J = 0 considered in this study, the size of the angular Hamiltonian matrix in each region is given by (lmax + 1) × (2mmax + 1) = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, 57
100, 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720, 66
720, 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 and 71
688 and 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808, respectively. Fortunately, the size of these matrices can be dramatically reduced by using the SDT (Sequential Diagonalization Truncation) technique.50 After applying SDT the dimension of the largest angular Hamiltonian matrix in each of the four regions is 13
808, respectively. Fortunately, the size of these matrices can be dramatically reduced by using the SDT (Sequential Diagonalization Truncation) technique.50 After applying SDT the dimension of the largest angular Hamiltonian matrix in each of the four regions is 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 008, 9412, 8401, and 6995. An efficient parallel numerical eigensolver (PARPACK) is then used to numerically diagonalize the sparse Hamiltonian matrices constructed at each sector.51 As mentioned above, the set of angular eigensolutions of eqn (18) form a basis for the one-dimensional CC propagation in ρ (see eqn (16) and (17)). The number of CCs propagated in this work was 820 in the APH region and 500 in the Delves region. In the Delves region, 338 uniformly spaced ρ values were used between ρm = 33.03a0 and the final asymptotic ρf = 144.6a0. Each sector in the APH and Delves regions was further sub-divided into 100 and 200 propagation steps, respectively. At ρ = ρm the Delves ro-vibrational basis functions include Li2(v = 0–8) and for each vibrational state the corresponding maximum rotational quantum numbers for Li2 are 62, 58, 54, 50, 44, 40, 34, 26 and 16, respectively. For the LiNa channel, the v = 0–6 vibrational states are included with corresponding maximum rotational quantum numbers 61, 56, 51, 44, 37, 28 and 15, respectively. Asymptotically at ρ = ρf the open ro-vibrational Jacobi basis functions at 1 nK collision energy include the single LiNa(v = 0, j = 0) reactant channel and the product Li2(v = 0–3) with maximum rotational quantum numbers 41, 35, 28, 18, respectively. We note that all of the above quantum dynamics calculations rigorously treat the identical particle exchange symmetry between the two identical 6Li nuclei.17 Thus, the calculations are repeated separately for each exchange symmetry, even and odd.
008, 9412, 8401, and 6995. An efficient parallel numerical eigensolver (PARPACK) is then used to numerically diagonalize the sparse Hamiltonian matrices constructed at each sector.51 As mentioned above, the set of angular eigensolutions of eqn (18) form a basis for the one-dimensional CC propagation in ρ (see eqn (16) and (17)). The number of CCs propagated in this work was 820 in the APH region and 500 in the Delves region. In the Delves region, 338 uniformly spaced ρ values were used between ρm = 33.03a0 and the final asymptotic ρf = 144.6a0. Each sector in the APH and Delves regions was further sub-divided into 100 and 200 propagation steps, respectively. At ρ = ρm the Delves ro-vibrational basis functions include Li2(v = 0–8) and for each vibrational state the corresponding maximum rotational quantum numbers for Li2 are 62, 58, 54, 50, 44, 40, 34, 26 and 16, respectively. For the LiNa channel, the v = 0–6 vibrational states are included with corresponding maximum rotational quantum numbers 61, 56, 51, 44, 37, 28 and 15, respectively. Asymptotically at ρ = ρf the open ro-vibrational Jacobi basis functions at 1 nK collision energy include the single LiNa(v = 0, j = 0) reactant channel and the product Li2(v = 0–3) with maximum rotational quantum numbers 41, 35, 28, 18, respectively. We note that all of the above quantum dynamics calculations rigorously treat the identical particle exchange symmetry between the two identical 6Li nuclei.17 Thus, the calculations are repeated separately for each exchange symmetry, even and odd.
3 Results
3.1 Potential energy surfaces for Li2Na
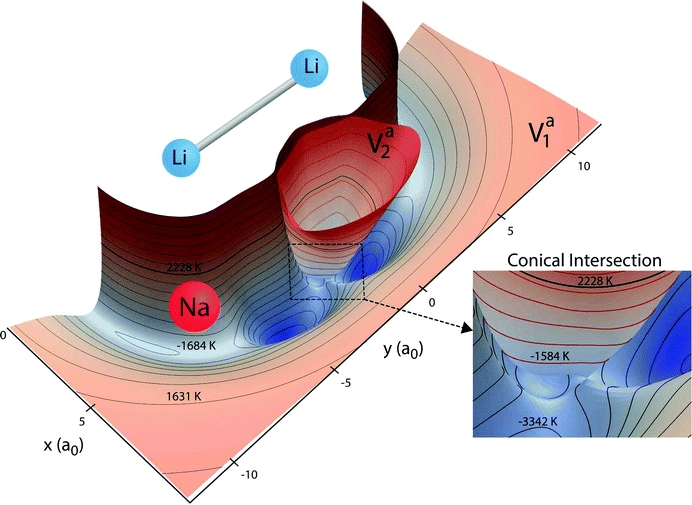
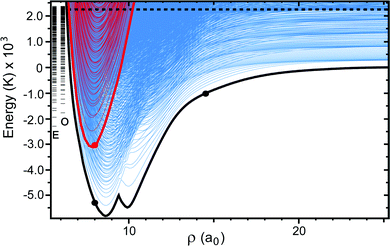
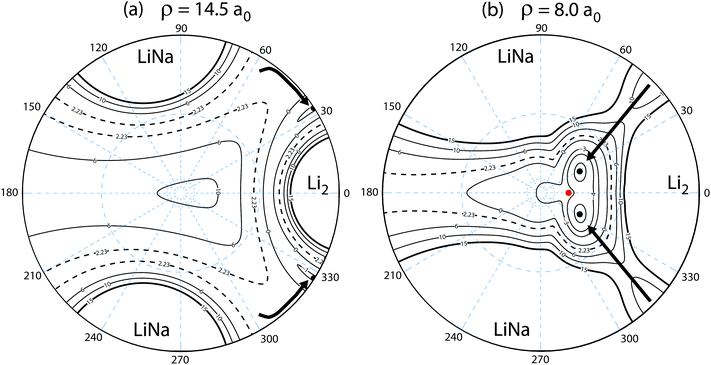
The Born–Oppenheimer electronic PESs are plotted in Fig. 1 for both the ground and first excited electronic states of the Li2Na molecule. The PESs in Fig. 1 are two-dimensional slices plotted for a fixed Li2 bond length of 6.25a0 (close to its equilibrium bond length) and show the topology of the effective interaction potential experienced by the Na nuclei in the vicinity of Li2. Notable features include the two deep attractive wells (blue colored regions) on the ground state surface (black contours) and the inverted cone of the excited electronic state (red contours). All energies are reported relative to the bottom of the asymptotic potential well for the Li2 + Na product channel. The minimum energy of the symmetric potential wells is −5814 K (see the thick solid black curve in Fig. 2). The ground and excited state PESs exhibit a conical intersection for T-shaped (i.e., C2v) geometries (see Fig. 1 inset). The minimum energy of the conical intersection is −3140 K (see the thick solid red curve in Fig. 2). The asymptotic energy of the Li + LiNa(v = 0, j = 0) reactant channel is shown by the thick black contour line at 2228 K (see also the thick horizontal dashed line in Fig. 2). From Fig. 1 we see that for ultracold collisions of Li with LiNa in its ground vibrational and rotational state, both the ground and excited electronic states are energetically accessible in the interaction region. Thus, both electronic states and the couplings between them must be included in the quantum dynamics calculations (see Section 2.2 for details).17 These non-adiabatic couplings include the GP associated with the conical intersection. As discussed in detail in the following section, the GP can lead to a dramatic enhancement or suppression of the ultracold rotationally resolved rate coefficients.21–23 We note that a traditional GP calculation21–23 based on only the ground adiabatic electronic state is not applicable for this system since the CI is located below the energy of the incident channel. Thus, a non-adiabatic fully coupled two electronic state calculation is required.17Fig. 2 plots the APH surface function energies (i.e., the eigenvalues εJpqt(ρξ) of eqn (18)) for the ground (blue) and excited (red) electronic states as a function of ρ. For visualization purposes, the surface function energies were computed for each electronic state separately (i.e., on an uncoupled single adiabatic electronic state). The black and red thick solid curves plot, respectively, the minimum energies of the ground (Va1) and excited (Va2) adiabatic electronic state PESs as a function of ρ. Asymptotically for large ρ, the ground state adiabatic surface function energies (blue) approach the diatomic Li2(v′, j′) and LiNa(v, j) rovibrational energies. The dashed horizontal black line denotes the energy of the Li + LiNa(v = 0, j = 0) reactant channel (2228 K) (see also the thick black contour line in Fig. 1). The excited electronic state is energetically open in the interaction region (small ρ) where the red curves drop below the black dashed horizontal line. The vertical series of short horizontal lines on the left edge of the plot denote the bound state energies of the cone states which are localized inside the cone (Va2) of the excited adiabatic electronic state (see Fig. 1). The E and O label the bound states of even and odd exchange symmetry, respectively. These bound states were computed numerically in full-dimensionality using the adiabatic excited electronic state PES (Va2) and could lead to Feshbach type scattering resonances.52 The large solid black and red dots denote particular points of interest and are discussed in the Appendix.
3.2 Rotationally resolved rate coefficients as a function of collision energy
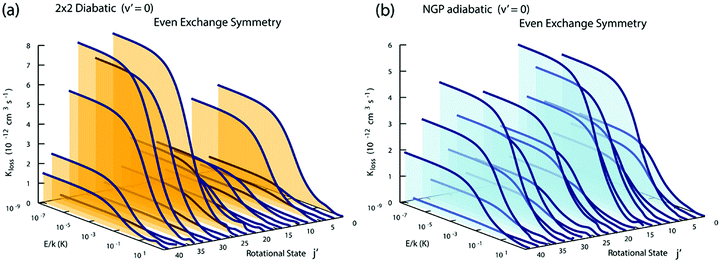
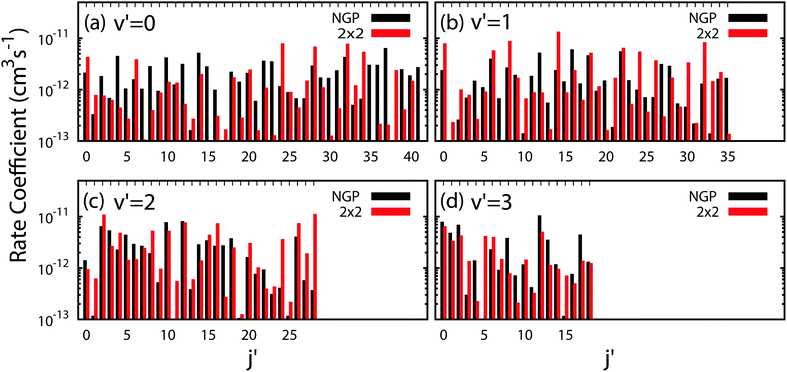
Fig. 3 and 4 plot the rotationally resolved rate coefficients for the Li + LiNa(v = 0, j = 0) → Li2(v′ = 0, j′) + Na reaction as a function of collision energy from 1 nK to 10 K for even and odd exchange symmetry, respectively. Unless otherwise stated, all rate coefficients include the appropriate nuclear spin statistical factors of 2/3 and 1/3 for even and odd exchange symmetry (associated with the two identical 6Li nuclei), respectively. At ultracold collision energies (<1 mK), only a single partial wave (i.e., l = 0 where l is the orbital angular momentum of Li about LiNa) contributes to the collision and the rate coefficient becomes finite (often referred to as the Wigner threshold regime).53,54 The specific values of the ultracold rate coefficients are sensitive to the PES but values reported here are numerically exact for the PESs computed in this study. The curves in Fig. 3(a) and 4(a) are from the coupled two-diabatic electronic states calculation (2 × 2) and the curves in Fig. 3(b) and 4(b) are from the calculation on a single adiabatic ground electronic state which does not include the GP (denoted as NGP for No GP). We see that many of the 2 × 2 ultracold rate coefficients are significantly enhanced or suppressed relative to the NGP ones. The rotationally resolved rate coefficients for the other product vibrational levels v′ = 1–3 show similar trends. A representative example is plotted in Fig. 5 for v′ = 3 and j′ = 5. The red curve in Fig. 5 is from the coupled two-diabatic electronic states calculation (2 × 2) and the black curve is from the NGP calculation on a single adiabatic ground electronic state. We see that in the ultracold limit the 2 × 2 rate coefficient (red) is significantly enhanced (by around 50 times) relative to the NGP one (black). As discussed in more detail below, the enhancement (suppression) is due to constructive (destructive) quantum interference between the direct and looping contributions to the total scattering amplitude.21 The GP associated with the conical intersection shown in Fig. 1 changes the sign of the interference term and hence the nature of the quantum interference from destructive to constructive and vice versa.14–16,21,22,55–62 Furthermore, due to the unique properties of ultracold collisions, according to Levinson's theorem63 the scattering phase shifts preferentially approach an integral multiple of π. Thus, the quantum interference often approaches its maximal values effectively turning the reaction on or off (i.e., a quantum switch!).21,22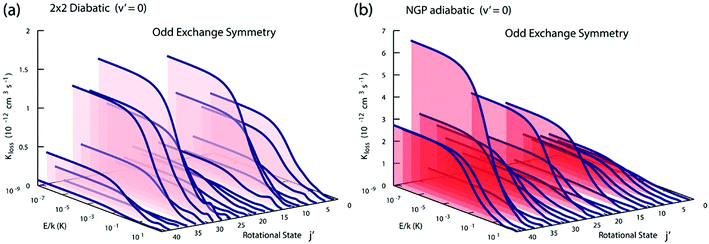 | ||
| Fig. 4 Same as in Fig. 3 except for odd exchange symmetry. | ||
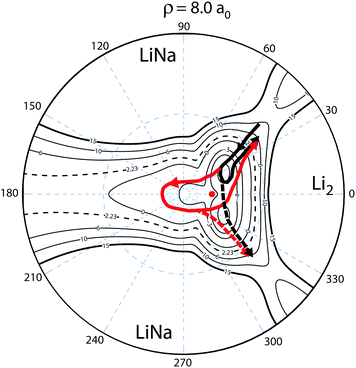
To understand this intriguing quantum interference mechanism in more detail, Fig. 6 plots a stereographic projection17,44 of the hypersphere for the adiabatic ground state PES (Va1) for Li2Na at a fixed hyperradius of ρ = 8a0. The north pole (θ = 0) is at the origin and the equator (θ = π/2) corresponds to the outer black circle. The azimuthal hyperspherical angle (ϕ) is indicated by the dashed blue radial lines. The smaller and larger dashed blue circles indicate the values of θ = 10° and θ = 53°, respectively. The conical intersection is indicated by the red dot and the two symmetric potential wells are clearly visible. These are the same features shown in Fig. 1 plotted in product Jacobi coordinates. The hyperspherical coordinates have the advantage of showing all channels (reactant and product) simultaneously. The dashed contour at 2228 K indicates the energy of the ultracold reactant Li + LiNa(v = 0, j = 0). It is clear that the CI is energetically accessible even at ultracold collision energies and will be encircled by the quantum mechanical wave function. The reaction pathways are indicated by the thick black and red curves and significant quantum interference can occur between the scattering amplitudes associated with these pathways. For clarity only the pathways from one of the symmetric Li + LiNa reactant channels is shown but both are included in the quantum mechanical calculations which rigorously treat the identical particle exchange symmetry (i.e., the two identical 6Li nuclei). We note that ϕ → −ϕ across the horizontal axis corresponds to an exchange of the two Li nuclei. Thus, the pathways from the other LiNa channel can be visualized by reflecting all of the red and black curves in Fig. 6 across the horizontal axis (ϕ = 0). The dashed (solid) black and red curves in Fig. 6 indicate a reactive process with (without) exchange of the identical 6Li nuclei. There are two primary quantum interference mechanisms occurring simultaneously during the reaction. First, both the exchange (dashed curves) and non-exchange (solid curves) pathways can undergo quantum interference with the contribution from the other LiNa channel. Second, each direct pathway (black) undergoes quantum interference with a looping pathway (red). In the following discussion we will focus on the second mechanism. The first mechanism is always present and is included in the rigorous quantum mechanical treatment of the identical particle exchange symmetry which leads to symmetric and antisymmetric functions with respect to ϕ → −ϕ.17 These symmetrized functions correlate asymptotically at large ρ to the even and odd rotational states of Li2 (see ref. 22 and 64 for a detailed discussion of the exchange symmetry quantum interference mechanism).
The quantum interference between two complex scattering amplitudes (e.g., ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) direct and
direct and ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) loop) is given by57
loop) is given by57
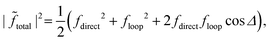 | (19) |
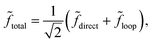 Δ denotes the relative phase between the two complex scattering amplitudes, and fdirect and floop denote their magnitudes. If the direct and looping scattering amplitudes are of comparable magnitude fdirect ≈ floop = f, then eqn (19) reduces to
Δ denotes the relative phase between the two complex scattering amplitudes, and fdirect and floop denote their magnitudes. If the direct and looping scattering amplitudes are of comparable magnitude fdirect ≈ floop = f, then eqn (19) reduces to|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) total|2 ≈ f2(1 + cos total|2 ≈ f2(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ). Δ). | (20) |
If Δ is near an integral multiple of π, Δ ≈ nπ where n is an integer, then from eqn (20) we see that for even and odd n, |![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) total|2 ≈ 2f2 and 0, respectively. That is, for even n the reaction is “on” and for odd n the reaction is “off”. As noted above, due to the unique properties of ultracold collisions,63 the relative phase shifts often approach an integral multiple of π and become effectively quantized.21–23 Also, the direct and looping scattering amplitudes often have similar magnitudes.21–23 Thus, the quantum interference between the black and red pathways shown in Fig. 6 often approaches its maximal values which effectively controls the reaction outcome.21 It is important to emphasize that this unique quantum interference mechanism (eqn (20)) occurs in ultracold scattering calculations based on a single adiabatic ground electronic state PES, as well as those based on a non-adiabatic coupled diabatic (2 × 2) electronic state representation. The critical difference is that the GP associated with the CI is included in the 2 × 2 diabatic calculations17 but not in the NGP single surface adiabatic calculations. The GP gives rise to an additional π phase shift along the looping (red) pathways so that Δ → Δ + π which changes the sign of the cos
total|2 ≈ 2f2 and 0, respectively. That is, for even n the reaction is “on” and for odd n the reaction is “off”. As noted above, due to the unique properties of ultracold collisions,63 the relative phase shifts often approach an integral multiple of π and become effectively quantized.21–23 Also, the direct and looping scattering amplitudes often have similar magnitudes.21–23 Thus, the quantum interference between the black and red pathways shown in Fig. 6 often approaches its maximal values which effectively controls the reaction outcome.21 It is important to emphasize that this unique quantum interference mechanism (eqn (20)) occurs in ultracold scattering calculations based on a single adiabatic ground electronic state PES, as well as those based on a non-adiabatic coupled diabatic (2 × 2) electronic state representation. The critical difference is that the GP associated with the CI is included in the 2 × 2 diabatic calculations17 but not in the NGP single surface adiabatic calculations. The GP gives rise to an additional π phase shift along the looping (red) pathways so that Δ → Δ + π which changes the sign of the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ term in eqn (20). Thus, when the GP is included the opposite interference occurs (i.e., constructive ↔ destructive) and the theoretically predicted reactivity is reversed. That is, for even n the reaction is “off” and for odd n the reaction is “on” (for additional details see the Appendix). The value of the integer n for a particular scattering process depends upon the details of the PES as discussed below. In practice, it is not computed directly but its parity can be inferred from an analysis of the calculated scattering amplitudes.
Δ term in eqn (20). Thus, when the GP is included the opposite interference occurs (i.e., constructive ↔ destructive) and the theoretically predicted reactivity is reversed. That is, for even n the reaction is “off” and for odd n the reaction is “on” (for additional details see the Appendix). The value of the integer n for a particular scattering process depends upon the details of the PES as discussed below. In practice, it is not computed directly but its parity can be inferred from an analysis of the calculated scattering amplitudes.
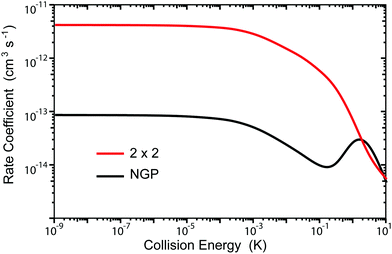
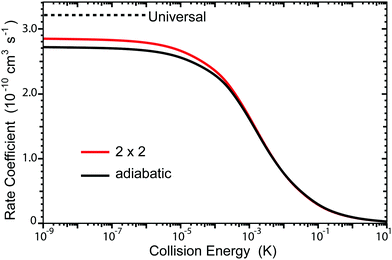
The total rate coefficient summed over all final vibrational and rotational states of Li2 are plotted in Fig. 7. The red and black curves correspond to the 2 × 2 and adiabatic (NGP) calculations, respectively. The horizontal black dashed line is the ultracold rate coefficient computed using a simple one-dimensional universal model based on just a long-range C6 potential ignoring all reflections.20 The quantum interference effects tend to wash out in the sum over final states so that the 2 × 2 and adiabatic total ultracold rate coefficients are similar in magnitude (i.e., K2×2/Kadiab ≈ 1.05 at Ec = 1.0 nK). Interestingly, both the 2 × 2 and adiabatic ultracold rate coefficients lie below the universal value (i.e., K2×2/Kuniv ≈ 0.89 and Kadiab/Kuniv ≈ 0.85 at Ec = 1.0 nK). Thus, the smaller 2 × 2 and adiabatic rates are most likely due to non-reactive (elastic) reflections that are included in the exact quantum mechanical calculations. The sensitivity of the rate coefficients to the accuracy of the PES was also investigated and is discussed in detail in the Appendix.
3.3 Ultracold rate coefficient distributions
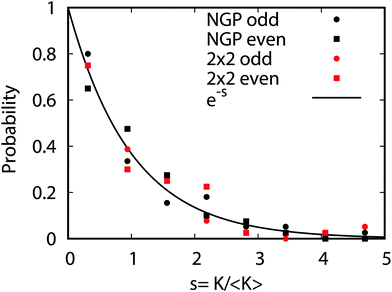
All of the rotationally resolved rate coefficients are plotted in Fig. 8 at the ultracold collision energy of 1 nK for each final vibrational product state of Li2 from v′ = 0 to 3. The red and black rate coefficients (vertical bars) correspond to the 2 × 2 and NGP calculations, respectively. Many of the 2 × 2 rate coefficients are significantly enhanced or suppressed relative to the NGP rate coefficients. As discussed above, this effect is due to the GP which is included in the 2 × 2 calculations but not in the NGP calculations. The sign change associated with the GP alters the nature of the quantum interference and hence the magnitude of the rate coefficients. For v′ = 0 (panel a) particularly large GP effects are seen in the product rotational states j′ = 4, 7, 15, 23, 30, 35–37 and 41 for which the 2 × 2 rate coefficients are suppressed relative to the NGP ones. In contrast, the product rotational states for j′ = 24, 34, and 38 show significantly enhanced 2 × 2 rates coefficients. For v′ = 1 (panel b) notably suppressed 2 × 2 rate coefficients are observed for the product rotational states j′ = 12, 20, 27, and 35 whereas notably enhanced 2 × 2 rate coefficients occur for j′ = 14, 21, 24, 26, 30, 32, and 33. For v′ = 2 (panel c) notably suppressed 2 × 2 rate coefficients are observed for the product rotational state j′ = 17 whereas notably enhanced 2 × 2 rate coefficients occur for j′ = 1, 11, 24, 27, and 28. Finally, for v′ = 3 (panel d) notably suppressed 2 × 2 rate coefficients are observed for the product rotational states j′ = 4, 8, 9, 13, and 17 whereas notably enhanced 2 × 2 rate coefficients occur for j′ = 3, 5, and 15. In summary, the magnitude of the GP effect on the ultracold rotationally resolved rate coefficients varies significantly across all values of the product ro-vibrational states of Li2(v′, j′).Fig. 9 plots the normalized distributions s = K/〈K〉 where 〈K〉 denotes the average value of the rate coefficients K for a given data set. The probability distributions are computed by binning the Kv′j′ into eight equally spaced intervals up to five times the average value. Four normalized data sets are plotted. The red and black data points denote the 2 × 2 and NGP rate coefficients, respectively. The circles and squares correspond to the results of even and odd exchange symmetry. The four data sets span all of the vibrational and rotational states shown in Fig. 8. For reference, the Poisson distribution (e−s) is also plotted (solid black curve). We see that on average all four data sets are consistent with the Poisson distribution. Thus, a statistical analysis of the seemingly random rotational rate coefficient distributions of Fig. 8 provides a unified description of all the results. We note that the Poisson nature of the rotational distributions was also reported previously for the ultracold K + KRb reaction from an NGP calculation on a single adiabatic electronic PES.12,13 This property appears to be very robust and is independent of the details of the PES and occurs for both the 2 × 2 and NGP results. For example, in the Appendix Fig. 16 and 17 the Poisson distributions are plotted for 25 different values of the PES scaling parameter λ for each exchange symmetry even and odd, respectively. The collective set of 100 distributions are consistent with the Poisson distribution. Though these distributions are presented at 1 nK, their validity extends to 10 μK due to the Wigner threshold behavior of the rate coefficients in this regime. The K + KRb results12,13 together with the present work confirms what appears to be a universal property of ultracold chemical reactions with a potential well supporting long-lived complex formation: the rotationally resolved rate coefficient probability distributions are Poissonian.
4 Conclusions
Many ultracold chemical reactions under active experimental investigation, such as Li + LiNa → Li2 + Na, K + NaK → K2 + Na, KRb + KRb → K2 + Rb2, and NaRb + NaRb → Na2 + Rb25,6,9,10 have a barrierless reaction pathway and a deep attractive potential well. In addition, the three atom systems are known to exhibit a C2v CI between the ground and first excited electronic states in the interaction region. This CI is energetically accessible even for ultracold collisions involving reactant diatomic molecules in their ground ro-vibrational state (e.g., LiNa(v = 0, j = 0)). The four atom systems are also expected to have CIs (possibly multiple CIs) that are energetically accessible. Thus, a standard Born–Oppenheimer calculation based on a single adiabatic electronic PES or even a generalized calculation which includes the GP either by the vector potential approach14,15 or a double-valued basis approach56 is not accurate for these systems. A non-adiabatic quantum mechanical dynamics calculation17 is required that includes both coupled electronic states using full-dimensional accurate ab initio PESs with experimentally based long-range and asymptotic diatomic potentials. In addition, a rigorous quantum mechanical treatment of the exchange symmetry due to the identical nuclei is also required.17 To the authors' knowledge, the first non-adiabatic calculations of this kind are reported in this work for the ultracold Li + LiNa(v = 0, j = 0) → Li2(v′, j′) + Na reaction. Indeed, we believe this work significantly advances the state-of-the-art in the theoretical treatment of experimentally relevant ultracold chemical reactions beyond the Born–Oppenheimer approximation.During the course of the reaction, two quantum interference mechanisms occur which ultimately govern the reaction outcome. One mechanism is the quantum interference between the two contributions from identical particle exchange symmetry. The second mechanism is the quantum interference between the two reaction pathways (direct and looping) which encircle the CI. Both of these mechanisms are included in all of the quantum mechanical calculations presented in this work (2 × 2 and NGP). Due to the unique properties of ultracold collisions, the quantum interference often approaches its maximal constructive or destructive values which leads to a significantly enhanced or suppressed rotationally resolved rate coefficient (i.e., the reaction is effectively turned on or off). Furthermore, the GP associated with the CI changes the sign on the interference term between the direct and looping pathways which reverses the nature of the quantum interference. Thus, a non-adiabatic calculation which includes the excited electronic state and its associated GP is crucial for obtaining the correct theoretical prediction of the rate coefficients. A conventional Born–Oppenheimer calculation based on a single adiabatic ground electronic state PES will give the opposite (incorrect) prediction whenever significant quantum interference occurs. Furthermore, a rigorous quantum mechanical treatment of the identical particle exchange symmetry (i.e., the exchange of the two identical 6Li nuclei) is also required in order to capture the quantum interference associated with exchange symmetry. Several PES scaling studies were undertaken which show that the large quantum interference effects are indeed due to interference between the direct and looping pathways. Furthermore, these PES scaling studies also confirm unambiguously that the GP is responsible for reversing the nature of the interference (i.e., constructive ↔ destructive) which leads to the dramatic enhancement or suppression of the 2 × 2 ultracold rate coefficients relative to the NGP ones. The novel quantum interference mechanism associated with ultracold collisions represents a realization of a molecular quantum switch. The large dynamic range of this quantum switch might be exploited by experimentalists to control the reaction outcome via the application of external fields and/or the selection of a particular initial quantum state.21–23 Interestingly, the interference effects mostly cancel out in the total rate coefficients (both 2 × 2 and NGP) when summed over all product rotational states. The total rate coefficients also exhibit non-universal behavior.
The rotationally resolved rate coefficient distributions are shown to exhibit Poisson behavior. The S matrix for open chaotic quantum systems obeys the statistics of unitary symmetric random matrices, one of which is the Poisson law behavior of the squares of off-diagonal matrix elements.65,66 Since state-to-state rates are directly proportional to the square of the corresponding S matrix element, this Poisson law behavior follows directly from the underlying classically chaotic motion of the reaction.67 Chaotic classical trajectories are extremely complicated and tangled for reactions with long-lived intermediate complexes, as such these results show that the ultracold LiNa + Li reaction proceeds via complex formation. Such intermediate complexes can be observed experimentally using a combination of mass spectrometry and velocity map imaging, as was recently demonstrated for the ultracold KRb + KRb → K2 + Rb2 reaction.10 As shown explicitly in this work for the first time, the Poisson nature of these rotational distributions is robust to variations in the PES, occurs for different chemical systems (i.e., both light Li2Na and heavy K2Rb12) and theoretical methods (i.e., both non-adiabatic (2 × 2) and adiabatic (NGP)). The robust and universal nature of the Poisson ultracold rotational rate coefficient distributions makes this property an ideal experimental observable. Considering the sensitivity of individual rotationally resolved rate coefficients to fine details of the PES a direct quantitative comparison of these with experimental measurements will be challenging and will likely require improvements to the PES.
In contrast to standard statistical theories which predict uniform product distributions for many complex-forming reactions,68 we find that at ultracold collision temperatures the product rotational distributions are significantly non-uniform (i.e., non-statistical). This is due in part to the unique properties of ultracold collisions which involve only a single-partial wave. At higher (thermal) energies many partial waves contribute which tend to wash-out the variations in the product distributions resulting in a uniform distribution. Statistical theories also ignore the detailed dynamics of the interaction region and therefore do not explicitly include the short-range quantum dynamics, non-adiabatic, and interference effects which are significantly amplified at ultracold temperatures and give rise to the large variations in the rotational distributions. Nevertheless, statistical theories can often provide a reasonable estimate of the total ultracold rate coefficients due to the large density of states associated with complex forming reactions with a deep attractive potential well and heavy nuclei.69 In an exact quantum mechanical calculation, the fluctuations in the rotational distributions average out in the sum over the large number of product states so that the total ultracold rate coefficient is often similar to the statistical one. However, we expect that the underlying distributions are all Poissonian and also occur in ultracold diatom–diatom reactions such as KRb + KRb and NaRb + NaRb. For additional analysis comparing statistical theories to exact quantum mechanical calculations, we refer the reader to recent work on the ultracold Li + LiYb reaction.11
The unique properties of ultracold collisions are still largely unexplored. We hope that the detailed theoretical results presented in this work will help stimulate new experimental and theoretical studies into the intriguing ultracold energy regime. For example, the extreme non-linear sensitivity of the quantum interference effects on the depth of the PES might be used for very accurate experimental probing and benchmarking of the molecular interactions, beyond anything used in the field at the present time. One could also imagine exploiting this ultra sensitivity in the search of new physics such as tightening the experimental bounds on possible variations in the physical constants (e.g., the proton to electron mass ratio). Clearly, ultracold molecules continue to show exceptional promise for future technological applications in quantum control, sensing and precision measurements.
Conflicts of interest
There are no conflicts to declare.A.1 Electronic ground and first excited state adiabatic potential energy surfaces
Fig. 10 plots the adiabatic ground electronic state potential energy surface for Li2Na (Va1) in hyperspherical coordinates. The north pole (θ = 0) of the hypersphere is projected onto the origin in the xy-plane. The equator (θ = π/2) is projected onto the outer circle. The values of the azimuthal angle (ϕ) are indicated by the dashed blue radial lines. The small (large) dashed blue circle about the origin indicates θ = 10° (53°). The barrierless reaction pathway is shown by the thick black curves with arrows indicating the reaction direction. The reaction proceeds along a collinear approach NaLi–Li (panel a) and then enters the attractive potential wells in the interaction region (panel b). The identical particle exchange symmetry (i.e., ϕ → −ϕ) associated with the two identical Li nuclei is rigorously accounted for in the quantum mechanical calculations. The black dots denote the location of the minimum energy of the PES for the specified fixed value of hyperradius: ρ = 14.5a0 (panel a) and ρ = 8.0a0 (panel b). The red dot in panel (b) denotes the location of the C2v conical intersection. The dashed contour line at −2.23 × 103 K corresponds to the energy of the reactant Li + LiNa(v = 0, j = 0) channel. The conical intersection lies at −3.14 × 103 K and is therefore energetically accessible even at ultracold collision energies. All energies are relative to the asymptotic Li2 + Na adiabatic ground electronic state energy minimum. We note that the sharp feature in the thick black curve (minimum energy curve) near ρ = 9.5a0 in Fig. 2 is due to a submerged barrier along the reaction path shown in Fig. 10(b).Fig. 11 is the same as Fig. 10 except that the adiabatic excited electronic state PES (Va2) is plotted at ρ = 8.0a0. The contours exhibit the typical inverted cone shape associated with a conical intersection. The excited state becomes degenerate with ground electronic state at the conical intersection (i.e., the red dots in Fig. 10 and 11). As also shown in Fig. 10, the dashed contour at −2.23 × 103 K lies above the energy of the conical intersection. Thus, the Born–Oppenheimer approximation breaks down necessitating a non-adiabatic coupled two electronic state quantum mechanical treatment.
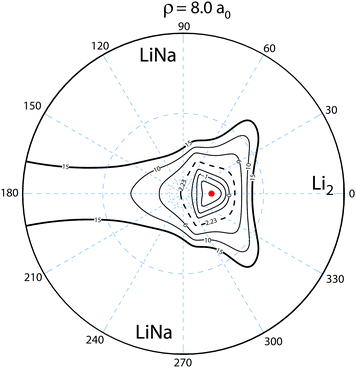 | ||
| Fig. 11 Same as in Fig. 10 except that the contour plot of the adiabatic excited electronic state of Li2Na (Va2) is plotted in hyperspherical coordinates for a fixed hyperradius ρ = 8a0. The contours lie between 15 × 103 and −2 × 103 K inclusive and the dashed contour at 2.23 × 103 K indicates the energy of the Li + LiNa ultracold collision. As in Fig. 10, the red dot indicates the location of the energetically accessible conical intersection. | ||
A.2 Reaction rate coefficients and potential scaling studies
Fig. 12 plots the ultracold total rate coefficient for the Li + LiNa(v = 0, j = 0) → Li2 + Na reaction as a function of the three-body potential scaling factor (λ). The ab initio computed three-body contribution to the potential energy surface (PES) was scaled by λ but the long-range and pairwise two-body potentials were left unchanged. This ensures that the asymptotic energies and long-range interactions are unchanged and that only the effective depth of the Li2Na PES is altered. Specifically, the 3-body components in the diabatic potentials V11, V22, and V12 (see eqn (9)) were scaled according to the following equation| Vij = Vpwij(R1,R2,θ) + λs(R1,R2,θ)V3Bij(R1,R2,θ), | (A.1) |
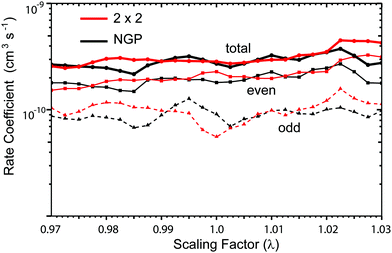
The computational time for each of the 100 λ calculations is primarily dominated by the surface function solutions (i.e., the diagonalization of eqn (18) at each ρξ) and the radial log-derivative propagation (i.e., the solution of the radial eqn (16) from ρi to ρf). All steps of the calculations are parallelized and can be efficiently distributed across a large number of CPUs simultaneously. For comparison, each set of 2 × 2 surface function calculations was performed using 288 CPUs and required tsf2×2 = 6.2 h whereas the NGP surface function calculations on the same number of CPUs required tsfNGP = 0.6 h. Each CPU is an Intel Haswell (Xeon E5-2650 v3) running at 2.3 GHz. The 2 × 2 and NGP log-derivative propagations used 16 CPUs (one for each collision energy) and required tlog2×2 = 8.8 and tlogNGP = 3.5 h, respectively. Thus, the total wall-clock time for one λ calculation was ttotal2×2 = tsf2×2 + tlog2×2 = 15.0 h and ttotalNGP = tsfNGP + tlogNGP = 4.1 h. The non-adiabatic 2 × 2 calculations require about ttotal2×2/ttotalNGP = 3.6 times more CPU time than the NGP ones. The 100 λ calculations were separately distributed across approximately 20 compute nodes (each node consists of 32 CPUs and 128 Gb memory) and were completed over the course of approximately three weeks.
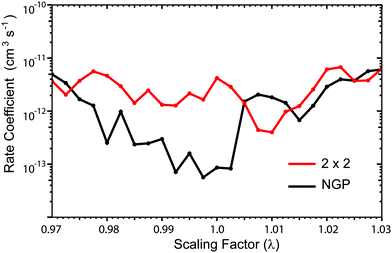
Fig. 13 plots the ultracold rotationally resolved rate coefficient for the Li + LiNa(v = 0, j = 0) → Li2(v′ = 3, j′ = 5) + Na reaction as a function of the three-body potential scaling factor (λ). The 2 × 2 and NGP results are presented in red and black, respectively. As the scaling factor increases or decreases away from λ = 1 (i.e., no scaling), dramatic and often sudden changes in both the 2 × 2 and NGP rate coefficients are observed. These large changes are due to the change in nature of the quantum interference from constructive to destructive and vice versa. The quantum interference occurs between the direct and looping contributions to the total scattering amplitude. The direct pathway proceeds straight from reactants to products through the Li2Na potential well whereas the looping pathway “loops around” and encircles the conical intersection (see Fig. 6 in the paper).
Let ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) direct = fdirecteiδdirect and
direct = fdirecteiδdirect and ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) loop = floopeiδloop denote the complex scattering amplitudes associated with the direct and looping pathways, respectively. The fdirect and floop are the real valued magnitudes and the δdirect and δloop are the real valued phases. The total scattering amplitude is the sum of the two:
loop = floopeiδloop denote the complex scattering amplitudes associated with the direct and looping pathways, respectively. The fdirect and floop are the real valued magnitudes and the δdirect and δloop are the real valued phases. The total scattering amplitude is the sum of the two: 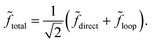 The cross sections and rate coefficients are computed from the modulus of the total scattering amplitude given by eqn (19) where the relative phase Δ = δloop − δdirect. The third term on the right hand side of eqn (19) is the interference term. If the looping and direct scattering amplitudes are comparable in magnitude: fdirect ≈ floop = f, then we obtain eqn (20). At ultracold collision energies the scattering phase shifts δloop and δdirect have a propensity to approach an integral multiple of π (i.e., Levinson's theorem): δdirect ≈ πndirect and δloop ≈ πnloop where the ndirect and nloop are integers. Thus the relative phase also approaches an integral multiple of π: Δ ≈ π(nloop − ndirect) ≈ nπ where the integer n = nloop − ndirect. This implies that the interference term cos
The cross sections and rate coefficients are computed from the modulus of the total scattering amplitude given by eqn (19) where the relative phase Δ = δloop − δdirect. The third term on the right hand side of eqn (19) is the interference term. If the looping and direct scattering amplitudes are comparable in magnitude: fdirect ≈ floop = f, then we obtain eqn (20). At ultracold collision energies the scattering phase shifts δloop and δdirect have a propensity to approach an integral multiple of π (i.e., Levinson's theorem): δdirect ≈ πndirect and δloop ≈ πnloop where the ndirect and nloop are integers. Thus the relative phase also approaches an integral multiple of π: Δ ≈ π(nloop − ndirect) ≈ nπ where the integer n = nloop − ndirect. This implies that the interference term cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ in eqn (20) approaches: cos
Δ in eqn (20) approaches: cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ ≈ 1 or cos
Δ ≈ 1 or cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ ≈ 0 for even and odd values of n, respectively. From Levinson's theorem we know that the integers ndirect and nloop denote the number of bound states supported along the direct and looping reaction pathways, respectively. Thus, the integer n is the relative number of bound states between these two pathways which in general is either even or odd. In practice, we never need to explicitly compute these integers (or Δ) but can infer the even or odd nature of n from the scattering amplitudes. Eqn (19) and (20) are valid for both the 2 × 2 and NGP calculations. However, the 2 × 2 calculations include the GP which gives rise to an additional sign change or π phase shift in the scattering amplitude for the looping pathway (relative to the NGP one). That is, δloop2×2 = δNGPloop + π + ε where ε represents other differences (due to non-adiabatic couplings) between the NGP and 2 × 2 scattering phase shifts. The GP phase shift is defined as δGPloop = δNGPloop + π, so that we can also write δloop2×2 = δGPloop + ε. If other non-adiabatic effects are small, then ε ≈ 0 and we obtain δloop2×2 ≈ δGPloop (and similarly δNGPdirect = δGPdirect ≈ δdirect2×2).
Δ ≈ 0 for even and odd values of n, respectively. From Levinson's theorem we know that the integers ndirect and nloop denote the number of bound states supported along the direct and looping reaction pathways, respectively. Thus, the integer n is the relative number of bound states between these two pathways which in general is either even or odd. In practice, we never need to explicitly compute these integers (or Δ) but can infer the even or odd nature of n from the scattering amplitudes. Eqn (19) and (20) are valid for both the 2 × 2 and NGP calculations. However, the 2 × 2 calculations include the GP which gives rise to an additional sign change or π phase shift in the scattering amplitude for the looping pathway (relative to the NGP one). That is, δloop2×2 = δNGPloop + π + ε where ε represents other differences (due to non-adiabatic couplings) between the NGP and 2 × 2 scattering phase shifts. The GP phase shift is defined as δGPloop = δNGPloop + π, so that we can also write δloop2×2 = δGPloop + ε. If other non-adiabatic effects are small, then ε ≈ 0 and we obtain δloop2×2 ≈ δGPloop (and similarly δNGPdirect = δGPdirect ≈ δdirect2×2).
Substituting the above expressions for the looping and direct phase shifts for δ2×2 and δNGP into the Δ in eqn (20) (and ignoring ε), we obtain
|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) NGP/2×2total|2 ≈ f2(1 ± cos(nπ)), NGP/2×2total|2 ≈ f2(1 ± cos(nπ)), | (A.2) |
|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) NGPtotal|2 ≈ 2f2 NGPtotal|2 ≈ 2f2 |
|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) total2×2|2 ≈ 0. total2×2|2 ≈ 0. | (A.3) |
If n is an odd integer, then eqn (A.2) gives
|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) NGPtotal|2 ≈ 0 NGPtotal|2 ≈ 0 |
|![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) total2×2|2 ≈ 2f2. total2×2|2 ≈ 2f2. | (A.4) |
In the ultracold limit, eqn (A.3) and (A.4) show that the quantum interference can approach its maximal values of 2f2 (constructive) or zero (destructive). The constructive or destructive nature of the interference is always opposite for the NGP and 2 × 2 calculations and can reverse if the integer n changes from being even to odd or vice versa. We note that the maximal values given by eqn (A.3) and (A.4) are not fully realized in practice since the direct and looping scattering amplitudes are not exactly equal in magnitude and their scattering phase shifts are not exactly an integer multiple of π. However, as discussed below, these limiting cases are useful for understanding and interpreting the large differences observed between the 2 × 2 and NGP results.
Armed with eqn (A.3) and (A.4), we can now understand and interpret the changes in the rate coefficients plotted in Fig. 13. First consider the scaling range between λ = 0.975 and 1.0025. In this region, the 2 × 2 rate coefficient is significantly enhanced relative to the NGP one (by 50 times for λ = 1). This enhancement is due to constructive quantum interference as shown in eqn (A.4) which implies n must be odd in this region. Fig. 14 plots the ratio of the magnitudes of the looping and direct scattering amplitudes averaged over the scattering angle as a function of the PES scaling factor. We see that for 0.98 ≤ λ ≤ 1.0025 the ratio is near unity which ensures maximal quantum interference. Fig. 15 plots cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ averaged over the scattering angle as a function of the PES scaling factor. In the region 0.975 ≤ λ ≤ 1.0025 we see that 〈cos
Δ averaged over the scattering angle as a function of the PES scaling factor. In the region 0.975 ≤ λ ≤ 1.0025 we see that 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ〉 lies near −1.0 (except for a few values between 0.9825 and 0.99). The negative cos
Δ〉 lies near −1.0 (except for a few values between 0.9825 and 0.99). The negative cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ is consistent with an odd value of n. As λ is decreased below 0.98, the ratio in Fig. 14 decreases rapidly to below 10−1. Thus, the direct scattering amplitude dominates and quantum interference effects become small. In this case, the 2 × 2 and NGP rate coefficients approach each other. Also in this region, the cos
Δ is consistent with an odd value of n. As λ is decreased below 0.98, the ratio in Fig. 14 decreases rapidly to below 10−1. Thus, the direct scattering amplitude dominates and quantum interference effects become small. In this case, the 2 × 2 and NGP rate coefficients approach each other. Also in this region, the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ term reverses sign for λ ≤ 0.9725 so that the nature of the quantum interference is reversed and now eqn (A.3) is relevant (i.e., n becomes even). Indeed, in this region the NGP rate coefficient is now larger than the 2 × 2 one. The change in n from being odd to even (or vice versa) is due to the sudden change in the relative number of bound states between the direct and looping pathways. Presumably this change is due to a bound (continuum) state leaving (entering) the well and becoming a continuum (bound) state as the well depth is decreased (increased) by the λ scaling. This explains the sudden change in sign of cos
Δ term reverses sign for λ ≤ 0.9725 so that the nature of the quantum interference is reversed and now eqn (A.3) is relevant (i.e., n becomes even). Indeed, in this region the NGP rate coefficient is now larger than the 2 × 2 one. The change in n from being odd to even (or vice versa) is due to the sudden change in the relative number of bound states between the direct and looping pathways. Presumably this change is due to a bound (continuum) state leaving (entering) the well and becoming a continuum (bound) state as the well depth is decreased (increased) by the λ scaling. This explains the sudden change in sign of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ between λ = 0.9725 and 0.975. Now consider the region 1.0025 < λ ≤ 1.0125. In this region the ratios in Fig. 14 lie between 1 and 10 and the cos
Δ between λ = 0.9725 and 0.975. Now consider the region 1.0025 < λ ≤ 1.0125. In this region the ratios in Fig. 14 lie between 1 and 10 and the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ are positive and approach + 1 for λ = 1.01. Again the positive cos
Δ are positive and approach + 1 for λ = 1.01. Again the positive cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ implies an even n (i.e., eqn (A.3) is relevant) and the NGP rate coefficient is larger than the 2 × 2 one. The quantum interference and hence the difference between the rate coefficients is largest in this region for λ = 1.01 where cos
Δ implies an even n (i.e., eqn (A.3) is relevant) and the NGP rate coefficient is larger than the 2 × 2 one. The quantum interference and hence the difference between the rate coefficients is largest in this region for λ = 1.01 where cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ ≈ 1. Between λ = 1.0125 and 1.015, the cos
Δ ≈ 1. Between λ = 1.0125 and 1.015, the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ term changes sign and becomes negative again reversing the nature of the quantum interference (i.e., n becomes odd again). The 2 × 2 rate coefficients are now larger than the NGP ones in Fig. 13. As λ is increased further, the cos
Δ term changes sign and becomes negative again reversing the nature of the quantum interference (i.e., n becomes odd again). The 2 × 2 rate coefficients are now larger than the NGP ones in Fig. 13. As λ is increased further, the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ term oscillates back to being positive again with a peak value at λ = 1.0275. In the region of large positive λ, the ratio in Fig. 14 continues to decrease rapidly which indicates that the direct pathway is dominant. Thus, the quantum interference decreases considerably and the 2 × 2 and NGP rate coefficients become comparable in magnitude as seen in Fig. 13. We note that a similar analysis was done for all of the other rotationally resolved rate coefficients and they are all consistent with eqn (A.3) and (A.4). The PES scaling studies show unambiguously that the significant enhancement or suppression of the 2 × 2 rate coefficients relative to the NGP ones is due to the GP.
Δ term oscillates back to being positive again with a peak value at λ = 1.0275. In the region of large positive λ, the ratio in Fig. 14 continues to decrease rapidly which indicates that the direct pathway is dominant. Thus, the quantum interference decreases considerably and the 2 × 2 and NGP rate coefficients become comparable in magnitude as seen in Fig. 13. We note that a similar analysis was done for all of the other rotationally resolved rate coefficients and they are all consistent with eqn (A.3) and (A.4). The PES scaling studies show unambiguously that the significant enhancement or suppression of the 2 × 2 rate coefficients relative to the NGP ones is due to the GP.
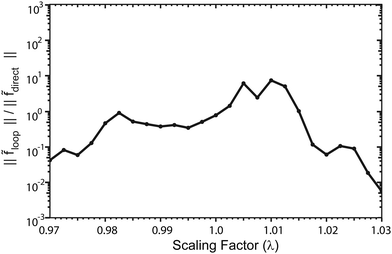 | ||
Fig. 14 The ratios of the modulus of the looping (![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) loop) and direct ( loop) and direct (![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) direct) scattering amplitudes averaged over the scattering angle are plotted as a function of the 3-body potential scaling parameter at the ultracold collision energy of 1 nK. The ratios correspond to the rotationally resolved rate coefficients plotted in Fig. 13. direct) scattering amplitudes averaged over the scattering angle are plotted as a function of the 3-body potential scaling parameter at the ultracold collision energy of 1 nK. The ratios correspond to the rotationally resolved rate coefficients plotted in Fig. 13. | ||
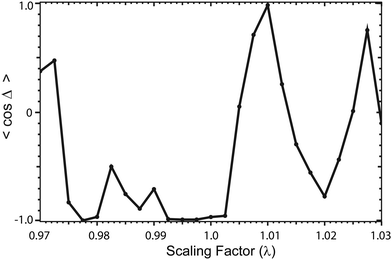 | ||
Fig. 15 The average cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ values are plotted as a function of the 3-body potential scaling parameter at the ultracold collision energy of 1 nK. The 〈cos Δ values are plotted as a function of the 3-body potential scaling parameter at the ultracold collision energy of 1 nK. The 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ〉 correspond to the rotationally resolved rate coefficients plotted in Fig. 13. Δ〉 correspond to the rotationally resolved rate coefficients plotted in Fig. 13. | ||
Fig. 16 and 17 plot the ultracold probability distributions of the rotationally resolved rate coefficients for the Li + LiNa(v = 0, j = 0) → Li2(v′, j′) + Na reaction for the NGP and 2 × 2 calculations, respectively. The normalized distributions s = K/〈K〉 (where 〈K〉 denotes the average value of the rate coefficients K for a given data set) are computed by binning the rate coefficient Kv′j′ into equally space bins up to 14 times the average value. In Fig. 16 and 17 the even and odd curves are plotted in dark and light blue (red), respectively. There are 25 curves for each exchange symmetry in each plot which correspond to the 25 values of the scaling parameter λ. On average, all of the curves are consistent with the Poisson distribution e−s (black curve).
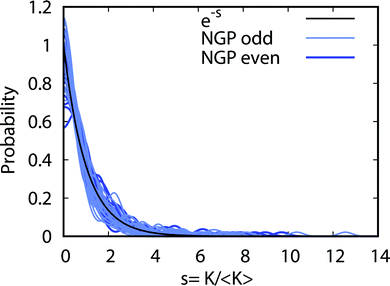 | ||
| Fig. 16 The probability distributions for all of the rotationally resolved rate coefficients for the Li + LiNa(v = 0, j = 0) → Li2(v′, j′) + Na reaction are plotted at the ultracold collision energy of 1.0 nK. The distributions correspond to the single surface adiabatic (NGP) calculations. The results for even and odd exchange symmetry are plotted in dark and light blue, respectively. Each curve plots the distribution for a different 3-body scaling parameter (see Fig. 13). The solid black curve is the Poisson distribution. | ||
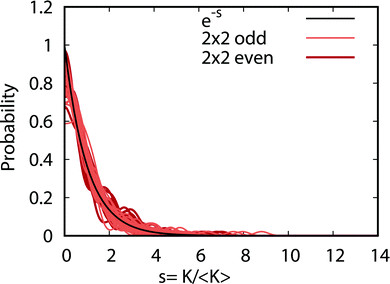 | ||
| Fig. 17 Same as in Fig. 16 except that the distributions for the coupled two-state diabatic (2 × 2) calculations are plotted. The results for even and odd exchange symmetry are plotted in dark and light red, respectively. | ||
Acknowledgements
B. K. K. acknowledges that part of this work was done under the auspices of the US Department of Energy under Project No. 20170221ER of the Laboratory Directed Research and Development Program at Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001). S. K. acknowledges support from the Army Research Office Grant No. W911NF-17-1-0563, the NSF Grant No. PHY-1619788 and PHY-1908634. J. F. E. C. acknowledges that part of this work was supported by the Marsden Fund of New Zealand (Contract No. UOO1923) and gratefully acknowledges support from the Dodd-Walls Centre for Photonic and Quantum Technologies. N. B. acknowledges partial support from NSF grant no. PHY-1806334 and ARO MURI grant no. W911NF-19-1-0283.Notes and references
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- S. Ospelkaus, K.-K. Ni, D. Wang, M. H. G. de Miranda, B. Neyenhuis, G. Quéméner, P. S. Julienne, J. L. Bohn, D. S. Jin and J. Ye, Science, 2010, 327, 853–857 CrossRef CAS.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356–359 CrossRef CAS.
- T. M. Rvachov, H. Son, A. T. Sommer, S. Ebadi, J. J. Park, M. W. Zwierlein, W. Ketterle and A. O. Jamison, Phys. Rev. Lett., 2017, 119, 143001 CrossRef.
- J. Rui, H. Yang, L. Liu, D.-C. Zhang, Y.-X. Liu, J. Nan, Y.-A. Chen, B. Zhao and J.-W. Pan, Nat. Phys., 2017, 13, 699–703 Search PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2018, 10, 561–567 CrossRef CAS.
- J. F. E. Croft, N. Balakrishnan, M. Huang and H. Guo, Phys. Rev. Lett., 2018, 121, 113401 CrossRef CAS.
- X. Ye, M. Guo, M. L. González-Martnez, G. Quéméner and D. Wang, Sci. Adv., 2018, 4, eaaq0083 CrossRef.
- M.-G. Hu, Y. Liu, D. D. Grimes, Y.-W. Lin, A. H. Gheorghe, R. Vexiau, N. Bouloufa-Maafa, O. Dulieu, T. Rosenband and K.-K. Ni, Science, 2019, 366, 1111–1115 CrossRef CAS.
- C. Makrides, J. Hazra, G. B. Pradhan, A. Petrov, B. K. Kendrick, T. González-Lezana, N. Balakrishnan and S. Kotochigova, Phys. Rev. A, 2015, 91, 012708 CrossRef.
- J. F. E. Croft, C. Makrides, M. Li, A. Petrov, B. K. Kendrick, N. Balakrishnan and S. Kotochigova, Nat. Commun., 2017, 8, 15897 CrossRef CAS.
- J. F. E. Croft, N. Balakrishnan and B. K. Kendrick, Phys. Rev. A, 2017, 96, 062707 CrossRef.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- B. Kendrick and R. T. Pack, J. Chem. Phys., 1996, 104, 7475–7501 CrossRef CAS.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45–57 Search PubMed.
- B. K. Kendrick, J. Chem. Phys., 2018, 148, 044116 CrossRef.
- B. K. Kendrick, Chem. Phys., 2018, 515, 387–399 CrossRef CAS.
- B. K. Kendrick, J. Phys. Chem. A, 2019, 123, 9919–9933 CrossRef CAS.
- H. Li, M. Li, C. Makrides, A. Petrov and S. Kotochigova, Atoms, 2019, 7, 36 CrossRef CAS.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Nat. Commun., 2015, 6, 7918 CrossRef CAS.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Phys. Rev. Lett., 2015, 115, 153201 CrossRef CAS.
- J. Hazra, B. K. Kendrick and N. Balakrishnan, J. Phys. Chem. A, 2015, 119, 12291–12303 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2015, a package of ab initio programs, 2015, see https://www.molpro.net Search PubMed.
- P. Fuentealba, L. Szentpály, H. Stoll, F. Fraschio and H. Preuss, THEOCHEM, 1983, 93, 213–219 Search PubMed.
- W. Müller, J. Flesch and W. Meyer, J. Chem. Phys., 1984, 80, 3297–3310 CrossRef.
- J. Mitroy, M. S. Safronova and C. W. Clark, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 202001 CrossRef.
- P. S. Żuchowski and J. M. Hutson, Phys. Rev. A, 2010, 81, 060703 CrossRef.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- B. Barakat, R. Bacis, F. Carrot, S. Churassy, P. Crozet, F. Martin and J. Verges, Chem. Phys., 1986, 102, 215–227 CrossRef CAS.
- C. Linton, F. Martin, A. Ross, I. Russier, P. Crozet, A. Yiannopoulou, L. Li and A. Lyyra, J. Mol. Spectrosc., 1999, 196, 20–28 CrossRef CAS.
- M. Steinke, H. Knöckel and E. Tiemann, Phys. Rev. A, 2012, 85, 042720 CrossRef.
- R. Abrol and A. Kuppermann, J. Chem. Phys., 2002, 116, 1035–1062 CrossRef CAS.
- B. K. Kendrick, J. Chem. Phys., 2018, 148, 044116 CrossRef.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections, World Scientific, 2004 Search PubMed.
- F. O. Ellison, J. Am. Chem. Soc., 1963, 85, 3540–3544 CrossRef CAS.
- T. Ho and H. Rabitz, J. Chem. Phys., 1996, 104, 2584–2597 CrossRef CAS.
- T.-S. Ho and H. Rabitz, J. Chem. Phys., 2000, 113, 3960–3968 CrossRef CAS.
- O. T. Unke and M. Meuwly, J. Chem. Inf. Model., 2017, 57, 1923–1931 CrossRef CAS.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300 CrossRef CAS.
- R. T. Pack and G. A. Parker, J. Chem. Phys., 1987, 87, 3888–3921 CrossRef CAS.
- B. K. Kendrick, R. T. Pack, R. B. Walker and E. F. Hayes, J. Chem. Phys., 1999, 110, 6673–6693 CrossRef CAS.
- G. A. Parker, R. B. Walker, B. K. Kendrick and R. T. Pack, J. Chem. Phys., 2002, 117, 6083–6102 CrossRef CAS.
- A. Teplukhin and D. Babikov, Chem. Phys. Lett., 2014, 614, 99–103 CrossRef CAS.
- B. Johnson, J. Comput. Phys., 1973, 13, 445–449 CrossRef.
- Z. Darakjian and E. F. Hayes, J. Chem. Phys., 1990, 93, 8793–8797 CrossRef CAS.
- J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1985, 82, 1400–1409 CrossRef CAS.
- R. Lehoucq, D. Sorensen and C. Yang, ARPACK Users' Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, Society for Industrial and Applied Mathematics, 1998 Search PubMed.
- H. Feshbach, Ann. Phys., 1958, 5, 357–390 CAS.
- E. P. Wigner, Phys. Rev., 1948, 73, 1002–1009 CrossRef CAS.
- N. Balakrishnan, V. Kharchenko, R. Forrey and A. Dalgarno, Chem. Phys. Lett., 1997, 280, 5–9 CrossRef CAS.
- C. A. Mead, J. Chem. Phys., 1980, 72, 3839–3840 CrossRef CAS.
- B. K. Kendrick, J. Phys. Chem. A, 2003, 107, 6739–6756 CrossRef CAS.
- J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, Science, 2005, 309, 1227–1230 CrossRef CAS.
- B. Zygelman, J. Phys. B: At., Mol. Opt. Phys., 2016, 50, 025102 CrossRef.
- I. G. Ryabinkin, L. Joubert-Doriol and A. F. Izmaylov, Acc. Chem. Res., 2017, 50, 1785–1793 CrossRef CAS.
- C. Xie, B. K. Kendrick, D. R. Yarkony and H. Guo, J. Chem. Theory Comput., 2017, 13, 1902–1910 CrossRef CAS.
- D. Yuan, Y. Guan, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, T. Xie, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Science, 2018, 362, 1289–1293 CrossRef CAS.
- Y. Xie, H. Zhao, Y. Wang, Y. Huang, T. Wang, X. Xu, C. Xiao, Z. Sun, D. H. Zhang and X. Yang, Science, 2020, 368, 767–771 CrossRef CAS.
- N. Levinson, Phys. Rev., 1953, 89, 755–757 CrossRef.
- J. F. E. Croft, J. Hazra, N. Balakrishnan and B. K. Kendrick, J. Chem. Phys., 2017, 147, 074302 CrossRef CAS.
- R. Blümel and U. Smilansky, Phys. Rev. Lett., 1988, 60, 477–480 CrossRef.
- F. J. Dyson, J. Math. Phys., 1962, 3, 140–156 CrossRef CAS.
- P. Honvault and J.-M. Launay, Chem. Phys. Lett., 2000, 329, 233–238 CrossRef CAS.
- H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1–68 Search PubMed.
- D. Yang, J. Huang, X. Hu, D. Xie and H. Guo, J. Chem. Phys., 2020, 152, 241103 CrossRef CAS.
| This journal is © the Owner Societies 2021 |