Open Access Article
Open Access ArticleExcitation and ionisation cross-sections in condensed-phase biomaterials by electrons down to very low energy: application to liquid water and genetic building blocks†
Pablo
de Vera
 *ab,
Isabel
Abril
*ab,
Isabel
Abril
 c and
Rafael
Garcia-Molina
c and
Rafael
Garcia-Molina
 a
a
aDepartamento de Física – Centro de Investigación en Óptica y Nanofísica, Universidad de Murcia, Murcia, Spain. E-mail: pablo.vera@um.es
bCurrently at European Centre for Theoretical Studies in Nuclear Physics and Related Areas (ECT*), Trento, Italy
cDepartament de Física Aplicada, Universitat d’Alacant, Alacant, Spain
First published on 10th February 2021
Abstract
Electronic excitations and ionisations produced by electron impact are key processes in the radiation-induced damage mechanisms in materials of biological relevance, underlying important medical and technological applications, including radiotherapy, radiation protection in manned space missions and nanodevice fabrication techniques. However, experimentally measuring all the necessary electronic interaction cross-sections for every relevant material is an arduous task, so it is necessary having predictive models, sufficiently accurate yet easily implementable. In this work we present a model, based on the dielectric formalism, to provide reliable ionisation and excitation cross-sections for electron-impact on complex biomolecular media, considering their condensed-phase nature. We account for the indistinguishability and exchange between the primary beam and excited electrons, for the molecular electronic structure effects in the electron binding, as well as for low-energy corrections to the first Born approximation. The resulting approach yields total ionisation cross-sections, energy distributions of secondary electrons, and total electronic excitation cross-sections for condensed-phase biomaterials, once the electronic excitation spectrum is known, either from experiments or from a predictive model. The results of this methodology are compared with the available experimental data in water and DNA/RNA molecular building blocks, showing a very good agreement and a great predictive power in a wide range of electron incident energies, from the large values characteristic of electron beams down to excitation threshold. The proposed model constitutes a very useful procedure for computing the electronic interaction cross-sections for arbitrary biological materials in a wide range of electron incident energies.
1 Introduction
Charged particles interacting with matter lose their energy mainly through electronic excitations and ionisations, which result in the ejection of secondary electrons and the ensuing generation of electron cascades,1 mostly having energies below 100 eV. Such electrons (even those with energies below ionisation threshold) are capable of inducing very harmful effects in organic and biological matter, either by means of electronic excitations leading to molecular fragmentation or by dissociative electron attachment.2,3 The characteristics of the electron cascade when reaching target sensitive molecules (e.g. DNA building blocks or polymeric lithographic resists) can be obtained through detailed Monte Carlo simulations,1,4–7 the reliability of whose predictions strongly depends on the accuracy of the cross-sections (i.e., interaction probabilities) with which they are fed for simulating the generation and propagation of these electrons through condensed matter. This knowledge is essential for the better understanding, through modelling, of numerous medical and technological applications, including radiation therapy for cancer8,9 or advanced nanofabrication techniques.10,11Plenty of experimental information is available on electron-impact ionisation cross-sections (total probabilities as well as energy spectra of ejected electrons) of relevant biomolecules (such as water or DNA nucleobases), however it is usually limited to the gas phase,12–17 without taking into account the condensed-phase nature of living organisms. Experimental data on electronic excitations are much scarcer and scattered16,18–21 and also limited just to molecules in the gas phase, with only a few exceptions.22 An alternative for gathering all relevant cross-sections resorts into theoretical calculations, where some very successful ab initio approaches are available for calculating both excitation and ionisation cross-sections.23,24 However, the required tools and background are usually rather complex and not accessible for a wide audience. There are also a number of very popular semiempirical models,25–27 which are easy to implement but, in return, remain generally limited to the ionisation process and/or they cannot provide the energy spectrum of the generated electrons, which is essential for following up their transport in the simulations.
A convenient alternative for studying ion-impact ionisation of condensed-phase organic and biological materials, based on the dielectric formalism,28,29 has the advantage that (i) it is relatively simple to implement, (ii) it provides both the total cross-sections and the energy and angular spectra of secondary electrons, and (iii) it only requires a few easily accessible parameters of the organic target (namely, their optical properties or just their atomic composition and density, together with their outer-shell ionisation thresholds). Thus, this procedure can be straightforwardly applied to any complex biological material, including liquid water, RNA/DNA and their building blocks, proteins30 or even subcellular compartments.31 The extension of this approach for electron projectiles requires accounting for a series of improvements. First, the indistinguishability and exchange between the primary and the struck electrons need to be appropriately considered both for electronic excitations and ionisations.32 Second, a series of low-energy modifications are necessary: (i) corrections32,33 to the perturbative first Born approximation (on which the dielectric formalism holds), and (ii) avoid counting ionisations attributed to low energy electrons that cannot ionise all the electronic levels of the target molecules.34
In this work, we extend the dielectric response model28,29 to electrons in a wide energy range, covering from the high energies typical of electron beams or delta-electrons down to the low energies characteristic of hot electrons. This extension introduces corrections to the first Born approximation to describe very low energy electrons (i.e., having a few tens of eV), and includes the indistinguishability and exchange, considering how electronic excitations and ionisations are differently affected by the target electronic structure.
The resulting methodology yields the total ionisation and excitation cross-sections, as well as the energy distribution of secondary electrons. Calculations for liquid water, all the DNA/RNA bases (adenine, thymine, guanine, cytosine and uracil) and tetrahydrofuran (THF, an important analogue molecule of the sugar component of the phosphate-deoxyribose backbone of DNA), in the condensed phase, are presented and compared to available experimental data, showing an excellent general agreement.
The model presented in this work provides a convenient and universal approach for reliably evaluating the main quantities involved in electron transport and effects within arbitrary organic and biological materials (accounting for their condensed-phase state) in a wide energy range. The methodology and data presented in this work will result very useful in the field of ionising radiation interaction with matter, either for medical or technological applications.
The work is organized as follows. In Section 2 we provide the theoretical background and introduce the necessary improvements, whose results are analysed and compared with available experimental data in Section 3. Finally, we present in Section 4 a summary and the conclusions of our work.
2 Theoretical framework
2.1 Electronic excitation and ionisation of biomaterials by swift charged particle impact
The doubly differential cross-section (DDCS – this and all other acronyms and abbreviations appearing in the manuscript are gathered in the ESI† for facilitating the reading –)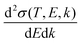 for the scattering of a charged particle, having kinetic energy T, with an atom or molecule gives the probability for the incident particle to lose some specific amount of energy E and of momentum ℏk as a result of the interaction. In the quantum theory of scattering, the DDCS can be related to the direct f(
for the scattering of a charged particle, having kinetic energy T, with an atom or molecule gives the probability for the incident particle to lose some specific amount of energy E and of momentum ℏk as a result of the interaction. In the quantum theory of scattering, the DDCS can be related to the direct f(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1,
1,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 2) and the exchange g(
2) and the exchange g(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1,
1,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 2) scattering amplitudes:35,36
2) scattering amplitudes:35,36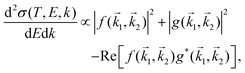 | (1) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 and ℏ
1 and ℏ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 2 are, respectively, the momentum of the scattered and excited particles in the final state;
2 are, respectively, the momentum of the scattered and excited particles in the final state; ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 −
1 − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 2. The last term in eqn (1) accounts for the interference between the direct and exchange scattering amplitudes.
2. The last term in eqn (1) accounts for the interference between the direct and exchange scattering amplitudes.
An incident ion and an excited electron are distinguishable particles, so the exchange and interference terms vanish in eqn (1). In such a case, the first Born approximation (FBA) relates the DDCS only to the direct scattering amplitude, 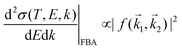 , and the dielectric formalism provides a compact expression for the DDCS for a charged particle scattered in a condensed-phase medium.1,37 This is valid when the energy loss is small in comparison with the energy of the primary particle, i.e., for incident ions or electrons much faster than the target electrons, and it is given by:
, and the dielectric formalism provides a compact expression for the DDCS for a charged particle scattered in a condensed-phase medium.1,37 This is valid when the energy loss is small in comparison with the energy of the primary particle, i.e., for incident ions or electrons much faster than the target electrons, and it is given by:
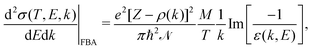 | (2) |
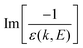 , represents the electronic excitation spectrum of the target material, with ε(k,E) = ε1(k,E) + iε2(k,E) being the complex dielectric function.
, represents the electronic excitation spectrum of the target material, with ε(k,E) = ε1(k,E) + iε2(k,E) being the complex dielectric function. ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the target atomic (or molecular) density, which relates the microscopic σ and the macroscopic cross-section Λ (or inverse mean free path, IMFP) as Λ = λ−1 =
is the target atomic (or molecular) density, which relates the microscopic σ and the macroscopic cross-section Λ (or inverse mean free path, IMFP) as Λ = λ−1 = ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) σ, with λ being the electronic inelastic mean free path.
σ, with λ being the electronic inelastic mean free path.
The ELF of the target material accounts for the excitation and ionisation spectrum of its outer- and inner-shell electrons:
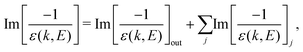 | (3) |
| Target | Liquid water | THF | Uracil | Adenine | Guanine | Cytosine | Thymine |
|---|---|---|---|---|---|---|---|
| Chemical formula | H2O | C4H8O | C4H4O2N2 | C5H5N5 | C5H5ON5 | C4H5ON3 | C5H6O2N2 |
| Atomic number Z | 10 | 40 | 58 | 70 | 78 | 58 | 66 |
| Atomic mass A | 18.0 | 72.11 | 112.09 | 135.13 | 151.13 | 110.10 | 126.11 |
| Density (g cm−3) | 1.00 | 0.8946 | 1.4047 | 1.3539 | 1.5839 | 1.3039 | 1.3647 |
| First binding energy B1 (eV) | 10.7948 | 9.7416 | 9.5049 | 8.4450 | 8.2450 | 8.9450 | 9.1450 |
| Last binding energy Bn (eV) | 32.3048 | 36.9716 | 37.9249 | 37.4850 | 39.2550 | 37.7050 | 37.8150 |
| Mean binding energy Bmean (eV) | 13.71 | 15.12 | 15.40 | 14.66 | 15.17 | 14.76 | 15.28 |
| Excitation threshold energy Eth (eV) | 7.0051 | 7.9452 | 3.6553 | 4.4754 | 4.3154 | 4.4654 | 4.5455 |
| Optical ELF | Exp.56 | Param. model39 | Exp.47 | Exp.57 | Exp.58 | Param. model39 | Exp.47 |
| Num. valence electrons Nval | 8 | 30 | 42 | 50 | 56 | 42 | 48 |
| Num. effective electrons Neff59 | 6 | 28 | 36 | 45 | 49 | 37 | 42 |
Fig. 1(a) illustrates schematically the electronic transitions in an insulating target (which is the case for biological matter). The outer-shell electrons of the material occupy the valence band, formed by localized states in the target molecules, while the conduction band, which hosts the mobile electrons, initially only contains the primary electron, moving with kinetic energy T. Between both bands, there are empty discrete states, to which electrons from the valence band can be promoted by excitation after receiving an energy transfer Ei. The processes of electronic excitation and ionisation are all contained in the ELF of the biological target, and they cannot be easily disentangled, except for some specific cases such as water.33,48,60–62 As an illustration of a typical biomaterial, Fig. 1(b) depicts the experimental optical ELF of adenine from 0 to 50 eV (circles),57 together with the prediction of the above mentioned parametric predictive model for biomaterials (dashed line)39 and the fitting to the experimental data by means of the MELF-GOS method (solid line).38 Electronic excitations start to appear for energy transfers E greater or equal than the first excitation threshold Eth, while ionisation processes will occur for larger energy transfers. Although the parametric model39 does not account for the excitation threshold, we applied a cutoff to the single-Drude function below the corresponding value (see Table 1).
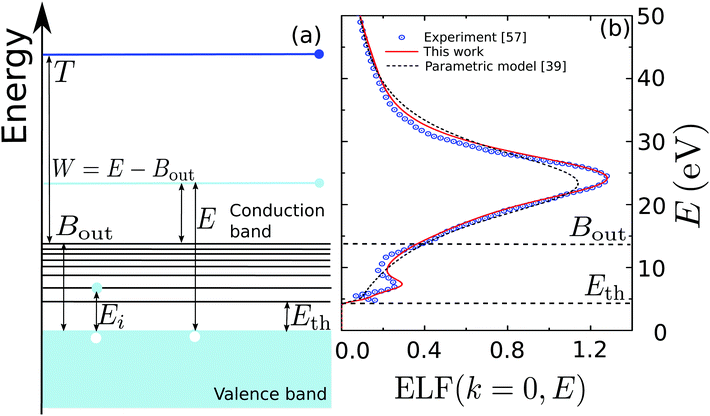 | ||
| Fig. 1 (a) Diagram of the possible electronic transitions in an insulator. Between the valence and the conduction bands there are localised states that can be reached when electrons in the valence band gain an energy Ei; see main text for details. (b) Optical energy loss-function of adenine as a function of the energy transfer E. Circles are experimental data for solid adenine,57 the solid line represents the MELF-GOS calculation,38 whereas the dashed line corresponds to the predictive parametric model39 (with a threshold energy Eth). | ||
When considering ion-impact ionisation28,29 we adopted some simplifying assumptions in order to disentangle the excitation and ionisation processes for arbitrary biomaterials. Since electronic excitations are mostly restricted to low energies, while most of the larger energy transfers produce ionisation, we defined a mean binding energy Bout for the outer shell electrons, obtained as a direct average of the target binding energies, which can be found either from experiment or from ab initio calculations. In this approach, it was assumed that any energy transfer E > Bout produces a secondary electron with kinetic energy W = E − Bout measured from the bottom of the conduction band (see Fig. 1(a)). Similarly, secondary electrons with energy W = E – Bj can be produced by ionisation of the inner shells, where Bj are the corresponding binding energies. In contrast, any energy transfer E < Bout is considered to be an electronic excitation, to some discrete and localised energy level through an energy transfer Ei, without electron ejection to the conduction band. This approximation for ion impact produced very good results in comparison with experimental data.28
The DDCS, eqn (2), can be used to obtain the angular distribution of secondary electrons by relating the momentum transfer to the ejection angle.29 It can also be integrated in momentum transfer in order to yield the energy distribution of secondary electrons, as well as in energy to obtain the total probabilities for ionisation and excitation.28 While the integration limits are straightforwardly deduced for the case of ion impact,28,29 a more detailed analysis of the possible electronic transitions is needed in the case of electron impact due to indistinguishability,32 for which the sketch of Fig. 1(a) is useful. The singly differential ionisation cross-section (SDCS) for electron impact is obtained as:
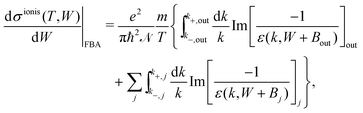 | (4) |
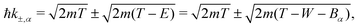 | (5) |
Further integration in energy of eqn (4) gives the total ionisation cross-section (TICS):
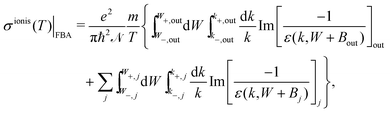 | (6) |
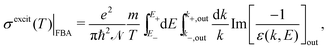 | (7) |
Let us now examine the integration limits in the energy transfer appearing in eqn (6) and (7). Within the current approximations, electronic excitations can be produced for energy transfers E between the excitation threshold Eth and the mean binding energy of the outer shell electrons Bout, as any larger transfer will lead to ionisation. Note that, when an incident electron has an energy T < Bout, the maximum energy that it can lose is T. Since the primary electron moves in the conduction band and the target electron is promoted to a lower discrete energy level, indistinguishability does not impose any limit to the amount of energy that the primary electron can lose for excitations in the range:
| E− = Eth, E+ = min[Bout,T]. | (8) |
For ionisation, the limits become:
| E− = Bα → W−,α = 0 | (9) |
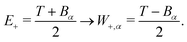 | (10) |
2.2 Mean binding energy for outer-shell electrons
The mean binding energy for outer shell electrons can be easily estimated from the ionisation energies for biomolecules reported in the literature, most frequently coming from quantum chemistry calculations.16,49,50 In previous works for ion impact,28,30Bout was calculated as a direct average of the binding energies Bi of the target outer shell electrons,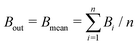 , with B1 and Bn being, respectively, the first and last outer-shell binding energies (see Table 1). However, it is known that the outermost the electronic shell is, the more it contributes to the ionisation cross-section,48,61 so this fact should be taken into account in some physically motivated manner (especially for low energy electron impact, where shell effects are deemed to be more important34). One of the simpler models for charged-particle impact-ionisation, namely the Rutherford cross-section,25 reflects this fact in the sense that the electron binding energy for the i-shell appears squared in the denominator. Thus, we will propose a mean binding energy Bmean for each material by weighting with Bi−2 the relative contribution of each outer-shell ionisation threshold Bi:
, with B1 and Bn being, respectively, the first and last outer-shell binding energies (see Table 1). However, it is known that the outermost the electronic shell is, the more it contributes to the ionisation cross-section,48,61 so this fact should be taken into account in some physically motivated manner (especially for low energy electron impact, where shell effects are deemed to be more important34). One of the simpler models for charged-particle impact-ionisation, namely the Rutherford cross-section,25 reflects this fact in the sense that the electron binding energy for the i-shell appears squared in the denominator. Thus, we will propose a mean binding energy Bmean for each material by weighting with Bi−2 the relative contribution of each outer-shell ionisation threshold Bi: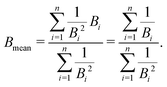 | (11) |
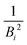 in the numerator are weights for each individual contribution to Bmean, while the denominator
in the numerator are weights for each individual contribution to Bmean, while the denominator 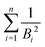 ensures normalisation (see Table 1). When using this criterion for estimating Bmean, the calculated ionisation SDCS for liquid water presents its maximum value at secondary electron kinetic energies W ∼ 10 eV, closer to the reference calculations by Emfietzoglou.63 Otherwise, the simple average of Bmean produces the maximum of the SDCS at energies W ≤ 5 eV, which is a behaviour closer to water vapour than to the liquid phase.60
ensures normalisation (see Table 1). When using this criterion for estimating Bmean, the calculated ionisation SDCS for liquid water presents its maximum value at secondary electron kinetic energies W ∼ 10 eV, closer to the reference calculations by Emfietzoglou.63 Otherwise, the simple average of Bmean produces the maximum of the SDCS at energies W ≤ 5 eV, which is a behaviour closer to water vapour than to the liquid phase.60
As noted by Tan et al.,34 a constant Bmean (independent of the projectile energy T) is only valid for electrons with large kinetic energies. When the primary electron has an energy T ≤ Bn, it is not capable of ionising all the possible electronic levels, and thus we define a new energy-dependent mean binding energy Bout(T):
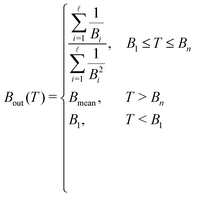 | (12) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the ionisation threshold immediately below T. As it will be discussed later, such a correction will notably improve the calculated cross-sections for electrons with energies T < Bn. It should be noted that electrons with energies below the first ionisation threshold B1 will, in fact, not be able to ionise the medium, and will be only capable of producing electronic excitations with the energy transfer limits given by eqn (8).
is the ionisation threshold immediately below T. As it will be discussed later, such a correction will notably improve the calculated cross-sections for electrons with energies T < Bn. It should be noted that electrons with energies below the first ionisation threshold B1 will, in fact, not be able to ionise the medium, and will be only capable of producing electronic excitations with the energy transfer limits given by eqn (8).
Noteworthy, the behaviour of Bout(T) is rather similar for the different biomolecules, and can be fitted, for convenience of the numerical implementation, with a logistic function of the form:
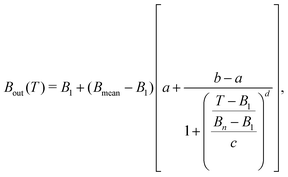 | (13) |
| Material | a | b·104 | c | d |
|---|---|---|---|---|
| Liquid water | 1.31752 | −6.62797 | 0.42317 | 1.31513 |
| THF | 1.103 | −1.04493 | 0.22376 | 1.51679 |
| Uracil | 1.2302 | 1.32923 | 0.32648 | 1.30721 |
| Adenine | 1.33102 | 0.826314 | 0.39745 | 1.19642 |
| Guanine | 1.24236 | 0.336896 | 0.32618 | 1.26275 |
| Cytosine | 1.2662 | 3.69257 | 0.36651 | 1.31606 |
| Thymine | 1.16425 | −0.170308 | 0.2776 | 1.40323 |
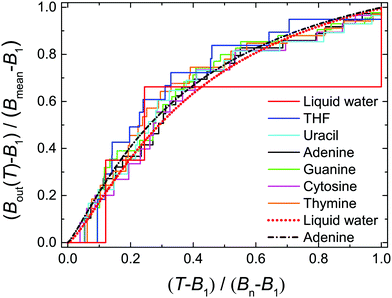 | ||
| Fig. 2 Normalised values of Bout(T) as a function of the normalised electron incident energy T for the biological materials studied in this work. Step functions correspond to the values provided by eqn (12), using quantum chemistry calculations for the binding energies,16,49,50 while dotted and dot-dashed lines correspond to fittings by means of eqn (13) for liquid water and adenine. | ||
2.3 Very low energy electrons: exchange effects and corrections to the Born approximation
When the electrons have a relatively low energy, the FBA for the DDCS, eqn (2), fails due to: (i) the exchange effects in the electron–electron interaction, arising from the indistinguishability of the scattered and the ejected electrons, which cannot be neglected since both have now comparable energies, and (ii) the energy loss is now comparable to the incident electron energy, so the scattering cannot be treated within a first order approximation. Therefore, the exchange terms in eqn (1) cannot be disregarded anymore and the DDCS has to be written as: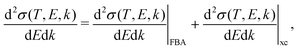 | (14) |
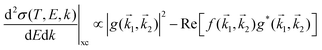 represents the exchange term. Several methods have been developed to account for this exchange term.36,64 Ochkur65 developed a modification of the first-order Born–Oppenheimer perturbation treatment66 by extrapolating the exchange effect for incident energies lower than the original approximation. The underlying argument was that the Born–Oppenheimer expression for the exchange scattering amplitude (eqn 3.24 in ref. 36) is correct at high energies, asserting that it is better to retain just the leading term in an expansion of g(
represents the exchange term. Several methods have been developed to account for this exchange term.36,64 Ochkur65 developed a modification of the first-order Born–Oppenheimer perturbation treatment66 by extrapolating the exchange effect for incident energies lower than the original approximation. The underlying argument was that the Born–Oppenheimer expression for the exchange scattering amplitude (eqn 3.24 in ref. 36) is correct at high energies, asserting that it is better to retain just the leading term in an expansion of g(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1,
1,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 2) in powers of 1/k0 (ℏk0 being the momentum of the primary electron before the collision) rather than the full Born–Oppenheimer expression. The Born–Ochkur (BO) approximation gives a convenient expression for the exchange scattering amplitude that retains the FBA component for the direct-scattering amplitude. The BO exchange amplitudes for the excitation36,65,67 and ionisation35,36,65 processes with momentum transfer
2) in powers of 1/k0 (ℏk0 being the momentum of the primary electron before the collision) rather than the full Born–Oppenheimer expression. The Born–Ochkur (BO) approximation gives a convenient expression for the exchange scattering amplitude that retains the FBA component for the direct-scattering amplitude. The BO exchange amplitudes for the excitation36,65,67 and ionisation35,36,65 processes with momentum transfer ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 0 −
0 − ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 are:
1 are: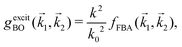 | (15) |
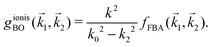 | (16) |
From eqn (2) and (14)–(16), the following expressions can be written for the exchange contribution to the excitation and ionisation DDCS:
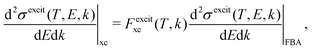 | (17) |
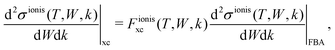 | (18) |
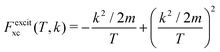 and
and 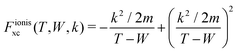 are the BO exchange correction factors to the DDCS|FBA given by eqn (2). It should be noted that the BO exchange term for ionisation, which is based on a quantum mechanical treatment of the problem, reproduces the classical Mott exchange for binary collisions25 at high electron energies. A similar expression for ionisation was used by ref. 68.
are the BO exchange correction factors to the DDCS|FBA given by eqn (2). It should be noted that the BO exchange term for ionisation, which is based on a quantum mechanical treatment of the problem, reproduces the classical Mott exchange for binary collisions25 at high electron energies. A similar expression for ionisation was used by ref. 68.
In the case of slow electrons (T ≤ 100 eV), the energy loss is no longer negligible with respect to the primary electron energy and the FBA becomes inaccurate. There exist several alternatives to correct the FBA at low energies, ranging from heuristic or phenomenological but easily implementable approaches,33 to more sophisticated theoretical models.64 Since in this work we aim at applying the method to arbitrary biological materials, we prefer to implement a simple scheme, which does not need the determination of additional parameters for the target material. This approach consists on accounting for a classical Coulomb-field correction, which considers the potential energy gained by the incident electron in the field of the target molecule. In practice, this means an increase of the kinetic energy T of the incident electron, which is replaced in eqn (2) in the following manner:33
| T → T′ ≃ T + 2Ei (for excitations), | (19) |
| T → T′′ ≃ T + 2Bα (for ionisations), | (20) |
The relevant TECS, ionisation SDCS and TICS quantities can now be expressed including low-energy corrections to the direct term plus the exchange term. The resulting TECS will be:
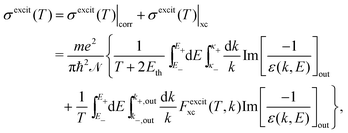 | (21) |
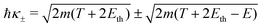 .
.
For ionisation, the SDCS is written as:
 | (22) |
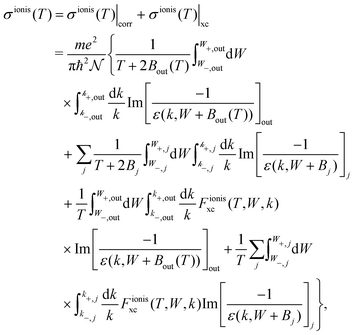 | (23) |
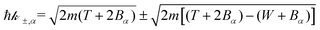 , with Bα = Bout(T) for the outer shells, eqn (12), and Bα = Bj for the inner shells j.
, with Bα = Bout(T) for the outer shells, eqn (12), and Bα = Bj for the inner shells j.
3 Results and discussion
In what follows we apply the present methodology to calculate ionisation singly differential (SDCS), total ionisation (TICS) and total excitation (TECS) cross-sections for the impact of electrons, in a wide energy range, on the relevant condensed-phase biological materials, namely liquid water and the DNA/RNA molecular components (THF, cytosine, adenine, guanine, uracil, and thymine), whose properties are summarised in Table 1. Our results will be compared to available experimental data for these targets, as well as analysed in the light of various scaling rules with the number of valence electrons. It is important to bear in mind for the discussion that all present calculations are performed for the condensed-phase materials, while most experimental data (excluding a few exceptions) are available for gas-phase targets only. Thus, some phase differences may be expected between experiments and calculations. Frequently, these will manifest in the form of lower cross sections for the condensed-phase with respect to the gas-phase materials, as a consequence of the dielectric screening due to the electron density in the condensed phase. For the few cases for which experimental data exist for the condensed phase, this will be explicitly mentioned in the corresponding discussion.3.1 Energy distributions of secondary electrons and total electronic cross sections
We start by considering liquid water, the most abundant material in living beings, whose ELF is experimentally available for several values of the momentum transfer56,70 and for which the MELF-GOS method produces excellent results in comparison with experiments for arbitrary momentum transfers.44,45 Let us begin by analysing how the different improvements of our model affect the calculated energy distribution of secondary electrons (i.e., the SDCS), which is a very relevant quantity affecting the density of inelastic events of the radiation track structure in living tissue, especially at the nanometre scale, and that will also determine the mechanisms by which secondary electrons damage organic molecules solvated in water.9 In order to compare with the available experimental data for water vapour,12 it is important to have in mind the differences in the energy spectra of the liquid and gaseous phases, which results in a shift of the position of the maximum in the energy spectrum from ∼3 eV (vapour) to ∼10 eV (liquid), according to detailed calculations.60,63Fig. 3 compares the present calculated SDCS (lines) for liquid water with the experimental data (symbols) for water vapour,12 for T = 100 and 1000 eV primary electrons. Solid lines depict the results we obtain when using Bmean = 13.71 eV (eqn (11)), while dotted lines employ the direct average of outer-shell binding energies introduced in previous works, Bmean = 18.13 eV.28,30 While both calculations lead to SDCS in a fair agreement with experiments at high energies, it is evident that the weighted Bmean gives the maximum of the SDCS at ∼10 eV, in agreement with the predictions for the liquid phase. In order to also assess the effect of the exchange (xc) and low-energy corrections (corr) introduced in this work, dashed lines in Fig. 3 depict the raw results from the FBA (eqn (4)). On the one hand, the exchange correction is needed to yield SDCS that correctly reproduce the primary peak observed at W ≃ T, which is due to the indistinguishability between the primary and the secondary electrons. On the other hand, the low-energy correction also diminishes the absolute values of the SDCS for the lower energies T, approaching calculations to experimental data (this effect is more clearly seen for T = 100 eV electrons).
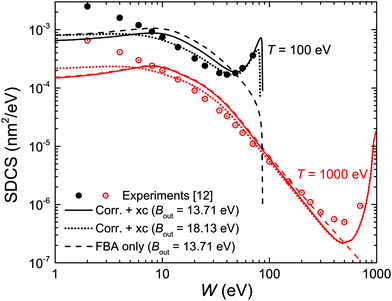 | ||
| Fig. 3 Ionisation singly differential cross-sections (SDCS) for 100 and 1000 eV electron impact in water. Symbols represent experimental data for water vapour12 and lines are our calculations for liquid water. Solid lines represent full calculations (eqn (22)) using the value of Bmean from eqn (12), while dotted lines employ a direct average for Bmean; dashed lines depict the raw FBA calculations (eqn (4)). | ||
Further comparison of the calculated energy distributions of secondary electrons ejected from water for different primary energies T is provided in Fig. 4(a), where our full calculations for the liquid (lines) are compared with all the available experimental data (symbols) for the gas phase.12 As can be seen, except for the differences expected between the gas and condensed phases (as explained above), there is a very good general agreement of the calculated SDCS with the experimental data, both in shape and absolute values. As the primary electron energy T grows, the height of the SDCS progressively drops, while the high-W tail extends to larger values, as a consequence of the larger primary electron energy and thus to the possibility to eject secondary electrons (or scattered primary electrons) of larger kinetic energies. In any case, the calculated SDCS are lower than the experimental ones for very low electron energies, W < 10 eV, which might be due to phase effects or to the uncertainty of the measured SDCS at these very low energies.
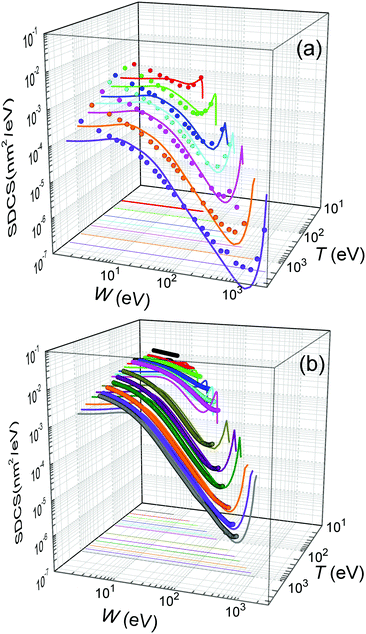 | ||
| Fig. 4 Energy distributions of the electrons generated by the impact of a primary electron (a) with energy T = 50, 100, 200, 300, 500, 1000 and 2000 eV in water, and (b) with energy T = 20, 30, 40, 60, 80, 100, 200, 400, 600, 800 and 1000 eV in THF. Solid lines represent our calculations for the condensed phases (eqn (22)), while symbols correspond to experimental data for water vapour12 and THF gas.71,72 | ||
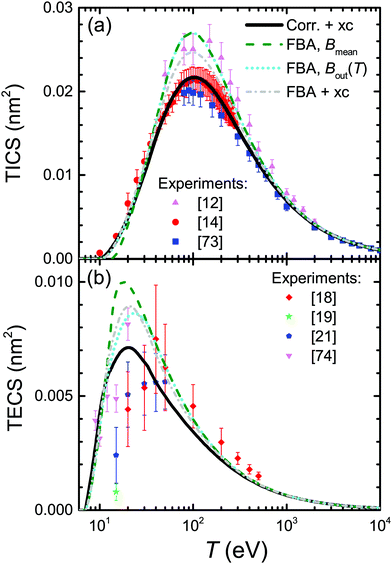
Plenty of experimental data is available for the total ionisation and excitation cross-sections of water, TICS and TECS, respectively, which allows further assessing the methodology and the different improvements accounted for in this work, as well as to evaluate the relative importance of the electronic ionisation and excitation processes for this relevant material. Fig. 5 shows the calculated and experimental TICS (a) and TECS (b) in water as lines and symbols, respectively. A wealth of experimental data is available for the electron-impact ionisation of water vapour, with a representative selection12,14,73 shown in the figure. The dashed line corresponds to the raw FBA calculation for liquid water, where no improvements are applied (eqn (6)), while the dotted line includes the energy-dependent Bout(T) defined by eqn (12). Even though both calculations yield results compatible with the experiments for large energies and even around the maximum, the use of Bout(T) clearly improves the results at energies ≤20 eV. While a constant mean binding energy makes the TICS to vanish for energies closer to Bmean = 13.71 eV, the energy-dependent binding energy accounts for low energy electrons being capable to ionise only a fraction of the outer shells, thus producing a progressive decrease of the TICS to zero as the electron energy approaches the first binding energy B1 = 10.79 eV.
Dash-dotted and solid lines in Fig. 5(a) account, respectively, for exchange and for exchange plus low-energy corrections. These improvements have the effect of lowering the TICS, especially around its maximum at T ∼ 100 eV. When both corrections are accounted for, the calculated TICS for liquid water drops towards the lower limit given by the scattered experimental data for the vapour around the maximum, remarkably coinciding with the most recent experimental data.14 This result is to some extent expected, as TICS for liquid water should be lower than for the gas phase, as a consequence of the dielectric screening effect provided by the electron density in the condensed phase.
The results for excitation of water, appearing in Fig. 5(b), require further explanations regarding the available experimental data (again for the gas phase). Measurements of electronic excitation cross-sections are usually restricted to some particular channels.18,19,21,74 However, data for many more transitions are provided in ref. 20, which is the most complete information currently available to the best of our knowledge. Since that work contains all the channels reported by the aforementioned authors, it is possible to use the (more complete) latter data to scale the former partial values as if all these channels were comprised, as our calculated TECS include all possible channels. Scaling factors have been estimated from Thorn's experiments20 as the ratio of the data for all 25 measured channels to the data for the specific channels at each particular electron energy, see ESI† for further details. This scaling was done previously32 accounting only for 6 channels (3B1, 1B1, 3A2, 1A2, 3A1, and 1A1) and not the 25 reported by ref. 20, and hence this is the reason for the difference between the data reported there32 with respect to the present work.
The meaning of the lines in Fig. 5(b) is the same as in Fig. 5(a). The raw FBA calculations for liquid water using a constant Bout (dashed line) already give a reasonable estimate for the TECS of water vapour in comparison with the scaled experimental data. However, introduction of Bout(T) (dotted line) improves the calculated TECS, even more when both exchange and low-energy corrections are also included (full line). Remarkably, the full calculation agrees rather well with the compilation of the (scaled) experimental data, having into account the dispersion of the different datasets and the considerable error bars. Thus, we deem that our calculation gives a reasonable estimate for the total excitation cross-section in water by electron impact. In any case, it is clear that electronic excitations only dominate the inelastic cross-section for energies <25 eV, with ionisation being the dominant process for larger electron energies.
The developed methodology allows us to obtain ionisation and excitation cross-sections for any condensed-phase biological material for which the atomic composition and density are known, irrespectively of whether its optical ELF has been experimentally or theoretically determined or not. For most of the materials studied in this work the experimental optical ELF is available (see Table 1), although there are no measurements for the two relevant DNA molecular components THF and cytosine, whose ELF has been obtained by the parametric predictive model.39
For the case of THF, our calculated ionisation SDCS by electron impact in the condensed phase are compared to available measurements for the gas phase71,72 in Fig. 4(b). As in the case of liquid water, the agreement between calculations and experimental data is rather good for the whole energy range of the emitted electrons, except for the differences expected between the condensed and gas phases, which also include, in this case, an underestimation of the SDCS for energies W ≤ 100 eV. As for the total cross-sections, full calculations (solid lines) are presented in Fig. 6(a) along with the available experimental data (symbols) and semiempirical binary-encounter Bethe (BEB) calculations27 (dash-dotted line). For the TICS, experiments are available only for the gas phase.14,16 Our calculations for condensed-phase THF agree well with most of the experiments at large energies and, around the maximum, they are very close to the data by ref. 14, the lowest among all experimental results. The differences with respect to the BEB calculations and other experiments can in principle be attributed to phase effects. As for the TECS, full condensed-phase calculations (solid line) are compared to the experimental data for the gas phase,16 as well as the recommended gas-phase data by ref. 75. Our calculations are in rather good agreement with ref. 16 and 75. Although we notably underestimate the data compiled in ref. 16 below 30 eV, it should be noted that the latter also includes, apart from electronic excitations, vibrational and rotational excitations, which we did not consider in our treatment. Comparison of calculations with a larger compilation of experimental data is shown in the ESI.†
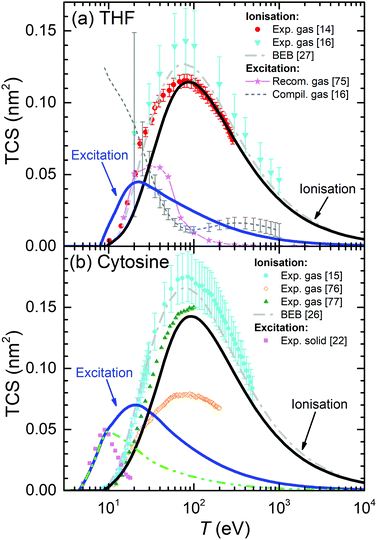 | ||
| Fig. 6 Total electronic cross-section (TCS) for electrons in (a) THF and (b) cytosine, as a function of the electron incident energy T. Solid lines correspond to our full condensed-phase calculations for TICS and TECS. Other lines and symbols represent experimental data: for THF, gas-phase TICS14,16 and TECS;16,75 for cytosine, gas-phase TICS15,76,77 and solid phase TECS.22 BEB calculations for THF27 and cytosine26 are depicted by dash-dotted lines. The dash-dot-dotted line in panel (b) depict results restricting the excitation process up to 9 eV for cytosine (see main text for details). | ||
Present results for the TICS and TECS for condensed-phase cytosine are presented in Fig. 6(b). The former are in fair agreement with the gas-phase experimental data from ref. 77, although they are lower than the gas-phase data from ref. 15 and much larger than the gas-phase results from ref. 76. Having into account the dispersion in the experimental data, the relatively good agreement between the data from ref. 15 and 77, as well as with the BEB calculations from ref. 26, makes these values plausible for the gas phase. Our calculations for solid cytosine are rather close to these data, although slightly below, most likely due to phase effects. As for the calculated TECS for the condensed phase, they correspond very well with the data for the solid form of cytosine22 up to 10–12 eV. A possible reason for the discrepancies for the larger energies is discussed below, in the light of the comparisons for other DNA bases. Comparison of calculations with a larger compilation of experimental data is shown in the ESI.†
It should be noted that the parametric model for predicting the optical ELF of these biomaterials39 does not give any information on the energy threshold for electronic excitations, Eth. For THF and cytosine, these values have been obtained from other sources (see Table 1). The sensitivity of the TECS on the choice of Eth for these materials is analysed on the ESI.†
The above results for THF and cytosine show the reliability of the methodology, even when the optical ELF of the material is not experimentally or theoretically available. However, in principle, results are expected to be more accurate when this information is at hand, as it is the case for the other DNA/RNA bases (adenine, guanine, thymine, and uracil), whose calculated condensed-phase TICS and TECS are shown by solid lines in Fig. 7. For adenine (panel (a)), experimental TICS for the gas phase15,78,79 and TECS for the solid phase22 are available (symbols). The calculated TICS is just slightly below the experiments from ref. 15 and 79 and the BEB calculations from ref. 26 (which agree well among themselves), and rather lower than the results from ref. 78. Such slight differences are, again, attributed to phase effects. Regarding the TECS, condensed-phase calculations give results in the same order of magnitude as the experiments in the solid,22 although with differences in shape and intensity that will be discussed in more details latter. Panels (b), (c) and (d) show the results for guanine, uracil and thymine, respectively. As for adenine, experimental TICS (in the gas phase) from ref. 15 and 79 and the BEB calculations from ref. 26 agree among themselves, with our results being slightly below, which we attribute to phase effects. In general, the experimental results from the Uzhgorod's group76,78,80,81 are rather different from data by other experimentalists although, for the particular cases of uracil80 and thymine,81 they give the maximum of the TICS at similar energies and close intensities as our calculations (these results being the only available for uracil). TECS are only experimentally available for solid thymine,22 which presents its onset at a similar energy as our calculations. Even though the slope of the experiments is slightly lower than in our calculations, the agreement is still fair.
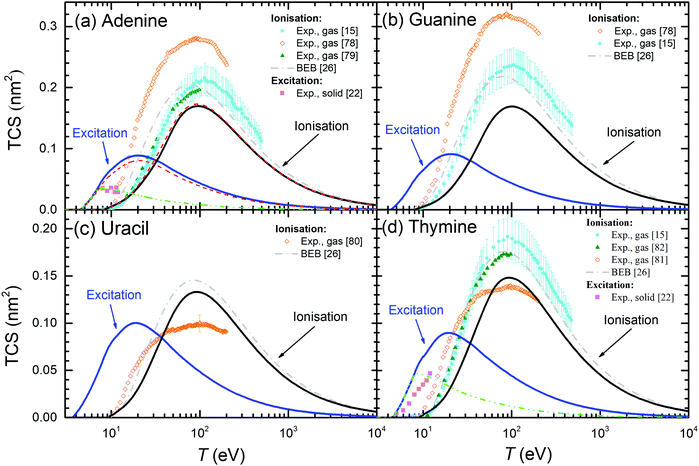 | ||
| Fig. 7 Total electronic cross-sections (TCS) for electrons in the DNA/RNA bases (a) adenine, (b) guanine, (c) uracil and (d) thymine, as a function of the incident energy T for excitation and ionisation processes. Solid lines are present full calculations for the condensed phases. Symbols correspond to experimental data: for electron ionisation in adenine (gas);15,78,79 in guanine (gas);15,78 in uracil (gas);80 in thymine (gas).15,81,82 For excitation processes: in solid adenine and thymine.22 BEB calculations (dash-dotted lines) are from ref. 26. Further calculations using the present model are presented under different assumptions: long-dashed lines (for adenine) show calculations using the optical ELF from the parametric model39 (with threshold Eth), while short-dashed lines depict results integrating eqn (21) up to 7.5 eV for adenine and up to 8 eV for thymine. | ||
In order to further benchmark the performance of the predictive model for the optical ELF,39 dashed lines in Fig. 7(a) depict the calculated TICS and TECS for electrons in adenine when using this parametric ELF, instead of the one experimentally measured. As can be seen, this option yields results which are very close to the calculations employing the experimental optical ELF, what gives confidence in the use of the model for predicting electron-impact cross-sections in arbitrary biomaterials for which information is not available, including complex biotargets such as DNA, proteins,28 or even cell compartments.31
One more clarification can be done regarding the comparison between the calculated and experimental TECS for THF (Fig. 6(a)), cytosine (Fig. 6(b)), adenine (Fig. 7(a)) and thymine (Fig. 7(d)). For these materials, measurements are available for the condensed phases from electron energy loss spectroscopy.22 These data are very relevant, since they are among the few available for the electron cross-sections determination in solid biomaterials. However, it has to be taken into account that the energy transfer range analysed in these experiments was limited to relatively low values. The experimental electron energy-loss spectrum (EELS) for THF was analysed up to 11.5 eV, for cytosine up to ∼9 eV, for adenine up to ∼7 eV, and for thymine up to ∼8.5 eV. Hence, there is a possibility that not all the electronic excitation channels are probed in the measured TECS, what might justify some discrepancies with our calculations. To check this possibility, we performed further calculations for these materials, artificially establishing an upper limit in the energy transfer given by E+ = min[Bout, T, Emax] (instead of eqn (8)), where Emax are the maximum energies analysed for electronic excitations in the experimental electron energy loss spectra. The results are shown in Fig. 6(a), (b) and 7(a), (d) by dash-dot-dotted lines. It can be seen that, especially for the cases of cytosine and adenine, these calculations resemble much more the experimental data: for cytosine, they give the maximum of the TECS at the same energy and with the same height as the experiments, although with a more progressive decrease; for adenine, the calculations with the limited energy loss range agree almost perfectly with the experimental data; for thymine, the agreement is less remarkable, with the position of the maximum shifted to slightly lower energies in the calculations, although with the maximum value similar to experiments. These findings indicate that our methodology for calculating the TECS for electron impact in biomaterials presents a very reasonable reliability, giving fair results for most of the targets for which there are measurements, either for the gas or the condensed phases.
3.2 Scaling rules for the total cross sections
Now that we count on with a collection of calculated excitation and ionisation cross-sections for electron impact in a wide variety of relevant biomaterials, we can further analyse the obtained results by testing the scaling rules for the ion-impact ionisation cross-sections of biomolecules,83,84 proposing that the TICS were proportional to the number of valence electrons per molecule. Such rules, which are closely related to the Bragg's additivity rule,85 have been shown useful for analysing and compiling electron and ion cross-sections for biomolecules.16,86 However, recently it has been pointed out that the number of valence electrons may not be the proper quantity for scaling the TICS,59 which instead should be better scaled as a function of the “effective” number of molecular electrons. Effective electrons were empirically defined in ref. 59 as the number of most weakly-bound electrons (i.e., with energy above some arbitrary threshold), thus being the easiest to be ejected. In the following, we will analyse both (the older and the new) scaling rules in the light of our calculated cross-sections for electron impact, not only for ionisation, but also for electronic excitation.Fig. 8(a) and (b) depict, respectively, the calculated TICS and TECS for the different biomaterials as a function of the number of valence electrons Nval (see Table 1) for several electron energies. As can be seen, neither TICS nor TECS scale well with the number of valence electrons Nval. The TECS present a rather more erratic behaviour, and somewhat saturate for Nval ≥ 45, and with cytosine presenting an unusually large TECS. Fig. 8(c) and (d) also show, respectively, the TICS and TECS for the different molecules and electron energies, but now as a function of the effective number of electrons Neff proposed by ref. 59 (see Table 1). Clearly, the linear scaling of the TICS is now better than as a function of Nval. However, the behaviour of the TECS is not improved at all.
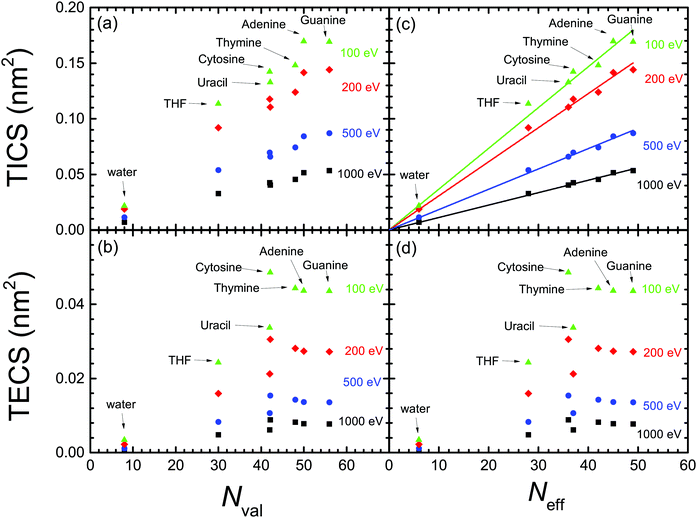 | ||
| Fig. 8 Dependence of the calculated (a) TICS and (b) TECS for biomaterials, for different electron energies (T = 100 eV, 200 eV, 500 eV and 1000 eV), as a function of the number of valence electrons for each biomolecule.83,84 Panels (c) and (d) represent the same as (a) and (b), but as a function of the effective number of valence electrons.59 The straight lines in panel (c) represent the linear fittings by means of eqn (24) with the parameters given in Table 3. | ||
From the above discussion, we can conclude that the proposed scaling laws for ion impact ionisation work well for the electron-impact TICS too. This is true, in principle, for the entire electron energy range, although the linear scaling works better for the larger electron energies. Also, the scaling laws seem more reliable when expressed as a function of the effective number of electrons59 (instead of the number of valence electrons), in the form:
| TICS(nm2) = βTICS(T)Neff, | (24) |
βTICS(T) = γTICS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T + δTICS, T + δTICS, | (25) |
| T (eV) | β TICS·103 (nm2/e−) | γ TICS·103 (nm2/e−) | δ TICS·103 (nm2/e−) | β SCS·102 (nm2/e−) | γ SCS·102 (eV nm2/e−) | δ SCS·10 (eV nm2/e−) |
|---|---|---|---|---|---|---|
| 100 | 3.7 | −1.14 | 9.0 | 12.04 | −3.11 | 26.96 |
| 200 | 3.1 | 11.34 | ||||
| 500 | 1.8 | 7.71 | ||||
| 1000 | 1.1 | 5.20 |
Nonetheless, the scaling in the TECS is not satisfactory, neither as a function of the number of valence nor of effective electrons. However, this deficiency does not seem to arise from limitations of the model, as the calculated TECS have been shown reasonably accurate in comparison with experimental data for water and THF vapour, as well as for solid cytosine, adenine and thymine. Thus, we attribute the less predictable behaviour of the TECS to the larger number of variables on which it depends, namely the features of the ELF (related to the number of valence electrons), but also to the values of both the electronic excitation threshold Eth and the mean binding energy of outer-shell electrons Bout(T), whose values cannot be, in principle, anticipated.
3.3 Stopping cross sections and their scaling
Finally, to complete our analysis of electronic excitation of biomaterials by electron impact, we provide another important quantity for assessing radiation biodamage, namely the electronic stopping cross-section (SCS) due to both electronic excitations and ionisations SCS = SCSexcit + SCSionis. The quantities SCSexcit and SCSionis are obtained by integrals similar to eqn (21) and (23) but replacing dE and dW by dE E and dW(W + Bα), respectively. The SCS gives a measure of the probability of energy deposition in a target molecule. This quantity was suggested92 as a convenient physical parameter for nanodosimetry studies, as it can be correlated with the damaging cross-sections for double-strand break formation in DNA. It should be noted that the SCS is a quantity closely related to the widely used quantity of the stopping power S (i.e., average of the energy lost by an electron per unit path length). Their relation is SCS = S/![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) , where
, where ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) is the target molecular density.
is the target molecular density.
The calculated SCS for all the relevant condensed-phase biomaterials are presented by lines in Fig. 9 (liquid water, THF and cytosine) and Fig. 10 (adenine, guanine, uracil, and thymine). For water (Fig. 9(a)), calculations are compared with compilations from various sources for liquid water87,88 and ice89,90 (ref. 89 and 90 come from Joy's compilation91). Our SCS is split into excitation and ionisation contributions, although comparison with other results can be only done for the total electronic SCS, which agrees well with ref. 87 for large energies down to the maximum (∼150 eV). Our calculations significantly underestimate the data for the lower energies.87–90 There are no data available for the comparison with THF (Fig. 9(b)).
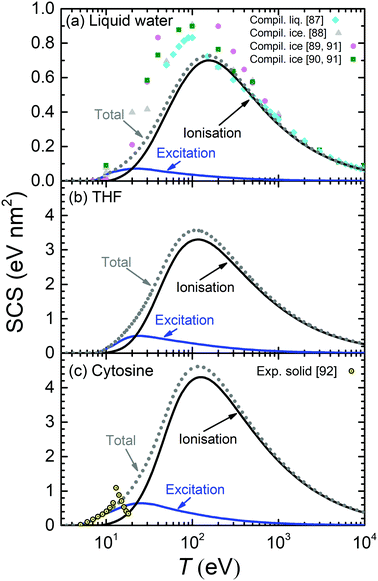 | ||
| Fig. 9 Calculated stopping cross-section SCS (lines) for electrons in (a) liquid water, (b) THF and (c) cytosine due to ionisation and electronic excitation. Total SCS (ionisation + ionisation) are represented by dotted lines. Symbols in the upper panel correspond to reference data for liquid water,87 ice88–91 and cytosine.92 | ||
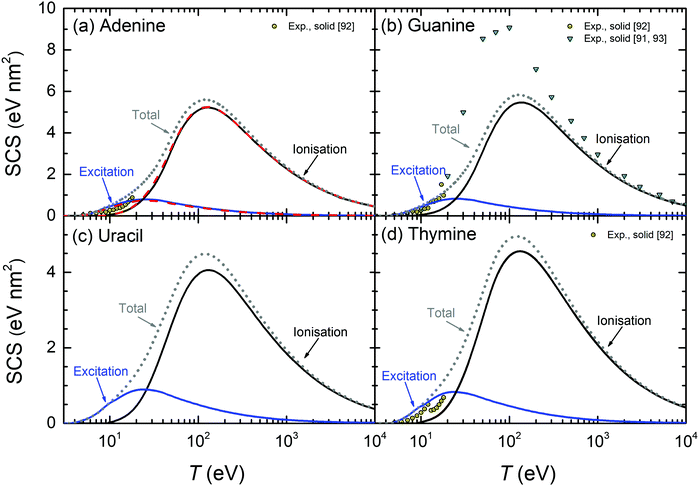 | ||
| Fig. 10 Calculated stopping cross-sections SCS (lines) for electrons in the solid DNA/RNA bases: (a) adenine, (b) guanine, (c) uracil and (d) thymine due to the processes of ionisation and electronic excitation. Total SCS (ionisation + excitation) are represented by dotted lines. For adenine, results obtained by using the parametric model for the optical ELF39 are presented by dashed lines. Symbols represent reference data.91–93 | ||
The calculated SCS for all the RNA/DNA bases (uracil, adenine, guanine, cytosine, and thymine) appear in Fig. 9(c) and 10. There are data for the four DNA bases at low energies (T ≤ 18 eV),92 although it is not clear whether they are experiments or calculations from the reading of the cited article. Our calculated total SCS agree nicely with this data. Only guanine has available SCS data in a higher energy range (20–104 eV).91,93 It is worth noting that Luo's SCS for liquid water90 and solid guanine93 are not a direct measurement, but they come from the experimental determination of the EELS for these materials.
The scaling behaviour of the total electronic SCS on the number of electrons has been analysed as well. It is found that the SCS also scales linearly with the effective number of electrons Neff in a way similar to eqn (24), i.e. SCS(eV nm2) = βSCS(T)Neff. As it happens for the TICS, the slope also depends on the electron energy by means of eqn (25), with the corresponding parameters γSCS and δSCS, given in Table 3.
4 Summary and conclusions
We have extended the dielectric response model, previously developed for the ion-impact ionisation of arbitrary condensed-phase organic media,28,30 to the case of excitations and ionisations induced by electrons in a wide energy range, due to their relevance in the direct damage of biological targets by different electronic excitations and ionising collisions. Especial attention has been paid to the proper description of very low energy electrons, as most of the secondary electrons produced by radiation have energies below 100 eV. These are nowadays recognised as the most important agents in radiation biodamage, since they are responsible for the development of the radiation track-structure (especially in the nanometre scale, typical of important biomolecules such as DNA).Such extension to incident electrons required the consideration of a series of improvements to the original model, namely: (i) accounting for the indistinguishability between the primary and the secondary electrons (which affects the range of possible energy transfers in the inelastic collisions), (ii) modification of the concept of an energy-independent mean binding energy for the targets outer-shell electrons when the primary particle has very low energy (in such a case, the projectile cannot ionise all the target's outer shells), (iii) inclusion of exchange interaction between the primary and scattered electrons (for both electronic excitations and ionisations), and (iv) introduction of low-energy corrections to the first Born approximation (FBA, on which the dielectric formalism is based) when the energy transfer is comparable to the primary electron energy. All these effects have been incorporated into our model, defining an energy-dependent mean binding energy for the outer-shell electrons on the basis of quantum chemistry data (which show a rather universal behaviour for all analysed materials), accounting for exchange factors for excitation and ionisation processes from the quantum-mechanical Born–Ochkur approximation, as well as implementing a simple Coulomb-field correction to the FBA, all the above allowing straightforward calculations of single differential and total cross-sections for arbitrary condensed-phase biomaterials.
As a result of such improvements, we have produced a comprehensive set of excitation and ionisation cross-sections for a wide set of biomolecules, including the main constituent of biological tissue, liquid water, as well as the relevant molecular components of DNA/RNA, namely the analogue molecule of the sugar component of the phosphate-deoxyribose backbone, THF, and all the bases adenine, guanine, cytosine, thymine and uracil. Such data comprises the well-studied total ionisation cross-sections (TICS), but also the energy distributions of secondary electrons (singly differential cross-sections, SDCS) as well as the total excitation cross-sections (TECS), for which available data are much scarcer. Moreover, we have calculated the stopping cross-sections (SCS), also related to biomolecular damage. This information is provided over a very wide electron energy range, which covers the high energies characteristic of electron beams, photoelectrons or delta-electrons produced by ion impact, as well as for electrons with kinetic energies down to electronic excitation threshold, so important in molecular damage, constituting by itself a comprehensive and important compilation of cross-sections.
The SDCS, TICS and TECS calculated for the condensed-phase materials have been compared with available experimental data that are limited to molecules in the gas phase, except for TECS in DNA bases. Particularly, plenty of experimental data is available for the SDCS and TICS for water and THF, the most studied molecules. The agreement between the model calculations and these experiments is remarkable, having into account the expected differences between the condensed and gas phases that, in this case, are mainly reflected in the position of the maximum of the energy spectra of secondary electrons, located at ∼10 eV for the condensed phase. Regarding their TECS, a good amount of data is available for water, this information being rather more limited for THF. In any case, the calculated TECS also agree remarkably well for water, and give a rather good estimate for THF in comparison with the available reference and recommended data.
As for the DNA/RNA bases, certain underestimation of the calculated TICS around their maxima is observed for some of them, which can be attributed, most likely, to the expected phase effects: in general, the cross-sections for the condensed phase are expected to be lower than for the gas phase, due to the dielectric screening in the electron gas in the solid; nonetheless, the generally large dispersion between different sets of experimental data prevents drawing more definitive conclusions. In any case, the shape and positions of the TICS agree well with experiments, and their absolute values follow well the linear scaling law with the number of effective valence electrons recently proposed on the basis of quantum calculations,59 which gives more confidence in the obtained results. Based on the calculations, we have provided parameters for linear equations predicting the TICS for biomaterials on the basis of their effective number of valence electrons.
Regarding the calculated TECS for the DNA bases, there is a general satisfactory agreement with experimental data in the condensed phase for energies below 10 eV. Deviations are identified for larger electron energies. However, it has been shown that, in several of these cases, such discrepancies seem to arise from the limited energy-loss range analysed in the electron energy loss spectroscopy experiments, as calculations limiting the energy-loss values to a similar range yield partial TECS that, at least for cytosine and adenine, and in part also for thymine, reproduce rather well the experimental results. The TECS, however, do not seem to scale well with the number of valence or effective electrons, what seems to arise from their dependence on a greater number of target material parameters apart from the number of electrons, namely the threshold energy for electronic excitations and the mean binding energy for outer-shell electrons.
Finally, the stopping cross-sections (SCS) due to both excitation and ionisation processes, relevant to evaluate electron-induced molecular damage, have been obtained and compared with the reference data available for liquid water and all the DNA/RNA bases. The agreement is in general rather good with the most recent datasets obtained from experiments and calculations by Rezaee et al. for ultra-low energy electrons,92 although our findings are lower than the compiled values for water and guanine for energies around the maximum. The obtained SCS also show a good linear dependence with the effective number of valence electrons.
All in all, having into account the generally good comparison between calculations and experiments and the dispersion inherent to the measured data, the proposed model is deemed to produce very good estimates for the electron excitation and ionisation cross-sections in biomaterials in the whole energy range. Moreover, the current approach delivers comprehensive information on these interactions, which is not limited to the TICS, as it happens with other simple models, but also provides the energy distributions of secondary electrons (SDCS) as well as the TECS, which are very difficult to obtain from other approaches, as far as we know. Very importantly, the model we have presented is relatively simple to implement, allowing the prediction of the electronic interaction cross-sections for organic or biological condensed-phase materials even when their optical electronic excitation spectrum is unknown (either experimentally or theoretically), by means of applying the parametric approach that provides the optical ELF of the material on the basis of its atomic composition and density,39 as well as the electronic excitation threshold energy. Thus, the proposed approach provides a very convenient tool for computing the electronic interaction cross-sections for arbitrary organic and biological materials. These not only include water and the RNA/DNA building blocks analysed here, but also complex biological materials such as proteins, lipids, sugars28,94 or even cell compartments,31 as well as other materials relevant for technological applications, such as polymeric resists95 or organometallic compounds.11 Finally, the exchange and low-energy corrections here implemented have been kept purposely simple, for the sake of the generality and usability of the model. Nonetheless, our approach is equally prepared for implementing other more rigorous quantum approaches for these corrections,64 as well as for more accurate estimates of the ELF by means of advanced ab initio techniques,96,97 which might increase its accuracy for very low energies, objectives which are left for future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Union's Horizon 2020 Research and Innovation programme under the Marie Sklodowska-Curie grant agreement no. 840752, from the Spanish Ministerio de Economía y Competitividad and the European Regional Development Fund (Project no. PGC2018-096788-B-I00), from the Fundación Séneca (Project no. 19907/GERM/15) and from the Conselleria d'Educació, Investigació, Cultura i Esport de la Generalitat Valenciana (Project no. AICO/2019/070). PdV acknowledges further financial support provided by the Spanish Ministerio de Economía y Competitividad by means of a Juan de la Cierva postdoctoral fellowship (FJCI-2017-32233).Notes and references
- H. Nikjoo, S. Uehara and D. Emfietzoglou, Interaction of Radiation with Matter, CRC Press, Boca Raton, 2012 Search PubMed.
- B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef.
- R. M. Thorman, R. Kumar, D. H. Fairbrother and O. Ingólfsson, Beilstein J. Nanotechnol., 2015, 6, 1904–1926 CrossRef CAS.
- M. Dapor, I. Abril, P. de Vera and R. Garcia-Molina, Phys. Rev. B, 2017, 96, 064113 CrossRef.
- S. Incerti, I. Kyriakou, M. A. Bernal, M. C. Bordage, Z. Francis, S. Guatelli, V. Ivanchenko, M. Karamitros, N. Lampe, S. B. Lee, S. Meylan, C. H. Min, W. G. Shin, P. Nieminen, D. Sakata, N. Tang, C. Villagrasa, H. N. Tran and J. M. Brown, Med. Phys., 2018, 45, e722–e739 CrossRef CAS.
- J. Schuemann, A. L. McNamara, J. Ramos-Méndez, J. Perl, K. D. Held, H. Paganetti, S. Incerti and B. Faddegon, Radiat. Res., 2019, 191, 125–138 CAS.
- M. Dapor, Transport of Energetic Electrons in Solids, Computer Simulation with Applications to Materials Analysis and Characterization, Springer International Publishing AGCham, Switzerland, 3rd edn, 2020 Search PubMed.
- D. Schardt, T. Elsässer and D. Schulz-Ertner, Rev. Mod. Phys., 2010, 82, 383–425 CrossRef.
- Nanoscale Insights into Ion-Beam Cancer Therapy, ed. A. V. Solov'yov, Springer International Publishing AG, Cham, Switzerland, 2017 Search PubMed.
- M. Huth, F. Porrati and O. V. Dobrovolskiy, Microelectron. Eng., 2018, 185-186, 9–28 CrossRef CAS.
- P. de Vera, M. Azzolini, G. Sushko, I. Abril, R. Garcia-Molina, M. Dapor, I. A. Solov’yov and A. V. Solov’yov, Sci. Rep., 2020, 10, 20827 CrossRef CAS.
- M. A. Bolorizadeh and M. E. Rudd, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 882–887 CrossRef CAS.
- Y. Itikawa and N. Mason, Phys. Rep., 2005, 414, 1–41 CrossRef CAS.
- J. N. Bull, J. W. L. Lee and C. Vallance, Phys. Chem. Chem. Phys., 2014, 16, 10743–10752 RSC.
- M. A. Rahman and E. Krishnakumar, J. Chem. Phys., 2016, 144, 161102 CrossRef CAS.
- M. U. Bug, W. Yong Baek, H. Rabus, C. Villagrasa, S. Meylan and A. B. Rosenfeld, Radiat. Phys. Chem., 2017, 130, 459–479 CrossRef CAS.
- W. Wolff, B. Rudek, L. A. Da Silva, G. Hilgers, E. C. Montenegro and M. G. Homem, J. Chem. Phys., 2019, 151, 064304 CrossRef.
- P. A. Thorn, M. J. Brunger, P. J. O. Teubner, N. Diakomichalis, T. Maddern, M. A. Bolorizadeh, W. R. Newell, H. Kato, M. Hoshino, H. Tanaka, H. Cho and Y.-K. Kim, J. Chem. Phys., 2007, 126, 064306 CrossRef CAS.
- M. J. Brunger, P. A. Thorn, L. Campbell, N. Diakomichalis, H. Kato, H. Kawahara, M. Hoshino, H. Tanaka and Y.-K. Kim, Int. J. Mass Spectrom., 2008, 271, 80–84 CrossRef CAS.
- P. A. Thorn, PhD thesis, Flinders University of South Australia, 2008.
- M. Matsui, M. Hoshino, H. Kato, F. F. Da Silva, P. Limão-Vieira and H. Tanaka, Eur. Phys. J. D, 2016, 70, 77 CrossRef.
- M. Michaud, M. Bazin and L. Sanche, Int. J. Radiat. Biol., 2012, 88, 15–21 CrossRef CAS.
- D. Bouchiha, J. D. Gorfinkiel, L. G. Caron and L. Sanche, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 975–986 CrossRef CAS.
- J. D. Gorfinkiel, Eur. Phys. J. D, 2020, 74, 51 CrossRef CAS.
- ICRU, Report 55 - Secondary Electron Spectra from Charged Particle Interactions, International Commission on Radiation Units and Measurements, Bethesda, Maryland, 1996.
- P. Możejko and L. Sanche, Radiat. Environ. Biophys., 2003, 42, 201–211 CrossRef.
- P. Możejko and L. Sanche, Radiat. Environ. Biophys., 2005, 73, 77–84 Search PubMed.
- P. de Vera, R. Garcia-Molina, I. Abril and A. V. Solov'yov, Phys. Rev. Lett., 2013, 110, 148104 CrossRef.
- P. de Vera, R. Garcia-Molina and I. Abril, Phys. Rev. Lett., 2015, 114, 018101 CrossRef CAS.
- P. de Vera, I. Abril, R. Garcia-Molina and A. V. Solov'yov, J. Phys.: Conf. Ser., 2013, 438, 012015 CrossRef.
- P. de Vera, E. Surdutovich, I. Abril, R. Garcia-Molina and A. V. Solov'yov, Eur. Phys. J. D, 2014, 68, 96 CrossRef.
- P. de Vera and R. Garcia-Molina, J. Phys. Chem. C, 2019, 123, 2075–2083 CrossRef CAS.
- D. Emfietzoglou and H. Nikjoo, Radiat. Res., 2005, 163, 98–111 CrossRef CAS.
- H. Q. Tan, Z. Mi and A. A. Bettiol, Phys. Rev. E, 2018, 97, 1–7 CrossRef.
- S. S. Prasad, Proc. Phys. Soc., London, 1965, 85, 57–59 CrossRef CAS.
- H. Rudge, Rev. Mod. Phys., 1968, 40, 564–590 CrossRef.
- J. Lindhard, Danske Matematisk-fysiske Meddelelser, 1954, 28, 1 Search PubMed.
- S. Heredia-Avalos, R. Garcia-Molina, J. M. Fernández-Varea and I. Abril, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 052902 CrossRef.
- Z. Tan, Y. Xia, M. Zhao, X. Liu, F. Li, B. Huang and Y. Ji, Nucl. Instrum. Methods Phys. Res., Sect. B, 2004, 222, 27–43 CrossRef CAS.
- S. Heredia-Avalos, I. Abril, C. D. Denton, J. C. Moreno-Marín and R. Garcia-Molina, J. Phys.: Condens. Matter, 2007, 19, 466205 CrossRef.
- C. D. Denton, I. Abril, R. Garcia-Molina, J. C. Moreno-Marín and S. Heredia-Avalos, Surf. Interface Anal., 2008, 40, 1481–1487 CrossRef CAS.
- C. D. Denton, I. Abril, J. C. Moreno-Marín, S. Heredia-Avalos and R. Garcia-Molina, Phys. Status Solidi B, 2008, 245, 1498–1504 CrossRef CAS.
- P. de Vera, I. Abril and R. Garcia-Molina, Appl. Radiation Isotopes, 2014, 83, 122–127 CrossRef CAS.
- R. Garcia-Molina, I. Abril, C. D. Denton, S. Heredia-Avalos, I. Kyriakou and D. Emfietzoglou, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 2647 CrossRef CAS.
- R. Garcia-Molina, I. Abril, S. Heredia-Avalos, I. Kyriakou and D. Emfietzoglou, Phys. Med. Biol., 2011, 56, 6475–6493 CrossRef CAS.
- ChemSynthesis. Chemical Database, https://www.chemsynthesis.com/base/chemical-structure-14512.html.
- M. Isaacson, J. Chem. Phys., 1972, 56, 1803–1812 CrossRef CAS.
- M. Dingfelder, D. Hantke, M. Inokuti and H. G. Paretzke, Radiat. Phys. Chem., 1998, 53, 1–18 CrossRef CAS.
- M. E. Galassi, C. Champion, P. F. Weck, R. D. Rivarola, O. Fojón and J. Hanssen, Phys. Med. Biol., 2012, 57, 2081–2099 CrossRef CAS.
- P. Bernhardt and H. G. Paretzke, Int. J. Mass Spectrom., 2003, 224, 599–611 CrossRef.
- D. Grand, A. Bernas and E. Amouyal, Chem. Phys., 1979, 44, 73–79 CrossRef CAS.
- A. Dwivedi, V. Baboo and A. Bajpai, J. Theor. Chem., 2015, 2015, 1–11 CrossRef.
- M. T. Nguyen, R. Zhang, P. C. Nam and A. Ceulemans, J. Phys. Chem. A, 2004, 108, 6554–6561 CrossRef CAS.
- S. D. Silaghi, M. Friedrich, C. Cobet, N. Esser, W. Braun and D. R. Zahn, Phys. Status Solidi B, 2005, 242, 3047–3052 CrossRef CAS.
- T. Yamada and H. Fukutome, Biopolymers, 1968, 6, 43–54 CrossRef CAS.
- H. Hayashi, N. Watanabe, Y. Udagawa and C. Kao, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6264–6266 CrossRef CAS.
- E. T. Arakawa, L. C. Emerson, S. I. Juan, J. C. Ashley and M. W. Williams, Photochem. Photobiol., 1986, 44, 349–353 CrossRef CAS.
- L. C. Emerson, M. W. Williams, I. Tang, R. N. Hamm and E. T. Arakawa, Radiat. Res., 1975, 63, 235–244 CrossRef CAS.
- A. M. Mendez, C. C. Montanari and J. E. Miraglia, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 55201–55211 CrossRef.
- D. Emfietzoglou, K. Karava, G. Papamichael and M. Moscovitch, Phys. Med. Biol., 2003, 48, 2355–2371 CrossRef CAS.
- D. Emfietzoglou and H. Nikjoo, Radiat. Res., 2007, 167, 110–120 CrossRef CAS.
- D. Emfietzoglou, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 257, 609–613 CrossRef CAS.
- D. Emfietzoglou, Radiat. Phys. Chem., 2003, 66, 373–385 CrossRef CAS.
- D. Emfietzoglou, I. Kyriakou, R. Garcia-Molina and I. Abril, Surf. Interface Anal., 2017, 49, 4–10 CrossRef CAS.
- V. I. Ochkur, Soviet Physics JETP, 1964, 18, 503–508 Search PubMed.
- J. R. Oppenheimer, Phys. Rev., 1928, 32, 361–376 CrossRef CAS.
- M. Inokuti, J. Phys. Soc. Jpn., 1967, 22, 971–973 CrossRef CAS.
- J. M. Fernández-Varea, R. Mayol, D. Liljequist and F. Salvat, J. Phys.: Condens. Matter, 1993, 5, 3593–3610 CrossRef.
- L. Vriens, Phys. Rev., 1966, 141, 88–92 CrossRef CAS.
- N. Watanabe, H. Hayashi and Y. Udagawa, Bull. Chem. Soc. Jpn., 1997, 70, 719–726 CrossRef CAS.
- W. Y. Baek, M. Bug, H. Rabus, E. Gargioni and B. Grosswendt, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 032702 CrossRef.
- M. U. Bug, PhD thesis, University of Wollongong, 2014.
- J. Schutten, F. J. de Heer, H. R. Moustafa, J. H. Boerboom and J. Kistenaker, J. Chem. Phys., 1966, 44, 3924–3928 CrossRef.
- K. Ralphs, G. Serna, L. R. Hargreaves, M. A. Khakoo, C. Winstead and V. McKoy, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 125201 CrossRef.
- M. C. Fuss, A. G. Sanz, F. Blanco, P. Limão-Vieira, M. J. Brunger and G. García, Eur. Phys. J. D, 2014, 68, 161 CrossRef.
- I. I. Shafranyosh, M. I. Sukhoviya and M. I. Shafranyosh, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 4155–4162 CrossRef CAS.
- P. J. van der Burgt, Eur. Phys. J. D, 2014, 68, 135 CrossRef.
- B. F. Minaev, M. I. Shafranyosh, Y. Svida, M. I. Sukhoviya, I. I. Shafranyosh, G. V. Baryshnikov and V. A. Minaeva, J. Chem. Phys., 2014, 140, 175101 CrossRef CAS.
- P. J. van der Burgt, S. Finnegan and S. Eden, Eur. Phys. J. D, 2015, 69, 173 CrossRef.
- I. I. Shafranyosh and M. I. Sukhoviya, J. Chem. Phys., 2012, 137, 184303 CrossRef CAS.
- I. I. Shafranyosh, M. I. Sukhoviya, M. I. Shafranyosh and L. L. Shimon, Tech. Phys., 2008, 53, 1536–1540 CrossRef CAS.
- P. J. van der Burgt, F. Mahon, G. Barrett and M. L. Gradziel, Eur. Phys. J. D, 2014, 68, 151 CrossRef.
- W. E. Wilson and L. H. Toburen, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 11, 1303–1308 CrossRef CAS.
- D. J. Lynch, L. H. Toburen and W. E. Wilson, J. Chem. Phys., 1976, 64, 2616–2622 CrossRef CAS.
- P. Sigmund and A. Schinner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2018, 415, 110–116 CrossRef CAS.
- M. Wang, B. Rudek, D. Bennett, P. de Vera, T. Buhr, W. Y. Baek, G. Hilgers and H. Rabus, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 93, 052711 CrossRef.
- D. E. Watt, Quantities for Dosimetry of Ionizing Radiations in Liquid Water, Taylor & Francis, London, 1996 Search PubMed.
- ICRU, Report 16 - Linear Energy Transfer, International Commission on Radiation Units and Meassurements, Washington D. C., 1970.
- J. A. LaVerne and A. Mozumder, J. Phys. Chem., 1985, 89, 4219–4225 CrossRef CAS.
- S. Luo, X. Zhang and D. C. Joy, Radiat. Eff. Defects Solids, 1991, 117, 235–242 CrossRef.
- D. C. Joy, Scanning, 1995, 17, 270–275 CrossRef CAS.
- M. Rezaee, D. J. Hunting and L. Sanche, Med. Phys., 2014, 41, 072502 CrossRef.
- S. Luo, PhD thesis, University of Tennessee, 1994.
- R. Garcia-Molina, I. Abril, I. Kyriakou and D. Emfietzoglou, Surf. Interface Anal., 2017, 49, 11–17 CrossRef CAS.
- P. de Vera, I. Abril and R. Garcia-molina, J. Appl. Phys., 2011, 109, 094901 CrossRef.
- H. T. Nguyen-Truong, J. Phys.: Condens. Matter, 2017, 29, 215501 CrossRef.
- M. Azzolini, T. Morresi, G. Garberoglio, L. Calliari, N. M. Pugno, S. Taioli and M. Dapor, Carbon, 2017, 118, 299–309 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04951d |
| This journal is © the Owner Societies 2021 |