Open Access Article
Open Access ArticleA first-principles study of rare earth quaternary Heusler compounds: RXVZ (R = Yb, Lu; X = Fe, Co, Ni; Z = Al, Si)
Hung-Lung
Huang
a,
Jen-Chuan
Tung
*b and
Horng-Tay
Jeng
 *acd
*acd
aDepartment of Physics, National Tsing Hua University, Hsinchu 30013, Taiwan. E-mail: jeng@phys.nthu.edu.tw
bCenter for General Education, China Medical University, Taiwan, Program of Digital Health Innovation, China Medical University, Taichung 40402, Taiwan. E-mail: jctung@mail.cmu.edu.tw
cPhysics Division, National Center for Theoretical Sciences, Hsinchu 30013, Taiwan
dInstitute of Physics, Academia Sinica, Taipei 11529, Taiwan
First published on 14th January 2021
Abstract
Rare earth equiatomic quaternary Heusler (EQH) compounds with chemical formula RXVZ (R = Yb, Lu; X = Fe, Co, Ni; Z = Al, Si) have recently attracted much attention since these materials are easily prepared and they also provide interesting properties for future spintronic applications. In this work, rare Earth-based EQH compounds in three types of structures are theoretically investigated through first-principles calculations based on density functional theory. We find that most of the studied rare Earth EQH compounds exhibit magnetic ground states including ferro-, antiferro-, and ferri-magnetic phases. Owing to the nearly closed shell f orbital in Lu and Yb, the spin magnetic moments mainly come from the 3d transition metal elements. In particular, in the type I structure, a large portion (7 out of 12) of EQH compounds are ferromagnetic half-metals (HMs) with integer magnetic moments ranging from 1 to 3 μB. In the type II structure, YbFeVAl is found to be a rare case of antiferro-magnetic (AFM) half-metal with zero total magnetic moments. Surprisingly, we also discover an unusual magnetic semiconductor LuCoVSi in the type III structure with a total spin magnetic moment of 3.0 μB and an indirect band gap of 0.2 eV. The structural and magnetic stabilities such as formation energy, magnetization energy as well as the mechanical stabilities such as the bulk, shear, and Young's moduli, and Poisson's, and Pugh's ratios of these EQH compounds are also investigated. Most of the studied compounds exhibit mechanical stability under the mechanical stability criteria and show elastic anisotropy. Our work provides guidelines for experimental researchers to synthesize useful materials in future spintronic applications.
I. Introduction
It is well known that Heusler compounds are intermetallic materials with rich magnetic properties.1–7 Since the first discovery of the Cu2MnSn Heusler alloys in 1903, Heusler compounds have become interesting and promising materials in both theoretical and experimental research fields. To date, thousands of members of Heusler compounds have been discovered with a wide range of physical properties, such as half-metallics, ferrimagnets,8–10 ferromagnets,11–13 shape memory alloys,14,15 and even tunable topological insulators.16,17 These properties are related to a high potential for spintronics, energy technologies, and magneto-caloric applications. The typical Heusler compounds are ternary alloys that have the chemical formula X2YZ and crystallize in the cubic L21 structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), where X and Y are different transition metal elements, and Z is an sp/main-group (group III, IV, or V) element.3,18 When one of the X's is substituted with a different transition metal M, a new equiatomic quaternary Heusler (EQH) compound with the stoichiometric composition of MXYZ (space group F
m), where X and Y are different transition metal elements, and Z is an sp/main-group (group III, IV, or V) element.3,18 When one of the X's is substituted with a different transition metal M, a new equiatomic quaternary Heusler (EQH) compound with the stoichiometric composition of MXYZ (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) is formed.3,19,20
3m) is formed.3,19,20
Half-metallic EQHs demonstrated through theoretical and experimental studies have attracted a lot of attention due to their superior magnetic and transport properties. Recently, some EQH compounds containing 4d transition metal elements or rare earth elements have been found to have intriguing properties.7,21 Some of them exhibit more robust half-metallic properties against interfering effect than general ternary Heusler alloys.22,23 Some of them are half-metallic magnets (HMMs) with larger spin–flip gaps than 3d transition metal based EQHs.24 Furthermore, some of EQHs are recently discovered as spin-gapless semiconductors (SGSs), which possess important and unique properties as follows: (1) the electrons in the valence band need less energy to get excited to the conduction band; (2) the excited electrons and holes can be fully spin-polarized simultaneously; (3) through the Hall effect, fully spin-polarized electrons and holes will be separated easily.25 It is also proposed that HMMs with EQH structures have lower-power dissipation than ternary Heusler alloys due to less disorder.3
As such, enormous attention has been devoted to searching for new spintronic materials through 4d transition metal/rare-earth element EQHs. In this work, we present a systematic theoretical investigation of the structural, electronic, magnetic, and mechanical properties of rare-earth-element-containing EQHs: YbXVZ and LuXVZ (X = Fe, Co, Ni; Z = Al, Si) based on first-principles density functional theory calculations. We demonstrate several intriguing phases such as ferromagnetic half-metal (HM), antiferromagnetic half-metal (AHM), and magnetic semiconductor (MSC) phases, which are important for future spintronics. In particular, since the latter two phases are rarely found, our work thus provides a good opportunity for experimentalists to pursue studies of such high-potential unusual materials.
II. Computational method
The ideal RXVZ (R = Lu, and Yb, X = Fe, Co, and Ni, Z = Si, and Al) full-Heusler alloys have the cubic L21 structure with the point group 225 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetric) as shown in Fig. 1. It consists of four interpenetrating fcc lattices with R, X, V, and Z atoms located at (0, 0, 0), (1/4, 1/4, 1/4), (1/2, 1/2, 1/2), and (3/4, 3/4, 3/4), respectively. Following the previous study by Wang et al.,21 we assume that the rare earth element R sits at (0, 0, 0). Therefore, there are three possible structures for the equiatomic quaternary Heusler compounds. These three possible structures are depicted in Fig. 1. Note that the type III structure is similar to that of normal Heusler compounds, A2BC, with A and B being transition metals and C being main group elements.
m symmetric) as shown in Fig. 1. It consists of four interpenetrating fcc lattices with R, X, V, and Z atoms located at (0, 0, 0), (1/4, 1/4, 1/4), (1/2, 1/2, 1/2), and (3/4, 3/4, 3/4), respectively. Following the previous study by Wang et al.,21 we assume that the rare earth element R sits at (0, 0, 0). Therefore, there are three possible structures for the equiatomic quaternary Heusler compounds. These three possible structures are depicted in Fig. 1. Note that the type III structure is similar to that of normal Heusler compounds, A2BC, with A and B being transition metals and C being main group elements.
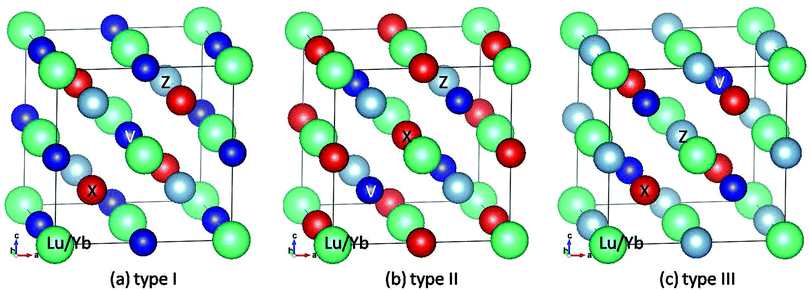 | ||
| Fig. 1 Crystal structures in conventional unit cells for three different types of rare earth-containing EQH compounds with the chemical formula RXVZ (R = Yb, Lu; X = Fe, Co, Ni; Z = Al, Si). | ||
The structural, electronic, and magnetic properties of RXVZ Heusler alloys are calculated by using the density functional theory as implemented using the Vienna ab initio simulation package (VASP).26,27 The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) was chosen for the exchange and correlation functional.28,29 The Γ-centered Monkhorst–Pack scheme with a k-mesh of 12 × 12 × 12 is used for Brillouin zone integration. The self-consistent total energy convergence criterion is set to be 1.0 × 10−6 eV. In all cases, a plane wave basis set with a cut-off energy of 450 eV was used. The equilibrium lattice constant, a, for all three types of structures is obtained using the structure optimization technique. The convergence criterion in the geometry optimization calculations was 1.0 × 10−6 eV. To calculate the total energy of the isolated atoms, we use a very large supercell with 20 Å of separation in all x, y, and z directions which should be wide enough to decouple the nearest atom. The electronic configurations used are 5p65d3 (Lu), 5p65d2 (Yb), 3d44s1 (V), 3d74s1 (Fe), 3d84s1 (Co), 3d94s1 (Ni), 3s23p1 (Al), and 3s23p2 (Si). Our calculated spin magnetization values for the Lu, Yb, V, Fe, Co, Ni, Al, and Si isolated atoms are 1.00 μB, 0.00 μB, 5.00 μB, 4.00 μB, 3.00 μB, 2.00 μB, 1.00 μB, and 2.00 μB, respectively.
III. Results and discussion
A Electronic and magnetic properties
In order to ensure the suitability of the DFT-GGA approach for EQHs, we have analysed three compounds CoFeCrGe, CoFeMnGe, and CoFeTiAl, which have been prepared and measured successfully in experiments as benchmarks shown in Table 1. It is clear that the lattice constants and magnetic moments calculated by DFT-GGA are in good agreement with the previous experimental results, indicating that the DFT-GGA approach is reliable for these kinde of compounds.Listed in Table 2 are the calculated lattice constants (Å), cohesive energy (eV f.u.−1), and formation energy (eV f.u.−1) of the rare Earth-based equiatomic Heusler compounds. The cohesive energy is calculated as the difference between the sum of the ground state total energies of the isolated atoms and the total energy of the quaternary Heusler compounds, i.e.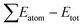 . The cohesive energy is the energy required to break alloys into isolated atoms. Consequently, high cohesive energy alloys are relatively stable compared to those with low cohesive energies. The formation energies (Ef) of RXVZ compounds are also calculated using
. The cohesive energy is the energy required to break alloys into isolated atoms. Consequently, high cohesive energy alloys are relatively stable compared to those with low cohesive energies. The formation energies (Ef) of RXVZ compounds are also calculated using
| Ef = Etot − (EbulkR + EbulkX + EbulkV + EbulkZ), |
| Lattice constant | Cohesive energy | Formation energy | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Å | eV f.u.−1 | eV f.u.−1 | |||||||
| X = Fe | Co | Ni | X = Fe | Co | Ni | X = Fe | Co | Ni | |
| Type I | |||||||||
| YbXVAl | 6.405 | 6.340 | 6.426 | 14.38 | 14.30 | 14.07 | 1.09 | 1.14 | 1.09 |
| YbXVSi | 6.246 | 6.249 | 6.341 | 15.69 | 15.50 | 15.31 | 0.84 | 1.01 | 0.91 |
| LuXVAl | 6.387 | 6.377 | 6.445 | 17.66 | 17.80 | 16.49 | 0.76 | 0.60 | 0.38 |
| LuXVSi | 6.242 | 6.277 | 6.358 | 18.95 | 18.94 | 18.76 | 0.54 | 0.52 | 0.42 |
| Type II | |||||||||
| YbXVAl | 6.538 | 6.464 | 6.526 | 14.46 | 14.23 | 14.48 | 1.01 | 1.21 | 0.68 |
| YbXVSi | 6.396 | 6.329 | 6.371 | 16.16 | 16.02 | 16.20 | 0.38 | 0.48 | 0.02 |
| LuXVAl | 6.372 | 6.428 | 6.473 | 17.91 | 18.33 | 17.09 | 0.51 | 0.07 | −0.23 |
| LuXVSi | 6.319 | 6.293 | 6.352 | 19.74 | 19.91 | 19.95 | −0.24 | −0.45 | −0.77 |
| Type III | |||||||||
| YbXVAl | 6.353 | 6.335 | 6.386 | 13.69 | 14.47 | 14.81 | 1.77 | 0.96 | 0.31 |
| YbXVSi | 6.213 | 6.146 | 6.241 | 15.84 | 16.29 | 16.41 | 0.69 | 0.21 | −0.19 |
| LuXVAl | 6.341 | 6.340 | 6.406 | 17.88 | 18.58 | 17.49 | 0.55 | −0.19 | −0.62 |
| LuXVSi | 6.205 | 6.207 | 6.294 | 19.67 | 20.12 | 19.62 | −0.18 | −0.66 | −0.44 |
We first summarize few general remarks regarding lattice constants here. As shown in Table 2, in all the three types of structures, the equilibrium lattice constants of RXVAl are larger than those of RXVSi. This is because that the Wigner–Seitz radius of aluminum is larger than that corresponding to silicon. Further, for all alloys except LuFeVAl and LuNiVSi, the type II lattice structure exhibits a larger equilibrium lattice constant than type I and III structures. Taking LuCoVAl as an example, the equilibrium lattice constants of type II is 6.428 Å, which is larger than 6.377 Å and 6.340 Å for type I and type III structures, respectively. Finally, for all alloys in all structures except type II YbNiVAl and YbNiVSi, RNiVZ has the largest equilibrium lattice constant.
As for the cohesive energies (equivalently the structure stability) of the RXVZ Heusler compounds listed in Table 1, in general, RXVSi is stabler than RXVAl in all three types of structures. Furthermore, the LuXVZ Heusler compounds are stabler than YbXVZ in all the structures. The stablest case among all listed in Table 1 is that of LuCoVSi in the type III structure with the largest cohesive energy of 20.12 (eV f.u.−1), whereas type III YbFeVAl is the most unstable with the smallest cohesive energy of 13.69 (eV f.u.−1).
Table 3 lists the calculated magnetic ground state, total spin moment (mt) (in μBμB f.u.−1), atomic spin moment (mR, mX, mV, and mZ) (μB per atom), and magnetization energy (eV f.u.−1). The magnetization energy is the energy difference between the magnetic and nonmagnetic phases. Previous studies21 show that type 3 is the most stable structure for LuCoVSi with the lattice constant and total magnetic moment of 6.26 Å and 3 μB f.u.−1, respectively. Our calculated results of 6.207 Å and 3 μB f.u.−1, respectively, as shown in Tables 2 and 3 are in good agreement with theirs. In the type I structure, the magnetic ground state of LuNiVSi, LuNiVAl, and YbNiVAl is ferromagnetic (FM), while YbFeVAl shows the ferrimagnetic (FiM) ground state. LuFeVAl is nonmagnetic (NM) and all the others are half-metals (HM) with integer magnetic moments. It is interesting that in general, vanadium exhibits a larger atomic spin moment than that of the magnetic elements Fe, Co, and Ni. Both ferro- and antiferro-magnetic couplings between V and Fe-Co-Ni are possible.
| RXVZ | Magnetic state | m t | m R | m X | m V | m Z | E M | M t |
|---|---|---|---|---|---|---|---|---|
| μ B | μ B per atom | (eV f.u.−1) | μ B | |||||
| Type I | ||||||||
| YbFeVAl | FiM | 0.06 | −0.11 | 2.16 | −1.85 | 0.023 | −0.141 | 0 |
| YbCoVAl | HM | 1.00 | 0.06 | −0.87 | 1.68 | −0.066 | −0.194 | 1 |
| YbNiVAl | FM | 2.13 | 0.07 | −0.09 | 2.09 | −0.115 | −0.518 | 2 |
| YbFeVSi | HM | 1.00 | 0.13 | −1.49 | 2.03 | −0.008 | −0.215 | 1 |
| YbCoVSi | HM | 2.00 | 0.12 | −0.51 | 2.12 | −0.046 | −0.340 | 2 |
| YbNiVSi | HM | 3.00 | 0.15 | 0.16 | 2.42 | −0.070 | −0.773 | 3 |
| LuFeVAl | NM | 0.00 | 1 | |||||
| LuCoVAl | HM | 2.00 | 0.30 | −0.40 | 1.87 | −0.037 | −0.310 | 2 |
| LuNiVAl | FM | 3.04 | 0.34 | 0.25 | 2.23 | −0.058 | −0.698 | 3 |
| LuFeVSi | HM | 2.00 | 0.38 | −0.48 | 1.80 | 0.003 | −0.116 | 2 |
| LuCoVSi | HM | 3.00 | 0.37 | 0.50 | 1.93 | −0.025 | −0.399 | 3 |
| LuNiVSi | FM | 3.99 | 0.50 | 0.57 | 2.47 | 0.004 | −0.720 | 4 |
| Type II | ||||||||
| YbFeVAl | AHM | 0.00 | −0.04 | 2.56 | −2.07 | −0.012 | −0.565 | 0 |
| YbCoVAl | FM | 2.82 | −0.03 | 0.99 | 1.64 | −0.001 | −0.171 | 1 |
| YbNiVAl | FM | 2.91 | 0.02 | 0.32 | 2.15 | 0.043 | −0.440 | 2 |
| YbFeVSi | FiM | 0.58 | −0.02 | 2.62 | −1.87 | 0.133 | −0.703 | 1 |
| YbCoVSi | FM | 2.99 | −0.02 | 1.19 | 1.59 | 0.013 | −0.313 | 2 |
| YbNiVSi | FM | 2.27 | 0.01 | 0.19 | 1.87 | −0.049 | −0.431 | 3 |
| LuFeVAl | FM | 1.43 | −0.07 | 0.33 | 1.11 | −0.018 | −0.056 | 1 |
| LuCoVAl | FM | 2.98 | −0.07 | 1.22 | 1.64 | 0.026 | −0.366 | 2 |
| LuNiVAl | FM | 2.50 | −0.04 | 0.33 | 1.97 | 0.003 | −0.439 | 3 |
| LuFeVSi | FM | 1.82 | 0.01 | 2.34 | −0.53 | 0.067 | −0.455 | 2 |
| LuCoVSi | FM | 2.96 | −0.03 | 1.26 | 1.53 | 0.030 | −0.349 | 3 |
| LuNiVSi | FM | 2.43 | 0.05 | 0.19 | 1.93 | −0.056 | −0.294 | 4 |
| Type III | ||||||||
| YbFeVAl | FM | 1.72 | −0.06 | 2.06 | −0.17 | −0.037 | −0.131 | 0 |
| YbCoVAl | FM | 1.80 | 0.10 | −0.53 | 2.05 | −0.015 | −0.417 | 1 |
| YbNiVAl | FM | 2.33 | 0.08 | −0.10 | 2.20 | −0.052 | −0.651 | 2 |
| YbFeVSi | HM | 1.00 | 0.24 | −1.82 | 2.29 | −0.009 | −0.400 | 1 |
| YbCoVSi | FM | 2.12 | 0.12 | −0.16 | 2.02 | −0.047 | −0.415 | 2 |
| YbNiVSi | FM | 3.00 | 0.26 | −0.03 | 2.48 | −0.042 | −0.559 | 3 |
| LuFeVAl | FM | 2.83 | 0.11 | 0.77 | 1.78 | −0.031 | −0.230 | 1 |
| LuCoVAl | FM | 2.20 | 0.15 | −0.24 | 2.10 | −0.025 | −0.581 | 2 |
| LuNiVAl | FM | 3.00 | 0.23 | −0.01 | 2.42 | −0.013 | −0.834 | 3 |
| LuFeVSi | HM | 2.00 | 0.27 | −0.73 | 2.15 | −0.002 | −0.412 | 2 |
| LuCoVSi | MSC | 3.00 | 0.26 | 0.06 | 2.34 | −0.011 | −0.656 | 3 |
| LuNiVSi | FM | 3.70 | 0.35 | 0.32 | 2.56 | 0.002 | −0.432 | 4 |
In the type II structure, YbFeVAl is the only half-metal material with zero spin magnetization, implying the rare antiferromagnetic half-metallic ground state while all the others are ferromagnetic metals. In general, the spin moment of Fe–Co–Ni (mX) in the type II structure is larger than that in type I and III structures. In the type III structure, we also find YbFeVSi, YbNiVSi, LuNiVAl, and LuFeVSi are half-metals. Very interestingly, we find that LuCoVSi is in the rare magnetic semiconductor ground state. In the type III structure, vanadium provides the main contributions to the spin magnetic moment, except YbFeVSi and YbFeVAl.
Slater and Pauling have shown that for binary magnetic compounds, the total spin magnetic moments of the L21 full Heusler compounds follow the so-called Slater–Pauling rule Mt = Zt − 24 as listed in Table 2 where Zt is the total number of valence electrons and Mt is the total spin magnetic moment in the unit cell. As shown in the table, the calculated magnetic moments somewhat follow the trend given by the Slater and Pauling rule.
The magnetization energy listed in Table 3 is the energy required to magnetize materials. The negative values for all the studied compounds therefore indicate the stability of the magnetic ground state in these materials. The magnetization energy is not only proportional to the total spin magnetization but also the spin configuration and the crystal structure. For example, in type I the total spin magnetization is 1.00, 2.00, and 3.00 (μB f.u.−1) for YbFeVSi, YbCoVSi and YbNiYSi, respectively, whereas their magnetization energies are −0.215, −0.340 and −0.773 (eV f.u.−1). The total spin magnetization of type II YbFeVAl is zero; however, the magnetization energy is −0.565 (eV f.u.−1). This is because of the large magnitude of atomic spin moments, though the total magnetization is zero.
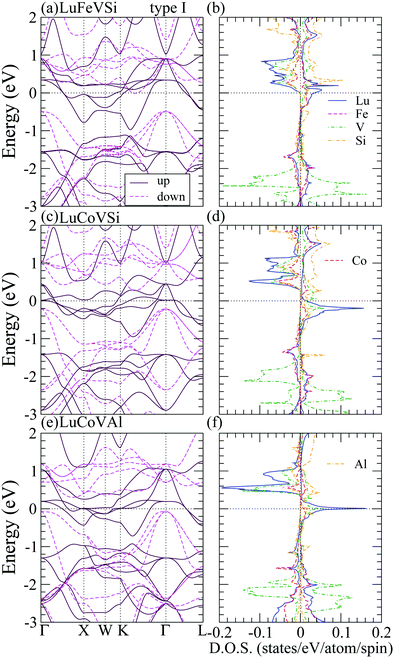
Table 3 indicates that most of the RXVZ Heusler alloys with the type I structure are in the ferromagnetic half-metallic ground state, whereas a few of them are in the ferrimagnetic, ferromagnetic, and non-magnetic metallic ground states. Fig. 2 shows the half-metallic band structure (BS) and density of states (DOS) of LuFeVSi, LuCoVSi, and LuCoVAl EQH compounds in the type I structure. They all have similar electronic structures with a conducting band in the spin up channel and an insulating band gap in the spin down channel at the Fermi level (Ef), leading to the half-metallic behavior with 100% spin polarized carriers at Ef. In particular, owing to the same number of valence electrons, LuFeVSi (Fig. 2(a and b)) and LuCoVAl (Fig. 2(e and f)) show more or less the same BS and DOS with Ef located at nearly the same position and having the same integer magnetic moment of 2 μB (Table 3) while in LuCoVSi (Fig. 2(c and d)), with one additional electron filled in the spin up d-band, the Fermi level hence locates at a higher position with a larger integer magnetic moment of 3 μB (Table 3). The energy band gap at Ef in LuFeVSi, LuCoVSi, and LuCoVAl are respectively 0.5, 0.5, and 0.3 eV in the spin minority states. The smaller gap in LuCoVAl is presumably due to the strong metallic character of Al with more dispersive bands. Besides, they all exhibit an indirect band gap in the minority spin channel. On the other hand, the BS and DOS of type I YbFeVAl in the ferrimagnetic (FiM) metal, YbNiVAl in the ferromagnetic (FM) metal, and LuFeVAl in the non-magnetic (NM) metal ground states are plotted in Fig. 3 for a comparison with the half-metallic (HM) electronic structures in Fig. 2.
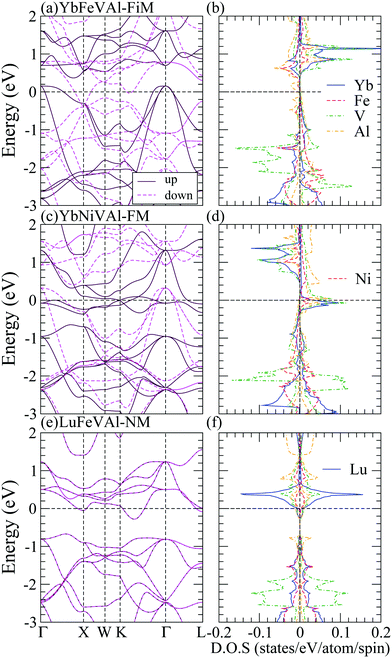 | ||
| Fig. 3 Band structures (left panels) and density of states (right panels) of YbFeVAl-FiM, YbNiVAl-FM, LuFeVAl-NM phases in the type I structure. The Fermi level is shifted to zero as the reference. | ||
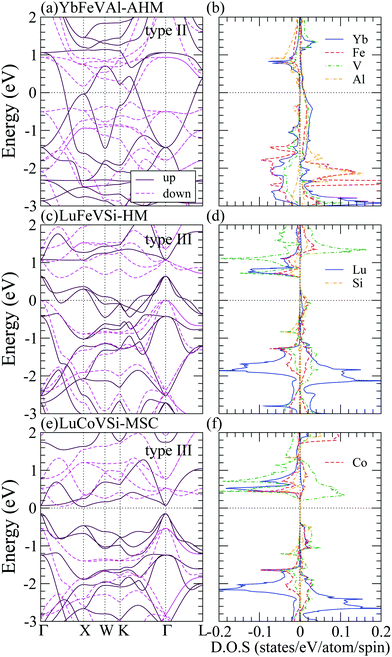
As shown in Table 3, RXVZ Heusler alloys in type II and III structures result in several interesting magnetic ground states. For example, type II YbFeVAl belongs to the rare category of an antiferromagnetic half-metal (AHM) with zero magnetic magnetization, and type III LuCoVSi turns out to be an unusual magnetic semiconductor (MSC) with an integer magnetic moment of 3 μB. The band structures (BS) and density of states (DOS) of these interesting magnetic phases together with those of a typical half-metal type III LuFeVSi are depicted in Fig. 4 for comparison. For type II YbFeVAl (Fig. 4(a and b)), the spin up channel is conducting while the spin down channel is insulating. The atom-decomposed DOS (Fig. 4(b)) demonstrates that Fe bands (red) are mainly in the majority spin whereas the V bands (green) are mainly in the minority spin, resulting in the AHM magnetic ground state. Such an intriguing electronic structure gives rise to a spin polarized transport behavior with the overall system remaining nonmagnetic, which is of high potential in future spintronic devices. There exists a direct energy band gap of 0.3 eV at the Fermi level in the minority spin channel (Fig. 4(a)). Note that this is the only direct band gap found in the minority spin among all the half-metallic cases studied in this work. All the other half-metals exhibit indirect band gaps similar to that of type III LuFeVSi in Fig. 4(c and d). As shown in the density of states in Fig. 2 and 4, Lu bands are relatively narrower than those of Yb. This is presumably due to the nearly closed shell electronic configuration of Lu with a relatively small orbital size and localized behavior. Consequently, the band dispersion is suppressed with a smaller bandwidth. Finally, Fig. 4(e and f) show that the type III LuCoVSi EQH compound is a magnetic semiconductor with an indirect band gap of 0.2 eV. Such a magnetic semiconductor ground state is very rare while of high importance in spintronics. We hope that this newly predicted magnetic semiconductor can be synthesized and applied for spintronic devices in the near future.
B Mechanical properties
To understand the mechanical properties and stability of a solid, we have calculated the elastic constants and related physical quantities of the rare-earth Heusler compounds RXVZ as discussed below. Since the EQH compounds studied in this work all have the cubic symmetry, we need only to consider three independent elastic constants, i.e., C11, C12, and C44. These independent elastic constants are determined by performing certain finite distortions of the lattice and calculating the elastic constants from the strain–stress relations. Once the elastic constants are obtained, we can determine the bulk modulus B, shear modulus G, Voigt shear modulus GV,34 Reuss shear modulus GR,35 Young's modulus E, anisotropy factor A, and the Poisson's ratio ν from the following equations: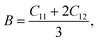 | (1) |
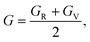 | (2) |
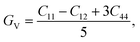 | (3) |
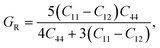 | (4) |
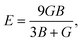 | (5) |
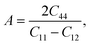 | (6) |
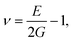 | (7) |
The mechanical stability criteria for the cubic structure37 are as follows:
| C44 > 0, | (8) |
| C12 < B < C11, | (9) |
| B > 0. | (10) |
As shown in Table 4, all the calculated C44 and B coefficients are positive. Consequently, the mechanical stability will be determined by eqn (9) or equivalently the sign of the anisotropy factor A in eqn (6). If the calculated coefficient A is negative, which indicates the violation of eqn (9), the structure is thus unstable. As can be seen in the table, most of the studied cases are mechanically stable except that YbNiVSi, LuNiVAl, LuCoVSi, and LuNiVSi in the type I structure, and YbNiVSi in the type II structure are mechanically unstable because of their negative value of the anisotropy factor A. In principle, the negative modules listed in Table 4 are related to the violation of eqn (9), in which C11–C12 can be understood as the elastic constant under the orthogonal distortion of the conserving volume. In addition to the anisotropy factor A, the instability of these unstable EQH compounds is also shown through the Reuss shear modulus GR. In addition, for type I YbNiVSi, the unstable features can further be found in the Hill shear modulus (G) and Young's modulus (E) as well. Apart from this, the remaining EQH compounds are all mechanically stable. Note that all EQH compounds in type III structure are stable, indicating that type III structure provides robust mechanical stability for the rare-earth Heusler compounds RXVZ.
| C 11 | C 12 | C 44 | B | G V | G R | G | E | A | ν | B/G | e | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPa | arb. unit | C m−2 | ||||||||||
| Type I | ||||||||||||
| YbFeVAl | 91.9 | 43.3 | 77.2 | 59.5 | 56.0 | 41.3 | 48.7 | 114.7 | 3.2 | 0.18 | 1.22 | −0.356 |
| YbCoVAl | 102.1 | 58.9 | 77.6 | 73.3 | 55.2 | 38.1 | 46.7 | 115.5 | 3.6 | 0.24 | 1.57 | −0.141 |
| YbNiVAl | 77.9 | 72.2 | 69.1 | 74.1 | 42.6 | 6.7 | 24.7 | 66.6 | 24.3 | 0.35 | 3.01 | −1.739 |
| YbFeVSi | 108.0 | 66.8 | 81.5 | 80.5 | 57.1 | 37.3 | 47.2 | 118.5 | 4.0 | 0.25 | 1.70 | −0.583 |
| YbCoVSi | 94.2 | 89.7 | 73.4 | 91.2 | 44.9 | 5.4 | 25.2 | 69.1 | 32.6 | 0.37 | 3.62 | −2.313 |
| YbNiVSi | 69.2 | 95.7 | 62.6 | 86.9 | 32.3 | −48.5 | −8.1 | −25.2 | −4.7 | 0.55 | −10.7 | −0.973 |
| LuFeVAl | 124.6 | 90.2 | 62.3 | 101.7 | 44.3 | 30.4 | 37.3 | 99.8 | 3.6 | 0.34 | 2.72 | −0.232 |
| LuCoVAl | 102.5 | 92.7 | 71.2 | 96.0 | 44.7 | 11.1 | 27.9 | 76.3 | 14.5 | 0.37 | 3.44 | −1.129 |
| LuNiVAl | 86.8 | 97.9 | 64.0 | 94.2 | 36.2 | −16.0 | 10.1 | 29.3 | −11.5 | 0.45 | 9.31 | −0.094 |
| LuFeVSi | 109.8 | 102.9 | 77.7 | 105.2 | 48.0 | 8.1 | 28.0 | 77.3 | 22.5 | 0.38 | 3.8 | −0.922 |
| LuCoVSi | 99.5 | 122.3 | 74.0 | 114.7 | 39.8 | −37.1 | 1.4 | 4.2 | −6.5 | 0.49 | 82.7 | −1.307 |
| LuNiVSi | 91.7 | 112.9 | 72.5 | 105.8 | 39.3 | −33.9 | 2.7 | 7.9 | −6.8 | 0.49 | 39.8 | −1.655 |
| Type II | ||||||||||||
| YbFeVAl | 92.6 | 58.8 | 63.4 | 70.1 | 44.8 | 30.2 | 37.5 | 95.5 | 3.8 | 0.27 | 1.87 | 1.076 |
| YbCoVAl | 81.3 | 76.3 | 58.5 | 78.0 | 36.1 | 5.9 | 21.0 | 57.8 | 23.4 | 0.38 | 3.72 | 0.122 |
| YbNiVAl | 70.4 | 70.1 | 58.0 | 70.2 | 34.9 | 0.4 | 17.6 | 48.8 | 386.7 | 0.38 | 3.98 | 0.642 |
| YbFeVSi | 124.3 | 68.9 | 73.9 | 87.4 | 55.4 | 44.3 | 49.9 | 125.7 | 2.7 | 0.26 | 1.75 | 0.017 |
| YbCoVSi | 106.3 | 85.0 | 75.3 | 92.1 | 49.4 | 22.0 | 35.7 | 94.9 | 7.1 | 0.33 | 2.58 | −0.015 |
| YbNiVSi | 94.6 | 96.7 | 65.8 | 96.0 | 39.1 | −2.7 | 18.2 | 51.3 | −62.7 | 0.41 | 5.28 | −0.085 |
| LuFeVAl | 113.3 | 91.8 | 88.3 | 99.0 | 57.3 | 22.7 | 40.0 | 105.8 | 8.2 | 0.32 | 2.47 | 1.088 |
| LuCoVAl | 75.9 | 69.7 | 61.7 | 71.8 | 38.3 | 7.2 | 22.7 | 61.7 | 19.9 | 0.36 | 3.16 | 0.847 |
| LuNiVAl | 80.9 | 63.3 | 59.1 | 69.2 | 39.0 | 18.0 | 28.5 | 75.1 | 6.7 | 0.32 | 2.43 | 0.618 |
| LuFeVSi | 156.3 | 131.0 | 75.8 | 139.4 | 50.5 | 25.3 | 37.9 | 104.3 | 6.0 | 0.38 | 3.68 | −0.153 |
| LuCoVSi | 108.1 | 84.3 | 77.7 | 92.2 | 51.4 | 24.2 | 37.8 | 99.4 | 6.5 | 0.32 | 2.44 | −0.062 |
| LuNiVSi | 128.7 | 108.8 | 68.9 | 115.4 | 45.3 | 20.5 | 32.9 | 90.1 | 6.9 | 0.37 | 3.51 | −7.192 |
| Type III | ||||||||||||
| YbFeVAl | 81.8 | 65.6 | 69.1 | 71.1 | 44.7 | 17.1 | 30.9 | 81.0 | 8.6 | 0.31 | 2.30 | −0.239 |
| YbCoVAl | 124.2 | 56.5 | 59.4 | 79.1 | 49.2 | 45.6 | 47.4 | 118.5 | 1.8 | 0.25 | 1.67 | −0.330 |
| YbNiVAl | 129.0 | 54.5 | 61.6 | 79.3 | 51.9 | 48.8 | 50.4 | 124.7 | 1.7 | 0.24 | 1.58 | −0.289 |
| YbFeVSi | 134.8 | 53.0 | 72.0 | 80.3 | 59.6 | 55.2 | 57.4 | 139.0 | 1.8 | 0.21 | 1.40 | −0.223 |
| YbCoVSi | 187.8 | 69.0 | 66.9 | 108.6 | 63.9 | 63.7 | 63.8 | 160.0 | 1.1 | 0.25 | 1.70 | −0.152 |
| YbNiVSi | 167.9 | 65.7 | 71.4 | 99.6 | 63.4 | 61.7 | 62.5 | 155.1 | 1.4 | 0.24 | 1.59 | −0.089 |
| LuFeVAl | 159.5 | 103.9 | 66.6 | 122.4 | 51.1 | 42.7 | 46.9 | 124.8 | 2.4 | 0.33 | 2.61 | −0.534 |
| LuCoVAl | 150.1 | 74.3 | 75.7 | 99.6 | 60.6 | 54.1 | 57.4 | 144.3 | 2.0 | 0.26 | 1.74 | −0.638 |
| LuNiVAl | 162.8 | 71.4 | 85.1 | 101.9 | 69.3 | 63.3 | 66.3 | 163.5 | 1.9 | 0.23 | 1.54 | −0.506 |
| LuFeVSi | 176.3 | 89.3 | 90.9 | 118.3 | 71.9 | 63.3 | 67.6 | 170.4 | 2.1 | 0.26 | 1.75 | −0.513 |
| LuCoVSi | 190.0 | 63.3 | 98.8 | 105.5 | 84.6 | 80.3 | 82.7 | 196.7 | 1.6 | 0.19 | 1.28 | 1.850 |
| LuNiVSi | 121.5 | 97.6 | 76.4 | 105.6 | 50.6 | 24.2 | 37.4 | 100.4 | 6.4 | 0.34 | 2.82 | −0.358 |
Generally, the Young's modulus E can present the stiffness of the material: a higher value of E indicates that the material is stiffer. As shown in Table 4, most of the E values are large. However it is very small for type I LuCoVSi (4.2 GPa), LuNiVSi (7.9 GPa), and YbNiVSi (−25.2 GPa). These low or even negative Young's modulus values E imply that these EQH compounds are very soft and tend to be mechanically unstable. In general, EQH alloys in the type III structure exhibit higher values of E, whereas the type I structure leads to lower E values. As a result, the general order of stiffness is type III > type II > type I.
The well known Pugh's ratio38 of B/G can be used to estimate the failure behavior of compounds. A material is classified to be ductile if B/G > 1.75, otherwise it is considered to be brittle. According to this empirical criterion, all type I and II EQH compounds except type I YbFeVAl, YbCoVAl, and YbFeVSi are ductile in nature. On the contrary, all EQH compounds in type III are brittle materials, except YbFeVAl, LuFeVAl, and LuNiVSi. This result is consistent with the trend of stiffness. In other words, the more stiff the material, the less ductile it is.
The Poisson's ratio provides useful information to understand the characteristics of the bonding forces in a material.39 It has been proved that ν = 0.25 is the lower limit of the central force solid, and ν = 0.5 is the upper limit of the infinite elastic anisotropy.40 It has also been suggested that brittleness and ductility can be judged considering the values ν < 1/3 and ν > 1/3, respectively.41 According to the above conditions, we can find that type I EQH compounds all show ductile behavior, except for YbFeVAl, YbCoVAl, and YbFeVSi. On the contrary, all type III EQH compounds exhibit a brittle nature, except for LuNiVSi. In between, one-half of type II EQH compounds are brittle, and the other half are ductile.
The anisotropy factor A, as shown in Table 4, of a solid can be used to predict whether the considered EQH compounds show mechanical anisotropy. A, also called the shear anisotropy factor, is defined as the ratio of the shear modulus between [001] and [1−10] directional stress on the shear plane (110). For a orthorhombic crystal, the shear modulus for a shear system (hkl)[uvw] is given by42,43
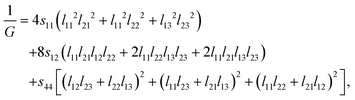 | (11) |
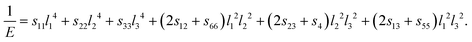 | (12) |
Therefore, the elastic anisotropy factor can be defined not only by the shear modulus but also by the bulk and Young's moduli. Moreover, there are other definitions of elastic anisotropy factors such as percentage anisotropy incompressibility and shear44 anisotropy. The shear anisotropic factors provide a measure of the degree of anisotropy in the bonding between atoms in different planes. As shown in Table 4, the value of A for all the studied EQH compounds is not equal to 1, which indicates that they are all elastic anisotropic. The difference of A from 1 (either larger or smaller than 1) provides an indication to estimate the level of elastic anisotropy acquired by the crystals.
To clarify the elastic anisotropy, we also present the orientation dependence of the shear modulus and Young's modulus as shown in Fig. 5 and 6, respectively. Fig. 5 shows the shear modulus corresponding to all directions on the (110) shear plane. It is clear that Fig. 5(b), (c), (f), and (i) show a complex cusp pattern for the type I structure and Fig. 5(i) for the type II structure, which means that these compounds are not stable. In addition, it can also be seen that the shear modulus show significant anisotropy. Indeed, the shear moduli G(100)[001] and G(100)1–10 are equivalent to C44 and (C11 − C12)/2, respectively. This indicates that A is the ratio between the x-intercept and the y-intercept. Further, Fig. 5 also illustrates a general trend that the anisotropic levels of type III EQH compounds are lower than those of type I and type II. On the other hand, Fig. 6 shows the Young's modulus with the tensile axis rotated from [100] to [010]. Similar to the shear modulus shown in Fig. 5, the Young's modulus (Fig. 6) also shows that all EQH compounds in the type III structure are more isotropic than those in type I and II structures.
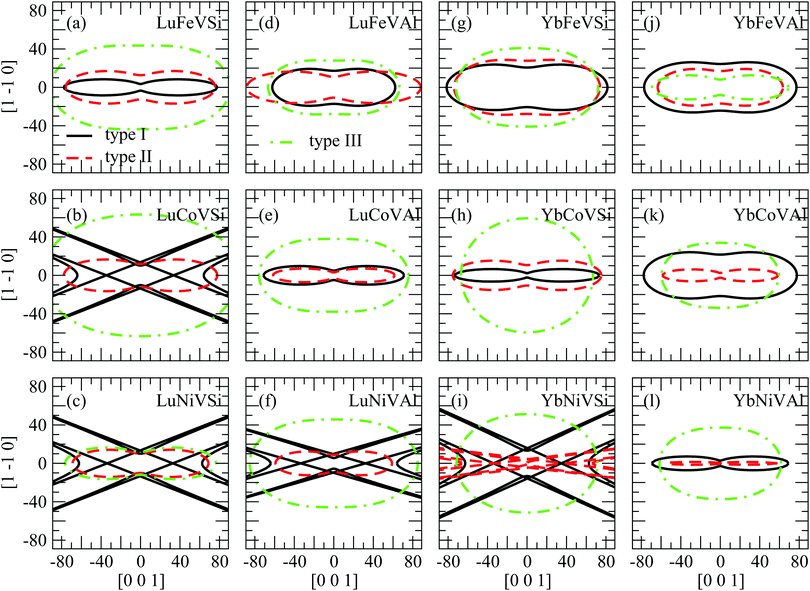 | ||
| Fig. 5 Contours of the shear modulus (G, in GPa) for shear stress along [001] to [1-10] on the (110) shear plane. | ||
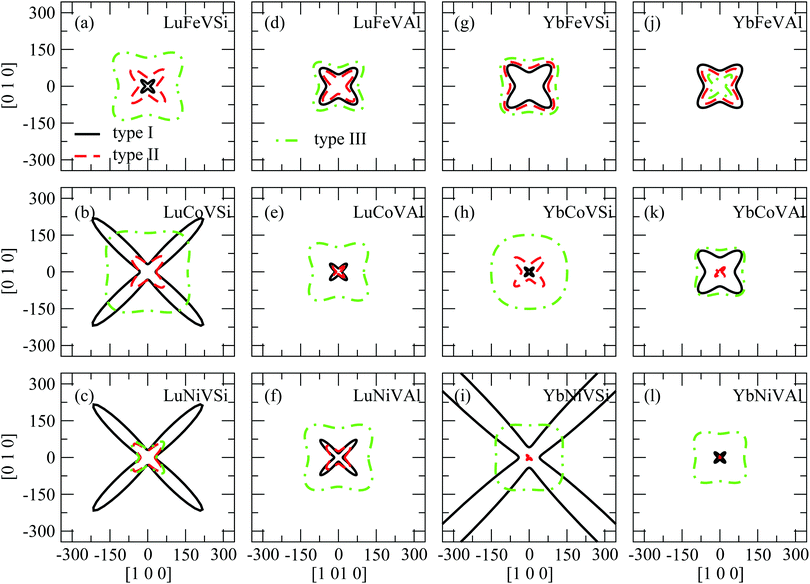 | ||
| Fig. 6 The directional Young's modulus (E, in GPa) with the tensile axis rotated from [100] to [010]. | ||
Piezoelectricity states that a material can generate electric dipole moments under external stress. This process can be reversed to produce stress on a material by applying an external electric field. For materials with the cubic symmetry, the piezoelectric tensor eij can be reduced to
 | (13) |
The calculated piezoelectric constant e14 is listed in Table 4 as e (C m−2). We found that for most of the studied rare earth EQH compounds, the piezoelectric constant |e| is small, usually less than 1 (C m−2). The commonly used piezoelectric material, lead zirconate titanate, exhibits a maximum value of piezoelectric tensor components in the range from 6 to 12 (C m−2).45 In general, materials with |e| > 3 might be useful for piezoelectrics. Over the 36 cases studied in this work, only one, i.e., type II LuNiVSi, exhibits an applicable piezoelectric constant of 7.192 C m−2.
IV. Conclusions
We have systematically studied the rare earth equiatomic quaternary Heusler compounds through first-principles calculations based on density functional theory. Twelve EQH compounds in three types of structures are considered. Most of the rare earth EQH compounds show magnetic ground states. 7 out of 12 EQH compounds in the type I structure are ferromagnetic half-metals with integer magnetic moments. Type II YbFeVAl is found to be the rare antiferromagnetic half-metal with zero total spin moment. Moreover, type III LuCoVSi is found to be an unusual magnetic semiconductor to have an integer magnetic moment of 3.00 μB and an indirect band gap of 0.2 eV. Both AHM and MSC phases are difficult to find but are of high potential in future spintronics. Structural and magnetic stability related factors formation energy, magnetization energy, as well as mechanical stability related factors such as the bulk, shear, and Young's modulus, and the Poisson's and Pugh's ratios of these EQH compounds are presented. Our work provides guidelines on the synthesis of useful materials for future spintronic devices.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by China Medical University, Taiwan (CMU108-N-25) and the Ministry of Science and Technology, Taiwan (MOST-107-2112-M-039-002-MY2, MOST-106-2112-M-007-012-MY3). The authors are also thankful for the support from the Academia Sinica, NCHC, CINC-NTU, AS-iMATE-109-13, and CQT-NTHU-MOE, Taiwan.References
- T. Graf, C. Felser and S. S. P. Parkin, Simple rules for the understanding of Heusler compounds, Prog. Solid State Chem., 2011, 39, 1 CrossRef CAS.
- C. Felser and A. Hirohata, Heusler Alloys, properties, growth, applications, Springer Series in Materials Science, 2016, p. 222 Search PubMed.
- L. Bainsla and K. G. Suresh, Equiatomic quaternary Heusler alloys: a material perspective for spintronic applications, Appl. Phys. Rev., 2016, 3, 031101 Search PubMed.
- C. Felser, L. Wollmann, S. Chadov, G. H. Fecher and S. S. P. Parkin, Basics and prospective of magnetic Heusler compounds, APL Mater., 2015, 3, 041518 CrossRef.
- Warren E. Pickett and S. Moodera Jagadeesh, Half metallic magnets, Phys. Today, 2001, 54, 39–44 CrossRef CAS.
- R. A. De Groot, et al., New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50, 2024 CrossRef CAS.
- L. Zhang, et al., Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-earth-element-based quaternary Heusler compounds, J. Alloys Compd., 2017, 718, 63 CrossRef CAS.
- I. Galanakis and E. Şaşioğlu, High TC half-metallic fully-compensated ferrimagnetic Heusler compounds, Appl. Phys. Lett., 2011, 99, 052509 CrossRef.
- N. Kervan, S. Kervan, O. Canko, M. Atis and F. Taskin, Half-Metallic Ferrimagnetism in the Mn2NbAl Full-Heusler Compound: a First-Principles Study, J. Supercond. Novel Magn., 2016, 29, 187–192 CrossRef CAS.
- D. Benea, R. Gavrea, M. Coldea, O. Isnard and V. Pop, Half-metallic compensated ferrimagnetism in the Mn-Co-V-Al Heusler alloys, J. Magn. Magn. Mater., 2019, 475, 229–233 CrossRef CAS.
- I. Asfour, H. Rached, S. Benalia and D. Rached, Investigation of electronic structure, magnetic properties and thermal properties of the new half-metallic ferromagnetic full-Heusler alloys Cr2GdSi1−xGex: An ab-initio study, J. Alloys Compd., 2016, 676, 440–451 CrossRef CAS.
- B. G. Yalcin, Ground state properties and thermoelectric behavior of Ru2VZ (Z = Si, ge, sn) half-metallic ferromagnetic full-Heusler compounds, J. Magn. Magn. Mater., 2016, 408, 137–146 CrossRef CAS.
- A. Kundu, S. Ghosh, R. Banerjee, S. Ghosh and B. Sanyal, New quaternary half-metallic ferromagnets with large Curie temperatures, Sci. Rep., 2017, 7, 1803 CrossRef.
- V. Srivastava and K. P. Bhatti, Ferromagnetic shape memory Heusler alloys, Solid State Phenom., 2012, 189, 189–208 CAS.
- Y.-K. Wang and J.-C. Tung, Structural, electronic and magnetic properties of Ni2XAl (X = V, Cr, Mn, Fe, and Co) Heusler alloys: An ab-initio study, Phys. Open, 2020, 2, 100008 CrossRef.
- A. K. Singh, S. D. Ramarao and S. C. Peter, Rare-earth based half-Heusler topological quantum materials: A perspective, APL Mater., 2020, 060903 CrossRef CAS , NPAM2020.
- X. T. Wang, et al., Three-dimensional topological insulators: case of quaternary Heusler compounds, Rare Met., 2015 DOI:10.1007/s12598-014-0421-1.
- A. J. Bradley and J. M. Rogers, The Crystal Structure of the Heusler Alloys, Proc. R. Soc. A, 1934, 144, 340 CAS.
- K. Özdoğan, E. Şasoşlu and I. Galanakis, Slater–Pauling behavior in LiMgPdSn-type multifunctional quaternary Heusler materials: Half-metallicity, spin-gapless and magnetic semiconductors, J. Appl. Phys., 2013, 113, 193903 CrossRef.
- L. Bainsla, et al., High spin polarization and spin splitting in equiatomic quaternary CoFeCrAl Heusler alloy, J. Magn. Magn. Mater., 2015, 394, 82 CrossRef CAS.
- X. Wang, et al., Rare earth-based quaternary Heusler compounds MCoVZ (M = Lu, Y; Z = Si, Ge) with tunable band characteristics for potential spintronic applications, IUCrJ, 2017, 4, 758 CrossRef CAS.
- S. Berri, et al., Robust half-metallic ferromagnet of quaternary Heusler compounds ZrCoTiZ (Z = Si, Ge, Ga and Al), Comput. Condens. Matter, 2014, 1, 26 CrossRef.
- X. Wang, et al., First-principles study of new quaternary Heusler compounds without 3d transition metal elements: ZrRhHfZ (Z = Al, Ga, In), Mater. Chem. Phys., 2017, 193, 99 CrossRef CAS.
- R. Guo, et al., First-principles study on quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In) with large spin-flip gap, RSC Adv., 2016, 6, 109394 RSC.
- G. Xu, et al., Highly-dispersive spin gapless semiconductors in rare-earth-element contained quaternary Heusler compounds, J. Phys. D: Appl. Phys., 2017, 50, 105003 CrossRef.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B, 1993, 48, 13115 CrossRef CAS.
- G. Kresse and J. Furthműller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- Y. Wang and J. P. Perdew, Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling, Phys. Rev. B, 1991, 44, 13298 CrossRef.
- Y. Wang and J. P. Perdew, Accurate and simple analytic representation of the electron–gas correlation energy, Phys. Rev. B, 1992, 45, 13244 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65, 1501–1509, DOI:10.1007/s11837-013-0755-4 , http://oqmd.org/materials/composition/C S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1, 15010, DOI:10.1038/npjcompumats.2015.10.
- Enamullah, Y. Venkateswara, S. Gupta, M. R. Varma, P. Singh, K. G. Suresh and A. Alam, Electronic structure, magnetism, and antisite disorder in CoFeCrGe and CoMnCrAl quaternary Heusler alloys, Phys. Rev. B, 2015, 92, 224413 CrossRef.
- V. Alijani, et al., Electronic, structural, and magnetic properties of the half-metallic ferromagnetic quaternary Heusler compounds CoFeMnZ (Z = Al, Ga, Si, Ge), Phys. Rev. B, 2011, 84, 224416 CrossRef.
- L. Basit, et al., Quaternary Heusler Compounds without Inversion Symmetry: CoFe1+xTi1−xAl and CoMn1+xV1−xAl, Eur. J. Inorg. Chem., 2011, 3950 CrossRef CAS.
- W. Voigt, Lehrbuch der kristallphysik, ed. B. G. Teubner, 1928 Search PubMed.
- A. Reuss and Z. Angew, Berchung der fiessgrenze von mischkristallen auf grund der plastizitätsbedingung fur einkristalle, J. Math. Mech., 1929, 9, 49 CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press, 1954 Search PubMed.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- W. Koster and H. Franz, Metall. Rev., 1961, 6, 1–56 CrossRef CAS.
- M. H. Ledbetter, in Materials at Low Temperatures, ed. R. P. Reed and A. F. Clarck, American Society for Metals, Metals Park, OH, 1983 Search PubMed.
- I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, in Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, ed. I. N. Frantsevich, Naukova Dumka, Kiev, 1983 Search PubMed.
- G. Ghosh, A first-principles study of cementite (Fe3C) and its alloyed counterparts: Elastic constants, elastic anisotropies, and isotropic elastic moduli, AIP Adv., 2015, 5, 087102 CrossRef.
- J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Metrices, Oxford University Press, Oxford, UK, 1985 Search PubMed.
- D. H. Chung and W. R. Buessem, The Elastic Anisotropy of Crystals, J. Appl. Phys., 1967, 38, 2010–2012 CrossRef CAS.
- Z. Wu and R. E. Cohen, Pressure-induced anomalous phase transitions and colossal enhancement of piezoelectricity in PbTiO3, Phys. Rev. Lett., 2005, 95, 037601 CrossRef.
| This journal is © the Owner Societies 2021 |