Interlayer separation in hydrogen titanates enables electrochemical proton intercalation

Abstract

Electrochemical proton intercalation into titanium oxides is typically limited to the near-surface region, necessitating the use of nanostructured high surface area materials to obtain high capacities. Here, we investigate the role of materials structure to extend intercalation beyond the near-surface region. Employing a series of hydrogen titanates (HTOs), we find that electrochemical protonation capacity significantly increases with interlayer structural protonation. The maximum capacity of ∼80 mA h g⁻¹ is achieved with H₂Ti₃O₇, which also undergoes reversible structural and optical changes during the de/intercalation process. Using quasi-elastic neutron scattering, we show that structural protons are highly confined in the HTO interlayer with only localized, but not translational, dynamics. Electrochemical protonation leads to a contraction of the H₂Ti₃O₇ interlayer without causing significant strain in the two-dimensional titanate layers. Density functional theory calculations indicate more favorable adsorption energy for intercalated protons in H₂Ti₃O₇ as compared to HTOs with fewer structural protons. We hypothesize that interlayer structural protons are the structural feature responsible for the high electrochemical protonation capacity in H₂Ti₃O₇ because they effectively decrease the interconnections between the titanate layers. This enables facile compensation of the electrochemically introduced strain via one-dimensional interlayer contraction. These results demonstrate the special structural requirements for bulk proton intercalation in titanium oxides, and offer a new materials design strategy for high energy density aqueous energy storage.

---

1. Introduction

Electrochemical energy storage devices such as lithium-ion batteries are now ubiquitous in modern life. Most of these devices utilize solid-state electrodes to store energy. As the use of electrochemical energy storage expands from portable electronics to electric vehicles and smart grids, there is an urgent need to correlate the properties of the electrode materials with electrochemical performance. These include the search for energy storage materials and mechanisms with high energy density and safety, as well as low cost.¹ Recently, the finding that highly concentrated aqueous electrolytes enable wide voltage windows (>3 V) has rekindled the search for high energy density and highly safe electrochemical energy storage in aqueous electrolytes.^2–6 Concomitant with this finding is the recent discovery that protons are likely the intercalating species into materials from many aqueous and non-aqueous electrolytes.^7–11 Together, these motivate the search for high capacity electrochemical proton intercalation in solid state materials, particularly ones that are also earth-abundant. From an even more fundamental standpoint, protons are unique intercalants because of their very low mass and volume (with a recently measured radius of 0.833 fm),¹² as compared to other cations. The electrochemical intercalation of protons is thus primarily concerned with the need to distribute the associated charge in the electrode material.

Titanium dioxide (TiO₂) is a highly versatile, abundant, non-toxic, and corrosion-resistant functional material that is used in many energy and environmental applications, such as photocatalysis, solar energy conversion, electrochromic devices, air/water purification, and electrochemical energy storage.^13,14 Upon cathodic polarization in an aqueous electrolyte, TiO₂ undergoes a surface reduction of Ti(IV) to Ti(III) due to the electrochemical intercalation of protons in the near-surface region, as indicated by the dependence of the capacity on the specific surface area.¹⁵ The synthesis of nanostructures is essential to enable this near-surface intercalation,^11,16,17 and leads to a proton intercalation capacity of up to ∼70 mA h g⁻¹.¹¹ Due to the abundance, safety, and lightweight of titanium and the potential of high energy density aqueous batteries, it is desirable to investigate materials design strategies, beyond nanostructuring, that lead to high capacity electrochemical proton intercalation in titanium oxides.

Here, we systematically investigate the role of materials structure in extending proton intercalation beyond the near-surface region of TiO₂ by characterizing the electrochemical behavior of a series of layered hydrogen titanates (HTOs; H₂Ti_3nO_6n+1, n = 1, 2, 4)¹⁸ as well as the completely dehydrated TiO₂(B). We show, for the first time, that the electrochemical proton intercalation capacity significantly increases with structural protonation of HTO (i.e., increasing H/Ti ratio), with the highest capacity obtained with H₂Ti₃O₇. Our quasi-elastic neutron scattering (QENS) results indicate that interlayer structural protons in HTOs are highly confined and exhibit primarily localized, but not translational, dynamics. We provide ex situ X-ray diffraction (XRD) results to show that electrochemical proton intercalation in H₂Ti₃O₇ is accompanied by a contraction of the interlayer spacing, but results in no significant strain in the two-dimensional titanate layers. Our density functional theory (DFT) results indicate that interlayer structural protons lead to a decreased adsorption energy for electrochemical H⁺ intercalation in H₂Ti₃O₇. We hypothesize that interlayer structural protons are the structural feature essential for electrochemical intercalation of H⁺ in titanates. Structural protons decrease covalent bond interconnection between titanate layers which may enable a more facile distribution of charge associated with electrochemical proton intercalation. In particular, the high degree of interlayer structural protons in H₂Ti₃O₇ may limit the strain caused by electrochemically intercalated protons to simply a one-dimensional contraction of the interlayer. This newly gained understanding of structural requirements for electrochemical protonation in titanates offers a new materials design strategy for high energy density aqueous energy storage.

2. Materials and methods

2.1 Synthesis of hydrogen titanates

Hydrogen titanates were synthesized via a modified procedure, as described in ref. 19. First, sodium trititanate (Na₂Ti₃O₇) was synthesized via a solid-state reaction between titanium oxide (TiO₂, Aeroxide P25, Sigma-Aldrich) and sodium carbonate (Na₂CO₃, anhydrous, Sigma-Aldrich). For homogenization of the precursors, 10 g of Na₂CO₃ was dissolved in 150 mL of deionized H₂O, followed by 20 g of TiO₂. The mixture was stirred at 70 °C until all water evaporated, ground in a pestle and mortar, then heated in an alumina crucible in a box furnace at 800 °C for 20 h with a heating rate of 2 K min⁻¹. Hydrogen trititanate (H₂Ti₃O₇) was obtained via a proton-exchange reaction of the as-synthesized Na₂Ti₃O₇ in 250 mL of 2 M HCl (Fisher Scientific) under magnetic stirring at 80 °C for 3 days. The sample was washed and centrifuged at 4500 rpm for 30 min three times in deionized H₂O until reaching a pH-value of ca. 5 and then dried at 80 °C overnight.

Hydrogen titanates with reduced interlayer structural protonation were obtained by annealing the as-synthesized H₂Ti₃O₇ at different temperatures. H₂Ti₆O₁₃ was obtained by holding at 175 °C for 6 h, H₂Ti₁₂O₂₅ at 280 °C for 7 h, and TiO₂(B) at 380 °C for 4 h with heating/cooling rates of 2 K min⁻¹.

2.2 Physical characterization

Thermogravimetric analysis (TGA) was carried out with a Seiko Exstar TG/DTA6200 using a heating rate of 2 K min⁻¹ to reach maximum temperatures of 175 °C, 280 °C, and 380 °C in an air atmosphere. X-ray diffraction (XRD) was conducted with a Rigaku SmartLab X-ray diffractometer with a copper Kα source in a Bragg–Brentano setup. Raman spectroscopy was performed with a WiTEC alpha300R confocal Raman microscope using an Nd:YAG laser with 532 nm wavelength and a 100× objective.

2.3 Neutron scattering

QENS experiments were conducted at the time-of-flight backscattering spectrometer (BASIS)²⁰ at the Spallation Neutron Source at Oak Ridge National Laboratory. The bandwidth of the incident neutron was centered at 6.4 Å, and the wavelength of the detected neutrons after scattering by the sample was λ₀ = 6.267 Å, as selected by the (111) Bragg reflection at 88° of the Si crystal analyzer. The Q-range of the collected data was between 0.5 Å⁻¹ to 1.5 Å⁻¹, obtained from an accessible range of energy transfer from −100 to 100 μeV with an overall energy resolution of 3.7 μeV. All samples (each ca. 7 g in ∼1 mm thick aluminum pouch) were loaded in unsealed cylindrical aluminum containers. The containers were heated to 80 °C and evacuated prior to QENS experiments to ensure evaporation of any surface water.

2.4 Electrode preparation

Electrode slurries were prepared by homogenizing 80 mass% of active material (H₂Ti₃O₇, H₂Ti₆O₁₃, H₂Ti₁₂O₂₅, or TiO₂(B)) with 10 mass% of carbon black (acetylene, 75 m² g⁻¹, Alfa Aesar) and 10 mass% of polyvinylidene fluoride (PVDF, Arkema Kynar KV 900) in a pestle and mortar and dispersing in N-methyl-2-pyrrolidone (NMP, Sigma-Aldrich) by magnetic stirring. The slurries were cast on glassy carbon substrates (Alfa Aesar) with a mass loading of about 0.7 mg cm⁻². Glassy carbon was used as the current collector due to its corrosion resistance in acidic electrolytes and low surface area, which minimizes the current from the hydrogen evolution reaction (HER) at cathodic potentials. For electrochemical in situ Raman measurements, the slurry was applied on screen-printed electrode substrates (Pine Research). All electrodes were dried at 80 °C overnight prior to use.

2.5 Electrochemical characterization

Electrochemical measurements were carried out in 50 mL three-neck round-bottom glass flasks (Sigma-Aldrich) in a half-cell setup using the slurry-coated glassy carbon as a working electrode, a platinum wire (99.997%, Alfa Aesar) as the counter electrode, and Ag/AgCl in saturated KCl solution (Pine Research) as the reference electrode. The electrolyte was 0.1, 0.5, 1.0, or 3.0 M H₂SO₄ (Fisher Scientific) in water, or 1 M Li₂SO₄ in water, as specified later. Cyclic voltammetry was performed using a VMP3 potentiostat/galvanostat (Bio-Logic).

2.6 In situ and ex situ electrochemical experiments

Electrochemical in situ Raman experiments were performed using a 20× immersion objective. Linear sweep voltammetry experiments were conducted using a potentiostat (Pine Instruments WaveNow) and screen-printed electrodes with a carbon counter electrode and a silver quasi-reference electrode (Pine Research Instrumentation). Raman spectra were recorded after scanning to the target potential with a rate of 10 mV s⁻¹ and holding for 30 s.

Electrochemical ex situ XRD measurements were conducted with the slurry-coated glassy carbon electrodes described above using a PANalytical Empyrean diffractometer with a copper source in a Bragg–Brentano setup. After charging to the desired potential, the electrodes were quickly removed from the three-neck flask and covered with a thin Mylar foil to limit oxidation by air.

2.7 Density functional theory

DFT calculations were performed using the Vienna ab initio Simulation Package (VASP)²¹ with the Perdew–Burke–Ernzerhof (PBE)²² form of the generalized-gradient-approximation exchange correlation functional. The projector augmented wave (PAW) potential was used to describe the electron–nuclei interaction.²³ An energy cutoff of 500 eV was used for the plane wave basis sets. The structures of H₂Ti₃O₇·H_x and H₂Ti₆O₁₃·H_x were simulated by a supercell containing 4 and 2 formula units, respectively. All degrees of freedom were relaxed with a force convergence criterion of 0.01 eV Å⁻¹ and energy convergence criterion of 10⁻⁵ eV. A 1 × 5 × 2 Monkhorst–Pack k point grid was adopted for Brillouin zone integration.²⁴ DFT-D3 was used to account for the van der Waals interaction.²⁵ To model the proton insertion energetics during electrochemical experiments, hydrogen atoms (H⁺ + e⁻) were inserted into the unit cell and the hydrogen adsorption energy was calculated as .

3. Results and discussion

3.1 Structure of hydrogen titanates

Layered HTOs were chosen as a model material system to investigate the effect of interlayer structural protonation on electrochemical H⁺ intercalation. The hydrogen titanate phase with the highest degree of interlayer structural protonation, H₂Ti₃O₇, will transform to TiO₂(B) over several discrete dehydration steps at elevated temperatures according to:

H₂Ti₃O₇ has a monoclinic crystal structure with a two-dimensional arrangement of titanate layers. Each layer consists of units of three edge-sharing TiO₆ octahedra that are connected to the next unit by corners, forming a step-like structure. According to prior neutron diffraction results, “structural protons” (protons incorporated upon exposure of the sodium titanate parent material to an acid solution) are bound to both bridging and terminal oxygens as hydroxyl groups and reside in the interlayer space, effectively separating the titanate layers.²⁶Fig. 1A shows the proposed crystal structures of the HTOs according to prior studies.^26–28 However, our DFT simulations show that the formation of an equal number of hydroxyl and water groups at bridging and terminal oxygens, respectively, leads to a more energetically relaxed structure (Fig. S1A and B, ESI†), which also aligns with our experimental XRD result (Fig. S1C, ESI†) and experimental data from Eguía-Barrio et al.²⁹

Fig. 1 (A) Proposed crystallographic structures of HTOs in different states of interlayer structural protonation according to crystal information files available from prior studies.^26–28 (B) Scanning electron micrograph of H₂Ti₃O₇.

The H₂Ti₃O₇ structure can be partially dehydrated to form the first intermediate phase H₂Ti₆O₁₃, which reduces the interlayer structural proton content by half and removes one terminal oxygen as compared to H₂Ti₃O₇. This causes the edge-sharing layers of TiO₆ octahedra to connect with an opposing layer by corner-sharing with a (previously) terminal oxygen.³⁰ Further interlayer structural dehydration results in increased interconnections between the titanate layers, yielding the second intermediate phase H₂Ti₁₂O₂₅.³¹ Full interlayer structural dehydration results in the monoclinic TiO₂(B) phase that exhibits entirely interconnected titanate layers.³¹ Overall, this step-wise increase in titanate layer interconnections upon dehydration of H₂Ti₃O₇ may lead to more constraints on the structure's ability to expand or contract along the a-unit cell direction.³² From a morphological standpoint, the synthesized H₂Ti₃O₇ consists of large, rod-like particles of up to 20 μm in length and several microns in diameter (Fig. 1B). Importantly, this morphology does not appear to change upon dehydration.

Thermogravimetric analysis was performed to confirm the structural proton content of the different HTOs (Fig. 2A). All TGA curves are characterized by an initial mass loss of <1 wt% caused by the desorption of surface water. Subsequent mass loss is caused by the dehydration of the interlayer in three distinct steps (Fig. S2, ESI†). Holding for 8 h at 175 °C led to a subsequent mass loss of 2.5%, which is slightly below the theoretical mass loss for the first dehydration step (removal of 0.5 H₂O from H₂Ti₃O₇ to form H₂Ti₆O₁₃). Annealing at 280 °C for 7 h led to a subsequent mass loss of 4.8 wt%, close to the theoretical value for the formation of H₂Ti₁₂O₂₅ from H₂Ti₃O₇. Finally, annealing at 380 °C for 4 h resulted in a subsequent mass loss of 5.9 wt%, slightly below the theoretical value for the removal of 1 H₂O from H₂Ti₃O₇ to form TiO₂.

Fig. 2 (A) Thermogravimetric analysis of H₂Ti₃O₇ in air with a heating rate of 2 K min⁻¹ at different temperatures and holding times (175 °C, 8 h, yielding H₂Ti₆O₁₃; 280 °C, 7 h, yielding H₂Ti₁₂O₂₅; 380 °C, 4 h, yielding TiO₂(B)). (B) X-ray diffractograms, and (C) Raman spectra of all four HTOs. Assignment of Raman modes in TiO₂(B) follows ref. 34.

The crystallinity of the synthesized titanates was analyzed by XRD (Fig. 2B). The diffraction pattern of the ion-exchanged H₂Ti₃O₇ matches with the structure of monoclinic H₂Ti₃O₇ (PDF 00-047-0561 (ICDD, 1997), “Model B” in Fig. S1, ESI†). The main peak at 11.2° 2θ corresponds to the (200) plane, indicating an interlayer distance of 7.9 Å between the titanate sheets. The intermediate phases of HTO synthesized at 175 °C and 280 °C show (200) signals at 12.1° 2θ and 14.2° 2θ, indicating decreased interlayer distances of 7.3 Å and 6.2 Å, respectively. The diffractograms match previous reports in the literature of the H₂Ti₆O₁₃ and H₂Ti₁₂O₂₅ phases, respectively.¹⁹ Full dehydration is achieved by annealing at 380 °C, with the diffractogram of the resulting material matching that of monoclinic TiO₂(B) (PDF 00-046-1238 (ICDD, 1996)).

We used Raman spectroscopy to analyze the interlayer bonding environment (Fig. 2C). A prior report on layered titanates assigned the broad peaks between 700 and 900 cm⁻¹ to Ti–O symmetric stretching modes, whose position changed depending on the interlayer species (proton vs. cation).³³ H₂Ti₃O₇ has two broad bands at 770 cm⁻¹ and 853 cm⁻¹, suggestive of two different bonding environments of the interlayer oxygens. A shift of these two signals to higher wavenumbers (868 cm⁻¹ and 915 cm⁻¹, respectively) in H₂Ti₆O₁₃ suggests stronger Ti–O bonds as compared to H₂Ti₃O₇. The spectrum of H₂Ti₁₂O₂₅ is very similar to that of TiO₂(B), indicating the close structural relationship between these materials which are separated in composition by the dehydration of just 0.25 H₂O. The Raman spectrum of TiO₂(B) is in good agreement with previous reports.³⁴

We utilized QENS to probe the dynamics of interlayer structural protons in HTOs. Fig. 3A shows the elastic neutron scattering intensity of all four HTOs as a function of temperature. The total elastic intensity, which in the measured scattering vector (Q) range is primarily due to incoherent neutron scattering by the protons, increases with a higher degree of interlayer structural protonation, as expected from the composition and TGA results. Both H₂Ti₃O₇ and H₂Ti₆O₁₃ show a nearly linear temperature dependence of the elastic intensity. This indicates the absence of a transition to a distinct regime of diffusive proton motion upon warming on the nano- to pico-second timescales probed by QENS. Fig. 3B shows the normalized elastic intensity as a function of temperature. The rapid decrease of the elastic intensity in H₂Ti₁₂O₂₅ and TiO₂(B) above ∼220 K is likely due to the presence of small amounts of water confined in 5–10 nm mesopores. This result strongly suggests that small amounts of water become trapped in closed pores of the HTOs during the dehydration process.

Fig. 3 (A) Raw and (B) low temperature-normalized elastic neutron scattering intensity integrated over the entire accessible Q-range (0.5–1.5 Å⁻¹) of all samples as a function of temperature. (C) Single Lorentzian peak fit and (D) Q- and T-dependent FWHM of quasi-elastic signal of H₂Ti₃O₇. (E) Single Lorentzian peak fit and (F) Q- and T-dependent FWHM of quasi-elastic signal of H₂Ti₆O₁₃.

The dynamics of interlayer structural protons in H₂Ti₃O₇ and H₂Ti₆O₁₃ were analyzed by fitting the QENS peaks (Fig. 3C and E). In both of these HTOs, a single Lorentzian peak can be fit to the experimental data. The full-width-half-maxima (FWHM) for Q = 0.5–1.5 Å⁻¹ (Fig. 3D and F) show only weak temperature- and Q-dependence. The weak Q-dependence indicates that the interlayer structural protons in both materials exhibit no translational motion on the timescale probed in the QENS experiment. However, the higher activation energy associated with H₂Ti₃O₇ compared to H₂Ti₆O₁₃ (Fig. S3, ESI†) is likely associated with stronger proton–proton interaction in the former compound. These results are significant because they demonstrate that structural protons are confined at their respective interlayer binding sites, where they decrease interconnection between the titanate layers.

3.2 Electrochemical characterization

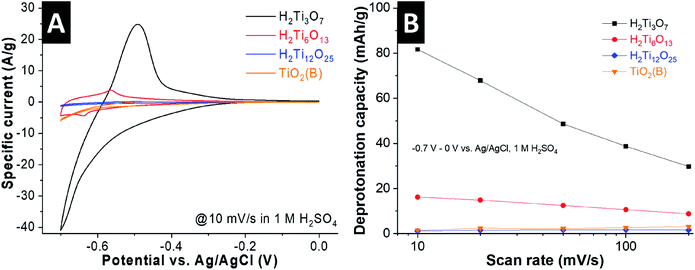
We performed cyclic voltammetry in 1 M H₂SO₄ to evaluate the H⁺ intercalation properties of the titanates as a function of interlayer structural protonation. The current responses of the materials at a scan rate of 10 mV s⁻¹ (70 s charging time) indicate drastically different electrochemical behavior (Fig. 4A). H₂Ti₃O₇ shows a continuous increase in cathodic current from ca. −0.4 V vs. Ag/AgCl and a strong peak at around −0.6 V, which we hypothesize to originate from H⁺ intercalation according to:

H₂Ti₃O₇ + xH⁺ + xe⁻ ↔ H_2+xTi₃O₇ (2)

Fig. 4 (A) Cyclic voltammograms of all four HTOs in a 1 M H₂SO₄ electrolyte at 10 mV s⁻¹. (B) Deprotonation capacity obtained by integrating the anodic current in the potential range from −0.7 V to 0 V vs. Ag/AgCl at scan rates between 10–200 mV s⁻¹.

Deintercalation of H⁺ is attributed to the anodic peak at around −0.55 V. Due to the onset of the hydrogen evolution reaction at these potentials, we compared the electrochemical proton intercalation capacity of the HTOs by calculating the charge passed from the anodic, and not cathodic, current, attributed to the deprotonation of the HTOs. At this scan rate, H₂Ti₃O₇ shows a deprotonation capacity of 82 mA h g⁻¹ (Fig. 4B), corresponding to 0.8 H⁺ per formula unit. This value is close to the theoretical capacity of 1 H⁺ per formula unit, vide infra, which leads us to conclude that the entire “bulk” of the H₂Ti₃O₇ particles is electrochemically protonated even at this relatively fast scan rate. We note that the coulombic efficiency (ratio between anodic and cathodic charge) is impacted by the competing hydrogen evolution reaction near the cathodic turnover potential especially at slow scan rates (Fig. S4, ESI†). Cyclic voltammograms of H₂Ti₃O₇ at rates up to 200 mV s⁻¹ are shown in Fig. S4A (ESI†), underlining the high magnitude of H⁺ intercalation in H₂Ti₃O₇ even at charging times as low as 3.5 seconds (∼30 mA h g⁻¹, corresponding to the deintercalation of 0.29 H⁺ per formula unit).

H₂Ti₆O₁₃ also shows one pair of redox peaks, but with a strongly decreased current magnitude. This indicates that the molar fraction of intercalating H⁺ is much lower than in H₂Ti₃O₇, only 16 mA h g⁻¹ (∼0.16 H⁺ per H₂Ti₆O₁₃) at 10 mV s⁻¹. For H₂Ti₁₂O₂₅ and TiO₂(B), we observe a further reduction in current and nearly negligible H⁺ storage capacity (Fig. S5, ESI†). The cyclic voltammograms of these samples shown in Fig. S4C and D (ESI†) illustrate a set of peaks at around −0.55 V vs. Ag/AgCl, with small overpotentials even at a high scan rate of 200 mV s⁻¹. We ascribe these to fast surface and near-surface intercalation of H⁺ into H₂Ti₁₂O₂₅ and TiO₂(B), as was previously reported for nanostructured TiO₂ materials cycled in the same potential range.^11,15,17,35 However, in these two HTOs the particle size is on the order of microns. Since intercalation of H⁺ is not feasible beyond the near surface, this leads to a lower specific capacity. These results demonstrate that interlayer structural protonation has a pronounced impact on the electrochemical H⁺ intercalation behavior of titanate materials, with a higher degree of structural protonation leading to the highest capacity.

To ascertain that the observed capacity was indeed due to H⁺ intercalation into H₂Ti₃O₇, we performed cyclic voltammetry in sulfuric acid electrolytes of different concentrations, from 0.1 to 3 M (Fig. S6, ESI†). As predicted from the Nernst equation, the proposed H⁺ intercalation redox peaks shift to more positive potentials with increasing concentration of H⁺ in the electrolyte. At the lower electrolyte concentrations, H⁺ intercalation occurs with the onset of the hydrogen evolution reaction (which limits the cathodic potential range) and leads to lower capacity (Fig. S6B, ESI†).

To our knowledge, this is the first report of electrochemical proton intercalation into H₂Ti₃O₇. However, Li⁺ intercalation into HTO materials from organic electrolytes has been widely studied in the literature.^19,36–38 Interestingly, the intercalation capacity for Li⁺ in organic electrolytes shows the opposite trend to the H⁺ intercalation shown here, that is, increasing structural protonation leads to a decrease in the Li⁺ intercalation capacity. To determine whether this was due to the non-aqueous electrolyte solvent, we performed cyclic voltammetry of H₂Ti₃O₇ in 1 M Li₂SO₄ aqueous electrolyte (Fig. S7, ESI†). There is no reversible Li⁺ intercalation observed in the aqueous electrolyte. This leads us to conclude that interlayer structural protonation enables electrochemical H⁺ intercalation into the bulk of titanates but does not benefit Li⁺ intercalation. We hypothesize that this is because H⁺ and Li⁺ prefer different intercalation sites. These results highlight the unique structural requirements for electrochemical proton intercalation, which appear to be determined by the ability of the solid lattice to easily distribute the electrochemical charge rather than to accommodate the volume of a cation, such as with Li⁺.

3.3 In situ Raman spectroscopy and ex situ X-ray diffraction

To correlate the structural changes of H₂Ti₃O₇ with electrochemical H⁺ intercalation, we performed in situ Raman spectroscopy in 1 M H₂SO₄. Fig. 5 shows the Raman spectra as a function of applied potential, along with the corresponding voltammetric response and optical micrographs of the measured region of the electrode (all Raman spectra were taken from the same region). At 0 V, the Raman spectrum is identical to that of pristine H₂Ti₃O₇ (Fig. 2A), indicating that no structural changes occur when the material is immersed in the electrolyte. The color of the H₂Ti₃O₇ particles appears bright white. During the cathodic scan to −1 V, a clear redox peak is visible at ∼−0.9 V (corresponding to ∼−0.6 V vs. Ag/AgCl) that is ascribed to H⁺ intercalation. The optical micrograph shows that the H₂Ti₃O₇ changed color to dark blue, which reveals the strong electrochromic effect of H₂Ti₃O₇ during electrochemical protonation. This has been described by Ghicov et al. for anatase TiO₂ nanotubes with an electrochemically protonated surface region, underlining that bulk H₂Ti₃O₇ particles show a similar electrochromic response as nanostructured TiO₂.¹⁵ At the same time, the Raman signal almost completely disappears, likely indicative of a semi-conductor to metal transition, which results in decreased interaction of the Raman laser with the sample volume.^39,40 However, the peak originally at 853 cm⁻¹, assigned to a Ti–O stretch, undergoes a shift to 892 cm⁻¹. This suggests an increased Ti–O binding energy after electrochemical proton intercalation that may be caused either by the contraction of the interlayer during electrochemical protonation, vide infra, or a more ionic Ti–O bond.³³ On the anodic scan, the optical micrographs reveal a gradual color change back to bright white, while at the same time the Raman signal increases in intensity and the Ti–OH stretching band continuously shifts back to the original position. This is significant as it illustrates that electrochemical H⁺ (de-)intercalation in bulk H₂Ti₃O₇ results in continuous, and highly reversible structural changes.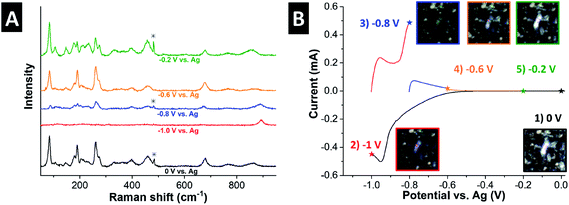

Fig. 5 (A) In situ Raman spectra of H₂Ti₃O₇ as a function of applied potential. The asterisk marks the peak from the sulfuric acid electrolyte.⁴⁰ (B) Corresponding voltammetric current response, including optical micrographs of the measured particle at the respective potentials.

The crystallographic changes that occur in H₂Ti₃O₇ during electrochemical H⁺ intercalation were analyzed by ex situ XRD (Fig. 6). In the charged state (−0.7 V vs. Ag/AgCl), the (200) peak shifts from 11.2° 2θ to 11.7° 2θ, corresponding to a contraction of the interlayer spacing from 7.88 Å to 7.56 Å. At the same time, the (201) peak shifts from 16.3° 2θ to 17.0° 2θ. Contrarily, the in-plane diffraction peak (003) remains at 29.7° 2θ in both the charged and uncharged state, indicating that the strain caused by the electrochemically intercalated H⁺ primarily leads to a contraction of the interlayer spacing, rather than a reorganization within the titanate layers. We hypothesize that the ability for facile interlayer contraction and expansion is due to the presence of interlayer structural protons. These prevent the interconnection of titanate layers in H₂Ti₃O₇ and reduce structural constraints along the a-unit cell direction. This structural feature may limit the electrochemically-induced strain to simply a one-dimensional contraction and expansion of the interlayer spacing. Due to the increased interconnection between the titanate layers in the other HTO phases, we hypothesize that electrochemically intercalated H⁺ would result in three-dimensional volume changes, including distortions within the titanate layers, which are associated with less favorable intercalation energetics, vide infra. Therefore, the extent of bulk electrochemical H⁺ intercalation is significantly reduced with decreased structural protonation.

Fig. 6 (A) Ex situ X-ray diffractograms of H₂Ti₃O₇ at the open circuit potential (OCP, ca. 0.4 V vs. Ag/AgCl) and at −0.7 V and (B) corresponding voltammetric current response.

3.4 Density functional theory

Density functional theory (DFT) was used to provide additional insight into the hypothesis that interlayer structural protonation enables facile electrochemical intercalation of H⁺ by calculating the H⁺ adsorption energy in H₂Ti₃O₇ and H₂Ti₆O₁₃. The computational results show that in a cell of 4 H₂Ti₃O₇ units, the first intercalated H⁺ adsorbs at a bridging oxygen in the interlayer to form a hydroxyl group, requiring an adsorption energy of 0.19 eV which is almost thermally neutral. Further intercalation proceeds with similarly low adsorption energies and leads to the formation of four hydroxyl groups at all free bridging oxygens (Fig. 7A). This corresponds to a theoretical capacity of 1 H⁺ per H₂Ti₃O₇. The simulated diffractograms show a continuous interlayer contraction with increased electrochemical protonation of the structure, and the simulated diffractogram of H₂Ti₃O₇·H_0.5 aligns with our ex situ XRD measurement (Fig. S9, ESI†). The incomplete electrochemical protonation during the ex situ measurement (ca. 0.5 H⁺ per H₂Ti₃O₇) is likely a consequence of the rapid sample oxidation in air, despite protection by Mylar film.

Fig. 7 DFT-calculated reaction sites and adsorption energies of electrochemically intercalated protons (green) in (A) H₂Ti₃O₇ and (B) H₂Ti₆O₁₃.

On the other hand, the DFT results show that electrochemical intercalation of the first H⁺ into a cell of 2 H₂Ti₆O₁₃ units would have to result in the conversion of a hydroxyl group at a bridging site to water, which causes a simultaneous distortion of the TiO₆ octahedra (Fig. 7B). This process is associated with a significantly higher adsorption energy of 0.59 eV as compared to H₂Ti₃O₇. The addition of a second H⁺ would lead to the formation of an additional hydroxyl group at a bridging oxygen with an adsorption energy of 0.56 eV. The DFT results illustrate how the presence of interlayer structural protons in H₂Ti₃O₇, which decrease titanate layer interconnections, allow for facile interlayer contraction to accommodate the charge associated with electrochemically intercalated H⁺. Contrarily, increased titanate layer interconnections in H₂Ti₆O₁₃ lead to more uphill energetics for comparably small amounts of intercalated H⁺ (Fig. 8).

Fig. 8 Comparison of the hydrogen adsorption energies for x electrochemically intercalated protons per formula unit of H₂Ti₃O₇ and H₂Ti₆O₁₃ as calculated by DFT.

4. Conclusions

In this mechanistic study, we analyzed the impact of interlayer structural protons in layered HTOs on their electrochemical H⁺ intercalation behavior. We found that H₂Ti₃O₇ – the material with the highest amount of interlayer structural protonation – showed a significantly higher electrochemical H⁺ intercalation capacity (about 0.8 H⁺ per H₂Ti₃O₇) compared to other HTOs. The titanate layers of H₂Ti₃O₇ readily contract to compensate for the strain induced by the insertion of H⁺ during electrochemical intercalation. We hypothesize that this is due to the presence of interlayer structural protons which separate the titanate layers. DFT calculations confirm a reduced adsorption energy for electrochemically intercalated H⁺ in the H₂Ti₃O₇ structure with only one-dimensional structural changes associated with interlayer contraction. Decreased structural proton content, as in H₂Ti₆O₁₃, leads to much higher adsorption energies associated with significant structural distortions. These results identify interlayer structural protons as the key structural feature that enables bulk electrochemical H⁺ intercalation of titanates for the development of future aqueous electrochemical energy devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of the Fluid Interface Reactions, Structures and Transport (FIRST) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences. This research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. This work was performed in part at the Analytical Instrumentation Facility (AIF) at North Carolina State University, which is supported by the State of North Carolina and the National Science Foundation (award number ECCS-1542015). The AIF is a member of the North Carolina Research Triangle Nanotechnology Network (RTNN), a site in the National Nanotechnology Coordinated Infrastructure (NNCI). The authors thank Dr David J. Wesolowski for critical comments on this manuscript.

References

1. X. Ji, Energy Environ. Sci., 2019, 12, 3203–3224.
2. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943.
3. M. R. Lukatskaya, J. I. Feldblyum, D. G. Mackanic, F. Lissel, D. L. Michels, Y. Cui and Z. Bao, Energy Environ. Sci., 2018, 11, 2876–2883.
4. N. Dubouis, P. Lemaire, B. Mirvaux, E. Salager, M. Deschamps and A. Grimaud, Energy Environ. Sci., 2018, 11, 3491–3499.
5. Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Nat. Energy, 2019, 4, 269–280.
6. Q. Dou, S. Lei, D.-W. Wang, Q. Zhang, D. Xiao, H. Guo, A. Wang, H. Yang, Y. Li and S. Shi, Energy Environ. Sci., 2018, 11, 3212–3219.
7. N. Sa, H. Wang, D. L. Proffit, A. L. Lipson, B. Key, M. Liu, Z. Feng, T. T. Fister, Y. Ren and C.-J. Sun, J. Power Sources, 2016, 323, 44–50.
8. S.-C. Lim, J. Lee, H. H. Kwak, J. W. Heo, M. S. Chae, D. Ahn, Y. H. Jang, H. Lee and S.-T. Hong, Inorg. Chem., 2017, 56, 7668–7678.
9. R. Verrelli, A. Black, C. Pattanathummasid, D. Tchitchekova, A. Ponrouch, J. Oró-Solé, C. Frontera, F. Bardé, P. Rozier and M. Palacín, J. Power Sources, 2018, 407, 162–172.
10. H. D. Yoo, J. R. Jokisaari, Y.-S. Yu, B. J. Kwon, L. Hu, S. Kim, S.-D. Han, M. Lopez, S. H. Lapidus and G. M. Nolis, ACS Energy Lett., 2019, 4, 1528–1534.
11. Y.-S. Kim, S. b. Kriegel, K. D. Harris, C. Costentin, B. Limoges and V. r. Balland, J. Phys. Chem. C, 2017, 121, 10325–10335.
12. N. Bezginov, T. Valdez, M. Horbatsch, A. Marsman, A. Vutha and E. Hessels, Science, 2019, 365, 1007–1012.
13. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
14. T. Berger, D. Monllor-Satoca, M. Jankulovska, T. Lana-Villarreal and R. Gómez, ChemPhysChem, 2012, 13, 2824–2875.
15. A. Ghicov, H. Tsuchiya, R. Hahn, J. M. Macak, A. G. Muñoz and P. Schmuki, Electrochem. Commun., 2006, 8, 528–532.
16. F. Fabregat-Santiago, E. M. Barea, J. Bisquert, G. K. Mor, K. Shankar and C. A. Grimes, J. Am. Chem. Soc., 2008, 130, 11312–11316.
17. A. Liu, D. Li, I. Honma and H. Zhou, Electrochem. Commun., 2006, 8, 206–210.
18. G.-N. Zhu, Y.-G. Wang and Y.-Y. Xia, Energy Environ. Sci., 2012, 5, 6652–6667.
19. S. Fleischmann, K. Pfeifer, M. Widmaier, H. Shim, Ö. Budak and V. Presser, ACS Appl. Energy Mater., 2019, 2, 3633–3641.
20. E. Mamontov and K. W. Herwig, Rev. Sci. Instrum., 2011, 82, 085109.
21. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
24. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
26. K. Kataoka, N. Kijima and J. Akimoto, Inorg. Chem., 2013, 52, 13861–13864.
27. K. Kataoka and J. Akimoto, J. Ceram. Soc. Jpn., 2016, 124, 710–713.
28. J. C. Pérez-Flores, F. García-Alvarado, M. Hoelzel, I. Sobrados, J. Sanz and A. Kuhn, Dalton Trans., 2012, 41, 14633–14642.
29. A. Eguía-Barrio, E. Castillo-Martınez, M. Zarrabeitia, M. A. Munoz-Márquez, M. Casas-Cabanasa and T. Rojo, Phys. Chem. Chem. Phys., 2015, 17, 6988–6994.
30. K. Kataoka, N. Kijima and J. J. S. S. I. Akimoto, Solid State Ionics, 2013, 252, 109–115.
31. M. Edisson Jr, P. M. Jardim, A. M. Bojan, C. R. Fernando, A. S. d. A. Marco, L. Z. José and S. A. Antonio, Nanotechnol., 2007, 18, 495710.
32. A. P. Giddy, M. T. Dove, G. S. Pawley and V. Heine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 697–703.
33. S.-H. Byeon, S.-O. Lee and H. Kim, J. Solid State Chem., 1997, 130, 110–116.
34. J. R. Jokisaari, D. Bayerl, K. Zhang, L. Xie, Y. Nie, D. G. Schlom, E. Kioupakis, G. W. Graham and X. Pan, Chem. Mater., 2015, 27, 7896–7902.
35. H. Tokudome and M. Miyauchi, Angew. Chem., Int. Ed., 2005, 44, 1974–1977.
36. S.-H. Lee, H.-K. Kim, J. H. Lee, S.-G. Lee and Y.-H. Lee, Mater. Lett., 2015, 143, 101–104.
37. J. Li, Z. Tang and Z. Zhang, Chem. Mater., 2005, 17, 5848–5855.
38. Y. Zhang, Z. Jiang, J. Huang, L. Y. Lim, W. Li, J. Deng, D. Gong, Y. Tang, Y. Lai and Z. Chen, RSC Adv., 2015, 5, 79479–79510.
39. R. Baddour-Hadjean and J.-P. Pereira-Ramos, Chem. Rev., 2009, 110, 1278–1319.
40. J. B. Mitchell, W. C. Lo, A. Genc, J. LeBeau and V. Augustyn, Chem. Mater., 2017, 29, 3928–3937.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta11098d

---