Enhanced Na+ pseudocapacitance in a P, S co-doped carbon anode arising from the surface modification by sulfur and phosphorus with C–S–P coupling†
Jie
Yan
ab,
Wei
Li
b,
Pingyuan
Feng
b,
Ruxing
Wang
a,
Mao
Jiang
b,
Jing
Han
b,
Shengling
Cao
b,
Kangli
Wang
*a and
Kai
Jiang
 *a
*a
aState Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, China 430074. E-mail: kjiang@hust.edu.cn; klwang@hust.edu.cn
bState Key Laboratory of Materials Processing and Die & Mould Technology, School of Materials Science and Engineering, Huazhong University of Science and Technology, Wuhan, Hubei, China 430074
First published on 2nd December 2019
Abstract
Enhanced phosphorus (7.2 wt%) and sulfur (15.7 wt%) co-doped carbon (PSC) is synthesized via a one-step sintering of carbon disulfide and red phosphorus in a vacuum. It is found that S atoms can act as immobilization sites for phosphorus by covalently bonding with P atoms in the form of C–S–P, and thus high-level doping of phosphorus can be realized. Owing to the high-level doping, this co-doped carbon shows enlarged interlayer spacing, improved charge transfer capability and strong adsorption of Na+ ions. When tested as an anode for sodium ion batteries, this PSC delivers a high reversible capacity of 513.8 mA h g−1 at 100 mA g−1, excellent rate capability of 181.8 mA h g−1 at 10 A g−1 and superior cycling stability with a capacity of 290.1 mA h g−1 after 1000 cycles at 1 A g−1.
Introduction
Sodium ion batteries are promising candidates for replacing lithium ion batteries due to the abundant sodium resources and the similar chemistry of sodium to that of lithium.1–9 However, due to the larger ionic size of Na+ ions than Li+ ions, the electrochemical performance and kinetics of sodium ion batteries are far inferior to those of lithium ion batteries.10,11 Therefore, searching for and exploiting advanced electrode materials to reversibly and rapidly accommodate Na+ ions is critical for the development of sodium ion batteries.Hard carbon, one of the most attractive anodes for sodium ion batteries,12,13 delivered a high reversible sodium storage capacity of ∼300 mA h g−1, first reported by Stevens and Dahn,14 but the rate performance and cycling stability were far from satisfactory. After that, various hard carbons have been reported with improved electrochemical performance via designing favorable carbon nanostructures, such as nanosheets,15 nanospheres,16 nanofibers,17,18 and coral-like porous carbon.19,20 However, these carbon nanostructures usually suffer from low initial coulombic efficiencies and complicated synthesis procedures, which limit their further applications. For example, the 3D porous carbon sheets delivered a high reversible capacity of 356.1 mA h g−1 at 0.1 A g−1 and maintained a capacity of 104.1 mA h g−1 even at a high rate of 10 A g−1, but the initial coulombic efficiency remains to be improved.15
From the perspective of the sodium storage mechanism in hard carbon, enlarging the interlayer distance of the graphite crystallite and creating more microvoids in hard carbon are the essential strategies to improve the electrochemical performance.21–26 Heteroatom doping (with heteroatoms such as N, S, and P) has been identified as an effective way to enhance the electrochemical behavior of carbon by expanding the interlayer spacing of carbon layers, introducing defects and modifying the electronic properties.27–31 Sulfur is one of the most appealing atoms due to the larger covalent radius (103 pm) than that of nitrogen (71 pm) and carbon (74 pm), which is favorable for further increasing the interlayer spacing and further improving the performance of hard carbon.32–34 Xu and co-workers demonstrated that sulfur doped carbon delivered a capacity of 150 mA h g−1 at 500 mA g−1, much higher than that of the undoped carbon of 60 mA h g−1, due to the increase of the interlayer distance from 0.37 nm to 0.41 nm after sulfur doping.32
Besides sulfur doping, phosphorus doping is also very attractive, because it can change the surface charge distribution due to the smaller electronegativity of the phosphorus atom (2.19) than that of carbon atom (2.55).35 When surface defects are induced by phosphorus doping, they can not only facilitate charge transfer, but also boost the reversible capacity and rate performance. For example, Yu and co-workers reported that a P-doped “honeycomb briquette” shaped carbon exhibited a high charge capacity of 393.4 mA h g−1 at 20 mA g−1, far exceeding that of the undoped hard carbon (HC).36 However, owing to the large covalent radius of phosphorus and the high bonding energy of phosphorus with carbon as well as the easy combination of phosphorus with oxygen (POx) outside the carbon plane, the doping contents of phosphorus in early reports were limited from 0.56 to 3 wt%.37–40
In this work, we propose a phosphorus and sulfur co-doped carbon (PSC) with a high level of both phosphorus (7.2 wt%) and sulfur (15.7 wt%) obtained by simply annealing red phosphorus (RP, 100 mg) and carbon disulfide (CS2, 250 μL) at 500 °C in a vacuum. In this phosphorus and sulfur co-doped carbon, S atoms can act as immobilization sites for phosphorus by covalently bonding with P atoms in the form of C–S–P, and so a high-level P doping can be realized. When used as an anode for sodium ion batteries, the P, S co-doped carbon delivered a high reversible capacity of 513.8 mA h g−1 at 100 mA g−1, and exhibited good rate performance and excellent cycling stability. It is found that the high co-doping level of both P and S can not only expand the interlayer distance, but can also facilitate the adsorption of sodium ions, which enhances its reversible capacity and rate capability.
Experimental
Synthesis of P, S co-doped carbons (PSCs)
The P, S co-doped carbon (PSC) was obtained by simply annealing the mixtures of red phosphorus and carbon disulfide in a vacuum sealed quartz tube at a certain temperature. Briefly, 5 g RP was purified in 75 ml deionized water in a 100 ml Teflon reactor at 200 °C for 10 h. After cooling, the purified RP was filtered and dried under vacuum at 80 °C for 12 h. Then 100 mg purified RP and different volumes of CS2 (100, 150, 250 and 300 μL) were sealed in a vacuum quartz tube and heated in a muffle furnace at different temperatures (400, 500 and 600 °C) for 24 h. The PSCs were obtained by washing with CS2 and ethyl alcohol three times and dried under vacuum at 80 °C for 12 h.Synthesis of S-doped carbon (SC)
S-doped carbon (SC) was prepared by annealing a mixture of sulfur (S, 150 mg) and benzene (C6H6, 100 μL) in a vacuum sealed quartz tube at a certain temperature and then washed with CS2 and ethyl alcohol three times.Materials characterization
The structural information on PSC was obtained by XRD using an X-ray diffractometer (D/MAXRB, 12 kW) with Cu Kα radiation (λ = 0.15406 nm). The morphologies of PSC were investigated using a field emission scanning electron microscope (FE-SEM, Sirion200) and TEM (TecnaiG220) coupled with an EDX spectrometer. Raman spectra were measured on a LabRAM HR800 Raman system using an Ar+ laser of 514.5 nm at RT. The surface elemental composition and chemical states were determined by XPS (AXIS-ULTRA DLD spectrometer) with a monochromatic Al Kα X-ray source. The nitrogen adsorption and desorption isotherms were collected at 77 K on a Tristar II 3020 instrument.Computational methods
All the calculations were performed within the framework of density functional theory (DFT) as implemented in the Vienna Ab initio Software Package (VASP 5.3.5) code within the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation and the projected augmented wave (PAW) method.41–44 The cutoff energy for the plane-wave basis set was set to 400 eV. The Brillouin zone of the surface unit cell was sampled by Monkhorst–Pack (MP) grids, with a k-point mesh for graphene structure optimizations.45 The graphene surface was determined using a 3 × 3 × 1 Monkhorst–Pack grid. The convergence criterion for the electronic self-consistent iteration and force was set to 10–5 eV and 0.01 eV Å−1, respectively. A 4 × 4 supercell of the graphene surface including 1 atomic layer was constructed to model the graphene catalyst in this work. A vacuum layer of 12 Å was introduced to avoid interactions between periodic images. The adsorption energy (Eads) of the surface species is defined by| Eads = Etotal − Esurface − Especies, |
Electrochemical measurements
Working electrodes were fabricated by grinding the active material, Super P and polyvinylidene difluoride (PVDF) in N-methyl-2-pyrrolidone (NMP) at a mass ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. The obtained slurry was coated onto a piece of copper foil, dried at 80 °C for 12 h in a vacuum and cut into small disks (diameter ∼ 10 mm) with a mass loading of 0.8–1.0 mg. CR 2025 coin cells were assembled by using sodium foil as the reference and the counter electrode, glass fiber as the separator and 1 mol L−1 NaClO4 in a mixture of ethylene carbonate (EC) and diethylcarbonate (DEC) (EC
10. The obtained slurry was coated onto a piece of copper foil, dried at 80 °C for 12 h in a vacuum and cut into small disks (diameter ∼ 10 mm) with a mass loading of 0.8–1.0 mg. CR 2025 coin cells were assembled by using sodium foil as the reference and the counter electrode, glass fiber as the separator and 1 mol L−1 NaClO4 in a mixture of ethylene carbonate (EC) and diethylcarbonate (DEC) (EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC, 1
DEC, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) with 5 wt% fluoroethylene carbonate (FEC) as the electrolyte. CV measurements were performed on an electrochemical workstation (CHI 604E, china) at a scan rate of 0.1 mV s−1. Electrochemical impedance spectra (EIS) were recorded in the frequency range from 100
1 by volume) with 5 wt% fluoroethylene carbonate (FEC) as the electrolyte. CV measurements were performed on an electrochemical workstation (CHI 604E, china) at a scan rate of 0.1 mV s−1. Electrochemical impedance spectra (EIS) were recorded in the frequency range from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 0.1 Hz. Galvanostatic charge/discharge tests with a cutoff voltage of 0.01–3 V were carried out on a battery testing system (LAND Electronic Co., China).
000 to 0.1 Hz. Galvanostatic charge/discharge tests with a cutoff voltage of 0.01–3 V were carried out on a battery testing system (LAND Electronic Co., China).
Results and discussion
The P, S co-doped carbon (PSC) is simply prepared by a one-step annealing of a mixture of red phosphorus (RP, 100 mg) and carbon disulfide (CS2, 250 μL) in a vacuum sealed quartz tube at 500 °C. The synthetic route is illustrated in Fig. 1a and a digital picture of the obtained material is shown in Fig. S1.† Owing to the strong interaction between phosphorus and sulfur,46 the sulfur in carbon disulfide can rapidly combine with phosphorus to form P4S7 (the corresponding XRD pattern is shown in Fig. S2†) by reaction (1).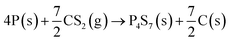 | (1) |
In this reaction, CS2 acts as both the carbon and the sulfur source, while red phosphorus serves as a desulfurizer and phosphorus source. The carbonization and P, S co-doping occur simultaneously during the desulfurization process of CS2. Such similar phenomenon is also observed in the case of Li and CS2 at 650 °C.47 Finally, pure PSC can be obtained by washing the products with CS2 and ethyl alcohol to remove P4S7.
The morphology of PSC at 500 °C is observed by field-emission scanning electron microscopy (FESEM) and transmission electron microscopy (TEM). As shown in Fig. 1b and c, PSC appears as a porous bulk structure that consists of carbon nanoparticles with an average size of 100 nm, as also confirmed by the TEM image in Fig. 1d. These nanopores are likely caused by the release of a large number of small P4S7 molecules during the reaction of CS2 with RP. The high-resolution TEM image (Fig. 1e) reveals an interlayer spacing of 0.41 nm, much larger than that of graphite (0.34 nm). EDS mapping confirms that sulfur, carbon, and phosphorus are uniformly distributed in PSC. Such a porous structure of PSC with an enlarged interlayer spacing is expected to facilitate the intercalation of Na+ ions into the carbon layers and improve its reversible capacity.
The influences of synthetic temperature on the structure, morphology and elemental composition of PSC were also investigated. As shown in Fig. S3,† when the synthetic temperature is 400 °C, the obtained PSC shows a compact bulk structure (Fig. S3a and d†) with poor crystallinity (Fig. S3g†) and low specific surface area (Fig. S3h†), indicating that this temperature is relatively low to attain sufficient carbonization. When the temperature is increased to 500 °C, PSC becomes porous (Fig. S3b and e†), and the XRD pattern displays typical disordered carbon characteristics (Fig. S3g†). When the temperature is further increased to 600 °C, the morphology (Fig. S3c and f†) and XRD pattern (Fig. S3g†) of PSC show no obvious changes, but the phosphorus and sulfur contents decrease significantly (Fig. S3i†). Taking the structure, morphology and elemental composition into consideration, the optimized temperature is determined to be 500 °C, at which PSC features a well-formed porous carbon structure and both high phosphorus and sulfur content.
Further structural information on the PSC at 500 °C was obtained by XRD and Raman analysis. As shown in Fig. 2a, the two broad peaks at around 22.5° and 43.5° in the XRD pattern of PSC correspond to the (002) and (100) diffractions of disordered carbon, respectively. Applying Bragg's law, the interlayer spacing of PSC is calculated to be ∼0.4 nm (well agreeing with the HRTEM result in Fig. 1e), much larger than that of SC (0.37 nm, Fig. S4a†), suggesting the significant role of P in enlarging the interlayer spacing. The Raman spectrum (Fig. 2b) shows two strong peaks at 1334 and at 1573 cm−1, which correspond to the D and G bands of PSC. The peak intensity ratio of D and G bands (ID/IG) of PSC is 1.089, much higher than that of SC (0.865, Fig. S4b†), indicating the existence of abundant defects in PSC caused by S and P co-doping, especially P-doping. Nitrogen adsorption and desorption isotherms were measured to evaluate the specific surface area and Barrett–Joyner–Halenda (BJH) pore size distribution of PSC. Based on the N2 adsorption/desorption isotherms (Fig. 2c), the Brunauer–Emmett–Teller (BET) surface area of PSC is calculated to be 56.7 m2 g−1. The typical type IV isotherms of PSC suggest the existence of a mesoporous structure, as confirmed by the narrow pore size distribution centered at ∼4 nm in Fig. 2d.
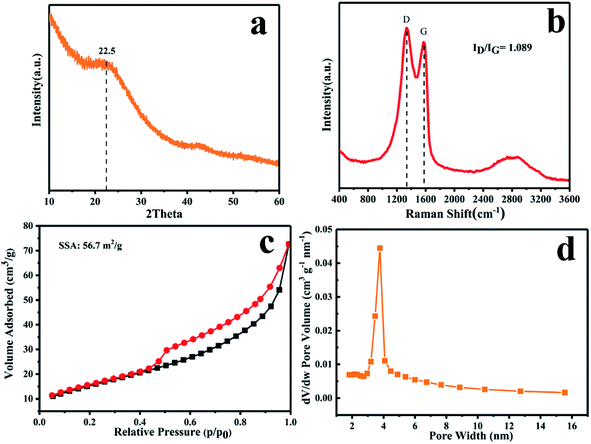 | ||
| Fig. 2 (a) XRD pattern, (b) Raman spectra, (c) N2 adsorption–desorption isotherms, and (d) pore size distribution of PSC. | ||
X-ray photoelectron spectroscopy (XPS) analysis was carried out to understand the chemical states of the elements of PSC. As shown in Fig. S5,† four elements, C, P, S and O, are detected, of which the phosphorus and sulfur contents are measured to be 7.2 and 15.7 wt%, respectively. The high resolution C 1s (Fig. 3a) spectrum of PSC exhibits five main peaks at binding energies of 284.5, 284.9, 285.5, 286.3 and 288.8 eV, which correspond to C–P, C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–S, C–O and C
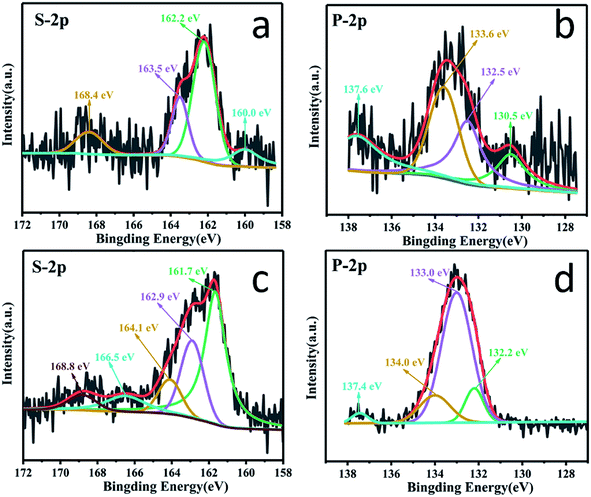
C, C–S, C–O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, respectively,48–51 demonstrating that S and P atoms are covalently bonded with C atoms. The S 2p spectrum (Fig. 3b) of PSC can be fitted into four peaks at 162.1, 164.1, 165.4 and 166.1 eV. The binding energy at 162.1 eV can be ascribed to the S–P bond,46,52 and those at 164.1 and 165.4 eV correspond to the C–S bond.53,54 The peak at 166.1 eV can be assigned to S–Ox, which is probably caused by the surface oxidation of phosphorus. The P 2p spectrum (Fig. 3c) of PSC can be deconvoluted into three main peaks at 132.7, 134.1 and 135.0 eV. The two weak peaks at 132.7 and 135.0 eV correspond to the P–C bond and P–Ox bond, respectively, while the major peak at 134.1 eV is ascribed to the P–S bond,46 which accounts for 45.5% of the total area of the P 2p spectrum. Therefore, a possible structure of PSC is illustrated in Fig. 3d. Since the direct bonding of P with three C atoms (point c in Fig. 3d) in the graphite layer needs high energy, a low level phosphorus doping (<3 wt%) is reported in most previous research studies. However, when S atoms are co-doped into PSC, they can not only act as immobilization sites and bridges to connect P and C (point b in Fig. 3d) to form C–S–P, but also reduce the stress generated by the large size of P atoms, leading to a high level phosphorus doping (7.2 wt%). Moreover, owing to the smaller electronegativity of phosphorus (2.19) than that of carbon (2.55) and sulfur (2.58), a high level phosphorus doping (7.2 wt%) may cause charge distribution of the surrounding carbon atoms and change the binding energy between the sodium ion and carbon atoms, which will be discussed in detail in the DFT calculation.
O bonds, respectively,48–51 demonstrating that S and P atoms are covalently bonded with C atoms. The S 2p spectrum (Fig. 3b) of PSC can be fitted into four peaks at 162.1, 164.1, 165.4 and 166.1 eV. The binding energy at 162.1 eV can be ascribed to the S–P bond,46,52 and those at 164.1 and 165.4 eV correspond to the C–S bond.53,54 The peak at 166.1 eV can be assigned to S–Ox, which is probably caused by the surface oxidation of phosphorus. The P 2p spectrum (Fig. 3c) of PSC can be deconvoluted into three main peaks at 132.7, 134.1 and 135.0 eV. The two weak peaks at 132.7 and 135.0 eV correspond to the P–C bond and P–Ox bond, respectively, while the major peak at 134.1 eV is ascribed to the P–S bond,46 which accounts for 45.5% of the total area of the P 2p spectrum. Therefore, a possible structure of PSC is illustrated in Fig. 3d. Since the direct bonding of P with three C atoms (point c in Fig. 3d) in the graphite layer needs high energy, a low level phosphorus doping (<3 wt%) is reported in most previous research studies. However, when S atoms are co-doped into PSC, they can not only act as immobilization sites and bridges to connect P and C (point b in Fig. 3d) to form C–S–P, but also reduce the stress generated by the large size of P atoms, leading to a high level phosphorus doping (7.2 wt%). Moreover, owing to the smaller electronegativity of phosphorus (2.19) than that of carbon (2.55) and sulfur (2.58), a high level phosphorus doping (7.2 wt%) may cause charge distribution of the surrounding carbon atoms and change the binding energy between the sodium ion and carbon atoms, which will be discussed in detail in the DFT calculation.
Cyclic voltammetry (CV) and galvanostatic charge/discharge measurements were performed to characterize the electrochemical properties of PSC. Fig. 4a shows the first four CV curves of PSC at a scan rate of 0.1 mV s−1 in the potential window of 0.01–3 V. An irreversible reduction peak appears at about 0.25 V in the first cycle and disappears in the second cycle, which is related to the formation of a solid electrolyte interphase (SEI) layer.6 In the subsequent cycle, there are two redox couples at 1.8/2.2 V and 1.1/1.85 V, which can be ascribed to the stepwise reactions between sodium and covalently bonded sulfur. The two reduction peaks at 1.8 and 1.1 V correspond to the formation of Na2S2 and Na2S,5,6 respectively. The reduction peak at about 0.01 V is related to intercalation of the sodium ions into carbon layers. Compared with S, no characteristic peak of P reacting with Na+ is observed in the CV curves, indicating the absence of P alloying with Na+. Besides, the quasi-rectangular shapes of the CV curves suggest the capacitive characteristic of this PSC, which is likely due to adsorption and diffusion of Na+ ions in doping/defect sites.
Fig. 4b shows the charge and discharge voltage profiles of PSC in the first three cycles at a current density of 100 mA h g−1. The PSC delivers an initial charge capacity of 519.9 mA h g−1 with an initial coulombic efficiency of 53.5%, much higher than that of SC (371.7 mA h g−1, 39.9%) (Fig. S6a†). In the second cycle, the PSC delivers a reversible discharge capacity of 513.8 mA h g−1 along with a high coulombic efficiency of 93.0%. In the subsequent cycles, the coulombic efficiency reaches and is retained at ∼100%. And the PSC still retains a high capacity of 401.3 mA h g−1 after 200 cycles (Fig. S6c†), which is also much higher than that of SC (Fig. S6b†). More significantly, PSC shows better cycling performance at both small and large current densities than SC (Fig. S6d†), which indicates that the introduction of P in PSC can enhance both the sodium storage capacity and structural stability. Obviously, the improved electrochemical performance of PSC compared to SC very likely originates from the larger interlayer spacing and stronger Na+ ion adsorption capability of PSC (Fig. S10†).
Moreover, the influence of the atomic ratio of P to S doped in carbon on the sodium storage capacity was also investigated. As shown in Table S1,† the atomic ratios of P to S doped in the PSCs (obtained after heating at 500 °C for 24 h) can be controlled by adjusting the atomic ratios of P to S in the raw materials and there is a positive correlation between them. The charge and discharge curves of PSCs with different P to S ratios are shown in Fig. S7.† It is found that the capacity of PSC increases with the decrease of P/S atomic ratios (Fig. S7a–c†). When the P/S atomic ratio lowers to the minimum value of 0.47 (corresponding to 100 mg RP with 250 μL CS2 in the raw materials), PSC can reach the highest capacity of 519.9 mA h g−1 and excellent cycling (Fig. S7d†).
Fig. 4c shows the capacity of the PSC electrode at different current densities from 0.1 to 10 A g−1. PSC delivers reversible capacities of 507.8, 409.2, 356.8, 318.5, 284.1 and 230.5 mA h g−1 at current densities of 0.1, 0.2, 0.5, 1.0, 2.0 and 5.0 A g−1, respectively. Even at a high current density of 10 A g−1, a capacity of 181.8 mA h g−1 can still be retained. When the current density returns to 0.1 A g−1, the capacity of PSC recovers to 415.9 mA h g−1, indicating the good stability of PSC at high rate charge and discharge.
The long cycle performance of PSC was further tested at a current density of 1 A g−1. As shown in Fig. 4e, a stable capacity of 290.1 mA h g−1 is yielded at 1 A g−1 after 1000 cycles and the coulombic efficiency is retained at nearly 100% during the cycling, which suggests the good structural stability of PSC. The morphologies of PSC electrode before and after 1000 cycles at 1 A g−1 were investigated. As shown in Fig. S8,† no obvious change is observed after long cycling at this high rate, demonstrating the robust structure of PSC. The Nyquist plots of the PSC after various cycles are shown in Fig. S9.† According to the equivalent circuit model, the SEI film resistance (RSEI) and charge transfer resistance (Rct) decrease in the first 5 cycles and remain stable after the following cycles, which is also consistent with the good cycling performance of PSC.
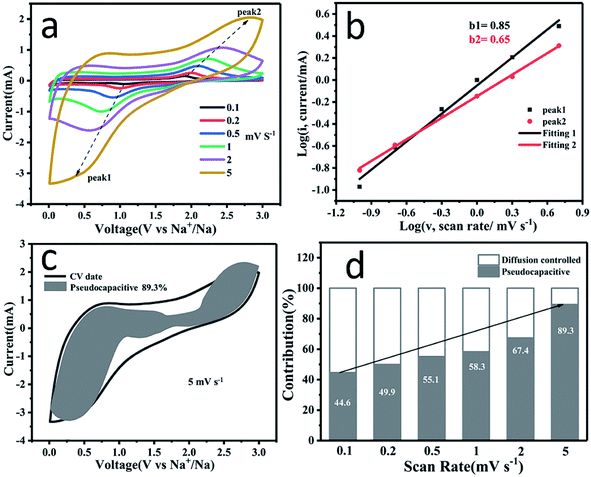
To further understand the high rate capability of PSC for SIBs, CV curves (Fig. 5a) at different scans rates (ν) ranging from 0.1 to 5 mV s−1 were recorded to estimate the rate-determining step of the reactions. According to Cottrell's equation, i = aνb, where the b value can be obtained by fitting the line of the log(ν)–log(i) curve. When the b value is 0.5, the reaction is a diffusion-controlled process; when the b value is 1, the reaction is a capacitive effect controlled process.55–57 As shown in Fig. 5b, the b values at peak 1 and peak 2 are 0.85 and 0.65, respectively, suggesting that the redox process is related to the capacitive process.
The capacitive contribution can be further quantified using the following formula:
| i(V) = k1ν + k2ν1/2 |
To investigate the origin of the dominant pseudocapacitive behavior and influence of P and S co-doping on the electronic structure of PSC, first principles calculations were used to estimate the adsorption energy of Na ions on the different sites of the PSC surface, the differential charge density (DCD) maps and the density of states (DOS) of PSC. As shown in Fig. 6a, the adsorption energy for the sodium ion is 0.53 eV for pure graphitic carbon. However, after P, S co-doping, the adsorption energies of Na+ ions in the carbon (Fig. 6b), sulfur (Fig. 6c) and phosphorus (Fig. 6d) sites in the P, S co-doped structure are about 0.05, −0.20 and −0.84 eV, respectively. Obviously, the introduction of phosphorus and sulfur atoms, especially phosphorus atoms, significantly facilitates the adsorption of sodium ions on the surface. Moreover, when single S or P is doped (Fig. S10†), it is demonstrated that the C–P sites have a stronger adsorption ability for Na+ than C–S sites, further suggesting that the effective adsorption sites for Na+ ions in the PSC are dominated by P-doping. Since the electronegativity of phosphorus (2.19) is smaller than that of carbon (2.55), the phosphorus atom acts as an electron donor to the adjacent carbon and sulfur atoms. Since the electronegativity of sulfur (2.58) is slightly larger than that of carbon, it acts as an electron acceptor from the adjacent carbon and phosphorus atoms.6,8,62–64 This can also be directly observed from the differential charge density (DCD) maps in Fig. 6a–d. These results confirm that doping with P and S atoms provides more active sites and makes Na+ ion adsorption more favorable, which enhances the sodium storage capability and rate capability.
The densities of states (DOSs) for the pure graphitic carbon and PSC are shown in Fig. 6e and f. Compared with pure graphitic carbon, the Fermi level in the PSC shifts right up to the conduction band, which is favorable for enhancing the electronic conductivity and chemical reactivity, and the electronic conductivity is measured to be 0.282 S m−1. Furthermore, the partial density of states (PDOS) of S is much higher than that of P in the PSC (Fig. 6g), implying that the increase in electronic states at the Fermi level is dominated by the S atom.36,63–65 Therefore, the enhanced Na+ ion adsorption capability and improved electronic conductivity facilitated by P, S co-doping contribute to the superior sodium storage and excellent rate performance.
XPS characterization of the PSC electrode at full discharge and charge was performed to verify the above calculation results. As shown in Fig. 7a, at the fully discharged state of 0.01 V, the binding energies of the S 2p spectrum clearly shift to lower energies of 160.0, 162.2 and 163.5 eV compared to those of pristine PSC, respectively, indicating the strong interaction between the S sites and Na+ ions, which is also supported by the ex situ results which indicate that the covalent S could interact with Na+ to form Na2Sx (x = 1–3) in the discharge process as revealed in Fig. S11,† contributing to an enhanced capacity. Similarly, in the spectrum of P 2p (Fig. 7b), the peaks assigned to P–C, P–S, and P–O also shift to lower energies of 130.5, 132.5 and 133.6 eV at 0.01 V, suggesting that the active sites around P atoms show distinct adsorption of Na+ ions (Fig. S11†). These results demonstrate that P, S co-doping, especially the C–S–P bonds, can facilitate a strong interaction with Na+ ions. When charged to 3 V (Fig. 7c), the strong peak at 161.7 eV (near the pristine PSC's 162.1 eV) corresponds to the recovery chemical environment of S–P bonding, indicating a good reversibility, while the binding energies of S 2p3/2 and S 2p1/2 peaks shift positively to 162.9 and 164.1 eV (lower than the pristine PSC's 164.1 and 165.4 eV), suggesting the partial oxidation of S. In the spectrum of P 2p (Fig. 7d) when fully charged to 3.0 V, the P–S bond at 133.0 eV regains intensity compared to the discharged state of the pristine PSC, indicating its recovery.
The excellent performance of the PSC anode in a half cell encouraged us to evaluate it application in full cells. Carbon coated Na3V2(PO4)3 (denoted as NVP@C, Fig. S12†) was used as the cathode and was synthesized by a simple solid-phase method reported in our previous work.66 The electrochemical performance of NVP@C is presented in Fig. S13;† it can deliver a specific capacity of 80 mA h g−1 at 100 mA g−1 with no decay after 550 cycles. Before the full cell assembly, the PSC electrode is pre-cycled in a half cell. The cycle performance and charge–discharge curves of the NVP@C//PSC full cell in a voltage window of 0.5–3.2 V are shown in Fig. 8. As can be seen, the NVP@C//PSC full cell can deliver a high initial capacity of ∼276 mA h g−1 (based on the active mass of the anode) at 500 mA g−1 and still maintain a stable capacity of 231 mA h g−1 after 270 cycles (Fig. 8a), corresponding to a capacity retention of 83.7%. Besides, the charge and discharge curves of the NVP@C//PSC full cell show an average discharge voltage of 1.5 V (Fig. 8b). The good performance of the NVP@C//PSC full cell demonstrates the possibility of using the PSC anode in a practical sodium ion full battery.
Therefore, the superior electrochemical performance of P and S co-doped carbon can be ascribed to the following aspects. Firstly, the porous structure of PSC with an enlarged interlayer spacing (∼0.41 nm) ensures sufficient penetration of electrolyte into the electrode and facilitates fast diffusion of Na+ ions; secondly, the abundant defects induced by P, S co-doping especially P-doping provide considerable active sites to accommodate Na ions, which not only improve the reversible capability but also the faradaic capacitance on the surface and high-rate discharge capability; thirdly, the increased electronic conductivity also boosts the charge transfer and benefits the high rate performance. As a result, the synergistic effects of unique porous structure and high level P, S co-doping are responsible for the high performance of PSC.
Conclusion
In summary, a high doping level P, S-co doped carbon is successfully synthesized by an economical and scalable method, and is applied as an anode for SIBs. The prepared PSC exhibits a high reversible capacity (513.8 mA h g−1 at 100 mA g−1), superior cycling performance (290.1 mA h g−1 at 1 A g−1 over 1000 cycles), and excellent rate capability (181.8 mA h g−1 at 10 A g−1). This excellent electrochemical performance of PSC can be attributed to its highly disordered porous structure, enlarged interlayer spacing and particularly a large number of active sites produced by sulfur and phosphorus doping. Theoretical calculations demonstrate that C–S–P bonds can facilitate the adsorption of sodium ions and improve the electronic conductivity, leading to excellent sodium storage performance. Our findings provide a new perspective to understand the sodium storage mechanism of carbon materials as anodes for SIBs.Conflicts of interest
The authors have no competing financial interests to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 21703073, 51622703, 51774148, and 51977097) and the China Postdoctoral Science Foundation Funded Project (Grant No. 2018 M642834). The authors acknowledge the Analytical & Testing Center of Huazhong University of Science and Technology.References
- P. Bai, Y. He, X. Zou, X. Zhao, P. Xiong and Y. Xu, Adv. Energy Mater., 2018, 8, 1703217 CrossRef.
- D. S. Bin, Y. Li, Y. G. Sun, S. Y. Duan, Y. Lu, J. Ma, A. M. Cao, Y. S. Hu and L. J. Wan, Adv. Energy Mater., 2018, 8, 1800855 CrossRef.
- L. Li, Y. Zheng, S. Zhang, J. Yang, Z. Shao and Z. Guo, Energy Environ. Sci., 2018, 11, 2310–2340 RSC.
- X. Wang, G. Li, F. M. Hassan, J. Li, X. Fan, R. Batmaz, X. Xiao and Z. Chen, Nano Energy, 2015, 15, 746–754 CrossRef CAS.
- W. Li, M. Zhou, H. Li, K. Wang, S. Cheng and K. Jiang, Energy Environ. Sci., 2015, 8, 2916–2921 RSC.
- Y. Liu, Y. Qiao, G. Wei, S. Li, Z. Lu, X. Wang and X. Lou, Energy Storage Materials, 2018, 11, 274–281 CrossRef.
- H. Li, K. Wang, M. Zhou, W. Li, H. Tao, R. Wang, S. Cheng and K. Jiang, ACS Nano, 2019, 13, 9533–9540 CrossRef CAS PubMed.
- X. Sun, C. Wang, Y. Gong, L. Gu, Q. Chen and Y. Yu, Small, 2018, 14, 1802218 CrossRef PubMed.
- P. Xiong, P. Bai, A. Li, B. Li, M. Cheng, Y. Chen, S. Huang, Q. Jiang, X. Bu and Y. Xu, Adv. Mater., 2019, 1904771, 1904771 CrossRef PubMed.
- Y. Fang, X. Y. Yu and X. W. D. Lou, Adv. Mater., 2018, 30, 1–6 Search PubMed.
- H. Li, K. Wang, S. Cheng and K. Jiang, ACS Appl. Mater. Interfaces, 2018, 10, 8016–8025 CrossRef CAS PubMed.
- R. E. Franklin, Proc. R. Soc. Lond. Ser A Math. Phys. Sci., 1951, 209, 196–218 CrossRef CAS.
- B. Xiao, F. A. Soto, M. Gu, K. S. Han, J. Song, H. Wang, M. H. Engelhard, V. Murugesan, K. T. Mueller, D. Reed, V. L. Sprenkle, P. B. Balbuena and X. Li, Adv. Energy Mater., 2018, 8, 1–10 Search PubMed.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271–1273 CrossRef CAS.
- H. Hou, C. E. Banks, M. Jing, Y. Zhang and X. Ji, Adv. Mater., 2015, 27, 7861–7866 CrossRef CAS PubMed.
- T. Chen, L. Pan, T. Lu, C. Fu, D. H. C. Chua and Z. Sun, J. Mater. Chem. A, 2014, 2, 1263–1267 RSC.
- Z. Wang, L. Qie, L. Yuan, W. Zhang, X. Hu and Y. Huang, Carbon, 2013, 55, 328–334 CrossRef CAS.
- P. Thomas and D. Billaud, Electrochim. Acta, 2002, 47, 3303–3307 CrossRef CAS.
- Z. L. Yu, S. Xin, Y. You, L. Yu, Y. Lin, D. W. Xu, C. Qiao, Z. H. Huang, N. Yang, S. H. Yu and J. B. Goodenough, J. Am. Chem. Soc., 2016, 138, 14915–14922 CrossRef CAS PubMed.
- S. Wenzel, T. Hara, J. Janek and P. Adelhelm, Energy Environ. Sci., 2011, 4, 3342–3345 RSC.
- M. Wahid, D. Puthusseri, Y. Gawli, N. Sharma and S. Ogale, ChemSusChem, 2018, 11, 506–526 CrossRef CAS PubMed.
- H. Hou, X. Qiu, W. Wei, Y. Zhang and X. Ji, Adv. Energy Mater., 2017, 7, 1602898 CrossRef.
- C. Bommier, T. W. Surta, M. Dolgos and X. Ji, Nano Lett., 2015, 15, 5888–5892 CrossRef CAS PubMed.
- S. Qiu, L. Xiao, M. L. Sushko, K. S. Han, Y. Shao, M. Yan, X. Liang, L. Mai, J. Feng, Y. Cao, X. Ai, H. Yang and J. Liu, Adv. Energy Mater., 2017, 7, 1700403 CrossRef.
- C. Matei Ghimbeu, J. Górka, V. Simone, L. Simonin, S. Martinet and C. Vix-Guterl, Nano Energy, 2018, 44, 327–335 CrossRef CAS.
- Y. Wen, K. He, Y. Zhu, F. Han, Y. Xu, I. Matsuda, Y. Ishii, J. Cumings and C. Wang, Nat. Commun., 2014, 5, 4033 CrossRef CAS PubMed.
- X. Hu, X. Sun, S. J. Yoo, B. Evanko, F. Fan, S. Cai, C. Zheng, W. Hu and G. D. Stucky, Nano Energy, 2019, 56, 828–839 CrossRef CAS.
- J. Yang, X. Zhou, D. Wu, X. Zhao and Z. Zhou, Adv. Mater., 2017, 29, 1604108 CrossRef PubMed.
- G. Zou, H. Hou, C. W. Foster, C. E. Banks, T. Guo, Y. Jiang, Y. Zhang and X. Ji, Adv. Sci., 2018, 5, 1800241 CrossRef PubMed.
- Z. Hong, Y. Zhen, Y. Ruan, M. Kang, K. Zhou, J. M. Zhang, Z. Huang and M. Wei, Adv. Mater., 2018, 30, 1802035 CrossRef PubMed.
- X.-W. D. Lou, Angew. Chem., Int. Ed. DOI:10.1002/anie.201910309.
- D. Xu, C. Chen, J. Xie, B. Zhang, L. Miao, J. Cai, Y. Huang and L. Zhang, Adv. Energy Mater., 2016, 6, 1501929 CrossRef.
- W. Li, K. Wang, S. Cheng and K. Jiang, ChemElectroChem, 2018, 5, 3206–3212 CrossRef CAS.
- Q. Jin, W. Li, K. Wang, P. Feng, H. Li, T. Gu, M. Zhou, W. Wang, S. Cheng and K. Jiang, J. Mater. Chem. A, 2019, 7, 10239–10245 RSC.
- H. He, D. Huang, Y. Tang, Q. Wang, X. Ji, H. Wang and Z. Guo, Nano Energy, 2019, 57, 728–736 CrossRef CAS.
- Y. Li, Y. Yuan, Y. Bai, Y. Liu, Z. Wang, L. Li, F. Wu, K. Amine, C. Wu and J. Lu, Adv. Energy Mater., 2018, 8, 1702781 CrossRef.
- Z. Li, C. Bommier, Z. Sen Chong, Z. Jian, T. W. Surta, X. Wang, Z. Xing, J. C. Neuefeind, W. F. Stickle, M. Dolgos, P. A. Greaney and X. Ji, Adv. Energy Mater., 2017, 7, 1602894 CrossRef.
- Z. Li, L. Ma, T. W. Surta, C. Bommier, Z. Jian, Z. Xing, W. F. Stickle, M. Dolgos, K. Amine, J. Lu, T. Wu and X. Ji, ACS Energy Lett., 2016, 1, 395–401 CrossRef CAS.
- G. Ma, Z. Xiang, K. Huang, Z. Ju, Q. Zhuang and Y. Cui, Part. Part. Syst. Charact., 2017, 34, 1600315 CrossRef.
- H. Hou, L. Shao, Y. Zhang, G. Zou, J. Chen and X. Ji, Adv. Sci., 2017, 4, 1600243 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- K. Georg and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- Y. Hu, B. Li, X. Jiao, C. Zhang, X. Dai and J. Song, Adv. Funct. Mater., 2018, 28, 1801010 CrossRef.
- G. Tan, R. Xu, Z. Xing, Y. Yuan, J. Lu, J. Wen, C. Liu, L. Ma, C. Zhan, Q. Liu, T. Wu, Z. Jian, R. Shahbazian-Yassar, Y. Ren, D. J. Miller, L. A. Curtiss, X. Ji and K. Amine, Nat. Energy, 2017, 2, 17090 CrossRef CAS.
- Y. Gao, H. Zhao, D. Chen, C. Chen and F. Ciucci, Carbon, 2015, 94, 1028–1036 CrossRef CAS.
- M. Latorre-Sánchez, A. Primo and H. García, Angew. Chem., Int. Ed., 2013, 52, 11813–11816 CrossRef PubMed.
- N. Parveen, M. O. Ansari, S. A. Ansari and M. H. Cho, J. Mater. Chem. A, 2015, 4, 233–240 RSC.
- J. Zhang, Y. Shi, Y. Ding, L. Peng, W. Zhang and G. Yu, Adv. Energy Mater., 2017, 7, 1602876 CrossRef.
- N. Tanibata, H. Tsukasaki, M. Deguchi, S. Mori, A. Hayashi and M. Tatsumisago, J. Mater. Chem. A, 2017, 5, 11224–11228 RSC.
- J. Ye, H. Zhao, W. Song, N. Wang, M. Kang and Z. Li, J. Power Sources, 2019, 412, 606–614 CrossRef CAS.
- J. Qian, F. Wu, Y. Ye, M. Zhang, Y. Huang, Y. Xing, W. Qu, L. Li and R. Chen, Adv. Energy Mater., 2018, 8, 1703159 CrossRef.
- Z. Liu, L. Zhang, L. Sheng, Q. Zhou, T. Wei, J. Feng and Z. Fan, Adv. Energy Mater., 2018, 8, 1802042 CrossRef.
- Y. Wang, Z. Wang, Y. Chen, H. Zhang, M. Yousaf, H. Wu, M. Zou, A. Cao and R. P. S. Han, Adv. Mater., 2018, 30, 1802074 CrossRef PubMed.
- Y. Fang, X. Y. Yu and X. W. Lou, Angew. Chem., Int. Ed., 2018, 57, 9859–9863 CrossRef CAS PubMed.
- B. Li, B. Xi, Z. Feng, Y. Lin, J. Liu, J. Feng, Y. Qian and S. Xiong, Adv. Mater., 2018, 30, 1705788 CrossRef PubMed.
- J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925 CrossRef CAS.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC.
- P. Feng, W. Wang, K. Wang, S. Cheng and K. Jiang, J. Alloys Compd., 2019, 795, 223–232 CrossRef CAS.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- Y. Qiao, M. Ma, Y. Liu, S. Li, Z. Lu, H. Yue, H. Dong, Z. Cao, Y. Yin and S. Yang, J. Mater. Chem. A, 2016, 4, 15565 RSC.
- C. Ling and F. Mizuno, Phys. Chem. Chem. Phys., 2014, 16, 10419 RSC.
- K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430 CrossRef.
- P. Feng, W. Wang, K. Wang, S. Cheng and K. Jiang, J. Mater. Chem. A, 2017, 5, 10261 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta11594c |
| This journal is © The Royal Society of Chemistry 2020 |