Constructing a tunable defect structure in TiO₂ for photocatalytic nitrogen fixation

Abstract

Photocatalytic systems capable of precisely regulating oxygen vacancy (OV) concentrations, which could help illuminate the effects of the OV concentration on N₂ fixation activity, are still scarce. Here, we demonstrate that excessive OVs in TiO₂, while increasing the adsorption activation capacity of N₂ molecules, exhibit disappointing activity due to a decrease in charge separation efficiency. With optimized OV concentration, TiO₂ can increase the charge separation efficiency 3-fold and show significant activation towards N₂ molecules. The normalized N₂ photofixation rate is 324.86 μmol h⁻¹ g⁻¹ (full spectrum) and the corresponding apparent quantum yield (AQY) under 365 nm illumination reaches 1.1%, which are relatively high levels compared to reports in the literature. The origin of this excellent activity is clearly attributable to the OV defect structures, which coordinate the charge separation efficiency and the dissociative adsorption capacity of N₂. This work establishes the relationship between OV concentration and activity, and helps to construct a highly efficient nitrogen-fixing photocatalyst by optimizing the OV concentration.

---

Introduction

Photocatalytic nitrogen fixation is highly promising and possesses significant potential with regard to sustainable energy solutions compared to the industrial Haber–Bosch process, which is carried out under a high temperature (300–550 °C) and pressure (15–25 MPa).^1–3 To drive its reactions, a photocatalyst must efficiently separate photogenerated carriers to minimize recombination and activate nitrogen molecules to enable their reaction with migrating photogenerated carriers.⁴ Unfortunately, due to the fast recombination of photogenerated carriers, most of these photocatalytic systems show disappointing activity. More than that, the rate-determining step of N₂ fixation is the cleavage of the N≡N triple bond.⁵ The strong triple bond of nitrogen (bond energy: 941 kJ mol⁻¹) is very stable and difficult to dissociate on the photocatalyst surface, which leads to a very low nitrogen fixation activity. It has remained a huge challenge to activate and split the highly stable N≡N bond for solar-driven N₂ fixation. Therefore, there is an urgent need to explore and construct high-efficiency photocatalysts for nitrogen fixation.

Recently, building defects in semiconductor photocatalysts has attracted attention as an approach for furnishing abundant active sites to activate N₂ molecules for challenging nitrogen fixation.^6–9 Despite the strong N≡N triple bonds, they can be activated and weakened through the transfer of electrons into the antibonding orbital of N₂ when absorbed on defect sites,¹⁰ which favors nitrogen molecules that then react with photogenerated electrons for the nitrogen reduction reaction. Zhang and co-workers first proposed that the oxygen vacancies (OVs) on the surface of BiOBr nanosheets can significantly improve the adsorption and activation of N₂ molecules, resulting in the successful reduction of N₂ to NH₃ at normal temperatures and pressures.¹¹ In addition, the OV-induced defect states can work as photoexcited electron acceptors to prevent electron/hole recombination, and facilitate the transfer of interfacial carriers from the photoexcited photocatalysts to pre-activated N₂ on the OV sites. Zhao et al. reported that the photoelectric separation efficiency can be increased tenfold by introducing OVs onto rutile TiO₂.¹² Sun's group found that defective SrTiO₃ can increase the charge separation efficiency by 5 times compared with common SrTiO₃.¹³ The high charge separation efficiency is beneficial to more photogenerated carriers participating in N₂ fixation reaction. Several defective inorganic and organic semiconductors have been used for N₂ activation and photofixation, such as TiO₂,⁵ Sb/TiO₂,¹⁴ Cu–TiO₂,¹⁵ Au/TiO₂,¹⁶ g-C₃N₄,^17,18 W₁₈O₄₉,¹⁹ MoO₃,²⁰ CuCr-LDH,²¹ BiOCl,²² BiOBr,¹¹ Bi₅O₇Br₄,²³ Bi₃O₄Br,²⁴ Bi₂WO₆,²⁵ and Bi₅O₇I.²⁶ However, systems capable of precisely regulating OV concentration which could help illuminate the effect of OV concentration on N₂ fixation activity are still scarce. A series of continuously adjustable OVs can be achieved to tailor the electronic structure and together serve as surface charge separation centers and adsorption activation sites for N₂ to further promote the N₂ fixation activity.

Here we choose the most common TiO₂ as a model photocatalyst to study the effect of OV concentration on nitrogen fixation activity. The OVs are constructed by a solid phase reduction with NaBH₄, and their concentration can be precisely regulated by the reduction temperature (310–360 °C). We demonstrate that the reduced TiO₂ with optimized OV concentration exhibits a 3-fold increase in charge separation efficiency and shows significant activation towards N₂ molecules. Excessive OVs, while increasing the adsorption activation capacity of N₂, exhibit disappointing activity due to a decrease in charge separation efficiency. The normalized N₂ photofixation rate is 324.86 μmol h⁻¹ g⁻¹ (full spectrum), which is 3.85 times that of the original TiO₂. It is immediately evident that the NH₄⁺ production rate under a full spectrum and the AQY in this work are at a relatively high level. This work establishes the relationship between OV concentration and N₂ fixation activity, and clarifies that the activity can be enhanced by optimizing the OV concentration to coordinate the charge separation efficiency and the dissociative adsorption capacity of N₂.

Experimental

Chemicals and materials

Pluronic@F-127 (F127) and standard ammonia solution (1000 mg L⁻¹ NH₄⁺ in water) were purchased from Sigma-Aldrich. Tetrabutyl titanate (TBT, AR, 98%), ethanol (AR, 99.7%), hydrochloric acid (AR, 36–38%) and acetic acid (AR, 99.5%) were purchased from Beijing Chemical Reagent Company. NaBH₄ (98%), hydrazine (80%) and 4-(dimethylamino) benzaldehyde (99%) were purchased from Aladdin Reagent Company. Methanol (AR, 99.5%) was purchased from Sinopharm Chemical Reagent Co., Ltd. All chemicals were used without any further purification.

Synthesis of anatase TiO₂

At room temperature, 8 g of F127, 11.5 mL of HCl, and 3.7 mL of acetic acid were dissolved in 150 mL of ethanol and then added to 30 mL of TBT. The mixture was agitated vigorously for 2 h, then subsequently evaporated at 100 °C in an electric oven for 12 h. Following this, the reaction was aged for 24 h. The as-prepared samples were annealed at 500 °C for 4 h at a heating rate of 2 °C min⁻¹ to remove remaining organic impurities and finally the anatase TiO₂ was obtained.

Preparation of reduced TiO₂

At room temperature, 2.0 g of anatase TiO₂ powders were mixed with 2 g of NaBH₄ and the mixtures were ground for 30 min. Then the mixtures were transferred into a glass bottle, and then heated to the designated temperature (310–360 °C) at a rate of 5 °C min⁻¹ in a tubular furnace and maintained at this temperature for 30 min under an Ar atmosphere. After cooling down to room temperature, the samples were washed with distilled water several times to remove the remaining impurities and dried in an oven at 60 °C for 12 h. According to the temperature of the reduction treatment, we named the samples R-x (x refers to the reduction temperature).

Characterization

Scanning electron microscope (SEM) images were measured on a JEOL JSM 4800F microscope. Transmission electron microscope (TEM) images were taken using a FEI Tecnai G2 F30 operated at 300 kV. The crystalline structure was recorded by using an X-ray diffractometer (XRD) (Bruker D8 Advance), using Cu Kα radiation (λ = 1.54056 A). The Brunauer–Emmett–Teller (BET) specific surface area was measured using an ASAP 2020 HD88 Surface Area and Pore Size Analyzer. The UV-Vis absorption spectra were recorded on a UV-2450 scanning spectrophotometer (Shimadzu). Fluorescence emission spectra were recorded on an FLS 9802 fluorescence spectrometer. X-ray photoelectron spectrum (XPS) analyses were performed on an ESCALAB 250Xi spectrometer with an Al-Kα (1486.6 eV) achromatic X-ray source. The EPR spectra were recorded using a Bruker EMX-8 spectrometer at 9.857 GHz at 100 K. The temperature-programmed desorption of N₂ (N₂-TPD) was tested with an Autosorb-iQ-C chemisorption analyser (Quantachrome, USA) with the temperature ranging from 0 to 773 K.

Photocatalytic nitrogen fixation

50 mg of the photocatalyst was added and dispersed in 100 mL of solution (10 mL of methanol, 90 mL of deionized water) under ultra-sonication for 15 min. Then high-purity N₂ was bubbled at a rate of 30 mL min⁻¹. And then the system was closed and illuminated with a 300 W Xe lamp. All runs were conducted at ambient pressure and 25 °C. 2 mL of the solution was taken out for ammonia detection every 10 min during the illumination. The concentration of ammonia was detected by ion chromatography (Metrohm IC).

AQY calculations of nitrogen fixation

The catalyst solution was irradiated by a 365 nm LED (2 W) for 1 h. The average intensity of irradiation was determined by an FZ-A spectroradiometer (Photoelectric Instrument Factory of Beijing Normal University). The AQY was calculated from the equation:

Quantification of hydrazine

The amount of hydrazine was measured based on the basis of the condensation of hydrazine with 4-(dimethylamino) benzaldehyde. The colored solutions formed had an absorption peak centered at 456 nm. A 0.1 mg mL⁻¹ stock solution of hydrazine monohydrate was prepared in 0.05 M H₂SO₄ solution. The standard solutions were freshly prepared. A solution of colored reagent was prepared by dissolving 1.09 g of 4-(dimethylamino) benzaldehyde with a mixture of 5.5 mL of concentrated HCl solution and 54.5 mL of ethanol. 1 mL of different concentrations of hydrazine solutions were added to 4 mL colorimetric tubes. Then, these solutions were mixed with 1 mL of colored reagent and were set aside for 20 min for full color development.

IPCE measurements

10 mg of the samples were dispersed in 100 mL of 0.2 mg mL⁻¹ I₂/acetone solution under ultrasonic treatment. A two-electrode process was used to deposit the samples at an applied potential of 30 V for 5 min. FTO glass substrates with a coated area of about 1 × 3 cm² were used for both electrodes. Then, the deposited electrode was dried at 200 °C for 30 min to remove I₂ residues. A conventional three electrode process was used to investigate the photoelectrochemical properties of samples in a quartz cell. An FTO photoanode with deposited samples, Hg/HgCl₂, and a Pt foil electrode acted as the working electrode, reference electrode, and counter electrode, respectively. A 0.5 M Na₂SO₃ aqueous solution was used as the electrolyte. The photoanode was illuminated by a 300 W Xe lamp with a monochromator. The illuminated area was 1 × 1 cm². The IPCE (incident photon-to-current conversion efficiency) was calculated from the following equation:

Surface photovoltage measurements

The surface photovoltage (SPV) measurement system consisted of a source of monochromatic light, a lock-in amplifier (SR 830-DSP) with a light chopper (SR 540) and a sample chamber. Monochromatic light was provided by a 300 W Xe lamp (Perfect Light Company Solaredge 700) and a monochromator (SBP500, Zolix). All measurements were operated at room temperature and under ambient pressure and samples were not pre-treated prior to the SPV measurement.

In situ DRIFT measurements

In situ diffuse-reflectance infrared Fourier transform spectroscopy (DRIFTS) was performed on a Nicolet iS50 FT-IR spectrometer. The TiO₂ catalyst was placed in the center of the reaction cell, followed by pumping out all gases with an ultrahigh vacuum pump. In our functional model, a layer of water molecules is necessary to provide protons. Before a large amount of molecular nitrogen was pumped to form a nitrogen atmosphere, it was pre-adsorbed on the surface by bubbling a small amount of water vapor. Finally, the full spectrum light was turned on and the IR signal was in situ collected through an MCT detector alongside the reaction the background spectrum was collected beforehand and automatically subtracted from the recorded spectrum.

DFT theoretical calculations

All the calculations were performed using first-principles density functional theory (DFT)+U calculations with the exchange-correlation energy functional, which were described by a generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation function. A (1 × 1) surface was applied to test the thickness of the atomic layers of the slabs for all the models, which was implemented by the CASTEP code in which a plane-wave pseudopotential approach and ultrasoft pseudopotentials were employed for all the atoms with a kinetic energy cutoff of 520 eV. A Monkhorst–Pack mesh for anatase was generated with k-points of 2 × 4 × 1. To simulate N₂ activation on the anatase surfaces, a (2 × 5) supercell was used and enabled by a VASP code in which the projector augmented wave (PAW) method represented the electron–ion interaction with a kinetic energy cutoff of 520 eV. During optimizations, the energy and force converged to 10⁻⁴ eV per atom and 0.01 eV Å⁻¹, respectively. The k-points were 5 × 5 × 1 for the anatase (101) supercell.

Results and discussion

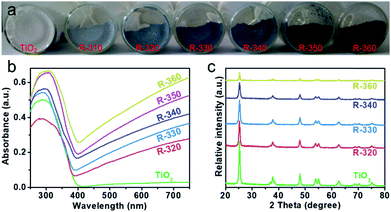
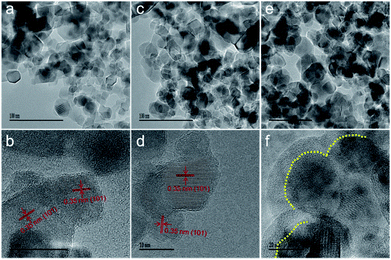
Constructing a suitable concentration of OV defects can extend visible light harvesting and facilitate the charge separation process, thereby improving the photocatalytic efficiency. However, an excess amount of OVs may generate a deep energy level as a recombination center for photoproduced carriers. Large quantities of anatase TiO₂ were prepared according to a sol–gel method by introducing a surfactant of F127 to control the particle sizes to below 50 nm. Subsequently, one-step solid phase reduction with NaBH₄ was used to obtain reduced TiO₂. Using the reducing properties of NaBH₄, the OV concentration can be regulated by controlling the reaction temperature (310–360 °C). According to the reduction temperature, we named the samples R-x (x refers to the reduction temperature). The adjustable colours of these reduced TiO₂ samples at different temperatures, as shown in Fig. 1a, gradually changed from white to light blue and finally to dark blue with an increase in the reduction temperature. The ultraviolet-visible diffuse reflectance spectra (UV-Vis DRS) are shown in Fig. 1b. Compared with the original anatase, a stronger absorption band in the visible-light region is present with a rise in the reaction temperature. These results are consistent with the colour changes in the samples (Fig. 1a). In addition, the visible light absorption may come from midgap states in the forbidden band, such as the OV defect band. The XPS valence-band analyses (Fig. S1†) indicate that the VB position was 1.74 eV below the Fermi level and did not change obviously before or after reduction. Therefore, we speculate that the OV defect band may be located below the CB, which is consistent with previous reports.^12,13,27 The X-ray powder diffraction pattern (XRD, Fig. 1c) indicates a typical anatase phase of TiO₂ (JCPDS no. 21-1272), and no additional diffraction peaks of other species are observed. However, a significantly wider and weaker main peak is shown with an increase in reduction temperature, which can be attributed to OVs, because of disorder-induced lattice strains and a decrease in crystallite dimension.²⁷

Fig. 1 Optical images (a), UV-vis DRS spectra (b) and XRD patterns (c) of anatase and reduced TiO₂.

The morphology of reduced TiO₂ is represented by scanning electron microscopy (SEM) and transmission electron microscopy (TEM). Fig. S2† shows the FE-SEM images of the nanoparticles with significant agglomeration after the reduction. Low resolution TEM (Fig. 2a, c and e) and high resolution TEM images (HR-TEM, Fig. 2b and d) show that the reduced TiO₂ are nanoparticles with a diameter of 20–50 nm and that 0.35 nm is the characteristic lattice fringe space of anatase TiO₂ (101). Interestingly, we observed the apparently amorphous structure of the R-360 surface (Fig. 2f), which matches well with the changes in XRD. The Brunauer–Emmett–Teller (BET) surface area and pore size distribution are characterized using N₂ adsorption–desorption isotherms (Fig. S3†). The original anatase exhibits BET surface area of 60.5 m² g⁻¹ calculated from the N₂ adsorption–desorption curve. After reduction treatment, the BET surface areas exhibit a slight reduction caused by nanoparticle agglomeration and are measured to be 57.2 (R-340) and 56.4 m² g⁻¹ (R-360), respectively.

Fig. 2 TEM and HR-TEM images of anatase (a and b), R-340 (c and d) and R-360 (e and f).

X-ray photoelectron spectroscopy (XPS) can furnish useful information regarding chemical binding and surface defects on the sample surfaces. The Ti 2p_3/2 and Ti 2p_1/2 peaks (Fig. 3a) show an obvious shift to low binding energies, indicating that Ti³⁺ doped TiO₂ is formed and the OV concentration increases as the reaction temperature goes up. Raman spectroscopy (Fig. 3b) is further used to illustrate the formation of OVs. With the increase in OV concentration, the strongest E_g mode area at 144 cm⁻¹ amplifies and exhibits a blue shift accompanied by peak broadening, compared with pristine TiO₂. As reported in previous studies, the shift and broadening of the peaks can be ascribed to the decrease in crystal domain size and nonstoichiometry.²⁸ Electron paramagnetic spectra (EPR) were recorded at 100 K to determine the presence of Ti³⁺. A strong EPR signal is observed at g = 1.95 (Fig. 3c), which could be assigned to Ti³⁺,²⁹ thus confirming the existence of the OVs in the reduced sample. The presence of Ti³⁺ results from the reduction of Ti⁴⁺ by NaBH₄. The photoluminescent peak intensity (Fig. 3d) of reduced TiO₂ reveals a significant decrease compared with pristine TiO₂, which indicates that these reduced TiO₂ samples have a relatively low radiative recombination rate of photogenerated electrons and holes. This fluorescence quenching is derived from the capture of photogenerated carriers by OV defects. These characterizations strongly illustrate the presence of OVs and the concentration increases as the reduction temperature increases.

Fig. 3 High-resolution Ti 2p XPS (a), Raman (b), low temperature EPR (c) and steady-state photoluminescence (d) spectra of anatase and reduced TiO₂.

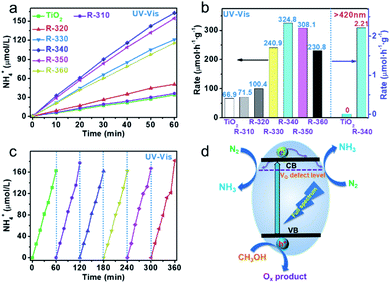
Successfully constructed reduced TiO₂ photocatalysts featuring regulatable defect structures allow an exploration of their N₂ fixation activity. The amount of NH₄⁺ produced was determined using cation exchange chromatography (Fig. S4†). A Xe lamp was used for illumination, and a 420 nm cutoff filter was employed to obtain the visible light. Control experiments indicated that ammonia cannot be generated in the absence of any of the following: illumination, N₂ or the reduced TiO₂ photocatalyst (Fig. S5†). Fig. 4a and b show the N₂ fixation and normalized N₂ fixation rate of anatase and reduced TiO₂. The amount of ammonia increases linearly with illumination (Fig. 4a). The normalized NH₄⁺ production rate is 66.94 μmol h⁻¹ g⁻¹ for 50 mg of anatase. By increasing the reduction temperature of the TiO₂ samples, the activity of NH₄⁺ production is also increased. However, an excessive reaction temperature (350–360 °C) results in a high OV concentration and a decrease in NH₄⁺ production rate. The appropriate concentration of OVs can be used as activation sites for nitrogen and separation centers for photogenerated carriers. Although the defect levels will weaken the reduction ability of photogenerated electrons, the activity of nitrogen fixation will be improved, as shown in the catalyst R-340. Excess OVs will become the recombination centers of photogenerated carriers and greatly reduce the reduction ability of photogenerated electrons, which has adverse effects on photocatalytic nitrogen fixation. The optimal reaction temperature is about 340 °C, the corresponding NH₄⁺ production rate is 324.86 μmol h⁻¹ g⁻¹ (full spectrum, 50 mg), which are 3.85 and 5.37 times that of pristine TiO₂ and Degussa P25 (Fig. S6†), respectively. Above all, R-340 shows obvious visible light activity at 2.21 μmol h⁻¹ g⁻¹, while no activity is shown for the original anatase. Fig. S7† shows the nitrogen fixation of R-340 in pure water, methanol/water and pure methanol. Compared with the activity in methanol/water, the activity was significantly improved under pure methanol conditions; while in pure water, the activity was very low. Considering that methanol is more easily oxidized by photogenerated holes than water, we think that the protons in ammonia may come mainly from methanol with a small part from water. The other potential reduction products, N₂H₄ and H₂, were quantified by the 4-(dimethylamino) benzaldehyde spectrophotometric method (Fig. S8†) and GC, respectively. In this work, NH₄⁺ was the only product without production of N₂H₄ and H₂. The activity shows almost no reduction after six cycles of photocatalytic experiment, indicating that R-340 has good photostability under a full spectrum (Fig. 4c). The morphology (Fig. S9†) and color (Fig. S10†) of the R-340 sample before and after photocatalytic reaction show no obvious change, which further confirms its photostability. We observed that irradiation of R-340 using a 365 nm LED can induce N₂ photofixation, with the apparent quantum yield (AQY) determined to be 1.1% at 365 nm. Table S1† compares photocatalytic data from the current study with previous data in the literature for N₂ photofixation. It is immediately evident that the NH₄⁺ production rate under a full spectrum and the AQY in this work are at a relatively high level. The origin of this excellent activity is clearly attributable to the OV defect structure and promotion of charge separation, visible light response and the activation of nitrogen molecules. Fig. 4d proposes a schematic diagram of photocatalytic N₂ fixation. The reduced TiO₂ is excited to generate photogenerated electrons and holes. Photoexcited electrons on the CB are then captured by the OV level below the CB. The N₂ molecules are activated at OV sites and react with the trapped photogenerated electrons to form NH₃. Photogenerated holes are consumed by the CH₃OH sacrificial agent.

Fig. 4 The full-spectrum N₂ fixation (a) and normalized N₂ fixation rate (b) data for anatase and reduced TiO₂. Recycling measurements of N₂ fixation for R-340 under full-spectrum irradiation (c). A schematic diagram of photocatalytic N₂ fixation (d). 50 mg of sample was dispersed in 100 mL of 10 vol% methanol solution under full-spectrum and visible-light irradiation for N₂ fixation, respectively.

In order to track the activation of N₂, in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) was used to detect intermediate products on the R-340 surface (Fig. 5). This highly sensitive spectroscopic technique allows the time-dependent transition of functional groups on the catalyst surface in a wet nitrogen flow to be studied under a full spectrum. Several absorption bands gradually strengthen with an increase in irradiation time from 0 to 160 min. The predominant overlapped absorption peaks ranging from 3600 to 2996 cm⁻¹ were ascribed to the ν(N–H) stretching mode of NH₃ and the ν(O–H) stretching mode of surface OH groups or adsorbed H₂O, respectively;¹⁶ while the two absorption peaks at 1700 and 1649 cm⁻¹ were attributed to the σ(N–H) bending mode.²³ Furthermore, the sharp peaks at 1397 cm⁻¹ and the weak peaks at 2876 and 1499 cm⁻¹ were assigned to the representative absorptions of NH₄⁺ and NH₃ molecules, respectively. In addition, another broad and weak peak located at 2108 cm⁻¹ was produced from the chemisorbed N₂. The wavenumber is shorter than the stretching wavenumber of free N₂ molecules (ν(gaseous N₂) = 2331 cm⁻¹) and larger than that of hydrazine (H₂N = NH₂) (1111 cm⁻¹), showing that the N≡N triple bond has weakened and the bond length has increased.³⁰ Fig. S11† shows the in situ DRIFTS in the N₂ fixation reaction of anatase TiO₂. In sharp contrast to R-340, the positions of all the peaks changed slightly. Moreover, the peak of nitrogen chemisorption at 2108 cm⁻¹ can hardly be observed, and the representative absorptions (1392, 2886 and 1496 cm⁻¹) of NH₄⁺ and NH₃ molecules are obviously weakened. These results show that OVs can activate nitrogen molecules and promote the formation of ammonia.

Fig. 5 In situ DRIFTS spectra detected as a function of time for the N₂ fixation reaction on R-340.

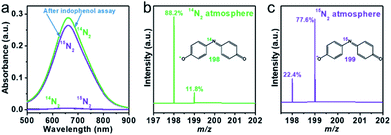
To verify the source of the ammonia from N₂ in our system, the photocatalytic N₂ reduction reaction was conducted with isotope-labeled ¹⁵N₂ gas.^5,15 100 mg of R-340 was dispersed in 100 mL of a methanol sacrificial solution and bubbled with Ar gas for 30 min. Thereafter, 50 mL of ¹⁵N₂ was injected into the closed reactor under full-spectrum irradiation for 10 h. A control experiment was performed by injecting 50 mL of high-purity ¹⁴N₂. Phenol solutions were added with NaClO as an oxidizing reagent and Na₂[Fe(CN)₅NO] as a catalyst. The resulting product ¹⁵NH₄⁺ was monitored according to the indophenol blue method, and further confirmed via liquid chromatography-mass spectroscopy (LC-MS). Both solutions presented an obvious absorption peak at 660 nm belonging to indophenol (Fig. 6a), and no peak appeared for either solution without light irradiation. Fig. 6b and c show the MS spectra of the indophenol solution from ¹⁴N₂ and ¹⁵N₂. The ¹⁴N₂ solution revealed two peaks at m/z 198 and m/z 199, which were attributed to the indophenol anion. Further, the ¹⁵N : ¹⁴N abundance ratio was significantly higher when ¹⁵N₂ was adopted as a nitrogen source. This test thus verifies that N₂ was the origin of NH₄⁺ in the photocatalytic reaction.

Fig. 6 The UV-vis absorption spectra of the solutions from N₂ reduction with ¹⁴N₂ or ¹⁵N₂ gas followed by an indophenol assay (a). MS spectra of obtained indophenol solutions from ¹⁴N₂ (b) and ¹⁵N₂ (c).

As aforementioned, the OV-induced defect states can work as photoexcited electron acceptors to prevent electron/hole recombination, and facilitate interfacial carrier transfer from the photoexcited photocatalysts to pre-activated N₂ on the OV sites. To further confirm this point of view, surface photovoltage spectroscopy (SPS), incident photon conversion efficiency (IPCE) measurement, N₂ temperature-programmed desorption (N₂-TPD) and steady-state photoluminescence (PL) spectroscopy were adopted. SPS is a powerful tool to further characterize charge separation at the nanoscale.^13,31Fig. 7a show the surface photovoltage (SPV) response of the original anatase, R-340 and R-360. A positive SPV response band in the range of 320–400 nm is detected, which is ascribed to the electron transition from VB to CB. The SPV response in R-340 is ∼3 times that of the original anatase, revealing a dramatic increase in charge separation efficiency. However, R-360 exhibits a significantly reduced SPV intensity and weak charge separation. The IPCE measurement (Fig. 7b) clearly shows that the conversion efficiency of the R-340 sample at 300 nm is approximately 10.9%, which is about a 2-fold increase compared to the original anatase. In case of R-360 sample, the conversion efficiency at 300 nm is only 1.3%. These results indicate that the OV-induced defect states can work as photoexcited electron acceptors to prevent electron/hole recombination, and promote charge separation; while excessive OVs act as recombination centres for photogenerated carriers, resulting in a decrease in charge separation efficiency, which corresponds to the decrease in nitrogen fixation activity shown in Fig. 4a and b. The N₂ temperature-programmed desorption (N₂-TPD, Fig. 7c) was used to study the adsorption and activation capacity of N₂. The pristine TiO₂ may contain trace OV defects itself due to the low formation energy of OVs, and the high surface energy and large specific surface area of ∼50 nm of TiO₂. All samples exhibited two N₂ desorption peaks at 130 and 365 °C, which were related to physical and chemical adsorption, respectively. With the increase in OV concentration, the adsorption and activation capacity of N₂ becomes stronger and stronger. This result shows that N₂ chemisorption occurs on OV sites, which is mainly caused by electron transfer from OVs into the antibonding orbital of N₂ when absorbed on defect sites.¹¹ This activation process favors nitrogen molecules that then react with photogenerated electrons for the nitrogen reduction reaction. Photoluminescence tests under different atmospheres (vacuum, argon and nitrogen) were used to investigate the activation behaviour of N₂ over OVs (Fig. 7d). Under an Ar atmosphere or vacuum, the R-340 presented a broader and more intense peak centred at about 420 nm compared to that under an N₂ atmosphere. Since the electrons captured at OV sites are usually in a metastable state, the quenching of the PL spectrum under an N₂ atmosphere may be due to the non-radiative transfer of captured electrons to the anti-bond orbital of adsorbed N₂.¹¹ This process greatly promoted the adsorption and dissociation of nitrogen molecules.

Fig. 7 The SPS (a) and IPCE (b) measurements of original anatase, R-340 and R-360. The N₂ TPD (c) data from original anatase, R-340 and R-360. Photoluminescence spectra under different atmospheres (vacuum, argon and nitrogen) of R-340 (d).

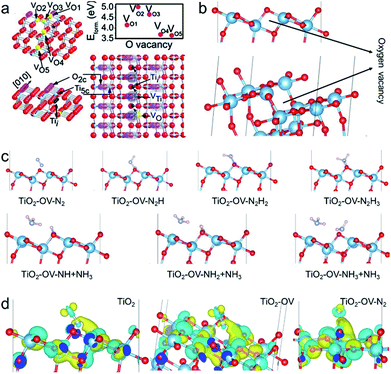
Density functional theory (DFT) calculations were employed to examine the possible N₂ activation on anatase TiO₂ (101) facets without and with OV. The OV energy of the anatase (101) crystal face is lowest in the secondary outer layer, so this configuration was also adopted in our calculations, as shown in Fig. 8a and b. Fig. 8c shows the theoretical calculation of each step of the photocatalytic nitrogen fixation. The chemisorption of N₂ on anatase (101) facets without OV was excluded due to their weak interactions. The OVs can adsorb and activate N₂ by transporting the available localized electrons back to the π antibonding orbital of N₂, while the activated N₂ with a negative charge greatly promotes the Lewis acid–base reaction activity at OV sites.²² As expected, after generating an OV on the surface, N₂ could be adsorbed on the OV through combining with the two nearest Ti atoms in the sublayer to form a terminal end-on bound structure. Since the N₂ fixation sites are diverse in the photocatalytic reactions, the model of an N₂ molecule on a Ti atom far away from OVs was considered. Due to the weak adsorption energy, the chemisorption of the N₂ molecule was excluded. The activation of the N≡N bond on the OV can be inferred via the N≡N bond length increasing to 1.138 Å, which is between the triple bond length (1.113 Å) of free N₂ and the double bond length (1.254 Å) of diazene (Fig. S12†). In addition, the adsorption energy was entirely negative during the whole process, indicating it is thermodynamically feasible for nitrogen fixation (Fig. S13†). Bader charge simulation and differential charge density were used to further explain the activation of nitrogen molecules at OV sites. As shown in Fig. 8d, the Ti atoms near the OVs accumulate more electrons, and these localized electrons are transferred to the adsorbed N₂ molecule. The number of electrons accumulated on the N₂ molecule increases, making the N≡N bond longer. Such interesting activation of the N₂ molecule can be found in many transition metal–N₂ complexes, in which the transitional metals (metal = Fe, Mo, Ru and Co) donate their available d-orbital electrons into the π N≡N antibonding system to activate the –N₂ ligand.

Fig. 8 O-vacancy configuration of the (101)-crystal facet outer layer of anatase phase TiO₂ (a and b). Theoretical calculations of each step of photocatalytic nitrogen fixation (c). Bader charge simulation and differential charge density data (d).

Conclusions

In summary, we have successfully designed and constructed a series of continuously adjustable defect structures on TiO₂. On one hand, an optimized concentration of OVs as electron acceptors can increase the charge separation efficiency 3-fold, while excessive OVs will result in a decrease in charge separation. On the other hand, N₂ adsorbed on OVs can be dissociated and activated through the transfer of electrons into the antibonding orbital of N₂, thus weakening the strong triple bond. In addition, the greater the concentration of OVs, the stronger the adsorption and activation behaviours of N₂. The defect structures were confirmed via XRD, TEM, XPS, Raman, EPR and PL studies, and the OV effects on N₂ fixation activity were also fully investigated according to SPV, IPCE, PL, N₂ TPD and DFT calculations. Finally, we further observed the formation of ammonia on the catalyst surface and the source of N via in situ DRIFTS and isotope-labeled ¹⁵N₂. Our results presented herein provide new insights into the construction of efficient nitrogen-fixing photocatalysts via optimizing the OV concentration to coordinate the charge separation efficiency and dissociative adsorption capacity of N₂.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was jointly supported by the Science and Technology Project of the Research Foundation of China Postdoctoral Science (2018M630982) and the Natural Science Foundation of China (51874199, 21601126). The computation experiments used the resources of the National Supercomputing Center in Shenzhen.

Notes and references

1. T. Rayment, R. Schlögl, J. Thomas and G. Ertl, Nature, 1985, 315, 311–313.
2. C. J. Van der Ham, M. T. Koper and D. G. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191.
3. D. E. Canfield, A. N. Glazer and P. G. Falkowski, Science, 2010, 330, 192–196.
4. G. Liu, H. G. Yang, J. Pan, Y. Q. Yang, G. Q. Lu and H.-M. Cheng, Chem. Rev., 2014, 114, 9559–9612.
5. H. Hirakawa, M. Hashimoto, Y. Shiraishi and T. Hirai, J. Am. Chem. Soc., 2017, 139, 10929–10936.
6. M. Cheng, C. Xiao and Y. Xie, J. Mater. Chem. A, 2019, 7, 19616–19633.
7. J. Li, H. Li, G. Zhan and L. Zhang, Acc. Chem. Res., 2016, 50, 112–121.
8. S. Bai, N. Zhang, C. Gao and Y. Xiong, Nano Energy, 2018, 53, 296–336.
9. M. Li, H. Huang, J. Low, C. Gao, R. Long and Y. Xiong, Small Methods, 2019, 3, 1800388.
10. K. C. MacLeod, D. J. Vinyard and P. L. Holland, J. Am. Chem. Soc., 2014, 136, 10226–10229.
11. H. Li, J. Shang, Z. Ai and L. Zhang, J. Am. Chem. Soc., 2015, 137, 6393–6399.
12. Z. Zhao, X. Zhang, G. Zhang, Z. Liu, D. Qu, X. Miao, P. Feng and Z. Sun, Nano Res., 2015, 8, 4061–4071.
13. G. Zhang, W. Jiang, S. Hua, H. Zhao, L. Zhang and Z. Sun, Nanoscale, 2016, 8, 16963–16968.
14. Z. Zhao, S. Hong, C. Yan, C. Choi, Y. Jung, Y. Liu, S. Liu, X. Li, J. Qiu and Z. Sun, Chem. Commun., 2019, 55, 7171–7174.
15. Y. Zhao, Y. Zhao, R. Shi, B. Wang, G. I. Waterhouse, L. Z. Wu, C. H. Tung and T. Zhang, Adv. Mater., 2019, 31, 1806482.
16. J. Yang, Y. Guo, R. Jiang, F. Qin, H. Zhang, W. Lu, J. Wang and J. C. M. Yu, J. Am. Chem. Soc., 2018, 140, 8497–8508.
17. G. Dong, W. Ho and C. Wang, J. Mater. Chem. A, 2015, 3, 23435–23441.
18. Y. Kofuji, Y. Isobe, Y. Shiraishi, H. Sakamoto, S. Tanaka, S. Ichikawa and T. Hirai, J. Am. Chem. Soc., 2016, 138, 10019–10025.
19. N. Zhang, A. Jalil, D. Wu, S. Chen, Y. Liu, C. Gao, W. Ye, Z. Qi, H. Ju and C. Wang, J. Am. Chem. Soc., 2018, 140, 9434–9443.
20. Y. Li, X. Chen, M. Zhang, Y. Zhu, W. Ren, Z. Mei, M. Gu and F. Pan, Catal. Sci. Technol., 2019, 9, 803–810.
21. Y. Zhao, Y. Zhao, G. I. Waterhouse, L. Zheng, X. Cao, F. Teng, L. Z. Wu, C. H. Tung, D. O'Hare and T. Zhang, Adv. Mater., 2017, 29, 1703828.
22. H. Li, J. Shang, J. Shi, K. Zhao and L. Zhang, Nanoscale, 2016, 8, 1986–1993.
23. S. Wang, X. Hai, X. Ding, K. Chang, Y. Xiang, X. Meng, Z. Yang, H. Chen and J. Ye, Adv. Mater., 2017, 29, 1701774.
24. J. Di, J. Xia, M. F. Chisholm, J. Zhong, C. Chen, X. Cao, F. Dong, Z. Chi, H. Chen and Y. X. Weng, Adv. Mater., 2019, 1807576.
25. S. Zhou, C. Zhang, J. Liu, J. Liao, Y. Kong, Y. Xu and G. Chen, Catal. Sci. Technol., 2019, 9, 5562–5566.
26. Y. Bai, L. Ye, T. Chen, L. Wang, X. Shi, X. Zhang and D. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 27661–27668.
27. H. Tan, Z. Zhao, M. Niu, C. Mao, D. Cao, D. Cheng, P. Feng and Z. Sun, Nanoscale, 2014, 6, 10216–10223.
28. Z. Wang, C. Yang, T. Lin, H. Yin, P. Chen, D. Wan, F. Xu, F. Huang, J. Lin and X. Xie, Adv. Funct. Mater., 2013, 23, 5444–5450.
29. F. Zuo, K. Bozhilov, R. J. Dillon, L. Wang, P. Smith, X. Zhao, C. Bardeen and P. Feng, Angew. Chem., Int. Ed., 2012, 51, 6223–6226.
30. H.-P. Jia and E. A. Quadrelli, Chem. Soc. Rev., 2014, 43, 547–564.
31. L. Kronik and Y. Shapira, Surf. Sci. Rep., 1999, 37, 1–206.

---

Footnote

† Electronic supplementary information (ESI) available: Additional SEM, BET, and photocatalysis data and DFT studies. See DOI: 10.1039/c9ta10471b

---