Revealing cooperative Li-ion migration in Li_1+xAl_xTi_2−x(PO₄)₃ solid state electrolytes with high Al doping

Abstract

Li_1+xAl_xTi_2−x(PO₄)₃ (LATP) is attracting attention as a promising inorganic solid electrolyte (ISE) with potential use in all-solid-state lithium-ion batteries. The objective of this paper is to examine and understand the effect of the Al-dopant concentration on the Li-ion diffusion of LATP using density functional theory and the molecular dynamics method. By comparing Li_1.16Al_0.16Ti_1.84(PO₄)₃ (LATP-0.16) and Li_1.33Al_0.33Ti_1.67(PO₄)₃ (LATP-0.33) with Li_1.5Al_0.5Ti_1.5(PO₄)₃ (LATP-0.50), LATP-0.50 is expected to have higher ionic conductivity. The trapping effect of Al-dopants on Li-ions is greatly reduced in LATP-0.50 due to the delocalization of polarization interactions and the depopulation of oxygen atoms, which results in a smooth energy landscape and destabilization of Li-ions. The energy difference of adjacent Li-ions and binding interaction of Li–Li due to a specific local configuration of two Li-ions alternately enable cooperative migration of Li-ions. This understanding of high Li-ion diffusion is important in interpreting the experimental results aiming to assess the effects of Al-dopants on Li-ion conductivity and can be used by researchers to engineer these materials for batteries.

---

Introduction

All-solid-state lithium batteries (ASSLBs) have been extensively studied due to their stability to lithium metal anodes and high safety.^1–4 One of the most important challenges in ASSLBs is to design solid electrolytes with high ionic conductivity.^5–7 Right now, the use of inorganic solid electrolytes (ISEs) is a field of continuous interest in ASSLBs,^8–11 but an optimum electrolyte is yet to be found. In terms of ionic conductivity, only a few ISEs have been considered on par with liquid electrolytes.^1,3 One approach for further improvement is to understand and fine-tune the already discovered fast Li-ion solid conductors such as Al-doped LiTi₂(PO₄)₃ (LTP) named Li_1+xAl_xTi_2−x(PO₄)₃ (LATP). The improvements in these materials can boost the properties of ISEs to a new level.¹²

Interstitial Li-ions created by the substitution of aliovalent Al³⁺ cations have been considered the source of ionic conductivity in LATP, and as a consequence, the ionic conductivity may increase with the concentration of interstitial Li-ions as some experiments have proved.^13–18 However, current experiments pay more attention to Li_1.2Al_0.2Ti_1.8(PO₄)₃ (LATP-0.20) or Li_1.3Al_0.3Ti_1.7(PO₄)₃ (LATP-0.30) rather than the Li_1.5Al_0.5Ti_1.5(PO₄)₃ (LATP-0.50) with higher Al-dopants.^17,19,20 To date, there has been no general agreement on the optimum Al-dopants in LATP.

Furthermore, interstitial migration in LATP, in particular, has a low barrier to enable high ionic conductivity.^21,22 Nevertheless, the structural and chemical origin of the interstitial migration is not understood, preventing the rational design of better ISEs. The well-defined atomistic structure of LATP provides us an ideal model system to probe the interstitial migration mechanism.

In this work, we chose to study three LATP systems with different compositions: Li_1.16Al_0.16Ti_1.84(PO₄)₃ (LATP-0.16), Li_1.33Al_0.33Ti_1.67(PO₄)₃ (LATP-0.33) and Li_1.5Al_0.5Ti_1.5(PO₄)₃ (LATP-0.50), along with LTP as a reference, to understand the ionic conductivity of LATP. Most research studies so far found that when the Al content was above 0.5, additional phosphate phases appear in LATP that slow down diffusion.^14,17,23,24 Therefore, in this work, we combine density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulation techniques to probe the Li-ion migration mechanism in LATP (0.0 ≤ x ≤ 0.5). In particular, the results obtained from DFT and long time-scale AIMD provide new insights into the mechanistic features of Al-dopants and lithium-ion (Li-ion) transport. These techniques have been applied successfully to a variety of studies on ionic or mixed conductors.^12,25–28

Results and discussion

Structural modeling

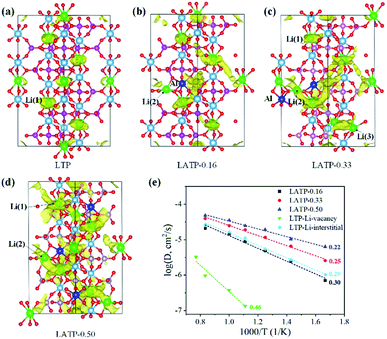
The LTP crystal structure has hexagonal symmetry and is composed of corner-sharing TiO₆-PO₄ units (Fig. 1a).^29–31 The distribution of Li-ions in Li(1) (6b), Li(2) (18e) and Li(3) (36f) positions is shown in the right inset of Fig. 1a. The Li(1) site is located in the LiO₆ octahedra, the Li(2) site is at each bend of the conduction channels, and the Li(3) site is adjacent to the Li(1) site along the conduction channel. The Li-ion diffusion pathway illustrated by the bond-valence method (analysis of valence mismatches)³² is a zigzag-shaped channel along the c-axis as shown in Fig. 1b. Li-ion migration within this system is restricted to within the channels of corner-sharing PO₄ tetrahedra and TiO₆ octahedra.

Fig. 1 (a) Polyhedral representation of the crystal structure of LTP and visualization of the local structure for Li-ion migration (right inset). (b) The potential diffusion pathway illustrated by the bond-valence mismatch method, and visualization of the positions of three Li-ions: M1 (6b), M2 (18e) and M3 (36f). (c) Local structure of LATP-0.16 with a configuration of two Li-ions.

To model LATP-0.16, LATP-0.33 and LATP-0.50, one, two, and three Ti atoms from the original twelve sites are replaced by Al atoms, respectively. The substitution of each Ti⁴⁺ by Al³⁺ needs an extra Li-ion for charge compensation and these Li-ions can occupy in either Li(2) or Li(3) sites. To check the stability of extra Li-ions at these two sites, the optimized local configuration of LATP-0.16 is calculated as shown in Fig. 1c. In the case of extra Li-ions occupying the Li(3) site, the interaction and steric effects between neighboring Li(1) and Li(3) positions lead to the displacement of Li(1)-ions and thus form two Li(3)-ions. In the case of extra Li-ions occupying the Li(2) site, the positions of neighboring Li(1)-ions are slightly displaced. The configuration energies of these two cases are nearly the same, suggesting that these configurations coexist in real experiments. In addition, Al-dopants in LATP tend to have a dispersed distribution rather than agglomeration according to the calculated configuration energy shown in Fig. S1 of the ESI.†

To study the influence of the Al-doping concentration on the stability of Al-dopants in LATP, we calculate the Al defect formation energy (Al-DFE) of LATP and phase decomposition energy (PDE) of LATP (detailed in the ESI†). The results suggest that the Al defect formation energies of LATP-0.33 (2.98 eV) and LATP-0.50 (3.10 eV) are very close. The decomposition energies of LATP-0.16, LATP-0.33 and LATP-0.50 are 262.41, 389.93, and 642.34 meV per atom, respectively. A positive value of Al-DFE or PDE signifies a thermodynamically unfavorable reaction. We note that the extent of Al defect formation and phase decomposition for LATP-0.33 is even a little higher than that for LATP-0.50. Now many experiments have successfully demonstrated the synthesis of LATP-0.50.¹⁷ Thus, the stability of the Al-dopant in LATP-0.50 is less problematic in practice because of the thermodynamically unfavorable reactions and the associated kinetic barrier.

Statistics of Li-ion hopping in LTP and LATP

To visualize the Li-ion diffusion paths and probe the transport mechanism, we perform lithium dynamic diffusion using the AIMD method on six LTP or LATP units. Fig. 2a–d show trajectory plots of Li-ion positions for LTP, LATP-0.16, LATP-0.33, and LATP-0.50 from an AIMD run (500 K), respectively. Fig. 2a clearly indicates small vibrations of Li-ions around their lattice sites, demonstrating a typical behavior of an ordered crystalline solid with no evidence of ion diffusion. This result suggests that Li-ion dynamics in LTP is a local oscillation. Comparing the shape and size of the spatial densities of the Li-ions obtained from the trajectory plots with those of the thermal ellipsoids from the neutron diffraction experiment,³³ we see a very good agreement.

Fig. 2 (a–d) The trajectory density (1 × 10⁻³ Å⁻³ isosurface level) of Li-ions in LTP, LATP-0.16, LATP-0.33 and LATP-0.50 obtained from 80 ps NVT AIMD simulations at 500 K. (e) Effects of Al-doping and carriers (Li-vacancies and Li-interstitials) on diffusivity in the LTP structure. The corresponding activation energies (in eV) are given. Data points at 600 K, 700 K, 800 K, 900 K, 1000 K and 1100 K in the AIMD simulations.

When two Al–Li pairs are present in LTP, i.e., LATP-0.33, there is some movement of the Li-ions (Fig. 2c). The diffuse distribution and overlapping of different Li positions indicate that Li-ions move through the interstitial sites, suggesting an interstitial mechanism. With the increasing of the Al-dopant (i.e., LATP-0.50 of Fig. 2c), all of the Li-ions are involved in the diffusion of lithium. To prove the effective hopping of Li-ions in LATP, we plotted the site displacement functions (SDFs) of Li-ion trajectories (Fig. S2 in ESI†) in LATP-0.50 obtained from 80 ps NVT AIMD simulations at 600 K. The SDF results suggest that the migration distance of Li-ions is more than 9 Å.

The calculated diffusivity and activation energy of LATP are plotted in Fig. 2e. We find that Al-doping enhances Li-ion conductivity. The increase in Li conductivity is consistent with the experimental observations that ISEs with a high Li-ion content tend to be better Li-ion conductors. The calculated activation energy for LTP (Li-ion migration via vacancies), LATP-0.16, LATP-0.33 and LATP-0.50 is 0.46, 0.30, 0.25, and 0.22 eV, respectively. In addition, we also calculate the interstitial migration by adding one interstitial Li-ion in LTP (with six LTP units). The calculated migration barrier is about 0.29 eV, suggesting that interstitial migration is more favourable than vacancy migration. Our results agree with those of the previous experiments that suggest LATP-0.50 has high Li-ion diffusivity.^13,14,34 The activation energy of LATP-0.50 is also in agreement with that obtained by lithium nuclear magnetic resonance (NMR) spectroscopy experiments (0.16–0.17 eV).¹³ The activation energy of LATP-0.50 is significantly lower than that of garnet-type Li₇La₃Zr₂O₁₂ (LLZO) (0.34 eV)³⁵ and is close to that of Li₁₀MP₂S₁₂ (M = Ge, Si, or Sn) groups (0.18–0.20 eV).³⁶ Therefore, the Li-ion conductivity in LATP-0.50 is among the best reported for solid electrolytes, and the related mechanism is sought to gain insight by the analysis of structural evolution during the Li-diffusion.

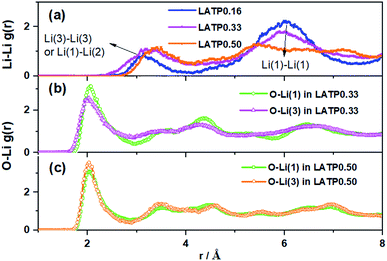
Valuable structural information can be obtained from radial distribution functions (RDFs), which often provide insight into the long-range (dis)order of a material. Fig. 3 shows the RDFs for Li–Li and partial RDFs for O–Li calculated over the simulation time. There are three important features. First, with the increase of the Al-dopant, the distance of Li–Li pairs (e.g. Li(1)–Li(1) and Li(3)–Li(3)) is reduced and the amplitude of the Li(3)–Li(3) peak becomes higher than that of Li(1)–Li(1) (Fig. 3a). Second, Li-ions originally in Li(3) sites are more mobile as demonstrated by the lack of structure beyond the first coordination shell (Fig. 3b), indicative of the greater disorder. Third, the partial RDF peaks for O–Li(1) and O–Li(3) in LATP-0.50 (Fig. 3c) are almost the same, indicating the faster Li-ion mobility, thus difficult to distinguish Li(3) and Li(1), which reveals the feature of cooperative Li-ion migration.

Fig. 3 RDFs for Li–Li interactions in LATP-0.16, LATP-0.33 and LATP-0.50 obtained from NVT (600 K, 80 ps) AIMD simulations. (a) Two sharp peaks located at 3.3 Å and 6.0 Å are for Li(1)–Li(1), Li(3)–Li(3) in LATP, respectively. (b) and (c) Partial RDFs for O–Li interactions in LATP-0.33 and LATP-0.50 obtained from NVT (600 K, 80 ps) AIMD simulations.

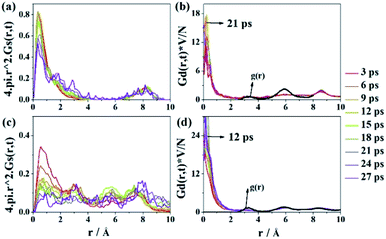
To further examine the Al-doping effect on Li conduction, statistical analysis of Li diffusion is performed by calculating the Li–Li space–time correlation functions³⁷ for LATP-0.16 and LATP-0.50, as shown in Fig. 4. The detailed introductions of the space–time correlation functions are shown in the ESI.† The defined G_s(r, t) gives the probability that, at time t, an atom will be located at a position that has a distance (r) from another location which is occupied by another atom at time zero. For LATP-0.16, in Fig. 4a, the G_s(r, t) plots show one peak appearing between 0 and 2.5 Å with weak time dependence, suggesting atomic vibrations around equilibrium positions. For LATP-0.50, in Fig. 4cG_s(r, t) curves have a much weaker intensity of peaks, indicating a lower probability of finding a Li-ion around its original position and showing a faster Li-ion mobility in LATP-0.50.

Fig. 4 (a) and (b) G_s(r, t) and G_d(r, t) of the van Hove correlation function for the Li motion (3–27 ps) obtained from NVT MD simulations at 900 K in LATP-0.16. (c) and (d) G_s(r, t) and G_d(r, t) functions for Li-ion motion in LATP-0.50.

The defined G_d(r, t) (right insets of Fig. 4) gives the probability of finding Li-ion j at a distance r after a time interval of t, in relation to the position of another Li-ion i at the initial time t = 0. When t = 0, G_d(r, t) is collapsed to the g(r) function of Li–Li. In the cooperative migration, r_j(t)–r_i(t = 0) progressively approaches zero with time and causes the G_d(r, t) contribution near r = 0 to increase rapidly. Actually, we can identify a characteristic time t_max above which the level of G_d(r, t) does not increase anymore, or it starts decreasing. This time scale can be taken as a measure for the average time required in order that a Li-ion is knocked-off with a different one; that is, a cooperative migration between Li-ions has been realized. For LATP-0.16 (Fig. 4d), t_max is estimated to be close to 21 ps; for LATP-0.50 (Fig. 4d), close to 12 ps. Comparing these time scales, it appears that the latter is shorter, as expected due to its cooperative nature. Therefore, high content Al-doping in the NASICON structure may modify the potential energy surface of Li-ions, which allows considerable Li-ion hopping to occur between lattice sites.

In addition, to evaluate whether Al-dopants could affect the stability of the skeleton, we plot the MSD (mean square displacement) of O (oxygen) and P (phosphorus) of LTP, LATP-0.16 and LATP-0.50 obtained from AIMD simulations at 500 and 900 K, as shown in Fig. S3 in ESI.† Comparison of LATP with LTP shows enhanced vibrations of O and P, which allow local relaxation and changes in Li coordination and thus enhance Li-ion conduction.

In summary, we find an ultra-fast Li-ion diffusion within LATP-0.50. From low to high Al-concentration, Li-ion diffusion changes from local oscillation to isolated hopping to superionic flow, and faster Li-ion mobility is achieved. However, further optimization towards the Al-concentration is constrained by the cost of computers due to a large number of atoms.

Analysis of the Li-ion migration energy profile and the electronic structure of LATP

To further understand the high ionic conductivity of LATP-0.50, we calculated the Li-ion migration energy profile using the climbing image nudged elastic band (cNEB) method through the cooperative migration of two-Li-ions, together with LATP-0.16 as a reference. The results are shown in Fig. 5. The cooperative migration of two Li-ions involves a concerted knock-off motion of Li(3)–Li(3) or Li(2)–Li(1) along the diffusion channel. For LATP-0.16 (Fig. 5a), the energy profile of cooperative migration suggests that Li-ions undergo migration in two stages: IM1 → IM4 and IM4 → IM7. In the IM1 → IM4 stage, Li-ion migration occurs near AlO₆-octahedra and the energy change between initial and final states IM1, IM2, IM3, and IM4 is very small. In the IM4 → IM7 stage, the energy difference between two local energy minimum structures (IM4 and IM6) is about 0.13 eV, which increases the energy barrier from 0.21 eV to 0.35 eV. The local energy minimum structures near AlO₆ octahedra are more stable than those far away from them, suggesting a trapping effect of Al-dopants.²¹

Fig. 5 (a) and (b) Energy profile and schematic drawing of the cooperative migration pathway of Li-ions in LATP-0.16 and LATP-0.50. The insets are the schematic drawing of intermediate states along the migration pathway.

For LATP-0.50, the energy profile of cooperative migration suggests that the energies of all local energy minimum structures are uniform and the Li trapping almost vanishes. More importantly, the energy barrier is also uniform and is approximately 0.22 eV, which is lower than that of LATP-0.16. This result is consistent with the AIMD calculations as shown in Fig. 2 and reveals an ultra-fast diffusion process cooperatively.

To understand the electronic structures, Fig. 6 shows the three-dimensional charge density difference obtained by subtracting the electronic charge of the LTP and Li-atoms from LATP. The yellow region represents electron accumulation. It is clear that there are more electrons localized on O-atoms. The higher negative charge on oxygen will lead to larger interaction energies of oxygen toward Li. This finding means that the AlO₆ groups are the polarization centers, which could provide strong interactions between Li and AlO₆. However, in LATP-0.50, the increase of AlO₆ groups delocalizes the effects by the mutual interaction and makes the potential surface more uniform. The Bader charge calculations also suggest that a higher negative charge exists on the O atoms surrounding the Al-dopant, increasing from −1.30 in TiO₆ to −1.50 in AlO₆. Therefore, the trapping effect of AlO₆ leads to the interaction between Li and O to be weakened in LATP-0.50, which can enhance the Li-diffusion.

Fig. 6 Charge density differences of LATP-0.16 and LATP-0.50 with respect to LTP and Li. The yellow region represents charge accumulation; the isosurface value is 1 × 10⁻³ e per ų.

Analysis of the cooperative migration mechanism

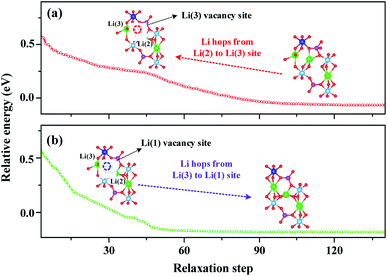
To explain this cooperative migration, we first divide the cooperative migration into two single-Li-ion hopping processes by fixing one of them and relaxing the other one, as shown in Fig. 7. The configuration energy for the single-Li-ion relaxation process in Fig. 7a and b displays an opposite trend, in which the single-Li-ion hopping processes need a much higher energy barrier than the cooperative migration. This analysis suggests that during the cooperative migration of two Li-ions, the Li-ions located at the high-energy sites migrate downhill, which cancels out a part of the energy barrier felt by other uphill-climbing Li-ions. This finding is in excellent agreement with the recent calculation by Mo et al.²² for fast Li-ion conductors. In addition, for the Li(2)O₅ structure, the Li(2) Bader charge change is +0.13 which is higher than that of Li(1) (+0.10). The higher the Li charge, the lower the covalence degree in Li–O bonds. According to that, Li(1) and Li(2) have different potential energy in the energy profile of LATP. Therefore, from an energy point of view, the energy difference between Li(2) and Li(1) results in a cooperative migration.

Fig. 7 Li-ion isolated hopping in LATP from DFT energy minimization. (a) Li hops from the Li(2) to Li(3) site, and (b) Li hops from the Li(3) to Li(1) site. The corresponding structures highlight the hopping path.

Next, by closely inspecting the intermediate states as shown in Fig. 5, we can further attribute the high ionic conductivity of LATP to the oxygen atoms' arrangement, which leads to the Li(3)O₄–Li(3)O₄ structures with unsymmetric tetrahedral sites for Li-ions to occupy. Therefore, we calculate the electron distribution of the Li(3)O₄–Li(3)O₄ configuration as shown in Fig. 8. We found that there is electron density in the vicinity of two Li-ions, suggesting the interaction between adjacent Li-ions. This charge density could attract two Li-ions causing two Li-ions to pair up. Such two Li-ion pairing is consistent with the results shown in Fig. 5 when the Li-ions migrate in pairs, and two Li(3)-ions proceed to the next neighboring Li-sites.

Fig. 8 Electron distribution of the Li(3)O₄–Li(3)O₄ structure with respect to the Ti₂(PO₄)₃ framework. The yellow region represents charge accumulation; the isosurface value is 1 × 10⁻³ e per ų.

In summary, we identify that the ultra-fast Li-ion diffusion within LATP-0.50 originates because of two fundamental reasons. One is the reduced Al-trapping effects for Li-ion hopping which helps to modify the potential energy surface and decreases the Li-ion migration barrier. Another is the interconnection among locally distorted LiO_n-polyhedra (Li(3)O₄ or Li(2)O₆) within LATP which reduces the distance between consecutive Li-sites. The energy difference of Li(2) and Li(1) and the binding interaction of two Li(3)-ions lead to cooperative migration. These two factors can be transformed into each other when Li-ions migrate along the diffusion channel.

Conclusions

In this work, an atomic-level investigation has allowed us to gain valuable insights into the Li-ion cooperative diffusion mechanism of LATP. Three important features are highlighted. (i) The highest Li conductivity is observed at the highest considered concentration of the Al-dopant, i.e., Li_1.5Al_0.5Ti_1.5(PO₄)₃. This opens up the possibility that LATP is among the best current solid electrolytes with cooperative ultra-fast Li-diffusion. (ii) A high concentration of the Al-dopant leads to a smooth energy landscape combining small energy barriers. (iii) Li-ion conduction occurs through a cooperative migration mechanism involving concerted knock-off motion of neighboring Li-ions via Li–Li interactions. An important feature is the unique Li(3)O₄–Li(3)O₄ structure, which allows considerable interaction between Li-ions. The energy difference of Li(2) and Li(1) and the binding interaction of two Li(3)-ions alternately enable the cooperative migration. These findings are believed to be important for the optimization and design of the next generation of inorganic solid-state electrolytes for ASSLBs and warrant further investigation.

Methods

All density functional theory calculations are carried out using the Vienna ab initio simulation package (VASP)³⁸ within the projector augmented wave (PAW) approach.³⁹ The generalized gradient approximation is adopted in the parameterization of Perdew, Burke, and Ernzerhof (PBE) to describe the exchange–correlation functional with a kinetic energy cut-off of 500 eV.^40,41 A k-mesh (2 × 2 × 1) was generated using the Monkhorst–Pack method to sample the Brillouin zone. All atomic positions and lattice parameters were allowed to relax until the forces on the atoms became less than 0.01 eV Å⁻¹. Convergence was completed when the residual forces were below 0.01 eV Å⁻¹ and the total energy difference was below 10⁻⁶ eV per atom.

To search for the possible Li-ion migration pathways and the corresponding migration barriers, the climbing image nudged elastic band (cNEB) method was used as implemented in the VASP.⁴² A chain of five initial images between two local energy minimum structures was first set by linear interpolation and then fully relaxed. The Al defect formation energy and phase decomposition energy are calculated and the equations are shown in ESI.†

For Li-ion diffusivity calculations, the AIMD method employing DFT-based force evaluation with a Verlet algorithm to integrate Newton's equations of motion was performed in VASP software. The NVT (or canonical) ensemble is selected by setting parameters in the input file and specifying a Nose–Hoover thermostat. A unit cell containing 136 atoms (16 formula units) and a Γ-point only k-point sampling are chosen for all calculations. The input structure was obtained from the PBE lattice relaxations. The system was equilibrated first under a constant pressure of 1 atm and at a temperature of 500 K for at least 5000-time steps (with a time step of 1 fs). The Li-ion dynamics are investigated using the AIMD under the NVT ensemble (at T = 500, 600, 700, 800, 900, and 1000 K) and a Nosé thermostat to give a simulation time of 80 ps with a time step 1 fs. In certain AIMD cases, the length of time and NVT temperature were set to be 30 ps and 900 K to check the hopping of Li-ions. For the ionic trajectory analyses by AIMD simulations, Python Materials Genomics (pymatgen)⁴³ and its add-on package pymatgen-diffusion were used.⁴⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by startup R&D funding from the One-Hundred Young Talents Program of Guangdong University of Technology (No. 22041331901), the Soft Science Research Project of Guangdong Province (No. 2017B030301013) and Shenzhen Science and Technology Research Grant (ZDSYS201707281026184). Wang was supported by the Assistant Secretary for Energy Efficiency and Renewal Energy of the U.S. Department of Energy under the Battery Materials Research (BMR) program.

Notes and references

1. B. Zhang, R. Tan, L. Yang, J. Zheng, K. Zhang, S. Mo, Z. Lin and F. Pan, Energy Storage Materials, 2018, 10, 139–159.
2. R. Chen, W. Qu, X. Guo, L. Li and F. Wu, Mater. Horiz., 2016, 3, 487–516.
3. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
4. Y. Wang and W.-H. Zhong, ChemElectroChem, 2015, 2, 22–36.
5. S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338.
6. Y. K. Shin, M. Y. Sengul, A. S. M. Jonayat, W. Lee, E. D. Gomez, C. A. Randall and A. C. T. v. Duin, Phys. Chem. Chem. Phys., 2018, 20, 22134–22147.
7. B. Zhang, L. Yang, L.-W. Wang and F. Pan, Nano Energy, 2019, 62, 844–852.
8. Z. Lin, Z. Liu, N. J. Dudney and C. Liang, ACS Nano, 2013, 7, 2829–2833.
9. C.-W. Ahn, J.-J. Choi, J. Ryu, B.-D. Hahn, J.-W. Kim, W.-H. Yoon, J.-H. Choi, J.-S. Lee and D.-S. Park, J. Power Sources, 2014, 272, 554–558.
10. Y. Xiayin, H. Bingxin, Y. Jingyun, P. Gang, H. Zhen, G. Chao, L. Deng and X. Xiaoxiong, Chin. Phys. B, 2016, 25, 018802.
11. X. Lu, G. Wu, J. W. Howard, A. Chen, Y. Zhao, L. L. Daemen and Q. Jia, Chem. Commun., 2014, 50, 11520–11522.
12. X. Zhao, Z. Zhang, X. Zhang, B. Tang, Z. Xie and Z. Zhou, J. Mater. Chem. A, 2018, 6, 2625–2631.
13. V. Epp, Q. Ma, E.-M. Hammer, F. Tietz and M. Wilkening, Phys. Chem. Chem. Phys., 2015, 17, 32115–32121.
14. M. Kotobuki and M. Koishi, Ceram. Int., 2013, 39, 4645–4649.
15. M. Kotobuki and M. Koishi, Journal of Asian Ceramic Societies, 2019, 7, 69–74.
16. B. Davaasuren and F. Tietz, Solid State Ionics, 2019, 338, 144–152.
17. C. Vinod Chandran, S. Pristat, E. Witt, F. Tietz and P. Heitjans, J. Phys. Chem. C, 2016, 120, 8436–8442.
18. S. Breuer, D. Prutsch, Q. Ma, V. Epp, F. Preishuber-Pflügl, F. Tietz and M. Wilkening, J. Mater. Chem. A, 2015, 3, 21343–21350.
19. M. Monchak, T. Hupfer, A. Senyshyn, H. Boysen, D. Chernyshov, T. Hansen, K. G. Schell, E. C. Bucharsky, M. J. Hoffmann and H. Ehrenberg, Inorg. Chem., 2016, 55, 2941–2945.
20. H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, Chem. Inf., 1990, 137, 1023–1027.
21. B. Lang, B. Ziebarth and C. Elsässer, Chem. Mater., 2015, 27, 5040–5048.
22. X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893.
23. K. Arbi, S. Mandal, J. M. Rojo and J. Sanz, Chem. Mater., 2002, 14, 1091–1097.
24. J. Liu, T. Liu, Y. Pu, M. Guan, Z. Tang, F. Ding, Z. Xu and Y. Li, RSC Adv., 2017, 7, 46545–46552.
25. X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18.
26. Z. Deng, Y. Mo and S. P. Ong, NPG Asia Mater., 2016, 8, e254.
27. R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430.
28. Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17.
29. L. O. Hagman, P. Kierkegaard, P. Karvonen, A. I. Virtanen, J. Paasivirta, L. O. Hagman, P. Kierkegaard, P. Karvonen, A. I. Virtanen and J. Paasivirta, Acta Chem. Scand., 1968, 22, 1822–1832.
30. M. Alami, R. Brochu, J. L. Soubeyroux, P. Gravereau, G. Le Flem and P. Hagenmuller, J. Solid State Chem., 1991, 90, 185–193.
31. D. T. Qui, S. Hamdoune, J. L. Soubeyroux and E. Prince, J. Solid State Chem., 1988, 72, 309–315.
32. S. Adams, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 278–287.
33. M. Giarola, A. Sanson, F. Tietz, S. Pristat, E. Dashjav, D. Rettenwander, G. J. Redhammer and G. Mariotto, J. Phys. Chem. C, 2017, 121, 3697–3706.
34. K. Hayamizu and S. Seki, Phys. Chem. Chem. Phys., 2017, 19, 23483–23491.
35. H. Buschmann, J. Dolle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392.
36. S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6, 148–156.
37. Y. Deng, C. Eames, B. Fleutot, R. David, J.-N. Chotard, E. Suard, C. Masquelier and M. S. Islam, ACS Appl. Mater. Interfaces, 2017, 9, 7050–7058.
38. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
41. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
42. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
43. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
44. Z. Deng, Z. Zhu, I.-H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta09770h

---