Open Access Article
Open Access ArticleMimicking coalescence using a pressure-controlled dynamic thin film balance†
Emmanouil
Chatzigiannakis
 a,
Peter
Veenstra
b,
Dick
ten Bosch
b and
Jan
Vermant
a,
Peter
Veenstra
b,
Dick
ten Bosch
b and
Jan
Vermant
 *a
*a
aDepartment of Materials, ETH Zürich, 8032 Zürich, Switzerland. E-mail: jan.vermant@mat.ethz.ch
bShell Global Solutions International B.V., 38000 Amsterdam, The Netherlands
First published on 5th August 2020
Abstract
The dynamics of thin films containing polymer solutions are studied with a pressure-controlled thin film balance. The setup allows the control of both the magnitude and the sign as well as the duration of the pressure drop across the film. The process of coalescence can be thus studied by mimicking the evolution of pressure during the approach and separation of two bubbles. The drainage dynamics, shape evolution and stability of the films were found to depend non-trivially on the magnitude and the duration of the applied pressure. Film dynamics during the application of the negative pressure step are controlled by an interplay between capillarity and hydrodynamics. A negative hydrodynamic pressure gradient promoted the thickening of the film, while the time-dependent deformation of the Plateau border surrounding it caused its local thinning. Distinct regimes in film break-up were thus observed depending on which of these two effects prevailed. Our study provides new insight into the behaviour of films during bubble separation, allows the determination of the optimum conditions for the occurrence of coalescence, and facilitates the improvement of population balance models.
1 Introduction
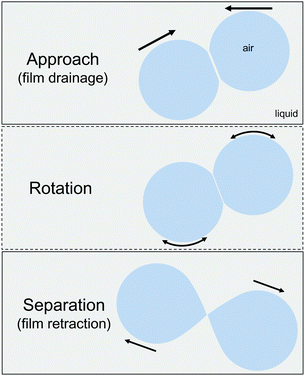
Coalescence is one of the most important processes that control the stability of emulsions and foams,1 as well as the morphology of two phase polymer blends.2 When two droplets or bubbles collide, they locally deform, forming a thin liquid film (TLF) between them (Fig. 1). The film drains due to the presence of a Laplace pressure in the droplets or bubbles, and when the thickness of the interstitial film reaches a critical value, it ruptures. Film rupture marks the beginning of coalescence.3,4 The total time that two droplets or bubbles stay into contact is controlled by the external flow conditions5 and their geometrical confinement.6 They initially approach each other and the formed film thins under what can be approximated to be a constant pressure. Depending on the imposed flow conditions the two droplets or bubbles can move towards each other along their centre–centre line (i.e. a head-on collision), or approach, rotate, and then either coalesce or move away from each other7 (i.e. a glancing collision). The pressure inside the separating film depends on the size and movement of the dispersed elements.8 For a head-on collision the pressure is positive, whereas for all other conditions it changes from positive to negative. For coalescence to occur, the total contact time between the two droplets or bubbles must be longer than the drainage and rupture time of the TLF. Coalescence has been extensively studied at the droplet level, using mostly the 4-roll mill7 and the droplet-probe AFM.9 However, these techniques do not have direct access to the details at the level of the interstitial film and the dynamics of film thinning are often inferred by comparing accessible measured properties, such as droplet trajectories, coalescence times and exerted forces, to simulations.The most common method to directly visualise the TLF and measure its thickness is interferometry.10–13 Its coupling with the thin film balance technique has been used since it was introduced by Sheludko in the 1960's, mainly to study the surface forces in equilibrium TLFs.10,14,15 More recently, it was used to study the complex interplay between hydrodynamics and dynamic deformation of surfaces that results in effects such as the formation of a dimple formation,16 evolution of fluctuations,17 spatiotemporal changes in surface stresses18 and a wide range of instabilities.19–23 So far almost all of the TFB studies involved the drainage of TLFs under a small constant pressure, which is controlled by the radius of the cavity where the film is formed. Two notable exceptions exist,24,25 which involved the forced drainage of foam films due to an extra pressure or flow rate applied by a syringe pump. Recently, competing droplet techniques were also coupled with interferometry, thus allowing a simultaneous force measurement and film visualisation.26,27 Although these studies have been crucial in elucidating the effect of surface stresses and forces on drainage, they have so far provided information relevant to the first part of the collision process, i.e. the approach phase. The experimental conditions necessitated unequally sized bubbles, with one of them staying undeformed during drainage and hence only head on collisions at high speeds (in the range of 102 μm s−1 to 1 mm s−1) were studied.
However, the second part of the collision, when the centres of mass of the bubbles or droplets separate, has been more difficult to investigate, yet it also plays a non-trivial role in coalescence. Leal and coworkers7 were the first to report that coalescence can occur between two droplets even when their centres of mass start to move away from each other. They attributed this behaviour to a change in the sign of the hydrodynamic pressure inside the interstitial film. This induces localised deformations of the droplets that actually decrease the local distance in the interstitial film as the centres of mass move away. The first observation of this local deformation was done by Bremond et al.28 while studying in a microfluidic platform the separation of two droplets that were initially into close contact. Lai et al.29 and later Chan et al.30 modelled this process, elucidated the dynamic nature of the deformation, and provided criteria for the stability of two separating droplets. The change in the hydrodynamic pressure gradient causes an inversion of curvature close to the rim of the film, which results in a local reduction in the separation distance between the two bubbles. It was shown that the deformation (or the local reduction in separation) evolves non-monotonically with time. Coalescence occurs when it is fast and pronounced enough to counteract the imposed separation. The models, despite the fact that they consider only the overall droplet deformation and not the film area and its retraction dynamics, were able to capture the general aspects of the AFM and microfluidic experiments that followed.31,32 However, a more detailed study of the local film dynamics is needed to improve our understanding and modelling of separation-driven coalescence.29,32 Because of the critical importance of capillarity to film retraction, it is imperative that this process is studied under direct film visualisation for two equally deformable surfaces. Since the studies mentioned above, separation-driven coalescence has been extensively used in microfluidic devices for the controlled production of droplets,33–35 has been related to avalanche phenomena and the phase-inversion of emulsions,36–38 and has been shown to affect the morphology of polymer blends.39
Despite the significance of this process, no study has so far addressed the detailed retraction dynamics of free-standing films, i.e. their behaviour when a change in the pressure gradient causes their thickening. In the present work we will use direct film visualisation during the retraction phase to elucidate the interplay between the destabilising dynamic deformation and the imposed hydrodynamic conditions. Earlier studies related to film retraction that involved direct film visualisation by interferometry have focused on supported films formed between a deformable interface and a solid surface.40–42 However, the behaviour of supported films has been found to be remarkably different compared to free-standing ones, i.e. those studied by the thin film balance technique or those formed between two droplets/bubbles. Specifically:
• The van der Waals disjoining pressure across two liquid/solid or air/solid interfaces is typically repulsive.43 Thus, film rupture cannot be examined and the interplay between drainage and surface forces is expected to be different.41,44
• The stress-boundary conditions in the upper and lower surface of the film are different, as the no-slip boundary condition almost always applies for the liquid/solid surface, while this is not the case for the air/liquid interface.18,45 Thus, the velocity profiles and the hydrodynamic forces will be different.
• The coupling of hydrodynamics to capillarity will be different as the lower surface is non-deformable and the asymmetry will play a major role.4
• The structural forces in a film near a solid wall have been found to be different than between two deformable surfaces.46
• The thinning velocities involved in these studies are usually much higher than those in the TFB technique (with the exception of certain studies done at very low approach speeds12,47).
Based on the current insights in separation-driven coalescence, it is safe to assume that film retraction may be as complicated as drainage, where small changes in the deformability, surface forces and stress-boundary conditions, can have substantial effects in the dynamics of the films.4,48 In the present work a freestanding thin film is used (i) to further study the interplay between capillarity and hydrodynamics in retraction (and later also the effect of surface forces) and (ii) to establish criteria for rupture during bubble separation and film thickening. These two effects can be studied in their full relevance only in free-standing films or in films formed between two deformable interfaces. A bike-wheel version of the thin film balance technique that was developed by Cascão-Pereira et al.49 is modified to study the dynamics of free-standing TLFs. The precise control of the pressure inside the film allowed us to study both the drainage and the retraction dynamics. Model systems consisting of non surface active polymer-solutions were studied, in which the viscosity can be varied. The simultaneous use of interferometry makes it possible to visualise the films and to decouple the effects that capillarity and hydrodynamics have on film dynamics. Criteria for the occurrence of film break-up during retraction were established and the optimum conditions for separation-driven coalescence were thus determined.
2 Materials and methods
2.1 Materials
The polyisobutylene grade in this study (BASF Oppanol B10SFN) has a weight-average molar mass of 36 kg mol−1 and a polydispersity index of 3.50 It is stabiliser-free and IR spectroscopy showed no presence of heteroatoms. n-Hexadecane was purchased from Acros Organics and has a purity of 99%. Hexadecane is a good solvent for polyisobutylene, with a Flory interaction parameter of χ ≃ 0.35.51 Solutions of four different concentrations were prepared (1, 5, 10, and 15 wt%). A critical overlap concentration of c* = 10 wt% was calculated from equation:52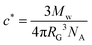 | (1) |
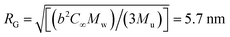 , where b is the C–C bond length, C∞ is the characteristic ratio, and Mu the molecular weight of the repeating unit.53 For polyisobutylene, it is b = 0.1505 nm,54 and C∞ = 6.7.55
, where b is the C–C bond length, C∞ is the characteristic ratio, and Mu the molecular weight of the repeating unit.53 For polyisobutylene, it is b = 0.1505 nm,54 and C∞ = 6.7.55
From dynamic light scattering measurements (ALV CGS3) compact goniometer with 22 mW HeNe laser light source at 25 °C a hydrodynamic radius of RH = 5.5 ± 0.1 nm was determined (average of 3 measurements). The bulk viscosity of all solutions was measured in an Anton Paar MCR302 rheometer with the double-gap Couette-cell geometry. The Newtonian flow curves of all polymer solutions were obtained for a shear rate of 10–100 s−1 at 25 °C. At least three measurements were done for each solution. The surface tension of all samples was measured at 25 °C using a Wilhelmy plate with a width of 19.62 mm and a thickness of 0.1 mm mounted on a balance (KSV Nima). Three measurements were conducted for each solution. The obtained values of the viscosity and surface tension are shown in Table 1.
| Concentration (wt%) | Viscosity (mPa s) | Surface tension (mN m−1) |
|---|---|---|
| 0 | 3.1 ± 0.156,57 | 27.4 ± 0.1 |
| 1 | 3.5 ± 0.1 | 27.3 ± 0.1 |
| 5 | 7.7 ± 0.1 | 27.3 ± 0.1 |
| 10 | 18.3 ± 0.2 | 27.4 ± 0.1 |
| 15 | 37.7 ± 0.3 | 27.4 ± 0.1 |
2.2 Methods
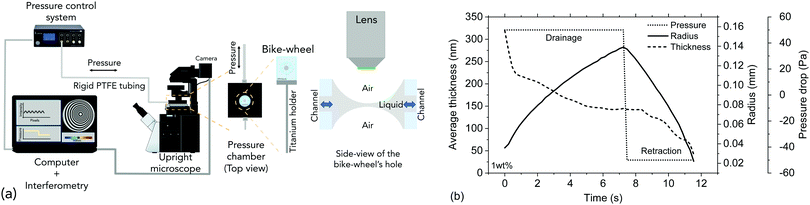
The dynamic thin film balance (TFB, Fig. 2a) technique consists of four main components: (i) an upright fixed-stage microscope, (ii) a pressure control system, (iii) an in-house fabricated aluminium pressure chamber, in which the (iv) bike-wheel microfluidic device is placed. The bike-wheel chip is a custom designed microfluidic device based on the initial design of Cascão-Pereira et al.49 It is fabricated using photolithography on borosilicate glass (by Micronit Microfluidics). It consists of: (i) a diamond-drilled hole with a diameter of 1 mm and a thickness of 400 μm, (ii) 25 channels (width of 45 μm and depth of 20 μm) connected to the hole, all leading to a circular channel of larger dimensions. The chip is glued onto a titanium holder using two-component epoxy. To ensure that the contact line between the liquid and the glass is pinned, the bike-wheel's outer surface is first hydrophilised by immersing it in a saturated NaOH ethanol solution and leaving it under microsonication for 20 min, and then hydrophobised with octadecyltrichlorosilane. More details regarding the bike-wheel microfluidic device and its fabrication can be found elsewhere.58 The pressure inside the chamber is controlled by an Elveflow MK3+ piezoelectric pressure control system which has a resolution of 1 Pa and a maximum pressure of 20 kPa. The response time is O(10−2 s), while the settling time after an initial overshoot (of ∼20%) is O(10−1 s). It is connected to the pressure chamber by rigid PTFE tubing with an inner diameter of 0.1 mm. The film visualisation is done with a Nixon Eclipse FN1 fixed stage upright microscope (to minimise vibrations) and a 10× long working distance objective, mounted onto an active noise cancelling table. The film is monitored by a Hamamatsu ORCA-Flash4.0 CMOS camera. A monochromatic wavelength of 508 nm was used for reflection. A sequence of images is saved (with a maximum of 10 ms temporal resolution) and is then converted to thickness using Sheludko equation:10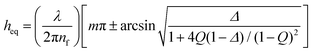 | (2) |
To explain the experimental procedure, an example of the evolution of the radius and the thickness of a 1 wt% polymer film are shown in Fig. 2b for a ±50 Pa pressure jump. Initially a thick film is created and its equilibrium pressure, Pc,applied, is determined. This point can be easily identified by varying the pressure in steps of 1 Pa until the first interference fringes appear when the thickness of the TLF is in the order of a few μm. Pc,applied is the sum of all the contributions in the static thick film PL,bw − P∞, where PL,bw is the Laplace pressure due the curvature in the Plateau border (which is ≈2σ/Rbw, with σ being the surface tension and Rbw the radius of the cell's hole), and P∞ is the pressure at the meniscus (under static conditions and at a large thickness, the hydrodynamic pressure, PH, and the van der Waals disjoining pressure, ΠvW (ESI†), are zero) (Fig. 3). Subsequently, the pressure inside the film was lowered using pressure drops, ΔP, in the range of 20 to 1000 Pa. The film began to drain and at a thickness of O(102 nm) the hydrodynamic pressure builds up, causing a radial expansion of the film. At least 25 measurements were done for each combination of ΔP and polymer concentration. The onset of film's expansion is identified as the beginning of drainage. At a certain point of drainage the applied pressure was changed sign (Pc,applied − ΔP) causing the inflow of liquid from the Plateau border to the film. Depending on the time allowed for the film to drain and the magnitude of the ΔP, the film could either rupture or get hydrodynamically stabilised by the inflow of liquid. The pressure balance in the thin film is given by:60
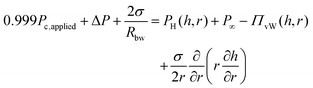 | (3) |
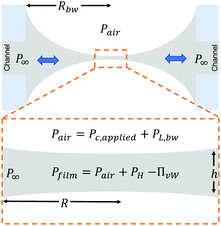 | ||
| Fig. 3 Pressure contributions in a thin liquid film in the dynamic TFB: the pressure difference Pfilm − P∞ drives the inflow and the outflow of liquid. | ||
The experimental protocol involves a first forced drainage of a film under a positive pressure difference across the film, followed by the retraction of the film because of an abrupt change in the sign of pressure. Therefore, it is equivalent to the procedure followed in the microfluidic experiments of Bremond et al.28 and Gunes et al.32 of approaching and separating droplets. The first time interval (+ΔP), during which the film drains and expands, corresponds to the approach phase of a collision between two bubbles. The second time interval (−ΔP), during which the film retracts (reduction in radius), corresponds to the separation phase of a collision. In the sections that follow we will first explain the main experimental results and then specifically focus on the drainage (+ΔP) and retraction (−ΔP) dynamics of the films. The consequences of our study on droplet and bubble coalescence will also be discussed.
3 Results and discussion
3.1 Film dynamics
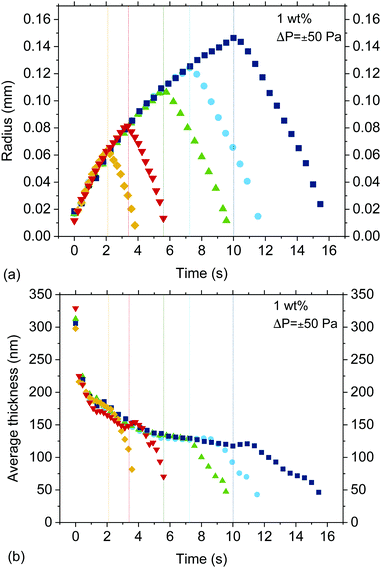
The outcome of the +ΔP/−ΔP cycle depends on the dynamics during both drainage and retraction. The evolution of the thickness and radius of several 5 wt% TLFs is shown in Fig. 4. The radius, R, was determined assuming that the end of the film region occurs at the first change of the order of interference (maximum intensity of the inner white ring for a 0th order of interference in the film). The thickness corresponds to the average one determined from the thickness profiles, according to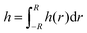 . During the drainage phase, the film thins while expanding, as expected. In this regime, the drainage and film expansion curves of all films coincide, confirming the very good pressure control in our experiment. At a certain point in time, which is different for each measurement shown in Fig. 4, the sign of the pressure step is changed. The resulting hydrodynamic pressure gradient causes the gradual reduction in the film radius. This observed reduction is caused by the inflow of liquid from the Plateau border towards the outer rim of the film. However, the centre part of the film, which is accessible to interferometry as it has a thickness in the range of 101–102 nm, continues to thin (Fig. 4). This is a manifestation of the same dynamic deformation that has been reported by various researchers during the separation of two droplets.28–31,61
. During the drainage phase, the film thins while expanding, as expected. In this regime, the drainage and film expansion curves of all films coincide, confirming the very good pressure control in our experiment. At a certain point in time, which is different for each measurement shown in Fig. 4, the sign of the pressure step is changed. The resulting hydrodynamic pressure gradient causes the gradual reduction in the film radius. This observed reduction is caused by the inflow of liquid from the Plateau border towards the outer rim of the film. However, the centre part of the film, which is accessible to interferometry as it has a thickness in the range of 101–102 nm, continues to thin (Fig. 4). This is a manifestation of the same dynamic deformation that has been reported by various researchers during the separation of two droplets.28–31,61
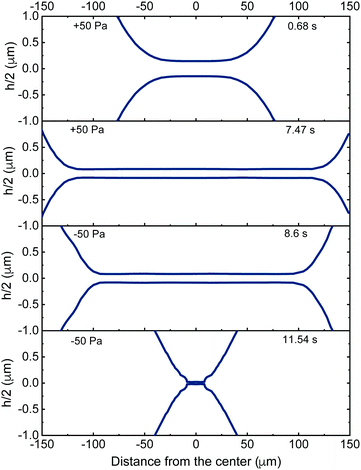
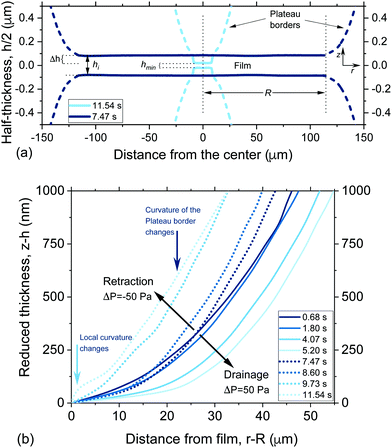
The interplay between capillarity and hydrodynamics, can be clearly seen in the time evolution of the thickness profiles of a retracting 5 wt% film (Fig. 5). In Fig. 5 both the thickness of the film (as determined using eqn (2)) and the thickness of the Plateau border are shown. The latter is determined from the interference fringes, given that the distance between two consecutive intensity maxima corresponds to a thickness difference of λ/(2πnf). The lower surface of the film is plotted assuming that it is symmetrical to the upper one that is visualised by interferometry. When the −ΔP is applied (at t = 7.47 s), the pressure in the Plateau border becomes larger than both the PL,bw and the PH inside the film. The new hydrodynamic conditions cause the flattening of the Plateau border that tends to reduce the thickness at the centre of the film. At the same time, there is an inflow of liquid that gradually thickens the outer rim of the film (observed as a reduction in film radius). In this specific case, the dynamic deformation was so pronounced that it counteracted the inflow of liquid. At t = 11.54 s the reduction in film thickness due to the overall deformation was so high that the critical thickness, hcrit, was reached and rupture occurred. The evolution of the shapes of the Plateau border and of the film are both controlled by the pressure balance of eqn (3). However, in the film region the PH and ΠvW are significant and contribute to the local deformation, while in the Plateau border they are negligible. To enable a better understanding of the involved processes, we will address separately the deformation in the film (local protuberance, h < 100 nm) and the Plateau border region (change in the curvature, h > 100 nm).
Given the good spatiotemporal resolution of the dynamic TFB technique, film retraction dynamics can be studied in a way that was previously inaccessible. Various effects that have not been reported before can be seen in Fig. 4 and 5:
• A second mode of deformation, i.e. a hesitation or a shoulder in the thickness profile h(t), can be observed close to the rim of the film just before rupture (Fig. 5).
• The rate of thinning (dh/dt) and the radial velocity (dR/dt) is faster during the retraction phase (−ΔP) than in the drainage phase (+ΔP) (Fig. 4). This effect is similar to the hysteresis in force between approach and retraction that has been observed in droplet-probe AFM experiments.4
• The outcome of a +ΔP/−ΔP cycle, i.e. whether the film will rupture or not, depends not only on the ratio of capillary to hydrodynamic forces during the retraction phase, but also on the film characteristics when the −ΔP is applied. The hydrodynamic pressure inside the film is a function of thickness, and thus the magnitude of the observed phenomena will depend on the extent that drainage has proceeded during the initial forced drainage, +ΔP phase. For the five measurements shown in Fig. 4, ruptured only occurred for td ≥ 7.2 s.
• The outcome of an approach/retraction cycle is very sensitive to the magnitude of the ΠvW(h), and thus in simulations it depends heavily on the Hamaker constant used (retarded or non-retarded).62 The main effect of ΠvW in such simulations is to set the critical thickness for rupture, hcrit,63 often estimated by balancing the Laplace pressure of the undeformed droplet to the attractive ΠvW. This procedure results in hcrit = [(RbwAH)/(12πσ)]1/3, where AH is the Hamaker constant. However, film retraction involves significant surface deformations and non-negligible hydrodynamic effects and the validity of this equation can be been questioned.64
In the following sections we will separately address the various effects described above.
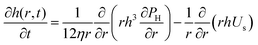 | (4) |
The coalescence times, tc, for forced drainage are shown in Fig. 6b as a function of the different pressure drops. The same trends are observed for all concentrations. For ΔP < PL,bw, drainage is slow and there is no strong dependency on ΔP. In this regime, capillary forces related to the macroscopic curvature (PL,bw) have been found to control drainage8 and the films were either planar or only slightly dimpled. For ΔP ≫ PL,bw, we cross over to a regime where the hydrodynamics dominate. Here, the tc is inversely proportional to ΔP in line with eqn (4) (based on eqn (3) for large pressure steps it is ΔP ≈ PH). In this regime, the films become pronouncedly dimpled, i.e. a thicker centre with a thinner rim develops. The observation of Ca-dependent regimes is a result of a well-known interplay between capillarity and hydrodynamics.4,16,64 During drainage, the outflow of liquid causes lower pressures where the velocities are high, leading to the formation of a dimple at the centre of the film and a thinner relatively planar region near its edge. Regardless of ΔP, rupture was preceded by the formation of dark spots which for low ΔP had a thickness slightly larger than h ≃ 4RH (Fig. 6a). The observation of these dark spots is an indication that osmotic pressure effects are present in the films and slow down drainage.66
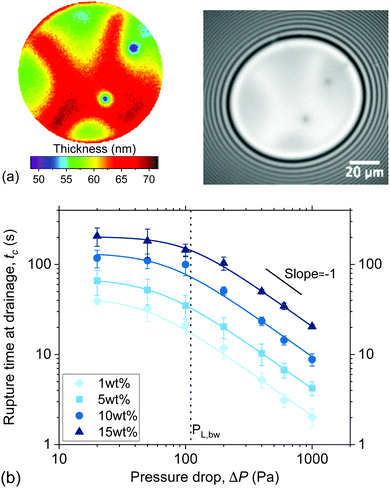 | ||
| Fig. 6 Film drainage: (a) interferometry image of a 5 wt% film draining at 50 Pa and the corresponding 3D thickness plot. Thickness corrugations and dark domains can be observed. (b) Coalescence times of all polymer solutions as a function of applied pressure drop. The measurements were done at constant ΔP to assess the dynamics of the films during drainage. Adapted from ref. 67. | ||
For the range of pressure drops investigated, a tc ∝ η relationship was observed, in agreement with the Stokes flow regime which underpins eqn (4). At low ΔP the film can be roughly approximated as planar due to the absence of a dimple. Integration of eqn (4) for a constant radius allows us to quantify the surface velocity by means of a mobility factor.68 For all films the mobility factors, n where found to be much smaller than what expected for the no-slip condition (n = 2), with n of O(10−1). Thus, no significant surface-stresses are observed in the films, agreeing with absence of surface active components in our system. Although the general behaviour of the films was found to be in accordance with the predictions of continuum models, in certain cases drainage was qualitative different. For concentrations close to c*, and ΔP ∼ PL,bw, drainage was not accompanied by the usual dimple formation. Rather, the dimple became unstable during drainage, and was washed out of the film. Thickness corrugations were then observed (Fig. 6a), which at high ΔP could take the form of vortices. The same observations have been made in surfactant-stabilised foam films and have been attributed to surface Marangoni stresses.69,70 In the polymer films they are caused by concentration gradients in the film, as well as by possible concentration differences between the film and the surrounding Plateau border, both of which give rise to osmotic pressure differences and stress inhomogeneities.
Similar osmotic pressure effects have been reported for other systems by various researchers.21,46,66,71,72 The osmotic pressure first contributes to the disjoining pressure by giving rise to structural forces, thus hindering drainage. Second, it can give rise to depletion effects, thus accelerating or decelerating drainage depending on the sign of the osmotic pressure gradient.21,46,72 In our experiments, we observed that the latter dynamic effect was negligible for all concentrations. Although as mentioned earlier, films with concentration close to c* where more prone to show asymmetric drainage, their drainage times did not deviate from the relative increase expected from the higher bulk viscosity. Similarly, the viscosity scalings of the drainage time and the film expansion (ESI†) indicated that the contribution of osmotic effects to the disjoining pressure was equal for all films, at least for the concentration ranges, molecular weights and molecular weight distributions investigated here.
A final aspect is the film expansion. In our experiments, the radius of the film does not remain constant but gradually increases until an equilibrium value is reached, just before rupture, Req (ESI†), and is equal to the one resulting from a pressure balance at the Plateau border:24,73
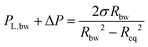 | (5) |
The time-dependence of the detailed surface deformation could be investigated experimentally in our work. In all of our experiments we observed that the curvature of the Plateau border increased gradually with time, at a rate that depended strongly on the initial conditions at the onset of retraction. In the film region, the maximum deformation, i.e. the most pronounced protuberance observed as a minimum film thickness, was always observed for the smallest radius (∼20 μm). Directly after that, the thickness of the film increased abruptly to h > 1 μm (upper limit of interferometry). This increase in the separation distance between the two surfaces, observed as a transition from a thin to a thick liquid film, took place faster than the temporal resolution of our technique (∼10 ms). Simulations and theoretical models indeed predict such a clear non-monotonic behaviour. However, analytical models predict a rapid decrease in the separation distance followed by a gradual increase.29,30 In contrast, numerical simulations predict the a gradual decrease in the separation distance followed by its rapid increase.30,61 Although the latter is in qualitative agreement to our observations, one notable difference is that the re-equilibration of the surface's shape occurs much faster in our experiments, which are pressure rather than velocity controlled.
The thickness profiles of a 5 wt% film (solid lines) and the surrounding Plateau border (dashed lines) at the onset (t = 7.47 s) and end (t = 11.54 s) of retraction are shown in Fig. 7a. The change in the pressure sign gradually changes the curvature of the Plateau border and its shape close to the film, the net effect of which cause a reduction in the local thickness of the film, equal to Δh. The shape of the Plateau border for a 5 wt% film (dashed line in Fig. 7a) before and after the change in the sign of the pressure drop is shown in more detail in Fig. 7b. The time dependence of the reduced thickness profiles, obtained after subtracting the thickness at the outer rim of the film (z − h) is plotted as a function of the distance from the edge of the film (r − R). Thus, the effect of deformation on film thickness is neglected and the change in the curvature of the Plateau border can be independently assessed. During drainage, the curvature of the Plateau border gradually increases, as the film expands towards its equilibrium radius (eqn (5)). The change in the pressure sign causes an initial abrupt increase in curvature observed as a flattening of the Plateau border (dark blue arrow). This flattening gets more pronounced as retraction proceeds. A second mode of deformation, i.e. a shoulder close to the radius of the film, can be observed just before rupture (light blue arrow). This deformation is the result of the dominance of the attractive ΠvW(h) over the other pressure contributions inside the film. It is caused by the increasing van der Waals interactions as the dynamic surface deformation causes the reduction of the film's thickness down to its critical value.
In our experiments, the change in the pressure sign was always accompanied by a collapse of the dimple and the abrupt transition to a planar film. This instability was observed for all the pressure drops applied. It occurred even at thicknesses larger than 100 nm where surface forces are negligible. The dimple washout is a hydrodynamic instability that has been observed in various other systems during film drainage at constant pressure.19,25,74 In our case, the dimple washout was fast and was triggered by the pressure change. It had a catastrophic effect on the thickness of the film and, thus facilitated film rupture during retraction. In contrast, simulations predict a gradual change in thickness31 and the hydrodynamic stabilisation of retracting films can be overestimated.
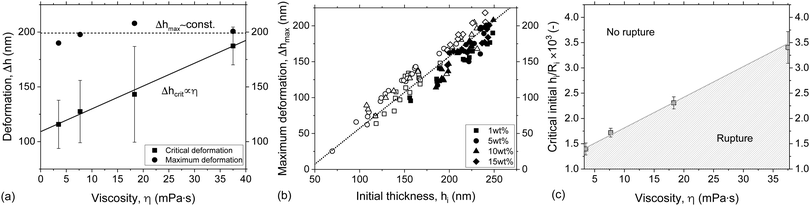
3.1.2.1 Effect of viscosity. The relative contributions of capillarity and hydrodynamics can be decoupled as we study films of different viscosities but with the same surface tension (see Table 1), while imposing the same +ΔP/−ΔP cycle (equal to ±50 Pa). In this way the net surface deformation in the film, measure as Δh, remains the same,29 while the increasing viscosity of the film is expected to decelerate the inflow from the Plateau border to the film. The negligible viscosity of the outer phase (air) also ensures that the increase in the viscosity does not influence the surface velocity (eqn (4)). However, this might not be the case in emulsion films, where the viscosity ratio of the inner and outer phase influences the momentum jumps across the interface75 and keeping this one constant would be more difficult. The +ΔP/−ΔP cycle will result in film rupture when capillary forces are strong enough to counteract the inflow of liquid and cause a decrease in the separation distance down to the critical thickness. In our experiments, the maximum surface deformation observed in the film region, i.e. the most pronounced protuberance, can be evaluated by subtracting the minimum attainable film thickness from the initial one at the start of the retraction phase, Δhmax = hi(td) − hmin (Fig. 7a). At rupture the gradual reduction in film thickness is interrupted at Δhcrit = hi(td) − hcrit. The same maximum observed deformation, within experimental error, was observed for all solutions. However, the evolution of the deformation was different, i.e. Δhmax was attained at longer times as the film viscosity was increased. As a result, the Δhcrit increased linearly with viscosity (Fig. 8a), in line with simulation results.29,30
The magnitude of the surface deformation of the film and its evolution depend on the ‘initial’ thickness before the reversal of the pressure. A linear relation between Δhmax and hi was observed (Fig. 8b). Furthermore, a critical hi/Ri was found to exist, above which rupture did not take place (Fig. 8c). The critical hi/Ri was proportional to viscosity. For a given −ΔP, the inflow of liquid from the Plateau border towards the film decreases with η. Thus, the hydrodynamic forces in the film decrease and stabilisation becomes more difficult. Similar results have been reported in previous droplet-probe AFM studies that involved the separation of two droplets at a constant speed.4,31 It was observed that the occurrence of coalescence depended sensitively on the initial distance between droplets. In our experiments, the separation speed corresponds to the thickening of the film. Therefore, it is not constant but depends on the pressure gradient ΔP/R, the thickness of the film and its viscosity.
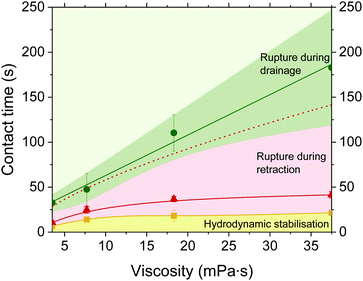
The critical hi/Ri can be related to a critical drainage time, td,crit, that must have elapsed before film retraction is started (Fig. 9), and thus obtain coalescence maps similar to simulation results of Berry and Dagastine.62 This drainage time results in a total contact time that is the sum of td + tr, where tr is the retraction time, i.e., the time between the application of −ΔP till rupture. The rupture times under the application of +ΔP (as in Fig. 6b) are also shown for comparison. The +ΔP/−ΔP cycle can either lead to rupture or not, depending on the imposed td. Three different regimes are observed. For t < td,crit (solid yellow line), the elapsed td is not enough to allow the drainage of the film down to the critical hi/Ri. Therefore, for this range of td, retraction does not result in rupture. The inflow of liquid overcomes the dynamic deformation and the film is hydrodynamically stabilised. This regime of hydrodynamic stabilisation is depicted as a yellow area. For t ≥ td,crit the elapsed drainage time is adequate to reach a hi/Ri smaller than the critical one of Fig. 9. If the change in the pressure sign is done after this td,crit then rupture will occur as capillary forces overcome the hydrodynamic ones. The distribution of elapsed td results in a distribution of rupture times during retraction (red area). The minimum film lifetime is shown as a solid red line. This line corresponds to the sum td + tr. Therefore, it is the minimum possible rupture time that can be achieved at retraction and corresponds to the film lifetime if the imposed drainage time is td,crit. The maximum rupture time observed after a +ΔP/−ΔP cycle is shown as a dashed red line. The rupture times if only +ΔP is applied are shown with the solid green line. The stochasticity of the rupture process results in a distribution of film lifetimes, shown here as both error bars and a green area. The efficiency of retraction to facilitate rupture can be assessed by comparing the red (+ΔP/−ΔP cycle) to the green area (+ΔP only). It is evident that rupture can occur much faster if the film drainage is followed by retraction. This is in agreement with the observation that coalescence in microfluidic platforms can be accelerated by separating two neighbouring droplets.28,32 However, applying a −ΔP might not accelerate rupture if the elapsed td before the onset of retraction, is long enough (overlap of green and red dashed line in Fig. 9).
When drainage is followed by retraction, the total time where the film remains stable increases with viscosity. This effect arises from the fact that the involved times and processes have different viscosity dependencies. When only +ΔP is applied, then the rupture time is linearly proportional to viscosity, tc ∝ η, in agreement to eqn (1). When a +ΔP/−ΔP cycle is applied, then the critical drainage time (yellow line), has a dependency of td ∝ η1/4. The minimum rupture time during retraction (solid red line) has a dependency of tr ∝ η1/2.
3.1.2.2 Effect of pressure. The second parameter that was systematically examined with respect to its influence on the outcome of film retraction was the magnitude of the pressure jumps. Seven different cycles of ±ΔP in the range of 20–1000 Pa were applied for various imposed drainage times on the 5 wt% films. By increasing the −ΔP during retraction, we change simultaneously the magnitude of the surface deformation and the rate of thickening of the film. In contrast to the effects of viscosity, we did not observe a clear dependency between the maximum deformation in the film's surface and the applied pressure. Changing the ΔP during drainage and retraction, does not only influence the surface deformation and the hydrodynamic forces, but also the dependency of both of them on the initial separation conditions. Nevertheless, we chose measurements at which the initial thickness at the onset of retraction was similar (hi = 310 ± 17 nm) and compared the maximum deformation observed for each ΔP (Fig. 10a). Only pressure drops up to 200 Pa were considered, as for higher ΔP the order of interference at the onset of retraction could not be determined with confidence. A trend of decreasing Δhmax with increasing ΔP can be observed in Fig. 10a. As mentioned earlier, the influence of ΠvW on the dynamics of the films is twofold. Firstly, it changes the pressure gradient that drives the inflow and outflow of liquid and, thus the radial velocities of the films, and, secondly, it causes film rupture. The average dR/dt as a function of applied pressure is shown in Fig. 10b. Whereas ΠvW is negligible during the initial stages of drainage, as the thickness of the film is large, it becomes comparable to ΔP during the whole retraction phase. This effect results in the different evolution of film radius, dR/dt, during drainage (+ΔP) and retraction (−ΔP). As the applied pressure drop increases, the imposed hydrodynamic pressure inside the film dominates over the attractive ΠvW. Thus, the measured dR/dt of the drainage and the retraction are equal for ΔP ≫ ΠvW.
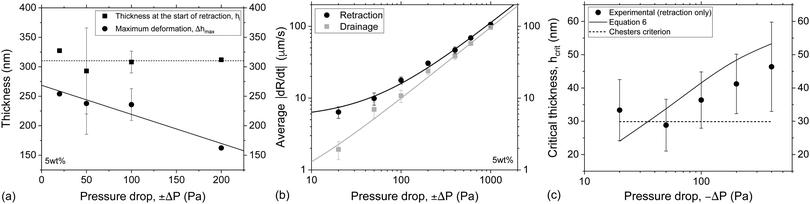 | ||
| Fig. 10 Effect of magnitude of the pressure jump on local film deformation: (a) the initial thickness of the 5 wt% films at the onset of the retraction phase and the maximum observed deformation as a function of pressure drop. (b) The average rates of film expansion and contraction as a function of pressure drop for the 5 wt% films. (c) The critical thickness for rupture of the 5 wt% films as a function of pressure drops. The predictions of eqn (6) and of Chesters criterion are also shown. | ||
It was also observed that the critical thickness of the film at rupture increases with pressure drop (Fig. 10c). The coupling between capillary fluctuations and hydrodynamic forces at the point of rupture leads to a dependence of hcrit on applied pressure drop, equal to:
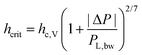 | (6) |
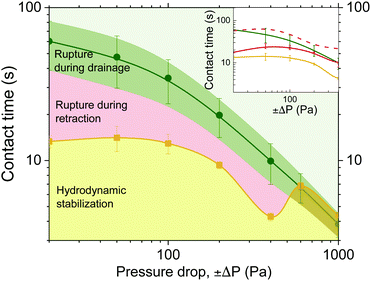
The effect of pressure on the drainage and rupture times of 5 wt% films is shown in the second coalescence map in Fig. 11 for various pressure steps (±ΔP, duration and sign). The colours of lines and areas are the same as in Fig. 9. The times of rupture for forced drainage in the absence of retraction, tc, give an upper boundary (green line). Compared to tc, retraction can accelerate film rupture up to a maximum factor of 4 (observed at low pressures). The critical drainage time, td,crit shows a slightly non-monotonic behaviour. The td,crit shows a maximum at 50 Pa and then gradually decreases with pressure. Moreover, the ratio between the minimum retraction time, tr, and td,crit, is maximum at low pressures and gradually increases up to a value of ∼1 at ΔP = ±400 Pa. Both effects are indicative of the increasing importance of ΠvW for low ΔP, as explained earlier. Berry and Dagastine62 have predicted a similar non-monotonic behaviour for the occurrence of coalescence as a function of approach speed between air bubbles separated by an aqueous film.
For ΔP ≥ ±600 Pa, it was not longer possible to induce rupture by changing the pressure sign. Rupture only occurred during the drainage phase, and thus in this regime td,crit = tc. The existence of a critical pressure, above which retraction does not result in rupture is in agreement with existing microfluidic experiments7,36 and simulations.62 Leal and coworkers, who studied the flow-induced coalescence of droplets with the 4-roll mill technique, were the first to report that droplet coalescence does not occur above a critical Capillary number, the value of which depends on the viscosity of the film and the collision angle.7,84,85 In their experiments however, droplet separation cannot be easily decoupled from the initial approach, and increasing the capillary number by the imposed flow rate also reduces the available time for drainage. Gunes et al.32 studied the separation-induced coalescence of droplets in microfluidic channels. The experimental procedure that they followed is similar to ours, as two droplets were pushed towards each other for a defined time and then separated at various speeds. It was observed that coalescence did not occur if the separation Capillary number was above a critical value. Vakarelski et al.,31 who used AFM to study the coalescence of air bubbles in water, did not observe a critical Capillary number in the employed range of separation speeds. Although the existence of a critical pressure, separation speed or capillary number will depend on the droplet size, the present results clearly confirm that for high enough pressure drops, the inflow of liquid causes the hydrodynamic stabilisation of the film in foams.
Capillarity slows down film thinning during the drainage phase through the formation of a dimple.16 In contrast, capillarity accelerates thinning during retraction by causing the protuberance of the film's surface near the Plateau border. Similarly, hydrodynamics destabilise the film during drainage and stabilise it during retraction. The overall efficiency of the process is controlled by the net ratio of the effects on capillary to hydrodynamic forces. The latter are controlled by the total pressure inside the film and, as explained earlier, show small differences between drainage and retraction due to the effect of ΠvW. Therefore, in our experiments retraction causes rupture more efficiently for ΔP < PL,bw. Likewise, both theory and experiments show that separation-induced coalescence is more efficient for large droplets.29,32 For ΔP ∼ PL,bw rupture during retraction is still feasible. However, the rupture times of the ±ΔP cycle are comparable to those of drainage at constant ΔP. In this regime, the net effect of the capillary and hydrodynamic forces is the same during drainage and retraction. Finally, for ΔP ≥ ±600 Pa the hydrodynamic forces dominate the process and rupture during retraction is completely prevented. The existence of this critical pressure (which is equivalent to a critical capillary number in flow-induced coalescence) causes the sigmoidal decrease of the coalescence efficiency that has been observed in microfluidic experiments32,35,86 when the flow rate is increased.
4 Conclusions
The dynamics of free-standing thin liquid films with polymer solutions of different viscosity was systematically studied using a dynamic thin film balance technique with precise pressure control. The approach and subsequent separation of two bubbles, which causes a change in the sign of the pressure gradient in the separating film, was imitated by directly applying comparable pressure drops (±ΔP) in free-standing films. The interplay between capillarity and hydrodynamics that causes rupture during retraction was experimentally assessed. It was confirmed that film retraction is accompanied by a dynamic protuberance in the film's surface, the temporal evolution of which was for the first time experimentally evaluated for free-standing films with attractive van der Waals interactions. The efficiency of this deformation to induce rupture during film retraction depended on the thickness at the end of drainage. A critical thickness-to-radius ratio was found to exist above which, the film is hydrodynamically stabilised. Whether two separating droplets will coalesce or not depends significantly on their initial distance, an aspect which was not yet explored.31 In agreement with observations in different systems7,36,62 hydrodynamic stabilisation was found to occur when the applied pressure drop was above a critical value.Rupture during film retraction was found to be more efficient when the imposed pressure drop was smaller than the Laplace pressure exerted by the curvature of the unperturbed Plateau border. Increasing the viscosity of the film also promoted rupture during retraction. Finally, we confirmed the important role of van der Waals interactions in the retraction dynamics,62 resulting in a distortion of the shape and accelerated retraction rates just before rupture. In conclusion, the dynamic TFB technique allows us to study film dynamics in a previously inaccessible way. The processes that can be mimicked are not limited in the approach and separation of two droplets. The exact pressure profile that is developed in the film during a glancing collision or during the oscillation of emulsions can also be imitated. The obtained coalescence maps enable a more accurate inclusion of coalescence criteria in population balance models.
As a final note it should be pointed out that the films in our study contained no surface-active components. The behaviour of films stabilised by surface-active species, in particular during retraction is still an open question. During retraction, Marangoni or viscoelastic stresses are expected to oppose the inflow of liquid and promote the local thinning of the film.87 However, surfactants also change the surface tension and hence also capillarity.48 Therefore, in films with stress-carrying surfaces, the interplay between capillarity and hydrodynamics that was described here is expected to be even richer. Moreover, the dynamic TFB technique gives access to the shape of the films at various hydrodynamic conditions, a capability that could potentially be utilised to back-calculate the pressure contributions and surface stresses from the thickness profiles by combining methods developed for films draining on surfaces88 and for pendant drop elastometry.89,90
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the ETH Energy Science Center Partnership with Shell for the financial support.References
- G. Narsimhan and E. Ruckenstein, Foams, Routledge, 2017, pp. 99–187 Search PubMed.
- U. Sundararaj and C. Macosko, Macromolecules, 1995, 28, 2647–2657 CrossRef CAS.
- I. B. Ivanov, Pure Appl. Chem., 1980, 52, 1241–1262 CAS.
- D. Y. Chan, E. Klaseboer and R. Manica, Soft Matter, 2011, 7, 2235–2264 RSC.
- V. G. Levich, Physicochemical Hydrodynamics, Prentice-Hall, 1962, vol. 115 Search PubMed.
- D. Chen, R. Cardinaels and P. Moldenaers, Langmuir, 2009, 25, 12885–12893 CrossRef CAS PubMed.
- L. Leal, Phys. Fluids, 2004, 16, 1833–1851 CrossRef CAS.
- H. Yang, C. C. Park, Y. T. Hu and L. G. Leal, Phys. Fluids, 2001, 13, 1087–1106 CrossRef CAS.
- R. R. Dagastine, R. Manica, S. L. Carnie, D. Chan, G. W. Stevens and F. Grieser, Science, 2006, 313, 210–213 CrossRef CAS PubMed.
- A. Sheludko, Adv. Colloid Interface Sci., 1967, 1, 391–464 CrossRef CAS.
- A. Zdravkov, G. Peters and H. Meijer, J. Colloid Interface Sci., 2003, 266, 195–201 CrossRef CAS PubMed.
- Y. Gao and L. Pan, Langmuir, 2018, 34, 14215–14225 CrossRef CAS PubMed.
- J. M. Frostad, D. Tammaro, L. Santollani, S. B. de Araujo and G. G. Fuller, Soft Matter, 2016, 12, 9266–9279 RSC.
- K. J. Mysels and M. N. Jones, Discuss. Faraday Soc., 1966, 42, 42–50 RSC.
- D. Exerowa and A. Scheludko, C. R. Acad. Bulg. Sci., 1971, 24, 47–50 Search PubMed.
- J. L. Joye, G. J. Hirasaki and C. A. Miller, Langmuir, 1992, 8, 3083–3092 CrossRef CAS.
- E. Manev, R. Tsekov and B. Radoev, J. Dispersion Sci. Technol., 1997, 18, 769–788 CrossRef CAS.
- E. Hermans, M. S. Bhamla, P. Kao, G. G. Fuller and J. Vermant, Soft Matter, 2015, 11, 8048–8057 RSC.
- J.-L. Joye, G. J. Hirasaki and C. A. Miller, Langmuir, 1994, 10, 3174–3179 CrossRef CAS.
- V. Bergeron, A. Jimenez-Laguna and C. Radke, Langmuir, 1992, 8, 3027–3032 CrossRef CAS.
- O. Velev, T. Gurkov, I. Ivanov and R. Borwankar, Phys. Rev. Lett., 1995, 75, 264 CrossRef CAS PubMed.
- V. C. Suja, A. Kar, W. Cates, S. Remmert, P. Savage and G. Fuller, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7919–7924 CrossRef CAS PubMed.
- Y. Zhang, S. Yilixiati, C. Pearsall and V. Sharma, ACS Nano, 2016, 10, 4678–4683 CrossRef CAS PubMed.
- S. Karakashev, Colloids Surf., A, 2010, 372, 151–154 CrossRef CAS.
- V. V. Yaminsky, S. Ohnishi, E. A. Vogler and R. G. Horn, Langmuir, 2010, 26, 8061–8074 CrossRef CAS PubMed.
- B. Liu, R. Manica, X. Zhang, A. Bussonniere, Z. Xu, G. Xie and Q. Liu, Langmuir, 2018, 34, 11667–11675 CrossRef CAS PubMed.
- B. Liu, R. Manica, Q. Liu, E. Klaseboer, Z. Xu and G. Xie, Phys. Rev. Lett., 2019, 122, 194501 CrossRef CAS PubMed.
- N. Bremond, A. R. Thiam and J. Bibette, Phys. Rev. Lett., 2008, 100, 024501 CrossRef PubMed.
- A. Lai, N. Bremond and H. A. Stone, J. Fluid Mech., 2009, 632, 97–107 CrossRef.
- D. Y. Chan, E. Klaseboer and R. Manica, Soft Matter, 2010, 6, 1809–1815 RSC.
- I. U. Vakarelski, R. Manica, X. Tang, S. J. O'Shea, G. W. Stevens, F. Grieser, R. R. Dagastine and D. Y. Chan, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11177–11182 CrossRef CAS PubMed.
- D. Z. Gunes, M. Bercy, B. Watzke, O. Breton and A. S. Burbidge, Soft Matter, 2013, 9, 7526–7537 RSC.
- L.-H. Hung, K. M. Choi, W.-Y. Tseng, Y.-C. Tan, K. J. Shea and A. P. Lee, Lab Chip, 2006, 6, 174–178 RSC.
- L. Mazutis, J.-C. Baret and A. D. Griffiths, Lab Chip, 2009, 9, 2665–2672 RSC.
- L. Mazutis and A. D. Griffiths, Lab Chip, 2012, 12, 1800–1806 RSC.
- D. Z. Gunes, X. Clain, O. Breton, G. Mayor and A. S. Burbidge, J. Colloid Interface Sci., 2010, 343, 79–86 CrossRef CAS PubMed.
- N. Bremond, H. Doméjean and J. Bibette, Phys. Rev. Lett., 2011, 106, 214502 CrossRef PubMed.
- M. D. Raj and R. Rengaswamy, Soft Matter, 2016, 12, 115–122 RSC.
- K. B. Migler, Phys. Rev. Lett., 2001, 86, 1023 CrossRef CAS PubMed.
- X. Zhang, P. Tchoukov, R. Manica, L. Wang, Q. Liu and Z. Xu, Soft Matter, 2016, 12, 9105–9114 RSC.
- L. Xie, C. Shi, X. Cui and H. Zeng, Langmuir, 2017, 33, 3911–3925 CrossRef CAS PubMed.
- C. Shi, X. Cui, L. Xie, Q. Liu, D. Y. Chan, J. N. Israelachvili and H. Zeng, ACS Nano, 2015, 9, 95–104 CrossRef CAS PubMed.
- R. F. Tabor, R. Manica, D. Y. Chan, F. Grieser and R. R. Dagastine, Phys. Rev. Lett., 2011, 106, 064501 CrossRef PubMed.
- R. A. Pushkarova and R. G. Horn, Langmuir, 2008, 24, 8726–8734 CrossRef CAS PubMed.
- R. R. Dagastine, G. B. Webber, R. Manica, G. W. Stevens, F. Grieser and D. Y. Chan, Langmuir, 2010, 26, 11921–11927 CrossRef CAS PubMed.
- R. F. Tabor, H. Lockie, D. Y. Chan, F. Grieser, I. Grillo, K. J. Mutch and R. R. Dagastine, Soft Matter, 2011, 7, 11334–11344 RSC.
- G. B. Webber, S. A. Edwards, G. W. Stevens, F. Grieser, R. R. Dagastine and D. Y. Chan, Soft Matter, 2008, 4, 1270–1278 RSC.
- N. Jaensson and J. Vermant, Curr. Opin. Colloid Interface Sci., 2018, 37, 136–150 CrossRef CAS.
- L. C. Pereira, C. Johansson, H. Blanch and C. Radke, Colloids Surf., A, 2001, 186, 103–111 CrossRef.
- BASF, Oppanol B Technical Information, 2005.
- P. Bataille and D. Patterson, J. Polym. Sci., Part A: Gen. Pap., 1963, 1, 3265–3275 CrossRef CAS.
- W. W. Graessley, Polymer, 1980, 21, 258–262 CrossRef CAS.
- C. Clasen, J. Plog, W.-M. Kulicke, M. Owens, C. Macosko, L. Scriven, M. Verani and G. H. McKinley, J. Rheol., 2006, 50, 849–881 CrossRef CAS.
- L. Bartell and R. Bonham, J. Chem. Phys., 1960, 32, 824–826 CrossRef CAS.
- U. Suter, E. Saiz and P. J. Flory, Macromolecules, 1983, 16, 1317–1328 CrossRef CAS.
- B. Coursey and E. L. Heric, J. Chem. Eng. Data, 1969, 14, 426–430 CrossRef CAS.
- G. P. Dubey and M. Sharma, J. Chem. Eng. Data, 2008, 53, 1032–1038 CrossRef CAS.
- P. J. Beltramo, R. Van Hooghten and J. Vermant, Soft Matter, 2016, 12, 4324–4331 RSC.
- T. M. Aminabhavi and G. Bindu, J. Chem. Eng. Data, 1994, 39, 529–534 CrossRef CAS.
- D. S. Valkovska, K. D. Danov and I. B. Ivanov, Adv. Colloid Interface Sci., 2002, 96, 101–129 CrossRef CAS PubMed.
- Y. Yoon, F. Baldessari, H. D. Ceniceros and L. G. Leal, Phys. Fluids, 2007, 19, 102102 CrossRef.
- J. D. Berry and R. R. Dagastine, J. Colloid Interface Sci., 2017, 487, 513–522 CrossRef CAS PubMed.
- A. Chesters, Chem. Eng. Res. Des., 1991, 69, 259–270 CAS.
- A. S. Hsu, A. Roy and L. G. Leal, J. Rheol., 2008, 52, 1291–1310 CrossRef CAS.
- O. Reynolds, Philos. Trans. R. Soc. London, 1886, 157–234 Search PubMed.
- A. Nikolov and D. T. Wasan, Langmuir, 1992, 8, 2985–2994 CrossRef CAS.
- E. Chatzigiannakis and J. Vermant, Phys. Rev. Lett., 2020 Search PubMed , under review.
- S. Jeelani and S. Hartland, J. Colloid Interface Sci., 1994, 164, 296–308 CrossRef CAS.
- S. I. Karakashev, D. S. Ivanova, Z. K. Angarska, E. D. Manev, R. Tsekov, B. Radoev, R. Slavchov and A. V. Nguyen, Colloids Surf., A, 2010, 365, 122–136 CrossRef CAS.
- M. S. Bhamla, C. Chai, M. A. Alvarez-Valenzuela, J. Tajuelo and G. G. Fuller, PLoS One, 2017, 12, e0175753 CrossRef PubMed.
- C. Browne, R. F. Tabor, F. Grieser and R. R. Dagastine, J. Colloid Interface Sci., 2015, 449, 236–245 CrossRef CAS PubMed.
- X. Chu, A. Nikolov and D. Wasan, J. Chem. Phys., 1995, 103, 6653–6661 CrossRef CAS.
- B. Toshev and I. Ivanov, Colloid Polym. Sci., 1975, 253, 558–565 CrossRef CAS.
- I. Ivanov and R. Jain, Dynamics and Instability of Fluid Interfaces, Springer, 1979, pp. 120–139 Search PubMed.
- S. A. Edwards, S. L. Carnie, O. Manor and D. Y. Chan, Langmuir, 2009, 25, 3352–3355 CrossRef CAS PubMed.
- A. Vrij, Discuss. Faraday Soc., 1966, 42, 23–33 RSC.
- J. Angarska, B. Dimitrova, K. Danov, P. Kralchevsky, K. Ananthapadmanabhan and A. Lips, Langmuir, 2004, 20, 1799–1806 CrossRef CAS.
- A. Malhotra and D. Wasan, Chem. Eng. Commun., 1986, 48, 35–56 CrossRef CAS.
- L. Wang and R.-H. Yoon, Colloids Surf., A, 2006, 282, 84–91 CrossRef.
- V. Simulescu, J. Angarska and E. Manev, Colloids Surf., A, 2008, 319, 21–28 CrossRef CAS.
- D. S. Ivanova and J. K. Angarska, Colloids Surf., A, 2013, 438, 93–103 CrossRef CAS.
- G. N. Sethumadhavan, A. D. Nikolov and D. T. Wasan, J. Colloid Interface Sci., 2001, 240, 105–112 CrossRef CAS PubMed.
- B. Liu, R. Manica, X. Zhang, A. Bussonnière, Z. Xu, G. Xie and Q. Liu, Langmuir, 2018, 34, 11667–11675 CrossRef CAS PubMed.
- Y. Yoon, M. Borrell, C. C. Park and L. G. Leal, J. Fluid Mech., 2005, 525, 355 CrossRef CAS.
- Y. Hu, D. Pine and L. G. Leal, Phys. Fluids, 2000, 12, 484–489 CrossRef CAS.
- Q. Zhou, Y. Sun, S. Yi, K. Wang and G. Luo, Soft Matter, 2016, 12, 1674–1682 RSC.
- Y. Yoon, A. Hsu and L. G. Leal, Phys. Fluids, 2007, 19, 023102 CrossRef.
- R. G. Horn, M. Asadullah and J. N. Connor, Langmuir, 2006, 22, 2610–2619 CrossRef CAS PubMed.
- M. Nagel, T. A. Tervoort and J. Vermant, Adv. Colloid Interface Sci., 2017, 247, 33–51 CrossRef CAS PubMed.
- J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage and J. Kierfeld, J. Colloid Interface Sci., 2018, 513, 549–565 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00784f |
| This journal is © The Royal Society of Chemistry 2020 |