 Open Access Article
Open Access ArticleModeling atomic force microscopy and shell mechanical properties estimation of coated microbubbles
A.
Lytra
a,
V.
Sboros
b,
A.
Giannakopoulos
c and
N.
Pelekasis
 *a
*a
aDepartment of Mechanical Engineering, University of Thessaly, Volos, 38334, Greece. E-mail: pel@uth.gr
bInstitute of Biological Chemistry, Biophysics and Bioengineering, Heriot-Watt University, Edinburgh EH14 4AS, UK
cSchool of Applied Mathematics, Physics and Mechanics, National Technical University of Athens, Athens, 15780, Greece
First published on 29th April 2020
Abstract
We present an extensive comparison with experimental data of our theoretical/numerical model for the static response of coated microbubbles (MBs) subject to compression from an atomic force microscope (afm). The mechanics of the MB's coating is described in the context of elastic thin shell theory. The encapsulated fluid is treated as compressible/incompressible pertaining to a gas/liquid, while the thinning of the liquid film between the MB and the afm cantilever is modeled via introduction of an interaction potential and the resulting disjoining pressure. As the external force increases, the experimental force–deformation (f–d) curves of MBs covered with polymer have an initial linear response (Reissner regime), followed by a non-linear curved downwards response (Pogorelov regime) where buckling takes place. On the other hand, the f–d curve for MBs covered with lipid monolayers initially follows the Reissner regime, but buckling is bypassed to a curved upwards regime where internal gas pressure dominates. The elastic properties, namely Young's modulus and shell thickness, for MB's covered with polymer can be estimated by combining the buckling point and the slope of the Reissner regime or the slopes of Reissner and Pogorelov regimes. Comparison of the present model with afm f–d curves for polymer shows satisfactory agreement. The area dilatation and bending moduli are shown to be the appropriate independent elastic parameters of MBs covered with phospholipid monolayers and are estimated by combination of the transition from Reissner to pressure dominated regime. Simulations and experiments in this case are in excellent agreement.
I. Introduction
Contrast agent microbubbles (MBs) have recently received significant attention, as they have a very positive impact in medical imaging via ultrasound1,2 and targeted drug delivery.3,4 Usually, they are coated with a biocompatible material, like polymer or lipid monolayer, that provides mechanical strength and reduces dissolution.3 Due to their small sub-capillary size, they are able to cross the entire vascular bed including abnormal vascular networks, such as the neovascularization of solid tumours.5 In the presence of an ultrasound field coated MBs oscillate, thus generating a strong back-scatter signal which allows for visualization of vital organs like liver,6 kidney,7etc., as well as blood flow8 to provide estimates of perfusion. Furthermore, after several cycles of oscillations they can be forced to collapse and release their payload in the vicinity of an area that is targeted for local treatment, thus significantly reducing side effects and increasing the efficacy of drug delivery.9,10The amount and the nature of the material that encapsulates the shell define the mechanical behavior of the MB. Considering the above fields of application, the mechanical properties, namely area dilatation and bending moduli, are of major importance since they determine the MB's amplitude of oscillation11 and dynamic response12,13 during acoustic interrogation, their window of stability before break-up takes place and their ability to travel across the vascular bed.14 Accurate estimation of these mechanical properties is a key to design their response in the presence of ultrasound. To this end, atomic force microscopy (afm) measurements have been proven to be a powerful and reliable tool to estimate the mechanical properties, because they rule out unnecessary coupling with dynamic effects and do not require consideration of the pertinent physical properties, such as shell viscosity and the viscosity of the surrounding liquid. In particular, MBs are compressed under the cantilever of an afm and the response is registered in force–deformation (f–d) curves.
AFM measurements are typically employed for the study of spherical capsules by employing the Hertz15 and Reissner16 theory, or appropriate combinations of them for varying shell thickness to particle radius ratio,17 and it is shown that as the ratio h/R decreases the Reissner theory becomes more appropriate with a correction factor depending on the cantilever and substrate shape. For soft cell-like spherical shells a variation of the Hertz theory, the Johnson–Kendall–Roberts model is employed that accounts for the surface energy of the cantilever and substrate,18 in order to obtain (f–d) curves and extract reliable predictions of the cell stiffness. For hollow polyelectrolyte or liquid filled shells analyses of afm measurements mainly focuses on the linear regime of the (f–d) curve17,19 where, for known shell thickness, the shell stiffness is recovered upon introducing the Reissner theory. Numerical simulations of the static response are then performed using commercial software packages such as Abaqus20 or Comsol17 in order to verify the f–d curve and shell deformation pattern. Simulations20 capture the linear regime as well elastic buckling in the Pogorelov21 regime however it was not always possible to capture the rich static response pattern exhibited by measurements involving mechanical indentation. In fact, theoretical and numerical studies that are performed in order to support such experiments in extracting shell properties are limited and usually omit crucial parameters such as the resistance of the encapsulated gas or liquid to compression.
Lulevich et al.22 investigated the response of liquid filled capsules with an afm and obtained a very different response pattern, i.e. an almost non-linear curved upwards f–d curve was identified right from the start of the experiment, without the classic Reissner response at low values of deformation that is usually observed in afm experiments. On the contrary, when harder shells are statically investigated via afm the linear regime becomes evident for small deformations,22–25 indicating the relative importance of the resistances to elongation/bending and volume compression. Furthermore, simulations using Abaqus captured the above pattern as well as instabilities in the form of horizontal plateaus, when transition from elastic to perfect plastic behavior was considered.23
Glynos et al.26 performed afm measurements of MBs coated with polymer (biSphere), where a rich f–d response was demonstrated. Initially, the f–d curve is linear while, with further increase of the applied force, the response becomes non-linear and nearly horizontal. Classic shell theory suggests that in the first regime the shape of the shell remains flattened and it is known as Reissner regime,16 while the non-linear response is associated with buckling in the contact area (Pogorelov regime21). A preliminary study by Lytra et al.27 suggested that proper coupling with the transition from Reissner to Pogorelov regime can estimate both Young's modulus and shell thickness from the f–d curve for MBs covered with polymer. It will be interesting to verify this prediction by resorting to simulations in view of the experimental evidence via unloading tests26 that plasticity effects are also possible during compression, which alters the response pattern via the onset of elasto-plastic buckling. The mechanical properties of MBs covered with phospholipid monolayers are the least studied and least understood in the literature. Among the first who performed afm measurements on Definity MBs was Buchner Santos et al.28 who found that these MBs are softer with a Young's modulus on the order of MPa. In addition, the f–d curve is almost linear for the most part of it and it is curved upwards at relatively high deformations. In the latter study the proposed model to estimate the Young's modulus is the one developed by Lulevich et al.,22 which however results in a radius dependent area dilatation modulus, while it is reported that the Reissner's model16 overestimates the Young's modulus. More recently, Abou-Saleh et al.29 also calculated the Young's modulus of lipid MBs using the afm, based on Reissner's model. In addition, they found that adding a functional coating on the outside of the shell the overall stiffness increases significantly. It is also interesting to note that when no extra coating is added on the shell surface the response is initially linear, followed by a non-linear curved upwards regime, while the extra coating results in a strong linear response.
Moreover, in classic shell mechanics the in plane stresses are proportional to area dilatation modulus, χ, and similarly the bending moments to the bending modulus, kb, via appropriate constitutive laws. In this context, the area dilatation modulus and the bending modulus are related to the 3d Young's modulus, E, and shell thickness, h, as χ = Eh and kb = Eh3/[12(1 − ν2)]. In the case of MBs covered with polymer, the shell thickness is relatively big and its structure could be characterized as more or less isotropic and homogeneous. Therefore, for polymeric shells, apart from the shell radius the independent shell parameters are the 3d Young's modulus and the shell thickness. On the other hand, MBs covered with lipid monolayers form a shell of very small thickness (1–5 nm) which is not easy to define or measure and as a result the shell structure is not entirely isotropic. Therefore, following studies on the mechanical behavior of lipid bilayer shells such as the red blood-cells,30 we propose that the independent parameters for MBs covered with lipid monolayers are the area dilatation and bending moduli and we want to investigate the validity of this discrepancy.
In order to capture the rich spectrum of static responses reported in afm measurements, pertaining to coated microbubbles and capsules, and provide reliable tools for accurate parameter estimation of the shell elastic properties, it is necessary to develop a flexible simulation technique that can accurately predict the load distribution on the interrogated MB as well as its deformed shape for a wide range of external forcing. Resorting to commercial software does not provide the degree of flexibility and robustness required to this end. Consequently, we have developed a numerical/theoretical model31 to account for the hydrophilic nature of the involved substrates and coated MBs, especially the ones coated with lipid monolayers, as a means to obtain the load distribution exerted on their shell by the slowly descending cantilever during an afm measurement. Such indentation experiments take place in an aqueous environment in which case, the thickness of the liquid film that surrounds the microbubble decreases as the cantilever approaches the shell, and as a result the disjoining pressure that keeps them apart increases while gradually deforming the shell. The disjoining pressure is a manifestation of the intermolecular forces32 between the shell and cantilever and depends on the nature of these two surfaces. Using this model it was possible to simulate31 the static response of both polymeric and lipid MBs. To this end, the previous model is extended to account for non-symmetric deformations with respect to the shell's equator, e.g. when the resting surface of the MB and the cantilever surface are of different geometry or possess very different wetting properties. Moreover, we have also modified our formulation in order to account for the case of an incompressible fluid being encapsulated in the shell and we investigate the possibility of a pure repulsive potential pertaining to afm measurements with air as the surrounding medium.
It should be stressed that we proceeded in this direction unaware of previous pioneer studies employing the interaction potential between the cantilever and the interrogated particle in order to obtain the distribution of the load that is exerted on the latter during the afm measurement. Particularly so when indentation studies are performed on drops and bubbles in order to obtain isothermal force–distance curves33 and through them the disjoining pressure isotherms,34 by invoking the DLVO theory that accounts for both van der Waals and double layer fources.32 In the study be Bhatt et al. (2001)34 such a short range repulsive/long range attractive potential is employed in order to solve the augmented Young–Laplace equation for the force exerted on a deformable drop/bubble as it interacts with two solid particles of comparable curvature that are emerged in a liquid of varying wetting properties. It was thus seen that in recovering the equilibrium disjoining pressure isotherm the actual interfacial deformation must be accounted for, rather than assuming an effective drop/bubble elasticity, and that in the linear force deformation regime compressibility of the drop/bubble is negligible. Consequently treating the inner fluid as a drop or bubble does not alter the f–d curve. This approach has been extensively and successfully used ever since for the analysis of forces on drops and bubbles, or between drops and bubbles in complex fluid systems with varying degrees of hydrophilicity, using afm.35–37 A similar type interaction potential is used in the present study for the static interrogation of coated microbubbles and liquid filled capsules and it was seen that, as long as we remain in the linear regime of the static response, the f–d curve is the same irrespective of the treatment of the pressure variation of the inner fluid. However, interesting variations arise as we enter the nonlinear regime of the shell static response.
The rest of the paper is organized as follows: the theoretical/numerical model is briefly discussed in Section II-A and the available analytical models in Section II-B; details of the extension of the methodology to account for non-planar cantilevers are provided in the Appendix. Then, the results and comparison with afm data are presented in Section III. Finally, Section IV contains the main conclusions and findings of the present study.
II. Modeling
A. Theoretical formulation
We consider an axisymmetric MB that is encapsulated by an elastic biomaterial (polymer or phospholipid monolayer), rests on a plane substrate and can be compressed by a plane or spherical cantilever, Fig. 1(a and b). In both cases the substrate and cantilevers have much higher elastic rigidity, thus we assume that after contact only the MB is deformed. In particular, based also on experimental observations, axisymmetric deformations are assumed throughout this study. Depending on the nature and geometry of the upper and lower surfaces the deformation can be symmetric or asymmetric with respect to the equatorial plane of the MB. During afm measurements the MB is submerged in a liquid solution, with the cantilever being initially positioned above the MB and gradually approaching it thereby increasing the exerted force. Consequently, in the present study we investigate the response as the distance between the cantilever and the solid substrate, zCS, decreases, rather than the distance, z0, between the cantilever and center of mass of the microbubble that was used in our previous modeling study.27 When a plane cantilever is considered the distance zCS is easily defined as the axial position of the cantilever, Fig. 1(a), whereas when a spherical one is employed zCS is defined as the axial position of its center, Fig. 1(b); the origin of the axis of symmetry z is located on the substrate in both cases. It will be seen in the following that when the cantilever and substrate are flat and similar in nature z0 = zCS/2.Due to the hydrophilic nature of the involved surfaces, the space between the cantilever and the north pole as well as between the substrate and the south pole of the coated bubble is occupied by an ultrathin liquid film with variable thickness, δ, which is squeezed by the action of the external force thus resulting in variations of the local pressure. The latter is known as disjoining pressure and is a measure of the intensity of the intermolecular forces between the interacting pair of surfaces whose strength is signified via an additional source of energy per unit surface that is attributed to the shell interface, wint, that reflects its interaction with the cantilever. In particular, a long range attractive-short range repulsive interaction potential is introduced herein in order to describe the above interaction, which has the following form32,34,38,39
 | (1) |
 | ||
Fig. 2 Dimensionless potential, ŵint = wint(δ)/w0, and dimensionless disjoining pressure, ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) = Π(δ)δA/w0, as a function of the relative distance from the cantilever/substrate, δ/δA. = Π(δ)δA/w0, as a function of the relative distance from the cantilever/substrate, δ/δA. | ||
On a different context, similar compression experiments are conducted for conventional spherical shells like table tennis balls.40 In this case, the shell is deformed as previously under a flat and rigid surface, but instead of a liquid the surrounding environment is air, which is a non-polar medium. Thus, a typical interaction potential32,34 contains only the repulsive term:
 | (2) |
For both types of interaction potential the total energy content of the shell, provided by the sum of strain, bending, intermolecular, gas compression and surface energy, reads as:
| UT = Wstr + Wb + Wint + Wc + Ws, | (3) |
 | (4a) |
 | (4b) |
The disjoining pressure Π arises as part of the minimization of the intermolecular energy with respect to the radial, σ, and axial, z, position of the shell and equals the derivative of the interaction potential in the normal direction:31
 | (5) |
 | (6) |
 | (7) |
The above equilibrium between the elastic tensions at the shell interface and the disjoining pressure is coupled with the internal pressure, PG, of the encapsulated gas. In particular, as the shell is compressed its volume is reduced and therefore the volume and internal pressure are linked via an isothermal equation:
| PGVγ = P0V0γ, | (8a) |
| m = const. ⇒ ρV = const. or V = V0 | (8b) |
The reference state is typically spherical and stress-free unless otherwise stated. A parametric study on the effect of pre-stress on the static response of coated microbubbles is not presented in the present article and is relegated to a future investigation. Nevertheless, it should be pointed out that in the presence of pre-stress a coated microbubble is expected to buckle as a result of static compression39–41 in which case transient break up takes place subject to further static or acoustic disturbance.27,44,45,47 This mechanism may explain the onset of collapse obtained in afm measurements of coated microbubbles at higher temperature levels,25 in which case large levels of pre-stress are present due to gas escaping out to the surrounding liquid as a result of increased diffusion rates through the shell.
The above problem is made dimensionless with the bubble radius at the reference state employed as characteristic length scale, R0. Hence, the problem formulation is governed by the following dimensionless numbers:
 | (9) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) denotes all the dimensionless lengths entering the problem, i.e. the height of the liquid film,
denotes all the dimensionless lengths entering the problem, i.e. the height of the liquid film, ![[small delta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b1.gif) , the position of the cantilever, ẑCS, the initial pre-stress, û and the cylindrical coordinates (
, the position of the cantilever, ẑCS, the initial pre-stress, û and the cylindrical coordinates (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ,ẑ), which for simplicity we keep in (σ,z) form. For polymeric shells that normally have thicker coatings, bending resistance is related to the elastic modulus and the shell thickness:43
,ẑ), which for simplicity we keep in (σ,z) form. For polymeric shells that normally have thicker coatings, bending resistance is related to the elastic modulus and the shell thickness:43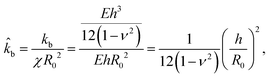 | (10) |
The above formulation is completed with the appropriate boundary conditions at the edges of the generatrix:
| σξξ = 0 at ξ = 0 and 1, | (11a) |
| zξ = 0 at ξ = 0 and 1, | (11b) |
| σ(ξ = 0) = σ(ξ = 1) = 0, | (11c) |
 | (12) |
B. Numerical solution and asymptotic models
The Galerkin finite element methodology (FEM) is employed for the numerical solution of the system of eqn (4), (8) and (11). The B-cubic splines48 are used as basis functions in order to accommodate the bending stresses. The unknown variables are the position (σ,z) of each node of the generatrix and the internal pressure, PG. An in-house Fortran code has been developed in this context,31,46 which was validated against analytical results available from the literature,49 and was recently extended to account for non-symmetric loading conditions. The validity of the numerical solution was tested against asymptotic results obtained using the theory of continuum mechanics,16,21 while new regimes in the static response pattern were identified31 as will also be illustrated in the next section that is dedicated to the comparison with afm measurements. More details on the model described in the previous section and the finite element methodology for its solution can be found in a previous article.31Microbubbles covered with polymeric biomaterial have relatively stiff shells in terms of their Young's modulus [2–20 GPa] and a shell thickness on the order of 20–40 nm. Therefore, the analytical solutions developed for convectional shells are more applicable with polymeric coatings in comparison with MB's covered with lipid monolayers. In particular, the f–d curve from afm measurements of polymeric shells is typically initially linear corresponding to the Reissner regime. Simulations and analysis suggest that in this regime the shell portion that lies immediately under the cantilever is flattened, while force and deformation are related via the Reissner equation:16
 | (13a) |
In the latter equation parameter Δ signifies the deformation of the pole that lies in the vicinity of the cantilever and is one half of the cantilever displacement, ΔC, that is usually registered as shell deformation in afm measurements for which the substrate and cantilever possess the same hydrophilic properties. The latter value, ΔC, incorporates the translation of the microbubble center of mass due to the same amount of deformation of the lower pole that is in contact with the substrate, see also Fig. 3(a). Therefore, when f–d curves are considered the horizontal axis should be marked with Δ in order to get an appropriate fitting of Reissner's equation, or an equivalent form of the previous relation can be used, namely
 | (13b) |
Moreover, as the external force increases, the response becomes non-linear and curved downwards. In this regime, buckling takes place in the area around the pole that is in contact with the cantilever and the analytical f–d relation has been described by Pogorelov21 as:
 | (14) |
Thus, combination of the linear regime of the static response curve with the Pogorelov regime can provide the Young's modulus and shell thickness.27,31 In addition, when buckling is observed, simulations31 suggest that the buckling point is encountered when
 | (15) |
When subjected to the same type of static load, MBs covered with lipids have a significantly different response pattern in experimentally obtained f–d curves, i.e. they initially exhibit a linear regime followed by a non-linear curved upwards28,29 regime. In this case, numerical simulations indicate27 that buckling is bypassed as the internal gas pressure is an equally important stiffness on the shell equilibrium, thus defining the new curved upwards regime. The first regime can be described by the Reissner relation eqn (15), while for the second regime we have developed an analytical expression31 to describe this type of response when the resistance to internal pressure change becomes important:
 | (16a,b) |
 | (17a,b) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b ≡ kb/(χR02) ≪ 1, it captures the curved up response pattern in f–d curves. Conversely, when bending is important it captures the linear part of the static response, Reissner regime, in which case the nature of the enclosed fluid, i.e. whether it is a gas or a liquid, does not affect the f–d curve. This was first pointed out by Bhatt et al.34 in their study of drop/bubble interaction with a solid particle for various geometric configurations and interaction potentials. In the following section the above response patterns will be identified in a number of experimental investigations of coated microbubbles via afm and will be recovered numerically with the proposed methodology, aiming at characterizing shell elastic properties.
b ≡ kb/(χR02) ≪ 1, it captures the curved up response pattern in f–d curves. Conversely, when bending is important it captures the linear part of the static response, Reissner regime, in which case the nature of the enclosed fluid, i.e. whether it is a gas or a liquid, does not affect the f–d curve. This was first pointed out by Bhatt et al.34 in their study of drop/bubble interaction with a solid particle for various geometric configurations and interaction potentials. In the following section the above response patterns will be identified in a number of experimental investigations of coated microbubbles via afm and will be recovered numerically with the proposed methodology, aiming at characterizing shell elastic properties.
III. Results
A. MB covered with polymer (![[P with combining circumflex]](https://www.rsc.org/images/entities/h3_i_char_0050_0302.gif) A ≪ 1)
A ≪ 1)
In the first part of this section we compare results obtained with the present methodology and experimental curves for MBs covered with polymers.17,19,20,26 This group of coated MBs is characterized by a relatively large Young's modulus, usually in the order of GPa, and relatively thick shells. Most characterization studies focus on the linear regime of the f–d curve.17,19 After the pioneering earlier studies by Updike and Kalnins,49 Elsner et al.20 were among the first to use the afm for characterization of the shell elastic properties, considering the nonlinear part as well. In particular, Elsner et al.20 performed compression tests in hollow polyeloctrolyte multilayer capsules (PMC). In both studies20,49 the response in the f–d curves is initially linear followed by a non-linear curved downwards regime indicating buckling of the shell near the contact area. Then, the curve is slightly curved upwards, which is attributed to the increase of the internal pressure as a result of volume reduction. Jumps and instabilities are observed at higher values of deformation where secondary effects govern the response, i.e. 3d deformations, plasticity, geometrical imperfections or even viscoelastic creep effects, which the present model does not account for. Nevertheless, we can compare our numerical model with the experimental curve of Elsner et al.,20 which involve hard polymeric microbubbles, at relatively lower deformations where elastic forces and gas compressibility dominate.
The shell thickness of a PAH/PSS capsule is h = 25 nm and the radius R0 = 7.9 μm. These values conform well with eqn (15), when it is considered for the estimation of the buckling point. In particular, eqn (15) implies that buckling takes place at Δ ≈ 63 nm, based on the above shell properties, which is in accordance with the buckling point obtained by the experimental curve, i.e. Δ ≈ 50–60 nm. Then employing the Reissner model on the experimental f–d curve, see also Fig. 4(a), we estimate the Young's modulus E ≈ 252 MPa, while Elsner et al. estimated it at E = 294 ± 32 MPa. This combined procedure for obtaining shell elastic properties was proposed in our earlier studies27,31 and is seen here to provide reliable estimates of available afm measurements. To illustrate this, we perform simulations of the measurements reported in ref. 20 using the model proposed in ref. 31 and described in Section II of the present article, assuming a weak interaction potential based on the nature of the symmetrically compressed shell, and employing the shell parameters obtained in the manner described above. As can be gleaned from Fig. 4(b) the f–d curve obtained by the FEM simulations predicts very well the buckling point, while slightly overestimating the slope. In addition, at higher deformations, i.e. Δ ≥ 100 nm, the FEM curve follows the curved upwards regime indicating an increase on the required force, with respect to the predictions of the Pogorelov theory, as a result of the increase of the internal pressure due to gas compressibility. The shape of the MB for selected values of deformation is presented in Fig. 4(c) for flat and buckled shapes. In addition, the disjoining pressure profiles along the radial coordinate σ for a range of values of deformation Δ, indicate that in the Reissner regime of small deformation the pressure is concentrated in the pole region and nearly assumes the form of a point load. As the deformation increases the pressure peak is translated towards the end of the contact area, while at the buckling regime the pressure distribution is that of a ring load concentrated at the edge of the dimpled region of the shell, Fig. 4(d). Finally, the components of the energy that constitute the equilibrium are presented in Fig. 4(e). Initially, the elastic energies due to stretching and bending dominate the response with stretching being the dominant energy before buckling. In the post buckling regime an exchange in the order takes place, with energy due to bending becoming dominant. Furthermore, after Δ ≥ 100 nm the energy due to gas compression starts increasing and becomes of the same order as elastic energies, which is manifested in the numerical f–d curve by the curved upwards regime. The above response pattern conforms with the findings of our earlier study31 on the static response of microbubbles coated by stiff polymeric shells that are characterized by very small bending resistance, i.e. very small ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b value, and non-vanishing resistance to compression, O(1)
b value, and non-vanishing resistance to compression, O(1) ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A value, in comparison with stretching resistance, as is the case with the shell that is interrogated in Fig. 4.
A value, in comparison with stretching resistance, as is the case with the shell that is interrogated in Fig. 4.
 | ||
Fig. 4 (a) Experimental curve f–d for a PAH/PSS MB with R0 = 7.9 μm and h = 25 nm by Elsner et al.20 (b) Comparison of numerical and experimental f–d curves. (c) Shape of deformed MBs for selected values of deformation. (d) Evolution of dimensionless disjoining pressure profiles ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) as function of the radial coordinate σ for selected values of deformation. (e) Evolution of dimensionless energy components Ŵi as function of deformation; simulation parameter for FEM: R0 = 7.9 μm, h = 25 nm, E = 252 MPa, ν = 0.33, γBW = 0 N m−1W0 = 10−5 N m−1, δA = 20 nm, neo-Hookean law with the corresponding dimensionless numbers, as function of the radial coordinate σ for selected values of deformation. (e) Evolution of dimensionless energy components Ŵi as function of deformation; simulation parameter for FEM: R0 = 7.9 μm, h = 25 nm, E = 252 MPa, ν = 0.33, γBW = 0 N m−1W0 = 10−5 N m−1, δA = 20 nm, neo-Hookean law with the corresponding dimensionless numbers, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 9.4 × 10−7, b = 9.4 × 10−7, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 1.3 × 10−1, Ŵ0 = 1.6 × 10−6 and A = 1.3 × 10−1, Ŵ0 = 1.6 × 10−6 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. BW = 0. | ||
In the same context, Glynos et al.26 employed the afm and demonstrated the mechanical response of MBs covered with biSphere (a polymer polylactide). In this case also the thickness of the coating is relatively large, i.e. h = O(20–40 nm). In particular, it was suggested50 that it varies linearly with the shell radius, i.e. h = 1.5 × 10−2R0. Thus, the Young's modulus, E, was estimated26via the slope of the linear part of the f–d curve by employing Reissner's model, and it was found to be on the order of 2–20 GPa. However, it should be noted that in the latter study Reissner's model was applied to f–d curves that employ the cantilever translation in the abscissa, which contains deformations from both poles. Therefore, in order to properly use Reissner's model, the horizontal axis of the experimental curve is divided by two and then we use the slope of the linear part of the f–d curve coupled with the nonlinear model pertaining to the Pogorelov regime, eqn (14), in order to obtain estimates of both shell thickness and Young's modulus, see also Fig. 5(a). The resulting values are E = 6 GPa and h = 36 nm, which we use as input in our numerical model, see also dashed curve in Fig. 5(b) and Table 1a. It should be stressed that in Fig. 5(b) the cantilever deflection, ΔC, is used in the abscissa in order to compare against the afm measurements reported in ref. 26. As can be gleaned from the dashed curve obtained by the simulations, the estimated values from the Reissner–Pogorelov transition overestimate the deformation corresponding to shell buckling, which is seen to take place at ΔC ≈ 180 nm instead of 65–70 nm indicated by the experiments.
 | ||
Fig. 5 (a) Fitting in experimental force–deformation curve. (b) Comparison of experimental and numerical results in force–deformation curves. The mechanical properties are obtained by defining the buckling point (solid curve) or using the properties of the buckling point in combination with the pre-stress assumption (dashed dot curve) and the transition for Reissner to Pogorelov regime (dashed curve). The extracted parameters, which have been used for every case, are shown in Table 1a and b. For every simulation, W0 = 10−3 N m−1, δA = 40 nm, ν = 0.42 and neo-Hookean law is assumed. (c–e) Shape of the MB for selected values of deformation. (f) Evolution of the dimensionless disjoining pressure profiles ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) along the radial coordinate σ for the cantilever-MB contact area. Figure (c–f) correspond to the buckling point assumption. The experimental curve was obtained by Glynos et al.26 along the radial coordinate σ for the cantilever-MB contact area. Figure (c–f) correspond to the buckling point assumption. The experimental curve was obtained by Glynos et al.26 | ||
| Radius (R0) | Thickness (h) | Young's modulus (E) | Surface tension (γBW) |
|---|---|---|---|
| (a) | |||
| 2 μm | 36 nm | 6 GPa | 0 |
| Dimensionless numbers | |||
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 3.3 × 10−5
b = 3.3 × 10−5 |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 9.4 × 10−4
A = 9.4 × 10−4 |
Ŵ 0 = 4.6 × 10−6 |
![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0
BW = 0 |
| (b) | |||
| 2 μm | 13 nm | 48 GPa | 0 |
| Dimensionless numbers | |||
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 4.3 × 10−6
b = 4.3 × 10−6 |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 3.2 × 10−4
A = 3.2 × 10−4 |
Ŵ 0 = 1.6 × 10−6 |
![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0
BW = 0 |
In order to resolve this discrepancy, upon noting that the buckling point in the experimental curve occurs at Δ = 33 nm or ΔC ≈ 66 nm based on the cantilever translation used in Fig. 5(b), eqn (15) provides the shell thickness, h = 13 nm. In this context Young's modulus is recovered, E = 48 GPa, from the linear part of the f–d curve by employing Reissner's model. The latter values are also incorporated in the numerical model, see also solid line in Fig. 5(b) and Table 1b, providing a more accurate simulation of the experimental f–d curve, until the onset of buckling. Furthermore, plotting the shape of the MB for indicative values of deformation, as predicted by the above simulation, we can see that solutions corresponding to the linear regime exhibit a flat contact area, while in the non-linear regime buckling takes place signified by dimple formation, Fig. 5(c–e). In addition, the MB is assumed to be compressed symmetrically at both poles, therefore the profiles of the disjoining pressure in the vicinity of the cantilever and substrate surfaces are identical, Fig. 5(f). Finally, the components of the total energy follow the same pattern as in the calculations performed in the context of Elsner et al.,20 as expected owing to the very small dimensionless bending resistance, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b < 10−5, that characterizes polymeric shells. However, the energy due to gas compression has no significant contribution in the simulations pertaining to the f–d curves reported in ref. 26, since the volume reduction is relatively small. This was anticipated based on the much smaller resistance to volume compression of the latter type shells,
b < 10−5, that characterizes polymeric shells. However, the energy due to gas compression has no significant contribution in the simulations pertaining to the f–d curves reported in ref. 26, since the volume reduction is relatively small. This was anticipated based on the much smaller resistance to volume compression of the latter type shells, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 9.4 × 10−4, and is confirmed by the profiles of the numerical f–d curves, Fig. 5(b), which do not exhibit a curved upwards regime; for more details see also the analysis in ref. 31.
A = 9.4 × 10−4, and is confirmed by the profiles of the numerical f–d curves, Fig. 5(b), which do not exhibit a curved upwards regime; for more details see also the analysis in ref. 31.
Nevertheless, the numerical simulations presented in Fig. 5(b) exhibit significant discrepancies compared to the experimental f–d curve, mainly pertaining to the extensive horizontal plateau obtained in the post-buckling regime of afm measurements. This type of response cannot be attributed to 3-d effects, since it occurs at lower deformation that expected for 3d buckling to take place,51 and this strongly indicates plastic deformations which was confirmed by unloading measurements in the context of the afm measurements reported in ref. 26 but also in earlier relevant experimental/theoretical studies.49 In particular, the horizontal plateau occurs right after buckling takes place in the f–d curve in the former experimental study.26 Consequently, we can presume that unstable behavior sets in such as elasto-plastic buckling or viscoelastic creep, soon after the onset of primary buckling. Similar findings of unstable behavior and discrepancies between loading and unloading measurements have been reported elsewhere,49 for deformations that lie beyond the onset of buckling, and was attributed to the impact of friction in the static response. In fact, simulations of the static response in the parameter range relevant to the latter study49 recover the post-buckling behavior captured in the experiments as the energetically favored response, while failing to follow the experimental curve to higher deformations in which regime Updike and Kalnins49 postulate the onset of the above mentioned instabilities. In such situations accurate estimation of the elastic properties probably requires additional parameters, e.g. the yield stress or shell viscosity, which are not a-priori known and their assessment is beyond the scope of the present study.
We also wish to employ our methodology in order to compare with experimental data obtained for larger polymeric shells which are surrounded by air, instead of being immersed in a liquid, during afm measurements. Such experiments are available in the literature for rubber shells by Updike and Kalnins49 or table tennis balls by Shorter et al.40 The size of these shells is a few centimeters with a thickness to radius ratio ∼1/100. In addition, their relatively big size allows for identification of buckling or other type of phenomena with a naked eye and direct comparison with instabilities in the profile of the f–d curve. Commercially available software packages are typically employed40,51 in the literature to simulate such experiments. Here, we use an interaction potential with only the repulsive term in order to account for the fact that the surrounding medium is air and consequently van der Waals repulsion is the predominant intermolecular force as the cantilever contacts the shell. In this fashion, we compare our numerical simulations with data obtained by Sorter et al.40 for a table tennis ball with R0 = 2 × 10−2 m. In this case, the f–d curve has an extensive linear regime followed by a non-linear one. The transition takes place at a sharp point, which conforms very well with eqn (15). Thus, we recover the value of the shell thickness from the buckling point to be h = 4 × 10−4 m. Subsequently, employing Reissner's model in the slope of the linear regime, eqn (13a), we estimate the Young's modulus, E = 2.8 MPa. It should be pointed out that the value used by Shorter et al. is E = 2.2 MPa. Then, performing simulations with a Hamaker potential we recover with satisfactory agreement the experimental response in terms of the f–d curve, Fig. 6(a). In the above simulations, we assumed, as Shorter et al.40 suggest, that variations in the internal gas pressure are negligible due to minute volume variations. As a result we set γ = 0 indicating an isobaric process. Otherwise, the increase of the internal pressure as a result of the volume reduction creates a strong curved upwards regime after the buckling point, which is not registered in the measured f–d curve. It should also be noted that a central aspect of the present calculations for bigger shells is the requirement for finer meshes. When we simulate MBs with a radius of several microns a mesh with 400 elements is sufficient to reproduce analytical49 or experimental results, while typical mesh refinement calculations with 800 or even 1600 elements give the same response pattern. However, it should be noted that a mesh with 400 or 1000 B-cubic splines failed to recover the experimental response and finer meshes with 1500, 2000 and 3000 elements are used in Fig. 6(a). Converged solutions with the relatively sparser meshes follow the non-linear response indicating buckling, but the deformed shape corresponds to unstable buckling solutions exhibiting multilobed shapes. The solutions with the finer meshes exhibit stable buckling shapes of the standard form with the dimple around the pole region, Fig. 6(b). Overall, in cases where the shell radius is very large and the transition region that connects the contact with the bulk of the shell is much smaller in comparison with the shell radius;31,46 typically on the order of the film thickness, δ, that occupies the region between the shell and substrate. As a result finer meshes are indeed necessary in order to obtain a reliable solution that captures details of the shape in the macroscale, O(R0), and the microscale, O(δ).
 | ||
Fig. 6 (a) Dimensionless force R0F/Eh3 as function of the dimensionless deformation Δ/h. Comparison between experiment and simulation employing the disjoining pressure model. The simulation parameters are R0 = 2 cm, h = 0.4 mm, E = 2.8 MPa, ν = 0.4, A = 10−10 N m, γ = 0 and the corresponding dimensionless numbers: ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 4 × 10−5, b = 4 × 10−5, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 0, Â = 2.2 × 10−10 and A = 0, Â = 2.2 × 10−10 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. (b) Evolution of shapes obtained with a 2000 elements mesh for selected values of dimensionless deformation. The experiment was conducted by Shorter et al.50 for a table tennis ball. BW = 0. (b) Evolution of shapes obtained with a 2000 elements mesh for selected values of dimensionless deformation. The experiment was conducted by Shorter et al.50 for a table tennis ball. | ||
B. MB covered with lipid monolayer (![[P with combining circumflex]](https://www.rsc.org/images/entities/h3_i_char_0050_0302.gif) A ≈ 1)
A ≈ 1)
In this section, we compare numerical results with experimental AFM data for MBs covered with a phospholipid28,29 shell. As was also pointed out in our earlier study,31 the static response pattern of this type of MBs differs significantly from MBs covered with a polymeric shell. In particular, there is an initial linear response that is identified as Reissner regime, but at higher deformations the f–d curve becomes non-linear and curved-up with a cubic dependence. This response type is in contrast with classic shell theory where, for a relative thin shell, transition to buckling is predicted at relatively large deformations and this is signified by a nonlinear and curved-down response pattern following the initial linear Reissner regime.31 For soft phospholipid shells, the encapsulated gas plays a central role in shell equilibrium, because its compressibility is comparable with the elastic rigidity. Thus, with increasing external force the shell volume decreases while the gas pressure increases as well, tending to relax the compressive tensions responsible for buckling. Fig. 7(a) describes the F–Δc/D0 curve for a Definity MB that was obtained by Buchner Santos et al.28 with the afm. In this curve we fit a linear and a cubic polynomial in the linear and non-linear regimes, respectively, in order to obtain the corresponding coefficients based on the approach presented in the previous section, combining the Reissner theory in eqn (13a) and the cubic law in (16b), maintaining a satisfactory regression parameter, ∼0.99, in both regimes. In this fashion we estimate the area dilatation and bending moduli as the two fundamental, independent elastic parameters, rather than the Young modulus and shell thickness,30 by invoking eqn (16b) in the non-linear regime and the slope of the linear regime in Reissner's law (13a); see also Fig. 7(a). In the case examined here the initial diameter is set to D0 = 4.2 μm and the Poisson ratio to ν = 0.5. Employing the above methodology on the data provided in ref. 28 we obtain for the area dilatation and bending moduli χ = 0.19 N m−1 and kb = 5.8 × 10−16 N m, respectively.
 | ||
Fig. 7 (a) Force as function of dimensionless deformation by Buchner Santos et al.28 for a Definity MB with D0 = 4.2 μm, solid lines describe linear and non-linear fitting. (b) Comparison of experimental and numerical F–Δ curves, the simulation parameters are: R0 = 2.1 μm, χ = 0.19 N m−1, kb = 5.8 × 10−16 N m, ν = 0.5, γBW = 0 N m−1, W0 = 10−4 N m−1 and δA = 50 nm, Mooney–Rivlin law. The dimensionless numbers are ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 6.9 × 10−4, b = 6.9 × 10−4, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 1.1, Ŵ0 = 5.2 × 10−4 and A = 1.1, Ŵ0 = 5.2 × 10−4 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. (c–e) Shape of the deformed MB for three indicative solutions at deformation Δc = 77 nm, Δc = 200 nm and Δc = 400 nm; the substrate is located at the origin of the axis and the cantilever is depicted with a horizontal line at the upper part of the MB. BW = 0. (c–e) Shape of the deformed MB for three indicative solutions at deformation Δc = 77 nm, Δc = 200 nm and Δc = 400 nm; the substrate is located at the origin of the axis and the cantilever is depicted with a horizontal line at the upper part of the MB. | ||
We next perform simulations using the above estimated values for the elastic properties and a relative weak potential, as there is no indication for strong adhesion, i.e. no significant pull-off force in the experiments. As can be gleaned from Fig. 7(b), the experimental and numerical curves are in excellent agreement. The FEM model accurately captures the linear regime, while slightly underestimating the force in the pressure dominated regime at high deformations. In addition, the shape of the MB for three indicative solutions is depicted in Fig. 7(c–e), where no buckling is observed. Instead, the shape near the poles remains flattened as the deformation increases and a progressively elongated contact area is exhibited. This behavior is in agreement with the parametric study performed in our earlier work31 pertaining to soft phospholipid shells characterized by large resistance to compression, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = O(1), in comparison with the area dilatation modulus. It should also be noted that for similar properties of the cantilever and substrate, as this is reflected in the intensity and nature of the interaction potential, the shape of the microbubble around the two poles is identical thus validating the assumption of symmetry across the equatorial plane of the microbubble.
A = O(1), in comparison with the area dilatation modulus. It should also be noted that for similar properties of the cantilever and substrate, as this is reflected in the intensity and nature of the interaction potential, the shape of the microbubble around the two poles is identical thus validating the assumption of symmetry across the equatorial plane of the microbubble.
It should be stressed at this point that Buchner Santos et al.28 adopt for the shell thickness a value of 5 nm, as proposed by the manufacturer of the statically interrogated MB's, and they estimate the Young's modulus to E = 10–50 MPa, based on their measurements. This corresponds to an area dilatation modulus in the range of χ = 0.05–0.25 N m−1 which is in good agreement with the estimate obtained in the present study. However, a shell with h = 5 nm and E = 10–50 MPa, upon applying the formula from classic shell mechanics (see also eqn (10) in Section II-A of the present study), corresponds to a bending resistance of kb ≈ (1–7) × 10−19 N m that is three orders of magnitude lower than the value estimated in the present study. Moreover, simulations with the parameter values estimated by Buchner Santos et al.28 indicate the onset of shell buckling. However, the afm measurements do not capture buckling within the reported deformation range. This corroborates our assertion that for MBs covered with phospholipid monolayers the area dilatation modulus and bending resistance constitute the proper set of independent shell parameters.
Further post-processing of the calculations with the FEM model can give a more detailed picture of the main force balance. In Fig. 8(a) we plot the components of the total energy as function of deformation. The dominant energies are the elastic components, i.e. stretching and bending, while at Δc = 300 nm we observe a slight increase of the energy due to gas compression which is reflected in the curved upwards regime in the numerical F–Δc curve. Surface energy is zero in this panel reflecting the assumption of zero surface tension and implying that the lipid monolayer fully covers the gaseous phase. This assumption is valid, especially for MBs with small size, where higher packing of lipids can be reached. Measurements of the surface tension for such type of MBs also suggest very small values.52,53 The profiles of the disjoining pressure are plotted as function of the radial coordinate σ in Fig. 8(b), for three indicative solutions at Δc = 77, 200 and 400 nm. The growth of the contact region near the north pole of the MB, σ = 0, in response to the movement of the cantilever results in an increase of the total force. The profile of the disjoining pressure resembles that of a point load placed at the pole region and is gradually displaced as the cantilever further squeezes the shell. Most of the loading is concentrated around the transition region, while at the contact area the disjoining pressure assumes lower values since the liquid film thickness increases tending to the characteristic length δA. This is a typical evolution of the disjoining pressure when the f–d curve follows the Reissner regime, Fig. 4(b). However, upon extending the simulation towards even higher deformations the disjoining pressure around the contact area is seen to form a plateau, indicating a slow thinning of the liquid film in response to the significant increase of the internal pressure,31 panel Fig. 8(b), in response to the increased repulsion from the cantilever. The contribution of the contact region in the total force is also evident in the nearly cubic increase with increasing deformation, Fig. 7(a and b), that reflects the O(Δ/R0)2 growth of pressure in that region.31 The plateau is followed by a local maximum in the disjoining pressure at the edge of the transition region,31 followed by a smooth attenuation towards the equator region, indicating the importance of the transition region in connecting the contact region with the outer shell where the loading is absent. Moreover, in the simulations portrayed in Fig. 7 and 8 the flat cantilever and substrate surfaces are characterized by the same properties (W0,δA) of the interaction potential. Therefore the two profiles must be symmetric for the same deformation and this is indeed reflected in the numerically obtained profiles of the disjoining pressure.
In the same context, Abou-Saleh et al.29 investigated the response of lipid MBs using the afm in an extensive range of deformations. They studied the effect of adding an extra functional coating on the mechanical response, where they measure a significant increase of the shell stiffness. The F–Δc curve of phospholipid MBs without extra coating follows the pattern previously described i.e. initially linear and at higher deformations curved upwards. Proceeding in the same manner as in the analysis of the Buchner Santos et al.28 curves, we employ the analytical models pertaining to the linear Reissner regime, eqn (13), and the ensuing nonlinear regime, eqn (16b), to extract the area dilatation and bending moduli, see also Fig. 9(a). Indeed, upon combining the Reissner with the non-linear regime, we calculate for the area dilatation modulus χ = 7.7 × 10−3 N m−1 and the bending modulus kb = 1.76 × 10−15 N m. Then, we employ the numerical model with the calculated elastic parameters and as can be gleaned from Fig. 9(b) the experimental and the numerical curves are in excellent agreement. In a similar fashion as in the simulations portrayed in Fig. 7, the deformed shape remains flattened for all deformations around the two pole regions where a progressively longer contact area is formed as the deformation increases, Fig. 9(c–e). It should also be stressed that in order to apply the Reissner relation, eqn (13a), the deformation Δ of the single pole must be employed corresponding to one half the displacement of the cantilever, Δc, reported in ref. 28 and 29, since the latter incorporates the deformation of both poles. The energy distribution and disjoining pressure profiles were also monitored in this case. However, they are not shown as they exhibit the same behavior as in the simulations pertaining to the afm measurements in ref. 28.
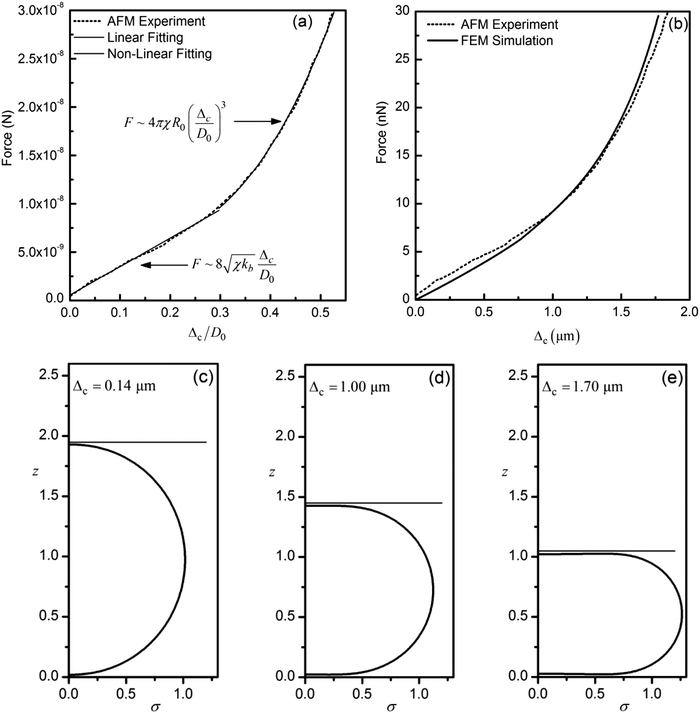 | ||
Fig. 9 (a) Force as function of dimensionless deformation by Abou-Saleh et al.29 for a MB covered with phospholipid and D0 = 3.5 μm, solid lines describe linear and non-linear fitting. (b) Comparison of experimental and numerical F–Δ curves, the simulation parameters are: R0 = 1.75 μm, χ = 7.7 × 10−3 N m−1, kb = 1.76 × 10−15 N m, ν = 0.5, γBW = 0 N m−1, W0 = 10−4 N m−1 and δA = 50 nm, Mooney–Rivlin law. The dimensionless numbers are ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 7.5 × 10−2, b = 7.5 × 10−2, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 2.3, Ŵ0 = 1.3 × 10−2 and A = 2.3, Ŵ0 = 1.3 × 10−2 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. (c–e) Shape of the deformed MB for three indicative solutions at deformation Δc = 0.14, 1.00 and 1.70 μm, the substrate is located at the origin of the axis and the cantilever is depicted with a horizontal line at the upper part of the MB. BW = 0. (c–e) Shape of the deformed MB for three indicative solutions at deformation Δc = 0.14, 1.00 and 1.70 μm, the substrate is located at the origin of the axis and the cantilever is depicted with a horizontal line at the upper part of the MB. | ||
C. Capsules with constant volume (![[P with combining circumflex]](https://www.rsc.org/images/entities/h3_i_char_0050_0302.gif) A → ∞)
A → ∞)
In this subsection simulations with our methodology are presented and compared against experimental data for monodisperse melamine formaldehyde (MF)22,24 and polydisperse poly-DL-lactic acid (PLA)22 shells using the afm22 and a micromanipulation rig.24 In both cases the shell contains an incompressible liquid instead of a gas and consequently the interrogated particles are referred to as microcapsules rather than microbubbles. One of the central aspects of the modeling of such capsules is the assumption of negligible drainage of water through the shell, which implies that the total volume remains constant. Therefore, in order to investigate the validity of the assumption of an impermeable shell and facilitate/validate the parameter estimation process, we perform simulations assuming constant volume for the PLA,22 and MF capsules.22,24
Afm measurements on PLA capsules22 exhibit a curved upwards regime in the f–d curve without an initial linear regime. Subsequent fitting of the experimental data on a theoretical expression that consists of an initial (Δ/R0)0.5 nonlinear regime where bending and stretching balance each other and a cubic rule, eqn (16b), an estimate was obtained for the Young's modulus of these capsules that is on the order of E ≈ 1 MPa, for an a priori known shell thickness h ≈ 20 nm based on the number of polyectrolyte bilayers and a typical bilayer thickness of 4 nm.22 Simulations performed in the context of the present study with the above shell parameter estimates recover the response pattern of the afm measurements as long as the deformation remains relatively small, Δ/R0 ≤ 0.2, thus identifying the limit of validity of the constant volume formulation. In particular, as can be gleaned from the f/d curve portrayed in Fig. 10(a), the numerical results obtained with the present methodology are in excellent agreement with the experimental curves,22 indicating a pronounced cubic curved upwards response pattern at the outset of the simulation, for both sizes that were interrogated. Thus, the force required to obtain large deformations was seen to increase significantly due to the dominant resistance to compression of the enclosed liquid that is a result of the requirement for constant volume. As was discussed in Section II-B in the context of eqn (17), this reflects the dominant contribution to the repulsive force on the shell from the contact region and affects the nature of the f–d curve which now exhibits an O(Δ/R0)3 dependence of the force on the shell deformation at the north pole. This is particularly so for the large capsules, Fig. 10(a), for which the bending resistance is less important hence the resistance to bending is not significant, and we can recover the above Young modulus value, E ≈ 1 MPa, via application of the cubic rule described by eqn (16b) on the afm curve. In fact, eqn (17) that contains the contribution of the contact and transition regions in the total force as the sum of the Reissner and cubic terms, can be used to describe the static response pattern of constant volume capsules. In the cases shown in Fig. 10(a) bending resistance is subdominant to stretching, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b is 2.8 × 10−6 and 1.1 × 10−5 and
b is 2.8 × 10−6 and 1.1 × 10−5 and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A is 20 and 10 when the radius of the shell R0 is 5 μm and 2 μm respectively, hence the Reissner term is subdominant in eqn (17). This is the type of behavior that was predicted in our previous theoretical/numerical study31 for capsules with very large resistance to compression, large
A is 20 and 10 when the radius of the shell R0 is 5 μm and 2 μm respectively, hence the Reissner term is subdominant in eqn (17). This is the type of behavior that was predicted in our previous theoretical/numerical study31 for capsules with very large resistance to compression, large ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A, that do not exhibit a marked Reissner regime in their f–d curves. Consequently, it is in agreement with the model proposed by Lulevich et al.,22 that accounts for the cubic nonlinearity but assumes a (Δ/R0)0.5 dependence in the initial part of the f–d curve instead of the linear Reissner regime, since it is the cubic part that provides the dominant contribution to the force.
A, that do not exhibit a marked Reissner regime in their f–d curves. Consequently, it is in agreement with the model proposed by Lulevich et al.,22 that accounts for the cubic nonlinearity but assumes a (Δ/R0)0.5 dependence in the initial part of the f–d curve instead of the linear Reissner regime, since it is the cubic part that provides the dominant contribution to the force.
 | ||
Fig. 10 (a) Comparison of experimental and numerical F–Δc curves assuming constant volume for two PLA capsules with R0 = 5 μm and R0 = 2 μm; (b and c) shape of the deformed capsule as obtained by simulations for R0 = 5 μm, when Δc/D0 = 0.1 and Δc/D0 = 0.2, respectively; (d) dimensionless disjoining pressure profiles ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) as function of the radial coordinate σ; (e) dimensionless energy components Ŵi as function of the dimensionless deformation Δc/D0, Simulation parameters for solid curve: R0 = 5 μm, E = 1 MPa, h = 25 nm, ν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, neo-Hookean law and the dimensionless numbers: as function of the radial coordinate σ; (e) dimensionless energy components Ŵi as function of the dimensionless deformation Δc/D0, Simulation parameters for solid curve: R0 = 5 μm, E = 1 MPa, h = 25 nm, ν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, neo-Hookean law and the dimensionless numbers: ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 2.78 × 10−6, b = 2.78 × 10−6, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 20, Ŵ0 = 4 × 10−4 and A = 20, Ŵ0 = 4 × 10−4 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. Simulation parameters for dashed curve: R0 = 2 μm, E = 1 MPa, h = 20 nm, ν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, neo-Hookean law and the dimensionless numbers: BW = 0. Simulation parameters for dashed curve: R0 = 2 μm, E = 1 MPa, h = 20 nm, ν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, neo-Hookean law and the dimensionless numbers: ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 1.1 × 10−5, b = 1.1 × 10−5, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 10, Ŵ0 = 5 × 10−4 and A = 10, Ŵ0 = 5 × 10−4 and ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) BW = 0. The experimental curves were obtained by Lulevich et al.22 BW = 0. The experimental curves were obtained by Lulevich et al.22 | ||
It should also be noted that based on the experimentally reported f–d curves the larger capsule, (R0 = 5 μm), is susceptible to instabilities, especially at high deformations. This might indicate collapse of the shell followed by water drainage, or it might also reflect the onset of elastoplastic buckling23,26 or creep displacement which are effects that are not accounted for in the shell model employed here. The evolution of the deformed shape of the capsule as the external force increases is illustrated in Fig. 10(b and c), where the upper contact area is seen to follow very smoothly the curvature of the rigid sphere that constitutes the tip of the cantilever, while the lower contact area remains flat. This type of deformation cannot be characterized as buckling of the upper contact area, because it is not the result of compressive stresses. Rather it resembles the gradual evolution of an indentation process affected by the cantilever tip onto the elastic shell surface. The slight asymmetry in the capsule shape at the two poles shown in panels Fig. 10(b and c) is a result of the spherical tip of the cantilever. Nevertheless, the radius of the glass sphere is much larger, in comparison with the capsule radius, and consequently its curvature does not introduce a significant discrepancy in comparison with the response of a plane cantilever or substrate. The slight asymmetry in the arrangement of the interrogated capsules is better visualized by plotting the profile of the disjoining pressure, panel Fig. 10(d), which exhibits plateau in its distribution along the contact area. Furthermore, due to the very large resistance to gas compression effected by the condition for constant volume, the internal pressure increases significantly as the force increases. This is illustrated by the gradually intensifying plateau in the contact region, Fig. 10(d), and the nonlinear behavior in the f–d curve, especially for large shells, that can be used to recover the area dilatation modulus as was shown above. Finally, the evolution of the solution is registered in terms of the energies that constitute the static equilibrium, Fig. 10(e), and it is seen that, for the parameter range considered pertaining to an incompressible liquid, most of the energy is due to stretching of the shell while bending is negligible.
Next, the simulation is repeated for the case of melamine formaldehyde (MF) capsules that were tested by Lulevich et al.22 and Mercade-Prieto et al.24 In both cases the response differs from the above described measurements with PLA shells since the shell possesses a larger bending resistance, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 1.1 × 10−5 and 4.8 × 10−4, respectively. In particular, in the measurements reported by Mercade-Prieto et al.24 using micromanipulation and compression of the microcapsules between two rigid flat surfaces, the initial linear – Reissner-part of the response is present in the small deformations regime of the experimental f–d curve, thus reflecting the balance between bending and stretching in the transition region of the shell, Fig. 3(a), before the curved upwards pattern is captured that was identified as the dominant force component for PLA shells. In this context, the importance of a simplified model for the approximation of the f–d curves of such capsules, as the one provided by eqn (17) of the present study, was pointed out. Simulations were also performed in the same study using ABAQUS and fitting was performed on the numerical data using an expression that contained linear and quadratic terms in the deformation. In this fashion, estimates were obtained of the shell shear modulus and thickness on the order of E = 1.17 GPa and h = 290 nm for microcapsules with rest radius on the order of R0 = 4.4 μm.
b = 1.1 × 10−5 and 4.8 × 10−4, respectively. In particular, in the measurements reported by Mercade-Prieto et al.24 using micromanipulation and compression of the microcapsules between two rigid flat surfaces, the initial linear – Reissner-part of the response is present in the small deformations regime of the experimental f–d curve, thus reflecting the balance between bending and stretching in the transition region of the shell, Fig. 3(a), before the curved upwards pattern is captured that was identified as the dominant force component for PLA shells. In this context, the importance of a simplified model for the approximation of the f–d curves of such capsules, as the one provided by eqn (17) of the present study, was pointed out. Simulations were also performed in the same study using ABAQUS and fitting was performed on the numerical data using an expression that contained linear and quadratic terms in the deformation. In this fashion, estimates were obtained of the shell shear modulus and thickness on the order of E = 1.17 GPa and h = 290 nm for microcapsules with rest radius on the order of R0 = 4.4 μm.
In the present study eqn (17) was employed to provide estimates of the shell elastic parameters by using the linear and cubic part of the static response curve in the manner described in the Section II-B. Thus, parameter values of the same order of magnitude were obtained with the ones provided in ref. 24, i.e. E = 0.36 GPa and h = 490 nm. Using the two available sets of shell parameters simulations were performed with the methodology proposed in the present study. It was thus seen that using the parameter estimates provided in ref. 24 fully recovers simulations performed with ABAQUS in the latter study while excellent agreement is obtained with the experimental data in both the linear and nonlinear parts of the f–d curve, Fig. 11(a). The shell is seen to progressively acquire more elongated shapes along the equator without buckling taking place, panel Fig. 11(b). This is a result of the incompressible nature of water enclosed in the shell that does not allow for bending to take place in the pole region as that would cause an abrupt volume reduction. Instead the contact region elongates to accommodate the additional energy provided by the interaction with the cantilever, panel Fig. 11(b). Furthermore, due to the larger bending resistance of MF shells, there is an identifiable linear part in the f–d curve where the linear Reissner regime holds before nonlinearity sets in. In fact, the numerical f–d curve obtained with the estimates provided upon applying the linear and cubic part of eqn (17) on the experimental f–d curve, accurately captures the linear regime while underestimating the force required to generate larger deformations since it ignores an intermediate quadratic part that follows the initial Reissner regime, before cubic effects dominate the static response, and consequently underestimates the Young's modulus E. Nevertheless, simulations with the parameter estimates obtained via the combination of linear and nonlinear regime incorporated in eqn (17), provide an overall accurate description of the experimental f–d curve and recover the aspects of the deformed shell illustrated in panels Fig. 11(b–d) for the same deformation. Subsequent improvement of the parameter estimates is possible by increasing the Young's modulus while reducing the shell thickness, in order to maintain the slope of the initial Reissner regime that is ∼Eh2, see also eqn (13a). In this manner excursions from the experimental f–d curve are minimized and the parameter estimates proposed in ref. 24 are recovered.
 | ||
Fig. 11 (a) Comparison of experimental and numerical F–Δ curves assuming constant volume for an MF capsule with R0 = 4.4 μm and E = 1.17 GPa, h = 290 nm (![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 4.8 × 10−4, b = 4.8 × 10−4, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 1.3 × 10−3), E = 0.36 GPa, h = 490 nm ( A = 1.3 × 10−3), E = 0.36 GPa, h = 490 nm (![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b = 1.4 × 10−3, b = 1.4 × 10−3, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A = 2.4 × 10−3), depicted with a solid and dashed line respectively; the rest of the simulation parameters areν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, for a shell obeying the neo-Hookean law. The experimental curve was obtained by Mercade-Prieto et al.24 (b) Shape of the deformed capsule, (c) dimensionless disjoining pressure profiles A = 2.4 × 10−3), depicted with a solid and dashed line respectively; the rest of the simulation parameters areν = 0.5, γBW = 0 N m−1, W0 = 10−5 N m−1 and δA = 50 nm, for a shell obeying the neo-Hookean law. The experimental curve was obtained by Mercade-Prieto et al.24 (b) Shape of the deformed capsule, (c) dimensionless disjoining pressure profiles ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) as function of the radial coordinate σ and (d) dimensionless energy components Ŵi as function of the dimensionless deformation Δc/D0, pertaining to the afm simulations depicted in the continuous f–d curve. as function of the radial coordinate σ and (d) dimensionless energy components Ŵi as function of the dimensionless deformation Δc/D0, pertaining to the afm simulations depicted in the continuous f–d curve. | ||
The absence of buckling is corroborated by plotting the disjoining pressure as the force increases, Fig. 11(c), that exhibits a point load distribution for small deformations that is indicative of the Reisner response, followed by a similar pattern with the simulations for the softer PLA capsules shown in Fig. 10(d), where the disjoining pressure forms a plateau in the contact region and gradually dominates the force exerted on the shell. Finally, the contribution to the total energy among the different stiffness components is provided in panel Fig. 11(d), indicating the dominant effect of stretching and bending resistances for small deformations. For large deformations the pattern of stretching energy dominating over bending is captured, as was also obtained in the context of our simulations with the PLA capsules depicted in Fig. 10(e).
Simulations performed in the present study in reference to the afm measurements by Lulevich et al.22 with MF capsules, using an average value for shell elasticity, E = 100 MPa, exhibit a very similar behavior with the simulations portrayed in Fig. 11 in the context of the experiments by Mercade-Prieto et al.;24 small ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A. However, it should be stressed that the response pattern in the experimental curve of the former study indicates rupture of the shell and water drainage at not very large deformations, as the authors of the latter study point out. Even though the present model does not predict rupture or any other kind of collapse it should be noted that the simulations break at around Δc/D0 > 0.25 due to inaccuracies in the calculation of the disjoining pressure distribution. It is conjectured that the excessive shell stretching in the two pole regions of such capsules as the external force increases, compromises the validity of the model employed since it neglects the importance of friction at the contact region. Finally, in the afm measurements reported by Mettu et al.25 where the effect of increasing temperature on the shell stiffness is investigated, the linear Reissner part in the f–d curve is also quite pronounced in view of the relatively large stiffness of the shell, E ≈ 15 MPa, and comparable resistance to compression,
A. However, it should be stressed that the response pattern in the experimental curve of the former study indicates rupture of the shell and water drainage at not very large deformations, as the authors of the latter study point out. Even though the present model does not predict rupture or any other kind of collapse it should be noted that the simulations break at around Δc/D0 > 0.25 due to inaccuracies in the calculation of the disjoining pressure distribution. It is conjectured that the excessive shell stretching in the two pole regions of such capsules as the external force increases, compromises the validity of the model employed since it neglects the importance of friction at the contact region. Finally, in the afm measurements reported by Mettu et al.25 where the effect of increasing temperature on the shell stiffness is investigated, the linear Reissner part in the f–d curve is also quite pronounced in view of the relatively large stiffness of the shell, E ≈ 15 MPa, and comparable resistance to compression, ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) A ≈ 0.2 for shell diameter and thickness on the order of 4.3 μm and 60 nm, respectively.
A ≈ 0.2 for shell diameter and thickness on the order of 4.3 μm and 60 nm, respectively.
IV. Conclusions
An extensive comparison was conducted in this study between AFM measurements of coated microbubbles (MB) and capsules and the theoretical/numerical model presented in our earlier study for the static response of MB's squeezed between two rigid flat plates. The thinning of the liquid film between the MB's coating and the cantilever results in an increase in the local pressure, known as the disjoining pressure. Employing a wall-bubble interaction potential we showed that it is possible to accurately capture force–deformation (f–d) curves of AFM experiments for a wide variety of experimental arrangements and materials and obtain reliable estimates of the bubble-shell elastic properties. In that sense it extends previous methodologies using various forms of interaction potentials for the study of free drops and bubbles subject to indentation, that mainly focused on the linear regime of the static response.Based on the assumption of axi-symmetry, valid for a wide range of deformations,51 the f–d curves pertaining to polymeric shells initially follow the linear Reissner regime, followed by a non-linear curved downwards regime (Pogorelov) that is associated with buckling around the contact area. As the external force further increases, a curved upwards regime is registered due to resistance to gas compression. The Reissner model in the linear regime with the buckling point that signals the Pogorelov regime, eqn (13a) and (15), provide the necessary information to calculate both the shell thickness and the Young modulus, based on data obtained at relatively small deformations.31 Simulations recover the static response of AFM measurements until, at higher deformations, instabilities associated with cantilever friction,49 changes in the elastic shell behavior20 or inelastic effects26 occur. Such phenomena cannot be captured by the present model, nevertheless they are not an issue in the parameter estimation of our methodology. The latter was also successfully applied on polymeric shells that coat large bubbles compressed in the open air.40,49 In this case, a purely repulsive potential was applied to properly capture the interaction between the shell and indenting cantilever with air in between, and accurately recover the shell mechanical properties.
A systematic comparison was also performed between our model and afm experiments28,29 that are available in the literature for MBs covered with soft phospholipid monolayers with significant resistance to volume compression, In these cases the typical sequence of Reissner and Pogorelov responses was not detected in the experimental or the numerical curves since buckling is bypassed and the shape around the contact area remains flattened. The area dilatation and bending moduli were estimated by combining the Reissner model and the asymptotic equation for the pressure dominated regime which is characterized by a nonlinear curved upwards response pattern,31eqn (17). The dominant force on the shell arises either in the transition or in the contact region of the shell, and reflects the balance between shell stretching and bending and between shell stretching and pressure change, respectively, in agreement with the experimental curves.28,29 This behavior strongly supports the validity of our assumption regarding MBs covered with lipid shells, namely that area dilatation and bending modulus constitute the primary independent elastic parameters.
When the shell encapsulates an incompressible liquid, buckling is not possible as well and simulations exhibit a strong curved upwards response in the f–d curves beginning from the small deformation regime when the bending stiffness is relatively unimportant, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) b ≈ 10−6, in conformity well with experimental findings.22 The f–d curves in both simulations and experiments exhibit a nearly cubic response at moderate deformations, in agreement with our previous findings31 in the parameter range for which stretching and resistance to volume compression constitute the dominant shell rigidities. In such cases the linear Reissner regime is weak and its effect is restricted in mitigating the cubic response. On employing the nonlinear estimate for the force deformation dependence, eqn (16b), we obtained reliable predictions of the area dilatation modulus. When the bending stiffness is comparable with the stretching stiffness, as for melamine formaldehyde shells,24 besides the nonlinear regime at large deformations, the linear regime is also present in the initial part of the f–d curves. Then eqn (17) constitutes a reliable first model of the response pattern that, coupled with simulations, provides optimal and accurate estimates of the Young's modulus and shell thickness.
b ≈ 10−6, in conformity well with experimental findings.22 The f–d curves in both simulations and experiments exhibit a nearly cubic response at moderate deformations, in agreement with our previous findings31 in the parameter range for which stretching and resistance to volume compression constitute the dominant shell rigidities. In such cases the linear Reissner regime is weak and its effect is restricted in mitigating the cubic response. On employing the nonlinear estimate for the force deformation dependence, eqn (16b), we obtained reliable predictions of the area dilatation modulus. When the bending stiffness is comparable with the stretching stiffness, as for melamine formaldehyde shells,24 besides the nonlinear regime at large deformations, the linear regime is also present in the initial part of the f–d curves. Then eqn (17) constitutes a reliable first model of the response pattern that, coupled with simulations, provides optimal and accurate estimates of the Young's modulus and shell thickness.
Finally, the above methodology accurately captures the contact stresses on a coated microbubble in the vicinity of a solid or flexible wall and is expected to assist the modeling of the trapping process of chemically modulated shells for the purpose of attaching them to specific substrates via application of ultrasound. In this fashion, the impact of intermolecular forces on the dynamic aspects of the wall-interaction and the resulting resonance frequencies and shell break-up threshold, will be essential for the control of trapped bubble pulsations near a substrate and the design of novel drug delivery protocols.
Conflicts of interest
There are no conflicts to declare.Appendix A: derivation of minimum distance between the MB and a cantilever
The liquid film thickness, which is incorporated in the interaction potential and the disjoining pressure, is defined as the minimum distance between the two surfaces, e.g. the cantilever and the microbubble or the substrate and the microbubble. When a flat cantilever is considered, Fig. 1(a), the minimum distance is:| δ = zCS − z, | (A-1) |
| δ = z, | (A-2) |
However, for a spherical cantilever or a cantilever with more complex geometry the minimum distance is defined by the Euclidean norm. We now present a methodology for calculating the disjoining pressure when the cantilever interacting with the shell is not flat and possesses a tip, e.g. a spherical tip as in the experiments reported in the literature of afm measurements.17,22,34 We consider a global cylindrical coordinated system (σ,z) with its origin located at the intersection between the axis of symmetry and the substrate plane. Then, the axial position of the cantilever is described as a known function of the cantilever radial coordinate σc:
| zc = f(σc), | (A-3) |
 . The point (σc,zc) on the cantilever surface that corresponds to the minimum distance from a point on the shell interface, lies on the line that is vertical at that point and connects the (σc,zc) with (σ,z), which can be mathematically described by the following relation
. The point (σc,zc) on the cantilever surface that corresponds to the minimum distance from a point on the shell interface, lies on the line that is vertical at that point and connects the (σc,zc) with (σ,z), which can be mathematically described by the following relation| (z − zc)zc′ + σ − σc = 0, | (A-4) |
 is the slope of the tangent at the point (σc,zc). Therefore, solving the system of eqn (A-1) and (A-2), the coordinates of the cantilever are calculated, where for a spherical cantilever we obtain:
is the slope of the tangent at the point (σc,zc). Therefore, solving the system of eqn (A-1) and (A-2), the coordinates of the cantilever are calculated, where for a spherical cantilever we obtain: | (A-5a,b) |
 | (A-6) |
Then the disjoining pressure can be calculated as:
 | (A-7a,b) |
 is easily calculated by differentiation of the interaction potential, while for the rest of partial derivatives further calculations are required taking into account the definition of the outwards pointing normal vector on the shell surface, Fig. 12. In particular, differentiation of eqn (A-6) with respect to radial and axial coordinates gives:
is easily calculated by differentiation of the interaction potential, while for the rest of partial derivatives further calculations are required taking into account the definition of the outwards pointing normal vector on the shell surface, Fig. 12. In particular, differentiation of eqn (A-6) with respect to radial and axial coordinates gives: | (A-8a,b) |
 | (A-8c,d) |
 | (A-9a,b) |
 | (A-9c,d) |
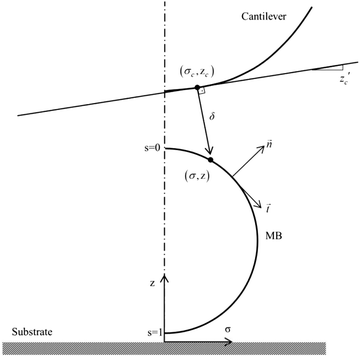 | ||
| Fig. 12 Minimum distance between a point on the shell surface and a cantilever of an arbitrary shape. | ||
Acknowledgements
A. Lytra, N. Pelekasis, V. Sboros and A. Giannakopoulos wish to acknowledge financial support from the operational program “Education and lifelong learning”-“Aristeia” (MIS 372620) via the “CONTAGEUSNUMSTADY” project, which was cofounded by the European Union (European Social Fund) and the Greek Ministry of Education (Grant Number: 2012SE01380000). V. Sboros also wishes to acknowledge financial support from the British Heart Found UK project grant (PG/10/021/28254) “Exploiting the understanding of the behaviour of microbubble contrast agents for improved microvascular imaging”.References
- B. A. Kaufmann, K. Wei and J. R. Lindner, Contrast Echocardiography, Curr. Prob. Cardiol., 2007, 32, 51 CrossRef PubMed.
- A. Stanziola, M. Toulemonde, Y. O. Yildiz, R. J. Eckersley and M. X. Tang, Ultrasound Imaging with Microbubbles [Life Sciences], IEEE Signal Process. Mag., 2016, 33, 111 Search PubMed.
- K. Ferrara, R. Pollard and M. Borden, Ultrasound Microbubble Contrast Agents: Fundamentals and Application to Gene and Drug Delivery, Annu. Rev. Biomed. Eng., 2007, 9, 415 CrossRef CAS PubMed.
- K. Kooiman, H. J. Vos, M. Versluis and N. de Jong, Acoustic behavior of microbubbles and implications for drug delivery, Adv. Drug Delivery Rev., 2014, 72, 28 CrossRef CAS PubMed.
- V. Sboros and M.-X. Tang, The assessment of microvascular flow and tissue perfusion using ultrasound imaging, Proc. Inst. Mech. Eng., Part H, 2010, 224(H2), 273–290 CrossRef CAS PubMed.
- G. Ferraioli and M. F. Meloni, Contrast-enhanced ultrasonography of the liver using SonoVue, Ultrasonography, 2018, 37, 25 CrossRef PubMed.
- P. Song, J. D. Trzasko, A. Manduca, R. Huang, R. Kadirvel, D. F. Kallmes and S. Chen, Improved Super-Resolution Ultrasound Microvessel Imaging with Spatiotemporal Nonlocal Means Filtering and Bipartite Graph-Based Microbubble Tracking, IEEE Trans. Ultrason. Eng., 2018, 65, 149 Search PubMed.
- M. Toulemonde, W. C. Duncan, C. H. Leow, V. Sboros, Y. Li, R. J. Eckersley, S. Lin, M. X. Tang and M. Butler, Cardiac flow mapping using high frame rate diverging wave contrast enhanced ultrasound and image tracking, 2017 Search PubMed.
- S. Kotopoulis, G. Dimcevski, O. Helge Gilja, D. Hoem and M. Postema, Treatment of human pancreatic cancer using combined ultrasound, microbubbles, and gemcitabine: A clinical case study, Med. Phys., 2013, 40, 072902 CrossRef PubMed.
- C. Sierra, C. Acosta, C. Chen, S. Y. Wu, M. E. Karakatsani, M. Bernal and E. E. Konofagou, Lipid microbubbles as a vehicle for targeted drug delivery using focused ultrasound-induced blood–brain barrier opening, J. Cerebr. Blood Flow Metabol., 2017, 37(4), 1236 CrossRef CAS PubMed.
- K. Tsiglifis and N. A. Pelekasis, Nonlinear radial oscillations of encapsulated microbubbles subject to ultrasound: The effect of membrane constitutive law, J. Acoust. Soc. Am., 2008, 123, 4059 CrossRef CAS PubMed.
- D. H. Thomas, P. Looney, R. Steel, N. Pelekasis, W. N. McDicken, T. Anderson and V. Sboros, Acoustic detection of microbubble resonance, Appl. Phys. Lett., 2009, 94, 243902 CrossRef.
- K. Efthymiou, N. Pelekasis, M. B. Butler, D. H. Thomas and V. Sboros, The effect of resonance on transient microbubble acoustic response: Experimental observations and numerical simulations, J. Acoust. Soc. Am., 2018, 143, 1392 CrossRef CAS PubMed.
- V. Sboros, Response of contrast agents to ultrasound, Adv. Drug Delivery Rev., 2008, 60, 1117 CrossRef CAS PubMed.
- H. Hertz and J. Reine, Angew. Math., 1882, 92, 156–171 Search PubMed.
- E. Reissner, Stresses and Small Displacements of Shallow Spherical Shells. II, J. Math. Phys., 1946, 25, 279 CrossRef.
- J. D. Berry, S. Mettu and R. R. Dagastine, Precise measurements of capsule mechanical properties using indentation, Soft Matter, 2017, 13(10), 1943–1947 RSC.
- M. Glaubitz, N. Medvedev, D. Pussak, L. Hartmann, S. Schmidt, C. A. Helm and M. Delcea, Soft Matter, 2014, 10, 6732–6741 RSC.
- F. Dubreuil, N. Elsner and A. Fery, Elastic properties of polyelectrolyte capsules studied by atomic-force microscopy and RICM, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 215 CrossRef CAS PubMed.
- N. Elsner, F. Dubreuil, R. Weinkamer, M. Wasicek, F. D. Fischer and A. Fery, Mechanical Properties of Freestanding Polyelectrolyte Capsules: a Quantitative Approach Based on Shell Theory, Springer Berlin, Heidelberg, 2006 Search PubMed.
- A. V. Pogorelov, Bendings of Surfaces and Stability of Shells, American Mathematical Society, 1988 Search PubMed.
- V. V. Lulevich, D. Andrienko and O. I. Vinogradova, Elasticity of polyelectrolyte multilayer microcapsules, J. Chem. Phys., 2004, 120, 3822 CrossRef CAS PubMed.
- R. Mercadé-Prieto, R. Allen, D. York, J. A. Preece, T. E. Goodwin and Z. Zhang, Compression of elastic–perfectly plastic microcapsules using micromanipulation and finite element modeling: Determination of the yield stress, Chem. Eng. Sci., 2011, 66, 1835 CrossRef.
- R. Mercadé-Prieto, B. Nguyen, R. Allen, D. York, J. A. Preece, T. E. Goodwin and Z. Zhang, Determination of the elastic properties of single microcapsules using micromanipulation and finite element modeling, Chem. Eng. Sci., 2011, 66, 2042 CrossRef.
- S. Mettu, M. Zhou, B. L. Tardy, M. Ashokkumar and R. R. Dagastine, Temperature dependent mechanical properties of air, oil and water filled microcapsules studied by atomic force microscopy, Polymer, 2016, 102, 333–341 CrossRef CAS.
- E. Glynos, V. Koutsos, W. N. McDicken, C. M. Moran, S. D. Pye, J. A. Ross and V. Sboros, Nanomechanics of Biocompatible Hollow Thin-Shell Polymer Microspheres, Langmuir, 2009, 25, 7514 CrossRef CAS PubMed.
- A. Lytra, N. Pelekasis, V. Sboros, E. Glynos and V. Koutsos, Static Response of Coated Microbubbles: Modeling Simulations and Parameter Estimation, Proc. IUTAM, 2015, 16, 123 CrossRef.
- E. Buchner Santos, J. K. Morris, E. Glynos, V. Sboros and V. Koutsos, Nanomechanical Properties of Phospholipid Microbubbles, Langmuir, 2012, 28, 5753 CrossRef CAS PubMed.
- R. H. Abou-Saleh, S. A. Peyman, K. Critchley, S. D. Evans and N. H. Thomson, Nanomechanics of Lipid Encapsulated Microbubbles with Functional Coatings, Langmuir, 2013, 29, 4096 CrossRef CAS PubMed.
- P. D. Zarda, S. Chien and R. Skalak, Elastic deformations of red bloodcells, J. Biomech., 1977, 10(4), 211–221 CrossRef CAS PubMed.
- A. Lytra and N. Pelekasis, Static response of coated microbubbles compressed between rigid plates: Simulations and asymptotic analysis including elastic and adhesive forces, Phys. Fluids, 2018, 30, 030711 CrossRef.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier Science, 2010 Search PubMed.
- D. E. Aston and J. C. Berg, Quantitative Analysis of Fluid Interface-Atomic Force Microscopy, J. Colloid Interface Sci., 2001, 235(1), 162–169 CrossRef CAS PubMed.
- D. Bhatt, J. Newman and C. J. Radke, Equilibrium Force Isotherms of a Deformable Bubble/Drop Interacting with a Solid Particle across a Thin Liquid Film, Langmuir, 2001, 17(1), 116–130 CrossRef CAS.
- R. F. Tabor, F. Grieser, R. R. Dagastine and D. Y. C. Chan, Measurement and analysis of forces in bubble and droplet systems using AFM, J. Colloid Interface Sci., 2012, 371(1), 1–14 CrossRef CAS PubMed.
- C. Shi, X. Cui, L. Xie, Q. X. Liu, D. Y. C. Chan, J. N. Israelachvili and H. B. Zeng, Measuring Forces and Spatiotemporal Evolution of Thin Water Films between an Air Bubble and Solid Surfaces of Different Hydrophobicity, ACS Nano, 2015, 9(1), 95–104 CrossRef CAS PubMed.
- L. Xie, C. Shi, X. Cui and H. Zeng, Surface Forces and Interaction Mechanisms of Emulsion Drops and Gas Bubbles in Complex Fluids, Langmuir, 2017, 33(16), 3911–3925 CrossRef CAS PubMed.
- M. J. Blount, M. J. Miksis and S. H. Davis, The equilibria of vesicles adhered to substrates by short-ranged potentials, Proc. R. Soc. London, Ser. A, 2013, 469 DOI:10.1098/rspa.2012.0729.
- I. Cantat, K. Kassner and C. Misbah, Vesicles in haptotaxis with hydrodynamical dissipation, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 10, 175–189, DOI:10.1140/epje/e2003-00022-1.
- R. Shorter, J. D. Smith, V. A. Coveney and J. J. C. Busfield, Axial compression of hollow elastic spheres, J. Mech. Mater. Struct., 2010, 5, 693 CrossRef.
- C. Pozrikidis, Modeling and Simulation of Capsules and Biological Cells, Taylor & Francis, 2003 Search PubMed.
- D. Barthès-Biesel, A. Diaz and E. Dhenin, Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation, J. Fluid Mech., 2002, 460, 211 CrossRef.
- S. Timoshenko and S. Woinowsky-Krieger, Theory of plates and shells, McGraw-Hill, 1959 Search PubMed.
- P. Marmottant, A. Bouakaz, N. d. Jong and C. Quilliet, Buckling resistance of solid shell bubbles under ultrasound, J. Acoust. Soc. Am., 2011, 129, 1231 CrossRef PubMed.
- K. Tsiglifis and N. A. Pelekasis, Parametric stability and dynamic buckling of an encapsulated microbubble subject to acoustic disturbances, Phys. Fluids, 2011, 23, 012102 CrossRef.
- A. Lytra, Numerical & theoretical study of the static response of coated microbubbles subject to uniform and distributed load: application on the estimation of the shell elastic properties, PhD thesis, University of Thessaly, 2017, http://thesis.ekt.gr/thesisBookReader/id/40137#page/1/mode/2up Search PubMed.
- K. Tsiglifis and N. Pelekasis, Dynamic simulations of insonated contrast agents, Phys. Fluids, 2013, 25, 032109 CrossRef.
- P. M. Prenter, Splines and Variational Methods, Wiley, 1975 Search PubMed.
- D. P. Updike and A. Kalnins, Axisymmetric Postbuckling and Nonsymmetric Buckling of a Spherical Shell Compressed Between Rigid Plates, J. Appl. Mech., 1972, 39, 172 CrossRef.
- T. Ottoboni, E. Tickner, R. Short and R. Yamamoto, Hollow microspheres with controlled fragility for medical use, US 6776761B2, 2004 Search PubMed.
- A. Vaziri, Mechanics of highly deformed elastic shells, Thin Wall Struct., 2009, 47, 692 CrossRef.
- T. Segers, L. de Rond, N. de Jong, M. Borden and M. Versluis, Stability of Monodisperse Phospholipid-Coated Microbubbles Formed by Flow-Focusing at High Production Rates, Langmuir, 2016, 32, 3937 CrossRef CAS PubMed.
- F. Jähnig, What is the surface tension of a lipid bilayer membrane?, Biophys. J., 1996, 71, 1348 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |


![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif)

