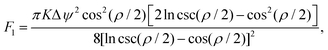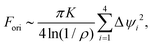DOI:
10.1039/D0SM00166J
(Paper)
Soft Matter, 2020,
16, 4682-4691
A theoretical phase diagram for an active nematic on a spherical surface
Received
29th January 2020
, Accepted 26th April 2020
First published on 11th May 2020
Abstract
Systems combining rod-shaped objects with self-generated motion such as suspensions of microtubules or growing bacterial colonies are commonly modeled as active nematics – nematic liquid crystals with an additional active stress term. Confining a 2D active nematic to the surface of a sphere generates novel behaviour as the four +1/2 nematic defects which are produced by the spherical geometry move round each other in an intricate dance. Here, these defects are modeled as point particles experiencing elastic forces from defect position and orientation, and self-propulsion due to activity. This model exhibits four qualitatively distinct types of trajectory state: two which are consistent with previous experimental and simulated trajectories; and two others, which are apparently novel and in regions of parameter space that may not yet have been explored. This work also explains a discrepancy between some previous point-particle models and the trajectories seen in experiments and simulations: this was due to a failure to fully account for the spherical geometry in the point-particle models.
I. Introduction
Interactions between topology and dynamics supply beautiful, useful and often non-intuitive phenomena across a wide range of scientific disciplines. Examples include the Kosterlitz–Thouless transition in solid-state physics,1 the dependence of DNA replication dynamics on its topological state,2 and the complex topological remodelling and inversions involved in embryogenesis or the growth of microorganism colonies.3
Recently, a synthetic experimental system has been developed that combines a topologically rich material, liquid crystals, with active motion provided by biological molecular motors, which offers an exciting arena for studying these dynamic topological effects. This system consists of suspensions of cytoskeletal filaments and motor-proteins.4–7 The filaments align to form bundles, gaining nematic order, and the molecular motors produce stresses between the filaments that then drive flow of the suspension.
This system has been applied to investigations of a wide range of novel phenomena.8 Initial work on bulk samples showed that the activity produces pairs of ±1/2 nematic defects, which then produce swirling motion over multiple lengthscales in a phenomenon described as ‘active turbulence’.5 Subsequent papers explored, e.g., nematic alignment of the defects themselves over longer length scales,6 the control of active nematics with magnetic fields,9 or active droplets with a surrounding passive nematic phase, where the active nematic distorts and interacts with the normal nematic disclinations in the passive phase.10
A second way to generate defects is to apply a topological constraint to the system. In particular, on the surface of a sphere,11 a total topological charge of +2 is required, a configuration which is achieved most favourably by four +1/2 defects.12 Due to their fore-aft asymmetry, these +1/2 defects then self-propel in the flow field they generate. Combined with elastic interactions between the defects, this produces a complex and coordinated dance where the defects oscillate between tetrahedral and great-circle configurations.11 Several models have since reproduced this oscillatory behaviour,11,13–16 but in doing so they predict at least three qualitatively different categories of defect trajectory. Presumably at most one of these corresponds to the experimental reality. One of the main aims of this paper is to determine to what extent all these different phenomena can be synthesized in a single theoretical framework, or whether some of the calculated defect trajectories are non-physical.
To this end, I develop here a coarse-grained, defect-level model, as in ref. 11, 14 and 15. This model can be parameterised just in terms of the defect self-propulsion speed and a defect reorientation time. Exploring the parameter space of this model then yields four distinct categories of defect trajectory. Two of these agree with trajectories obtained in two separate previous models,14,16 indicating that these models were simply exploring different regions of parameter space. The two other trajectory types, with either 2 or 4 co-rotating circles, have, to my knowledge, not been previously observed or predicted. On the other hand, counter-rotating circles, that have been predicted previously,11,15 are not predicted here: I show that these are indeed non-physical artefacts of a failure to fully account for the spherical geometry of the surface.
The paper is arranged as follows: in Section II I develop the coarse-grained model. In Section III I catagorise the various defect trajectories this model produces, and generate a numerical phase diagram. All these trajectories have a higher symmetry than the original system (fewer degrees of freedom), and in Section IV I am therefore next able to write down much simpler equations describing their dynamics, and apply linear stability analysis to reproduce the phase boundaries obtained numerically. In Section V I compare my results with those of previous models and in Section VI I discuss the implications for future theoretical and experimental work.
II. A point-particle model
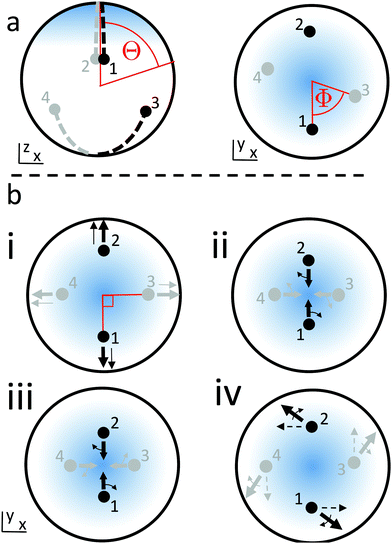
To introduce the model briefly: the only entities in the final model are 4 +1/2 nematic defects that move on the surface of a sphere. Other features of the sphere, i.e., the nematic director field and flow field, are taken into account as effective interactions between the defects. This results in three types of interaction: the defects repel each other spatially; they align or anti-align their axes of symmetry; and they self-propel, see Fig. 1a. The trajectories of the defects are then determined by the stiffness of the spatial and orientational interaction potentials; by the self-propulsion speed; and by friction coefficients associated with relaxation of the various degrees of freedom. The model is developed from several previous analytic treatments of the problem11,14,15 which themselves are built on the mature theory of passive nematics.8,17
 |
| | Fig. 1 (a) Schematic of the contributions to the dynamics for two defects interacting via the elastic energy, giving repulsion and alignment (red), and self-propelling along their axes (black). The nematic director field is indicated in blue. (b) Diagram of the spherical coordinate system discussed in the text. Orientations are defined for defect 1. Defects on the near or far hemisphere are shown with solid or hollow circles, respectively. | |
A. Elastic energy of the nematic texture
I model an active nematic on the surface of a sphere of radius R with four +1/2 defects. Each defect has a typical core radius rc ≪ R, within which the usual nematic order is lost. Outside these four, circular regions, full nematic order is assumed. On a 2D surface, the elastic energy density of a nematic director field depends on the degree and type – bend or splay – of the local curvature of the nematic director. For mathematical convenience I make use of the typical single elastic constant (SEC) approximation, in which the splay K11 and bend K33 elastic constants are set equal, i.e., K11 = K33 = K. Defining the nematic director field n = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αeθ + sin
αeθ + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αeϕ with orientation angle α, the elastic energy12
αeϕ with orientation angle α, the elastic energy12| |  | (1) |
where the integral is over the defect-free subset S′ of the total spherical surface S. The defects themselves will have a different internal structure, e.g., in the microtubule-based systems the defect core is typically devoid of microtubules.8 However, these details are not taken into account at this coarse-grained level, and the defect structure is just subsumed into the constant terms.
The four defects have positions xi = R × {sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi, sin
ϕi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi, cos
ϕi, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi} defined by the polar θi and azimuthal ϕi angles of each defect, and the radius R of the sphere. Each defect has an orientation vector pi = eθi
θi} defined by the polar θi and azimuthal ϕi angles of each defect, and the radius R of the sphere. Each defect has an orientation vector pi = eθi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi + eϕi
ψi + eϕi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi, which points along the symmetry axis of the defect, see Fig. 1. Previous work12,15 has shown that, for a given set of defect positions xi, eqn (1) can be minimized with a particular director field that can be determined by a stereographic projection onto the equatorial plane. This minimizing director field is
ψi, which points along the symmetry axis of the defect, see Fig. 1. Previous work12,15 has shown that, for a given set of defect positions xi, eqn (1) can be minimized with a particular director field that can be determined by a stereographic projection onto the equatorial plane. This minimizing director field is
| | 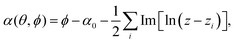 | (2) |
where
z = cot(
θ/2)e
iϕ, and
α0 is a scalar parameter (potentially time-dependent) that produces a uniform rotation of each nematogen within the local tangent plane of the sphere. The defect orientations associated with this minimizing texture, which I label
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i
i, are
| |  | (3) |
as shown in
ref. 15.
The elastic energy incurred by the minimizing director field I will refer to as the ‘positional’ part of the energy because it depends only on the defect positions. It is12
| |  | (4) |
with
βij the angular distance between defects cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βij
βij = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj
θj + sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj
θj![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
ϕi −
ϕj). Note that
α0 does not appear in
eqn (4). This is because, in the SEC approximation, the elastic energy is invariant with respect to rotations of the entire nematogen orientation field
n(
θ,
ϕ) by a constant value.
12 Whether defects are pointing towards or away from each other, or at some arbitrary angle to each other, does not affect the energy, as long as the defect orientations are coupled through
eqn (3) with some value of
α0. In other words, changing the value of
α0 merely modifies the distribution of bend and splay deformations, but, since in the SEC approximation bend and splay deformations are energetically equivalent, this does not affect the elastic energy.
However, in a dynamical system, the nematic director field, and hence the defects, will not always be in the minimum-energy configurations specified by eqn (2) and (3). To take account of this, I allow the defect orientations ψi to deviate from the equilibrium values ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i. These deviations will produce a localized additional torsion of the nematic director field, and an associated ‘orientational’ energy Fori. This orientational energy has already been calculated in the planar case,18 and I perform the analogous calculation for a spherical geometry in the appendix. To lowest order in the dimensionless defect size ρ = rc/R the result is
i. These deviations will produce a localized additional torsion of the nematic director field, and an associated ‘orientational’ energy Fori. This orientational energy has already been calculated in the planar case,18 and I perform the analogous calculation for a spherical geometry in the appendix. To lowest order in the dimensionless defect size ρ = rc/R the result is
| | 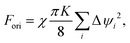 | (5) |
where Δ
ψi =
ψi −
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i
i is the deviation from the equilibrium orientation, and
χ = 2/ln(1/
ρ) is the dimensionless parameter which specifies the ratio of orientation to positional contributions. As in the planar case,
18 there is a simple quadratic dependence on the orientational deviation and a logarithmic scaling with the defect size.
B. Defect dynamics
As shown in Fig. 1b +1/2 defects have a single symmetry axis, with a ‘head’ and ‘tail’ at either end of this axis. In an active nematic, backflow causes them to self-propel either towards the head or the tail, depending on whether the activity is contractile or extensile,13 with orientation vector pi = eθi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi + eϕi
ψi + eϕi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi at some fixed speed uadv.15 As discussed above, the SEC approximation does not make a global distinction between defect heads and tails because the elastic energy is invariant w.r.t. α0, so, without loss of generality, I specify that the defects are self-propelled towards their heads, as observed in experiments on microtubules and molecular motors.11
ψi at some fixed speed uadv.15 As discussed above, the SEC approximation does not make a global distinction between defect heads and tails because the elastic energy is invariant w.r.t. α0, so, without loss of generality, I specify that the defects are self-propelled towards their heads, as observed in experiments on microtubules and molecular motors.11
The total instantaneous velocity of each defect is given by adding the elastic and self-propulsion contributions
with ∇
iF the gradient on the spherical surface of the total elastic energy
F =
Fpos +
Fori with respect to the position of the
ith defect, and
ξ a phenomenological frictional drag term.
The dynamics of the orientation angle ψi is
| |  | (7) |
where d
t indicates the time derivative and
ξrot is a phenomenological rotational friction term. Since both
ξ and
ξrot must be determined by the microscopic dynamics of the nematogens, they will not necessarily be independently variable. However, to the best of my knowledge, a detailed microscopic theory of the effective friction on defects has not yet been developed, so I have left these as free parameters in the model.
The second term in eqn (7) is necessary to account for parallel transport, i.e., the rotation of the orientation in the coordinate system of the sphere which is due to the spherical geometry itself. This term ensures that, in the absence of external torques and forces, each defect moves along a great circle, which is the physically expected result. To give a familiar analogy: if a ship at the equator is initially moving north-east, and continues to move north-east, it will trace out a spiral helix ending at the north pole, a so called loxodrome. In order instead to trace out a great circle, the compass direction of the ship, i.e., ψ, must rotate just as specified by the second term in eqn (7).
In the same way, parallel transport should produce dynamics in the equilibrium defect orientations ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i as the defects move. However, because each of these orientations is slaved to α0, independent parallel transport of each
i as the defects move. However, because each of these orientations is slaved to α0, independent parallel transport of each ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i is not possible. Instead, I apply the requirement that, in the absence of any elastic energy contribution, the equilibrium orientations should adjust so as to minimize the squared rate of change of the deviation of the orientations from their equilibrium values. In other words, the constraint on the equilibrium defect orientations should produce the minimum additional disturbance in the local environment of each defect. Mathematically, this is
i is not possible. Instead, I apply the requirement that, in the absence of any elastic energy contribution, the equilibrium orientations should adjust so as to minimize the squared rate of change of the deviation of the orientations from their equilibrium values. In other words, the constraint on the equilibrium defect orientations should produce the minimum additional disturbance in the local environment of each defect. Mathematically, this is
| |  | (8) |
where the ‖ superscript refers to the part of the motion just due to parallel transport obtained by setting the elastic energy contribution to zero. This minimum is obtained when the condition
| | 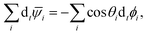 | (9) |
is met,
i.e., when the mean orientation of the equilibrium defects is rotated due to parallel transport at the same rate as the mean defect orientations themselves. By taking the time derivative of
eqn (3) and substituting this into
eqn (9) one obtains, after some algebra, dynamics for
α0 of
| |  | (10) |
where the first term comes from switching on the elastic-energy contribution again, and
ξα is another phenomenological drag constant coupled to the overall nematic field orientation
α0.
C. Non-dimensionalization
To make the system dimensionless, distances are scaled by R, energies by F0 = πK/8, velocities by u0 = πK/(8ξR), and times by t0 = R/u0. Dimensionless parameters are denoted ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ,
, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , ũ, and the two orientational friction constants become
, ũ, and the two orientational friction constants become ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot = ξrot/(R2ξ) and
rot = ξrot/(R2ξ) and ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) α = ξα/(R2ξ). The dimensionless speed is ν = uadv/u0, and the dimensionless elastic energy is thus
α = ξα/(R2ξ). The dimensionless speed is ν = uadv/u0, and the dimensionless elastic energy is thus| | 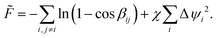 | (11) |
It is also helpful to write down the derivatives of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) w.r.t. the various translational coordinates
w.r.t. the various translational coordinates| | 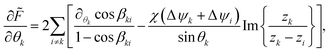 | (12) |
| |  | (13) |
and orientational coordinates| | 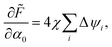 | (14) |
| |  | (15) |
The dimensionless velocities of the orientational and positional variables are then
| |  | (16) |
| | 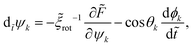 | (17) |
| |  | (18) |
where I define the complex velocity
15| | | Ũk = ũk·eθk + iũk·eϕk, | (19) |
and the gradient operator
| |  | (20) |
III. Numerical defect trajectories
Trajectories were generated by integrating the non-dimensional versions of the dynamic equations, eqn (16)–(18), using the ODE23 function in MATLAB with relative and absolute tolerances of 10−5. The initial conditions were randomized, with coordinates drawn uniformly from the relevant ranges, taking account of the spherical geometry: {cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi} ∈ [−1,1]; {ϕi} ∈ [0,2π); α ∈ [0,π); {Δψi} ∈ [0,2π). The parameters of the motion were selected from ranges specified below.
θi} ∈ [−1,1]; {ϕi} ∈ [0,2π); α ∈ [0,π); {Δψi} ∈ [0,2π). The parameters of the motion were selected from ranges specified below.
Five distinct types of final state were observed, labelled S, A, C, I, and F, see Fig. 2. It was found that all states had  (to within the precision of the calculation), so each calculation was run until that condition had been obtained, and then a few oscillatory cycles were recorded. States were then characterized by examination of the trajectories, and of the inter-defect spacings βij.
(to within the precision of the calculation), so each calculation was run until that condition had been obtained, and then a few oscillatory cycles were recorded. States were then characterized by examination of the trajectories, and of the inter-defect spacings βij.
 |
| | Fig. 2 Categories of trajectory identified with (for a–d) plots of the inter-defect distances βij. Coloured lines show defect trajectories, usually over one period, black dots are a snapshot of defect position. Bold letters with highlighted colours correspond to the usage in Fig. 3. On the βij plots the dotted and dashed lines indicate the square-planar and regular tetrahedral configurations. (a) Four intertwined defect trajectories with cubical symmetry (A) with low dimensionless activity ν = 1, and τ = 0. (b) As for a, but with high activity, ν = 100. (c) Four intertwined trajectories having a period incommensurate with the circumference of the sphere (I) with ν = 1, τ = 10. (d) As for c, but now showing several periods. (e) Two co-rotating defect pairs (C) indicated by bicolour lines, with ν = 1, τ = 4. (f) Four co-rotating circles (F) with ν = 1.7, τ = 4.75. | |
State S (not shown) has static defects forming an isoceles tetrahedron (disphenoid). The orientational energy has relaxed, i.e., {Δψi} = 0. The regular tetrahedron is the ground state of the equivalent passive system,12 and static tetrahedral states have been observed at low activity in experiments11 and all the various models considered.11,13–16 Even though these defects are static, it is important to note that there will still be flow in the surrounding nematic director field,13,15 which can drive, e.g., droplet motion.11
State A has active defects tracing out 4 equivalent closed loops whose axes of rotation are arranged in a tetrahedron, and whose shape grades from approximately cubic at low speed, Fig. 2a, to great circles at high speed, Fig. 2b. The defect configuration oscillates between a tetrahedral and a great-circle arrangement, as seen experimentally.11 This state was previously identified in simulations.13,16 As in state S, the orientational energy has relaxed, {Δψi} = 0.
State C has co-rotating small circles centred around opposite poles, Fig. 2e, with π/2 phase between the two pairs of defects. This state has two distinct and fixed βij values, corresponding to inter-pair and intra-pair distances, and the Δψi has non-zero, equal and opposite fixed values for the two defect pairs. This orientation difference is maintained by a balance between the orientational part of the energy and the parallel-transport term in eqn (7), which continually rotates the defect orientation away from equilibrium.
State I again has co-rotating paired defects, again π/2 out of phase, but the pairs periodically cross the equator and exchange places, see Fig. 2c. There is again oscillation between tetrahedral and great-circle configurations, but this is not commensurate with the orbital frequency, resulting in precession, which eventually fills the space in a band around the equator, Fig. 2d. In comparison with state A the symmetry of the configuration means that there are only two independent values of βij corresponding to inter- and intra-pair distances. This state was identified in an earlier coarse grained model.14
State F has four individual co-rotating circles, Fig. 2f. These rotate at a single frequency, requiring that each defect moves at a unique speed.
Fig. 3 shows the location of these trajectory types in parameter space. The parameter τ = ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot/(2χ) is a dimensionless time scale for orientational relaxation. For simplicity, I set all the orientational relaxation rates equal, i.e.,
rot/(2χ) is a dimensionless time scale for orientational relaxation. For simplicity, I set all the orientational relaxation rates equal, i.e., ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot =
rot = ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) α = 1. As I will show below, this should not affect the steady state dynamics. The numerical calculations were repeated 10 times at each point, with the coloured dots indicating the trajectory types found there. Most regions of the phase diagram have at least two bistable states. Solid lines indicate analytical boundaries, obtained from local linear stability analysis, again as discussed below.
α = 1. As I will show below, this should not affect the steady state dynamics. The numerical calculations were repeated 10 times at each point, with the coloured dots indicating the trajectory types found there. Most regions of the phase diagram have at least two bistable states. Solid lines indicate analytical boundaries, obtained from local linear stability analysis, again as discussed below.
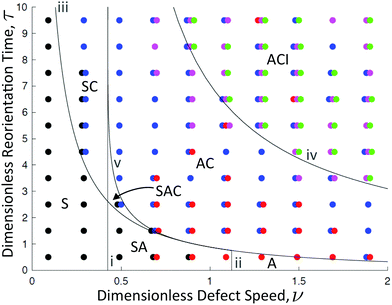 |
| | Fig. 3 Phase diagram. Symbols are from 10 repeats and colours indicate trajectory type as on Fig. 2: S = black; A = red; C = blue; I = green; F = pink. Solid lines denote theoretical phase boundaries obtained from linear stability, as described in the text, and letters indicate the types of trajectory predicted by this analysis (F is not included because linear stability analysis was not performed for this state). | |
IV. Analytical calculations
A. Dynamics on subspaces of reduced dimensionality
Apart from state F, which I will not study in detail, the states share several common symmetries. The four defect trajectories in each case are interchangable by reflection and rotation; each defect is essentially doing the same thing at the same time. It is thus possible to rewrite the equations of motion for these states in terms of much reduced parameter sets. Specifically, the trajectories can be described instantaneously as isoceles tetrahedra, with pairs of equal and opposite values of Δψi. Hence one can reduce the parameter set to five coordinates, which are indicated by Θ, Φ,  , ΔΨ and ϕ1, as illustrated in Fig. 4, plus global rotations of the initial coordinates, with
, ΔΨ and ϕ1, as illustrated in Fig. 4, plus global rotations of the initial coordinates, with| | | {θi} = {Θ,Θ,π − Θ,π − Θ}, | (21) |
| | | {ϕi} = {ϕ1,ϕ1 + π,ϕ1 + Φ,ϕ1 + Φ + π}, | (22) |
| |  | (23) |
| | | {Δψi} = {ΔΨ,ΔΨ,−ΔΨ,−ΔΨ}, | (24) |
and, from eqn (3)| |  | (25) |
 |
| | Fig. 4 (a) Lateral and polar views of the reduced configuration of the defects, as described in the text. The two near defects are shown in black, the two far defects in grey. ϕ1 = 0 here. (b) Schematic of the geometry of the critical configurations corresponding to four of the five state transitions discussed in the text, polar views. Solid arrows indicate the orientation of defects, dashed lines show the direction of their motion (where different), and thin arrows indicate the direction in which the defects move or turn when they become unstable. These configurations all have Φ = π/2. | |
Solving the equations of motion, eqn (16)–(18), in this reduced system then gives
| | 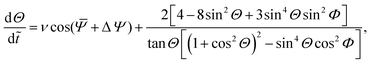 | (26) |
| | 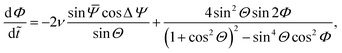 | (27) |
| | 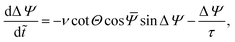 | (28) |
| |  | (29) |
As one would expect, the dynamics of this four-dimensional system is independent of the overall rotation of the system, specified by
ϕ1, whose dynamics are
| |  | (30) |
The dimensionality of the system can be further reduced by specializing to either the S and A states, or the C and I states, which adds extra symmetries:
States S and A: here one has the further condition that {ΔΨi} = 0, so that one can reduce eqn (26)–(30) to three dimensions Θ, Φ,  with dynamics
with dynamics
| | 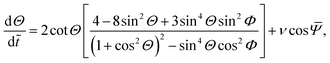 | (31) |
| |  | (32) |
| |  | (33) |
with overall rotation given by
| | 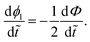 | (34) |
States C and I: both these states have Φ = π/2 and  . This leads to 2-dimensional dynamics in Θ, ΔΨ
. This leads to 2-dimensional dynamics in Θ, ΔΨ
| |  | (35) |
| |  | (36) |
The overall rotation is
| |  | (37) |
For the circular state C,
Θ and Δ
Ψ are both constant, so this trajectory corresponds to a fixed point in the
Θ, Δ
Ψ plane.
B. Linear stability analysis
The fixed points of eqn (26)–(37) correspond to static tetrahedra and corotating circles. Systematic local linear stability analysis around these points yields the five boundaries in Fig. 3, which are seen to reasonably describe the structure of the phase diagram. The algebra associated with the local stability analysis is standard, see e.g., ref. 19, so here I just present a geometrical picture of these transitions, together with analytic results where these are available. The transitions, as illustrated in Fig. 4 are:
Transition i: this marks the first point at which a static tetrahedron becomes unstable w.r.t. the active state. For static tetrahedra, S, the steady state is determined by solving for dψi/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = dθi/d
= dθi/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = dϕi/d
= dϕi/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0. Physically, this corresponds to the defects being trapped in a position where the elastic force exactly balances the active propulsion, i.e., where p points along the gradient of
= 0. Physically, this corresponds to the defects being trapped in a position where the elastic force exactly balances the active propulsion, i.e., where p points along the gradient of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , and where
, and where 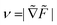 , as indicated by the contours in Fig. 5a, coloured according to the value of ν. The solid black line is the separatrix between the unstable (outside) and stable (inside) states, which I determine numerically.
, as indicated by the contours in Fig. 5a, coloured according to the value of ν. The solid black line is the separatrix between the unstable (outside) and stable (inside) states, which I determine numerically.
 |
| | Fig. 5 Dynamics in reduced dimensions. (a) The contours in Θ, Φ space of a static tetrahedron at values of ν indicated by the colour bars. Contours within the solid black curve are stable, and those outside are unstable. At a critical ν* ∼ 0.4 shown by the dashed line the defects can escape the static configuration. T and GC indicate the regular tetrahedral and regular great circle configurations, respectively. (b) Trajectories in the Θ, ΔΨ plane obtained from eqn (35) and (36) for ν = 1.6, τ = 10. Black lines show points where d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) Θ = 0 (dashed) and d Θ = 0 (dashed) and d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ΔΨ = 0 (solid). Intersections of these lines are classified as saddle points (SP), stable fixed points (FP) corresponding to corotating circles C, and limit cycles (LC) corresponding to precession I. ΔΨ = 0 (solid). Intersections of these lines are classified as saddle points (SP), stable fixed points (FP) corresponding to corotating circles C, and limit cycles (LC) corresponding to precession I. | |
The first static state to become unstable is symmetrical with all defects moving towards the equator, Fig. 4b. At a critical activity of  , where
, where  , the golden ratio, and a critical angle of
, the golden ratio, and a critical angle of 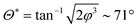 , defect 1 moves fast enough to overcome the repulsion from defects 3–4 (these critical values can be obtained just by considering the stability of eqn (31) with
, defect 1 moves fast enough to overcome the repulsion from defects 3–4 (these critical values can be obtained just by considering the stability of eqn (31) with 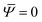 and Φ = π/2). The contour for ν = ν* is indicated by the dashed line in Fig. 5a; as can be seen, this is the first value of ν for which the contour crosses the separatrix, corresponding to the first value where the stable states encircling the regular tetrahedral point meet the unstable states around the great-circle position. This transition is therefore a saddle-node bifurcation.19 One can see from Fig. 5a that the great circle configuration is an unstable fixed point, i.e., a maximum in the potential landscape. Interestingly, if differences in the bend and splay elastic constants are allowed for, i.e., moving beyond the SEC approximation, then the great-circle configuration can itself become the stable configuration of the passive system:20,21 in this case, one might expect this active trajectory to be preserved, but to emerge from stable great circle configurations rather than from stable tetrahedra.
and Φ = π/2). The contour for ν = ν* is indicated by the dashed line in Fig. 5a; as can be seen, this is the first value of ν for which the contour crosses the separatrix, corresponding to the first value where the stable states encircling the regular tetrahedral point meet the unstable states around the great-circle position. This transition is therefore a saddle-node bifurcation.19 One can see from Fig. 5a that the great circle configuration is an unstable fixed point, i.e., a maximum in the potential landscape. Interestingly, if differences in the bend and splay elastic constants are allowed for, i.e., moving beyond the SEC approximation, then the great-circle configuration can itself become the stable configuration of the passive system:20,21 in this case, one might expect this active trajectory to be preserved, but to emerge from stable great circle configurations rather than from stable tetrahedra.
Transition ii: this marks the last stable static tetrahedron. This tetrahedron is also symmetrical, but now with all defects moving towards the pole, Fig. 4b, i.e., with  and Φ = π/2. At this point, the defects are able to rotate and move past each other into the active state. The relevant equation for the critical values of ν** and Θ** is 0 = 3
and Φ = π/2. At this point, the defects are able to rotate and move past each other into the active state. The relevant equation for the critical values of ν** and Θ** is 0 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos6
cos6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** − 2
Θ** − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos4
cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** + 7
Θ** + 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** − 4, which has solution Θ** ≈ 40° and ν** = 8
Θ** − 4, which has solution Θ** ≈ 40° and ν** = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**
Θ**![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**/(1 + cos2
Θ**/(1 + cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**)2 = 1.12.
Θ**)2 = 1.12.
Transition iii: this marks the first point at which a static tetrahedron becomes unstable w.r.t. the co-rotating circular state. This occurs through a supercritical pitchfork bifurcation:19 a continuous transition between a polar-oriented tetrahedron (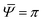 , Φ = π/2), and corotating circles initially moving at arbitrarily small speeds either anticlockwise (as shown, Fig. 4b) or clockwise. This boundary is found to have the analytical form
, Φ = π/2), and corotating circles initially moving at arbitrarily small speeds either anticlockwise (as shown, Fig. 4b) or clockwise. This boundary is found to have the analytical form
| |  | (38) |
Transition iv: marks the first point at which the co-rotating circular state becomes unstable w.r.t. stable limit cycles corresponding to state I, as shown in Fig. 5b. The co-rotating circular states found above this boundary have values of ΔΨ greater than π, see Fig. 5b, i.e., the defects are under significant orientational strain, and it would probably be difficult to reach such states in practice.
Transition v: marks the boundary where all tetrahedra are either unstable w.r.t. co-rotating circles C or w.r.t. the active state A. This boundary is determined numerically, i.e., for each value of ν I identify a critical τ for which all points in the relevant contour in Fig. 5a become linearly unstable w.r.t. perturbations of Δψ.
V. Comparison with previous models and experiment
In this study two distinct categories of trajectory (A and I) have been found that exhibit the oscillations between tetrahedral and great-circle trajectories found in experiments.11 Because the experiments are subject to noise the precise form of the trajectory found there is difficult to determine. However, several observations indicate that state A is the most correct here. First, the inter-defect distances shown in ref. 11 are grouped into three pairs as in state A. Second, the defects rapidly span the whole sphere rather than being confined to a band. Third, there appears to be a simple transition from the static to active state with no indication of the co-rotating circular state C which would be expected at intermediate activity values if state I represented the active state found in ref. 11. I conclude from this that the dimensionless reorientation time associated with the experiments in ref. 11 is low, probably τ < 1.
I turn now to previous theoretical treatments of this problem. These encompass several different approaches, often in the same publication. Some have used a point-particle approximation for the defects, where the individual nematogens, e.g., microtubules, are coarse grained out.11,14,15 Others have simulated the nematogens as interacting, active particles,14,16 or have used a continuum nematohydrodynamic approach.13
States equivalent to A have been identified in two previous papers.13,16 The continuum hydrodynamics of ref. 13 yields closed deterministic trajectories that are very similar to A. In ref. 16, the nematogens themselves are treated as noisy active particles, so the trajectory is also more noisy, but again three pairs of inter-defect distances are found, which is strongly indicative of a state like A.
State I has been identified in another coarse-grained model.14 This state was not found in the more detailed simulations undertaken in the same paper, and this was taken as an indication of a qualitative difference between these types of model. The identification here of a wide range of different trajectory types on a single phase diagram indicates instead that simple differences in parameter values, in particular the defect reorientation time, can account for some of the apparent differences between modeling techniques.
The two states with co-rotating circles have not, to the best of my knowledge, been identified previously. However, state C may be similar to the band-like states seen in ref. 16. Again, noise makes it difficult to identify rotations of the defects there, and the defects, which are near the poles, eventually coalesce into two +1 defects. In the current model, calculating the full nematic texture and flow field would aid this comparison. Interestingly, ref. 16 identifies a state consisting of stochastic flipping between a band-like structure and the state equivalent to A. This is consistent with the bistability between states A and C identified here.
Another state that has been used to explain the experimental great-circle to tetrahedral oscillations consists of pairs of counter-rotating circles,11,15 but this does not agree visually with the experimental observation of 4 distinct trajectories spanning the whole vesicle. Furthermore, this state is found neither in the current work nor in the two other modeling papers considered.14,16 This discrepancy is explained by examination of the defect equations of motion in ref. 11 and 15. Both papers fail to include parallel transport, i.e., the second term is lacking from the equivalent of eqn (7), e.g., eqn (S5) and (S8) in the supplementary information of ref. 11. As discussed above, this omission gives non-physical motion along loxodromic trajectories in the absence of inter-defect torque. In ref. 15, this issue is not immediately apparent, because the defect orientation is slaved to the parameter α0, so that it is not possible to apply their model to a single defect. However, the α0 dynamics also require a contribution from parallel transport, whereas in ref. 15α0 is assumed constant. I repeated the numerical calculations above, neglecting the parallel transport term, and did indeed obtain counter-rotating defect pairs. These trajectories are thus artefacts of the failure to account for parallel transport. Interestingly, one simulation that does include the effects of parallel transport has produced counter-rotating defect pairs, but this was on an oblate spheroidal surface, where the anisortropy presumably leads to extra effective torques on the defects that can balance the parallel transport contribution.14
Various other states arise in the more fine-grained simulations.13,14,16 Some of these probably arise from the relaxation of the SEC approximation there, e.g., in ref. 13, a transition to another complex state with cubical symmetry, at a value equivalent to ν ≈ 3, is found only with extensile flow. From the point of view of the SEC point-particle model, the contractile or extensile nature of the flow is irrelevant, so this is not captured here. Other states, where the defects merge or proliferate, or exhibit noisy trajectories, are clearly not accessible to the coarse-grained model studied here.16
VI. Conclusion
In conclusion, I have calculated a phase diagram for an active nematic confined to the surface of a sphere based on a point-particle representation of defect dynamics. This is parameterised just in terms of the defect self-propulsion speed and a defect reorientation time. The phase diagram revealed four distinct categories of defect trajectory, which I compared to previous experimental and theoretical results. One of these categories, an interweaving dance spanning the whole sphere, corresponded well to previous experimental and simulation results.13,16 Analysis of the governing equations excluded a competing hypothesis consisting of counter-rotating pairs of defects circling around the poles.11,15 Two other types of trajectory, pairs and quartets of corotating circles, have not to the best of my knowledge been predicted or observed previously, though they are similar to the equatorial band state in ref. 16.
The predictions made here may be experimentally testable, e.g., by increasing the activity in the active nematic to cross the phase boundary into co-rotating circles, or by assessing bistability between static and active states. Nevertheless, it is likely that breakdown of the point-particle description will limit our ability to explore some regions of the phase diagram. Specifically, at high activity, spontaneous formation of defect pairs will become predominant.11 Similarly, it is not clear to this author what microscopic parameters control the relative orientational and translational timescales, so that experimental exploration of this dimension of the phase diagram may be challenging. From a theoretical point of view, further studies containing several different levels of modeling detail as in ref. 14, or taking into account, e.g., the finite size of defects, or differences between the bend and splay elastic constants,20 would be very helpful. The relatively simple equations for the final states determined here should aid those pursuing such investigations.
Conflicts of interest
There are no conflicts of interest to declare.
Appendix: derivation of the contribution to the energy arising from defect orientation
I start with eqn (1), the general expression for the free energy, and write α = αeq + ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) , with αeq the equilibrium nematogen orientation field and
, with αeq the equilibrium nematogen orientation field and ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) the additional orientation field produced by the non-equilibrium defect orientations Δψi. Eqn (1) can then be written as
the additional orientation field produced by the non-equilibrium defect orientations Δψi. Eqn (1) can then be written as| | 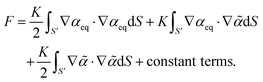 | (A.1) |
The 2nd term vanishes because αeq is a minimal solution. Hence the additional orientational free energy contribution is| |  | (A.2) |
I now calculate the director field ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) that minimizes Fori subject to the constraint that each defect is rotated by an angle Δψi. I am interested here in the small-defect limit ρ = rc/R → 0, so will calculate the energy only to lowest order in ρ.
that minimizes Fori subject to the constraint that each defect is rotated by an angle Δψi. I am interested here in the small-defect limit ρ = rc/R → 0, so will calculate the energy only to lowest order in ρ.
Consider first a single defect in isolation, which is rotated by angle Δψ around its centre causing deformation of the director field around the defect. Without loss of generality I suppose that this defect is centred at the north pole, θ = 0. A simple rotation of the defect requires that the orientation at the edge of the defect ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) (θ = ρ) = −Δψ/2. This boundary condition is axisymmetric so the minimizing texture will also be axisymmetric, so that
(θ = ρ) = −Δψ/2. This boundary condition is axisymmetric so the minimizing texture will also be axisymmetric, so that ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) =
= ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) (θ).
(θ).
I also apply the constraint that the average distortion is zero, i.e., 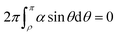 . This is necessary because otherwise the minimum energy distortion is achieved by a uniform rotation of the director field, which contributes zero elastic energy due to the SEC approximation. The constraint is imposed by minimizing the Lagrangian
. This is necessary because otherwise the minimum energy distortion is achieved by a uniform rotation of the director field, which contributes zero elastic energy due to the SEC approximation. The constraint is imposed by minimizing the Lagrangian
| |  | (A.3) |
where
λ is a Lagrange multiplier. This yields the Euler–Lagrange equation
| |  | (A.4) |
The director field that solves this equation, fits the boundary condition at the defect edge, and satisfies the constraint on the average distortion is
| | 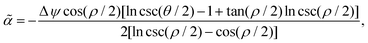 | (A.5) |
which is identical apart from additive constants to an analogous expression obtained to determine the positional part of the energy in
ref. 12 (eqn (A29) there). To lowest order in
ρeqn (A.5) is
| |  | (A.6) |
I now determine the limits of this expression near to the defect (
θ ∼
ρ) and far away (
θ ≫
ρ). For
θ ∼
ρ,
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
=
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1) whereas for
θ ≫
ρ,
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
=
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1/ln(1/
ρ)) ≪ 1.
The energy density f1 is obtained by substituting eqn (A.5) into f1 = (K/2)∇![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ·∇
·∇![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) to give
to give
| |  | (A.7) |
which, to lowest order in
ρ is
| |  | (A.8) |
Again, for
θ ∼
ρ,
f1 =
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1/[
ρln(1/
ρ)]
2) ≫ 1, while for
θ ≫
ρ,
f1 =
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1/ln(1/
ρ)
2) ≪ 1. Hence both the distortion of the director field and the energy density are localized around the defect itself (where
θ ∼
ρ).
The final potential energy from a single defect is
| | 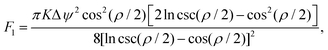 | (A.9) |
which, to lowest order in
ρ is
| |  | (A.10) |
Because the energy and distortion are localized one can then treat the total energy as just as sum over the energy of the individual defects,
i.e., to lowest order in
ρ| | 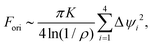 | (A.11) |
which corresponds to
eqn (5) in the main text.
Acknowledgements
I thank Alys Jepson, Nick Koumakis and Wilson Poon for introducing me to this problem, and Joost de Graaf for helpful comments on an early draft of the manuscript. All data associated with this paper are included in the paper itself.
References
- J. M. Kosterlitz and D. J. Thouless, J. Phys. C: Solid State Phys., 1973, 6, 1181 CrossRef CAS.
- C. Brackley, J. Johnson, A. Bentivoglio, S. Corless, N. Gilbert, G. Gonnella and D. Marenduzzo, Phys. Rev. Lett., 2016, 117, 018101 CrossRef CAS PubMed.
- P. A. Haas and R. E. Goldstein, J. R. Soc., Interface, 2015, 12, 20150671 CrossRef PubMed.
- P. Guillamat, J. Ignés-Mullol, S. Shankar, M. C. Marchetti and F. Sagués, Phys. Rev. E, 2016, 94, 060602 CrossRef PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431 CrossRef CAS PubMed.
- S. J. De Camp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110 CrossRef CAS PubMed.
- G. Henkin, S. J. DeCamp, D. T. N. Chen, T. Sanchez and Z. Dogic, Philos. Trans. R. Soc., A, 2014, 372, 20140142 CrossRef PubMed.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5498 CrossRef CAS PubMed.
- P. Guillamat, Ž. Kos, J. Hardoüin, J. Ignés-Mullol, M. Ravnik and F. Sagués, Sci. Adv., 2018, 4, 1 Search PubMed.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135 CrossRef CAS PubMed.
- V. Vitelli and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 21711 CrossRef CAS PubMed.
- R. Zhang, Y. Zhou, M. Rahimi and J. J. De Pablo, Nat. Commun., 2016, 7, 13483 CrossRef CAS PubMed.
- F. Alaimo, C. Köhler and A. Voigt, Sci. Rep., 2017, 7, 1 CrossRef CAS PubMed.
- D. Khoromskaia and G. P. Alexander, New J. Phys., 2017, 19, 103013 CrossRef.
- S. Henkes, M. C. Marchetti and R. Sknepnek, Phys. Rev. E, 2018, 97, 042605 CrossRef CAS PubMed.
-
P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1995 Search PubMed.
- X. Tang and J. V. Selinger, Soft Matter, 2017, 13, 5481 RSC.
-
S. H. Strogatz, Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering, CRC Press, 2018 Search PubMed.
- H. Shin, M. J. Bowick and X. Xing, Phys. Rev. Lett., 2008, 101, 1 Search PubMed.
- M. N. T. Lopez-Leon, A. Fernandez-Nieves and C. Blanc, Phys. Rev. Lett., 2011, 106, 247802 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αeθ + sin
αeθ + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αeϕ with orientation angle α, the elastic energy12
αeϕ with orientation angle α, the elastic energy12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi, sin
ϕi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi, cos
ϕi, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi} defined by the polar θi and azimuthal ϕi angles of each defect, and the radius R of the sphere. Each defect has an orientation vector pi = eθi
θi} defined by the polar θi and azimuthal ϕi angles of each defect, and the radius R of the sphere. Each defect has an orientation vector pi = eθi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi + eϕi
ψi + eϕi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi, which points along the symmetry axis of the defect, see Fig. 1. Previous work12,15 has shown that, for a given set of defect positions xi, eqn (1) can be minimized with a particular director field that can be determined by a stereographic projection onto the equatorial plane. This minimizing director field is
ψi, which points along the symmetry axis of the defect, see Fig. 1. Previous work12,15 has shown that, for a given set of defect positions xi, eqn (1) can be minimized with a particular director field that can be determined by a stereographic projection onto the equatorial plane. This minimizing director field is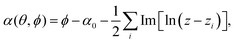
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i, are
i, are

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βij = cos
βij = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj + sin
θj + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi
θi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj
θj![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕi − ϕj). Note that α0 does not appear in eqn (4). This is because, in the SEC approximation, the elastic energy is invariant with respect to rotations of the entire nematogen orientation field n(θ,ϕ) by a constant value.12 Whether defects are pointing towards or away from each other, or at some arbitrary angle to each other, does not affect the energy, as long as the defect orientations are coupled through eqn (3) with some value of α0. In other words, changing the value of α0 merely modifies the distribution of bend and splay deformations, but, since in the SEC approximation bend and splay deformations are energetically equivalent, this does not affect the elastic energy.
cos(ϕi − ϕj). Note that α0 does not appear in eqn (4). This is because, in the SEC approximation, the elastic energy is invariant with respect to rotations of the entire nematogen orientation field n(θ,ϕ) by a constant value.12 Whether defects are pointing towards or away from each other, or at some arbitrary angle to each other, does not affect the energy, as long as the defect orientations are coupled through eqn (3) with some value of α0. In other words, changing the value of α0 merely modifies the distribution of bend and splay deformations, but, since in the SEC approximation bend and splay deformations are energetically equivalent, this does not affect the elastic energy.
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i. These deviations will produce a localized additional torsion of the nematic director field, and an associated ‘orientational’ energy Fori. This orientational energy has already been calculated in the planar case,18 and I perform the analogous calculation for a spherical geometry in the appendix. To lowest order in the dimensionless defect size ρ = rc/R the result is
i. These deviations will produce a localized additional torsion of the nematic director field, and an associated ‘orientational’ energy Fori. This orientational energy has already been calculated in the planar case,18 and I perform the analogous calculation for a spherical geometry in the appendix. To lowest order in the dimensionless defect size ρ = rc/R the result is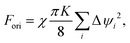
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i is the deviation from the equilibrium orientation, and χ = 2/ln(1/ρ) is the dimensionless parameter which specifies the ratio of orientation to positional contributions. As in the planar case,18 there is a simple quadratic dependence on the orientational deviation and a logarithmic scaling with the defect size.
i is the deviation from the equilibrium orientation, and χ = 2/ln(1/ρ) is the dimensionless parameter which specifies the ratio of orientation to positional contributions. As in the planar case,18 there is a simple quadratic dependence on the orientational deviation and a logarithmic scaling with the defect size.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi + eϕi
ψi + eϕi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψi at some fixed speed uadv.15 As discussed above, the SEC approximation does not make a global distinction between defect heads and tails because the elastic energy is invariant w.r.t. α0, so, without loss of generality, I specify that the defects are self-propelled towards their heads, as observed in experiments on microtubules and molecular motors.11
ψi at some fixed speed uadv.15 As discussed above, the SEC approximation does not make a global distinction between defect heads and tails because the elastic energy is invariant w.r.t. α0, so, without loss of generality, I specify that the defects are self-propelled towards their heads, as observed in experiments on microtubules and molecular motors.11

![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i as the defects move. However, because each of these orientations is slaved to α0, independent parallel transport of each
i as the defects move. However, because each of these orientations is slaved to α0, independent parallel transport of each ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) i is not possible. Instead, I apply the requirement that, in the absence of any elastic energy contribution, the equilibrium orientations should adjust so as to minimize the squared rate of change of the deviation of the orientations from their equilibrium values. In other words, the constraint on the equilibrium defect orientations should produce the minimum additional disturbance in the local environment of each defect. Mathematically, this is
i is not possible. Instead, I apply the requirement that, in the absence of any elastic energy contribution, the equilibrium orientations should adjust so as to minimize the squared rate of change of the deviation of the orientations from their equilibrium values. In other words, the constraint on the equilibrium defect orientations should produce the minimum additional disturbance in the local environment of each defect. Mathematically, this is
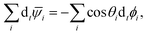

![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ,
, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , ũ, and the two orientational friction constants become
, ũ, and the two orientational friction constants become ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot = ξrot/(R2ξ) and
rot = ξrot/(R2ξ) and ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) α = ξα/(R2ξ). The dimensionless speed is ν = uadv/u0, and the dimensionless elastic energy is thus
α = ξα/(R2ξ). The dimensionless speed is ν = uadv/u0, and the dimensionless elastic energy is thus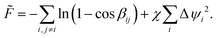
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) w.r.t. the various translational coordinates
w.r.t. the various translational coordinates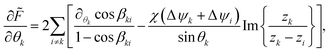

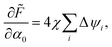


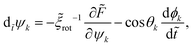


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi} ∈ [−1,1]; {ϕi} ∈ [0,2π); α ∈ [0,π); {Δψi} ∈ [0,2π). The parameters of the motion were selected from ranges specified below.
θi} ∈ [−1,1]; {ϕi} ∈ [0,2π); α ∈ [0,π); {Δψi} ∈ [0,2π). The parameters of the motion were selected from ranges specified below.
 (to within the precision of the calculation), so each calculation was run until that condition had been obtained, and then a few oscillatory cycles were recorded. States were then characterized by examination of the trajectories, and of the inter-defect spacings βij.
(to within the precision of the calculation), so each calculation was run until that condition had been obtained, and then a few oscillatory cycles were recorded. States were then characterized by examination of the trajectories, and of the inter-defect spacings βij.
![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot/(2χ) is a dimensionless time scale for orientational relaxation. For simplicity, I set all the orientational relaxation rates equal, i.e.,
rot/(2χ) is a dimensionless time scale for orientational relaxation. For simplicity, I set all the orientational relaxation rates equal, i.e., ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) rot =
rot = ![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/char_e119.gif) α = 1. As I will show below, this should not affect the steady state dynamics. The numerical calculations were repeated 10 times at each point, with the coloured dots indicating the trajectory types found there. Most regions of the phase diagram have at least two bistable states. Solid lines indicate analytical boundaries, obtained from local linear stability analysis, again as discussed below.
α = 1. As I will show below, this should not affect the steady state dynamics. The numerical calculations were repeated 10 times at each point, with the coloured dots indicating the trajectory types found there. Most regions of the phase diagram have at least two bistable states. Solid lines indicate analytical boundaries, obtained from local linear stability analysis, again as discussed below.
 , ΔΨ and ϕ1, as illustrated in Fig. 4, plus global rotations of the initial coordinates, with
, ΔΨ and ϕ1, as illustrated in Fig. 4, plus global rotations of the initial coordinates, with

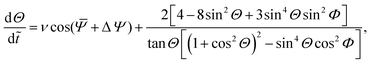
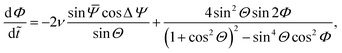
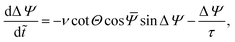


 with dynamics
with dynamics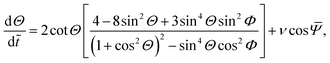


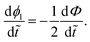
 . This leads to 2-dimensional dynamics in Θ, ΔΨ
. This leads to 2-dimensional dynamics in Θ, ΔΨ


![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = dθi/d
= dθi/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = dϕi/d
= dϕi/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0. Physically, this corresponds to the defects being trapped in a position where the elastic force exactly balances the active propulsion, i.e., where p points along the gradient of
= 0. Physically, this corresponds to the defects being trapped in a position where the elastic force exactly balances the active propulsion, i.e., where p points along the gradient of ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , and where
, and where 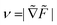 , as indicated by the contours in Fig. 5a, coloured according to the value of ν. The solid black line is the separatrix between the unstable (outside) and stable (inside) states, which I determine numerically.
, as indicated by the contours in Fig. 5a, coloured according to the value of ν. The solid black line is the separatrix between the unstable (outside) and stable (inside) states, which I determine numerically.
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) Θ = 0 (dashed) and d
Θ = 0 (dashed) and d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ΔΨ = 0 (solid). Intersections of these lines are classified as saddle points (SP), stable fixed points (FP) corresponding to corotating circles C, and limit cycles (LC) corresponding to precession I.
ΔΨ = 0 (solid). Intersections of these lines are classified as saddle points (SP), stable fixed points (FP) corresponding to corotating circles C, and limit cycles (LC) corresponding to precession I. , where
, where  , the golden ratio, and a critical angle of
, the golden ratio, and a critical angle of 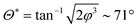 , defect 1 moves fast enough to overcome the repulsion from defects 3–4 (these critical values can be obtained just by considering the stability of eqn (31) with
, defect 1 moves fast enough to overcome the repulsion from defects 3–4 (these critical values can be obtained just by considering the stability of eqn (31) with 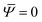 and Φ = π/2). The contour for ν = ν* is indicated by the dashed line in Fig. 5a; as can be seen, this is the first value of ν for which the contour crosses the separatrix, corresponding to the first value where the stable states encircling the regular tetrahedral point meet the unstable states around the great-circle position. This transition is therefore a saddle-node bifurcation.19 One can see from Fig. 5a that the great circle configuration is an unstable fixed point, i.e., a maximum in the potential landscape. Interestingly, if differences in the bend and splay elastic constants are allowed for, i.e., moving beyond the SEC approximation, then the great-circle configuration can itself become the stable configuration of the passive system:20,21 in this case, one might expect this active trajectory to be preserved, but to emerge from stable great circle configurations rather than from stable tetrahedra.
and Φ = π/2). The contour for ν = ν* is indicated by the dashed line in Fig. 5a; as can be seen, this is the first value of ν for which the contour crosses the separatrix, corresponding to the first value where the stable states encircling the regular tetrahedral point meet the unstable states around the great-circle position. This transition is therefore a saddle-node bifurcation.19 One can see from Fig. 5a that the great circle configuration is an unstable fixed point, i.e., a maximum in the potential landscape. Interestingly, if differences in the bend and splay elastic constants are allowed for, i.e., moving beyond the SEC approximation, then the great-circle configuration can itself become the stable configuration of the passive system:20,21 in this case, one might expect this active trajectory to be preserved, but to emerge from stable great circle configurations rather than from stable tetrahedra. and Φ = π/2. At this point, the defects are able to rotate and move past each other into the active state. The relevant equation for the critical values of ν** and Θ** is 0 = 3
and Φ = π/2. At this point, the defects are able to rotate and move past each other into the active state. The relevant equation for the critical values of ν** and Θ** is 0 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos6
cos6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** − 2
Θ** − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos4
cos4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** + 7
Θ** + 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ** − 4, which has solution Θ** ≈ 40° and ν** = 8
Θ** − 4, which has solution Θ** ≈ 40° and ν** = 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**
Θ**![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**/(1 + cos2
Θ**/(1 + cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ**)2 = 1.12.
Θ**)2 = 1.12.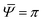 , Φ = π/2), and corotating circles initially moving at arbitrarily small speeds either anticlockwise (as shown, Fig. 4b) or clockwise. This boundary is found to have the analytical form
, Φ = π/2), and corotating circles initially moving at arbitrarily small speeds either anticlockwise (as shown, Fig. 4b) or clockwise. This boundary is found to have the analytical form
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) , with αeq the equilibrium nematogen orientation field and
, with αeq the equilibrium nematogen orientation field and ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) the additional orientation field produced by the non-equilibrium defect orientations Δψi. Eqn (1) can then be written as
the additional orientation field produced by the non-equilibrium defect orientations Δψi. Eqn (1) can then be written as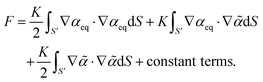

![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) that minimizes Fori subject to the constraint that each defect is rotated by an angle Δψi. I am interested here in the small-defect limit ρ = rc/R → 0, so will calculate the energy only to lowest order in ρ.
that minimizes Fori subject to the constraint that each defect is rotated by an angle Δψi. I am interested here in the small-defect limit ρ = rc/R → 0, so will calculate the energy only to lowest order in ρ.
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) (θ = ρ) = −Δψ/2. This boundary condition is axisymmetric so the minimizing texture will also be axisymmetric, so that
(θ = ρ) = −Δψ/2. This boundary condition is axisymmetric so the minimizing texture will also be axisymmetric, so that ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) =
= ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) (θ).
(θ).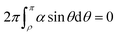 . This is necessary because otherwise the minimum energy distortion is achieved by a uniform rotation of the director field, which contributes zero elastic energy due to the SEC approximation. The constraint is imposed by minimizing the Lagrangian
. This is necessary because otherwise the minimum energy distortion is achieved by a uniform rotation of the director field, which contributes zero elastic energy due to the SEC approximation. The constraint is imposed by minimizing the Lagrangian

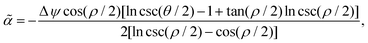

![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) =
= ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) whereas for θ ≫ ρ,
(1) whereas for θ ≫ ρ, ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) =
= ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/ln(1/ρ)) ≪ 1.
(1/ln(1/ρ)) ≪ 1.
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ·∇
·∇![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) to give
to give

![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/[ρln(1/ρ)]2) ≫ 1, while for θ ≫ ρ, f1 =
(1/[ρln(1/ρ)]2) ≫ 1, while for θ ≫ ρ, f1 = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/ln(1/ρ)2) ≪ 1. Hence both the distortion of the director field and the energy density are localized around the defect itself (where θ ∼ ρ).
(1/ln(1/ρ)2) ≪ 1. Hence both the distortion of the director field and the energy density are localized around the defect itself (where θ ∼ ρ).