Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single molecule protein stabilisation translates to macromolecular mechanics of a protein network†
Matt D. G.
Hughes
 a,
Sophie
Cussons
a,
Sophie
Cussons
 bc,
Najet
Mahmoudi
bc,
Najet
Mahmoudi
 d,
David J.
Brockwell
d,
David J.
Brockwell
 bc and
Lorna
Dougan
bc and
Lorna
Dougan
 *ab
*ab
aSchool of Physics and Astronomy, Faculty of Engineering and Physical Sciences, University of Leeds, Leeds, UK. E-mail: L.Dougan@leeds.ac.uk
bAstbury Centre for Structural Molecular Biology, University of Leeds, Leeds, UK
cSchool of Molecular and Cellular Biology, Faculty of Biological Sciences, University of Leeds, Leeds, UK
dISIS Neutron and Muon Spallation Source, STFC Rutherford Appleton Laboratory, Leeds, UK
First published on 11th June 2020
Abstract
Folded globular proteins are attractive building blocks for biopolymer-based materials, as their mechanically resistant structures carry out diverse biological functionality. While much is now understood about the mechanical response of single folded proteins, a major challenge is to understand and predictably control how single protein mechanics translates to the collective response of a network of connected folded proteins. Here, by utilising the binding of maltose to hydrogels constructed from photo-chemically cross-linked maltose binding protein (MBP), we investigate the effects of protein stabilisation at the molecular level on the macroscopic mechanical and structural properties of a protein-based hydrogel. Rheological measurements show an enhancement in the mechanical strength and energy dissipation of MBP hydrogels in the presence of maltose. Circular dichroism spectroscopy and differential scanning calorimetry measurements show that MBP remains both folded and functional in situ. By coupling these mechanical measurements with mesoscopic structural information obtained by small angle scattering, we propose an occupation model in which higher proportions of stabilised, ligand occupied, protein building blocks translate their increased stability to the macroscopic properties of the hydrogel network. This provides powerful opportunities to exploit environmentally responsive folded protein-based biomaterials for many broad applications.
1. Introduction
Folded proteins are nanoscale machines responsible for a vast array of sophisticated biological functions. Acting in isolation or as part of larger, often complex machinery, proteins perform their function through structural and mechanical changes.1–3 Harnessing this diverse functionality within a programmable structural and mechanical hydrogel would create a transformative and innovative technology. Hierarchical structure and mechanics are crucial to biological systems4,5 as they allow for smaller molecules (e.g. proteins6 and polysaccharide7) to be used in the construction of large scale biological structures (e.g. cell cytoskeletons) with properties such as structural support and repetitive energy dissipation.8–13 For example, α-helical lamin protein domains that define the lattice-like network of the cell's nucleus, provide both crucial structural support, as well as aiding in the coupling of mechanical signals to complex biochemical processes in the cell.14 The staggered architecture in a collagen microfibril permits energy dissipation through molecular sliding, rather than snapping and can withstand GPa of pressure. While as yet less understand than their synthetic and flexible counterparts,4 hierarchical biopolymer networks show diverse behaviour including reversible softening under compression,15 as well as both stiffening16 and negative normal stress under shear.17 This richness of behaviour can serve as inspiration for new functional materials. However, a predictive framework for biopolymer networks has proven to be a significant challenge. A fundamental goal in this field is to bridge the gap between the mechanical properties of a single biopolymer and the collective response of a network of such polymers.18With the development of single molecule force spectroscopy (SMFS) techniques, we now have a wealth of information about the mechanical properties of individual proteins.19–23 This includes proteins which exhibit mechanical properties, which can be finely tuned through ligand binding.24–30 These studies have shown that the native, folded state of protein molecules display a wide range of mechanical stabilities (pNs to nNs).19,31 Hydrogels formed of cross-linked folded proteins thus offer the opportunity to design novel smart materials that exploit the protein's intrinsic properties and functions, resulting in hydrogel networks that are inherently functional with unique properties. In the last decade folded protein-based networks have emerged as an exciting new class of biomaterial motivated by the work of Li et al.,32–35 which demonstrates their ability to mimic the mechanical properties of muscle, form highly elastic and stimuli-responsive materials, and dynamically regulate their properties. However, the ability to rationally design protein hydrogels with predictable and tuneable structural and mechanical properties remains a fundamental challenge. A notable exception is the recent study of Wu et al., which examined the balance between protein building blocks and cross-linker.36 However, it is critical that we progress our understanding of the translation of mechanical properties from single protein to crosslinked network. Here we report a novel, rationally designed protein hydrogel that translates the nanoscale function of a single protein ligand binding to the macroscopic mechanical properties of a cross-linked37 protein network.
2. Experimental section
2.1 Materials
Tris(2,2′-bipyridyl)dichlororuthenium(II) hexahydrate (Ru(BiPy)3), sodium persulfate (NaPS), D-(+)Maltose monohydrate, sodium phosphate dibasic, and sodium phosphate monobasic were obtained from Sigma-Aldrich and used without further treatment. N-Terminal hexa-histidine tagged MBP was expressed and purified as described below.2.2 Protein preparation
A pMal-c5x vector, with a stop codon inserted at position 378 by Q5 mutagenesis, was transformed into the expression host Escherichia coli BL21 (DE3) pLysS competent cells. Selected colonies were grown overnight in Lysogeny Broth (LB) at 37 °C, 200 rpm to form starter cultures. 2 ml of these starter cultures were used to inoculate 0.5 l of auto-induction media38 in 2.5 l conical flasks, these cultures were incubated for 48 hours at 37 °C, 200 rpm. Cells were harvested at 8000 rpm for 45 minutes, and the pellet resuspended in lysis buffer (0.1% Triton X-100, 1 mM PMSF, 20 mM benzamidine, 20 mM Tris, 300 mM NaCl, 10 mM imidazole, pH 8), homogenised and incubated for 1 hour in the presence of DNAase. To ensure complete lysis, cell solutions were passed through a cell disruptor (30 kpsi, 25 °C) before centrifuging at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 25 min to pellet the cell debris and collect the lysate.
000 rpm for 25 min to pellet the cell debris and collect the lysate.
To purify the MBP from the lysate, it was loaded onto a Ni-NTA resin column over night at 2 ml min−1 to ensure maximum binding of the hexa-histidine-tagged MBP. The column was then equilibrated in wash buffer (20 mM Tris, 300 mM NaCl, 10 mM imidazole, pH 8), before the protein was eluted with elution buffer (20 mM Tris, 300 mM NaCl, 500 mM imidazole, pH 8) in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to wash buffer. The purified protein was dialysed into water and freeze dried for storage at −20 °C. Average MBP yields of 250 mg l−1.
3 to wash buffer. The purified protein was dialysed into water and freeze dried for storage at −20 °C. Average MBP yields of 250 mg l−1.
2.3 Sample preparation
Hydrogel samples are prepared by mixing in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio a 200 mg ml−1 stock of MBP protein and 2× crosslink reagent stock for final protein and reagent concentrations of 100 mg ml−1 MBP, 30 mM NaPS, 100 μM Ru(BiPY). Maltose and NaCl are added to the protein stock and reagent stock at concentrations of 20 mM and 400 mM for final hydrogel concentrations of 10 mM and 200 mM respectively. All stocks were dissolved in 25 mM phosphate buffer.
1 ratio a 200 mg ml−1 stock of MBP protein and 2× crosslink reagent stock for final protein and reagent concentrations of 100 mg ml−1 MBP, 30 mM NaPS, 100 μM Ru(BiPY). Maltose and NaCl are added to the protein stock and reagent stock at concentrations of 20 mM and 400 mM for final hydrogel concentrations of 10 mM and 200 mM respectively. All stocks were dissolved in 25 mM phosphate buffer.
2.4 Rheometry
The mechanical properties of hydrogels were determined using an Anton Parr MCR 502 stress controlled rheometer (Anton Parr GmbH, Austria) in parallel plate configuration (with a plate diameter of 8 mm). Time sweep measurements were conducted at a frequency and shear strain of 1 Hz and 0.5%, respectively. All samples were gelated under a blue LED (peak emission at 452 nm) run at a current of 0.48 A. To prevent evaporation, during this process low viscosity silicone oil (approx. 5 ct) was placed around the geometry. The silicone oil should present no schematic error on rheometric data as this is below the rheometer's torque range. All measurements were performed at room temperature. The modified form of the Langmuir equation is defined as: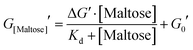 | (1) |
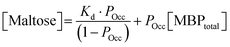 | (2) |
2.5 Differential scanning calorimetry
DSC scans were performed on a TA Q20 DSC with a refrigerated cooling system (RCS90, TA Inst.) Hermetically seal aluminium sample pans (Tzero pans, TA inst.) were used to hold 10 mg of each sample. An empty pan was used as a reference. Samples were heated from 30 to 95 °C at 10 °C min−1. To determine the bind affinity of maltose the curves are fit with the Langmuir thermal shift equation: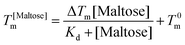 | (3) |
2.6 Circular dichroism (CD)
Far-UV circular dichroism spectra of MBP hydrogels were acquired on a Chirascan plus circular dichroism spectrometer (Applied PhotoPhysics) with a bandwidth of 2 nm, a step size of 1 nm, and a path length of 10 μm. The samples contain different concentrations of maltose from 0 to 10 mM and were measured at temperatures: 23 °C. The mean residue ellipticity (MRE) at each wavelength was obtained by: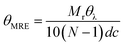 | (4) |
2.7 Small angle scattering (SAS)
SAS curves were fitted using SASview in accordance with eqn (5).| I(Q) = VblockΔρ2[ϕBlockP(Q) + ϕClusterP(Q)S(Q)] + background | (5) |
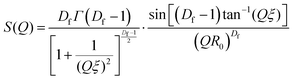 | (6) |
2.8 Small angle neutron scattering (SANS)
SANS measurements were conducted on the time-of-flight diffractometer instruments ZOOM and LOQ at ISIS Spallation Source (Didcot, UK). The Q ranges explored on the LOQ and ZOOM instruments are 0.006–0.24 Å−1 and 0.0025–0.43 Å−1 respectively. Temperatures were controlled by an external circulating thermal bath. Samples were loaded and gelled in 1 mm path length quartz cuvettes.2.9 Small angle X-ray scattering (SAXS)
SAXS measurements were conducted in the Materials Characterisation Laboratory of the ISIS Spallation Source, on the Nano-inXider SAXS equipment. Samples were loaded and gelled in 1 mm path length glass capillary tubes. The Q range investigated was 0.0045–0.37 Å−1, and measurements were made at room temperature.3. Results and discussion
3.1 Selection of hydrogel building block
Maltose binding protein was selected as a model system to investigate the relationship between building block stability and the macroscopic properties of a cross-linked MBP hydrogel. This 370 residue protein from E. coli is highly expressing (250 mg l−1 of cell culture (Methods)), has 14 solvent-exposed tyrosine residues (allowing formation gel network42via residue specific photo-chemical crosslinking) and binds the sugar maltose with a dissociation constant (Kd) of (1.20 ± 0.05) μM.43,44 The crystal structure of MBP have been determined by X-ray crystallography in the presence45 and absence46 of maltose (Fig. 1) and no significant difference is seen in the size or shape of the protein (RMSD = 4 Å).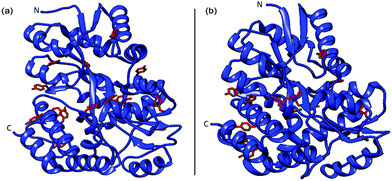 | ||
| Fig. 1 Crystal structures of MBP both apo (a) (PDB code: 1JW5) and with maltose bound (b) (PDB code: 1Y4C). Where tyrosine residues are coloured red and the bound maltose is coloured magenta, for clarity. | ||
An increase in the thermal stability of MBP of 8–14 °C, depending on pH, is noted upon the binding of maltose.47 A number of SMFS studies have successfully demonstrated that the mechanical stability of single proteins can be modulated upon ligand binding.27,48–52 A previous study showed that the mechanical stability of MBP is modulated upon ligand binding of maltose. In the case of MBP, in the structure two lobes are connected by a hinge region that changes from an open to close state upon binding of maltose (Fig. 1). Bertz and Rief demonstrated that when stretched from its N–C termini, binding of maltose to MBP did not change the mechanical stability of MBP.53 When protein engineering was used to control the pulling direction such that the two lobes of MBP are forced to move apart along the hinge axis upon stretching, the binding of maltose enhanced the mechanical stability of MBP by 12% (specifically extended via residues 53 and 141).54 The measured increase in mechanical stability was attributed to 11 additional hydrogen bonds in the maltose binding site upon ligand binding.55 This study highlighted the importance of hydrogen bonding for the mechanical stability of proteins.48,54,56,57 The majority of crosslinking tyrosine residues (9 out of 14) are located either side of the hinge region of MBP (Fig. 1), consistent with the hinge axis reported by Rief et al. (these tyrosine are all within 26 Å of the maltose binding site in agreement with residues 53 (25 Å from binding site) and 141 (35 Å from binding site)). Given the prior work of Rief et al. which demonstrated the importance of pulling direction and insertion of the ligand in the binding site of MBP, we would expect cross-linking of tyrosines across the hinge region and the presence of maltose to result in an increase in the mechanical stability of chemically cross-linked MBP. These properties make MBP an ideal protein to investigate the effects of mechanical stabilisation at the molecular level on the mechanical properties of a hierarchically structured macroscopic system.
3.2 Modulation of hydrogel mechanics
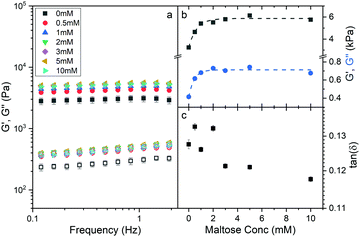
To investigate whether an increase in the stability of MBP changes the macroscopic properties of a cross-linked MBP hydrogel, concentrated solutions of MBP (100 mg ml−1, 7.4% vol frac.) were photochemically crosslinked (Methods) in the presence of 0 mM to 10 mM maltose (Fig. 2a).The frequency sweep curves (Fig. 2a) of MBP hydrogels as determined by applied shear rheology show how the storage, G′, and loss, G′′, moduli which are the real and imaginary component of the complex shear modulus and are a measure of hydrogel elasticity and inelasticity respectively. Both moduli decrease as the frequency decreases and decrease linearly below 2 Hz, the slopes of this region differ between the storage and loss moduli and appear to diverge implying that the elastic behaviour is dominant even over long timescales. Fitting the linear region between 0.1 and 2 Hz allows for the determination of the storage and loss modulus at 1 Hz (Fig. 2b) and by extension tan(δ) (Fig. 2c) as a function of maltose concentration. In addition, the exponent of the power law dependence of the storage and loss moduli can be extracted as a function of maltose concentration (Fig. S1, ESI†), and show little variation between maltose concentrations. The storage and loss moduli appear to increase sharply as a function of maltose concentration, with the former reaching an upper plateau at just over 2 mM maltose, and the latter at approximately 1 mM. It is interesting to consider what sets the critical concentration of 2 mM maltose for the storage modulus beyond which mechanical properties are insensitive to maltose content. One possibility is that the saturation point of the system is reached, and all the MBP building blocks have maltose bound. This seems intuitive given the MBP protein concentration is approximately 2 mM, and we revisit this explanation later in the paper. While the addition of maltose increases the storage and loss moduli of the hydrogels, the ratio of loss to storage modulus remains relatively unchanged (approximately 0.125) suggesting that the degree of elasticity is the same in the presence and absence of maltose. The initial results show that the addition of maltose increases mechanical stability of the MBP hydrogels without changing the relative elasticity. To further investigate the effects of maltose on the hydrogels mechanical properties the hydrogels are next investigated under load.
Fig. 3a shows shear stress–strain loading curves up to 50% strain of MBP hydrogels from applied rotational rheology. A maximum strain of 50% was chosen as this corresponds to the beginning of the strain stiffening region as determined by strain amplitude ramp experiments (Fig. S2, ESI†). Additional stress–strain curves for maximum load strains of 10% and 30% were also performed (Fig. S3, ESI†). For all measured maltose concentrations, the stress–strain curves in Fig. 3a show clear linear elasticity up to shear strains of at least 15% (Fig. S4, ESI†). In this work the behaviour of hydrogels in the linear regime is focused on, but it is important to note that biopolymer gels exhibit rich non-linear58–60 and delayed yielding behaviour,61–63 which would warrant subsequent studies and future work. Fitting the linear region of the stress–strain curves (Fig. S4, ESI†) and extracting the gradient yields a measurement of the storage modulus, G′. The storage modulus appears to increase sharply as a function of maltose concentration, reaching an upper plateau at just over 2 mM maltose, in good agreement with the values extracted from the frequency sweep data (Fig. 2). The stress–strain curves all show some level of residual strain at 0 Pa suggesting the gels have not yet fully recovered from the applied force, this residual strain appears to show no trend with maltose concentration (Fig. S5, ESI†). To determine that this residual strain was not indicative of permanent damage to the gels progressive strain loads were performed on the same sample (with appropriate time between to wait for relaxation of the sample). This showed that the sample followed the same load path each time demonstrating, that no permanent damage was caused (Fig. S6, ESI†).
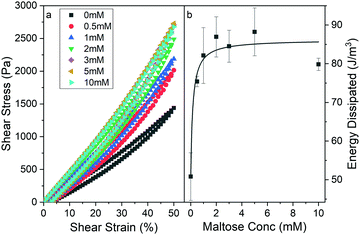 | ||
| Fig. 3 (a) Stress–strain curves of chemically crosslinked MBP hydrogels (final concentrations: 100 mg ml−1 MBP, 30 mM NaPS, 100 μM Ru) as a function of maltose concentration. Samples were strained to 50% at a rate of 1%/s and then unloaded down to 0% at the same rate. (b) Energy dissipation during load–unload cycle of MBP hydrogels as a function of maltose concentration. Solid line shows fit to Langmuir type model (eqn (S1), ESI†). | ||
In addition, the stress–strain curves (Fig. 3a) display more prominent hysteresis behaviour in the presence of increasing maltose concentrations. This hysteresis is indicative of the energy dissipated during loading and unloading and suggests that MBP hydrogels formed in the presence of higher concentrations of maltose dissipate more energy upon straining and relaxing. The area enclosed by the stress–strain provides a quantitative measure of the energy dissipated to the internal energy of the material. Calculating the energy dissipated from the curves in Fig. 3a as a function of maltose concentration, generates the graph in Fig. 3b. The energy dissipation, like the storage modulus, increases and plateaus with maltose concentration. In folded protein hydrogels, the main source of energy dissipation is believed to be force-induced unfolding,32,64 where more energy is required to unfold the more robust ligand bound MBP. Thus, increasing the maltose concentration results in stiffer gels with increased energy dissipation. Interestingly the efficiency can be measured from the curves in Fig. 3a and suggests that the same number of protein domains are unfolded irrespective of maltose concentration in order to accommodate the 50% strain on the system (Fig. S7a, ESI†). The invariance of the hydrogel efficiency with maltose is consistent between other measured load strains (Fig. S7a, ESI†), even with lower energy dissipation measured at lower strains (Fig. S7b, ESI†) suggesting that the number of protein domains being unfolded is invariant of maltose concentration but is dependent on the maximum applied strain.
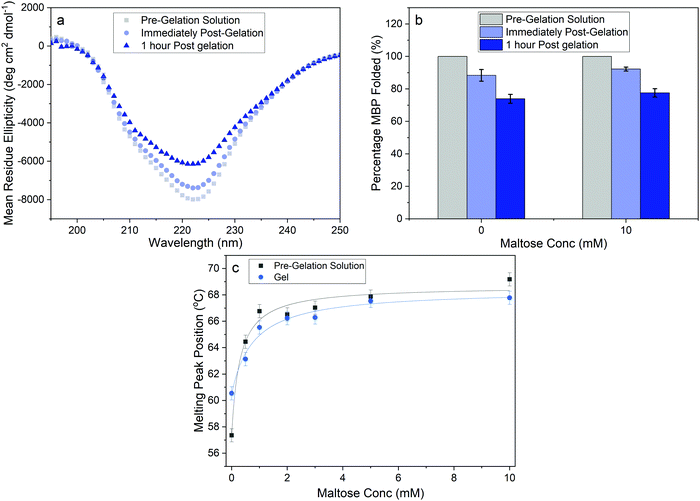
To quantify the proportion of folded MBP in our cross-linked hydrogels we performed CD experiments of MBP in solution and in the cross-linked hydrogel, both in the presence and absence of maltose. CD allows for measurement of the secondary structure of MBP and Fig. 4a shows the mean residue ellipticity spectra of MBP pre- and post-gelation, in the absence of maltose. In both the MBP solution and the hydrogel, the spectra exhibit the expected secondary structure profile for the α–β protein MBP, with negative peaks at 222 nm and 209 nm signalling α-helices and a positive peak at 195 nm signalling the presence of β-sheets. The small shift in magnitude of the peaks in the mean residue ellipticity signal post gelation shows that there is a reduction in the amount of folded protein present, both immediately following gelation and 1 hour post-gelation. The spectra can be used to extract the relative folded fraction of MBP protein post-gelation in the absence and presence of maltose (Fig. 4b), at times that are comparable to the rheology experiments. In both samples the relative folded fraction shows an initial reduction of approximately 10%, and a further reduction of ∼15% after 1 hour. These experiments show that while gelation results in unfolding of a proportion of the MBP protein, the folded population dominates and is relatively unchanged with increasing maltose concentration ((74 ± 3)% folded MBP in the absence, and (77 ± 3)% in presence, of maltose). This insignificant difference is unlikely to account for the over (1.7 ± 0.2)-fold increase in storage modulus (Fig. 2b), as if we consider the proteins as springs in parallel we would expect the sample with 10 mM maltose to have 1.7× as much folded protein in situ, compared to the sample with 0 mM maltose.
Previous studies have demonstrated that maltose bound MBP is more thermodynamically stable.47 To determine if enhanced thermal stabilisation is still present in a cross-linked hydrogel, we used differential scanning calorimetry, a technique which measures the heat flow in and out of a material upon heating and cooling. We first measured the melting temperature, Tm, of MBP in solution in the absence of maltose, obtaining a value of 58 °C in good agreement with published literature.47 We then measured Tm as a function of maltose concentration and observed an increasing Tm with increasing maltose concentration (Fig. 4c). The same DSC experiments were also completed for the MBP hydrogels, showing similar results. The increase in Tm in the hydrogels shows a slower rate of increase to the max Tm, compared to the solution data (Fig. 4c), suggesting a lower apparent Kd value. Using the DSC data and applying the Langmuir thermal shift equation (Methods), we extracted the apparent Kd values of maltose to MBP both in pre-gelation solution (290 ± 90) μM and in situ in the gel (800 ± 200) μM. The values obtained are larger than previously determined in literature (1.20 ± 0.05) μM,43,44 likely due to comparable protein (2.4 mM) and ligand (0–10 mM) concentrations in the present study causing high depletion of ligands, which is not consistent with the assumptions in binding assays that the change in ligand concentration due to binding is negligible. The apparent binding affinity allows us to calculate the number of maltose bound MBP, or ‘occupied protein’ as a function of concentration (Fig. 5, inset). By combining the rheology (Fig. 2 and 3), CD (Fig. 4a and b) and DSC (Fig. 4c) results we propose an ‘occupation model’ to describe the observed modulation of the mechanical properties of MBP hydrogels. With increased maltose concentration the probability of MBP binding to maltose increases. We expect that this would result in a greater number of mechanically more robust maltose bound MBP, or ‘occupied’ MBP. This enhancement of the mechanical stability of the folded protein building block translates to the cross-linked folded protein hydrogel, which exhibits increased mechanical strength (Fig. 5).
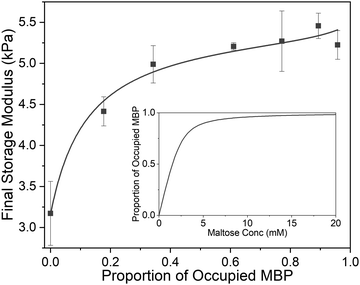 | ||
| Fig. 5 Final storage modulus as a function of proportion of ligand occupied MBP. Fitted using eqn (1) and (2) (Methods). Where the concentration of MBP, ΔG′ and G0′ are taken to be 2.4 mM, 2.25 Pa and 3.16 Pa respectively. (inset) The proportion of occupied MBP as a function of maltose concentration as modelled by eqn (2) using the values 2.4 mM and 800 μM for MBP concentration and apparent MBP: maltose dissociation constant (as extracted from DSC data), respectively. | ||
From Fig. 5 it is clear that the trend of storage modulus with the proportion of more stable ‘occupied MBP’ is not linear (as would be expected from a simple springs in parallel model), increasing rapidly at low proportion and slower at higher proportions (>0.2). This result demonstrates that the translation of stability across length scales in hierarchically structure network is highly non-trivial. Since the storage modulus increases as the proportion of ‘occupied’ MBP increases, we are able to fit Fig. 5 with a modified form of the Langmuir binding equation (Methods) and extract the apparent Kd value. The Kd value extracted from the rheology data (Fig. 5) was found to be (300 ± 100) μM, compared to (290 ± 90) μM (in pre-gel solution) and (800 ± 200) μM (in situ in the gel) extracted from the DSC data (Fig. 4c). A similar value for apparent Kd of (400 ± 200) μM was extracted from the rheology data in Fig. 3b. While these value do not match exactly with those found in the DSC experiments it is of the correct order of magnitude and is still over two-orders of magnitude larger than that previously determined in low concentration MBP solutions.
In Fig. 2b it was noted that above a critical concentration of 2 mM maltose the storage modulus was insensitive to maltose content, suggesting a saturation of the MBP binding sites. However, Fig. 5 (inset) shows that the proportion of occupied MBP is only 0.6 at 2 mM maltose concentration, implying the critical concentration is not a saturation point of available protein–ligand binding sites. Instead, it suggests that the network mechanics plateaus when a 0.6 proportion of MBP is occupied, implying a 0.4 proportion of MBP makes little contribution to the mechanical properties of the network. We examine this further in Fig. 5 which shows the steepest rate of increase in final storage modulus between 0 and 0.2 occupation, implying the mechanics of the protein network can be dominated by relatively few (1 in 5) protein building blocks. So we have shown that by controlling the proportion of mechanically robust ‘occupied’ MBP we are able to tune the storage modulus of hydrogels constructed from MBP. In addition our results imply that only a small proportion of the protein building blocks contribute to the mechanical stability of the network and approximately 40% effectively may not contribute at all.
3.3 Modulation of hydrogel structure
We have shown that the mechanical strength of a protein network is determined by the stability of the protein building block. This increase in the shear modulus of the network could, however, also arise due to an alteration of the mesoscopic structure. In order to investigate this possibility small angle neutron (SANS) and X-ray (SAXS) scattering measurements were employed, (Fig. 6a and b).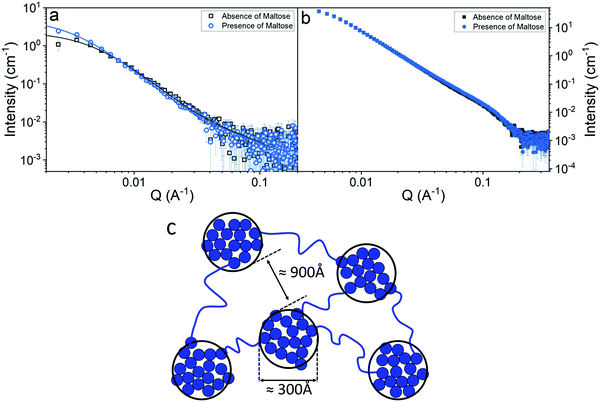 | ||
| Fig. 6 SANS curves (a) and SAXS curves (b) of folded MBP hydrogels, (final concentrations: MBP 100 mg ml−1, NaPS 30 mM, Ru 100 μm) in the absence (grey) and presence (blue) of 10 mM Maltose. Solid lines show fits to eqn (5). (c) Schematic representation of the predicted structure MBP hydrogels. | ||
Fig. 6a and b show the scattering curves of MBP hydrogels, in the absence and presence of maltose (illuminated by neutron and X-ray beams respectively). In both graphs very little difference can be seen between samples, suggesting that the differences in the mechanical properties of the gel are not due to a mesoscopic structural change. However, it is important to note that there is a difference in the gels at lower Q values of the SANS measurements, representing differences between the gels at larger length scales, highlighting the need for lower Q value measurements in order to structurally characterise protein-based hydrogels. To facilitate fitting of the data, SANS and SAXS measurements were also performed on 5–10 mg ml−1 MBP in solution (Fig. S8, ESI†) to determine the form factor of the MBP building block. Analysis of these data sets show that there is negligible change in the form between samples in the presence and absence of maltose. Fitting the data in Fig. 6a and b (see Methods) allows us to extract quantitative information about the structure of folded protein-based hydrogels (Table 1).
Previous structural characterisation of folded protein based hydrogel, (using a two-Lorentzian function) suggested the presence of clusters of crosslinked folded protein with fractal-like nature in the gel.65 Based on these findings a fractal structure factor is used to model the scattering in this work (see Methods). Three key parameters can be extracted from the data. The first two are; the correlation length representing the size of the clusters of crosslinked proteins and the fractal dimension of these clusters. The correlation length is over 10× larger than the radius of gyration of the MBP subunit unit (approx. 21 Å), this decade of separation between relevant length scales gives confidence in the validity of the fractal fit used. The third parameter here termed ‘Kiessig’ length is one that is only present in our SANS data and is extracted through peak to peak analysis of the Kiessig fringes (Fig. S9, ESI†). Kiessig fringes are the result of an interference effect due to the scattering from two separated interfaces (where the separation is much larger than the incident wavelength) such that the Bragg condition is satisfied.66,67 So the emergence of such fringes implies the existence of a repeating length scale of approximately 1000 Å in the system. The lack of definition in these fringes is what leads to the large error in these values but also is indicative that the length scale is not well defined in the system i.e. has a large standard deviation. The only parameter that genuinely varies between samples is the correlation length of the clusters, which increases in the presence of maltose, however this increase in length is not very significant (two MBP diameters). The invariance of the fractal dimension and the small change in the cluster size implies that the structure of the hydrogel is approximately the same in the absence and presence of maltose. The consistency of the gel network's structural motifs (in the presence and absence of 10 mM maltose) demonstrates that the increase in shear modulus of the network is due to the increase in stability of the protein building block, not a change in the mesoscopic structure caused by this increased stability.
Together, the parameters extracted from the scattering data shows that folded MBP hydrogels contain fractal-like clusters (Df ∼ 2.4 for SANS, 2.6 for SAXS) that vary in size from 250 Å to 340 Å with an additional preserved length scale of ∼1000 Å, and that this structure is unchanged by the addition of maltose. Combining the results of the scattering measurements with CD spectroscopy experiments, which demonstrate that there is a population of unfolded protein present in the gels, we propose a structural model of our hydrogels (Fig. 6c). Our proposed structure consists of fractal-like clusters of crosslinked folded MBP proteins linked together by strands of unfolded protein giving rise to an inter-cluster distance of ∼1000 Å. It is worth noting at this point that the Kiessig fringes we see in our data are not well defined and since these fringes arise due to Bragg interference this suggests that the length scale, we extract is also not well defined, i.e., has a large distribution of sizes. We speculate that this structure is critically regulated by the rupture force of the protein building block, instead of other mechanisms such as diffusion limited cluster aggregation, as increasing the stability of the building block appears to lead to a larger cluster size, suggesting force plays a crucial role in the formation of this architecture.
3.4 Modulation of hydrogel dynamics
Stabilisation of the protein building block through ligand binding leads to an enhancement in the storage modulus of the gels, however analysis of the kinetics of gel formation performed by rheology concurrently during light induced gel formation reveals other effects of ligand binding.The gelation curves in Fig. 7a, show the evolution of the storage modulus with time as a function of maltose concentration. The gelation curves all have the same general shape, i.e., during illumination they increase to a maximum value before relaxing to a final value (G∞′), which increases as a function of maltose concentration in agreement with end point rheology data (Fig. 2b). While the presence of maltose increases the storage modulus of the gel, the gelation time remains the same in the presence and absence of maltose (Fig. S10, ESI†). In previously literature68 it has been noted that such overshoot behaviour during gelation can be due to deswelling of the gel causing slipping between the sample and the rheometer plate. To investigate this possibility we consider the measured force normal to the plane of shear during gelation (Fig. S11, ESI†) and calculate a maximum negative (downwards) stress of −1 kPa, several times small than previously reported (−3.2 kPa).69 Nonetheless they are of the same order, so the possibility of slippage due to contraction may be present and will be the subject of further investigation. Assuming slippage is not present, here we present an explanation for the gelation behaviour.
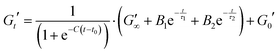 | (7) |
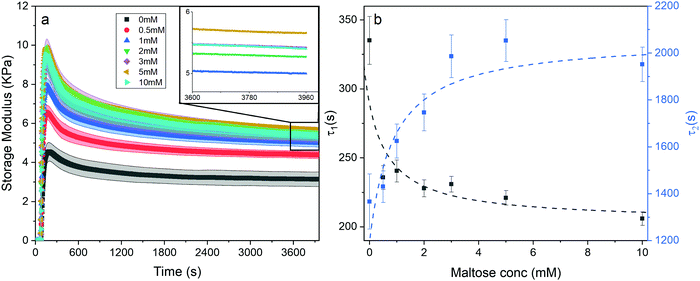 | ||
| Fig. 7 (a) Gelation curves (showing storage modulus vs. time) of chemical crosslinked MBP hydrogels (final concentrations: 100 mg ml−1 MBP, 30 mM NaPS, 100 μM Ru) as a function of maltose concentration. Illuminated at t = 60 s till t = 360 s. (inset) Magnification of the boxed section in Fig. 7a, with the error bar ribbon removed for clarity. (b) Relaxation time constant of the first and second relaxation mode, τ1 (black) and τ2 (blue) as a function of maltose concentration. | ||
In order to analyse these relatively complex kinetic profiles in more detail we fitted an empirical function to these data sets (shown in eqn (7). Example of fit shown in Fig. S12, ESI†).
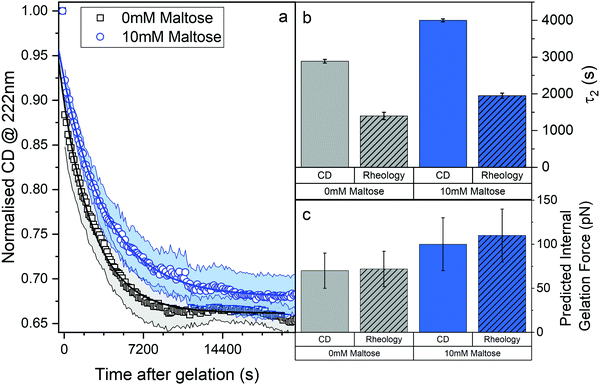
Eqn (7) shows the functional form of the gelation curves and contains two key components. The first is the sigmoidal component, which models the initial increase in the storage modulus up to the final value G∞′, where C is the rate of increase and t0 the midpoint position of the increase to the maximum in the storage modulus. The second are the two exponential terms that model the relaxation of the gels from the maximum value to the final value G∞′. Two exponential terms are required to adequately fit the gelation curves, implying that there are two distinct relaxation modes for the hydrogels during formation, one modelled by the time constant τ1 and the other by τ2. The two time constants differ by approximately a factor of 10 from each other and Fig. 7b shows how these time constants vary as a function of maltose concentration. The two time constants show inverse relationships to one another. Two possible mechanisms that could be attributed to these relaxation modes are the relaxation of the newly percolated crosslinked network into a lower energy state, and the unfolding of the MBP domains.
We employed CD to measure the evolution of the secondary structure of MBP solutions and hydrogels over the course of 10 hours, shown in Fig. 8a. (Note that these curves were corrected for dehydration in the samples over the long course of the measurements.) The normalised CD curves show a decaying relationship that plateaus to the same value of approximately 67% folded protein, taking a different amount of time to reach this plateau. The time constants of this decay (Fig. 8b) are approximately (2900 ± 50) s and (4000 ± 50) s in the absence and presence of 10 mM maltose, respectively. These values are almost exactly a factor of two larger than those determined from rheology, implying that the longer τ2 relaxation is due to the unfolding of the MBP building block. The factor of two difference may be due to the application of external strain on the system during gelation on the rheometer that is not present in the CD measurements. Interestingly we can use these time constants to predict the forces present in the gel during gelation,70 shown in Fig. 8c. The applied force during gelation lowers the energy barrier of unfolding in a linear manner. The energy being defined as Fxu at force, F where xu is the measure of the distance to the unfolded state in the energy landscape. The expression for the rate constant of unfolding at force, F (ku,F) is defined as:
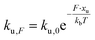 | (8) |
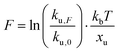 | (9) |
4. Conclusions
We have demonstrated that increasing the stability of MBP through ligand binding results in enhanced mechanical characteristics of the hydrogels. Using both SANS and SAXS we have shown that the addition of maltose does not affect the mesoscale structure of our hydrogel adding further evidence that the enhancement in protein stability at the molecular level scales directly to the macroscale. We propose an occupation model of this modulation, due to increased probability of more robust ligand bound MBP with increasing maltose concentration. A wealth of literature on the reinforcement of gels using so-called ‘fillers’ exists, in which large particles are added to fill space in the gel matrix leading to reinforcement of the gel and an increase mechanical strength.71,72 By contrast in the present study, rather than filling the space within gel network pores, we modify the molecular building block stability, namely MBP, and demonstrate the translation of increased stability to the mechanical stability of the gel network. In addition our data suggests that by stabilising only 20% of the folded protein blocks the mechanical properties of the protein network can be significantly increased. While the underlying mechanism is not known it is likely heavily related to the hierarchical structure of the network.We use our scattering data and combine it with the results of CD to postulate a structure of folded protein-based hydrogels, where there are fractal-like clusters of crosslinked folded MBP proteins linked together by strands of unfolded proteins, due to the stresses of gelation. With this structural model in place we speculate that the architecture of networks formed by mechanically labile folded proteins is critically limited and regulated by the rupture force of the protein building block.
We also investigated the effect of maltose stabilisation on the kinetics of hydrogel formation. During gel formation, after the initial crosslinking reaction there is a relaxation to a final plateau shear modulus. Assuming slippage is not present, by fitting these gelation curves with a bespoke empirical function we find that there is an increase in the time constant of this relaxation. Using CD, we are able to demonstrate that this increase in relaxation time is also due to the stabilising effect of maltose on the MBP domain. These results are interesting and warrant further investigation of the modulation of the relaxation behaviour under permanent strain, which would be important and relevant for biomedical and biomechanical applications.
By controlling the proportion of building block subunits with enhanced stability it is possible to tune the mechanical and dynamical behaviour of a network of such subunits. Furthermore, this tuning of the mechanical and dynamical properties of the hydrogel network does not come at the expense of altering the mesoscopic structure. This is an important step in understanding and, in future, exploiting the translation of building block stability on network behaviour and opening the door to environmentally responsive hydrogels with many broad applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was supported by a grant from the Engineering and Physical Sciences Research Council (EPSRC) (EP/P020088X/1) to Prof. L. Dougan. Matthew Hughes is supported by a White Rose Industrial Biotechnology studentship network. We acknowledge ISIS Neutron and Muon Spallation Source for access to the LOQ and ZOOM beamlines (experiment number RB1820509 on LOQ, and screening experiment on ZOOM), and for the use of the Nano-inXider SAXS system in the Materials Characterisation Laboratory. Additionally, we acknowledge funding from the Wellcome Trust for Chirascan, grant code 094232, and Dr G. Nasir Khan for his support. We are grateful to Dr Daniel Baker for discussions and support in rheology. Many thanks to members of the Dougan group (in particular Dr Ben Hanson and Dr Anders Aufderhorst-Roberts) and David Head for helpful discussion and feedback. The data repository for this paper can be found at https://doi.org/10.5518/799.References
- O. Lieleg, M. M. A. E. Claessens and A. R. Bausch, Soft Matter, 2010, 6, 218–225 RSC.
- Y. Mulla, F. C. Mackintosh and G. H. Koenderink, Phys. Rev. Lett., 2019, 122, 218102 CrossRef CAS PubMed.
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 485–492 CrossRef CAS PubMed.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Clarendon Press, 1986 Search PubMed.
- J. Illingworth, Biochem. Educ., 1987, 15, 101 CrossRef.
- E. S. Chhabra and H. N. Higgs, Nat. Cell Biol., 2007, 9, 1110–1121 CrossRef CAS PubMed.
- K. H. Caffall and D. Mohnen, Carbohydr. Res., 2009, 344, 1879–1900 CrossRef CAS PubMed.
- P. de Almeida, M. Jaspers, S. Vaessen, O. Tagit, G. Portale, A. E. Rowan and P. H. J. Kouwer, Nat. Commun., 2019, 10, 609 CrossRef CAS PubMed.
- M. Simonet Roda, E. Griesshaber, A. Ziegler, U. Rupp, X. Yin, D. Henkel, V. Häussermann, J. Laudien, U. Brand, A. Eisenhauer, A. G. Checa and W. W. Schmahl, Sci. Rep., 2019, 9, 598 CrossRef PubMed.
- F. Ajalloueian, G. Lemon, J. Hilborn, I. S. Chronakis and M. Fossum, Nat. Rev. Urol., 2018, 155–174 CrossRef PubMed.
- M. J. Buehler and Y. C. Yung, Nat. Mater., 2009, 175–188 CrossRef CAS PubMed.
- K. A. Jansen, A. J. Licup, A. Sharma, R. Rens, F. C. MacKintosh and G. H. Koenderink, Biophys. J., 2018, 114, 2665–2678 CrossRef CAS PubMed.
- M. Fernandez-Castano Romera, R. P. M. Lafleur, C. Guibert, I. K. Voets, C. Storm and R. P. Sijbesma, Angew. Chem., Int. Ed., 2017, 56, 8771–8775 CrossRef CAS PubMed.
- J. Swift, I. L. Ivanovska, A. Buxboim, T. Harada, P. C. D. P. D. P. Dingal, J. Pinter, J. D. Pajerowski, K. R. Spinler, J.-W. J. W. Shin, M. Tewari, F. Rehfeldt, D. W. Speicher and D. E. Discher, Science, 2013, 341, 1240104 CrossRef PubMed.
- O. Chaudhuri, S. H. Parekh and D. A. Fletcher, Nature, 2007, 445, 295–298 CrossRef CAS PubMed.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194 CrossRef CAS PubMed.
- P. A. Janmey, M. E. McCormick, S. Rammensee, J. L. Leight, P. C. Georges and F. C. MacKintosh, Nat. Mater., 2007, 6, 48–51 CrossRef CAS PubMed.
- C. P. Broedersz and F. C. Mackintosh, Rev. Mod. Phys., 2014, 86, 995–1036 CrossRef CAS.
- T. Hoffmann, K. M. Tych, M. L. Hughes, D. J. Brockwell and L. Dougan, Phys. Chem. Chem. Phys., 2013, 15, 15767 RSC.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Science, 1997, 276, 1109–1112 CrossRef CAS PubMed.
- A. F. Oberhauser, P. E. Marszalek, H. P. Erickson and J. M. Fernandez, Nature, 1998, 393, 181–185 CrossRef CAS PubMed.
- Y. Cao and H. Li, Nat. Mater., 2007, 6, 109–114 CrossRef CAS PubMed.
- Y. Chen, S. E. Radford and D. J. Brockwell, Curr. Opin. Struct. Biol., 2015, 30, 89–99 CrossRef CAS PubMed.
- X. Hu and H. Li, FEBS Lett., 2014, 588, 3613–3620 CrossRef CAS PubMed.
- J. P. Junker, F. Ziegler and M. Rief, Science, 2009, 323, 633–637 CrossRef CAS PubMed.
- S. R. K. Ainavarapu, L. Li, C. L. Badilla and J. M. Fernandez, Biophys. J., 2005, 89, 3337–3344 CrossRef CAS PubMed.
- J. P. Junker, K. Hell, M. Schlierf, W. Neupert and M. Rief, Biophys. J., 2005, 89, L46–8 CrossRef CAS PubMed.
- M. Carrion-Vazquez, T. Yoo and H. Li, Proc. Natl. Acad. Sci. U. S. A., 2008, 96, 3694–3699 CrossRef PubMed.
- J. Oroz, A. Valbuena, A. M. Vera, J. Mendieta, P. Gómez-Puertas and M. Carrión-Vázquez, J. Biol. Chem., 2011, 286, 9405–9418 CrossRef CAS PubMed.
- M. Sikora, J. I. Sułkowska and M. Cieplak, PLoS Comput. Biol., 2009, 5, e1000547 CrossRef PubMed.
- M. L. Hughes and L. Dougan, Rep. Prog. Phys., 2016, 79, 076601 CrossRef PubMed.
- S. Lv, D. M. Dudek, Y. Cao, M. M. Balamurali, J. Gosline and H. Li, Nature, 2010, 465, 69–73 CrossRef CAS PubMed.
- J. Fang, A. Mehlich, N. Koga, J. Huang, R. Koga, X. Gao, C. Hu, C. Jin, M. Rief, J. Kast, D. Baker and H. Li, Nat. Commun., 2013, 4, 2974 CrossRef PubMed.
- S. Lv, T. Bu, J. Kayser, A. Bausch and H. Li, Acta Biomater., 2013, 9, 6481–6491 CrossRef CAS PubMed.
- S. Lv, Y. Cao and H. Li, Langmuir, 2012, 28, 2269–2274 CrossRef CAS PubMed.
- J. Wu, P. Li, C. Dong, H. Jiang, B. Xue, X. Gao, M. Qin, W. Wang, B. Chen and Y. Cao, Nat. Commun., 2018, 9, 620 CrossRef.
- J. W. Bjork, S. L. Johnson and R. T. Tranquillo, Biomaterials, 2011, 32, 2479–2488 CrossRef CAS.
- F. W. Studier, Protein Expression Purif., 2005, 41, 207–234 CrossRef CAS.
- L. A. Feigin and D. I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, 1987 Search PubMed.
- J. Teixema, Small-Angle Scattering by Fractal Systems, 1988, vol. 21 Search PubMed.
- S. H. Chen and J. Teixeira, Phys. Rev. Lett., 1986, 57, 2583–2586 CrossRef CAS PubMed.
- L. Zhang and X. Mao, New J. Phys., 2018, 20, 063034 CrossRef.
- P. G. Telmer and B. H. Shilton, J. Biol. Chem., 2003, 278, 34555–34567 CrossRef CAS PubMed.
- I. H. Walker, P. Hsieh and P. D. Riggs, Appl. Microbiol. Biotechnol., 2010, 88, 187–197 CrossRef CAS PubMed.
- S. L. LaPorte, C. M. Forsyth, B. C. Cunningham, L. J. Miercke, D. Akhavan and R. M. Stroud, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1889–1894 CrossRef CAS PubMed.
- X. Duan and F. A. Quiocho, Biochemistry, 2002, 41, 706–712 CrossRef CAS PubMed.
- V. Novokhatny and K. Ingham, Protein Sci., 1997, 6, 141–146 CrossRef CAS PubMed.
- S. R. K. Ainavarapu, L. Li, C. L. Badilla and J. M. Fernandez, Biophys. J., 2005, 89, 3337–3344 CrossRef CAS PubMed.
- Y. Cao, T. Yoo, S. Zhuang and H. Li, J. Mol. Biol., 2008, 378, 1132–1141 CrossRef CAS PubMed.
- Y. Cao, M. M. Balamurali, D. Sharma and H. Li, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15677–15681 CrossRef CAS PubMed.
- M. Zocher, C. Zhang, S. G. F. Rasmussen, B. K. Kobilka and D. J. Müller, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E3463–E3472 CrossRef CAS PubMed.
- C. C. Wang, T. Y. Tsong, Y. H. Hsu and P. E. Marszalek, Biophys. J., 2011, 100, 1094–1099 CrossRef CAS.
- M. Bertz and M. Rief, J. Mol. Biol., 2008, 378, 447–458 CrossRef CAS.
- M. Bertz and M. Rief, J. Mol. Biol., 2009, 393, 1097–1105 CrossRef CAS PubMed.
- J. C. Spurlino, G. Y. Lu and F. A. Quiocho, J. Biol. Chem., 1991, 266, 5202–5219 CAS.
- C. Nick Pace, J. Martin Scholtz and G. R. Grimsley, FEBS Lett., 2014, 2177–2184 CrossRef CAS PubMed.
- M. Schlierf and M. Rief, J. Mol. Biol., 2005, 354, 497–503 CrossRef CAS PubMed.
- M. Pouzot, T. Nicolai, L. Benyahia and D. Durand, J. Colloid Interface Sci., 2006, 293, 376–383 CrossRef CAS PubMed.
- J. M. Y. Carrillo, F. C. MacKintosh and A. V. Dobrynin, Macromolecules, 2013, 46, 3679–3692 CrossRef CAS.
- B. Keshavarz, T. Divoux, S. Manneville and G. H. McKinley, ACS Macro Lett., 2017, 6, 633–667 Search PubMed.
- T. Baumberger and O. Ronsin, J. Chem. Phys., 2009, 130, 061102 CrossRef CAS PubMed.
- D. Bonn, H. Kellay, M. Prochnow, K. Ben-Djemiaa and J. Meunier, Science, 1998, 280, 265–267 CrossRef PubMed.
- M. Leocmach, C. Perge, T. Divoux and S. Manneville, Phys. Rev. Lett., 2014, 133, 038303 CrossRef.
- L. R. Khoury and I. Popa, Nat. Commun., 2019, 10, 5439 CrossRef PubMed.
- M. a. Da Silva, S. Lenton, M. Hughes, D. J. Brockwell and L. Dougan, Biomacromolecules, 2017, 18, 636–646 CrossRef CAS.
- H. Kiessig, Ann. Phys., 1931, 402, 715–768 CrossRef.
- C. Hammond, The Basics of Crystallography and Diffraction, 2nd edn, 2002.
- H. Zhang, M. Yoshimura, K. Nishinari, M. A. K. Williams, T. J. Foster and I. T. Norton, Biopolymers DOI:10.1002/1097-0282(200107)59:1<38::AID-BIP1004>3.0.CO;2-A.
- B. Mao, T. Divoux and P. Snabre, J. Rheol., 2016, 60, 473–489 CrossRef CAS.
- D. J. Brockwell, G. S. Beddard, E. Paci, D. K. West, P. D. Olmsted, D. A. Smith and S. E. Radford, Biophys. J., 2005, 89, 506–519 CrossRef CAS PubMed.
- L. Ducloué, O. Pitois, J. Goyon, X. Chateau and G. Ovarlez, Soft Matter, 2014, 10, 5093–5098 RSC.
- D. B. Genovese, Adv. Colloid Interface Sci., 2012, 171–172 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm02484k |
| This journal is © The Royal Society of Chemistry 2020 |