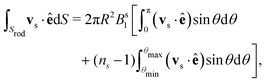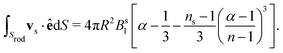DOI:
10.1039/D0SM00616E
(Paper)
Soft Matter, 2020,
16, 6400-6412
Squirmer rods as elongated microswimmers: flow fields and confinement
Received
8th April 2020
, Accepted 9th June 2020
First published on 25th June 2020
Abstract
Microswimmers or active elements, such as bacteria and active filaments, have an elongated shape, which determines their individual and collective dynamics. There is still a need to identify what role long-range hydrodynamic interactions play in their fascinating dynamic structure formation. We construct rods of different aspect ratios using several spherical squirmer model swimmers. With the help of the mesoscale simulation method of multi-particle collision dynamics we analyze the flow fields of these squirmer rods both in a bulk fluid and in Hele-Shaw geometries of different slab widths. Based on the hydrodynamic multipole expansion either for bulk or confinement between two parallel plates, we categorize the different multipole contributions of neutral as well as pusher-type squirmer rods. We demonstrate how confinement alters the radial decay of the flow fields for a given force or source multipole moment compared to the bulk fluid.
1 Introduction
Swimming at the micron scale and understanding how microorganisms overcome the constraints of low-Reynolds-number hydrodynamics have attracted a lot of attention among physicists.1–3 Intriguing features such as active turbulence,4,5 swarming,6,7 polar patterns,8 and vortex formation,8,9 which arise from the active nature of the fluid, still pose challenges to scientists. The fluid environment and the flow fields initiated by microswimmers strongly determine both their isolated motion and their appealing collective patterns, which they develop in non-equilibrium.10 But also the elongated body shapes4,7,8 and geometric confinement11–15 of microswimmers significantly contribute to their single and collective dynamics. However, it is still a matter of current debate to completely identify the individual contributions of direct steric and long-range hydrodynamic interactions.2,16,17 By introducing an active squirmer rod in this article, we aim to contribute to the discussion with a detailed analysis of its flow field in bulk and Hele-Shaw geometry.
Artificial microscopic swimmers with various locomotion mechanisms have recently been constructed to study the principal properties of their individual and collective motion. Examples mostly include spherical microswimmers.6,18–21 Elongated and flexible active constituents are realized by polar biofilaments in motility assays8 or at a fluid–fluid interface,7 while bacteria provide a natural realization of active rods.4
Combining elements of the Toner–Tu22 and Swift–Hohenberg23 theories, continuum models for bacterial microswimmers have been developed that are able to reproduce pattern formation such as vortices and active turbulence.4,24–26 Alternative continuum theories for active matter based on liquid-crystal hydrodynamics reproduce the creation, annihilation, and motion of liquid-crystal defects27 or are able to describe the dynamics of the intracellular cytoskeleton gel.2,28
In contrast, particle-based simulations are employed to study the collective dynamics of active rods. In the famous Vicsek model coarse-grained aligning interactions are able to reproduce dynamical states such as flocking and swarming.29–31 Langevin dynamics simulations of active rods4,32,33 or active filaments34,35 suggest that many properties might already emerge from short-ranged steric interactions. However, also implicit hydrodynamic pair interactions are included in such simulations to provide more realistic models with novel dynamic states.36,37 An extension to single active filaments exists.38,39 Explicit hydrodynamic simulation schemes have been applied, as well. For example, the lattice Boltzmann method was used to investigate the properties of microswimmers with various shapes40–42 while with the method of multi-particle collision dynamics collective phases of spherical43–45 and ellipsoidal microswimmers46,47 were studied, as well as realizations of pusher and puller-type swimmers.48,49
In this work, we introduce and characterize single squirmer rods with the idea to model elongated microswimmers in their fluid environment. They then can be used to disentangle the effect of direct steric and long-range hydrodynamic interactions in their collective behavior. The squirmer model swimmer45,50,51 is a good model for spherical artificial microswimmers such as Janus particles52–54 and also biological organisms such as Volvox.55 Squirmers have in common that they propel themselves by an axisymmetric surface–velocity field, which acts on the surrounding fluid.45,56,57 In biological systems this is realized by cilia, located all over the cell surface, which perform synchronized collective non-reciprocal motions. The squirmer has frequently been used in hydrodynamic simulations of the collective behavior of microswimmers42,58,59 and also by our own group,43–45,60–62 where we rely on the mesoscale method of multi-particle collision dynamics.45,63,64
In this article we use squirmers to build rigid rod-shaped microswimmers of different aspect ratios and perform large-scale simulations with multi-particle collision dynamics. We explore their hydrodynamic flow fields both in a bulk fluid and in a Hele-Shaw geometry with varying cell width, where we keep the squirmer rod in the midplane to mimic the fluid interface in the experiments of ref. 7 (cf.Fig. 1).
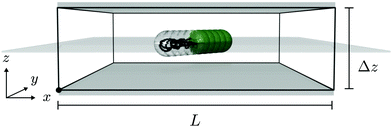 |
| | Fig. 1 Perspective view of a squirmer rod moving in the midplane (in light gray) of a Hele-Shaw cell with slab width Δz. Periodic boundary conditions along the x and y directions are used. | |
In our analysis, we rely on the hydrodynamic multipole expansion both in the bulk fluid10,40,50,65 and between two parallel plates.12–14 This will enable us to categorize the different multipoles of both neutral as well as pusher-type squirmer rods and to determine the different radial decays of their multipole flow fields.
The paper is organized as follows. In Section 2 we introduce the squirmer rod and the methods to generate and analyze its flow fields. We present the results of our analysis in Section 3 and conclude in Section 4.
2 System and methods
The hydrodynamics of the squirmer rod at small Reynolds numbers is determined by the Stokes equations including the incompressibility condition,| | η∇2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u − ∇p + f u − ∇p + f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 ∇·u 0 ∇·u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. 0. | (1) |
Here, η is the viscosity of the fluid, u(r) the fluid velocity, p(r) the pressure, and f(r) denotes a body force at point r. In the following we introduce the squirmer-rod model, the fundamental solutions of the Stokes equations both in bulk and a Hele-Shaw cell, in order to characterize its hydrodynamic multipole moments, and details of the method of multi-particle collision dynamics (MPCD) to simulate the flow fields together with the relevant parameters.
2.1 Squirmer rod model
To investigate the influence of shape anisotropy of microswimmers and their hydrodynamic interactions on collective motion, we introduce a new model of squirming active rods. To construct them, we arrange several spherical squirmers [cf.Fig. 2(a)] on a line to form a rigid body as shown in Fig. 2(b). On the one hand, this closely resembles the actual rod shape of many biological microswimmers such as bacteria, on the other hand the model can be extended to a flexible swimmer body by introducing bending rigidity in future works. In concrete, we always take Nsq = 10 spherical squirmers and vary the squirmer distance d [cf.Fig. 2(b)] to form rods of different aspect ratios α = lS/2R, where lS is the rod length. We do not go beyond a maximum squirmer distance of d ≈ 0.8R, which amounts to a maximum rod length lS = 9.5R, so that the surface is still smooth enough that swimmers can slide past each other. Each of the individual squirmers of a rod propels itself by an imposed axisymmetric surface slip-velocity field of a neutral squirmer,45,56,57| | vs = Bs1[(ê·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s) s)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s − ê] s − ê] | (2) |
that acts on the surrounding fluid. Here, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s is the unit vector along xs, which points from the squirmer center to its surface, and unit vector ê indicates the orientation and swimming direction of the squirmer. In the case of a single squirmer, the induced flow field in a bulk fluid agrees with the velocity field of a pure source-dipole singularity with strength B1 = Bs1R3 as explained in the following section. The squirmer parameter Bs1 also determines the swimming speed v0, which amounts to v0 = 2/3Bs1 for a single squirmer.
s is the unit vector along xs, which points from the squirmer center to its surface, and unit vector ê indicates the orientation and swimming direction of the squirmer. In the case of a single squirmer, the induced flow field in a bulk fluid agrees with the velocity field of a pure source-dipole singularity with strength B1 = Bs1R3 as explained in the following section. The squirmer parameter Bs1 also determines the swimming speed v0, which amounts to v0 = 2/3Bs1 for a single squirmer.
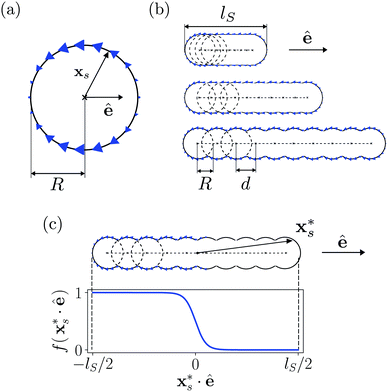 |
| | Fig. 2 (a) Schematic of a single squirmer of radius R and with orientation given by the unit vector ê. The surface slip-velocity field of a neutral squirmer is indicated by blue arrows. (b) Schematic of the squirmer rod model. Always, nsq = 10 spherical squirmers are placed on a straight line with distance d to form active rods. All squirmer orientations ê are aligned with the rod axis. (c) Implementation of a pusher type squirmer rod. The surface slip velocity on the rod surface is multiplied by the envelop function f(xs*·ê) of eqn (3) such that the slip-velocity field is concentrated on the rear of the rod. | |
Having the surface velocity field distributed over the whole squirmer rod [cf.Fig. 2(b)], our model resembles ciliated microorganisms such as Paramecium. In contrast, bacteria like E. coli propel themselves with a bundle of rotating flagella that pushes fluid backwards while the cell body does not have any surface velocity field. To implement squirmer rods of such a pusher or also of puller type, we use the envelope function
| | 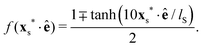 | (3) |
Here,
xs* is a vector from the center of mass of the rod to any point on the surface [
cf.Fig. 2(c)] and 10/
lS is the step width of the envelope function. Multiplying the surface velocity field with
f(
xs*·
ê), concentrates the slip velocity field on the rear half of the rod for the – sign in
f and thereby a pusher squirmer rod is realized, while the + sign generates a puller.
2.2 Fundamental solutions of Stokes flow in bulk
To provide an understanding of the flow field u(r) that squirmer rods initiate in a bulk fluid and how they interact hydrodynamically, we review the multipole expansion of u(r).50,66 It is composed of singular solutions of the Stokes equations including the Stokeslet as the flow field of the leading force monopole, which has to vanish for force-free microswimmers, the flow field of the source dipole, and their higher-order derivatives. We introduce the polar angle θ relative to the squirmer-rod axis via cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = ê·r/r. Then, in spherical coordinates r, ϕ, and θ the respective radial and polar components of the velocity field can be written as50,66
θ = ê·r/r. Then, in spherical coordinates r, ϕ, and θ the respective radial and polar components of the velocity field can be written as50,66| | 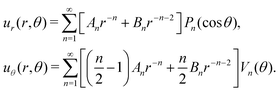 | (4) |
Here, Pn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) are the ordinary Legendre polynomials and
θ) are the ordinary Legendre polynomials and| | 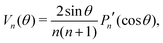 | (5) |
where ′ means derivative with respect to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Due to the rotational symmetry of a squirmer rods about its axis, the flow field is independent of the azimuthal angle ϕ and the azimuthal velocity component uϕ vanishes. The multipole coefficients An and Bn describe the strength of the nth-order force and source multipoles, where B1 belongs to the source dipole. To determine them, we calculate the nth expansion or Legendre coefficient of the radial component of the flow field in eqn (4),
θ. Due to the rotational symmetry of a squirmer rods about its axis, the flow field is independent of the azimuthal angle ϕ and the azimuthal velocity component uϕ vanishes. The multipole coefficients An and Bn describe the strength of the nth-order force and source multipoles, where B1 belongs to the source dipole. To determine them, we calculate the nth expansion or Legendre coefficient of the radial component of the flow field in eqn (4),| | 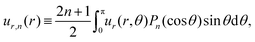 | (6) |
using the completeness relation of the Legendre polynomials, which gives| | | ur,n(r) = Anr−n + Bnr−n−2. | (7) |
Thus, from the simulated flow fields of the squirmer rods, in particular, from the radial decay of ur,n(r), we can infer their leading force and source multipole moments. We will demonstrate this in Section 3.1. Note that the nth force and source monopole can be clearly distinguished by their radial decay.
2.3 Fundamental solutions of Stokes flow in Hele-Shaw geometry
In a seminal paper Liron and Mochon12 determined the Stokeslet solution between two infinitely extended parallel plates with no-slip boundary condition (cf. Hele-Shaw geometry in Fig. 1) using an infinite series of image forces. For a force parallel to the plates (x − y plane), the x, y components of the resulting Stokeslet flow field are long-range and consist of a Poiseuille flow profile g(z) along the plate normal times the flow field of a two-dimensional source dipole in the plane (cf. Appendix A). As in the bulk fluid65 one can generate the flow fields of higher-order force moments by applying the directional derivative ê·∇p to the Stokeslet flow field.14 Here, ∇p is the nabla operator acting on the position of the Stokeslet singularity and the unit vector ê gives the direction of the force multipole in the x − y plane, which we assume to be uniaxial for simplicity. Likewise, by applying the Laplace operator ∇p2 to the Stokeslet flow field, one obtains the flow field of a source dipole, which here is up to a factor identical to the Stokeslet flow field.14 Higher source multipole moments are again generated by directional derivatives.
Relevant for the squirmer rod will be the flow fields of the source dipole (uSD), force dipole (uFD), force quadrupole (uSD), and source octupole (uSD):†
| | | u(r) = uSD(r) + uFD(r) + uFQ(r) + vSO(r) + …. | (8) |
To determine these contributions from the simulated flow field of the squirmer rod, we first average over the
z coordinate and then treat the resulting velocity field
ũ(
ρ,
φ) in the
x–
y plane using polar coordinates
ρ,
φ. As we demonstrate in Appendix A, for a microswimmer oriented along the
x axis,
ê =
êx, the multipole expansion for the radial component of the flow field gives
| | 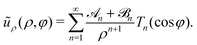 | (9) |
Here,
Tn(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ) = cos(
nφ) are the Chebyshev polynomials of the first kind and
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n
n,
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n
n are the respective coefficients of the force and source multipole moments. They start with
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 1
1 for the force monopole, which does not exist for a force-free swimmer, and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1
1 for the source dipole, and so on.
It immediately becomes obvious that in contrast to the bulk fluid one cannot distinguish the flow fields of force and source multipoles with the same angular dependence (same order n) by the radial decay. We note that the coefficients scale differently with the slab width Δz. In Appendix A we motivate ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n ∝ Δz and
n ∝ Δz and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n ∝ 1/Δz. However, our simulated data are not always sufficiently accurate to discriminate both cases. So, we assign the relevant multipole assuming that it is preserved from the bulk fluid. The multipole expansion captures the distribution of force and source multipoles in leading order. This distribution generated by the rod surface should remain the same in the Hele-Shaw geometry. However, since we deal with a voluminous rod in contrast to a point-like source, higher-order terms enter to fulfill the boundary conditions on both the rod surface and the bounding plates. The flow fields of these terms will decay faster than the leading bulk moments at some distance from the rod.
n ∝ 1/Δz. However, our simulated data are not always sufficiently accurate to discriminate both cases. So, we assign the relevant multipole assuming that it is preserved from the bulk fluid. The multipole expansion captures the distribution of force and source multipoles in leading order. This distribution generated by the rod surface should remain the same in the Hele-Shaw geometry. However, since we deal with a voluminous rod in contrast to a point-like source, higher-order terms enter to fulfill the boundary conditions on both the rod surface and the bounding plates. The flow fields of these terms will decay faster than the leading bulk moments at some distance from the rod.
Finally, exploiting the orthogonality relations of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nφ = Tn(cos
nφ = Tn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ), we extract the multipole moments from eqn (9) by projecting ũρ(ρ,φ) on the Chebyshev polynomials,
φ), we extract the multipole moments from eqn (9) by projecting ũρ(ρ,φ) on the Chebyshev polynomials,
| | 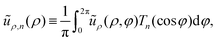 | (10) |
which yields
| |  | (11) |
In both the bulk fluid and Hele-Shaw geometry we can restrict our focus on a particular set of Stokes flow singularities. These will be the source dipole (
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1
1), force dipole (
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2
2), force quadrupole (
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3
3), and source octupole (
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3
3).
2.4 MPCD fluid model
To model the fluid in our simulations, we apply the method of multi-particle collision dynamics together with the Andersen thermostat and angular momentum conservation (MPCD-AT+a).44 The method solves the Navier–Stokes equations and thereby can also treat hydrodynamic interactions between the active squirmer rod and the confining walls of the Hele-Shaw geometry.63,64 Furthermore, it also includes thermal fluctuations. The MPCD method considers point-like particles that represent the fluid and defines rules for (i) their motion and (ii) their collisions such that the resulting hydrodynamic flow field fulfills the Navier–Stokes equations. These rules are applied in alternating steps. We shortly introduce the essential features of the MPCD method and refer to ref. 45 for more details.
During the streaming step (i) the point particles with masses m0, positions xi(t), and velocities vi(t) move ballistically during time Δt,
| | | xi(t + Δt) = xi(t) + vi(t)Δt. | (12) |
During this step fluid particles collide with confining walls or the surface of the squirmer rod. By applying the so-called bounce-back rule
44,45 the collisions either enforce the no-slip boundary condition on confining walls or the slip-velocity field on the squirmer-rod surface. In addition, the collisions also transfer both linear and angular momentum, in particular, to the squirmer rod. This changes the center-of-mass and angular momentum of the rigid rod, which is calculated relative to the center-of-mass. In Appendix B we present formulas for the mass
mrod and moment-of-inertia tensor
Irod of the rigid squirmer rod.
For the collision step (ii), the simulation volume is divided by a cubic lattice and the fluid particles are grouped into the cubic unit cells of linear size a0 and centered around ξ. First, for the nξ particles in each cell with volume ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ξ the mean velocity vξ and center-of-mass position xξ are determined. Then, in the center-of-mass frame the fluid particles are assigned new random velocities δvi from a Boltzmann-distribution with temperature T0. To restore overall momentum conservation, the total change in linear momentum,
ξ the mean velocity vξ and center-of-mass position xξ are determined. Then, in the center-of-mass frame the fluid particles are assigned new random velocities δvi from a Boltzmann-distribution with temperature T0. To restore overall momentum conservation, the total change in linear momentum, 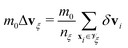 , has to be subtracted from the new velocities, while an additional term containing the difference of the angular momentum before the collision
, has to be subtracted from the new velocities, while an additional term containing the difference of the angular momentum before the collision 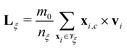 , and the change in angular momentum,
, and the change in angular momentum, 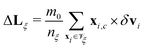 , is added to preserve angular momentum. Here xi,c denotes the particle position relative to the center-of-mass position xξ. Thus, the collision step can be summarized by
, is added to preserve angular momentum. Here xi,c denotes the particle position relative to the center-of-mass position xξ. Thus, the collision step can be summarized by
| | | vnewi = vξ + δvi − Δvξ − xi,c × Iξ−1(Lξ − ΔLξ), | (13) |
Here,
Iξ is the moment-of-inertia tensor of the distribution of particles inside
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ξ
ξ calculated in the center-of-mass frame. During this step immersed boundaries are represented by so-called “ghost” particles. They are added to the collision cells divided by the boundaries and interact with the other fluid particles. These ghost particles are assigned the local velocity of the translating and rotating squirmer rod plus a random thermal velocity drawn from a Boltzmann distribution. The changes of linear and angular momentum of the ghost particles during the collision step are then added to the squirmer rod to ensure linear and angular momentum conservation. Finally, before performing each collision step, the lattice is randomly shifted to ensure Galilean invariance.
Given the center-of-mass and angular momentum of the rigid squirmer rod, its location and orientation are updated 10 times during each collision step using a standard leapfrog algorithm.67 The rod is treated as single rigid body the position and orientation vector of which is updated following ref. 67. To keep the squirmer rod in the midplane of the Hele-Shaw cell, we only use the x and y component of the fluid force acting on the rod to integrate its motion in time throughout the simulation. Due to the symmetry about the midplane only Brownian forces are acting on the squirmer normal to the midplane. Note due to this constraint we do not observe any oscillatory trajectories between the plates as observed in ref. 68.
We have implemented the MPCD model fluid together with the squirmer-rod model in C++ and CUDA to enable the use of graphic cards. Because the main performance bottleneck in MPCD is memory access, we integrate a sorting algorithm and lookup table following ref. 69. Additionally, we use variable size cooperative thread groups to add dynamic load balancing to our MPCD collision routines in CUDA.
2.5 Geometry and fluid parameters
For the MPCD fluid we use a density of n0 = 10/a03 fluid particles per cell and the same mass density ρ0 = m0n0 for the immersed squirmer rod. With time step 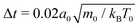 one obtains a dynamic fluid viscosity of
one obtains a dynamic fluid viscosity of 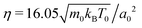 .44 Throughout this work, the radius and the squirner parameter of the single squirmer are chosen as R= 3a0 and
.44 Throughout this work, the radius and the squirner parameter of the single squirmer are chosen as R= 3a0 and 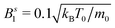 , respectively.
, respectively.
To determine how the hydrodynamic moments of the squirmer flow field in a bulk fluid varies with the aspect ratio α in Section 3.1, we simulate single rods in a cubic box of linear size L = 100a0 using periodic boundary conditions in all three dimensions. For all other bulk simulations in Sections 3.1 and 3.3, we use box sizes of L = 180a0 with periodic boundary conditions. We begin by simulating the system for a time 104Δt to equilibrate the MPCD fluid flow and then average the flow fields over the time interval from 104Δt to 5 × 106Δt. To determine the radial component vr(r,θ) of the velocity field, we also exploit the rotational symmetry of the flow fields by averaging about the rod axis. Using eqn (6), we then obtain the expansion coefficients ur,n(r) for different multipole order n and extract the strengths of the hydrodynamic moments by fitting ur,n(r) from eqn (7) to the curves determined from the simulated flow fields.
For the simulations in Hele-Shaw geometry in Sections 3.2 and 3.3, we use box sizes of L = 200a0 with no-slip walls and periodic boundary conditions along the x and y directions. For the slab width we investigate the three values Δz/R = 2.7, 6.0, and 9.3. When determining the flow fields in the Hele-Shaw geometry, the total simulation time is increased up to 107Δt to compensate for the fact that the flow field cannot be averaged about the rod axis.
3 Results
In the following, we present our results. We first discuss the flow field of a neutral squirmer rod in the bulk fluid and how it depends on the aspect ratio α. We then study neutral squirmer rods in Hele-Shaw geometries of different slab widths and illustrate the different far-field behavior compared to the bulk fluid. Finally, we look at a squirmer rod of pusher type moving in both bulk fluid and the Hele-Shaw geometry.
3.1 Neutral squirmer rods in bulk fluid
In the bulk fluid, rods of different aspect ratio α create flow fields as shown in Fig. 3. In all panels (a), (b), and (c) only a part of the simulated fluid volume is shown. In the case of the spherical squirmer, α = 1, in Fig. 3(a) we observe a perfect match with the theoretical prediction for the flow field of a source dipole moment. For a short squirmer rod with α = 1.75 the flow field already becomes stretched along the rod [cf.Fig. 3(b)]. At higher aspect ratio, α = 4.0, the flow field shows a strong deviation from the one of a source dipole moment, with the streamlines buckling inwards at the sides of the rod. Thus, we expect higher-order moments to contribute strongly to squirmer rods with higher aspect ratios α.
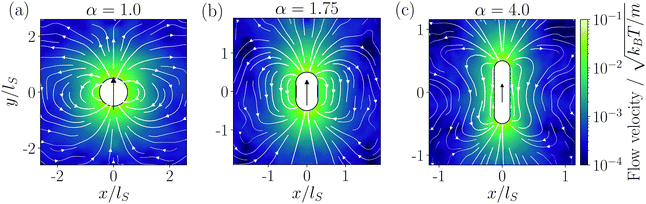 |
| | Fig. 3 Simulated flow fields of an active squirmer rod for different aspect ratios α = 1 (a), α = 1.75 (b), and α = 4.0 (c) shown in the laboratory frame. The color-coded magnitude of the velocity field and streamlines are presented. In each case only a part of the simulated fluid volume is shown. | |
To provide a quantitative analysis, we apply eqn (6) and decompose the flow field into its different angular contributions with the nth-order Legendre coefficients ur,n(r). As an example, we show in Fig. 4(a) the measured ur,n(r) as data points for a squirmer rod of α = 4 and also include fitted polynomials in r−1 as solid lines.
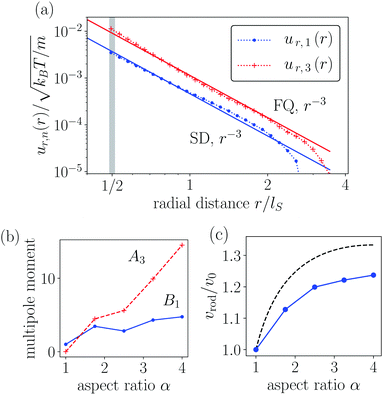 |
| | Fig. 4 (a) Radial Legendre coefficients ur,n(r) of the simulated flow field of a neutral squirmer rod with aspect ratio α = 4.0 calculated from eqn (6) (symbols) and with fitted power laws (solid lines). SD and FQ stand for source dipole and force quadrupole, respectively. (b) Hydrodynamic multipole moments in units of the squirmer parameter Bs1R3 plotted versus aspect ratio α. (c) Swimming speed vrod of a squirmer rod plotted versus α. vrod is normalized by the swimming speed v0 = 2/3Bs1 of a single squirmer at α = 1. Simulation data (blue dots) and analytical values as given by eqn (15) (dashed black line). | |
All radial velocity components ur,n(r) either show distinct power law behavior as for n = 1 and 3 or vanish. The first-order coefficient ur,1(r) clearly shows a pure 1/r3 decay, indicating a zero force monopole moment A1 while the source dipole moment B1 is present, as expected. This is consistent with the fact that we consider microswimmers free of external forces. Consistent with the head–tail symmetry of the forces, the squirmer rods exert on the fluid, we do not observe a force dipole moment, A2 = 0, since the second-order coefficient ur,2(r) vanishes. Furthermore, the third-order contribution ur,3(r) is also present and decays with 1/r3, which indicates an additional force quadrupole moment A3. We elaborate on its origin further below. Both curves ur,1(r) and ur,3(r) fall off from the theoretically predicted power law at large r due to the finite size of the simulation box. They also show small deviations from the power law, which we attribute to the flow fields of the image swimmers introduced by the use of periodic boundary conditions. All other coefficients ur,n(r) are too small to be distinguished from noise and hence can be neglected in the following. Thus, the flow field of a neutral squirmer rod is a superposition of a source dipole moment (B1 ≠ 0), and a force quadrupole moment (A3 ≠ 0), which both decay as 1/r3. In Fig. 4(b) we plot the two moments normalized by the squirmer parameter Bs1versus the aspect ratio α. They both increase roughly linearly in α. While the source-dipole moment B1 shows a modest increase in α starting from B1 = Bs1R3 for α = 1, the force quadrupole moment A3 increases much more strongly from zero and clearly dominates beyond α = 2.
The additional force quadrupole does not break the head–tail symmetry of the squirmer rod, which we therefore denote as neutral. However, the corresponding flow field clearly affects the shape of the overall flow field as we saw in Fig. 3. Since its angular dependence is governed by the third-order Legendre polynomial P3(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) compared to P1(cos
θ) compared to P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) of the source dipole, it will influence the hydrodynamic interactions with other squirmer rods, also because its flow field shows the same radial decay, 1/r3.
θ) of the source dipole, it will influence the hydrodynamic interactions with other squirmer rods, also because its flow field shows the same radial decay, 1/r3.
To shed some light on the origin of the force quadrupole, we determined the local force Fhyd(yi), with which the spherical squirmer component i placed at yi along the rod axis acts on the surrounding fluid. Of course, the rod is force free, thus all the forces Fhyd(yi) add up to zero, 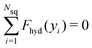 . The forces from the terminal squirmers i = 1 and i = Nsq are mainly determined by fluid pressure. They cancel each other up to some remaining force, Fhyd,p = Fhyd(y1) + Fhyd(yNsq). In the following, we refer the force of the other squirmers on this remaining force, δFhyd(yi) = Fhyd(yi) − Fhyd,p/(Nsq − 2), so that they sum up to zero:
. The forces from the terminal squirmers i = 1 and i = Nsq are mainly determined by fluid pressure. They cancel each other up to some remaining force, Fhyd,p = Fhyd(y1) + Fhyd(yNsq). In the following, we refer the force of the other squirmers on this remaining force, δFhyd(yi) = Fhyd(yi) − Fhyd,p/(Nsq − 2), so that they sum up to zero: 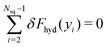 . In Fig. 5(a) we plot the relative force δFhyd(yi), the schematic in Fig. 5(b) rationalizes the different signs of δFhyd(yi). In the center of the rod (y = 0), the relative local force is negative due to the surface velocity of the squirmer rod pushing fluid backwards, while at both ends of the rod the fluid is dragged with the rod. This generates the observed force quadrupole.
. In Fig. 5(a) we plot the relative force δFhyd(yi), the schematic in Fig. 5(b) rationalizes the different signs of δFhyd(yi). In the center of the rod (y = 0), the relative local force is negative due to the surface velocity of the squirmer rod pushing fluid backwards, while at both ends of the rod the fluid is dragged with the rod. This generates the observed force quadrupole.
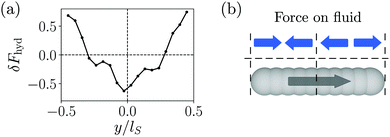 |
| | Fig. 5 (a) Local relative force δFhyd(yi), with which the squirmer rod acts on the fluid, plotted along the long axis y of the squirmer rod. The aspect ratio is α = 4. The dots correspond to the axial positions yi of the constituent squirmers and the line is a guide to the eye. Note, in contrast to the rest of the article, Nsq = 20 squirmers are used to compose the rod in order to generate a smoother surface. (b) Sketch of δFhyd(y) (blue arrows) to illustrate the force quadrupole. The grey arrow indicates the swimming velocity. | |
Finally, as we show in Fig. 4(c), the swimming speed vrod of the rod increases with α and then saturates. With increasing aspect ratio the swimming speed is more and more determined by the maximum surface velocity around the equator of the constituent squirmers and thus the speed increases. At large α the cap regions of the squirmer rod become irrelevant and the swimming speed saturates. To calculate an analytic expression for the swimming speed, we average the surface slip-velocity field vs of the squirmer rod over the whole surface with area Srod.70 For the component along the squirmer axis ê we obtain
| | 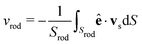 | (14) |
| | 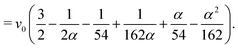 | (15) |
The derivation is sketched in Appendix C. Note that the first two terms on the right-hand side of
eqn (15) result when a perfect spherocylinder with the maximum slip velocity
Bs1 = 3
v0/2 on the straight region is assumed. For
α = 1 we reproduce the swimming velocity
v0 of the spherical squirmer.
Fig. 4(c) shows the analytic expression overestimates the swimming speed. The reason is that the surface average of
eqn (14) to calculate the swimming speed only applies to spherical shapes since then the hydrodynamic surface stress for a passive sphere is constant along the surface.
70 This is used in the derivation of
eqn (14) and obviously no longer valid for the passive squirmer rod.
3.2 Neutral squirmer rods in Hele-Shaw geometry
To discuss the flow fields of a squirmer rod in the confining Hele-Shaw geometry, we start with Fig. 6 where we show the color-coded strength of the flow field and streamlines in the midplane of the cell (upper panel) and the cross-sectional plane (lower panel). For a squirmer rod of α = 4.0 and similar to the bulk fluid [cf.Fig. 2(c)], we observe how the streamlines at the sides of the rod buckle inwards (upper panel of Fig. 6) due to the flow field of the force quadrupole moment. However, as explained in Section 2.3 and detailed in Appendix A, in the Hele-Shaw geometry the flow field of the source dipole with moment ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1 is of longer range than the one of the force quadrupole with moment
1 is of longer range than the one of the force quadrupole with moment ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3. Indeed, already at a distance lS from the rod the buckling of the flow lines is much weaker compared to the bulk fluid [cf.Fig. 3(c)] and the flow field assumes the shape of a pure source dipole.
3. Indeed, already at a distance lS from the rod the buckling of the flow lines is much weaker compared to the bulk fluid [cf.Fig. 3(c)] and the flow field assumes the shape of a pure source dipole.
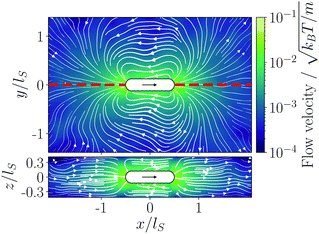 |
| | Fig. 6 Simulated flow field of a squirmer rod with aspect ratio α = 4.0 in a Hele-Shaw geometry with slab width Δz = 6R = 18a0 shown in the laboratory frame. The color-coded magnitude of the velocity field v and streamlines are presented. Upper panel: Flow field in the midplane; lower panel: flow field in the cross-sectional plane indicated by the red dashed line in the upper panel. | |
In the lower panel of Fig. 6, further away from the rod (|x/lS| > 1) the streamlines are approximately parallel to the bounding plates in agreement with the Poiseuille flow profile of the single force and source multipoles as detailed in Appendix A. However, in the direct vicinity of the rod, |x/lS| < 3/4, near-field flow along the z direction occurs, which is due to terms with exponential decay in the full hydrodynamic solution in a slab geometry.
We now present a more quantitative analysis of the simulated flow fields in Fig. 7 and 8. As for the bulk fluid, we decompose the flow fields into the different angular contributions given by the Chebyshev polynomials Tn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) using eqn (10). Since from the radial decay of the expansion coefficients ũρ,n(ρ) we cannot distinguish between the force multipole of nth order and the source multipole of n + 1th order, we are guided by the analysis in the bulk fluid from Section 3.1 and attribute the expansion coefficients ũρ,1(ρ) and ũρ,3(ρ), plotted in Fig. 7 and 8, to a source dipole (SD) and force quadrupole (FQ), respectively.
φ) using eqn (10). Since from the radial decay of the expansion coefficients ũρ,n(ρ) we cannot distinguish between the force multipole of nth order and the source multipole of n + 1th order, we are guided by the analysis in the bulk fluid from Section 3.1 and attribute the expansion coefficients ũρ,1(ρ) and ũρ,3(ρ), plotted in Fig. 7 and 8, to a source dipole (SD) and force quadrupole (FQ), respectively.
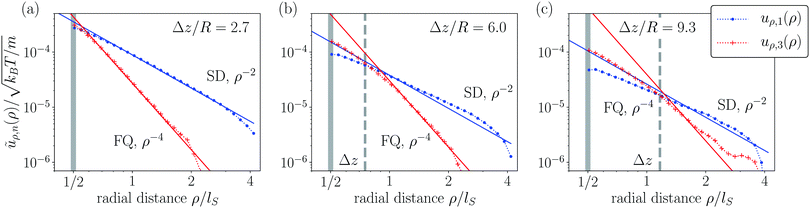 |
| | Fig. 7 Multipole analysis of the simulated flow field of a neutral squirmer rod with aspect ratio α = 4 for different slab widths of the Hele-Shaw cell: (a) Δz = 2.7R, (b) Δz = 6.0R and (c) Δz = 9.3R. As in the bulk fluid the radial decays of the expansion coefficients ũρ,n(ρ) feature a source dipole (n = 1, blue dots) and force quadrupole (n = 3, red pluses). The solid lines show fits with the corresponding power laws of ρ−2 and ρ−4, respectively. Grey vertical bar: the coefficients ũρ,n(ρ) were determine for radial distances ρ ≥ lS/2. The gray vertical dashed line indicates ρ = Δz. | |
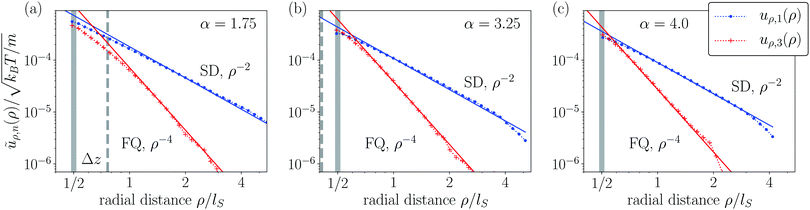 |
| | Fig. 8 Multipole analysis of the simulated flow field of a neutral squirmer rod confined in a Hele-Shaw cell with slab width Δz = 2.7R for different aspect ratios: (a) α = 1.75, (b) α = 3.25, and (c) α = 4.0. Otherwise, the same description as in Fig. 7 is used. | |
In Fig. 7 we plot ũρ,1/3(ρ) averaged over the cell height for different slab widths Δz. For a small width Δz = 2.7R = 0.34lS the coefficients are in very good agreement with the expected power-law decay: 1/ρ2 for the source dipole and 1/ρ4 for the force quadrupole. Both power laws fit well over the whole range of the radial distance. For slab width Δz = 6R = 0.75lS the measured coefficients ũρ,n(ρ) approach the predicted power-law decays at a radial distance of approximately ρ/lS = 1. This is larger than the slab width, where we expect the far-field solutions of the different multipoles to become valid. At this distance the corresponding streamlines shown in the lower panel of Fig. 6 are parallel to the bounding plates as predicted by the multipole flow fields. Finally, increasing the slab width further to Δz = 9.3R = 1.2lS the measured coefficients ũρ,n(ρ) show clear deviations from the expected power-law decay over the whole range of the radial distance ρ. All in all, when we vary the slab width, the force quadrupole moment stays the same, while the source dipole moment increases with decreasing Δz.
In Fig. 8 we choose the smallest slab width Δz/R = 2.7, where we obtained the best agreement in the previous figure and plot the coefficients ũρ,1/3(ρ) for different aspect ratios α. Again there is very good agreement between the coefficients and the expected power law decay. Only at radial distance smaller than lS one realizes deviations, as expected. This is, in particular, visible in plot (a).
3.3 Pusher-type squirmer rods
As explained in Section 2.1 we also implemented a pusher-type squirmer rod with aspect ratio α = 4.0 and show our analysis in Fig. 9. In the bulk fluid, the force dipole now dominates the flow field as the new coefficient ur,2(r) demonstrates, which decays with 1/r2 starting from r ≈ lS. Compared to the neutral squirmer rod and the dominating force dipole, the flow field of the source dipole is roughly an order of magnitude smaller. We also observe a deviation from the expected 1/r3 decay (as indicated by the solid line) to a decay of roughly 1/r2. One explanation might be the hydrodynamic interaction of the squirmer rod with its images due to the periodic boundary conditions, which especially affects the weaker multipole moments. Compared to the neutral rod, the force-dipole field is more long-ranged and therefore hydrodynamic interactions between the images are stronger, which especially influences the field of higher-order multipoles. Very different from the neutral squirmer rod, the third-order coefficient ur,3(r) changes sign at a radial distance of r ≈ lS from positive to negative with increasing r. This is why we plot the magnitude of the coefficients ur,n(r). It is tempting to fit the 1/r5 decay of a source octupole with positive moment B3 at distances r/lS < 1, while at r/lS >1 we indicate the decay of a force quadrupole with negative moment A3. Again, the latter is probably strongly disturbed by the periodic images, resulting in a decay of roughly 1/r2, similar to our observations before. In conclusion, since the flow fields of both the source dipole and force quadrupole are one order of magnitude weaker compared to the force dipole, the overall flow field is well described by the latter.
 |
| | Fig. 9 Absolute values of the radial Legendre coefficients |ur,n(r)| of the simulated flow field of a pusher-type squirmer rod with aspect ratio α = 4.0 calculated from eqn (6) (symbols) and with fitted power laws (solid lines). FD, FQ stand for force dipole and quadrupole, while SD, SO mean source dipole and octupole, respectively. | |
In Fig. 10 we analyze the flow field of the pusher-type squirmer rod in the Hele-Shaw geometry for different slab widths. In addition to the findings for the neutral squirmer rod (cf.Fig. 7), we also observe the force dipole. Compared to the bulk fluid, it now has a stronger radial decay, ũρ,2(ρ) ∝ 1/ρ3, as described by theory. At distances ρ/lS < 1.3 the strong but shorter ranged force-dipole flow field dominates, while for ρ/lS > 1.3 the slower decay of the source-dipole field takes over. Increasing the slab width, the flow field of the force dipole always dominates in the given radial range [cf.Fig. 10(b) and (c)]. The reason is the green curve shifts upwards while the blue curve shifts downwards with increasing Δz. Thus, the dipole-force moment increases with Δz in qualitative agreement with ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n ∝ Δz (cf. Section 2.3), while the source-dipole moment decreases with Δz again in qualitative agreement with
n ∝ Δz (cf. Section 2.3), while the source-dipole moment decreases with Δz again in qualitative agreement with ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n ∝ 1/Δz.
n ∝ 1/Δz.
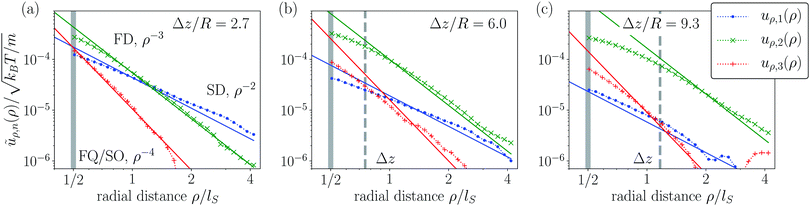 |
| | Fig. 10 Multipole analysis of the simulated flow field of a pusher-type squirmer rod with aspect ratio α = 4 for different slab widths of the Hele-Shaw cell: (a) Δz = 2.7R, (b) Δz = 6.0R and (c) Δz = 9.3R. In addition to the source dipole (n = 1, blue dots) and force quadrupole/source octupole (n = 3, red pluses), the force dipole (n = 2, green crosses) is observed. Otherwise, the same description as in Fig. 7 is used. | |
The third-order coefficient ũρ,3(ρ) ∝ 1/ρ4 does not change very significantly in one direction with increasing Δz. We take this as an indication that both the force quadrupole and source octupole contribute to the flow field. A more detailed analysis of ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3 and
3 and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3 is not feasible with the hydrodynamic MPCD method since due to thermal fluctuations it requires long averaging in order to obtain smooth flow lines at large distances. Therefore, larger system sizes would require an immense computational effort.
3 is not feasible with the hydrodynamic MPCD method since due to thermal fluctuations it requires long averaging in order to obtain smooth flow lines at large distances. Therefore, larger system sizes would require an immense computational effort.
4 Summary and conclusion
In this paper we introduced the squirmer rod as a new model for elongated microswimmers. By varying aspect ratio and surface slip-velocity field, it is able to describe artificial and biological microswimmers of different shape and propulsion type, such as pushers, pullers, and neutral swimmers. To quantify the generated hydrodynamic flow fields of the squirmer rod, we determined the hydrodynamic multipole moments both in the bulk fluid and the Hele-Shaw geometry, by projecting the simulated flow fields on Legendre or Chebyshev polynomials, respectively. The corresponding expansion coefficients showed the expected radial decay.
The flow field of the neutral squirmer rod in the bulk fluid shows the expected source dipole, while a force quadrupole moment develops linearly with increasing aspect ratio and becomes dominant beyond α = 2. It is due to a non-uniform distribution of the force, with which the rod acts on the fluid. By taking an average of the surface slip-velocity field over the rod surface, the actual swimming velocity is overestimated. In the Hele-Shaw geometry the radial decay of the multipole flow fields changes as predicted by theory. Especially at low slab width Δz we find a good match with our simulations. The flow field of the source dipole now decay as 1/ρ2 and dominates at radial distances ρ > Δz for all α and Δz over the field of the force quadrupole, which now decays as 1/ρ4.
For the pusher-type squirmer rod with noticeable elongation we observe that the flow field is composed of four hydrodynamic moments: force dipole, source dipole, force quadrupole, and source octupole. In bulk the force dipole completely dominates the flow field and determines the radial decay with 1/r2. However, in the Hele-Shaw geometry the radial decay changes to 1/ρ3 and is less long-ranged. Nevertheless, for larger slab widths and the recorded radial distances it dominates the flow field, while for small slab widths we see a cross over to the longer-ranged source-dipole field. This is in qualitative agreement with the expected behavior of the strength of the multipole moments with increasing slab width: the force dipole becomes stronger while the source dipole weakens. Finally, in the Hele-Shaw geometry the flow fields of force quadrupole and source octupole have the same radial decay. Varying slab width suggests that they both contribute.
Our work shows how elongated microswimmers generate additional hydrodynamic multipole moments compared to swimmers of spherical shape, which leads to a more complex appearance of the generated flow field. Since rods experience additional torques in a non-uniform flow field via the strain-rate tensor71 this will generate different behavior in suspensions of squirmer rods compared to their pure steric interactions. Furthermore, the source dipole is predicted to be the dominant hydrodynamic moment in a Hele-Shaw geometry,13 which we confirm for neutral squirmer rods for varying slab width. However, for pusher and puller rods the dominance of the force dipole depends on the slab width and radial distance.
Therefore, in the continuation of this work, we plan to investigate the collective dynamic behavior of the squirmer rods introduced in this work. Thereby we will gain an understanding how hydrodynamic interactions through the self-generated flow fields contribute to different types of dynamic behavior such as swarming in active nematics or active turbulent phases. As a further extension of the presented model, we plan to introduce bending rigidity between the different components of the squirmer rod to model active flexible filaments used, for example, in ref. 7 and 8.
Conflicts of interest
There are no conflicts to declare.
A Force and source multipole moments in Hele-Shaw geometry
In their seminal paper Liron and Mochon derived Green's function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) for solving the Stokes equations in a Hele-Shaw cell of width Δz (cf.Fig. 1) using an infinite series of image point forces.12 For a point force along the z axis normal to the bounding plates, the Stokeslet decays exponentially and the same applies to the flow field component u3(r) along the z direction. In the following we concentrate on the case, where the point force is directed along unit vector ê in the x–y plane and only flow in this plane is monitored. Then the main feature of the Stokeslet is the long-range flow field of a two-dimensional hydrodynamics source dipole, which appears in the second line,
for solving the Stokes equations in a Hele-Shaw cell of width Δz (cf.Fig. 1) using an infinite series of image point forces.12 For a point force along the z axis normal to the bounding plates, the Stokeslet decays exponentially and the same applies to the flow field component u3(r) along the z direction. In the following we concentrate on the case, where the point force is directed along unit vector ê in the x–y plane and only flow in this plane is monitored. Then the main feature of the Stokeslet is the long-range flow field of a two-dimensional hydrodynamics source dipole, which appears in the second line,| | 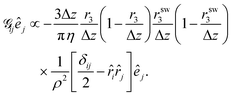 | (16) |
Here, the indices i, j ∈ {1, 2} belong to the x–y plane, ρ is the corresponding radial distance from the point force, and ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) the radial unit vector. In the first line on the right hand side a Poiseuille flow profile is visible, which vanishes at the plate locations r3 = 0 and Δz, and an equivalent term with the z coordinate of the swimmer, rsw3, appears.
the radial unit vector. In the first line on the right hand side a Poiseuille flow profile is visible, which vanishes at the plate locations r3 = 0 and Δz, and an equivalent term with the z coordinate of the swimmer, rsw3, appears.
In the Stokes flow regime any flow field surrounding a solid body can be written as the sum of hydrodynamic multipoles or singularities, which can be derived from the Stokeslet in eqn (16). For the flow field of the squirmer rod we list the relevant terms:
| | | u(r) = uFD(r) + uFQ(r) + uSD(r) + uSO(r)…. | (17) |
Since the squirmer rod is force free, there only appears the flow field of a force dipole [
uFD(
r)] and, in addition, the flow fields of a force quadrupole [
uFQ(
r)], a source dipole [
uSD(
r)], and a source octupole [
uSO(
r)].
14,65
Following ref. 14 and 65 we derive the flow fields of force multipoles with uniaxial symmetry from the Stokeslet in eqn (16) by applying the directional derivative ê·∇pn times on ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ijêj, where ∇p acts on the location of the point force. For n = 1 and 2 we thus obtain the respective flow fields of a hydrodynamic force dipole,
ijêj, where ∇p acts on the location of the point force. For n = 1 and 2 we thus obtain the respective flow fields of a hydrodynamic force dipole,
| | 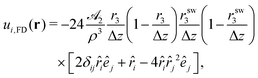 | (18) |
and force quadrupole,
| | 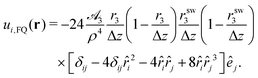 | (19) |
Note that we allocated a factor Δ
z from the Stokeslet to the force-multipole moments, so that we have
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n
n ∝ Δ
z. Again following
ref. 14 and 65, we derive the flow field of a source dipole by the operation,
ui,SD(
r) ∝ ∇
p2![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ijêj
ijêj. While the second derivative with respect to
rsws removes the term with
rsws and generates a factor 1/Δ
z2, the remaining two-dimensional Laplace operator acting on the source dipole term gives zero. Thus, one arrives at
| | 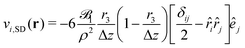 | (20) |
which is nearly identical to the Stokeslet. Flow fields of higher source multipoles are generated by the directional derivate
ê·∇
p acting on
vSD(
r). Of relevance is the second derivative, which gives the flow field of a source octupole:
| | 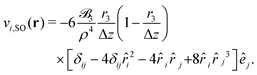 | (21) |
Again, we have allocated a factor 1/Δ
z to the source-multipole moments, so that we have
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n
n ∝ 1/Δ
z. In the following, we restrict ourselves to a squirmer rod oriented along the
x-axis and swimming in the midplane of the Hele-Shaw cell,
i.e.,
ê =
êx and
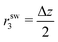
. To convert the flow fields in the Hele-Shaw geometry to a form similar to the one used in free Stokes flow, we switch to cylindrical coordinates (
ρ,
φ,
z). We eliminate the
z-dependence of the multipole flow fields by integrating over the Poiseuille profile along
z, project the resulting velocity field on the radial direction, and arrive at
| | 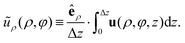 | (22) |
The resulting radial velocity component can also be decomposed into cell-height averaged multipole moments
ũρ,n. For the relevant multipole moments we have
| | ũρ(ρ,φ) = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ũρ,FD(ρ,φ) + ũρ,FQ(ρ,φ) + ũρ,SD(ρ,φ) +ũρ,SO(ρ,φ) + …. ũρ,FD(ρ,φ) + ũρ,FQ(ρ,φ) + ũρ,SD(ρ,φ) +ũρ,SO(ρ,φ) + …. | (23) |
which we calculate using
eqn (18)–(21). For the force dipole and quadrupole, we obtain
| | 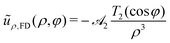 | (24) |
and
| |  | (25) |
respectively. The source dipole and octupole give
| | 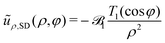 | (26) |
and
| | 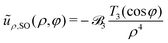 | (27) |
respectively, where the
Tn(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ
φ) = cos(
nφ) are Chebyshev polynomials of the first kind. These formulas agree with the general result given in
eqn (9) in the main text. Using
eqn (10) and (11), we can then determine the force and source moments
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2
2,
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3
3,
1, and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3
3 by a numerical fit of the power law
ρ−n to
ũρ,n(
ρ).
B Moment-of-inertia tensor of the squirmer rod
The moment-of-inertia tensor Irod of the squirmer rod can be calculated applying Steiner's theorem to the constituent parts of the squirmer rod. First, we calculate the masses mmid and mcap as well as the moment-of-inertia tensors Imid and Icap of the middle segments and end caps relative to their respective centers of mass. Due to the rotational symmetry around the rod axis, Irod, Imid and Icap have two degenerate eigenvalues in the x−y plane perpendicular to the rod axis and a different eigenvalue along the rod axis ê = ẑ.
In each of the constituent parts of the squirmer rods, we use cylindrical coordinates (ρ,φ,z), where z = 0 is the center of each spherical squirmer. The constituent parts are sections of spheres of radius R that extend from z = hmin to z = hmax. Integration over the enclosed volume with constant mass density ρ0, gives the mass
| | 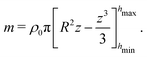 | (28) |
For the middle segments of the rod, −
hmin =
hmax =
d/2, and for the end caps
hmin = −
d/2 and
hmax =
R.
Based on the known formula for the moment-of-inertia tensor for a solid body with uniform mass density ρ0, 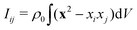 , we first calculate the Izz components of the constituent parts. Integrating ρ0ρ2 over the enclosed volume yields
, we first calculate the Izz components of the constituent parts. Integrating ρ0ρ2 over the enclosed volume yields
| | 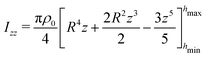 | (29) |
For the component
Ixx the integrand becomes
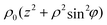
, which yields
| | 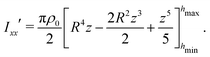 | (30) |
We attach a dash here since for the end caps the mass distribution is not symmetric about
z = 0 and therefore the center of mass of the caps does not coincide with the reference point
x = 0, for which
Ixx′ was calculated. For further use below, we need the moment of inertia
Ixx for a rotation axis perpendicular to the
z axis through the center of mass and calculate it using Steiner's theorem:
Ixx =
Ixx′ −
mzcom2. The distance
zcom between
z = 0 and the center of mass follows by integrating
zρ0/
m over the enclosed volume,
| | 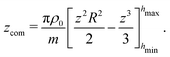 | (31) |
For the middle segments the mass distribution is symmetric about
z = 0 and hence
Ixx =
Ixx′.
We now use the previous results to calculate the relevant moments of inertia Irod,ij for the squirmer rod. For the moment Irod,zz the relevant rotational axis along ẑ goes through all the centers of mass of the ns segments. Thus, we can just add up their moments of inertia:
| | | Irod,zz = 2Icap,zz+ (ns − 2)Imid,zz. | (32) |
For the remaining non-zero moments,
Irod,xx =
Irod,yy, we have to shift the respective moments of the middle segments and end caps,
Imid,xx and
Icap,xx, using their distances from the rod's center of mass and Steiner's theorem:
| | 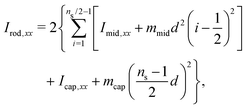 | (33) |
for an even number of squirmers per rod
ns.
C Swimming velocity
In principle, following ref. 70 the swimming velocity of a squirmer of arbitrary shape can be calculated analytically using the reciprocal theorem.70 If (v,σ) are the velocity and stress tensor that solve the Stokes equation for the force-free swimmer and (v′,σ′) the corresponding fields for a passive object of the same shape pulled now by a force F′, then| | 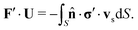 | (34) |
Here U is the swimming velocity, ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the surface normal, vs the slip velocity at the swimmer surface and S the surface of the swimmer's body. For a sphere of radius R the acting force is F′ = −6πηRU′, where U′ is the translational velocity, and the surface force density
the surface normal, vs the slip velocity at the swimmer surface and S the surface of the swimmer's body. For a sphere of radius R the acting force is F′ = −6πηRU′, where U′ is the translational velocity, and the surface force density 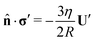 is constant and proportional to U′. Thus, for a sphere the swimming velocity U is simply the negative average of the surface slip velocity vs
is constant and proportional to U′. Thus, for a sphere the swimming velocity U is simply the negative average of the surface slip velocity vs| | 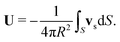 | (35) |
To provide an estimate for the swimming velocity of the squirmer rod, we apply the approximation that the surface force density is constant along the surface of the passive rod, when pulled by force F′ along its long axis. The estimate for the swimming velocity is thus the average of the surface slip velocity vs as given in eqn (14).
To determine the swimming velocity, we calculate the surface of the squirmer rod,
| | 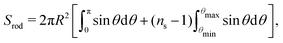 | (36) |
which adds up the surface of one complete sphere and
ns − 1 middle segments of a sphere. The integration limits for the polar angles of the middle segments are
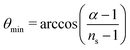
and
θmax = π −
θmin. We obtain
Srod![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
4π
R2α. Similarly, we integrate the scalar product of the surface velocity
vs and the orientation vector
ê| | vs·ê = Bs1(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1) θ − 1) | (37) |
over the surface of one complete sphere and
ns − 1 middle segments,
| | 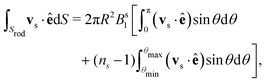 | (38) |
and obtain
| | 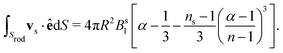 | (39) |
The swimming velocity of the squirmer rod is ultimately given by
eqn (15).
Acknowledgements
We thank Felix Rühle and Josua Grawitter for helpful discussions on the topic of the manuscript. We also acknowledge financial support from the Collaborative Research Center 910 funded by Deutsche Forschungsgemeinschaft.
References
- E. Lauga and T. R. Powers, Phys. Rev. Lett., 2009, 72, 096601 Search PubMed.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308 CrossRef CAS PubMed.
- D. Nishiguchi, I. S. Aranson, A. Snezhko and A. Sokolov, Nat. Commun., 2018, 9, 1–8 CrossRef PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef.
- T. Sánchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431 CrossRef PubMed.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 268102 CrossRef PubMed.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- J. Blake and A. Chwang, J. Eng. Mech., 1974, 8, 23–29 Search PubMed.
- N. Liron and S. Mochon, J. Eng. Mech., 1976, 10, 287–303 Search PubMed.
- T. Brotto, J.-B. Caussin, E. Lauga and D. Bartolo, Phys. Rev. Lett., 2013, 110, 038101 CrossRef PubMed.
- A. J. Mathijssen, A. Doostmohammadi, J. M. Yeomans and T. N. Shendruk, J. Fluid Mech., 2016, 806, 35–70 CrossRef.
- S. Thutupalli, D. Geyer, R. Singh, R. Adhikari and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5403–5408 CrossRef CAS PubMed.
- D. L. Koch and G. Subramanian, Annu. Rev. Fluid Mech., 2011, 43, 637–659 CrossRef.
- M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Condens. Matter Phys., 2019, 11, 441–466 CrossRef.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- D. Nishiguchi and M. Sano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052309 CrossRef PubMed.
- C. C. Maass, C. Krüger, S. Herminghaus and C. Bahr, Annu. Rev. Condens. Matter Phys., 2016, 7, 171–193 CrossRef CAS.
- J. Toner and Y. Tu, Phys. Rev. Lett., 1995, 75, 4326 CrossRef CAS PubMed.
- J. Swift and P. C. Hohenberg, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 319 CrossRef.
- J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bär and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 CrossRef PubMed.
- J. Dunkel, S. Heidenreich, M. Bär and R. E. Goldstein, New J. Phys., 2013, 15, 045016 CrossRef.
- S. Heidenreich, J. Dunkel, S. H. Klapp and M. Bär, Phys. Rev. E, 2016, 94, 020601 CrossRef PubMed.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 1–13 CrossRef CAS PubMed.
- F. Jülicher, S. W. Grill and G. Salbreux, Rep. Prog. Phys., 2018, 81, 076601 CrossRef PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS PubMed.
- G. Grégoire and H. Chaté, Phys. Rev. Lett., 2004, 92, 025702 CrossRef PubMed.
- H. Chaté, F. Ginelli, G. Grégoire, F. Peruani and F. Raynaud, Eur. Phys. J. B, 2008, 64, 451–456 CrossRef.
- H. Wensink and H. Löwen, J. Phys.: Condens. Matter, 2012, 24, 464130 CrossRef CAS PubMed.
- M. C. Bott, F. Winterhalter, M. Marechal, A. Sharma, J. M. Brader and R. Wittmann, Phys. Rev. E, 2018, 98, 012601 CrossRef CAS PubMed.
- Ö. Duman, R. E. Isele-Holder, J. Elgeti and G. Gompper, Soft Matter, 2018, 14, 4483–4494 RSC.
- K. Prathyusha, S. Henkes and R. Sknepnek, Phys. Rev. E, 2018, 97, 022606 CrossRef CAS PubMed.
- M. Hennes, K. Wolff and H. Stark, Phys. Rev. Lett., 2014, 112, 238104 CrossRef PubMed.
- H. Jeckel, E. Jelli, R. Hartmann, P. K. Singh, R. Mok, J. F. Totz, L. Vidakovic, B. Eckhardt, J. Dunkel and K. Drescher, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1489–1494 CrossRef CAS.
- A. Laskar, R. Singh, S. Ghose, G. Jayaraman, P. S. Kumar and R. Adhikari, Sci. Rep., 2013, 3, 1–5 Search PubMed.
- A. Laskar and R. Adhikari, Soft Matter, 2015, 11, 9073–9085 RSC.
- J. de Graaf, H. Menke, A. J. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- A. Pandey, P. S. Kumar and R. Adhikari, Soft Matter, 2016, 12, 9068–9076 RSC.
- M. Kuron, P. Stärk, C. Burkard, J. De Graaf and C. Holm, J. Chem. Phys., 2019, 150, 144110 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef.
- J. Blaschke, M. Maurer, K. Menon, A. Zöttl and H. Stark, Soft Matter, 2016, 12, 9821–9831 RSC.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 61 CrossRef PubMed.
- M. Theers, E. Westphal, G. Gompper and R. G. Winkler, Soft Matter, 2016, 12, 7372–7385 RSC.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- F. J. Schwarzendahl and M. G. Mazza, Soft Matter, 2018, 14, 4666–4678 RSC.
- F. J. Schwarzendahl and M. G. Mazza, J. Chem. Phys., 2019, 150, 184902 CrossRef PubMed.
- M. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801 CrossRef PubMed.
- S. Jiang, Q. Chen, M. Tripathy, E. Luijten, K. S. Schweizer and S. Granick, Adv. Mater., 2010, 22, 1060–1071 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- T. J. Pedley, D. R. Brumley and R. E. Goldstein, J. Fluid Mech., 2016, 798, 165–186 CrossRef CAS PubMed.
- T. Ishikawa, M. Simmonds and T. Pedley, J. Fluid Mech., 2006, 568, 119–160 CrossRef.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef PubMed.
- G.-J. Li and A. M. Ardekani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013010 CrossRef PubMed.
- J.-T. Kuhr, J. Blaschke, F. Rühle and H. Stark, Soft Matter, 2017, 13, 7458–7555 RSC.
- F. Rühle, J. Blaschke, J.-T. Kuhr and H. Stark, New J. Phys., 2018, 20, 025003 CrossRef.
- J.-T. Kuhr, F. Rühle and H. Stark, Soft Matter, 2019, 15, 5685–5694 RSC.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
-
G. Gompper, T. Ihle, D. Kroll and R. Winkler, Advanced computer simulation approaches for soft matter sciences III, Springer, Berlin, 2009, pp. 1–87 Search PubMed.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- J. Blake, Math. Proc. Cambridge Philos. Soc., 1971, 70, 303–310 CrossRef.
-
M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, Oxford, 2017 Search PubMed.
- J. de Graaf, A. J. Mathijssen, M. Fabritius, H. Menke, C. Holm and T. N. Shendruk, Soft Matter, 2016, 12, 4704–4708 RSC.
- M. P. Howard, A. Z. Panagiotopoulos and A. Nikoubashman, Comput. Phys. Commun., 2018, 230, 10–20 CrossRef CAS.
- H. A. Stone and A. D. Samuel, Phys. Rev. Lett., 1996, 77, 4102 CrossRef CAS PubMed.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
Footnote |
| † Although the source quadrupole shares the same radial dependence as the force dipole in the Hele-Shaw geometry, it is not considered in this list for two reasons. First, we solely observe a force dipole in the bulk fluid but no source quadrupole. Second, the strength of ũρ,2(ρ) grows with the slab width Δz in our simulations, which identifies it as a force dipole rather than a source quadrupole. We will elaborate on this further below. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Holger
Stark
* and
Holger
Stark
 *
*

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u − ∇p + f
u − ∇p + f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 ∇·u
0 ∇·u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.
0.![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s)
s)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s − ê]
s − ê]![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) s is the unit vector along xs, which points from the squirmer center to its surface, and unit vector ê indicates the orientation and swimming direction of the squirmer. In the case of a single squirmer, the induced flow field in a bulk fluid agrees with the velocity field of a pure source-dipole singularity with strength B1 = Bs1R3 as explained in the following section. The squirmer parameter Bs1 also determines the swimming speed v0, which amounts to v0 = 2/3Bs1 for a single squirmer.
s is the unit vector along xs, which points from the squirmer center to its surface, and unit vector ê indicates the orientation and swimming direction of the squirmer. In the case of a single squirmer, the induced flow field in a bulk fluid agrees with the velocity field of a pure source-dipole singularity with strength B1 = Bs1R3 as explained in the following section. The squirmer parameter Bs1 also determines the swimming speed v0, which amounts to v0 = 2/3Bs1 for a single squirmer.

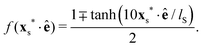
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = ê·r/r. Then, in spherical coordinates r, ϕ, and θ the respective radial and polar components of the velocity field can be written as50,66
θ = ê·r/r. Then, in spherical coordinates r, ϕ, and θ the respective radial and polar components of the velocity field can be written as50,66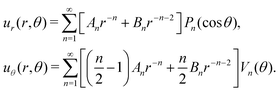
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) are the ordinary Legendre polynomials and
θ) are the ordinary Legendre polynomials and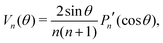
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Due to the rotational symmetry of a squirmer rods about its axis, the flow field is independent of the azimuthal angle ϕ and the azimuthal velocity component uϕ vanishes. The multipole coefficients An and Bn describe the strength of the nth-order force and source multipoles, where B1 belongs to the source dipole. To determine them, we calculate the nth expansion or Legendre coefficient of the radial component of the flow field in eqn (4),
θ. Due to the rotational symmetry of a squirmer rods about its axis, the flow field is independent of the azimuthal angle ϕ and the azimuthal velocity component uϕ vanishes. The multipole coefficients An and Bn describe the strength of the nth-order force and source multipoles, where B1 belongs to the source dipole. To determine them, we calculate the nth expansion or Legendre coefficient of the radial component of the flow field in eqn (4),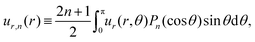
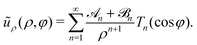
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) = cos(nφ) are the Chebyshev polynomials of the first kind and
φ) = cos(nφ) are the Chebyshev polynomials of the first kind and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n,
n, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n are the respective coefficients of the force and source multipole moments. They start with
n are the respective coefficients of the force and source multipole moments. They start with ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 1 for the force monopole, which does not exist for a force-free swimmer, and
1 for the force monopole, which does not exist for a force-free swimmer, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1 for the source dipole, and so on.
1 for the source dipole, and so on.
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n ∝ Δz and
n ∝ Δz and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n ∝ 1/Δz. However, our simulated data are not always sufficiently accurate to discriminate both cases. So, we assign the relevant multipole assuming that it is preserved from the bulk fluid. The multipole expansion captures the distribution of force and source multipoles in leading order. This distribution generated by the rod surface should remain the same in the Hele-Shaw geometry. However, since we deal with a voluminous rod in contrast to a point-like source, higher-order terms enter to fulfill the boundary conditions on both the rod surface and the bounding plates. The flow fields of these terms will decay faster than the leading bulk moments at some distance from the rod.
n ∝ 1/Δz. However, our simulated data are not always sufficiently accurate to discriminate both cases. So, we assign the relevant multipole assuming that it is preserved from the bulk fluid. The multipole expansion captures the distribution of force and source multipoles in leading order. This distribution generated by the rod surface should remain the same in the Hele-Shaw geometry. However, since we deal with a voluminous rod in contrast to a point-like source, higher-order terms enter to fulfill the boundary conditions on both the rod surface and the bounding plates. The flow fields of these terms will decay faster than the leading bulk moments at some distance from the rod.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nφ = Tn(cos
nφ = Tn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ), we extract the multipole moments from eqn (9) by projecting ũρ(ρ,φ) on the Chebyshev polynomials,
φ), we extract the multipole moments from eqn (9) by projecting ũρ(ρ,φ) on the Chebyshev polynomials,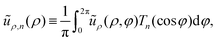

![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1), force dipole (
1), force dipole (![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2), force quadrupole (
2), force quadrupole (![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3), and source octupole (
3), and source octupole (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3).
3).
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ξ the mean velocity vξ and center-of-mass position xξ are determined. Then, in the center-of-mass frame the fluid particles are assigned new random velocities δvi from a Boltzmann-distribution with temperature T0. To restore overall momentum conservation, the total change in linear momentum,
ξ the mean velocity vξ and center-of-mass position xξ are determined. Then, in the center-of-mass frame the fluid particles are assigned new random velocities δvi from a Boltzmann-distribution with temperature T0. To restore overall momentum conservation, the total change in linear momentum, 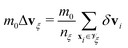 , has to be subtracted from the new velocities, while an additional term containing the difference of the angular momentum before the collision
, has to be subtracted from the new velocities, while an additional term containing the difference of the angular momentum before the collision 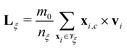 , and the change in angular momentum,
, and the change in angular momentum, 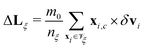 , is added to preserve angular momentum. Here xi,c denotes the particle position relative to the center-of-mass position xξ. Thus, the collision step can be summarized by
, is added to preserve angular momentum. Here xi,c denotes the particle position relative to the center-of-mass position xξ. Thus, the collision step can be summarized by![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ξ calculated in the center-of-mass frame. During this step immersed boundaries are represented by so-called “ghost” particles. They are added to the collision cells divided by the boundaries and interact with the other fluid particles. These ghost particles are assigned the local velocity of the translating and rotating squirmer rod plus a random thermal velocity drawn from a Boltzmann distribution. The changes of linear and angular momentum of the ghost particles during the collision step are then added to the squirmer rod to ensure linear and angular momentum conservation. Finally, before performing each collision step, the lattice is randomly shifted to ensure Galilean invariance.
ξ calculated in the center-of-mass frame. During this step immersed boundaries are represented by so-called “ghost” particles. They are added to the collision cells divided by the boundaries and interact with the other fluid particles. These ghost particles are assigned the local velocity of the translating and rotating squirmer rod plus a random thermal velocity drawn from a Boltzmann distribution. The changes of linear and angular momentum of the ghost particles during the collision step are then added to the squirmer rod to ensure linear and angular momentum conservation. Finally, before performing each collision step, the lattice is randomly shifted to ensure Galilean invariance.
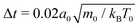 one obtains a dynamic fluid viscosity of
one obtains a dynamic fluid viscosity of 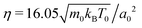 .44 Throughout this work, the radius and the squirner parameter of the single squirmer are chosen as R= 3a0 and
.44 Throughout this work, the radius and the squirner parameter of the single squirmer are chosen as R= 3a0 and 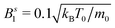 , respectively.
, respectively.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) compared to P1(cos
θ) compared to P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) of the source dipole, it will influence the hydrodynamic interactions with other squirmer rods, also because its flow field shows the same radial decay, 1/r3.
θ) of the source dipole, it will influence the hydrodynamic interactions with other squirmer rods, also because its flow field shows the same radial decay, 1/r3.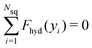 . The forces from the terminal squirmers i = 1 and i = Nsq are mainly determined by fluid pressure. They cancel each other up to some remaining force, Fhyd,p = Fhyd(y1) + Fhyd(yNsq). In the following, we refer the force of the other squirmers on this remaining force, δFhyd(yi) = Fhyd(yi) − Fhyd,p/(Nsq − 2), so that they sum up to zero:
. The forces from the terminal squirmers i = 1 and i = Nsq are mainly determined by fluid pressure. They cancel each other up to some remaining force, Fhyd,p = Fhyd(y1) + Fhyd(yNsq). In the following, we refer the force of the other squirmers on this remaining force, δFhyd(yi) = Fhyd(yi) − Fhyd,p/(Nsq − 2), so that they sum up to zero: 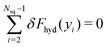 . In Fig. 5(a) we plot the relative force δFhyd(yi), the schematic in Fig. 5(b) rationalizes the different signs of δFhyd(yi). In the center of the rod (y = 0), the relative local force is negative due to the surface velocity of the squirmer rod pushing fluid backwards, while at both ends of the rod the fluid is dragged with the rod. This generates the observed force quadrupole.
. In Fig. 5(a) we plot the relative force δFhyd(yi), the schematic in Fig. 5(b) rationalizes the different signs of δFhyd(yi). In the center of the rod (y = 0), the relative local force is negative due to the surface velocity of the squirmer rod pushing fluid backwards, while at both ends of the rod the fluid is dragged with the rod. This generates the observed force quadrupole.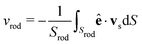
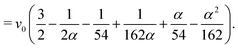
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 1 is of longer range than the one of the force quadrupole with moment
1 is of longer range than the one of the force quadrupole with moment ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3. Indeed, already at a distance lS from the rod the buckling of the flow lines is much weaker compared to the bulk fluid [cf.Fig. 3(c)] and the flow field assumes the shape of a pure source dipole.
3. Indeed, already at a distance lS from the rod the buckling of the flow lines is much weaker compared to the bulk fluid [cf.Fig. 3(c)] and the flow field assumes the shape of a pure source dipole.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) using eqn (10). Since from the radial decay of the expansion coefficients ũρ,n(ρ) we cannot distinguish between the force multipole of nth order and the source multipole of n + 1th order, we are guided by the analysis in the bulk fluid from Section 3.1 and attribute the expansion coefficients ũρ,1(ρ) and ũρ,3(ρ), plotted in Fig. 7 and 8, to a source dipole (SD) and force quadrupole (FQ), respectively.
φ) using eqn (10). Since from the radial decay of the expansion coefficients ũρ,n(ρ) we cannot distinguish between the force multipole of nth order and the source multipole of n + 1th order, we are guided by the analysis in the bulk fluid from Section 3.1 and attribute the expansion coefficients ũρ,1(ρ) and ũρ,3(ρ), plotted in Fig. 7 and 8, to a source dipole (SD) and force quadrupole (FQ), respectively.

![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n ∝ Δz (cf. Section 2.3), while the source-dipole moment decreases with Δz again in qualitative agreement with
n ∝ Δz (cf. Section 2.3), while the source-dipole moment decreases with Δz again in qualitative agreement with ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n ∝ 1/Δz.
n ∝ 1/Δz.
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3 and
3 and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3 is not feasible with the hydrodynamic MPCD method since due to thermal fluctuations it requires long averaging in order to obtain smooth flow lines at large distances. Therefore, larger system sizes would require an immense computational effort.
3 is not feasible with the hydrodynamic MPCD method since due to thermal fluctuations it requires long averaging in order to obtain smooth flow lines at large distances. Therefore, larger system sizes would require an immense computational effort.![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) for solving the Stokes equations in a Hele-Shaw cell of width Δz (cf.Fig. 1) using an infinite series of image point forces.12 For a point force along the z axis normal to the bounding plates, the Stokeslet decays exponentially and the same applies to the flow field component u3(r) along the z direction. In the following we concentrate on the case, where the point force is directed along unit vector ê in the x–y plane and only flow in this plane is monitored. Then the main feature of the Stokeslet is the long-range flow field of a two-dimensional hydrodynamics source dipole, which appears in the second line,
for solving the Stokes equations in a Hele-Shaw cell of width Δz (cf.Fig. 1) using an infinite series of image point forces.12 For a point force along the z axis normal to the bounding plates, the Stokeslet decays exponentially and the same applies to the flow field component u3(r) along the z direction. In the following we concentrate on the case, where the point force is directed along unit vector ê in the x–y plane and only flow in this plane is monitored. Then the main feature of the Stokeslet is the long-range flow field of a two-dimensional hydrodynamics source dipole, which appears in the second line,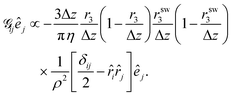
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) the radial unit vector. In the first line on the right hand side a Poiseuille flow profile is visible, which vanishes at the plate locations r3 = 0 and Δz, and an equivalent term with the z coordinate of the swimmer, rsw3, appears.
the radial unit vector. In the first line on the right hand side a Poiseuille flow profile is visible, which vanishes at the plate locations r3 = 0 and Δz, and an equivalent term with the z coordinate of the swimmer, rsw3, appears.
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ijêj, where ∇p acts on the location of the point force. For n = 1 and 2 we thus obtain the respective flow fields of a hydrodynamic force dipole,
ijêj, where ∇p acts on the location of the point force. For n = 1 and 2 we thus obtain the respective flow fields of a hydrodynamic force dipole,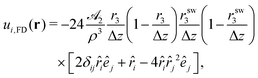
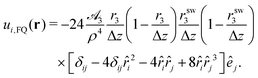
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) n ∝ Δz. Again following ref. 14 and 65, we derive the flow field of a source dipole by the operation, ui,SD(r) ∝ ∇p2
n ∝ Δz. Again following ref. 14 and 65, we derive the flow field of a source dipole by the operation, ui,SD(r) ∝ ∇p2![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) ijêj. While the second derivative with respect to rsws removes the term with rsws and generates a factor 1/Δz2, the remaining two-dimensional Laplace operator acting on the source dipole term gives zero. Thus, one arrives at
ijêj. While the second derivative with respect to rsws removes the term with rsws and generates a factor 1/Δz2, the remaining two-dimensional Laplace operator acting on the source dipole term gives zero. Thus, one arrives at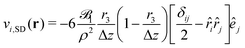
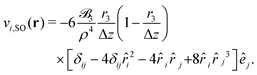
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) n ∝ 1/Δz. In the following, we restrict ourselves to a squirmer rod oriented along the x-axis and swimming in the midplane of the Hele-Shaw cell, i.e., ê = êx and
n ∝ 1/Δz. In the following, we restrict ourselves to a squirmer rod oriented along the x-axis and swimming in the midplane of the Hele-Shaw cell, i.e., ê = êx and 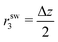 . To convert the flow fields in the Hele-Shaw geometry to a form similar to the one used in free Stokes flow, we switch to cylindrical coordinates (ρ,φ,z). We eliminate the z-dependence of the multipole flow fields by integrating over the Poiseuille profile along z, project the resulting velocity field on the radial direction, and arrive at
. To convert the flow fields in the Hele-Shaw geometry to a form similar to the one used in free Stokes flow, we switch to cylindrical coordinates (ρ,φ,z). We eliminate the z-dependence of the multipole flow fields by integrating over the Poiseuille profile along z, project the resulting velocity field on the radial direction, and arrive at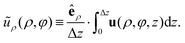
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ũρ,FD(ρ,φ) + ũρ,FQ(ρ,φ) + ũρ,SD(ρ,φ) +ũρ,SO(ρ,φ) + ….
ũρ,FD(ρ,φ) + ũρ,FQ(ρ,φ) + ũρ,SD(ρ,φ) +ũρ,SO(ρ,φ) + ….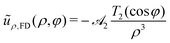

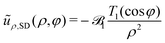
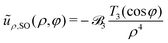
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) = cos(nφ) are Chebyshev polynomials of the first kind. These formulas agree with the general result given in eqn (9) in the main text. Using eqn (10) and (11), we can then determine the force and source moments
φ) = cos(nφ) are Chebyshev polynomials of the first kind. These formulas agree with the general result given in eqn (9) in the main text. Using eqn (10) and (11), we can then determine the force and source moments ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 2,
2, ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) 3,1, and
3,1, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 3 by a numerical fit of the power law ρ−n to ũρ,n(ρ).
3 by a numerical fit of the power law ρ−n to ũρ,n(ρ).
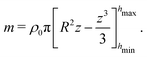
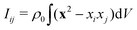 , we first calculate the Izz components of the constituent parts. Integrating ρ0ρ2 over the enclosed volume yields
, we first calculate the Izz components of the constituent parts. Integrating ρ0ρ2 over the enclosed volume yields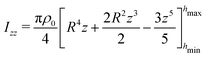
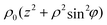 , which yields
, which yields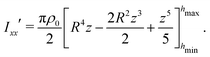
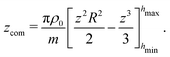
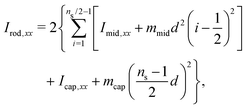
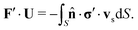
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) the surface normal, vs the slip velocity at the swimmer surface and S the surface of the swimmer's body. For a sphere of radius R the acting force is F′ = −6πηRU′, where U′ is the translational velocity, and the surface force density
the surface normal, vs the slip velocity at the swimmer surface and S the surface of the swimmer's body. For a sphere of radius R the acting force is F′ = −6πηRU′, where U′ is the translational velocity, and the surface force density 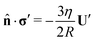 is constant and proportional to U′. Thus, for a sphere the swimming velocity U is simply the negative average of the surface slip velocity vs
is constant and proportional to U′. Thus, for a sphere the swimming velocity U is simply the negative average of the surface slip velocity vs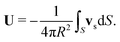
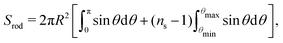
 and θmax = π − θmin. We obtain Srod
and θmax = π − θmin. We obtain Srod![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4πR2α. Similarly, we integrate the scalar product of the surface velocity vs and the orientation vector ê
4πR2α. Similarly, we integrate the scalar product of the surface velocity vs and the orientation vector ê![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)
θ − 1)