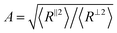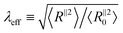Compression-induced anti-nematic order in glassy and semicrystalline polymers

Abstract

We provide new insights into the molecular origin of the asymmetry between uniaxial tensile and compressive deformation of glassy and semicrystalline polymers using molecular dynamics simulations. The difference between the two responses strongly depends on the chain length and is the largest at intermediate chain lengths. Irrespective of chain length, the intra- and interchain organization of polymers under extension and compression are remarkably distinct. The chains align along the tensile axis leading to a global nematic order of the bonds and end-to-end vectors, whereas compression reorganizes polymers to lie in planes perpendicular to the compressive axis resulting in the emergence of an anti-nematic order and destruction of crystallinity. Regardless of the initial glassy or semicrystalline structure, the deformed state of polymers at large strains converge towards the same kind of structure that only depends on the deformation mode.

---

The mechanical responses of glassy and semicrystalline polymers under various loading conditions have been the subject of intensive experimental^1–7 and theoretical^8–19 investigations. However, the effect of deformation mode on conformational and microstructural rearrangement of polymers, especially in the strain-hardening regime, still remains elusive.^1,6,10,13,20 Gaining chain-level insights into deformation mechanisms of polymers is experimentally challenging due to the small length scales involved. Thus, this challenge has been taken over by molecular simulations that allow a direct access to various intra- and inter-chain statistical measures during the plastic flow of polymeric solids.^{9,10,12–15,17,19,21,22} The simulation studies investigating the effect of deformation mode have mainly focused on glasses.^10,15,20 In the case of semicrystalline polymers, the effect of deformation mode in conjunction with chain length on the conformational changes and structural rearrangements remains largely unexplored. The few available studies are atomistic simulations of semicrystalline polymers that are limited to small length scales.^13,14 For instance, molecular simulations investigating the dependence of deformation mode in semicrystalline polymers focused only on a layered semicrystalline morphology as part of a larger spherulite structure.¹³

Using large-scale molecular dynamics (MD) simulations of a crystallizable coarse-grained polymer model,²³ we investigate the conformational and microstructural rearrangements of glassy and semicrystalline polymers of varying chain lengths during uniaxial tensile and compressive deformations. We find that the orientational order of chains under compression is entirely different from that under extension regardless of the chain length and the underlying structure. The chains align themselves under extension leading to a net nematic order. Contrarily, a uniaxial compression constrains the chains to lie within planes perpendicular to the deformation axis leading to the emergence of an anti-nematic order akin to the electric-field induced anti-nematic order observed in charged platelet suspensions.²⁴ To our knowledge, this is the first report of compression-induced anti-nematic order in solid-like polymers.

The crystallizable polymer model is a bead-spring chain with a triple-well bending potential that is obtained from coarse-graining of the atomistic simulation of polyvinyl alcohol, the so-called CG-PVA model.^23,25 Upon slow cooling of the melt, chains undergo a crystallization transition and form semicrsytalline structures consisting of randomly oriented crystallites with 2D hexagonal order immersed in a network of amorphous strands.²⁶ Short chains transform into polycrystalline structures composed of extended chain conformations, whereas longer ones form chain-folded lamella-like structures²³ as shown in Fig. 1. For a rapid quench, polymers undergo a glass transition.^17,19 Our prior investigation of tensile response of both amorphous and semicrystalline polymers¹⁹ showed that the response of long polymer glasses is dominated by the entanglement network whereas that of long semicrystalline polymers is determined by an interplay of the two interpenetrated networks of entanglements and tie chains (amorphous strands connecting the crystalline domains).¹⁹ Here, we focus on the underlying origin of asymmetry in tensile and compressive deformation of glassy and semicrystalline polymers.

Fig. 1 Conformations of CG-PVA polymers with different degrees of polymerization N in the semicrystalline state at T = 0.2.

We perform MD simulations using LAMMPS.²⁷ Distances in the CG-PVA model^25,26 are reported in units of σ = 0.52 nm, the bond length is b₀ = 0.5σ. A 6-9 Lennard-Jones potential is used to model the non-bonded interactions with the range and strength σ_LJ = 0.89σ and ε_LJ = 1.511k_BT₀ where T₀ = 550 K is the reference temperature.²⁶ The time unit from the conversion relation of units is τ = 1.3 ps. The Lennard-Jones potential is truncated and shifted at r_c = 1.6σ. Temperatures T = T_real/T₀ and pressures P = P_realσ³/ε are reported in reduced units. The equilibrated polymer melts are obtained at T = 1 and P = 8 equivalent to T₀ = 550 K and P₀ = 1 bar in atomistic simulations.²³ Glassy and semicrystalline samples of different chain lengths, N = 5, 20, 50, 300 and 1000, see ESI†²⁸ for more details, are obtained by cooling the melts from T = 1 to T = 0.2 at cooling-rates Ṫ = −10⁻³τ⁻¹ and Ṫ = −10⁻⁶τ⁻¹, respectively. Both glass transition T_g and crystallization T_c temperatures increase with chain length ranging from T_g ≈ 0.38 and T_c ≈ 0.63 for N = 5 to saturation values of T^∞_g ≈ 0.56 to T^∞_c ≈ 0.9 for N > 100, see Fig. S1 in ESI.†²⁸ The polymer gyration radii span from R_g ≈ 0.7σ for N = 5, comparable to monomers size, to R_g ≈ 15σ for N = 1000 ≫ N_e where N_e ≈ 40 is the entanglement length of semicrystalline polymers.²⁹ We use a local nematic order parameter to identify ordered and amorphous regions¹⁷ which in combination with a cluster analysis allows us to determine the volume distribution of crystalline domains.^17,19 The average linear dimensions of crystallites is in the range 14.5 ≤ L_crys/σ ≤ 48. It varies non-monotonically with N with a maximum at N = 20 given by L_crys/σ ≈ 48 and the average size of tie chains increases with N as 5 < N_tie < 30 for 20 ≤ N < 1000, see ref. 19 and Table S1 in ESI.†

The samples are deformed in the y-direction with a constant true strain-rate of [small epsi, Greek, dot above] = ±10⁻⁵τ⁻¹ while in the x and z-directions we impose the same pressure as in the undeformed samples. We restrict the maximum strain to |ε_max| = 1.8 to avoid bond scission monitored by examining the maximum extension on the covalent bonds. |ε_max| = 1.8 corresponds to a macroscopic stretch ratio λ ≡ L^‖/L^‖₀ of about 6 (1/6) for extension (compression) where L^‖₀ and L^‖ are the undeformed and instantaneous box length in the y direction parallel to the deformation axis. The volume increase is at most 10% for both glassy and semicrystalline polymers at |ε_max|, see Fig. S2 in ESI† ²⁸ and these systems behave nearly as an incompressible fluid implying that the stretch ratio in any of the perpendicular directions, x and z, follows .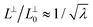

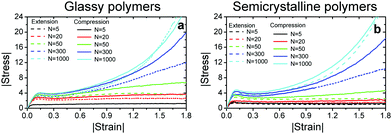
Fig. 2a and b present the magnitude of stress Σ versus magnitude of strain ε obtained under compression and extension for glassy and semicrystalline polymers, respectively. For all the samples, the elastic regime at small strains is followed by a plastic flow at larger strains. For the shortest chain length N = 5 with a gyration radius comparable to the monomer size, we observe a stress plateau beyond the yield point and the compressive and tensile responses of both glassy and semicrystalline polymers are almost identical. For longer polymers, we observe a strain-hardening regime, the slope of which increases with the chain length.¹⁹ The dependence of T_g on chain length and finite persistence length [small script l]_p ≈ 5σ are the key factors for the dependence of mechanical behavior of glassy polymers on the chain length even for N > N_e.³⁰ For both glassy and semicrystalline polymers, the compressive stress is larger than the tensile stress. The compressive elastic moduli and flow stress Σ_f (roughly estimated as the maximum value of the stress in the overshoot region) of polymers with N > 5 are about 15–20% higher in agreement with the prior experimental and simulation reports for glassy polymers.^10,20,31,32 This difference can be attributed to a slightly larger monomer density under compression relative to that under extension, see Fig. S2 in ESI.†²⁸ The difference between the two responses in the strain-hardening regime is a non-monotonic function of chain length and notably large at intermediate chain lengths N = 50 and 300. For the longest chain length N = 1000, the compressive and tensile responses become similar especially if we plot |Σ| − |Σ_f| versus |ε|, see Fig. S3 in ESI.†²⁸

Fig. 2 The magnitude of true stress in units of ε_LJ/σ³versus true strain magnitude from uniaxial compression (solid lines) and tensile (dashed lines) deformation of (a) glassy and (b) semicrystalline polymers with chain lengths N = 5, 20, 50, 300 and 1000 as given in the legends.

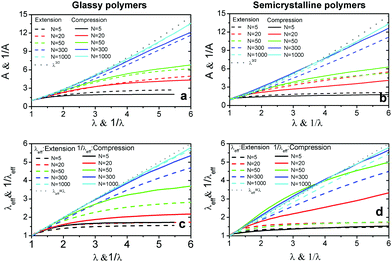
To understand the molecular origin of compressive–tensile asymmetry, we first inspect the degree of conformational anisotropy of chains at different stages of deformation. The chains elongate along the tensile axis whereas their lateral extents shrink. Under compression, the chains contract in direction parallel to the deformation axis whereas they stretch isotropically in planes perpendicular to it. We quantify the degree of conformational anisotropy A as the ratio of RMS components of the chain end-to-end vectors R in the parallel and perpendicular directions, i.e.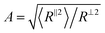 where 〈R^‖2〉 ≡ 〈R^y2〉 and 〈R^⊥2〉 ≡ (〈R^x2〉 + 〈R^z2〉)/2. In an affine deformation for which the chains follow the macroscopic deformation, we expect A = λ^3/2. Fig. 3a and b show A and 1/A as a function of macroscopic stretch λ and 1/λ for glassy and semicrystalline polymers under tensile and compressive deformations, respectively. We note that for the longest chain length, A_extension ≈ 1/A_compression and the anisotropy of conformations follows that of the box, i.e., λ^3/2. The conformational anisotropy of short chains is remarkably smaller than the macroscopic anisotropy because they entail a lesser number of degrees of freedom to follow the macroscopic stretching.

Fig. 3 The degree of conformational anisotropy for (a) glassy and (b) semicrystalline polymers under tensile deformations as a function of macroscopic stretch λ = L^‖/L^‖₀ (dashed lines) and 1/A versus 1/λ for the same systems under compression (solid lines). The gray dotted lines correspond to the box anisotropy described by λ^3/2. The effective microscopic stretch versus λ for (c) glassy and (d) semicrystalline polymers under extension (dashed lines) and 1/λ_effversus 1/λ for the same samples under compression (solid lines). The dotted grey lines shows the affine limit for which λ_eff= λ.

Next, we compare the microscopic stretch ratio of the chains with the macroscopic one λ. The effective microscopic stretch ratio is defined as 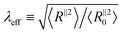.⁹ Under an affine uniaxial deformation, λ_eff = λ and the changes in 〈R^α2〉 are consistent with a volume conserving uniaxial macroscopic deformation, i.e., 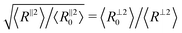. The effective stretch ratio λ_eff has recently been identified as an important parameter controlling the strain hardening behavior of amorphous and semicrystalline polymers.^9,19 When λ_eff(λ) of two samples are similar, independently of the chain length, their responses in the strain-hardening regime are also alike. Fig. 3c and d display λ_eff as a function of the macroscopic stretch λ for tensile deformation and 1/λ_effversus 1/λ for compression of glassy and semicrystalline polymers, respectively. Starting from the same initial configuration, samples deform more affinely under compression than under extension. Similar to the results for tensile deformation,¹⁹ under compression polymers in semicrystalline state deform less affinely than their glassy counterparts. However, the samples of long polymers N = 1000 exhibit a more affine behavior irrespective of deformation mode and their underlying structure. The differences between the λ_eff in extension and 1/λ_eff in compression remarkably reflect the compressive–tensile asymmetry observed in the stress responses shown in Fig. 2. The difference between the microscopic stretches is large when the asymmetry between the two responses is significant. Particularly, we observe a big contrast between compressive and tensile deformation of semicrystalline polymers of N = 50. The chains of this sample are mainly in stretched conformations with at most one fold leading to a large persistence segment s_p ≈ 20, see Fig. S4 and S5 in ESI.†²⁸ Hence, under extension they exhibit a slight degree of unfolding and stretching and their deformation mainly proceeds via reorientation of extended chain conformations with the tensile axis. Under compression, the stretching of the chains in planes perpendicular to the deformation axis leads to buckling of chains and a greater extent of chain unfolding. This leads to a notably different behavior of λ_eff of N = 50 semicrystalline polymers under compression relative to other chain lengths.

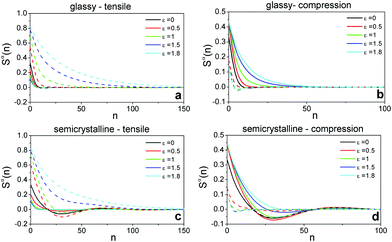
To inspect the conformational changes under deformation, we compute the components of intrachain bond–bond correlation functions given by S^α(n) = 〈b^α_ib^α_i+n〉 where b^α_i is the component α of ith unit bond vector b_i of a chain and 1 ≤ n ≤ N − 1 is the curvilinear distance between any two monomers along the chain backbone. Fig. 4 presents the intrachain bond–bond correlations of glassy and semicrystalline polymers of N = 1000 in the directions parallel S^‖(n) ≡ S^y(n) and perpendicular S^⊥(n) ≡ (S^x(n) + S^z(n))/2 to the deformation axis at different strain magnitudes. In undeformed isotropic samples S^α(0) = 〈b^α2_i〉 = 1/3. For the undeformed semicrystalline polymers, we observe a minimum at n ≈ 30 reflecting the average length of chain folds. Under tensile deformation, the parallel correlations S^‖(n) increase whereas the perpendicular correlations S^⊥(n) decrease and the minimum of S^α(n) observed for undeformed semicrystalline polymers disappears at large deformations. The results confirm unfolding of chains and their alignment with the tensile direction.^17,18 On the contrary, under uniaxial compression the intrachain correlations of both glassy and semicrystalline polymers shrink in the parallel direction and grow in the perpendicular direction. Because the chains can stretch at any direction perpendicular to the deformation axis, we observe a lesser degree of chain unfolding in comparison to extension-induced chain stretching at equal strain magnitudes.

Fig. 4 Anisotropic intrachain bond–bond orientational correlation functions against the curvilinear distance n along chain backbones at different tensile and compressive strain magnitudes ε for glassy (a and b) and semicrystalline polymers (c and d) with chain length N = 1000. The dashed lines depict the intrachain correlations parallel to the deformation axis S^‖(n) ≡ S^y(n) and the solid lines correspond to the average intrachain correlations in the perpendicular directions S^⊥(n) ≡ (S^x(n) + S^z(n))/2.

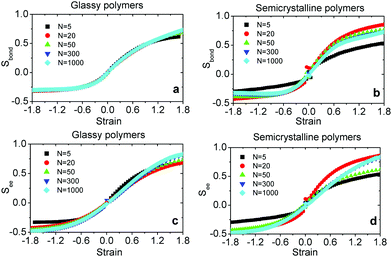
Fig. 4 shows that not only the correlation lengths of the S^‖(n) and S^⊥(n) change upon deformation but also their starting values S^α(0) evolve. These changes are expected, because the mean squared projections of bond vector components S^α(0) are related to the eigenvalues of the global nematic tensor of bond orientation vectors 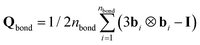where n_bond is the total number of bonds in the system. Especially, the eigenvalue with the largest magnitude S_bond is given by S_bond = 1/2(3S^‖(0) − 1). S_bond varies in the range −0.5 ≤ S_bond ≤ 1. In an isotropic state, the three eigenvalues are null and S_bond = 0. The degeneracy is lifted as soon as the structure gets anisotropic. Two extreme cases can be envisaged. When all the bond vectors are aligned in the same direction, S_bond → 1 leading to a perfect uniaxial nematic alignment. On the other hand, when all the bonds are perpendicular to the director, without any preferred azimuthal direction, a perfect uniaxial anti-nematic order described by S_bond → −0.5 emerges. The evolution of S_bond is presented in Fig. 5a and b. Under both compression and extension, the director of the nematic tensor Q_bond is aligned with the deformation axis. Under extension, reorientation of bonds with the tensile axis leads to increase of S_bond with strain and it approaches unity at large ε. Under compression, negative strains, S_bond gradually decreases and becomes more negative. A negative S_bond is an evidence of anti-nematic order reflecting a distinct arrangement of bonds under compression and a notable destruction of initial crystalline order, see Fig. S6 in ESI.† As the polymeric material is uniaxially compressed, the chains elongate isotropically in directions perpendicular to the compressive axis. Consequently, a large fraction of bond vectors are oriented in planes orthogonal to the deformation axis.

Fig. 5 The global nematic order parameter of bonds S_bond for glassy (a) and semicrystalline (b) polymers of different chain lengths, N, as a function of strain in both compression (negative strain) and tensile deformation modes. Likewise, the strain-dependence of the nematic order parameter of chains end-to-end vector S_ee for glassy (c) and semicrystalline (d) polymers.

To examine the collective organization of the chains, we calculate the nematic order tensor associated with the chain end-to-end orientation vectors R̂_i ≡ R_i/R_i obtained as 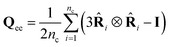where n_c is the total number of chains. Likewise, we define S_ee as the eigenvalue of Q_ee with the largest magnitude varying in the range −0.5 ≤ S_ee ≤ 1. Fig. 5c and d show the evolution of S_ee as a function of strain for glassy and semicrystalline polymers, respectively. We observe a very similar trend to that of S_bond, nematic and anti-nematic order under extension and compression, respectively. However, the absolute values of S_ee are larger than the corresponding ones for S_bond, especially in the compressive regime where S_ee → −0.5 already at ε ≈ −1.5 for N > 5. The emergent anti-nematic order suggests that a local buckling mechanism may be at play under compression as supported by our visual inspections.²⁸ We observe a non-monotonic behavior of both S_bond and S_ee as a function of N for semicrystalline polymers which reflects the initial non-monotonic dependence of crystallinity degree on N; see Table S1 (ESI†).

We conclude by highlighting our main findings and suggestions for future directions. The degree of asymmetry between the tensile and compressive responses depends on both the underlying structure (degree of crystallinity) and the chain length. The two responses become similar for very short N ≪ N_e and long chains N ≫ N_e. Even when the two responses are similar, the nature of inter- and intra-chain organization under the two deformation modes is very distinct. Alignment of chains along the tensile axis leads to a nematic order of bond and end-to-end vectors, whereas reorganization of polymers under compression results in an anti-nematic order. Deformation mode also affects the crystalline domains differently. During tensile deformation, the crystalline domains of semicrystalline polymers are fragmented and reoriented along the tensile axis^17,18 and eventually at large strains the initial hexagonal order of semicrystalline polymers²⁶ is replaced by a nematic order. Under compression the degree of crystallinity is dramatically reduced as a consequence of anti-nematic ordering. Notably, at large strains configurations of semicrystalline and glassy polymers become similar as a result of chain unfolding and reorientation. Thus, the same kind of order appears in both glassy and semicrystalline polymers under identical deformation modes but the degree of ordering at a given strain depends on the chain length and the underlying structure. The convergence towards affine limit also depends on both the underlying structure and deformation mode. The approach to affine limit occurs quicker under compression, leading to a large degree of compressive–tensile asymmetry at intermediate chain lengths. Moreover, the finite persistence length [small script l]_p ≈ 5b₀ seems to affect the convergence behavior when we compare our results to those of flexible polymer glasses under compression. The latter exhibits an affine behavior already for N > N_e.^9,10

Finally, we point out that the observed compressive–tensile asymmetry can not be captured by affine entropic network models which attribute the strain-hardening to a loss of conformational entropy of polymers.³³ The stress in the strain-hardening regime predicted by these theories is given by Σ − Σ_f = G_H(λ² − 1/λ), where G_H is the strain-hardening modulus. This leads to a weaker stress response under compression relative to extension at equal strain magnitudes. Our findings reinforce the significance of the effective microscopic stretch λ_eff^9,19 for the description of the strain-hardening behavior. Nonetheless, the mechanical response is determined by a complex interplay of intra- and interchain organization in conjunction with the relevant length scales, i.e. [small script l]_p and N_e for glassy polymers and [small script l]_p, N_e, L_crys and N_tie for semicrystalline polymers. As such, the new insights from our simulations provide the necessary input for development of physics-based constitutive models for solid-like polymers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Kurt Binder for helpful discussions. S. J.-F. acknowledges financial support from the German Research Foundation (http://www.dfg.de) within SFB TRR 146 (http://trr146.de). The computations were performed the supercomputer clusters Mogon I and II at Johannes Gutenberg University Mainz (hpc.uni-mainz.de).

Notes and references

1. M. C. Boyce and E. M. Arruda, Polym. Eng. Sci., 1990, 30, 1288–1298.
2. Y. Men, J. Rieger and G. Strobl, Phys. Rev. Lett., 2003, 91, 095502.
3. S. Humbert, O. Lame and G. Vigier, Polymer, 2009, 50, 3755–3761.
4. P. Lin, S. Cheng and S.-Q. Wang, ACS Macro Lett., 2014, 3, 784–787.
5. J. Liu, P. Lin, S. Cheng, W. Wang, J. W. Mays and S.-Q. Wang, ACS Macro Lett., 2015, 4, 1072–1076.
6. T. A. Tervoort and L. E. Govaert, J. Rheol., 2000, 44, 1263–1277.
7. D. J. A. Senden, J. A. W. van Dommelen and L. E. Govaert, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1483–1494.
8. J. Rottler and M. O. Robbins, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011507.
9. R. Hoy and M. O. Robbins, Phys. Rev. Lett., 2007, 99, 117801.
10. T. Ge and M. O. Robbins, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1473–1482.
11. Jatin, V. Sudarkodi and S. Basu, Int. J. Plast., 2014, 56, 139–155.
12. S. Lee and G. C. Rutledge, Macromolecules, 2011, 44, 3096–3108.
13. J. M. Kim, R. Locker and G. C. Rutledge, Macromolecules, 2014, 47, 2515–2528.
14. I.-C. Yeh, J. W. Andzelm and G. C. Rutledge, Macromolecules, 2015, 48, 4228–4239.
15. E. F. Oleinik, M. A. Mazo, I. A. Strelnikov, S. N. Rudnev and O. B. Salamatina, Polym. Sci., Ser. A, 2018, 60, 1–49.
16. J. van Dommelen, D. Parks, M. Boyce, W. Brekelmans and F. Baaijens, J. Mech. Phys. Solids, 2003, 51, 519–541.
17. S. Jabbari-Farouji, J. Rottler, O. Lame, A. Makke, M. Perez and J. L. Barrat, ACS Macro Lett., 2015, 4, 147–151.
18. S. Jabbari-Farouji, J. Rottler, O. Lame, A. Makke, M. Perez and J. L. Barrat, J. Phys.: Condens. Matter, 2015, 27, 194131.
19. S. Jabbari-Farouji, O. Lame, M. Perez, J. Rottler and J.-L. Barrat, Phys. Rev. Lett., 2017, 118, 217802.
20. I. A. Strelnikov, M. A. Mazo, N. K. Balabaev, E. F. Oleinik and A. A. Berlin, Dokl. Phys. Chem., 2014, 457, 108.
21. H. Cho, J. C. Weaver, E. Pöselt, P. J. in't Veld, M. C. Boyce and G. C. Rutledge, Adv. Funct. Mater., 2016, 26, 6938–6949.
22. A. J. Parker and J. Rottler, ACS Macro Lett., 2017, 6, 786–790.
23. H. Meyer and F. Müller-Plathe, J. Chem. Phys., 2001, 115, 7807–7810.
24. I. Dozov, E. Paineau, P. Davidson, K. Antonova, C. Baravian, I. Bihannic and L. J. Michot, J. Phys. Chem. B, 2011, 115, 7751–7765.
25. S. Jabbari-Farouji, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 1376–1392.
26. H. Meyer and F. Müller-Plathe, Macromolecules, 2002, 35, 1241–1252.
27. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
28. S. Jabbari-Farouji and D. Vandembroucq, 2019, ESI†.
29. C. Luo and J. Sommer, ACS Macro Lett., 2013, 2, 31–34.
30. J. T. Seitz, J. Appl. Polym. Sci., 1993, 49, 1331–1351.
31. I. M. Ward and J. Sweeney, Mechanical Properties of Solid Polymers, Wiley, Chichester, UK, 3rd edn, 2013.
32. N. Inoue, A. Yonezu, Y. Watanabe, H. Yamamura and B. Xu, ASME. J. Eng. Mater. Technol., 2017, 139(2), 021002.
33. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003.

---

Footnote

† Electronic supplementary information (ESI) available: More details on configurations of polymers. See DOI: 10.1039/c9sm01848d

---