Entropy estimates of a hard sphere system by data compression of Monte Carlo simulation data

Abstract

Data compression algorithms remove redundant information from a file. The extent to which a file size is reduced is a measure of the entropy. Recently, it has been suggested to use this technique to find the entropy from a simulation of a physical system. Here, we apply this technique to estimate the entropy from Monte Carlo simulations of the hard sphere system. Numerical results compare well with the limited available entropy estimates from the laborious thermodynamic integration method, while this new algorithm is much faster. Our results show the phase transition by calculation of the entropy for a large number of densities. A common tangent method is used to find the coexistence densities for the fluid–solid phase transition. The upper density deviates from the established density from the literature, while the lower density compares very well.

---

Introduction

It is well known that the hard sphere system has a first order phase transition from a disordered fluid-like organisation below a volume fraction ϕ_f ≈ 0.494 to a crystalline ordering above a volume fraction ϕ_s ≈ 0.545. A set of particles that do not interact until they touch, and then experience an infinitely strong repulsion, has a temperature independent phase diagram. In other words, the phase transition is purely entropic in nature. In the region ϕ_f < ϕ < ϕ_s the overall system can gain entropy by having a subset of its particles ordered in a close, typically FCC, packing so that the remainder of the particles have more space available to be in the fluid-like disordered state by increasing the translational entropy. After this transition was found by computer simulations,^1,2 careful experiments that approximated the hard sphere system confirmed the phase transition.³

As entropy rules in this system, one would expect that in computer simulations of the hard sphere system this quantity should be focused on in large detail. However, entropy estimates from computer simulations of the hard sphere system are surprisingly rare and have been calculated only for a handful of densities.^4–6 The simple reason is that the state of the art method for this, thermodynamic integration, is computationally tedious and expensive. It requires (for the solid branch) a series of simulations in between the Einstein crystal and the hard sphere system, making this method time consuming. Alternatives to estimating the entropy from computer simulation data might improve this situation. Data compression algorithms may provide such an alternative route.

Data compression algorithms, not to be confused with physical volume compression, are designed to remove redundant information from a file. They have come to a good level of maturity and are highly efficient, which is why they are commonly used in data storage. The compression ratio, that is the file size after the compression relative to the original file size, is known to be related to the Shannon entropy, which is a measure of the information content in the file. This Shannon entropy is equivalent to the physical entropy of a system when the file that is compressed contains the relevant physical information (conformations, snapshots, etc.) of the system of interest. Briefly, physical entropy is a measure of repetition and compression algorithms remove repetitious data, giving a direct relation between the two.

Recently, Avinery et al. suggested to use this method to compute the entropy from computer simulations of a physical system. They tested the method successfully for the energy ladder, various variants of the 2D Ising model, the Gaussian chain in two dimensions and a protein-folding problem.⁷ The general idea is to store physical quantities to a data file, such as distances or angles for multiple snapshots of a physical system. The data compression algorithm is then applied to this data file, reducing its file content based on the repetition within the initial data. This compression factor is then correlated with the physical entropy of the system. The method is simplest to implement if the system has discrete states such as the energy ladder, because data files are inherently discretized as well. Small systematic deviations from the known entropy of this system are attributed to the imperfections of the data compression algorithms. For systems that contain particles in continuous space, there is the issue of introducing ‘bins’ to keep the number of distinguishable states finite. In the latter case, it is clear that one obtains the entropy subject to a constant. In all cases, the method requires reference files that contain a representative number of snapshots for the lowest and largest entropy contents in the system. The file size after compression of a simulation with different parameters can then be scaled between the file sizes corresponding to minimal and maximal entropies to obtain the physical entropy of the system.

We have performed a series of Monte Carlo simulations for the hard sphere system. These simulations are relatively simple, because one only has to check for ‘overlap’ to reject or accept a translational move. As the hard sphere system is a three-dimensional and continuous system, to be translated to a one-dimensional, discrete data file such that it can be used by file compression algorithms, the data should be handled in such a way that as little information as possible is lost and that results are fully converged. Afterwards, using the compression algorithm, the entropy is then measured as a function of volume fraction (system box sizes or, equivalently, particle sizes).

In the following sections, we first give more details on the MC simulations, after which we focus on the key steps that lead to the entropy estimates regarding the compression algorithm and present the entropy versus volume fraction curve. Moreover, the coexistence densities will be given as calculated by the new algorithm as a justification for its use in physical systems. In the Discussion section, we reflect on the accuracy of the method, especially with regards to the coexistence densities, and the applicability of data compression as a tool for the entropy estimates.

Simulation and compression details

Monte Carlo simulations have been carried out for the hard sphere system consisting of N particles with diameter depending on the volume fraction ϕ and placed in the unit cube with periodic boundaries. Initially, the particles are configured according to an FCC lattice. Each Monte Carlo step (involving N trials) consists of consecutively displacing per trial 1 particle randomly in each x, y and z direction limited by a maximal movement distance such that 40–60% of the moves are rejected. One rejects a move if the displaced particle overlaps with any other, otherwise the move is accepted. At first, the maximal displacement is determined, which is then fixed to run the rest of the simulation to store relevant data. The typical length of the simulation to obtain accurate results is in the order of 10⁷ MC steps.

Data are stored in a binary file, being a very elementary file type in which pure binary numbers are stored (or values 0–255 per byte) without containing any other redundant information. This is of great importance in the compression algorithm, since even the commas in comma-separated value files increase the entropy by around 20% depending on the system at hand (not shown). Storing the data is therefore a delicate process and should be handled carefully. In this section, we present several steps in the processing of the physical data from the MC simulations to the data that are stored in a binary file.

As a general remark, data compression algorithms try to find as much repetition as possible, but it might not find every piece of repetition. Therefore, after convergence, the estimated entropy will always be higher than the true entropy. While comparing different methods of storing data, one should therefore strive for the lowest entropy.

Entropy calculation

As discussed before, entropy is directly related to the compression ratio φ. As a scale for the entropy, the two cases of minimal and maximal entropies need to be generated, giving compression ratios φ_min and φ_max, respectively. Typically, in the case of hard spheres this means we store the positions of the particles in an FCC configuration for every uncorrelated MC step for the minimal entropy and generate random coordinates for every particle and every uncorrelated MC step for the maximal entropy. The estimate for the correlation time is discussed below. The incompressibility content is then defined by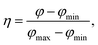which attains a value between 0 and 1. The entropy can then be determined using a linear map from η to S as a first order approximation:

S = ηS_max + (1 − η)S_min, (2)

where the minimal and maximal entropies for the discretised hard sphere system are given by

S_min= 0, S_max = D ln n_s, (3)

in units of k_B, where D is the amount of degrees of freedom and n_s is the number of discretisation bins. Using coordinates relative to the center of mass or spherical coordinates with respect to the previous particle in the list, we find that D = 3(N − 1). Therefore, the entropy for the hard sphere system is given by

S = 3(N − 1)η ln n_s, (4)

with η being dependent on the volume fraction ϕ.

Discretisation

Each degree of freedom will be discretised using the same amount of bins n_s. If the number of bins is too small, displacements within the system become unnoticeable, resulting in more repetitious data and an entropy that is too low. In contrast, using an enormous amount of bins creates a lot of data and is therefore less optimal in data storage and memory management.

To determine the optimal amount of bins we run a simulation per volume fraction and discretise using a variable number of bins up to 65 536 (as allowed by using 2 bytes of storage per degree of freedom). In the end, the differences in entropy, rather than their absolute values, are important and should remain constant. Therefore, a guideline for choosing the number of bins is to find the amount of bins above which the difference between the measured entropy and the maximal entropy remains constant. The result is given in Fig. 1, depicting these differences using varying amounts of bins for different volume fractions. A properly converged estimate should result in the difference between the measured entropy and the maximal entropy being constant with respect to an increase in the amount of bins. Therefore, a guideline for choosing the number of bins is to find the number above which this difference plateaus. We find that the maximal amount of bins using 2 bytes is optimal as differences are constant at least up to a volume fraction of 0.7, after which changes in the system can only be detected by having more precise discretisation. Using 256 bins by storing in a single byte results in unconverged values within the region of phase coexistence, while utilising 2 bytes results in full convergence in this region. Further discretisation is therefore unneeded, unless densities near close packing are to be studied.

Fig. 1 The entropy difference relative to maximal entropy for different amounts of bins at multiple packing fractions, 10⁶ MC steps, 32 particles, 200 as correlation time (see the text) and using the minimum of spherical coordinates ordered with a Hilbert curve (see the text) or an FCC lattice.

Ordering and coordinate systems

The particles in a three-dimensional space need to be represented in a one-dimensional data file. We therefore have a choice in the ordering of the particles. The goal is to find as much repetition in local clusters in the system as possible. Particles close together in space should be represented by coordinates that are placed close together in the data file as well. A space-filling Hilbert curve is known to preserve the locality and has been used in two-dimensional systems before.⁷ Here, we utilise the 3D Hilbert curve, ordering particles along this curve. In this case, only the recursively defined Hilbert curve after 3 iterations is needed, as the number of points on this curve exceeds the number of particles in our system. Moving along the vertices of this curve, a particle is added to the list if it is contained in the subcube surrounding this vertex and because it is a space-filling curve, all particles in the simulation box will be ordered this way. Initially, particles are ordered following the generation of the FCC lattice. We have observed that ordering using the Hilbert curve improved the entropy in the fluid regime, since this curve introduces more locality. In contrast, in the crystalline region we find that it does not improve the entropy as the initial ordering is already local. Each measurement is therefore taken to be the lowest of these two orderings.

Now there is still the question of which coordinate system to use. The data could be stored using the naive x, y and z coordinates, but the translational entropy within a simulation box with periodic boundaries should be excluded. A way to remove the collective translational degree of freedom is to use Cartesian coordinates with respect to the centre of mass. However, the use of spherical coordinates gave slightly better results: in this case the translational freedom is excluded by storing coordinates relative to the previous particle in the ordered list with the first particle being set at the origin. Spherical coordinates consistently result in a lower entropy as compared to other coordinate systems. Hence, what is stored in the data file are the spherical coordinates of particles in relation to the previous particle in the ordering.

Overhead

Data compression algorithms generate overhead, which for our purpose is unnecessary data. This is a general problem due to data compression and does not only hold for the hard sphere system. Typically, lossless algorithms are in use, such as LZMA and DEFLATE, which ensure that the original file content can be regenerated. Then, upon removal of redundant information, the algorithm needs to reintroduce bits as a reference to an earlier occurrence of the data. The latter contributes to the overhead in the compressed files, which influences the compression ratio and therefore such data compression algorithms are not per se optimal for our purpose. Moreover, the 8-bit representation of each number contains leading and trailing zeroes, giving rise to unneeded information, e.g., the six zeroes in front of the representation of 2: 00000010. However, one can implement a strategy to correct for this. When storing different values of n_s in a file, the expected compression ratio will converge to log₂(n₂)/8 in the limit of large file sizes. The overhead factor r(n_s) is then defined by the fraction that the compression ratio of the compressed random file with n_s different values is above the expected compression ratio. This value can then be used to correct for a file with physical information by decreasing the obtained compression ratio φ by r(n_s). Note, however, that the overhead depends on the specific algorithm. We have used the DEFLATE algorithm implemented in MATLAB through the zip() command. The overhead will differ from the presented overhead values for other compression algorithms. The overhead for using 2 bytes per value as calculated for the zip() implementation in MATLAB is given in Fig. 2.

Fig. 2 Percentage overhead relative to the expected compression file size at a varying number of different values stored in files of size 10⁷ bytes using 2 bytes per value for the zip() implementation in MATLAB.

Correlation time

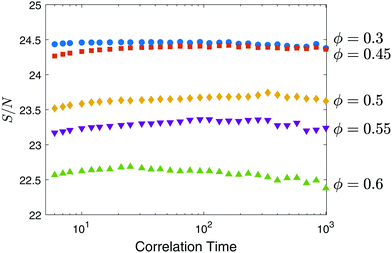
Due to the nature of Monte Carlo simulations, ‘temporal’ correlations might be present in the data. To circumvent this unnecessary correlation in the stored data, we determine the correlation ‘time’ for the simulation, i.e., how long temporal correlations exist in the MC trajectory. It is important to wait until this correlation time has passed before a new data point is stored into the file. To this end, we have ran simulations using a fixed number of MC steps between sample storages and call this number the imposed correlation time. For a given correlation time, we have evaluated the entropy by data compression. The optimal correlation time is then estimated from the ‘saturation’ point: storing data with a lower frequency did no longer affect the entropy. Examples for this procedure are shown in Fig. 3 for a system of 32 particles at volume fractions between 0.3 and 0.6. As can be seen, especially for the low volume fractions, the entropy per particle is roughly constant. In other words, the result does not strongly depend on the presented range of frequencies of storages (range of imposed correlation time), which means that the optimal correlation time in these cases may be as low as approximately 10 MC steps. The optimal correlation time seems to be an increasing function of the density. This is better seen for lower imposed correlation times than shown in Fig. 3. For ϕ = 0.55, we might already have a two or three-fold increase. That is why an optimal correlation time of order 100 was typically used for the data production (cf. the caption of Fig. 4).

Fig. 3 The estimate for the entropy versus imposed correlation time (number of MC steps per sample storage). Number of particles N = 32 using 2 bytes per value with, as an example, number of bins n_s = 5000 and 10⁶ total MC steps.

Fig. 4 Entropy per particle for system sizes consisting of 32, 108 and 256 particles as well as an extrapolation to an infinite system size using 65 530 bins, correlation times of, respectively, 100, 200 and 400 MC steps and the minimum entropy of ordering using a Hilbert curve or an FCC lattice.

Results

Using the file compression algorithm as described in the previous section, the entropies against volume fraction curves have been calculated for various system sizes as well as an extrapolated curve to infinite system size. For 32 particles and the extrapolation, the entropy per particle curve against volume fraction is given in Fig. 4a. Error bars have not been included in the figure as these are smaller than the symbols used, except within the region of phase coexistence, where the error is slightly larger due to a system sometimes behaving as a solid or as a fluid. The extrapolation has been performed at each volume fraction using system sizes of 32, 108 and 256 particles with S/N scaling linearly with 1/N. Various extrapolation curves are shown in Fig. 4b. The accuracy of the extrapolated entropy relies on the accuracy of each of the points. In fact, we have just 3 system sizes to estimate the value for N → ∞. This is not much and we should note that with increasing N, simulations need to be longer in order to get results that have comparable accuracies.

The values of the coexistence densities have been determined by the common tangent method on the entropy per volume versus volume fraction curve as this corresponds to equal chemical potential and pressure. As the entropy per volume is a steeply increasing function of the particle volume fraction, the quality of the common tangent is not easily recognised. That is why the common tangent is subtracted from the entropy per unit volume curve. This shifted entropy per volume curve now has two equally high local maxima: one at the fluid and one at the solid binodal densities. An example for N = 32 is presented in Fig. 5. The error bars in the solid branch are indicated, which represent the statistical fluctuations of 20 independent ‘measurements’ per density and tend to grow slightly with increasing density. The estimated coexistence densities on the fluid and solid branches (for N → ∞) are given by ϕ_f = 0.49(7) and ϕ_s = 0.57(5), respectively.

Fig. 5 Entropy per volume, shifted such that the common tangent is a horizontal line, against volume fraction for the hard sphere system consisting of 32 particles by using 65 530 bins, a correlation time of 100 MC steps and the minimum taken by ordering using a Hilbert curve or an FCC lattice. The data points near the fluid and solid binodal are fitted by a cubic polynomial to pinpoint the binodal values. Error bars are 1 standard deviation for 20 independent measurements.

Discussion and conclusion

The entropy for a couple of volume fractions has been computed in a previous study by thermodynamic integration⁶ to which our results can be compared, see Table 1. As we know the entropy up to an additive constant, we focus on entropy differences. The entropy as computed by the compression algorithm is always higher than the true entropy and this overestimate may be larger with increasing volume fraction. This suggests that differences in entropy using the new algorithm are smaller than the true differences, which might explain why we have found smaller differences than the ones from the literature.

Table 1 Entropy differences for N → ∞ as compared to the literature⁶ with volume fractions ϕ₁ = 0.544993, ϕ₂ = 0.575828 and ϕ₃ = 0.602139

Δϕ	ΔSlit/N	ΔScompr/N
ϕ 1 − ϕ3	1.32	1.15 ± 0.02
ϕ 1 − ϕ2	0.67	0.60 ± 0.02
ϕ 2 − ϕ3	0.64	0.55 ± 0.02

---

Above we have shown that the file compression method used to estimate the entropy leads to a wider two-phase region for the hard sphere system than currently found in the literature. In particular, our data suggest a higher value for the upper binodal value, while the lower binodal value compares very well with the literature. Experimental estimates for this upper binodal value have relied on the observation of an interface between a fluid and a solid phase. This interface disappears when the binodal value is reached. Even in micro-gravity experiments, the upper binodal was found to be close to ϕ_s = 0.545.⁸ Playing the role of devil's advocate, one could argue that in the formation of a solid phase, grain boundaries and imperfections exist which take long to anneal. This might result in a (temporal) too low density of the solid phase. In such a scenario, the interface between the fluid and solid phase disappears at a too low overall particle density. However, possible kinetic traps that might have prevented the solid phase to find its proper density have rarely been discussed. Theoretical estimates of the upper limit rely on a more laborious process where the entropy is estimated by thermodynamic integration. Subsequently, one then should compute the pressure for various densities and find the density at which the pressure in the solid phase equals that in the fluid. Such projects have been performed multiple times and resulted in similar upper binodal values of ϕ_s = 0.545 from which our result differs.

In the search for an explanation of our excessively large two-phase region, we should recall that the compression algorithm will always slightly overestimate the entropy. As for the relevant binodal, it is necessary to consider the thermodynamic limit and, therefore, our estimate for the width of the two-phase region must also include ‘extrapolation’ errors. Systematic errors in the entropy estimates depending on density may lead to the erroneous placement of the binodal values. Finally, as shown in Fig. 5, the fitted curve used to find the local maximum might also have influenced the estimate of the upper binodal value. Excluding a few points in the two-phase region and at very high densities might lead to a shift of the estimated binodal to a slightly lower value. With this in mind, we should judge the quality of our result for the upper binodal value. The differences in entropy change between our results and the ones from the literature in Table 1 do not appear to be large enough to explain the large disparity in the estimated binodal values. However, it is generally known that small changes in the actual values may influence the positioning of binodal points greatly. At this stage of developments to estimate the entropy from file compression, one should be cautious to draw too strong conclusions about the position of the binodal. It remains of interest to understand why the entropy compression algorithm gave such a wide two-phase coexistence result and insights into the causes may lead to further improvements of the compression method.

Although the upper binodal value does not match with the previously found results from other methods, we still argue that this entropy estimation method using compression algorithms has high potential. It is extremely quick and easy to implement, and the method can be used to measure the entropy during a single simulation, in a similar way as we can measure, e.g., the energy or some correlation functions. Such an entropy measuring tool may be used in yet unexplored terrain. For example, by inspection of the compressed file one can find out where in the system a lot of compressions could be realised and where not. Physically, this means that one can trace the region in a system where relatively high or relatively low entropy densities exist. Hence, we can obtain entropy information with spatial resolution. When simulations are done for systems that are out of equilibrium, one can try to quantify the entropy production⁹ with spatial resolution. Such results cannot be generated by the classical thermodynamic integration method.

Finally, we note that the entropy estimation by file compression can also be applied to experimental data. For example, one can nowadays find the coordinates of particles by microscopy as a function of time. By storing these coordinates in a file similarly as is done in a simulation, one can find estimates of the entropy by the file compression strategy. Knowing the entropy as a function of time (and space) may lead to improved insights in the way a system evolves towards equilibrium.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Simone Dussi and Simeon Stoyanov for having insightful discussions on the hard sphere model and the use of the compression algorithm for further research.

References

1. B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208.
2. W. G. Hoover and F. H. Ree, J. Chem. Phys., 1968, 49, 3609.
3. P. N. Pusey and W. van Megen, Nature, 1986, 320, 340.
4. D. Frenkel and A. J. C. Ladd, J. Chem. Phys., 1984, 81, 3188.
5. J. M. Polson, E. Trizac, S. Pronk and D. Frenkel, J. Chem. Phys., 2000, 112, 5339.
6. C. Vega and E. G. Noya, J. Chem. Phys., 2007, 127, 154113.
7. R. Avinery, M. Kornreich and R. Beck, Phys. Rev. Lett., 2019, 178102.
8. Z. Cheng, P. M. Chaikin, W. B. Russel, W. V. Meyer, J. Zhu, R. B. Rogers and R. H. Ottewill, Mater. Des., 2001, 22, 529.
9. S. Martiniani, P. M. Chaikin and D. Levine, Phys. Rev. X, 2019, 9, 011031.

---