Open Access Article
Open Access ArticleSpin multiplicity effects in doublet versus singlet emission: the photophysical consequences of a single electron†
Caleb M.
Wehrmann‡
 ,
Muhammad
Imran‡
,
Muhammad
Imran‡
 ,
Craig
Pointer
,
Craig
Pointer
 ,
Lisa A.
Fredin
,
Lisa A.
Fredin
 *,
Elizabeth R.
Young
*,
Elizabeth R.
Young
 * and
Mark S.
Chen
* and
Mark S.
Chen
 *
*
Department of Chemistry, Lehigh University, Bethlehem, PA 18015, USA. E-mail: mschen@lehigh.edu; ery317@lehigh.edu; laf218@lehigh.edu
First published on 10th September 2020
Abstract
Ambient-stable fluorescent radicals have recently emerged as promising luminescent materials; however, tailoring their properties has been difficult due to the limited photophysical understanding of open-shell organic systems. Here we report the experimental and computational analysis of a redox pair of π-conjugated fluorescent molecules that differ by one electron. A π-dication (DC) and π-radical cation (RC) demonstrate different absorption spectra, but similar red emission (λemiss,max = ∼630 nm), excitation maxima (λexc,max = ∼530 nm), fluorescence lifetimes (1–10 ns), and even excited-state (non-emissive) lifetimes when measured by transient absorption spectroscopy. Despite their experimental similarities, time-dependent density functional theory (TDDFT) studies reveal that DC and RC emission mechanisms are distinct and rely on different electronic transitions. Excited-state reorganization occurs by hole relaxation in singlet DC, while doublet RC undergoes a Jahn-Teller distortion by bending its π-backbone in order to facilitate spin-pairing between singly occupied molecular orbitals. This relationship between the excited-state dynamics of RC and its π-backbone geometry illustrates a potential strategy for developing π-conjugated radicals with new emission properties. Additionally, by comparing TDDFT and CIS (configuration interaction singles) excitations, we show that unrestricted TDDFT accurately reproduces experimental absorption spectra and provides an opportunity to examine the relaxed excited-state properties of large open-shell molecules like RC.
Introduction
Photoluminescence (PL) is the process in which a photogenerated excited state relaxes via emission of a photon.1 Since many photochemical applications are dependent on absorption or emission-related phenomena (or both), investigations that clarify the photophysical mechanisms of PL and related processes are critical to the development of photoactive materials for chemical sensing,2 photocatalysis,3 and light-emitting diodes.4All PL is classified as either fluorescence or phosphorescence based on whether emission occurs by radiative decay from an excited state with spin multiplicity that is the same as or higher than the ground state, respectively. Most organic compounds possess an even number of electrons resulting in all paired spins (i.e. they are closed-shell molecules). Consequently, fluorescence derives from singlet excited states (Sn), while phosphorescence derives from triplet excited states (Tn). Recently, however, photophysical phenomena that derive from excitation of doublet ground states (i.e. an odd number of electrons that leads to one unpaired spin) have begun to be considered with reports of emissive, air-stable, organic radicals (i.e. open shell molecules) that demonstrate short luminescence lifetimes (<10 ns).5 Fluorescence and phosphorescence in monoradicals instead derive from doublet (Dn) or quartet (Qn) excited states, respectively.
Spin multiplicity effects have been studied in other luminescent compounds, particularly for metal complexes.6 However, such an investigation has been difficult with organic molecules because it requires a single electron redox pair that shows sufficient stability and photoluminescence in both closed- and open-shell oxidation states.
Due to challenges in achieving persistence in air, nearly all examples of ambient stable, emissive organic radicals stabilize unpaired spin using a triarylmethyl motif.5,7 While these fluorescent radicals have already shown utility in various applications, their photophysical properties have yet to be compared with their redox-related anion or cation.
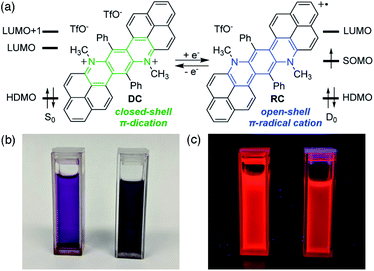
Herein we report a recently discovered phenalenyl-based,8 stable π-radical cation (RC) that shares red fluorescence with its dicationic, closed-shell precursor (DC) (Fig. 1).9 Despite their electronic differences, both species show remarkably similar emission, solvent-dependent behaviours, and even excited-state dynamics. Specifically, although different electronic transitions are responsible for emission in DC and RC, the observed wavelengths are near-identical between species because of significant structural and electronic reorganization in excited RC. This reorganization arises from spin-(un)pairing in the singly occupied molecular orbitals of RC, which is a key distinguishing feature between the electronic structures of doublet and singlet excited states. Disentanglement of the different excited-state manifolds of this single electron redox pair of emissive π-conjugated organics is accomplished through the powerful combination of steady-state and time-resolved spectroscopies and quantum mechanical calculations.
Results and discussion
Absorption and photoluminescence
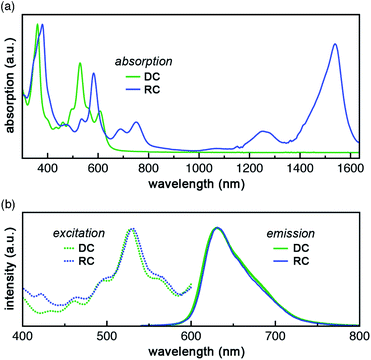
DC and RC share two strong absorption bands at 530–540 nm and 590–610 nm (in acetonitrile) that arise from electronic transitions originating from the doubly occupied molecular orbital manifold into the unoccupied molecular orbital manifold. Additionally, RC shows several longer wavelength features (>650 nm) that are associated with promotion of the unpaired electron (Fig. 2a, vide infra).9Despite these differences in absorption features, DC and RC share a surprisingly near-identical red emission (λemiss,max = 632 nm and λemiss,max = 630 nm, respectively, solid lines Fig. 2b) upon irradiation at wavelengths higher in energy than the highest doubly occupied molecular orbital (HDMO) to lowest unoccupied molecular orbital (LUMO) energy gap (i.e. λexc < 650 nm, dotted lines). The highest photoluminescence (PL) intensity was achieved with excitation wavelengths of ∼530 nm. To identify what electronic transitions are responsible for PL, we measured the PL excitation (PLE) spectrum that corresponds to the λemiss,max for both DC and RC. The maximum PLE intensity for DC is 530 nm, as shown in Fig. 2b (dotted green line), and the maximum PLE intensity for RC is 534 nm (dotted blue line Fig. 2b and S3†). The PL lifetimes of DC and RC are measured to be 1.42 ns and 3.40 ns, respectively, which are typical for organic fluorescence. Although RC shows several lower energy absorption peaks, irradiation at longer wavelengths (λexc > 650 nm) does not result in emission wavelengths shorter than 1350 nm, likely due to competing non-radiative decay pathways (Table S3†). Moreover, excitation of RC at varying wavelengths (λexc) leads to only one emission peak, which suggests that there is only one emissive excited state (Fig. S3†).
Relative photoluminescence quantum yields (PLQY, ΦPL) of DC and RC were determined by calibration to known standards and found to be 11.8% and 5.8%, respectively, which are values within the range of other fluorescent radicals.5,7 In combination with PL lifetimes (τPL), these PLQY values enable us to calculate radiative (kr) and non-radiative (knr) decay rates (eqn (1) and (2)). For DC, kr = 8.3 × 107 s−1 and knr = 62.1 × 107 s−1, and for RC, kr = 1.7 × 107 s−1 and knr = 27.7 × 107 s−1. Interestingly, despite the clear difference in quantum yields, DC and RC show near-identical rates of radiative and non-radiative decay.
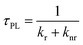 | (1) |
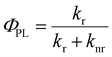 | (2) |
The photochemical similarities between DC and RC are extraordinary, and might even lead one to suspect that they result from the generation of a common species upon irradiation. However, absorption spectra recorded before and after each PL measurement (Fig. S5†) verified that distinct samples of DC and RC remained homogeneous and did not decompose. The near-identical PLE (λexc,max) and PL (λemiss,max) maxima, suggest that fluorescence in both compounds must rely on very similar orbital transitions, which can only arise if there are some similarities in the electronic structure of DC and RC (vide infra and Fig. S18†). Since the emission of DC is redshifted from all of its absorption bands, we can infer that emission originates from the lowest singlet excited state (S1). In contrast, the emission of RC occurs at shorter wavelengths than multiple absorption bands, which indicates that RC violates Kasha's rule.10
Solvent effects
Changes to solvent polarity lead to alterations in steady-state characteristics that provide insight to the nature of these transitions. Spectroscopic characterization of DC was carried out in acetone and ethyl acetate, in addition to acetonitrile (ACN) reported above. DC in acetone produces similar spectra to those obtained in ACN; however, the PLQY increases from 11.8% up to 16.2% (Table 1). Solvation in ethyl acetate leads to even further PLQY increases (26.0%), a longer PL lifetime (1.96 ns), and a redshifted emission (λmax = 642 nm) when compared to ACN. These data are indicative of a decrease in the dipole moment of DC upon excitation, such that the excited state is more stabilized by less polar solvents.| Solvent | Dielectric constant (F m−1) | Exc λmax (nm) | PL λmax (nm) | PL lifetime (ns) | PLQY (%) | k r (107 s−1) | k nr (107 s−1) | τ 1 (ps) | τ 2 (ns) | τ 3 (μs) |
|---|---|---|---|---|---|---|---|---|---|---|
| π-dication (DC) | ||||||||||
| ACN | 37.5 | 530 | 632 | 1.42 (0.02) | 11.8 (0.7) | 8.3 | 62.1 | 76 (12) | 2.1 (0.3) | 1.8 (0.1) |
| Acetone | 20.7 | 529 | 632 | 1.52 (0.01) | 16.2 (3.0) | 10.7 | 55.1 | 59 (6) | 2.1 (0.3) | 1.7 (0.1) |
| Ethyl acetate | 6.02 | 532 | 642 | 1.96 (0.08) | 26.0 (1.4) | 13.3 | 37.7 | 114 (38) | 2.3 (0.3) | 2.6 (0.3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| π-radical cation (RC) | ||||||||||
| ACN | 37.5 | 534 | 630 | 3.40 (0.15) | 5.8 (0.6) | 1.7 | 27.7 | 106 (25) | 2.9 (0.1) | 1.8 (0.2) |
ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM (1 DCM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
— | 534 | 632 | 4.23 (0.1) | 11.8 (1.9) | 2.8 | 20.9 | 15.4 (0.7) | 3.0 (0.3) | 2.4 (0.3) |
ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM (1 DCM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
— | 536 | 635 | 3.96 (0.12) | 10.1 (0.6) | 2.6 | 22.7 | 10.8 (0.1) | 3.1 (0.4) | 2.4 (0.2) |
| DCM | 8.93 | 537 | 634 | 3.32 (0.02) | 9.1 (0.2) | 2.7 | 27.4 | 11 (1.0) | 2.8 (0.3) | 3.4 (0.5) |
Due to RC being soluble in dichloromethane (DCM), but not in acetone or ethyl acetate, the solvent polarity was varied for RC by using mixtures of ACN and DCM. A solvent trend is less apparent with RC because the solvent mixtures (Table 1) do not show intermediate values. Instead solvent mixtures of RC produce PLQYs and PL lifetimes greater than either ACN or DCM alone. RC in neat DCM displays a PLQY of 9.1% and shows only a small increase in PL lifetime compared to ACN.
Transient absorption (TA) spectroscopy
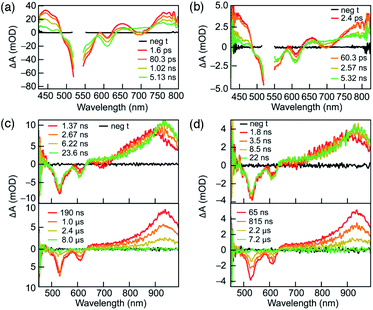
To understand their excited-state evolution, DC and RC were analysed by TA spectroscopy in ACN from picosecond to microsecond time ranges (Fig. 3). Absorption spectra recorded before and after each TA experiment were found to be identical, which verified that neither compound experienced photoinduced decomposition (Fig. S5†). Both compounds demonstrate near-identical TA features that, like their similarities in PL excitation and emission, arise from similar ground-state electronic structures of DC and RC (Fig. S16–S18,†vide infra).Similar TA spectra are not expected between related redox species; however, the significant delocalization of charge and spin in both compounds lead to negligible differences in their electronic structures. These common TA features appear to result from comparable relative energy level spacings between the higher unoccupied molecular orbitals (vide infra and Fig. S18†) in DC and RC that produce similar induced absorptions. Therefore, it is difficult to distinguish the transient absorption spectra of RC from DC in the visible absorption region. The α-SUMO-related for transitions for RC correspond to lower energy absorption features that lie outside the detection window of our TA analysis (>800 nm). The visible TA spectra show negative ΔA centred at ∼530 nm and ∼610 nm corresponds to ground-state bleaching of both DC and RC. The appearance of positive ΔA peaks, convolved with the ground-state bleach, are centred at 450 nm, 650 nm, and > 750 nm and represent the formation of the initial excited state. The excited-state growths at wavelengths greater than 750 nm obscure the expected ground-state bleach of the RC at ∼750 nm due to the convolution of the two signals. The initial excited state decays to form an intermediate species with a very broad positive signal between 650 and 850 nm (Fig. 3a and b). During the first 25 nanoseconds (Fig. 3c and d, top tile), the signal > 700 nm continues to slightly redshift ending up as a peak at ∼950 nm (Fig. 3c and d). Concomitant decay of the 950 nm peak and recovery of the ground-state bleach is observed in less than 10 μs and corresponds with return to the ground state.
The solvent-dependence of DC and RC excited-state evolution were evaluated for DC in ethyl acetate and acetone, and for RC in DCM and varying ratios of ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM (1
DCM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), along with ACN (vide supra) (Fig. S6 and S7†). The TA spectra obtained for each solvent condition show features very similar to those observed in acetonitrile, thereby suggesting that the formation of similar excited state species occurs independent of solvent.
2), along with ACN (vide supra) (Fig. S6 and S7†). The TA spectra obtained for each solvent condition show features very similar to those observed in acetonitrile, thereby suggesting that the formation of similar excited state species occurs independent of solvent.
Due to the complicated spectral evolution observed for DC and RC, global analysis fitting was performed to extract individual lifetime components of the spectral evolution. Each component is referred to as a decay-associated difference spectrum (DADS). Global analysis fitting for DC and RC yielded three lifetimes, each associated with a separate DADS, and each decaying at different timescales: ps, ns, or μs ranges (Table 1, Fig. S8 and S9†). The shortest lifetime (τ1) is assigned to rapid vibrational relaxation and transition to a lower energy excited state. For DC, τ1 is not affected by solvent polarity; however, a trend is present in the DADS of RC. Since the τ1 values for the ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM solvent mixtures (Table 1) are more similar to DCM, we postulate that these convoluted solvent trends at shorter time scales are due to RC possessing a preferential solvent shell of DCM even when ACN is present.
DCM solvent mixtures (Table 1) are more similar to DCM, we postulate that these convoluted solvent trends at shorter time scales are due to RC possessing a preferential solvent shell of DCM even when ACN is present.
The lifetimes of the second DADS component (τ2) for DC and RC are ∼2 ns and ∼3 ns, respectively, with no distinguishable trend with solvent. The τ2 component is assigned to radiative decay responsible for the observed fluorescence, based on the agreement between τ2 lifetimes measured by TA and time-resolved PL lifetimes.
The lifetimes of the third and longest-lived DADS component (τ3) fall within 1–4 μs for DC and RC. Lifetimes of this order of magnitude often result from spin or symmetry forbidden transitions back to the ground state. We propose that the long-lived DC species (τ3) represents an excited triplet state based on its decay lifetime and the similarity of its absorption (λmax ∼950 nm) with the calculated energy differences between the first (T1) and higher (Tn) triplet excited states (Table S8†). This assignment is supported by the fluorescence detection of singlet oxygen when DC is irradiated (530 nm) in the presence of molecular oxygen, since oxygen sensitization commonly proceeds by energy transfer from excited triplets (Fig. S4†).11 The long-lived lifetime of the doublet RC might, by analogy, be assumed to result from relaxation from a quartet that forms during intersystem crossing from the doublet excited state. However, the calculated quartet (Q1, Table S1†) is isoenergetic with the excited-state, which suggests that there is no driving force for intersystem crossing and thus the long lifetime likely results from doublet symmetry forbidden transitions (vide infra).
The lifetime of the longest-lived species (τ3) increases with decreasing solvent dipole moment. For DC, ethyl acetate produces the longest lifetime (2.6 μs) compared to acetone or ACN (Table 1). For RC, DCM yields the longest lifetime (3.4 μs), ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM mixtures show intermediate lifetimes (2.4 μs), and ACN leads to the shortest lifetime of 1.8 μs. These trends between solvent polarity and τ3 lifetimes support the formation of excited states with a lower dipole moment than the ground states. For such species, less polar solvents are more effective for stabilization of the excited state, thereby promoting longer τ3 lifetimes.
DCM mixtures show intermediate lifetimes (2.4 μs), and ACN leads to the shortest lifetime of 1.8 μs. These trends between solvent polarity and τ3 lifetimes support the formation of excited states with a lower dipole moment than the ground states. For such species, less polar solvents are more effective for stabilization of the excited state, thereby promoting longer τ3 lifetimes.
Quantum mechanical calculations
Clarification of the emission mechanisms in DC and RC was achieved through quantum chemical calculations. Structure optimizations were performed in Gaussian D.01 (ref. 12) using the hybrid B3LYP functional and a double-ζ basis set with polarization and dispersion [6-31g+(d,p)] to best model the delocalized π-networks. An ACN polarization continuum model of solvation13 was applied to allow for more charge localization, and GD3 empirical dispersion was used to account for the diffuse π-bonds. A closed-shell restricted formalism was used to optimize the singlet ground state of DC, whereas an unrestricted formalism was necessary to optimize the doublet ground state of RC due to its unpaired electron. While a restricted formalism forces electrons to pair in occupied molecular orbitals in the conventional spin-up–spin-down manner, an unrestricted formalism results in α (spin down) and β (spin up) sets of singly occupied orbitals. Therefore, in RC the singly occupied molecular orbital (SOMO) becomes the α-SOMO and each doubly occupied orbital is computed as two (one α and one β) SOMOs, such that the HDMO is the α-SOMO-1 and β-SOMO.One of the most ubiquitous uses of time-dependent (TD)14 implementations of DFT is to model the absorption spectra of singlet ground state molecules. However, when it is applied to organic and inorganic systems of higher multiplicity, large spin-contamination leads to errors in orbital transition assignments by as much as 3 eV.15 In contrast, the configuration interaction (CI) description of orbital overlap between non-singlet orbitals, makes CI singles (CIS) highly effective for predicting absorption spectra and excitation energies, even of higher spin systems. The main limitation for CIS is that it is resource intensive and thus recent implementations of excited state geometry optimization16 are still severely limited to small π-conjugated systems. Alternatively, TDDFT is known to effectively optimize excited states of even large systems, making it an attractive method to simulate the photophysical properties of fluorescent radicals. Because most TDDFT implementations presume that ground state orbitals possess singlet multiplicity, it is important to check if excitations between the highly delocalized doublet Kohn-Sham orbitals of RC accurately reflect experimental data.17
Notably, the ground-state structures of DC and RC are nearly identical across a range of hybrid functionals, which indicates that the presence (or absence) of one electron does not greatly affect overall bonding and geometry. This structural similarity is probably due to highly delocalized frontier molecular orbitals, which extend throughout the entire π-backbone. The nature of the molecular orbitals of DC and RC are remarkably similar, despite the splitting of the occupation of orbitals and the addition of an electron in RC. The molecular orbitals differ only in energies, but not in their ordering, symmetry, or spacing (Fig. S16 and S17†). For example, the DC LUMO is the same π-symmetry as the α-SOMO in RC. These unusual similarities between DC and RC provide an explanation for their near-identical PL and TA spectra (vide supra, Fig. S18†). As discussed above, the common TA spectral features of DC and RC likely originate from their having comparable relative energy levels between higher unoccupied molecular orbitals.
Interestingly, the α-SOMO and β-LUMO energy levels in RC differ by much less (0.96 eV) than analogous MOs calculated for the reported triarylmethyl radicals,5,7 which leads to the low energy transitions seen in the absorption spectra of RC. In addition, DC and RC excitations modeled by CIS and TDDFT with various common functionals14 are all remarkably similar (Fig. S20 and S21†).
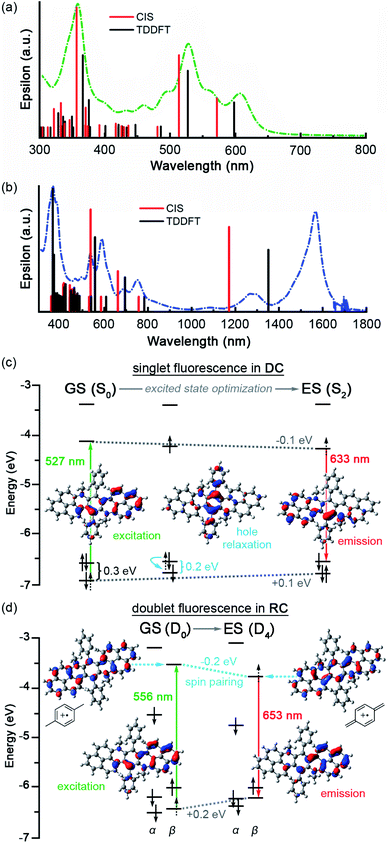
CIS and TDDFT predict very similar absorption for DC with only a minor blue shift from the experimental absorption spectra (Fig. 4a, Tables S5–S7, S10–S15†). Similarly, CIS and TDDFT provide similar predictions for RC absorption and match experimental excitations in the visible range. However, despite our experimental observation of two near-infrared (NIR) peaks at 1276 and 1565 nm (Fig. 4b), both methods predict only one NIR electronic transition: α-SOMO → α-LUMO at 1170 nm and 1350 nm with CIS/D3-B3LYP and TDDFT/D3-B3LYP, respectively (Tables S16–S18 and S20–S25†). As CIS and TDDFT only calculate electronic transitions, we can be relatively certain that only one electronic transition occurs in this region. Considering that the two experimental NIR bands differ by the characteristic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching frequency (1511 cm−1), we can infer that the lower energy peak (1565 nm) is the 0 → 0 vibronic transition of the α-SOMO → α-LUMO excitation, while the higher energy peak (1276 nm) represents the 0 → 1 vibronic transition. Of the methods and hybrid functionals explored, CIS/CAM-B3LYP provided the closest match (1509 nm) to experiment (Table S22†).
C stretching frequency (1511 cm−1), we can infer that the lower energy peak (1565 nm) is the 0 → 0 vibronic transition of the α-SOMO → α-LUMO excitation, while the higher energy peak (1276 nm) represents the 0 → 1 vibronic transition. Of the methods and hybrid functionals explored, CIS/CAM-B3LYP provided the closest match (1509 nm) to experiment (Table S22†).
CIS and TDDFT proved relatively accurate for calculating the visible transitions across various functionals. The strong agreement between CIS and TDDFT suggests that linear response TDDFT can be used to model the excited states and resultant excitations not only for the singlet excited state manifold of DC but also unrestricted doublet manifold of RC.
For DC, TDDFT/D3-B3LYP assigns the two lowest energy excitations (599 and 527 nm) to HDMO → LUMO and HDMO-1 → LUMO, respectively. The S2 excited state, which results when an electron is promoted from HDMO-1 to LUMO, is identified as the electronic state from which the experimental excited-state dynamics originate because its calculated transition energy most closely matches the experimental excitation wavelengths (∼530 nm). Optimization of the excited state (S2) leads to barely any conformational change but a significant decrease in dipole moment (2.24 → 2.04 D), which strongly agrees with stabilization of the excited state in less polar solvents (Fig. S12 and S14†). The electronic structure of the optimized excited state (S2) indicates that at its relaxed geometry S2 emits via a LUMO → HDMO transition.
These data suggest that fluorescence in DC proceeds by excitation (527 nm) from HDMO-1 (−6.90 eV) to LUMO (−4.14 eV) that is followed by rapid hole relaxation (on the S2 surface near the S0 geometry). This assignment is based on the HDMO–HDMO-1 contraction that occurs early in the TDDFT optimization path from S0 to S2 geometries (Fig. 4c and S14†). The excited state (S2) then radiatively decays (632 nm) via an electronic transition from LUMO (−4.22 eV) to HDMO (−6.54 eV) that obeys Kasha's rule (Table S9†).
In RC, the excitation that best matches the experimental excitation energy (∼534 nm) corresponds to a HDMO-1 → LUMO type excitation (β-SOMO-1 → β-LUMO, in the doublet orbitals), too. Optimization of this excited state (D4) leads to a lower dipole moment (2.95 → 2.70 D), more quinoidal character, and a Jahn-Teller distortion that manifests as greater bending in the π-backbone. As observed in cycloparaphenylenes, increased curvature facilitates quinoidization and spin-pairing stabilization.18,19 In particular, the low lying β-LUMO electron seems to spin-pair with the electron in the α-SOMO, leading to additional stabilization of the newly populated β-LUMO energy level. This effect is highlighted by the greater decrease in α-SOMO and β-LUMO (∼0.2 eV) energy levels versus the LUMO (∼0.1 eV) in excited DC where spin-pairing is not possible. In addition, spin-unpairing between the α-SOMO-2 and β-SOMO-1 leads to significant destabilization (∼0.2 eV) of these orbitals (Fig. 4d and S17†).
Therefore, we propose that RC fluorescence proceeds by excitation (556 nm) from β-SOMO-1 (−6.43 eV) to β-LUMO (−3.53 eV) to form the D4 excited state, that upon relaxation to a Jahn-Teller distorted geometry radiatively decays (653 nm) from β-LUMO (−3.74 eV) to β-SOMO-1 (−6.23 eV). The hole relaxation observed in the excited state optimization of DC is not present in the D4 optimization of RC (Fig. S15†). We postulate that hole relaxation is absent in RC because of the difference in intrinsic charge on the molecule: a photogenerated hole in a dication (DC) is hotter than one in a cation (RC).
The mixing of spin multiplicities is small for molecules only containing light atoms, and therefore the oscillator strength (orbital overlap) between the different spin states is also small for organic molecules. Despite this, it is well known that many closed-shell organic molecules can phosphoresce from a triplet state. A small population of ISC to the triplet occurs, despite the small overlap, due to an energetic driving force between excited singlet states and the triplet states. These triplets are long-lived due to the spin forbidden nature of the radiative decay back to the singlet surface. In RC, the spin–orbit coupling is small and there is no driving force to form a quartet through ISC, either at the ground-state geometry or to a relaxed Q1 state (Table S1†). However, there is significant driving force for IC to D2 and D1 from the relaxed excited-state (D4) supporting formation of a long-lived doublet state. For this state to be long-lived the return to the ground-state must be symmetry forbidden.
Photoresponse of the single electron redox pair
From these data, we can construct a full picture of the photo-physical behaviour for both species (Fig. 5). For DC, initial excitation (530 nm) leads to formation of S2, which rapidly under-goes internal conversion (76 ps) via hole relaxation to the lowest excited singlet (S1). The observed red emission (632 nm, 2.1 ns) is the result of radiative decay from S1 to S0 so that fluorescence in DC follows Kasha's rule. Additionally, DC can also undergo intersystem crossing to access an excited triplet state (Tn) that decays more slowly (1.8 μs) to the ground state (S0).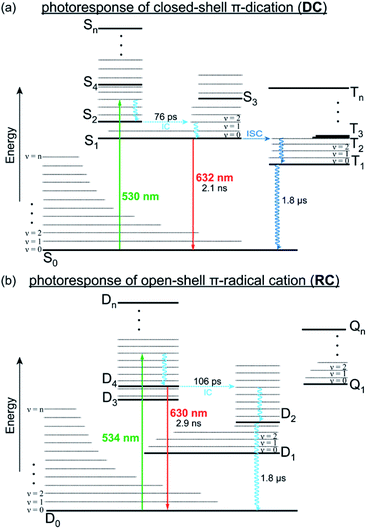 | ||
| Fig. 5 Jablonski plots that illustrate the relaxation pathways of DC (a) and RC (b) from their respective excited states, either through radiative (solid lines) or vibronic (wavy lines) transitions. | ||
Regarding RC, excitation (534 nm) generates a thermally excited D4 that relaxes to its lowest vibrational state prior to radiative decay back to D0 to provide the observed anti-Kasha fluorescence (630 nm, 2.9 ns). Alternatively, relaxation of RC can also proceed by internal conversion (106 ps) from D4 to lower doublet excited states, which is expected to be slow (1.8 μs) since they represent symmetry forbidden transitions with minimal overlap (Fig. S19†). These lower doublet excited states must instead relax through low frequency (ν < 100 cm−1) vibrational modes, many of which consist of wags along the π-backbone (Table S2†). Generally, π-conjugated molecules are less contorted and therefore only show vibrations along ancillary moieties (Table S4†). The presence of these low energy vibrations however, likely explain why DC and RC demonstrate knr > kr and have relatively low fluorescence quantum yields. They also highlight a structural property that we can look to synthetically modify in order to develop fluorescent radicals with different emission wavelengths and higher quantum efficiencies.
Conclusions
Although the steady-state and time-resolved spectroscopic behaviors of DC and RC appear identical, TDDFT calculations reveal the consequences of a single unpaired electron. In the absence of an electron, DC is an electrophilic dicationic singlet (S0) that favors hole relaxation prior to emission. Relaxation of the photoexcited state may also proceed through a triplet excited state that is long-lived because of the spin forbidden transition to the ground state. With the addition of an electron, RC is a cationic doublet (D0) that achieves spin-pairing between the excited electron and the α-SOMO in the excited state (D4) through a Jahn-Teller distortion. The slow decay process in RC proceeds through an excited state that shares the same multiplicity (doublet) as the ground state, but is long-lived due to its symmetry forbidden transition. This clarification of doublet excited state dynamics in RC is significant since it suggests that tailoring π-backbone flexibility should enable the development of luminescent radicals with new and more efficient emission properties. Furthermore, our computational studies demonstrate the accuracy of unrestricted TDDFT for simulating the excitations and emissions of a large, π-conjugated, open-shell molecule like RC, which is representative of a growing class of novel organic materials.Author contributions
C. M. W. performed the TDDFT calculations, M. I. synthesized the molecules and collected the absorption and photoluminescence data, and C. P. performed the transient absorption spectroscopy. L. A. F., E. R. Y., and M. S. C. designed the experiments and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Portions of this research were conducted with research computing resources provided by Lehigh University and the TG-CHE190011 allocation from Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Financial support for this research comes from Lehigh University and the Charles E. Kaufman New Investigator Award (KA2015-79201) of The Pittsburgh Foundation. The authors thank the NSF Major Research Instrumentation program (CHE-1428633) for funding that established the laser facility.Notes and references
- N. J. Turro, J. C. Scaiano and V. Ramamurthy, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Mill Valley, 2010 Search PubMed.
- (a) H.-W. Liu, L. Chen, C. Xu, Z. Li, H. Zhang, X.-B. Zhang and W. Tan, Chem. Soc. Rev., 2018, 47, 7140–7180 RSC; (b) D. Wu, A. C. Sedgwick, T. Gunnlaugsson, E. U. Akkaya, J. Yoon and T. D. James, Chem. Soc. Rev., 2017, 46, 7105–7123 RSC; (c) H. Zhu, J. Fan and X. Peng, Acc. Chem. Res., 2016, 49, 2115–2126 CrossRef CAS; (d) M. H. Lee, J. S. Kim and J. L. Sessler, Chem. Soc. Rev., 2014, 44, 4185–4191 RSC.
- (a) W. Chen, Z. Huang, N. E. S. Tay, B. Giglio, M. Wang, H. Wang, Z. Wu and D. A. Nicewicz, Science, 2019, 364, 1170–1174 CrossRef CAS; (b) N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS; (c) N. Corrigan, S. Shanmugam, J. Xu and C. Boyer, Chem. Soc. Rev., 2016, 45, 6165–6212 RSC; (d) J. C. Theriot, C.-H. Lim, H. Yang, M. D. Ryan, C. B. Musgrave and G. M. Miyake, Science, 2016, 352, 1082–1086 CrossRef CAS.
- (a) T. Chatterjee and K.-T. Wong, Adv. Opt. Mater., 2019, 7, 1800565 CrossRef; (b) T. Huang, W. Jiang and L. Duan, J. Mater. Chem. C, 2018, 6, 5577–5596 RSC; (c) Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020 CrossRef CAS; (d) C. Adachi, Jpn. J. Appl. Phys., 2014, 53, 060101 CrossRef.
- (a) Y. Teki, Chem.–Eur. J., 2020, 26, 980–996 CrossRef CAS; (b) X. Ai, Y. Chen, Y. Feng and F. Li, Angew. Chem., Int. Ed., 2018, 57, 2869–2873 CrossRef CAS; (c) S. Dong, A. Obolda, Q. Peng, Y. Zhang, S. Marder and F. Li, Mater. Chem. Front., 2017, 1, 2132–2135 RSC; (d) Y. Hattori, T. Kusamoto and H. Nishihara, Angew. Chem., Int. Ed., 2014, 53, 11845–11848 CrossRef CAS; (e) O. Armet, J. Veciana, C. Rovira, J. Riera, J. Castaner, E. Molins, J. Rius, C. Miravitlles, S. Olivella and J. Brichfeus, J. Phys. Chem., 1987, 91, 5608–5616 CrossRef CAS.
- W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubicek, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Perrson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T.-C. Weng, D. Zhu, K. Wärnmark, V. Sundström and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523 RSC.
- (a) H. Guo, Q. Peng, X.-K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J.-L. Brédas and F. Li, Nat. Mater., 2019, 18, 977–984 CrossRef CAS; (b) X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Nature, 2018, 563, 536–540 CrossRef CAS; (c) S. Kimura, A. Tanushi, T. Kusamoto, S. Kochi, T. Sato and H. Nishihara, Chem. Sci., 2018, 9, 1996–2007 RSC; (d) Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 CrossRef CAS.
- (a) C. M. Wehrmann, R. T. Charlton and M. S. Chen, J. Am. Chem. Soc., 2019, 141, 3240–3248 CrossRef CAS; (b) T. Kubo, Chem. Rec., 2015, 15, 218–232 CrossRef CAS; (c) S. K. Pal, M. E. Itkis, R. W. Reed, R. T. Oakley and R. C. Haddon, Science, 2005, 309, 281–284 CrossRef CAS.
- M. Imran, C. M. Wehrmann and M. S. Chen, J. Am. Chem. Soc., 2020, 142, 38–43 CrossRef CAS.
- T. Itoh, Chem. Rev., 2012, 112, 4541–4568 CrossRef CAS.
- (a) P. R. Ogilby, Chem. Soc. Rev., 2010, 39, 3181–3209 RSC; (b) A. Greer, Acc. Chem. Res., 2006, 39, 797–804 CrossRef CAS; (c) M. C. DeRosa and R. J. Crutchley, Coord. Chem. Rev., 2002, 233–234, 351–371 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef; (b) G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef.
- (a) N. S. Hill and M. L. Coote, Annu. Rep. Comput. Chem., 2019, 15, 203–285 Search PubMed; (b) W. Liu and Y. Xiao, Chem. Soc. Rev., 2018, 47, 4481–4509 RSC; (c) T. W. Schmidt, Int. Rev. Phys. Chem., 2016, 35, 209–242 Search PubMed; (d) S. Hirata, T. J. Lee and M. Head-Gordon, J. Chem. Phys., 1999, 111, 8904 CrossRef CAS.
- (a) B. Suo, K. Shen, Z. Li and W. Liu, J. Phys. Chem. A, 2017, 121, 3929–3942 CrossRef CAS; (b) S. Grimme and M. Parac, ChemPhysChem, 2003, 3, 292–295 CrossRef; (c) D. J. Tozer, R. D. Amos, N. C. Handy, B. O. Roos and L. Serrano-Andres, Mol. Phys., 1999, 97, 859–868 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS.
- C. He, Z. Li, Y. Lei, W. Zou and B. Suo, J. Phys. Chem. Lett., 2019, 10, 574–580 CrossRef.
- M. Matsumoto, I. Antol and M. Abe, Molecules, 2019, 24, 209 CrossRef.
- (a) E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410 RSC; (b) Y. Segawa, A. Fukazawa, S. Matsuura, H. Omachi, S. Yamaguchi, S. Irle and K. Itami, Org. Biomol. Chem., 2012, 10, 5979–5984 RSC; (c) T. Iwamoto, Y. Watanabe, Y. Sakamoto, T. Suzuki and S. Yamago, J. Am. Chem. Soc., 2011, 133, 8354–8361 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04211k |
| ‡ C. M. W. and M. I. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |