Synthesis of a d² kagome lattice antiferromagnet, (CH₃NH₃)₂NaV₃F₁₂

Abstract

The ground-state of S = 1 kagome lattice antiferromagnets (KLAFs), in the presence of strong geometric frustration and the smallest integer spin, has the potential to host a range of non-trivial magnetic phases including a quantum spin liquid. The effect of local geometry and metal-ion electronic structure on the formation of these predicted phases remain unknown due to, in part, the lack of an ideal analyte. Herein, a kagome lattice compound, (CH₃NH₃)₂NaV₃F₁₂ (1-V), featuring a single distinct V³⁺ (d²) site in the R3̄m space group, was synthesized hydrothermally. In this S = 1, d² system, the trivalent vanadium ions are tetragonally compressed due to Jahn–Teller distortion. The interlayer methylammonium cations show static positional disorder with three possible orientations. The negative Curie–Weiss temperature and dominant antiferromagnetic interactions make 1-V a candidate to study S = 1 KLAF physics. The frequency-dependence of ac magnetic susceptibility and the heat capacity results suggest that 1-V has a spin glass ground state. This freezing of the spin dynamics may be due to competing exchange interactions, structural imperfection arising from the static disorder of the interlayer methylammonium cations or the presence of ‘defect’-like spins.

---

Introduction

Kagome lattice antiferromagnets (KLAFs) have attracted great interest due to their potential to host novel magnetic states.^1,2 The ground states of the KLAFs have not been well-determined partially due to the lack of appropriate analytes,³ but progress has been made by synthetic chemists recently.⁴ The synthesis of iron and chromium jarosites in single crystal form provided access to S ≥ 3/2 KLAFs for study.^5–8 The ground state of Herbertsmithite, the first realization of a structurally perfect S = 1/2 KLAF, matches the theoretical results of a gapped spin liquid state.^9–11 Several lanthanide-based kagome lattice compounds with a potential J_eff = 1/2 spin have also been synthesized recently and show interesting magnetic behaviors.^12–15S ≥ 3/2 systems are governed by thermal fluctuations which leads to long-range ordering despite significant geometric frustration.^6,16 However, several theoretical studies suggest that the ground state of S = 1 KLAFs could be a trimerized, hexagonal, or quantum spin liquid (QSL) state.^16–19 This intermediate spin regime is important for understanding the transition between materials governed exclusively by quantum fluctuations and those governed by thermal fluctuations. However, the accessible ground states of S = 1 KLAFs are still elusive since the realization of ideal, S = 1 KLAF compounds remains an open synthetic challenge.

Several S = 1 kagome lattice compounds have been synthesized before, but few compounds are close to an ideal S = 1 KLAF. The vanadium jarosites, AV₃(OH)₆(SO₄)₂ with A = Na⁺, K⁺, Rb⁺, Tl^+, and NH₄⁺, have nearly perfect kagome lattices but have dominant ferromagnetic interactions.²⁰ Compounds with kagome lattice and S = 1 spins also include BaNi₃(OH)₂(VO₄)₂ (ref. 21) and [C₆N₂H₈][NH₄]₂[Ni₃F₆(SO₄)₂],²² which show features of both antiferromagnetic and ferromagnetic interactions. The Ni₃V₂O₈ has S = 1 and a kagome-staircase lattice which deviates from a planar 2-D kagome structure.²³ The KV₃Ge₂O₉ has a perfect kagome lattice above 50 K and strong antiferromagnetic interactions between spins.²⁴ Nonetheless, below 50 K, the structure of KV₃Ge₂O₉ is orthorhombic, and the C-centered symmetry is broken.²⁵ Structural phase transitions can also be observed in m-N-methylpyridinium α-nitronyl nitroxide·BF₄·1/3(acetone), m-(MPYNN)·BF₄·1/3(acetone), and Na₂Ti₃Cl₈.^26–28 The YCa₃(VO)₃(BO₃)₄ is an interesting S = 1 KLAF with a possible QSL state.^29,30 The short interlayer distance (∼2.9 Å) in comparison to the distance between neighboring vanadium within layers (∼5.3 Å) and the weak ferromagnetic interactions deviate this compound from an ideal two-dimensional S = 1 KLAF analyte. As a result, there is no phase stable kagome lattice system with S = 1 ions that are antiferromagnetically coupled and does not present structural perturbations. Recently, a group of compounds, A₂BV₃F₁₂, with dominantly antiferromagnetic interactions and a large distance between layers, have been reported.^24,31 However, the kagome lattices in these materials are distorted. Herein, building on our synthesis of the S = 1/2 KLAF, (CH₃NH₃)₂NaTi₃F₁₂ (1-Ti),³² the analogous compound (CH₃NH₃)₂NaV₃F₁₂ (1-V), an S = 1 kagome lattice antiferromagnet, is reported.

Results and discussion

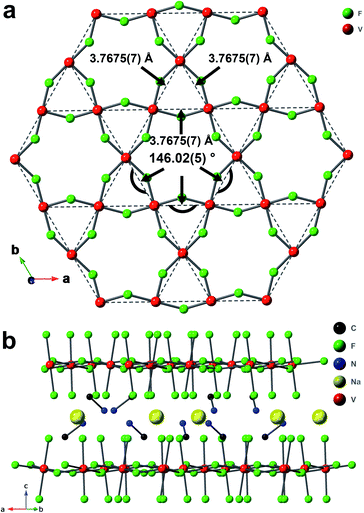
The material 1-V was synthesized hydrothermally by mixing V₂O₅, ethylene glycol (EG), CH₃NH₂·HCl, NaF, HF, and water. This synthetic method is developed based on a related methodology.³³ The crystal structure of 1-V was determined by single crystal X-ray diffraction (SCXRD) on a brown-green crystal (∼0.187 mm × 0.14 mm × 0.124 mm, Fig. S1†) at 300 K.³⁴ The lack of an obvious difference between the experimental powder X-ray diffraction (PXRD) pattern and the pattern simulated from the SCXRD structure (Fig. S2†) suggests the bulk-purity of as-synthesized 1-V. One unique vanadium site sits in an octahedral VF₆ environment (Fig. S4a†). The axial V–F bond length, d_axial, and the equatorial bond length, d_equi. are 1.8842(12) and 1.9697(6) Å, respectively, which indicate a compressed Jahn–Teller distortion. The vanadium is trivalent and has a d² electron configuration based on the bond valence sum calculation (valence of 3.162(1) for V³⁺),³⁵ X-ray photoelectron spectroscopy (XPS) results (Fig. S7b†), and the UV-vis-NIR diffuse reflectance spectra (Fig. S8†). The V³⁺ sites form a kagome layer (Fig. 1a) with all the distances between the neighboring V³⁺ equal to 3.7675(7) Å. The bridging fluoride ligands connect the V³⁺ ions with a V–F–V angle of 146.02(5)°.

Fig. 1 (a) The {V₃F₆} kagome lattice layer in 1-V viewed parallel to the crystallographic c-axis. (b) View of interlayer Na⁺ and disordered MA⁺ in 1-V, carbon atoms on C1 sites, and hydrogen atoms are omitted for clarity. The positions of nitrogen atoms for methylammonium are selected from three possible sites.

The vanadium kagome layers are separated by methylammonium (MA⁺) cations and sodium cations (Fig. 1b). The distance between layers is 6.367(1) Å. Similar to 1-Ti, the MA⁺ cations are disordered, and an analogous disorder model was applied to the MA⁺ in 1-V (Fig. S4b†). The nitrogen atoms occupy three crystallographically equivalent sites with 1/3 atom occupancy for each site, which suggests that each MA⁺ cations have three possible orientations. The distances between the hydrogen atoms of the amine group and their neighboring fluorides range from 1.9267(14) Å to 2.4581(10) Å and indicate the formation of H–F hydrogen bonding interaction.³⁶

The crystal structure of 1-V is very similar to that of 1-Ti. The structural features of these two compounds are listed in Table 1.³² The θ_mp, which is the angle between the C–N bond of MA⁺ (the MA⁺ is composed of C1 and one of the nitrogen sites with C–N bond length of 1.44(3) Å for 1-V and 1.42(2) Å for 1-Ti) and (001) crystal plane in two compounds is 20.9(6)° in 1-Ti and 23.8(6)° in 1-V (demonstrated in Fig. S5†). The difference between the θ_mp value in 1-Ti and 1-V suggests that the inclusion of an organic cation provides essential flexibility in the structure to accommodate different sized trivalent cations in the with the same connectivity. The change in the θ_mp (the MA⁺ tilting angle) reflects changes in the size of the hexagonal pocket as the trivalent cation is varied.

Table 1 Structural comparison of 1-V and 1-Ti, SCXRD data are measured under 300 K for 1-V and 298 K for 1-Ti, M stands for V in 1-V and Ti in 1-Ti

	1-V	1-Ti
Space group	R3̄m	R3̄m
a, b/Å	7.5349(13)	7.7046(2)
c/Å	19.100(3)	18.9645(6)
d axial : dequi	0.9566(10)	0.9386(5)
∠M–F–M/°	146.02(5)	146.09(4)
Nearest-neighboring metal center distance/Å	3.7675(5)	3.8523(1)
Layer distance/Å	6.367(1)	6.3215(2)
θ mp/°	23.6(8)	20.9(6)

---

Several S = 1 kagome lattice compounds, such as Na₂Ti₃Cl₈ (ref. 27) and KV₃Ge₂O₉,²⁵ undergo phase transitions from R3̄m to lower symmetries. The SCXRD data of 1-V were also collected at 100 K, and there is no change in the measured lattice symmetry between 300 K and 100 K (Table S2†).¹⁷ Additionally, no feature of first-order phase transition was observed either in the differential scanning calorimetry from 183 K to 473 K (Fig. S9†) or in the heat capacity measurement from 2 K to 140 K at 0 T (Fig. 2d) which indicates that the R3̄m space group is maintained down to 2 K. The lack of phase transition and the absence of diffuse scattering in the precession image of (0kl) plane at 300 K and 100 K (Fig. S3†) indicates that the disorder of MA⁺ cations is static.³²

Fig. 2 (a) Temperature dependence of magnetic susceptibility in 1-V under 0.001 T ZFC and FC conditions. The dashed orange line is the fit from 150 K to 300 K using a modified Curie–Weiss law. Inset: Temperature dependence of magnetic susceptibility from 1.8 K to 8 K in 1-V under 0.001 T FC and ZFC condition. (b) Magnetic field dependence of magnetization in 1-V at 1.8 K from 0 to 14 T. The red dashed line is the linear fit magnetization curves from 10 to 14 T. The orange dots are magnetization data after the subtraction of the linear contribution. The green dashed line is the Brillouin function for 2.84(3)% of free S = 1 spins when g = 2. Inset: Magnetization curves of 1-V between −1 and 1 T at 1.8 K. The measurement was performed from 0 T to 14 T, from 14 T to −1 T and from −1 T to 0 T. (c) The temperature dependence of the real part of ac susceptibility from 1.8 K to 5 K under 0 T with different frequencies in 1-V. The black dashed arrow is shown to demonstrate the shift of the peak with frequency. (d) The temperature dependence of specific heat divided by temperature under 0 T and 9 T from 2 K to 140 K.

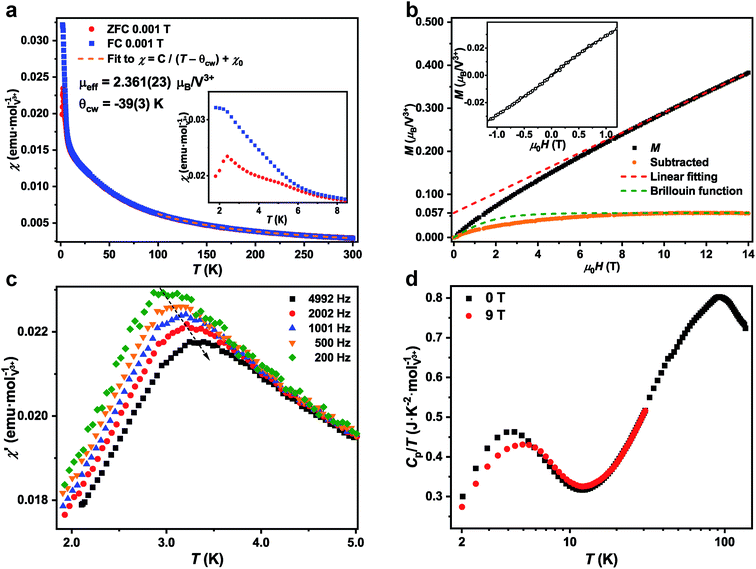
The dc magnetic susceptibility measurement of 1-V was performed from 1.8 K to 300 K under field cooled (FC) and zero field cooled (ZFC) conditions under 0.001 T (Fig. 2a). Fits of the susceptibility data from 150 K to 300 K to the modified Curie–Weiss law with a temperature-independent contribution (see ESI† for details) yield a Curie–Weiss temperature of θ_cw = −39(3) K. This result suggests that the dominant interactions between spins are antiferromagnetic. The θ_cw is similar to the value of these A₂BV₃F₁₂-type KLAFs with lattice distortion (Table 2).³¹ The effective magnetic moment of μ_eff = 2.361(23) μ_B/V³⁺ deviates from the theoretical value of 2.83 μ_B for S = 1 spin but is close to the value observed for several A₂BV₃F₁₂ compounds.^31,37 A change in slope around 8 K in the temperature-dependence of inverse susceptibility can be observed. This change in slope could be due to several effects including the formation of short-range magnetic ordering or the single-ion anisotropy of V³⁺ in the tetragonal environment. The strong single-ion anisotropy in the V³⁺, d², cations has been observed in several systems such as in the alum doped with vanadium(III) cations and in the vanadium fluorides.^20,31,38

Table 2 Comparison between the structural information and the magnetic properties of the 1-V and other S = 1 KLAFs compounds

Compounds	Space group	D M–M (Å)	Layer distance (Å)	θ cw (K)	T c (K)	Frustration parameter^c	Description of the compound	Ref.
a D M–M indicates the distance between the nearest-neighboring metal (S = 1) centers. b T c represents any cooperative-ordering transition temperature. c Frustration parameter f = −θcw/Tc. The frustration parameters of compounds with dominant ferromagnetic interactions are not shown here since the frustration parameter is an empirical measure of frustration and applied mainly to antiferromagnetic systems.^1 d In m-(MPYNN)·BF4·1/3(acetone), the S = 1 spin is composed of two ferromagnetically coupled spins, the distance between spins is therefore hard to determine. e The antiferromagnetic coupling constant, J1, between S = 1 spins is −3.1 K.
1-V	R3̄m	3.7675(5)	6.367(1)	−39(3)	2.3	16.2	2D kagome lattice with one distinct V^3+ site, antiferromagnet	This work
Rb2NaV3F12	P21/m	3.680–3.709	6.168	−50 (H⊥ab)	8.0	6.25	Distorted 2D kagome lattice, antiferromagnet	31
Cs2NaV3F12	P21/m	3.707–3.732		−21 (H⊥ab)	4.9	4.28	Distorted 2D kagome lattice, antiferromagnet	31
Cs2KV3F12	P21/c	3.734–3.743		−29 (H⊥ab)	2.5	11.6	Distorted 2D kagome lattice, antiferromagnet	31
NaV3(OH)6(SO4)2	R3̄m	3.642, 3.643	5.617	+53	33	N.A.	Nearly perfect kagome lattice, ferromagnet	20 and 44
MV3(OH)6(SO4)2, M = Na^+, K^+, Rb^+, Tl^+ and NH4^+	R3̄m	3.636–3.642	5.800–5.973	52–54	29–31	N.A.	Nearly perfect kagome lattice, ferromagnet	20 and 45
BaNi3(OH)2(VO4)2	C2/c	2.908, 2.938	7.028	10	15	N.A.	Distorted kagome lattice, both ferromagnetic and antiferromagnetic	21
[C6N2H8][NH4]2[Ni3F6(SO4)2]	R3̄	3.658	8.731	−60	10	6	Perfect kagome lattice, both ferromagnetic and antiferromagnetic	22 and 46
(NH4)2(C2H8N)[V3F12]	P21/m	3.711, 3.722	6.932	−30	15	2	Distorted kagome lattice, both ferromagnetic and antiferromagnetic	37
KV3Ge2O9	P63/mmc (above 50 K)	2.931	6.855	−250	∼60 (structural phase transition	∼4.2	Perfect kagome lattice at high temperature, orthorhombic phase below 50 K, antiferromagnet	24 and 25
YCa3(VO)3(BO3)4	P3̄	5.244–5.262	2.898	−453	<1.5	>302	Distorted kagome lattice, antiferromagnet, short interlayer distance, QSL candidate	29 and 30
m-MPYNN)·BF4·1/3(acetone)	P3c1 (above 129 K)	N.A.^d	11.81	N.A.^e	128.7 (structural phase transition)	N.A.	Kagome lattice antiferromagnet
Ni3V2O8	Cmca	2.942, 2.968	5.710	−30	2.6, 4, 6.4, 9	<11.6	Kagome-staircase lattice, antiferromagnet	23

---

Strong interlayer or intralayer ferromagnetic interactions have been observed in several S = 1 kagome lattice compounds (Table 2). The negative θ_cw (inset of Fig. 2a) indicates that 1-V has dominantly antiferromagnetic interactions, which is similar to the other A₂BV₃F₁₂ compounds.^31,37 Therefore, the 1-V, with a non-distorted kagome lattice and dominantly antiferromagnetic interactions is a candidate material to study the ground state of S = 1 KLAFs. The frustration parameter f = |θ_cw/T_c| (T_c represents any cooperative-ordering transition temperature) is an empirical measurement of frustration.¹ The f in 1-V is 16.2, which indicates strong frustration and is larger than the value for the previously reported S = 1 KLAFs except for the YCa₃(VO)₃(BO₃)₄ (ref. 29) (Table 2).

The FC and ZFC susceptibility curves under 0.001 T increase monotonically with decreasing temperature until 2.4 K where a peak is found in the ZFC curve. This peak can be observed from 0.005 T to 0.1 T, and the position of the peak does not change as a function of applied field (Fig. S10†). The divergence between FC and ZFC curves from 1.8 K to 8 K as shown in the inset of Fig. 2a suggests the freezing of spins at low temperatures. The spin freezing behavior is supported by the frequency dependence of the real part of the ac susceptibility, χ′ (Fig. 2c), and the sudden onset of the imaginary part of the ac susceptibility, χ′′, (Fig. S12†) from 1.8 K to 5 K under 0 T.³⁹ Additionally, a maximum that shifts to higher temperatures with increasing frequency can also be observed around 3 K. The empirical parameter X, which is used to express the freezing temperature observed in χ′ vs. frequency dependence, is around 0.06 in 1-V and is within the range for insulating spin glasses.⁴⁰ A broad peak centers at 4.4 K is found in the temperature dependence of specific heat under 0 T, and this broad peak shifts to 4.9 K and reduces in intensity under 9 T (Fig. 2d). A typical spin glass shows a peak in both dc and ac magnetic susceptibility, a divergence between FC and ZFC dc magnetic susceptibility curves, a frequency dependence of the χ′, and a sudden onset of χ′′ near spin glass transition temperature (T_f).³⁹ The heat capacity of a spin glass shows a broad peak at a temperature higher than the T_f.³⁹ Therefore, the physical properties of 1-V are consistent with those of a spin glass.

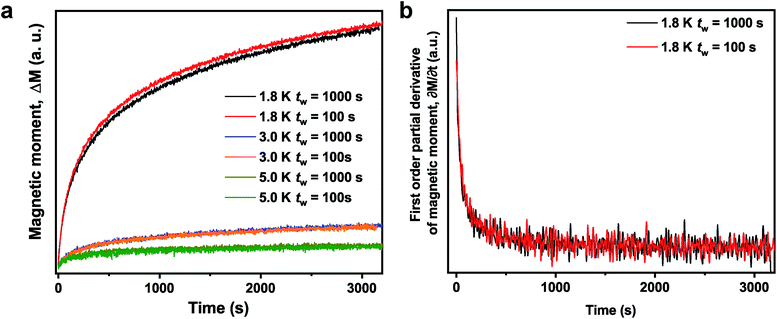
In an ageing experiment, a spin glass presents a divergent response to the application of applied field which implies nonequilibrium dynamics.^41–43 On 1-V, an ageing experiment was performed by cooling the sample under zero field from 50 K (above the T_f in 1-V) to the measurement temperature (T_m). At T_m, the sample was aged for the waiting time, t_w, seconds. Then, a small magnetic field (0.0025 T) was applied and the magnetization as a function of time was recorded. The results are shown in Fig. 3. The magnetic moment as function of time shows a clear dependence on t_w. This dependence is observed only at 1.8 K (not at 3.0 K or 5.0 K) which is consistent with a spin glass behavior below T_f for 1-V.⁴³ The time dependence of magnetization at 1.8 K can be fit by the stretched exponential function as shown in Fig. S15†.⁴⁷ The increase of time constant τ with longer t_w is indicative of a stiffening of the spin relaxation.⁴⁷ An inflection point is absent in the first derivative of the time dependence of magnetization as shown in Fig. 3b. However, an inflection point can be observed close to the t_w for a typical metallic spin glass, such as CuMn.⁴² The ageing behavior of 1-V is close to the behavior in La_0.5Sr_0.5CoO₃ which can be described as a cluster glass or mictomagnet (one category of spin glass) due to the formation of large magnetic clusters.⁴⁸

Fig. 3 (a) Time dependence of magnetic moment change under 25 Oe after ZFC from 50 K to 1.8 K, 3.0 K, and 5.0 K for different waiting time, t_w = 100 and 1000 seconds in 1-V. (b) Time dependence of the first order partial derivative of magnetic moment under 25 Oe after ZFC from 50 K to 1.8 K with t_w = 100 and 1000 seconds.

The isothermal magnetization of 1-V at 1.8 K is shown in Fig. 2b. No hysteresis is observed in the magnetization curves of 1-V between −1 T and 1 T (inset of Fig. 2b). A high-resolution of isothermal magnetization measurement was conducted in a short loop as shown in Fig. S16† and an observable hysteresis is noted. While this is a small hysteresis, it is consistent with the assignment of the 1-V as a spin glass. The magnetization under 14 T is 0.383 μ_B/V³⁺ which is around 19% of the saturated value for V³⁺ ions (2 μ_B/V³⁺ when g = 2). The magnetization increases rapidly below 10 T and is linearly dependent on the field above 10 T. The magnetization is far from saturation at accessible fields and is indicative the significant geometric frustration and the strong antiferromagnetic interaction.

One possible way to analyze the isothermal magnetization result is that the magnetization could be consisted of two components, the defect (M_d) and the intrinsic (M_i) contributions, which is a similar approach to that utilized for 1-Ti. After the subtraction of the linear dependent component (M_i, red dashed line in Fig. 2b, this component is determined by the linear fitting of the isothermal magnetization data above 10 T), around 3% of ‘defect’-like S = 1 spins (M_d) could be identified as shown in the orange dots in Fig. 2b. These ‘defect’-like spins saturate rapidly below 10 T, but still deviate from the Brillouin function for 2.84(3)% of free S = 1 spins (green dashed line in Fig. 2b). However, the XPS results have largely ruled out the existence of vanadium species with different oxidation states in 1-V and no impurity phases can be observed in laboratory PXRD. Therefore, the origin of the non-linear region in isothermal magnetization result at low field still requires further structural, spectroscopic, and physical studies.

The 1-V and 1-Ti are structurally similar (Table 1) and share some similar physical properties (Table S3†). Both compounds have dominant antiferromagnetic interactions and are highly frustrated. Frequency dependence can be observed in the real part of ac magnetic susceptibility in both 1-V and 1-Ti, while a peak can only be found in 1-V around 3 K. Evidence of ‘defect’-like spins can be observed in both compounds and no chemical impurities are identified by laboratory PXRD in either material.

It should be noted that recent theoretical studies propose that the introduction of structural disorder in KLAFs could lead to a spin glass state.^49,50 It is possible that the magnetic freezing behaviors observed in both compounds are induced by the disordered methylammonium cations. It is also noticeable that θ_cw in 1-V is higher than that in 1-Ti (−36 K vs. −140 K) which implies stronger antiferromagnetic interactions between spins in 1-Ti than in its isostructural 1-V. The weaker antiferromagnetic coupling in 1-V could originate from additional, competing, ferromagnetic exchange interaction due to the extra d electron in either d_xz or d_yz orbitals for V³⁺ in comparison to Ti³⁺.³⁷ Similar phenomenon has been observed in the jarosites with V³⁺, Cr³⁺ and Fe³⁺.^4,20 Therefore, we cannot rule out the contribution from the potential competing ferromagnetic exchange interaction to the spin glass state in 1-V despite of the dominant antiferromagnetic interactions between spins. In addition, the ‘defect’-like spins could also lead to the spin glass state since several spin glasses are induced by the inclusion of intrinsic ‘impurities’ such as the metallic alloy CuMn with 0.9% Mn.⁴⁰

Conclusions

In summary, an S = 1 kagome lattice antiferromagnet, 1-V, was synthesized hydrothermally, providing access to this intermediate spin regime on a highly frustrated, non-distorted kagome lattice. As a result, effects of local symmetry and d orbital population, along with the organic cation disorder on the resultant ground state, can be examined. This compound crystallizes into an R3̄m space group and one distinct V³⁺ (d²) site is found. No first-order phase transition was observed, and the methylammonium cations show static positional disorder. Compound 1-V, with θ_cw = −39(3) K and f = 16.2, is a strongly frustrated antiferromagnet and is a candidate to study the ground state of S = 1 KLAFs. The ac and dc magnetic susceptibility, heat capacity measurement, and magnetic ageing experiments suggest a spin glass state in 1-V at low temperature. The spin glass like behaviour may be due to competing exchange interactions, structural imperfections arising from the static disorder of the interlayer methylammonium cations, or the presence of ‘defect’-like spins.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Studies were supported by the Beckman Foundation as part of a Beckman Young Investigator Award to H. S. L. Single-crystal diffraction experiments were performed at the Georgia Institute of Technology SCXRD facility directed by Dr John Bacsa. We thank Prof. Martin Mourigal for the access to a PPMS. This work was performed in part at the Georgia Tech Institute for Electronics and Nanotechnology, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (grant ECCS-1542174). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement no. DMR-1644779 and the State of Florida.

Notes and references

1. A. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453–480.
2. L. Balents, Nature, 2010, 464, 199–208.
3. A. Harrison, J. Phys.: Condens. Matter, 2004, 16, S553.
4. D. G. Nocera, B. M. Bartlett, D. Grohol, D. Papoutsakis and M. P. Shores, Chem.–Eur. J., 2004, 10, 3850–3859.
5. D. Grohol, D. G. Nocera and D. Papoutsakis, Phys. Rev. B: Condens. Matter, 2003, 67, 064401.
6. D. Grohol, K. Matan, J.-H. Cho, S.-H. Lee, J. W. Lynn, D. G. Nocera and Y. S. Lee, Nat. Mater., 2005, 4, 323–328.
7. K. Okuta, S. Hara, H. Sato, Y. Narumi and K. Kindo, J. Phys. Soc. Jpn., 2011, 80, 063703.
8. K. Matan, D. Grohol, D. G. Nocera, T. Yildirim, A. B. Harris, S. H. Lee, S. E. Nagler and Y. S. Lee, Phys. Rev. Lett., 2006, 96, 247201.
9. M. P. Shores, E. A. Nytko, B. M. Bartlett and D. G. Nocera, J. Am. Chem. Soc., 2005, 127, 13462–13463.
10. M. Fu, T. Imai, T.-H. Han and Y. S. Lee, Science, 2015, 350, 655–658.
11. S. Yan, D. A. Huse and S. R. White, Science, 2011, 332, 1173–1176.
12. M. Sanders, J. Krizan and R. Cava, J. Mater. Chem. C, 2016, 4, 541–550.
13. M. Ashtar, J. Guo, Z. Wan, Y. Wang, G. Gong, Y. Liu, Y. Su and Z. Tian, Inorg. Chem., 2020, 59, 5368–5376.
14. P. Bordet, I. Gelard, K. Marty, A. Ibanez, J. Robert, V. Simonet, B. Canals, R. Ballou and P. Lejay, J. Phys.: Condens. Matter, 2006, 18, 5147.
15. Z. Dun, J. Trinh, M. Lee, E. Choi, K. Li, Y. Hu, Y. Wang, N. Blanc, A. Ramirez and H. Zhou, Phys. Rev. B: Condens. Matter, 2017, 95, 104439.
16. H. J. Changlani and A. M. Läuchli, Phys. Rev. B: Condens. Matter, 2015, 91, 100407.
17. K. Hida, J. Phys. Soc. Jpn., 2000, 69, 4003–4007.
18. C. Xu and J. E. Moore, Phys. Rev. B: Condens. Matter, 2007, 76, 104427.
19. W. Li, S. Yang, M. Cheng, Z.-X. Liu and H.-H. Tu, Phys. Rev. B: Condens. Matter, 2014, 89, 174411.
20. D. Papoutsakis, D. Grohol and D. G. Nocera, J. Am. Chem. Soc., 2002, 124, 2647–2656.
21. D. E. Freedman, R. Chisnell, T. M. McQueen, Y. S. Lee, C. Payen and D. G. Nocera, Chem. Commun., 2012, 48, 64–66.
22. J. Behera and C. Rao, J. Am. Chem. Soc., 2006, 128, 9334–9335.
23. N. Rogado, G. Lawes, D. A. Huse, A. Ramirez and R. J. Cava, Solid State Commun., 2002, 124, 229–233.
24. S. Hara, H. Sato and Y. Narumi, J. Phys. Soc. Jpn., 2012, 81, 073707.
25. E. Takagi, T. Aoyama, S. Hara, H. Sato, T. Kimura and Y. Wakabayashi, Phys. Rev. B: Condens. Matter, 2017, 95, 104416.
26. D. J. Hinz, G. Meyer, T. Dedecke and W. Urland, Angew. Chem., Int. Ed., 1995, 34, 71–73.
27. Z. A. Kelly, T. T. Tran and T. M. McQueen, Inorg. Chem., 2019, 58, 11941–11948.
28. T. Kambe, Y. Nogami, K. Oshima, W. Fujita and K. Awaga, J. Phys. Soc. Jpn., 2004, 73, 796–799.
29. W. Miiller, M. Christensen, A. Khan, N. Sharma, R. B. Macquart, M. Avdeev, G. J. McIntyre, R. O. Piltz and C. D. Ling, Chem. Mater., 2011, 23, 1315–1322.
30. H. J. Silverstein, R. Sinclair, A. Sharma, Y. Qiu, I. Heinmaa, A. Leitmäe, C. R. Wiebe, R. Stern and H. Zhou, Phys. Rev. Mater., 2018, 2, 044006.
31. M. Goto, H. Ueda, C. Michioka, A. Matsuo, K. Kindo, K. Sugawara, S. Kobayashi, N. Katayama, H. Sawa and K. Yoshimura, Phys. Rev. B: Condens. Matter, 2017, 95, 134436.
32. N. Jiang, A. Ramanathan, J. Bacsa and H. S. La Pierre, Nat. Chem., 2020, 12, 691–696.
33. D. W. Aldous, N. F. Stephens and P. Lightfoot, Inorg. Chem., 2007, 46, 3996–4001.
34. X-ray crystallographic data for 1-V at 300 K and 100 K can be found at the Cambridge Crystallographic Data Centre (CCDC) under deposition numbers CCDC 1987388 and 1987389†.
35. N. Brese and M. O'keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
36. C. N. R. Rao, E. V. Sampathkumaran, R. Nagarajan, G. Paul, J. N. Behera and A. Choudhury, Chem. Mater., 2004, 16, 1441–1446.
37. F. H. Aidoudi, L. J. Downie, R. E. Morris, M. A. de Vries and P. Lightfoot, Dalton Trans., 2014, 43, 6304–6307.
38. P. L. Tregenna-Piggott, H. Weihe, J. Bendix, A.-L. Barra and H.-U. Güdel, Inorg. Chem., 1999, 38, 5928–5929.
39. K. Binder and A. P. Young, Rev. Mod. Phys., 1986, 58, 801.
40. J. A. Mydosh, Spin glasses: an experimental introduction, CRC Press, 2014.
41. P. Granberg, L. Sandlund, P. Nordblad, P. Svedlindh and L. Lundgren, Phys. Rev. B: Condens. Matter, 1988, 38, 7097.
42. L. Lundgren, P. Svedlindh, P. Nordblad and O. Beckman, Phys. Rev. Lett., 1983, 51, 911.
43. J. A. Mydosh, Spin glasses: an experimental introduction, CRC Press, 1993.
44. D. Grohol, D. Papoutsakis and D. G. Nocera, Angew. Chem., Int. Ed., 2001, 40, 1519–1521.
45. D. Grohol and D. G. Nocera, J. Am. Chem. Soc., 2002, 124, 2640–2646.
46. J. Behera, A. Sundaresan, S. K. Pati and C. Rao, ChemPhysChem, 2007, 8, 217–219.
47. N. Khan, P. Mandal and D. Prabhakaran, Phys. Rev. B: Condens. Matter, 2014, 90, 024421.
48. M. Itoh, I. Natori, S. Kubota and K. Motoya, J. Phys. Soc. Jpn., 1994, 63, 1486–1493.
49. M. Schmidt, F. Zimmer and S. Magalhaes, J. Phys.: Condens. Matter, 2017, 29, 165801.
50. T. Bilitewski, M. E. Zhitomirsky and R. Moessner, Phys. Rev. Lett., 2017, 119, 247201.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic, spectroscopic, and crystallographic details (PDF and CIF). CCDC 1987388 and 1987389. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03323e

---