Open Access Article
Open Access ArticleDimensional reduction of the small-bandgap double perovskite Cs2AgTlBr6†
Bridget A.
Connor
 a,
Raisa-Ioana
Biega
b,
Linn
Leppert
a,
Raisa-Ioana
Biega
b,
Linn
Leppert
 *b and
Hemamala I.
Karunadasa
*b and
Hemamala I.
Karunadasa
 *ac
*ac
aDepartment of Chemistry, Stanford University, Stanford, California 94305, USA. E-mail: hemamala@stanford.edu
bInstitute of Physics, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: l.leppert@utwente.nl
cStanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
First published on 5th June 2020
Abstract
Quantum confinement effects in lower-dimensional derivatives of the ABX3 (A = monocation, X = halide) single perovskites afford striking optical and electronic changes, enabling applications ranging from solar absorbers to phosphors and light-emitting diodes. Halide double perovskites form a larger materials family, known since the late 1800s, but lower-dimensional derivatives remain rare and prior work has revealed a minimal effect of quantum confinement on their optical properties. Here, we synthesize three new lower-dimensional derivatives of the 3D double perovskite Cs2AgTlBr6: 2D derivatives with mono- (1-Tl) and bi-layer thick (2-Tl) inorganic sheets and a quasi-1D derivative (1'-Tl). Single-crystal ellipsometry studies of these materials show the first clear demonstration that dimensional reduction can significantly alter the optical properties of 2D halide double perovskites. This large quantum confinement effect is attributed to the substantial electronic delocalization of the parent 3D Ag–Tl perovskite. Calculations track the evolution of the electronic bands with dimensional reduction and the accompanying structural distortions and show a direct-to-indirect bandgap transition as the 3D perovskite lattice is thinned to a monolayer in 1-Tl. This bandgap transition at the monolayer limit is also evident in the calculations for 1-In, an isostructural, isoelectronic analogue to 1-Tl in which In3+ replaces Tl3+, underscoring the orbital basis for the direct/indirect nature of the bandgap. Thus, in complement to the massive compositional diversity of halide double perovskites, dimensional reduction may be used as a systematic route for harnessing electronic confinement effects and obtaining new electronic structures.
1. Introduction
In recent years, double perovskites have risen to the forefront of synthetic efforts in halide perovskites, driven in part by the substitutional flexibility of this family of materials. The A2BB'X6 (A = 1+ cation, X = halide) double perovskite structure splits the charge of the 2+ octahedral B-site metal present in ABX3 single perovskites between two distinct octahedral sites, accommodating cations with charges from 1+ to 4+. This increased flexibility has afforded a class of materials with an astonishing array of optoelectronic properties. Exhibiting bandgaps large1,2 and small,3–6 direct7,8 and indirect,9–12 symmetry-allowed and symmetry-forbidden,5,13,14 double perovskite band structures demonstrate how a diverse range of properties can arise from substitutions at a single atomic site.Dimensional reduction15 of the 3D double perovskite lattice to create lower-dimensional hybrid analogues offers yet more fertile ground for exploration. Indeed, studies performed since the 1990s have shown that dimensional reduction dramatically tunes the electronic structure in lead- and tin-halide single perovskites.16–18 However, although double perovskites constitute a larger family of materials, known since the late 1800s,19 the effects of dimensional reduction have not yet been elucidated. We recently probed the effects of dimensional confinement on halide double perovskites by synthesizing 2D derivatives of 3D Cs2AgBiBr6.20 Unexpectedly, however, the optical properties of the layered double perovskites with monolayer- (n = 1, (BA)4AgBiBr8; BA = butylammonium, 1-Bi) and bilayer-thick (n = 2, (BA)2CsAgBiBr7; 2-Bi) inorganic sheets were strikingly similar. This is in stark contrast to the well-studied Pb and Sn single perovskites, whose optical properties show a large and systematic variation with n.18,21–23 Indeed, even nanoparticles of the Ag–Bi perovskites24,25 have not displayed the dramatic effects of quantum confinement seen in Pb-perovskite nanoparticles.26,27
It is important to determine if the minimal effect of quantum confinement observed in 1-Bi and 2-Bi is a general feature of 2D halide double perovskites, or whether it is specific to this Ag–Bi composition. However, the dearth of known 2D halide double perovskites does not allow us to answer this question. Prior to preparation of this manuscript only two other B-site combinations, AuI–AuIII (ref. 28) and CuI–BiIII,29 were known for this structure type (a third (AgI–InIII) was recently reported30). In the AuI–AuIII perovskites, I3− coordination to Au is thought to perturb the electronic structure relative to the 3D analogues,28 while in the case of the CuI–BiIII composition, there is no 3D analogue for comparison.29 Thus, neither family allows us to study the optoelectronic effects of dimensional reduction.
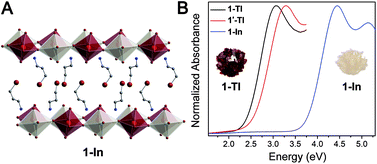
To reveal the optical and electronic effects of dimensional confinement in double perovskites, we focused on a composition with a delocalized electronic structure, Cs2AgTlBr6, featuring an unusually small bandgap (0.95 eV) and large band dispersion.5 Herein, we present the effects of dimensional reduction on the optoelectronic properties of Cs2AgTlBr6 through the synthesis of a family of new double perovskites: two 2D n = 2 perovskites ((A)2CsAgTlBr7; A = phenethylammonium (PEA), 2-TlPEA and A = butylammonium (BA), 2-TlBA), a 2D n = 1 perovskite ((3-BPA)4AgTlBr8; 3-BPA = 3-bromopropylammonium, 1-Tl), and a quasi-1D n = 1 perovskite ((HIS)2AgTlBr8; HIS = histammonium, 1′-Tl). We also synthesized the n = 1 Ag–In double perovskite ((3-BPA)4AgInBr8, 1-In) as an isoelectronic and isostructural analogue to 1-Tl. Although the Ag–Tl and Ag–In layered perovskites are structurally similar to their Ag–Bi analogues, even showing similar metal coordination environments, their optical and electronic properties differ significantly. We characterize the optical properties of the Ag–Bi and Ag–Tl perovskites through ellipsometry. Whereas quantum confinement has a minimal impact on the optical properties of the layered Ag–Bi perovskites, we observe substantial optical changes upon dimensional reduction of the Ag–Tl materials, making this the first demonstration of clear optical changes induced by electronic confinement in lower-dimensional halide double perovskites. Importantly, our ellipsometry measurements allow us to trace the origin of the difference in optical behavior between the Ag–Tl and Ag–Bi perovskites to the more delocalized electronic character of the Ag–Tl materials. Finally, using density functional theory (DFT), we further explore direct-to-indirect gap transitions that occur in Ag–Tl and Ag–In perovskites when the 3D parent lattice is thinned to a monolayer at the n = 1 limit.
2. Results and discussion
2.1. Structure
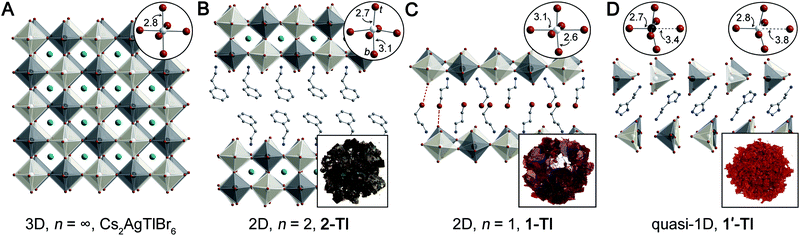 | ||
| Fig. 1 Single-crystal X-ray diffraction structures of (A) Cs2AgTlBr6 (ref. 5) and three new lower-dimensional derivatives: (B) (PEA)2CsAgTlBr7 (2-TlPEA; PEA = phenethylammonium), (C) (3-BPA)4AgBiBr8 (1-Tl; 3-BPA = 3-bromopropylammonium) with dotted lines showing Br⋯Br interactions, and (D) (HIS)2AgTlBr8 (1′-Tl; HIS = histammonium). Top insets show the metal coordination spheres (t = terminal, b = bridging) and bottom insets show the colors of the crystals. Black, white, teal, brown, blue, and gray spheres represent Tl, Ag, Cs, Br, N, and C atoms, respectively. H and disordered atoms omitted for clarity. | ||
In the 3D rock-salt halide double perovskite (or elpasolite) structure, the divalent B-site cations of the ABX3 structure are replaced by an ordered arrangement of two different B-site cations yielding the general formula A2BB'X6. Recently, renewed interest in these materials has greatly expanded the structural and electronic diversity of the perovskite family.5,7,8,10–12,32 However, lower-dimensional analogues of elpasolites remain rare.20,28–30,33 Seeking to expand the diversity of lower-dimensional double perovskites to better understand their optoelectronic properties, we synthesized several dimensionally reduced derivatives of Cs2AgTlBr6 and of the isoelectronic but unreported Cs2AgInBr6. See the ESI† for synthetic details and materials characterization.
As is frequently observed for d10 transition metal centers,39 the Ag–Br octahedra of 1-Tl display an axial compression, with two short terminal Ag–Br bonds (2.5665(1) Å) perpendicular to the plane of the sheets and four long bridging Ag–Br bonds (3.0576(1) Å and 3.1421(1) Å) parallel to the plane of the sheet (Fig. 1C, inset). This distortion is analogous to that observed in 1-Bi,20 though larger in magnitude (Table S3†).
The quasi-1D connectivity in 1'-Tl induces an obvious optical effect evidenced by the substantial color difference between this material (red-orange, Fig. 1D) and 1-Tl (maroon, Fig. 1C). We quantify this difference using thin-film transmission spectra which reveal a substantial blueshift (ca. 220 meV) of the spectrum of 1′-Tl relative to that of 1-Tl (Fig. 2B). Additionally, band structure calculations point to decreased electronic dimensionality in 1′-Tl arising from its quasi-1D connectivity (section 2.4).
Although Cs2AgInCl6 has been reported,8 to date there are no reports of the successful synthesis of the bromide analogue. The octahedral tolerance factor (μ) of In3+ coordinated by six bromides suggests that Cs2AgInBr6 may be unstable.8 The additional structural flexibility afforded by the 2D perovskite lattice diminishes the relevance of stability criteria like μ, explaining the isolation of 1-In.
2.2. Contrasting optical properties of AgI–MIII layered perovskites (M = Tl, Bi)
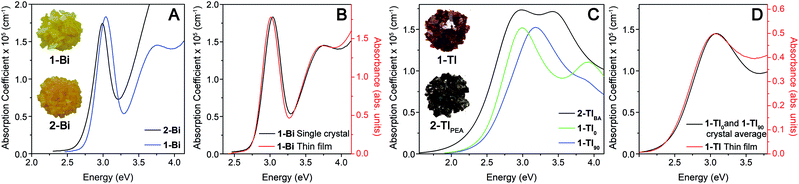
The variation of absorption coefficient (α) with photon energy obtained from ellipsometry measurements of crystals of 1-Tl, 2-TlBA, 1-Bi, and 2-Bi is shown in Fig. 3A and C. Notably, for 1-Bi and 2-Bi, the ellipsometry traces have very similar shapes to the thin-film transmission spectra, validating the use of ellipsometry as a probe of strong absorption events (Fig. 3B and S8†).20 It is important to note that, because ellipsometry and thin-film transmission measurements are only sensitive to a material's strongest absorptions, the absorption onsets observed in these spectra do not necessarily correspond to the bandgap onset because weak absorption from indirect or symmetry-forbidden direct gaps (with absorption coefficients <104 cm−1) are not evident.
For 1-Bi, 2-Bi, and 2-TlBA, the ellipsometry spectra did not vary substantially as the crystal was rotated and only one representative trace is shown (see ESI†). In contrast, for 1-Tl, the spectra obtained in different orientations differ significantly (Fig. S10†). We find that two distinct orientations of 1-Tl, defined as 0° and 90°, give unique ellipsometry spectra represented by the traces 1-Tl0 and 1-Tl90 in Fig. 3C. The average of these unique spectra looks very similar to the thin-film transmission spectrum of 1-Tl (Fig. 3D) consistent with the fact that the thin-film transmission measurement employs unpolarized light incident on a multi-crystalline thin film, where the in-plane unit-cell vectors are randomly oriented. The underlying electronic origin of the optical anisotropy in 1-Tl is currently under investigation.
The ellipsometry spectra of the 2D Ag–Bi perovskites change very little with n. Both 1-Bi and 2-Bi display a narrow, isolated absorption feature at ca. 3.0 eV that shifts minimally (ca. 50 meV) between the two materials (Fig. 3A). Fits to the ellipsometry data yield essentially the same full width at half maximum (fwhm, 0.29 eV) for this transition in both n = 1 1-Bi and n = 2 2-Bi (see ESI†).
In contrast, the lowest-energy feature in the Ag–Tl perovskites shows a substantial dependence on n. The spectra of 1-Tl0 and 2-TlBA exhibit a lowest-energy absorption feature peaked at nearly the same energy (ca. 3.0 eV), though in both cases, the feature is substantially broader than the peak in 1-Bi and 2-Bi (Fig. 3C). Fits of these spectra indicate that the lowest-energy feature in 2-TlBA is much broader than that of 1-Tl. Using a series of Lorentzian-like oscillators to fit the spectra according to the new amorphous dispersion formula, we find a broadening parameter for the major oscillator describing this lowest-energy feature in 2-TlBA that is ca. 41% larger than in the case of 1-Tl0 and ca. 19% larger than in the case of 1-Tl90 (see ESI†). Thus, in contrast to the 2D Ag–Bi perovskites whose optical spectra are essentially unaffected by n value, the optical spectra of the 2D Ag–Tl perovskites evolve substantially with changing n.
2.3. Contrasting electronic properties of AgI–MIII layered perovskites (M = Tl, Bi)
The significantly greater width of the absorption features in the Ag–Tl perovskites and the larger influence of dimensionality on their breadth suggest greater electronic delocalization. Delocalized wavefunctions yield dispersive bands and give rise to broad optical transitions. In addition, quantum confinement forces increased localization of the wavefunction, leading to narrowing of absorption features and pronounced effects of dimensional reduction.
Our ellipsometry studies demonstrate the substantial effect of n value on the optical properties of the Ag–Tl perovskites, making this the first demonstration of clear quantum confinment effects in 2D double perovskites, and trace this observation to the delocalized electronic character of the Ag–Tl perovskites. Despite this, we do not observe any spectral signatures of excitonic behavior resembling those observed upon quantum confinement of the well-studied Pb perovskites. Sharp excitonic absorption features observed in 2D Pb perovskites through single-crystal reflectance spectroscopy,40 ellipsometry,41 and thin-film transmission spectroscopy42 are absent in our materials. Indeed, clear excitonic features have not been seen in any composition of halide double perovskite to date. Additionally, although (001) Pb–Br perovskites show bright excitonic emission at room temperature,43 neither 1-Tl, 2-TlBA, nor any other composition of low-dimensional halide double perovskite has shown excitonic photoluminescence to date. Thus, any excitonic states in these materials are expected to differ from those of the well-studied Pb perovskites.
2.4. Electronic effects of dimensional reduction
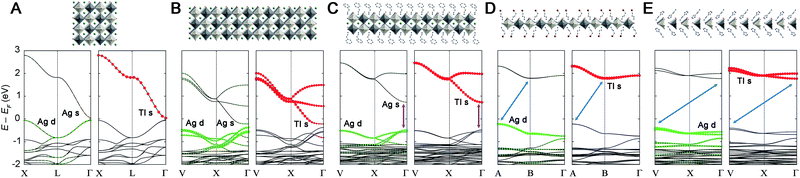
Previously, we found that the Ag–Bi double perovskites with ∞ ≥ n > 1 have an indirect bandgap between analogous k-points. This band structure changed significantly at the n = 1 limit, affording a direct bandgap.20 This indirect-to-direct gap transition is reminiscent of the effects of exfoliating bulk MoS2 to individual layers.44,45 Although Cs2AgTlBr6 (ref. 5) is electronically distinct from Cs2AgBiBr6,11,12 we see a similar bandgap transition upon dimensional reduction. Consistent with prior work,5 we find that 3D Cs2AgTlBr6 has a direct bandgap at the Γ point with a valence band maximum (VBM) composed entirely of Ag d and Br p orbitals and a conduction band minimum (CBM) composed mainly of Tl s and Br p orbitals with a smaller contribution from Ag s orbitals (Fig. 4A). The band structure of 2-TlPEA is analogous to that of the parent 3D material; we find a direct bandgap at the Γ point and similar orbital make-up of the VBM and CBM (Fig. 4C). The similar shape of the band dispersion in the band structures of Cs2AgTlBr6 (plotting the X → L → Γ path) and 2-TlPEA (plotting the analogous V → X → Γ path, see ESI†) further highlights the analogy between the electronic structures of the 3D perovskite and its n = 2 derivative. Nevertheless, a distinguishing feature of the band structure of 2-TlPEA is the lack of band dispersion along the layer stacking direction (Γ → Z) which reflects the electronically 2D nature of this material (Fig. S25†). We also constructed a model n = 3 system by relaxing the structure of an n = 3 slab cut from the 3D material (see ESI†). The band structure of this model n = 3 system shows the same close analogy to the 3D band structure as 2-TlPEA (Fig. 4B). This suggests that all Ag–Tl double perovskites with n ≥ 2 have analogous band structures.Interestingly, further dimensional reduction of the Ag–Tl perovskite lattice to the n = 1 limit yields substantial changes in band structure. The band structure of 1-Tl reveals an indirect gap between the A point in the VB and the B point in the CB (Fig. 4D). Additionally, the Ag s-orbital contribution is greatly reduced in the CB and the bandgap transition becomes an almost pure Ag-to-Tl MMCT. Once again, we find no dispersion along the layer stacking direction (Γ → Z) in 1-Tl, evidencing its electronically 2D nature (Fig. S25†).
Structural distortions of the inorganic lattice can significantly affect band dispersion and therefore, the direct/indirect nature of the bandgap.20 To separate the effects of dimensional reduction and the accompanying structural distortion, we constructed model n = 1 and 2 Ag–Tl materials (1M and 2M, respectively) with bond lengths and angles identical to those found in the cubic 3D structure (see ESI†). We find that the band structure of 2M (Fig. S23D†) retains a direct bandgap at Γ, and the band structure of 1M retains an indirect bandgap, although here, the CBM shifts from B to Γ (Fig. S23B†). This result indicates that the direct-to-indirect bandgap transition observed when moving from Cs2AgTlBr6 to 1-Tl is driven by dimensional reduction.
To further probe this direct-to-indirect bandgap transition at the n = 1 limit, we calculated the band structure of the isoelectronic n = 1 perovskite 1-In using the SCXRD structure. This material has an orbital makeup analogous to 1-Tl with s-orbital character in the CB. However, due to the significantly higher energy of the In 5s orbitals relative to the Tl 6s orbitals, the CB shifts up in energy and we calculate a 1.3 eV larger bandgap for 1-In than for 1-Tl (Table S7†), consistent with our experimental observation of a ca. 1.4 eV blueshifted absorption onset in 1-In (Fig. 2B). Calculations still predict a direct-to-indirect bandgap transition when the 3D Ag–In parent lattice is thinned to a monolayer; our calculations show an indirect bandgap in 1-In, consistent with a recent calculation for an analogous structure.30 The indirect gap in 1-In occurs between the A point in the VB and the Γ point in the CB (Fig. S24†), analogous to 1M, whereas a direct bandgap has been reported at the Γ point for the 3D analogue Cs2AgInCl6.8 This finding highlights the significance of orbital symmetry in dictating the direct/indirect nature of the bandgap in both 3D double perovskites46,47 and their layered derivatives.
Despite the significant structural distortions of the inorganic lattice of 1′-Tl, this quasi-1D structure retains an indirect bandgap similar to that of the less distorted 2D 1-Tl (Fig. 4E). However, we find substantially less band dispersion in 1′-Tl, consistent with lower dimensionality caused by increased structural distortion of the inorganic lattice.
3. Conclusion
We report several new lower-dimensional analogues of the 3D double perovskite Cs2AgTlBr6. The n = 1 and n = 2 2D perovskites, 1-Tl and 2-TlPEA/BA, are structurally similar to the analogous Ag–Bi perovskites (1-Bi and 2-Bi) (Fig. S21†). In 1′-Tl, structural distortions produce a lattice with quasi-1D connectivity. Unlike the n = 1 (1-Bi) and 2 (2-Bi) layered derivatives of 3D Cs2AgBiBr6, which are a similar shade of yellow, the lower-dimensional derivatives of 3D Cs2AgTlBr6 show significantly different colors for the 2D n = 2 (2-TlPEA/BA; black) and n = 1 (1-Tl; maroon) members and the quasi-1D structure (1′-Tl; red-orange). Single-crystal ellipsometry measurements underscore this difference. In the Ag–Bi perovskites, the strong low-energy absorption is dominated by narrow features that change very little as n varies, suggesting localized molecule-like character. In contrast, much broader features with a stronger dependence on n dominate in the Ag–Tl analogues, suggesting delocalized electronic character that is more sensitive to quantum confinement. We attribute this difference to the replacement of Bi 6p orbitals in the CB of the Ag–Bi perovskites with diffuse, spherically symmetric Tl 6s orbitals in the CB of the Ag–Tl perovskites, which promotes enhanced orbital interaction leading to greater electronic delocalization.We also find that all members of the Ag–Tl perovskite family with n ≥ 2 have analogous band structures, exhibiting direct bandgaps. In contrast, the band structure of n = 1 1-Tl displays significant differences, most notably, an indirect bandgap. This indirect bandgap is retained in 1′-Tl despite the quasi-1D connectivity of the inorganic lattice. Importantly, using calculations on undistorted model structures, we find that this direct-to-indirect bandgap transition is driven by dimensional reduction rather than by the accompanying structural distortions of the lattice. We also synthesize 1-In as an isoelectronic, isostructural analogue of 1-Tl. Despite the higher energy of the CB in the Ag–In perovskites, calculations show a similar direct-to-indirect bandgap transition, demonstrating that the analogous symmetry of the bands preserves the change in electronic structure upon dimensional reduction. Our studies of dimensional reduction of 3D halide double perovskites so far have revealed an indirect-to-direct bandgap transition at the n = 1 limit of Cs2AgBiBr6 (ref. 20) and a direct-to-indirect bandgap transition at the n = 1 limit of Cs2AgTlBr6. This substantial change in band structure observed at the inorganic monolayer limit in two electronically distinct double perovskites is intriguing and understanding the generality of this phenomenon warrants further study.
Electronic confinement effects in Pb-halide single perovskites have yielded widely varying phenomena, generating materials with applications ranging from solar-cell absorbers with high open-circuit voltages48 to phosphors with emissions ranging from the visible to the near-IR.27,49 This work shows that tuning the dimensionality of the inorganic sublattice can also afford significant changes in the optoelectronic properties of the much larger family of halide double perovskites, particularly when the parent 3D double perovskite has substantial electronic delocalization.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Department of Energy, Office of Science, Basic Energy Sciences (DOE, BES), Division of Materials Sciences and Engineering under Contract DE-AC02-76SF00515. SC-XRD studies were performed at beamlines 11.3.1 and 12.2.1 at the Advanced Light Source (ALS) at the Lawrence Berkeley National Laboratory and at the Stanford Nano Shared Facilities, supported by the National Science Foundation (ECCS-1542152). B. A. C. is supported by an NSF graduate fellowship (DGE-114747). R. I. B. and L. L. acknowledge support by the Bavarian State Ministry of Science, Research, and the Arts through the grant “Solar Technologies go Hybrid”, the Elite Network Bavaria, the German Research Foundation through SFB840, and computational resources provided by the Bavarian Polymer Institute. Work at the ALS was supported by the DOE, BES (DE-AC02-05CH11231). We thank A. H. Slavney for helpful discussions and Dr S. J. Teat for crystallographic advice.Notes and references
- F. Pelle, B. Jacquier, J. P. Denis and B. Blanzat, J. Lumin., 1978, 17, 61–72 CrossRef CAS.
- P. S. Bryan and S. A. Ferranti, J. Lumin., 1984, 31–32, 117–119 CrossRef CAS.
- H. L. Wells, Am. J. Sci., 1922, 3, 315–326 CrossRef CAS.
- V. Auger and T. Karantassis, C. R. Hebd. Seances Acad. Sci., 1925, 180, 1845–1847 CAS.
- A. H. Slavney, L. Leppert, A. Saldivar Valdes, D. Bartesaghi, T. J. Savenije, J. B. Neaton and H. I. Karunadasa, Angew. Chem., Int. Ed., 2018, 57, 12765–12770 CrossRef CAS PubMed.
- M.-G. Ju, M. Chen, Y. Zhou, H. F. Garces, J. Dai, L. Ma, N. P. Padture and X. C. Zeng, ACS Energy Lett., 2018, 3, 297–304 CrossRef CAS.
- Z. Deng, F. Wei, S. Sun, G. Kieslich, A. K. Cheetham and P. D. Bristowe, J. Mater. Chem. A, 2016, 4, 12025–12029 RSC.
- G. Volonakis, A. A. Haghighirad, R. L. Milot, W. H. Sio, M. R. Filip, B. Wenger, M. B. Johnston, L. M. Herz, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2017, 8, 772–778 CrossRef CAS PubMed.
- M. Retuerto, T. Emge, J. Hadermann, P. W. Stephens, M. R. Li, Z. P. Yin, M. Croft, A. Ignatov, S. J. Zhang, Z. Yuan, C. Jin, J. W. Simonson, M. C. Aronson, A. Pan, D. N. Basov, G. Kotliar and M. Greenblatt, Chem. Mater., 2013, 25, 4071–4079 CrossRef CAS.
- A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS PubMed.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579–2585 CrossRef CAS PubMed.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS PubMed.
- W. Meng, X. Wang, Z. Xiao, J. Wang, D. B. Mitzi and Y. Yan, J. Phys. Chem. Lett., 2017, 8, 2999–3007 CrossRef CAS PubMed.
- E. G. Tulsky and J. R. Long, Chem. Mater., 2001, 13, 1149–1166 CrossRef CAS.
- X. Hong, T. Ishihara and A. V. Nurmikko, Solid State Commun., 1992, 84, 657–661 CrossRef CAS.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- D. B. Mitzi, C. A. Feild, W. T. A. Harrison and A. M. Guloy, Nature, 1994, 369, 467–469 CrossRef CAS.
- C. W. Cross and W. F. Hillebrand, Am. J. Sci., 1883, 26, 271–294 CrossRef.
- B. A. Connor, L. Leppert, M. D. Smith, J. B. Neaton and H. I. Karunadasa, J. Am. Chem. Soc., 2018, 140, 5235–5240 CrossRef CAS PubMed.
- J. Calabrese, N. L. Jones, R. L. Harlow, N. Herron, D. L. Thorn and Y. Wang, J. Am. Chem. Soc., 1991, 113, 2328–2330 CrossRef CAS.
- X. Hong, T. Ishihara and A. V. Nurmikko, Phys. Rev. B, 1992, 45, 6961–6964 CrossRef CAS PubMed.
- D. B. Mitzi, S. Wang, C. A. Feild, C. A. Chess and A. M. Guloy, Science, 1995, 267, 1473–1476 CrossRef CAS PubMed.
- S. E. Creutz, E. N. Crites, M. C. De Siena and D. R. Gamelin, Nano Lett., 2018, 18, 1118–1123 CrossRef CAS PubMed.
- Y. Bekenstein, J. C. Dahl, J. Huang, W. T. Osowiecki, J. K. Swabeck, E. M. Chan, P. Yang and A. P. Alivisatos, Nano Lett., 2018, 18, 3502–3508 CrossRef CAS PubMed.
- L. C. Schmidt, A. Pertegás, S. González-Carrero, O. Malinkiewicz, S. Agouram, G. M. Espallargas, H. J. Bolink, R. E. Galian and J. Pérez-Prieto, J. Am. Chem. Soc., 2014, 136, 850–853 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- L. M. Castro-Castro and A. M. Guloy, Angew. Chem., Int. Ed., 2003, 42, 2771–2774 CrossRef CAS PubMed.
- L.-Y. Bi, Y.-Q. Hu, M.-Q. Li, T.-L. Hu, H.-L. Zhang, X.-T. Yin, W.-X. Que, M. S. Lassoued and Y.-Z. Zheng, J. Mater. Chem. A, 2019, 7, 19662–19667 RSC.
- L. Mao, S. M. L. Teicher, C. C. Stoumpos, R. M. Kennard, R. A. DeCrescent, G. Wu, J. A. Schuller, M. L. Chabinyc, A. K. Cheetham and R. Seshadri, J. Am. Chem. Soc., 2019, 141, 19099–19109 CrossRef CAS PubMed.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC.
- F. Wei, Z. Deng, S. Sun, F. Xie, G. Kieslich, D. M. Evans, M. A. Carpenter, P. D. Bristowe and A. K. Cheetham, Mater. Horiz., 2016, 3, 328–332 RSC.
- M. K. Jana, S. M. Janke, D. J. Dirkes, S. Dovletgeldi, C. Liu, X. Qin, K. Gundogdu, W. You, V. Blum and D. B. Mitzi, J. Am. Chem. Soc., 2019, 141, 7955–7964 CrossRef CAS PubMed.
- L. Pauling, in The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell University Press, Ithaca, New York, 3 edn, 1960, ch. 7, pp. 257–264 Search PubMed.
- A. Lemmerer and D. G. Billing, CrystEngComm, 2010, 12, 1290–1301 RSC.
- M. D. Smith, L. Pedesseau, M. Kepenekian, I. C. Smith, C. Katan, J. Even and H. I. Karunadasa, Chem. Sci., 2017, 8, 1960–1968 RSC.
- V. Gómez, O. Fuhr and M. Ruben, CrystEngComm, 2016, 18, 8207–8219 RSC.
- S. Sourisseau, N. Louvain, W. Bi, N. Mercier, D. Rondeau, F. Boucher, J.-Y. Buzaré and C. Legein, Chem. Mater., 2007, 19, 600–607 CrossRef CAS.
- L. E. Orgel, J. Chem. Soc., 1958, 4186–4190, 10.1039/JR9580004186.
- T. Ishihara, J. Takahashi and T. Goto, Solid State Commun., 1989, 69, 933–936 CrossRef CAS.
- S. Zhang, P. Audebert, Y. Wei, A. Al Choueiry, G. Lanty, A. Bréhier, L. Galmiche, G. Clavier, C. Boissière, J.-S. Lauret and E. Deleporte, Materials, 2010, 3, 3385–3406 CrossRef CAS.
- C.-q. Xu, S. Fukuta, H. Sakakura, T. Kondo, R. Ito, Y. Takahashi and K. Kumata, Solid State Commun., 1991, 77, 923–926 CrossRef CAS.
- K. Tanaka, T. Takahashi, T. Kondo, K. Umeda, K. Ema, T. Umebayashi, K. Asai, K. Uchida and N. Miura, Jpn. J. Appl. Phys., 2005, 44, 5923–5932 CrossRef CAS.
- A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS PubMed.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- A. H. Slavney, B. A. Connor, L. Leppert and H. I. Karunadasa, Chem. Sci., 2019, 10, 11041–11053 RSC.
- T. T. Tran, J. R. Panella, J. R. Chamorro, J. R. Morey and T. M. McQueen, Mater. Horiz., 2017, 4, 688–693 RSC.
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235 CrossRef CAS PubMed.
- M. D. Smith, B. A. Connor and H. I. Karunadasa, Chem. Rev., 2019, 119, 3104–3139 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. The CIFs for 1-In, 1-Tl, 1'-Tl, and 2-TlPEA have been deposited in the CCDC 1943974–1943977, respectively. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01580f |
| This journal is © The Royal Society of Chemistry 2020 |