Open Access Article
Open Access ArticleUnderstanding and controlling the efficiency of Au24M(SR)18 nanoclusters as singlet-oxygen photosensitizers†
Mikhail
Agrachev‡
 a,
Wenwen
Fei‡
a,
Wenwen
Fei‡
 a,
Sabrina
Antonello
a,
Sabrina
Antonello
 a,
Sara
Bonacchi
a,
Sara
Bonacchi
 a,
Tiziano
Dainese
a,
Tiziano
Dainese
 a,
Alfonso
Zoleo
a,
Alfonso
Zoleo
 a,
Marco
Ruzzi
a,
Marco
Ruzzi
 *a and
Flavio
Maran
*a and
Flavio
Maran
 *ab
*ab
aDepartment of Chemistry, University of Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: marco.ruzzi@unipd.it; flavio.maran@unipd.it
bDepartment of Chemistry, University of Connecticut, 55 North Eagleville Road, Storrs, 06269 Connecticut, USA
First published on 19th February 2020
Abstract
Singlet oxygen, 1O2, can be generated by molecules that upon photoexcitation enable the 3O2 → 1O2 transition. We used a series of atomically precise Au24M(SR)18 clusters, with different R groups and doping metal atoms M. Upon nanosecond photoexcitation of the cluster, 1O2 was efficiently generated. Detection was carried out by time-resolved electron paramagnetic resonance (TREPR) spectroscopy. The resulting TREPR transient yielded the 1O2 lifetime as a function of the nature of the cluster. We found that: these clusters indeed generate 1O2 by forming a triplet state; a more positive oxidation potential of the molecular cluster corresponds to a longer 1O2 lifetime; proper design of the cluster yields results analogous to those of a well-known reference photosensitizer, although more effectively. Comprehensive kinetic analysis provided important insights into the mechanism and driving-force dependence of the quenching of 1O2 by gold nanoclusters. Understanding on a molecular basis why these molecules may perform so well in 1O2 photosensitization is instrumental to controlling their performance.
Introduction
Singlet oxygen, 1O2, is the first excited state (1Δg) of molecular oxygen. Depending on the experimental conditions, its lifetime can span several orders of magnitude.1–31O2 eventually converts to ground-state triplet oxygen (3Σg−), 3O2. Because singlet oxygen is significantly more reactive than triplet oxygen, it finds uses in several applications, especially organic synthesis, photocatalysis, and nanomedicine (photodynamic therapy).4–9 Singlet oxygen10–12 can be produced by direct excitation, although 3O2 → 1O2 is a spin-forbidden transition with a very low absorption coefficient. A more efficient way to generate singlet oxygen is by using photosensitizers.10,13 The sensitizer is photoexcited to its singlet state, undergoes intersystem crossing (ISC) to form the excited triplet state, and then transfers energy to triplet oxygen to yield 1O2; the last step is efficient because the overall angular moment is now conserved. Suitable photosensitizers are molecules that exhibit a sufficiently high value of the excited triplet-state energy (the 3Σg− to 1Δg excitation energy, Eexc, is 94 kJ mol−1), a high quantum yield for ISC, and a sufficiently long triplet lifetime. On the other hand, it has been long acknowledged that the sensitizer and/or products of its photoreactions can also quench singlet oxygen by converting it back to 3O2.14,15 These quenching reactions may significantly diminish the 1O2 lifetime and, consequently, affect the overall efficiency of the photosensitization process. An ideal photosensitizer should, therefore, maximize generation efficiency and minimize deactivation. This is not, however, an easy task to achieve.10The detection of singlet oxygen in fluid solution is routinely carried out by optical spectroscopy. The most specific probe of singlet oxygen is 1275 nm 1O2 → 3O2 phosphorescence, particularly when it is monitored in a time-resolved experiment. To overcome the low-sensitivity limitations, several approaches have been proposed, mostly relying on the introduction of a fluorescent probe activated by energy transfer from 1O2. For example, phthalocyanines, naphthalocyanines, and porphyrazines exhibit strong delayed luminescence upon energy transfer from two 1O2 molecules.16 This luminescence is emitted in the visible-light region and its quantum yield exceeds that of 1O2 phosphorescence by 2–4 orders of magnitude. These molecules, however, are also good sensitizers for the formation of 1O2, thereby complicating detection. Chemical traps have also been extensively employed.17 Singlet oxygen rapidly and irreversibly reacts with aromatic compounds to yield endoperoxides that do not fluoresce and whose absorption spectrum differs significantly from that of the original molecule. However, chemical traps may also be reactive toward other reactive oxygen species. Because of the difficulties associated with direct detection and indirect methods, alternative approaches for the detection of 1O2 generated by photosensitizers are thus sought.
Possible photosensitizer candidates that meet several of the aforementioned requirements are atomically precise gold nanoclusters, Aun(SR)m (where SR = thiolate). Nowadays, many of these clusters can be prepared in a very pure, controlled state.18 This implies full molecular control on the structure and properties, which cannot be achieved with the larger gold nanoparticles. Because the electronic structure and thus the optical properties of these clusters depend on the values of n and m, ultrasmall gold nanoclusters might be, in principle, optimized for the efficient production of 1O2. So far, the research in this field has been quite limited,19–33 with very few examples describing the behavior of truly atomically precise gold nanoclusters. This is the case of Au25(SR)18, which is a stable cluster that shows distinct electrochemical,34 optical,18 and magnetic features,35,36 and is consistently considered the benchmark system for understanding and controlling many properties of gold nanoclusters.37,38 Kawasaki et al. were the first to describe the formation of singlet oxygen using Au25(SR)18 (HSR = phenylethanethiol or captopril) as the photosensitizer.19 The photosensitization was detected optically and with chemical quenchers. Au38(SC2H4Ph)240, another well-established molecular cluster, was found to be significantly less efficient. More recently, Ho-Wu et al. compared the photosensitization efficiency of Au25, Ag32, Au144, larger gold nanoparticles, and a conventional dye photosensitizer.29 This study, which was carried out with indirect optical methods (1,3-diphenylisobenzofuran quencher), concluded that Au144 provides the most efficient system. A size dependence order of Au144 > Au38 > Au25 was observed for the aerobic oxidation of D-glucose on carbon-supported clusters.31 The efficiency of 1O2 generation using Au38S2(SAdm)20 (SAdm = adamantanethiolate) nanoclusters was found to be higher than that of Au25(SC2H4Ph)18−.32 The ultrasonic activation of Au25(Captopril)18 to generate 1O2 was also demonstrated.33
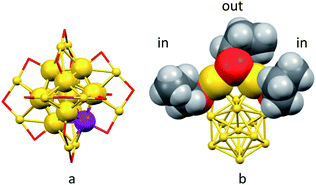
Here we describe the photosensitizing behavior of a series of Au25(SR)18−, where R = n-C3H7 (C3), n-C4H9 (C4), and C2H4Ph (C2Ph) (hereafter, we will indicate the number of carbon atoms of the alkyl chain simply as Cn), and monodoped Au24M(SR)180 (M = Cd, Hg) clusters (Fig. 1). Besides studying the effect of the protecting ligand, the analysis was extended to monodoped clusters because their optical and especially electrochemical behaviors show significant differences from those of the undoped clusters.39 Regarding detection, we relied on continuous-wave and, especially, time-resolved electron paramagnetic resonance techniques (CWEPR and TREPR, respectively). TREPR spectroscopy provides an efficient and sensitive method to detect even very low concentrations of 1O2 generated by photosensitization in solution.40,41 Moreover, TREPR is selective toward singlet oxygen, which is unequivocally detected and identified, while other reactive oxygen species are not revealed. As we will show, TREPR allowed us to characterize in detail the photosensitization behavior of the investigated clusters, and could confirm that the cluster's excited state responsible for the generation of singlet oxygen is indeed a triplet. Most notably, we found that proper design of the redox properties of the cluster yields results comparable to those of tetraphenylporphirin (TPP), which is a well-known reference photosensitizer.10 Finally, we carried out a comprehensive kinetic investigation on the 1O2 quenching mechanism by gold nanoclusters as a function of driving force and obtained important mechanistic insights into the reasons why properly devised gold nanoclusters may perform very well in 1O2 photosensitization.
Results and discussion
1O2 photosensitization with TREPR detection
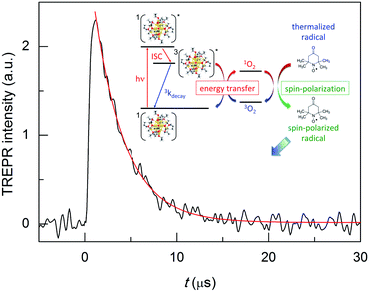
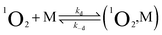
TREPR spectroscopy is especially suitable to study the kinetics of photogenerated paramagnetic species exhibiting lifetimes ranging from a few to several hundred μs.42 TREPR detection of 1O2 is based on the radical triplet pair (RTP) mechanism.43 Triplet quenching by a stable free radical, such as a nitroxide (which is a doublet, 2R, and generally exhibits three, very similar CWEPR lines due to the hyperfine interaction of the unpaired electron with the N nucleus), induces populations of radical spin sublevels that differ significantly from those at thermal equilibrium. This phenomenon, which is commonly referred to as chemically induced dynamic electron polarization,44 can be sensitively detected by TREPR in the form of transient intensities of the EPR signals associated with the radical probe. Importantly, polarization may also be caused by a singlet state, as in the case of 1O2.45,46Briefly, photoexcitation of the sensitizer fundamental singlet state (1PS) yields a singlet excited state (1PS*) that is quickly converted into a triplet state (3PS*) via ISC. In the absence of oxygen, the excited triplet state undergoes quenching by interaction with a nitroxide radical, and polarized emissive TREPR signals are observed. The emissive polarization is interpreted according to quartet-precursor RTP (Q-RTP) theory,47 as described by eqn (1):
| 3PS* + 2R → 1PS + 2R*↓ | (1) |
| 3PS* + 3O2 → 1PS + 1O2 | (2) |
| 1O2 + 2R → 3O2 + 2R*↑ | (3) |
All clusters were prepared and characterized by mass spectrometry, NMR spectroscopy, and UV-vis spectroscopy as described previously.39,48–50 Special attention was paid to controlling properly the charge state.51,52 TREPR experiments were carried out in toluene at 240 K, and refer to 1 mM clusters and 0.5 mM 2,2,6,6-tetramethyl-4-oxo-1-piperidinyloxy (TEMPONE), unless otherwise stated. In TREPR, a laser pulse (we used 4 ns at 532 nm) triggers the aforementioned photochemical reaction/s and eventually generates the polarized paramagnetic species (2R*↑ or 2R*↓). The ensuing EPR transient is recorded at a given value of the magnetic field (B). This procedure is applied by scanning B until the entire field range is covered. The sequence is then repeated many times, and the corresponding series of transients are averaged. The resulting TREPR spectrum is usually displayed in a 3D form (Fig. 2), where the TREPR intensity is plotted as a function of B and time (t). No field modulation is applied and thus the observed signals do not exhibit the derivative shape typical of the corresponding CWEPR spectra (Fig. 3c and d).
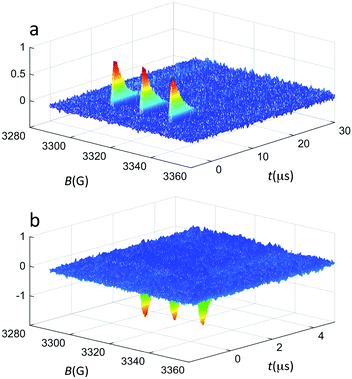 | ||
| Fig. 2 TREPR surfaces recorded for 0.5 mM TEMPONE and 1 mM Au25(SC3)18− in (a) air-saturated and (b) deaerated toluene solution at 240 K. The z-axis shows the TREPR intensity (a.u.). | ||
Fig. 2a shows the spectrum obtained using Au25(SC3)18− as the photosensitizer under aerobic conditions. The TREPR spectrum of TEMPONE consists of three signals of equal intensity that decay in a few μs. The polarized TREPR signals show the net absorptive character expected when the overall photosensitization process (excitation, ISC, and energy transfer) is efficient and followed by step (3). In the control experiment carried out in the absence of oxygen, only emissive polarization is observed (Fig. 2b). According to the Q-RTP mechanism, the emissive polarized transient spectra are consistent with the direct interaction of the nitroxide with the triplet state of Au25(SR)18−. The extent of emissive polarization strongly depends on the quantum yield of the latter and the actual lifetime of the cluster triplet state. In this connection, the different time scales of the transients in the two plots of Fig. 2 are worth noticing. These results already allow us to draw a very important conclusion. So far, photoexcitation of clusters has been generically described as generating excited states, as no conclusive evidence about the formation of an excited triplet state could be gathered. In the first report on singlet oxygen generation by photoexcited Au clusters, the term triplet state was used for the very same reason that the photoexcited cluster was generating 1O2.19 On the other hand, singlet oxygen may form in several different ways.53 In the present context, the TREPR results observed under anaerobic conditions definitely prove that, indeed, photoexcitation of Au25(SR)18− eventually leads to an excited triplet state.46
Analysis of the 1O2 lifetime and validation of the TREPR method
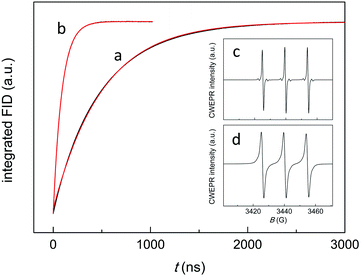
The decay kinetics depends on several parameters. In a deaerated solution, the decay of the emission-polarized signals (Fig. 2b) is determined by the lifetime of the cluster triplet state and the characteristic magnetic-relaxation times of the nitroxide, T1 and T2.54T1, which is the spin-lattice longitudinal relaxation time, can be determined independently, by pulsed EPR inversion recovery experiments (Fig. 3, trace (a)), to be 499.1(0.6) ns. In the absence of the cluster, we obtained a virtually identical value of 501.8(0.7) ns (r2 = 1.000). T2 is the transverse spin–spin relaxation time and could be estimated to be 0.43(0.01) μs from the reciprocal of the full-width-at-half-height of the integral of the CWEPR spectrum shown in Fig. 3c, as illustrated in Fig. S1.† In deaerated solution, the reciprocal of the TREPR decay rate-constant value obtained from the emission data (Fig. S2†) is 0.45(0.01) μs (r2 = 0.983), and therefore, is comparable to the relaxation parameters of TEMPONE. These results point to the TEMPONE spin relaxation as a particularly relevant factor determining the TREPR decay kinetics and thus imply that the lifetime of the cluster triplet state should be shorter than ∼0.3 μs.In the presence of air, the CWEPR spectrum of TEMPONE shows broader peaks (Fig. 3d). The T1 measured by pulsed EPR inversion recovery experiments in the presence of Au25(SC3)18− (Fig. 3b) is now only 64(0.2) ns (r2 = 1.000), that is, about one order of magnitude shorter than the T1 determined under anaerobic conditions. Similarly, T2 decreases from 0.43 to 0.04 μs. These effects are caused by the known interaction of TEMPONE with triplet oxygen.55 Under aerobic conditions, the decay of the TREPR signals also depends on the singlet-oxygen lifetime. A scheme of the general process is provided in the inset of Fig. 4. The average of the TREPR transients (Fig. 4) can be fit to a single exponential (r2 = 0.969) yielding an observed decay rate constant (kΔ) of 3.02 × 105 s−1, which corresponds to a lifetime (τΔ) of 3.31(0.05) μs. τΔ is thus nearly two orders of magnitude longer than the corresponding T1 value, and this indicates that now the observed decay of spin polarization is only controlled by the 1O2 lifetime. In other words, while the polarized signals decay on the T1 time scale, there is still some singlet oxygen in solution that continuously contributes to generating further polarization in the TEMPONE molecules. Under these conditions, the decay of the TREPR signal lifetime can thus be used to calculate the singlet-oxygen lifetime.
Under any given experimental conditions, the observed 1O2 lifetime is determined by the species present in solution.10 In the absence of solutes other than oxygen, on the other hand, the intrinsic 1O2 decay pseudo-first order rate constant (kSΔ) only depends on the solvent (S) through two terms (eqn (4)):
| kSΔ = knr[S] + kr[S] | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 and 34.6 μs.56 These lifetimes are significantly longer than the lifetime of 3.31 μs obtained with the TEMPONE/Au25(SC3)18− system, and therefore, show that in our experimental conditions significant quenching of singlet oxygen must take place. Comparison of τΔ with τSΔ (hereafter, we will refer to the most recent determination, 34.6 μs)56 yields a relative τΔ decrease of 100(τSΔ − τΔ)/τSΔ = 90.4%.
57 and 34.6 μs.56 These lifetimes are significantly longer than the lifetime of 3.31 μs obtained with the TEMPONE/Au25(SC3)18− system, and therefore, show that in our experimental conditions significant quenching of singlet oxygen must take place. Comparison of τΔ with τSΔ (hereafter, we will refer to the most recent determination, 34.6 μs)56 yields a relative τΔ decrease of 100(τSΔ − τΔ)/τSΔ = 90.4%.
Besides the solvent, there are two possible candidates as quenchers: TEMPONE and the cluster itself. To address this issue, we carried out further experiments. The majority of photosensitizers currently employed in photodynamic therapy are cyclic tetrapyrrolic structures, such as porphyrin derivatives.58 It is thus instructive to compare the polarized signals observed for Au25(SC3)18− with those obtained for tetraphenylporphyrin (TPP), which is a well-known reference photosensitizer, yet showing some quenching of 1O2.59 TPP was used at the same concentration of the cluster (1 mM) and qualitatively gave the same TREPR spectrum, but for the two differences that the signal intensity at its maximum is ∼3 times larger than for Au25(SC3)18− and, particularly important, the decay is much slower (Fig. 5). It should be noted that for t < 0.5 μs the presence of a negative spike indicates that a (small) fraction of the TPP molecules in their triplet excited state (for TPP, the fraction of singlet excited state species that undergo radiationless decay to form the triplet excited state is ΦT = 0.71;60 in the presence of oxygen, this value is expected to increase slightly)61 react with TEMPONE according to Q-RTP theory (eqn (1)). The fact that the TREPR intensity maximum is attained at 1.5–2 μs indicates that the majority of the TPP triplet reacts with 3O2 within less than 1 μs. This is in keeping with a lifetime of 196 ns measured for the TPP triplet state in aerated toluene at room temperature.62
The best fit of the decay data obtained for t > 3 μs gives kΔ = 3.54 × 104 s−1 (r2 = 0.999), corresponding to a lifetime τΔ of 28.2(0.1) μs. This shows that TPP is, as expected, a very good photosensitizer. Comparison of this τΔ value with τSΔ, however, evidences a relative τ decrease of 18.5%. To obtain information on a possible effect of TEMPONE as a quencher, we carried out further TPP photosensitization experiments in which the TEMPONE concentration was varied, as exemplified by the two traces in Fig. 5. We obtained: [TEMPONE] = 0.2 mM, kΔ = 3.36 × 104 s−1, and τΔ = 29.8(0.4) μs; ([TEMPONE] = 0.1 mM, kΔ = 3.66 × 104 s−1, and τΔ = 27.4(0.6) μs). The very similar τΔ values, therefore, show that under our experimental conditions the TEMPONE concentration does not affect the observed 1O2 lifetime. Besides confirming that indeed TPP acts as a quencher, these results also indicate that despite the intense TREPR signals, TEMPONE polarization must involve a very small amount of 1O2 present in solution. These tests validated the TREPR methodology and indicated that 0.5 mM TEMPONE could be consistently used with no detectable effect on the 1O2 lifetime. The experiments described below were carried out under these conditions.
Tuning the photosensitizing properties of Au25 nanoclusters
The TREPR data confirm that Au25(SR)18− can be used as a photosensitizer.19 They also show that the 1O2 lifetime measured in the presence of Au25(SC3)18− is much shorter than τSΔ. The cluster is, therefore, not only a good sensitizer but also a good quencher, as observed for many sensitizers.10 We will now specifically focus on this aspect. The decay of singlet oxygen can proceed by physical quenching, leading to deactivation of 1O2, and chemical reactions, in which 1O2 irreversibly reacts with some other species in solution.10 In the presence of a generic molecule (M) capable of quenching or chemically reacting with 1O2, eqn (4) must include further terms (eqn (5)):10,56| kΔ = knr[S] + kr[S] + kq[M] + kcr[M] | (5) |
The easiest way to tune the properties of Au25 is to change the capping ligands. While this change does not affect the structure and the absorption spectrum,18,69 other properties, especially the electrochemical potentials,34,70 may change appreciably. Finally, the ligands provide a nanoenvironment surrounding the cluster core that determines the effective dielectric constant70 and porosity of the capping monolayer,69 and these factors may exert an influence on the quenching mechanisms of the excited states and ultimately the effective singlet-oxygen lifetime. To gain insights into this aspect, we compared the outcome of TREPR measurements carried out on Au25 clusters capped by SC3, SC4, and SC2Ph thiolates. The ligand choice was primarily dictated by their ability to change the E° of the Au25(SR)180/Au25(SR)18− redox couples quite significantly.70,71
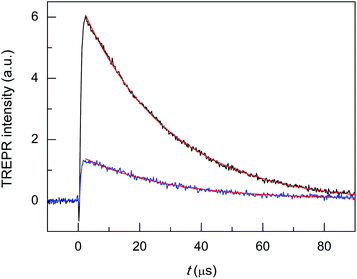
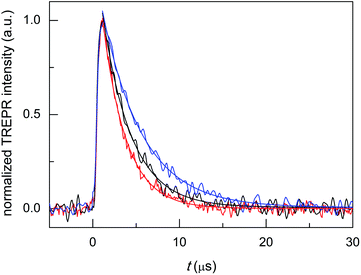
Au25(SC4)18− and Au25(SC2Ph)18− display TREPR surfaces similar to that of Au25(SC3)18−. Fig. 6 compares the reinforced absorptive-polarized transient signals observed upon 1O2 photosensitization by Au25(SC4)18−, Au25(SC3)18−, and Au25(SC2Ph)18− (red, black, and blue traces, respectively). The growth of the polarized signals occurs within 1 μs (that is, a bit faster than for TPP) and the maximum signal intensities are very similar, pointing to similar photosensitization efficiency (in Fig. 6 the intensities are normalized for the sake of better comparison of the transients).
Monoexponential fit to the decay data reveals small, yet clearly detectable differences in the value of kΔ, which increases in the order Au25(SC2Ph)18− (2.17 × 105 s−1, r2 = 0.990) < Au25(SC3)18− (3.02 × 105 s−1, r2 = 0.974) < Au25(SC4)18− (3.69 × 105 s−1, r2 = 0.986); the corresponding lifetimes τΔ are 4.61(0.05), 3.31(0.05), and 2.71(0.04) μs, respectively. This order indeed matches that of the decreasing E° of the anionic clusters (DCM/0.1 M TBAH, 298 K, E vs. SCE), which are −0.077, −0.171, and −0.188 V, respectively.70,71 These data point to the ease of oxidation (lower E° value) as an important factor enhancing the cluster quenching ability and are thus in keeping with the effect noted for other sensitizer families.10
Overall, these results evidence a detectable effect of the cluster oxidation potential on the singlet-oxygen decay kinetics and thus confirm an active role of the cluster also as a quencher. With alkanethiolate ligands, however, the potentials cannot be changed substantially.34,70 A more substantial way to modify the physicochemical properties of gold nanoclusters is by doping their core with other metals. We thus focused on modifying Au25(SC4)18− to prepare the corresponding Au24M(SC4)180 clusters, with M = Hg, Cd. For these metals, monodoping is conveniently accomplished by carrying out the metal exchange on a preformed Au25(SR)18− cluster by using a salt or thiolate of the exogenous metal.39,72–74 We focused on these two metals because they both dope the cluster on one of the icosahedron positions, as we could demonstrate very recently.39 While in their neutral state, the resulting Au24M(SC4)180 clusters are diamagnetic and thus match the same magnetic state of anion Au25(SC4)18−.
Monodoping affects the HOMO–LUMO gap. The values that can be estimated from the electrochemical peaks are:39,70 Au, 1.30 eV; Hg, 1.28 eV; Cd, 1.41 eV. Similar differences are found for the optical bandgaps.39,75 These differences are indeed noteworthy because, for example, a progressive change in the number of carbon atoms from 2 to 12 in Au25(SCn)18 does not affect the HOMO–LUMO gap, which remains constant at 1.30 eV.70 Besides these differences, Hg and Cd doping affects the electrochemical potentials very significantly. In particular, the first oxidation of the Au24M(SC4)18 clusters occurs (E° values) at −0.188 (Au), +0.364 (Hg), and +0.332 V (Cd).39 In electrochemical terms, a positive shift of the first oxidation step by more than 0.5 V is indeed massive.
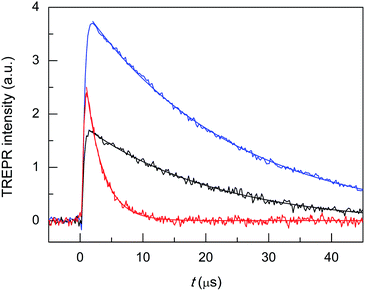
Hg doping induces remarkable changes in the TREPR transients (Fig. 7, black trace). First, in Au24Hg(SC4)180 the photosensitization efficiency is about two thirds that of Au25(SC4)18− (red trace). This decrease may be caused by a shorter triplet lifetime, a less efficient cluster-to-oxygen energy transfer to form singlet oxygen, or a lower quantum yield for the formation of the triplet. In this context, an important piece of information is provided in a recent study by Zhou et al. about the excited-state lifetime of similar (R = C2Ph) clusters, as the values determined for Au24Hg(SC2Ph)180 and Au25(SC2Ph)18− are 50 and 100 ns, respectively.75 The observed TREPR intensities are indeed in rather good agreement with this ratio, and therefore, we may arguably conclude that the efficiency of singlet-oxygen generation is mainly determined by the cluster triplet lifetime. Regarding the hypothesis of a less efficient cluster-to-oxygen energy transfer, we note that the HOMO–LUMO gap of Au24Hg(SC4)180 (1.28 eV) is slightly smaller than for Au25(SC2Ph)18− (1.30 eV): the same should be true also for the corresponding triplet states and this may affect the cluster-oxygen energy transfer, although to a very small extent. Finally, ISC in the cluster should occur on a low ns timescale and very efficiently (ΦT = 0.87), as evaluated by Wen et al. for films of BSA-protected Au25 clusters.76
The most important effect brought about by the introduction of a single Hg atom, however, is to increase the singlet-oxygen lifetime by more than one order of magnitude: 19.5(0.2) (kΔ = 5.13 × 104 s−1, r2 = 0.990) vs. 2.71 μs (kΔ = 3.69 × 105 s−1), which indicates that the mechanism of 1O2 quenching is much less efficient than for the corresponding Au25 cluster. Still, compared with the reference τSΔ of 34.6 μs, the relative τΔ decrease is quite significant: 43.6%.
To make the cluster even more performing, the foreign-metal atom should minimize quenching effects without losing the photosensitization efficiency or possibly even increasing it with respect to Au25. The doped cluster should, therefore, exhibit electrochemical properties similar to those of Au24Hg(SC4)180, a more significant population of the photogenerated triplet state, and ultimately, allow for a longer 1O2 lifetime. A cluster that satisfies these requirements is Au24Cd(SC4)180, as it is almost as resistant toward oxidation as Au24Hg(SC4)180 (0.332 V vs. 0.364 V), its HOMO–LUMO gap is the largest of the three SC4 clusters, and according to Zhou et al.75 its excited-state lifetime (in supposedly aerated solution) is 200 ns (R = C2Ph), i.e., two and four times longer than those of Au25(SC2Ph)18− and Au24Hg(SC2Ph)180, respectively. In this regard, it is worth mentioning that TREPR (emission decay lifetime of 0.44(0.01) μs, r2 = 0.988) points to a higher limit of ∼0.3 μs for the lifetime of the triplet of Au24Cd(SC4)180 under anaerobic conditions (Fig. S4†), as already noted and discussed for Au25(SC3)18−. These general expectations of better performance are fully met: use of the Cd-doped cluster yields a longer singlet-oxygen lifetime (kΔ = 4.31 × 104 s−1, r2 = 0.999, and τΔ = 23.2(0.09) μs) than Au24Hg(SC4)180, a smaller relative τΔ decrease (32.9%) and a more significant photosensitization efficiency (Fig. 7, blue trace). In particular, the maximum intensity of the TREPR signals is ∼1.5 times larger than that observed for Au25(SC4)18− and more than two times larger than that of Au24Hg(SC4)180. The photosensitization efficiency of Au24Cd(SC4)180 is significant also in comparison with that of the TPP photosensitizer, as the TREPR signal intensity of the former is ∼1/2 that of TPP. The fact that the amount of triplet excited state obtained from Au24Cd(SC4)180 is quite significant is also supported by the presence of the negative spike for t < 0.5 μs, which, as already commented upon for TPP, is attributed to the Q-RTP component (eqn (1)).
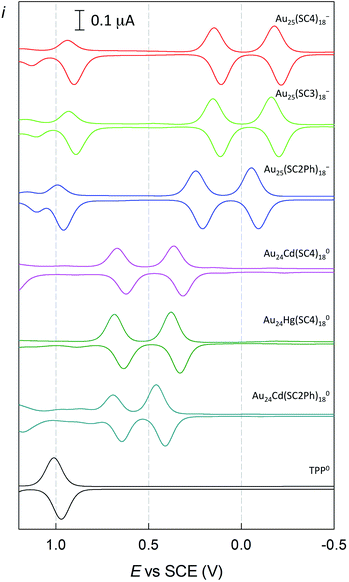
Finally, we tested the Cd-doped cluster that has an even more positive oxidation potential, Au24Cd(SC2Ph)180, whose E° is 0.430 V (vs. 0.332 V for Au24Cd(SC4)180).39 The DPV curves (oxidation region) of all clusters investigated and TPP are gathered in Fig. 8. Also for this cluster we estimate (Fig. S5:† TREPR emission decay lifetime of 0.44(0.01) μs, r2 = 0.989) a higher limit of ∼0.3 μs for its triplet lifetime under anaerobic conditions. Indeed, the photosensitization outcome further improves (Fig. 9, blue trace), as the observed singlet-oxygen lifetime is even longer (kΔ = 3.58 × 104 s−1, r2 = 0.997, and τΔ = 27.9(0.25) μs). In particular, this τΔ value and the relative τΔ decrease, 19.3%, are virtually identical to those of TPP (Fig. 9, black trace), 28.2(0.1) μs and 18.5%, though the latter is more difficult to oxidize by as much as 0.563 V (Fig. 8). Besides the redox potentials, a comparison between the aforementioned estimated lifetime values (aerobic vs. anaerobic conditions) obtained for the Cd-doped clusters and TPP (whose triplet-state lifetime in the absence of oxygen increases by orders of magnitude)13,62 shows that despite the much shorter intrinsic lifetime of their triplet state, the Cd-doped clusters are perfectly fine to accomplish the 1O2 photosensitization job very efficiently.
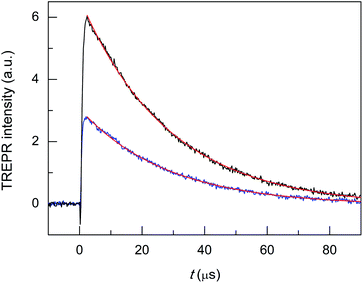 | ||
| Fig. 9 TREPR transients and corresponding exponential fit to the data for air-saturated toluene solutions of 0.5 mM TEMPONE and 1 mM Au24Cd(SC2Ph)180 (blue) and TPP (black). Temperature = 240 K. | ||
Chemical quenching
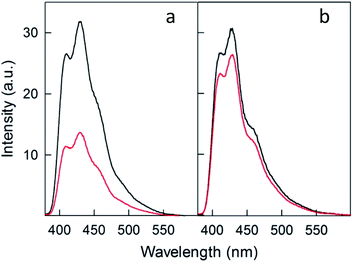
To compare further the performance of doped and undoped clusters, we performed photosensitization experiments in the presence of 9,10-diphenylanthracene (DPA), which reacts with singlet oxygen to yield the endoperoxide 9,10-diphenyl-9,10-epidioxyanthracene (DPA-O2) with rate constants on the order of 106 M−1 s−1.77 Its formation can be conveniently monitored through the decrease in the excitation and fluorescence spectra of DPA. Fig. 10 compares the fluorescence spectra of DPA in air-saturated toluene (at room temperature) containing the photosensitizer Au24Cd(SC4)180 (panel a) or Au25(SC4)18− (panel b) before and after 10 min pulsed irradiation (carried out as in the TREPR experiments) with a 532 nm laser at 240 K (for details, see the Experimental section).For Au24Cd(SC4)180, the strong emission band of DPA at ∼430 nm (excitation at 360 nm) is markedly quenched (by 56.9%), which confirms its particular efficiency as a photosensitizer. Instead, when Au25(SC4)18− is used as photosensitizer, only 13.6% quenching of the DPA emission is observed at ∼430 nm. The different behavior of the two clusters is also quantitatively detected in the excitation spectra obtained at 450 nm: Au24Cd(SC4)180 causes a strong decrease of the absorption band of DPA (56.9%), whereas the variation is much less significant for Au25(SC4)18− (11.0%) (Fig. S6 and S7†). The absorption spectra of the solutions of the two clusters, which only show the optical features of the nanoclusters because their concentration is 100 times larger than that of DPA (the molar extinction coefficients of DPA,78 Au24Cd(SC4)180, and Au25(SC4)18− are 1.4 × 104 M−1 cm−1 (372.5 nm), 4.68 × 104 M−1 cm −1 (398 nm) and 4.58 × 104 M−1 cm −1 (401 nm), respectively), exhibit no differences before and after laser irradiation (Fig. S8 and S9†), thereby pointing to their photostability (no change of the spectrum associated with cluster oxidation) under the given experimental conditions. These results thus show that Au24Cd(SC4)180 is a significantly better photosensitizer than Au25(SC4)18−, in full agreement with the TREPR results.
Mechanism of physical quenching by Au25 nanoclusters
The sequence of the observed τΔ values is in very good agreement with the cluster oxidation potentials (Fig. 11).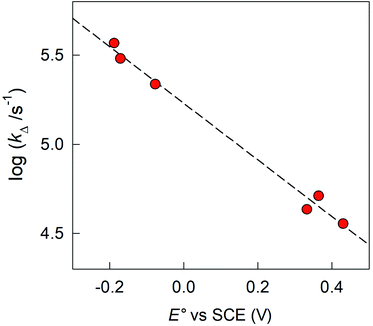 | ||
| Fig. 11 Dependence of the 1O2 decay rate constant kΔ on the formal potentials for the oxidation of the clusters. The dashed line shows the linear fit to the data. | ||
Due to the aforementioned considerations regarding kr and kcr, eqn (5) can be simplified to eqn (6):
| kΔ = knr[S] + kq[M] | (6) |
 | (7) |
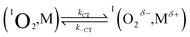 | (8) |
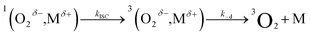 | (9) |
 | (10) |
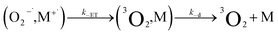 | (11) |
 | (12) |
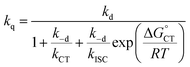 | (13) |
We start by considering Au25(SC4)18−, which exhibits a less positive oxidation potential and the fastest quenching rate, and then we will discuss the differences caused by making the cluster oxidation more difficult. For this cluster, kΔ = 3.69 × 105 s−1. The term kq[M] can be obtained from eqn (6) by subtracting the rate constant for the intrinsic 1O2 lifetime (τSΔ = 34.6 μs and kSΔ = knr[S] = 2.89 × 104 s−1). Hence, a value of kq = 3.40 × 108 M−1 s−1 is calculated using [M] = 1 mM.
The diffusion rate constants kd and k−d are estimated to be 1.9 × 1010 M−1 s−1 and 2 × 1010 s−1, respectively (see the ESI†). The equilibrium constant KCT, and thus 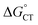 , is unknown. However,
, is unknown. However, 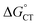 , which refers to the transfer of the charge fraction δ, is conceivably related to
, which refers to the transfer of the charge fraction δ, is conceivably related to 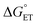 ,10 which is the free energy for full ET between the cluster and singlet oxygen (eqn (10)). kCT may be similarly estimated (eqn (14)) using a Marcus expression for the activation free energy ΔG≠CT (eqn (15)).
,10 which is the free energy for full ET between the cluster and singlet oxygen (eqn (10)). kCT may be similarly estimated (eqn (14)) using a Marcus expression for the activation free energy ΔG≠CT (eqn (15)).
kCT = Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−ΔG≠CT/RT] exp[−ΔG≠CT/RT] | (14) |
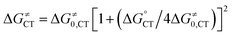 | (15) |
The process is considered adiabatic and thus occurring at the contact distance between singlet oxygen and the cluster, as supported by recent results.80–82 The frequency factor Z is estimated (see the ESI†) by taking into account the role of solvent friction in determining the rate of crossing the barrier.83 ΔG≠0,CT is the intrinsic barrier, that is, the value of ΔG≠CT at zero driving force. In analogy to the ET intrinsic barrier (ΔG≠0,ET), ΔG≠0,CT can be seen as composed of a solvent reorganization term, ΔG≠0,s,CT, and an inner component, ΔG≠0,i,CT, which describes the molecular deformation of bond lengths and angles of the reacting system. For a full ET,84,85 ΔG≠0,ET can be calculated from the homogeneous self-exchange (ΔG≠0,ET)hom,ex values of the two redox couples (here, M+˙/M and 1O2/O2−˙) (eqn (16)):
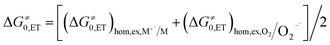 | (16) |
The values of the two (ΔG≠0,ET)hom,ex terms can be obtained from the corresponding heterogeneous intrinsic barriers through eqn (17):86
| (ΔG≠0)hom,ex = 2(ΔG≠0)het − (ΔG≠0,s)hom,ex | (17) |
Both kCT and KCT require calculating 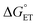 and how to relate it to
and how to relate it to 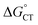 . Additionally, kCT requires converting ΔG≠0,ET into ΔG≠0,CT. For 1O2 quenching,
. Additionally, kCT requires converting ΔG≠0,ET into ΔG≠0,CT. For 1O2 quenching, 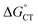 is usually taken as a fraction f of
is usually taken as a fraction f of 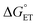 to account for the partial character δ of ET in the formation of the exciplex.10
to account for the partial character δ of ET in the formation of the exciplex.10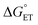 can be estimated, according to Rehm and Weller,89,90 with eqn (18). Because the process here considered involves a neutral and a charged species, 1O2/Au25(SC4)18−, the coulombic term associated with the formation of charges is zero. To avoid confusion, the actual charge of the Au25 cluster is made explicit.
can be estimated, according to Rehm and Weller,89,90 with eqn (18). Because the process here considered involves a neutral and a charged species, 1O2/Au25(SC4)18−, the coulombic term associated with the formation of charges is zero. To avoid confusion, the actual charge of the Au25 cluster is made explicit.
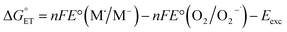 | (18) |
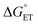 , and therefore, E°(1O2/O2−˙) will be taken as E°(O2/O2−˙) − Eexc/F = −0.850 + 0.974 = 0.124 V (for details, see the ESI†).
, and therefore, E°(1O2/O2−˙) will be taken as E°(O2/O2−˙) − Eexc/F = −0.850 + 0.974 = 0.124 V (for details, see the ESI†).
As to the fraction f of 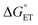 , it has been proposed that δ ∼ f1/2, as inferred from experimental trends involving neutral donors.10 Because of the charge here involved, however, we will use a linear dependence (eqn (19)) in which δ simply replaces n = 1 in eqn (18). Hence:
, it has been proposed that δ ∼ f1/2, as inferred from experimental trends involving neutral donors.10 Because of the charge here involved, however, we will use a linear dependence (eqn (19)) in which δ simply replaces n = 1 in eqn (18). Hence:
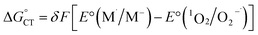 | (19) |
Regarding the conversion of ΔG≠0,ET into ΔG≠0,CT, we consider that ΔG≠0,s,CT should also depend on the square of δ, whereas ΔG≠0,i,CT has been previously considered as, possibly, independent of it, although differences were noted between different classes of compounds.91 The actual dependence of ΔG≠0,CT on δ is indeed unclear, especially in solvents of a very low dielectric constant and/or when ΔG≠0,i,CT is dominant, as noted above for Au25 clusters.69–71,87 Here, to balance contributions, we will consider a simple linear dependence, ΔG≠0,CT ∼ δΔG≠0,ET.
k
CT can now be obtained from the appropriate preexponential factor (eqn (14) and S1,† with Z = 4.6 × 1010 s−1), provided that a reasonable δ value is used in eqn (19). As δ is unknown, we will follow an approach similar to that used for other series of photosensitizers.10,66,67 In ETs, the transfer coefficient α is introduced to describe how the activation free energy responds to changes in the reaction driving force, that is, 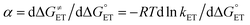 . Because of the quadratic expression relating ΔG≠ET to
. Because of the quadratic expression relating ΔG≠ET to 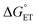 , α is expected to be 0.5 at zero driving force.85 We will focus on the three Au25 clusters, which are self-consistent in terms of cluster charge. The corresponding driving forces for ET (eqn (18)) range from −0.312 (SC4) to −0.201 (SC2Ph) eV, that is, these processes are exergonic, yet not too far from
, α is expected to be 0.5 at zero driving force.85 We will focus on the three Au25 clusters, which are self-consistent in terms of cluster charge. The corresponding driving forces for ET (eqn (18)) range from −0.312 (SC4) to −0.201 (SC2Ph) eV, that is, these processes are exergonic, yet not too far from 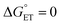 . The corresponding log
. The corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kqvs.
kqvs.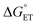 plot provides a slope corresponding to a very small α value of 0.10. Adjusting δ in eqn (19) shows that α ∼ 0.5 is obtained when δ = 0.2. This figure corresponds to
plot provides a slope corresponding to a very small α value of 0.10. Adjusting δ in eqn (19) shows that α ∼ 0.5 is obtained when δ = 0.2. This figure corresponds to 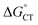 values ranging from −0.06 to −0.04 eV. This value of δ is indeed quite similar to those previously proposed for 1O2 quenching by other photosensitizers.10,66,67 We also should note that δ is expected to decrease for more positive reaction free energies.79 Using δ = 0.2, the remaining quantities in eqn (13) are defined. Hence, an experimental rate constant (SC4) of kq = 3.40 × 108 M−1 s−1 corresponds to
values ranging from −0.06 to −0.04 eV. This value of δ is indeed quite similar to those previously proposed for 1O2 quenching by other photosensitizers.10,66,67 We also should note that δ is expected to decrease for more positive reaction free energies.79 Using δ = 0.2, the remaining quantities in eqn (13) are defined. Hence, an experimental rate constant (SC4) of kq = 3.40 × 108 M−1 s−1 corresponds to 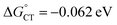 , kCT = 1.8 × 1010 s−1, and kISC = 1.8 × 107 s−1. For common photosensitizers, ISC is a fast process, with rate constant values estimated to be ∼1010 s−1.66 Despite the several inputs and assumptions and the resulting comparatively small kISC value, this kinetic analysis would suggest that the same CT–ISC mechanism proposed for 1O2 quenching by other photosensitizers is plausible. Different assumptions on the preexponential factor Z do not affect the value of kISC, as already observed.66
, kCT = 1.8 × 1010 s−1, and kISC = 1.8 × 107 s−1. For common photosensitizers, ISC is a fast process, with rate constant values estimated to be ∼1010 s−1.66 Despite the several inputs and assumptions and the resulting comparatively small kISC value, this kinetic analysis would suggest that the same CT–ISC mechanism proposed for 1O2 quenching by other photosensitizers is plausible. Different assumptions on the preexponential factor Z do not affect the value of kISC, as already observed.66
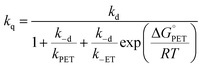 | (20) |
It is worth making a comment about the spin constrains. For this ET pathway, the singlet-triplet spin transition rate might affect the overall back ET rate in eqn (11). Indeed, spin-forbidden transitions can be orders of magnitude slower than the corresponding allowed transition.93 Both caged species formed in eqn (10) are radicals and the exchange interaction between them gives rise to nondegenerate singlet and triplet states (spin-correlated radical pair). In the present case, the singlet state has a higher energy and, as the precursor is a singlet (1O2), it is initially more populated. Therefore, the back ET rate constant should be considered as an upper limit. However, the rate is still large enough to make 3O2 formation a very rapid step.
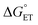 in eqn (18) (with E°(M+˙/M) in place of E°(M˙/M−)) requires adding the coulombic term, as now two opposite charges form. This correction can be performed for CT according to Rhem–Weller,89,90 who considered this term as negative (stabilization of the opposite charges) (eqn (21)):
in eqn (18) (with E°(M+˙/M) in place of E°(M˙/M−)) requires adding the coulombic term, as now two opposite charges form. This correction can be performed for CT according to Rhem–Weller,89,90 who considered this term as negative (stabilization of the opposite charges) (eqn (21)):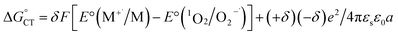 | (21) |
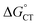 . For photoinduced ETs, coulombic stabilization has been shown to be especially important for dielectric constants smaller than 13.94
. For photoinduced ETs, coulombic stabilization has been shown to be especially important for dielectric constants smaller than 13.94
It is useful to compare TPP and Au24Cd(SC2Ph)180, which exhibit very similar kq values of 6.5 × 106 and 6.9 × 106 M−1 s−1, respectively. For TPP, the decrease of 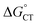 caused by the coulombic term depends on the value of δ: for example, it is 0.032 and 0.008 eV for δ = 0.2 and 0.1, respectively. In the absence of further information, however, we will keep using δ = 0.2. The CT–ISC path can reproduce the experimental kq value when kISC is set to 2.4 × 1010 s−1, which is indeed a reasonable value for a molecular system such as TPP.66 For the sake of argument, the use of a very small δ value of 0.1 would lower kISC to 7.5 × 108 s−1. Regardless, there is no competition from the ET path (eqn (10) and (11)), as kPET drops by several orders of magnitude.
caused by the coulombic term depends on the value of δ: for example, it is 0.032 and 0.008 eV for δ = 0.2 and 0.1, respectively. In the absence of further information, however, we will keep using δ = 0.2. The CT–ISC path can reproduce the experimental kq value when kISC is set to 2.4 × 1010 s−1, which is indeed a reasonable value for a molecular system such as TPP.66 For the sake of argument, the use of a very small δ value of 0.1 would lower kISC to 7.5 × 108 s−1. Regardless, there is no competition from the ET path (eqn (10) and (11)), as kPET drops by several orders of magnitude.
For Au24Cd(SC2Ph)180, the situation is more intriguing. Reproducing the observed kq value, requires kISC = 3.7 × 107 s−1, which, if one considers the error introduced by the various approximations, is probably the same as that calculated for Au25(SC4)18−. On the other hand, the independently estimated kPET, 3.2 × 106 s−1, leads (eqn (20)) to kq = 5.3 × 106 M−1 s−1, which is also comparable to the experimental value of 6.9 × 106 M−1 s−1. We are thus facing the same mechanistic competition addressed for the undoped Au25 clusters.
Conclusions
Diamagnetic Au24M(SR)18 clusters are shown to be effective singlet-oxygen photosensitizers. As to their efficiency as singlet-oxygen quenchers, we show that it can be modulated quite precisely by changing the ligands and/or one of the Au atoms. The use of very sensitive TREPR spectroscopy allowed us to determine 1O2 lifetimes ranging from 2.71 to 27.9 μs. The latter, which was measured for Au24Cd(SC2Ph)180, is virtually the same as that of TPP, a well-known reference photosensitizer.Analysis of the results leads to three main conclusions.
(1) We have described the first kinetic analysis of the quenching mechanism/s by gold nanoclusters. The Au25 clusters have unusually low E° values, yielding almost unprecedented92 negative 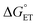 values. 1O2 quenching involves both CT–ISC and ET–ISC mechanisms, although the latter appears to be the most probable: indeed, for the ET–ISC mechanism the kq value is fully calculated according to eqn (20), whereas for the CT–ISC mechanism the kISC is adjusted to reproduce the experimental kq value viaeqn (13). Therefore, the actual kISC might be even smaller. This is also supported by the fact that 1O2 quenching by the corresponding Au24M doped clusters also appears to be possible through both mechanisms. The ET–ISC mechanism is made possible because the substantially more positive E° values of these doped clusters are largely compensated by the coulombic term (eqn (21)). This would imply that the use of a more polar solvent, which decreases the value of the coulombic term89,90 and may even revert its sign,94 would remove the feasibility of the ET–ISC mechanism, leaving CT–ISC as the only plausible quenching mechanism.
values. 1O2 quenching involves both CT–ISC and ET–ISC mechanisms, although the latter appears to be the most probable: indeed, for the ET–ISC mechanism the kq value is fully calculated according to eqn (20), whereas for the CT–ISC mechanism the kISC is adjusted to reproduce the experimental kq value viaeqn (13). Therefore, the actual kISC might be even smaller. This is also supported by the fact that 1O2 quenching by the corresponding Au24M doped clusters also appears to be possible through both mechanisms. The ET–ISC mechanism is made possible because the substantially more positive E° values of these doped clusters are largely compensated by the coulombic term (eqn (21)). This would imply that the use of a more polar solvent, which decreases the value of the coulombic term89,90 and may even revert its sign,94 would remove the feasibility of the ET–ISC mechanism, leaving CT–ISC as the only plausible quenching mechanism.
(2) Despite the possibility of quenching 1O2 through two mechanisms, we have detected the striking effect that the kISC values estimated for the nanoclusters are consistently smaller than those estimated for other molecular systems (and here shown for TPP) by no less than two orders of magnitude. This observation is obviously beneficial in terms of using this family of nanoclusters as 1O2 photosensitizers with minimum 1O2 quenching efficacy and makes these materials extremely promising for practical applications. Indeed, this large difference in kISC values points to something special in the interaction between nanoclusters and 1O2. Minaev concluded that, to achieve an efficient intersystem crossing enhancement, there should be a non-linear encounter geometry between 1O2 and the quencher molecular axes.68,93 This condition is typically fulfilled for common molecules, as quenching can be treated as a series of random encounters. Instead, ligand-protected gold nanoclusters are composed of a hard core and a dynamic capping layer,69 which is a feature not present in regular molecules. When inside the monolayer, interactions of 1O2 with the ligands may give rise to orientation-specific interactions with the Au orbitals. In this framework, our results would suggest that an approximately axial collision takes place, as this orientation, according to Minaev, does not lead to strong ISC. More generally, it is conceivable that the limited orientations imposed by the capping monolayer can make ISC substantially less favored than in common molecular systems, where all relative orientation geometries and, therefore, ISC contributions are possible.
(3) The sequence of the observed τΔ values illustrated in Fig. 11 demonstrates that the efficiency of Au24M(SR)18 clusters as a singlet oxygen quencher is a function of their E° value. We thus expect that a more positive E° would allow us to obtain even better results and possibly reach the physiological limit of τSΔ = 34.6 μs, i.e., no physical quenching by the cluster. According to Fig. 11, whose linear fit has a good r2 value of 0.990, the “ideal” cluster should have an oxidation potential at least more positive than ∼0.5 V vs. SCE in DCM/0.1 M TBAH. We believe that this target is indeed reachable through proper selection of the ligands to cap a cluster of the Au24Cd(SR)180 family, which also appears to have the longest triplet lifetime.
These results, methodologies, insights, and conclusions are expected to provide further ideas and incentive for using atomically precise gold nanoclusters as efficient photosensitizers, which is a topic of current interest for both fundamental and applied research.95,96
Experimental
TREPR
For the TREPR measurements, a pulsed laser beam from a Nd:YAG laser (Quantel Brilliant, pulse length 5 ns, pulse energy 5 mJ, and pulse repetition rate 20 Hz) was used for the optical excitation of the samples at 532 nm. At this wavelength, the absorption of all Au24M(SR)18 clusters is significantly larger than for nitroxides. The measurements were carried out by using a Bruker ER200D (X-band) spectrometer with an extended detection bandwidth (6 MHz), disabling the magnetic field modulation and working in a direct detection mode. The temperature of the sample inside the EPR cylindrical cavity (8 mm optical access) was controlled to 240 K by using a variable-temperature nitrogen flow system. The time-dependent EPR signals were digitized using a digital oscilloscope (LeCroy Model LT344) with a maximum acquisition rate of 500 megasample/s synchronized with the laser pulse. The time resolution of the instrument was ∼150 ns. Data collection was performed with a personal computer and software that allowed controlling the magnetic field and setting the digital oscilloscope. Typically, 300 transient signals were averaged under on-resonance conditions and subtracted from those accumulated off-resonance to eliminate the background signal induced by the laser pulse. A complete two-dimensional data set that shows the EPR signal as a function of both time and magnetic field consists typically of a set of transient signals, containing 500 points each, recorded at 128 different magnetic field positions. The 500 × 128 matrix gave a two-dimensional time/field data set from which the transient spectra were extracted.Electrochemistry
The DPV and CV measurements were carried out in DCM/0.1 M TBAH, under an Ar atmosphere, in a glass cell, at 25 °C. For DPV we used a CHI 660c electrochemical workstation, whereas for the electrode kinetics, CV experiments we used an EG&G-PARC 173/179 potentiostat-digital coulometer, an EG&G-PARC 175 universal programmer, and a Nicolet 3091 12-bit resolution digital oscilloscope. The working electrode was a glassy carbon microdisk (9.1 × 10−4 cm2), prepared and activated as already described.97 The counter electrode was a Pt wire. A silver wire, which was kept in a tube filled with the same electrolyte solution and separated from the main compartment by a Vycor frit, served as a quasi-reference electrode. At the end of the experiments, its potential was calibrated after addition of ferrocene; the ferricenium/ferrocene redox couple has E° = 0.460 V (SCE) in DCM/0.1 M TBAH. All potential values are reported against the SCE. Standard DPV parameters were employed: peak amplitude = 50 mV, pulse width = 0.05 s, increments per cycle = 2 mV, and pulse period = 0.1 s. For CV, we applied positive feedback correction to minimize the ohmic drop between the working and the reference electrodes. The standard heterogeneous rate constant,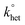 , for oxygen reduction on a glassy carbon electrode was determined by the analysis of the CVs obtained at various scan rates (v). In DCM/TBAH 0.1 M, the separation between the cathodic and anodic peak potentials is large also at low v values (e.g., 0.228 V at 0.2 V s−1) pointing to a small
, for oxygen reduction on a glassy carbon electrode was determined by the analysis of the CVs obtained at various scan rates (v). In DCM/TBAH 0.1 M, the separation between the cathodic and anodic peak potentials is large also at low v values (e.g., 0.228 V at 0.2 V s−1) pointing to a small 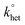 value. The latter was determined by digital simulation of the experimental CVs. For digital simulation, we used DigiSim 3.03 software, using a step size of 1 mV and an exponential expansion factor of 0.5.
value. The latter was determined by digital simulation of the experimental CVs. For digital simulation, we used DigiSim 3.03 software, using a step size of 1 mV and an exponential expansion factor of 0.5.
Author contributions
M. A. carried out most of the TREPR measurements and analyses; W. F. prepared and characterized all clusters; S. A. carried out the electrochemical experiments; M. A., T. D. and S. B. conducted the chemical quenching experiments; A. Z. and M. R. contributed to the TREPR study; S. A. and F. M. carried out the kinetic analysis; M. R. and F. M. designed the research; M. A., S. A., M. R., and F. M. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the University of Padova (P-DiSC-2018: Magnetic detection of singlet oxygen photosensitized by gold nanoclusters; P-DiSC-2017: Gold Nose) and Fondazione CARIPARO (grant: GoldCat).References
- K. H. Becker, W. Groth and U. Schurath, Chem. Phys. Lett., 1971, 8, 259–262 CrossRef CAS.
- (a) F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1995, 24, 663–1021 CrossRef CAS; (b) F. Wilkinson and J. G. Brummer, J. Phys. Chem. Ref. Data, 1981, 10, 809–999 CrossRef CAS.
- M. Ruzzi, E. Sartori, A. Moscatelli, I. V. Khudyakov and N. J. Turro, J. Phys. Chem. A, 2013, 117, 5232–5240 CrossRef CAS PubMed.
- I. Amato, Science, 1993, 262, 32–33 CrossRef CAS PubMed.
- A. Greer, Acc. Chem. Res., 2006, 39, 797–804 CrossRef CAS PubMed.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Molecular Oxygen and Organic Photochemistry, in Modern Molecular Photochemistry of Organic Molecules, University Science Books, Sausalito, 2010, ch. 14, pp. 1001–1042 Search PubMed.
- A. A. Ghogare and A. Greer, Chem. Rev., 2016, 116, 9994–10034 CrossRef CAS PubMed.
- Y. Nosaka and A. Y. Nosaka, Chem. Rev., 2017, 117, 11302–11336 CrossRef CAS PubMed.
- D. E. Dolmans, D. Fukumura and R. K. Jain, Nat. Rev. Cancer, 2003, 3, 380–387 CrossRef CAS PubMed.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1757 CrossRef CAS PubMed.
- P. R. Ogilby, Chem. Soc. Rev., 2010, 39, 3181–3209 RSC.
- M. Bregnhøj, M. Westberg, B. F. Minaev and P. R. Ogilby, Acc. Chem. Res., 2017, 50, 1920–1927 CrossRef PubMed.
- M. C. DeRosa and R. J. Crutchley, Coord. Chem. Rev., 2002, 233–234, 351–371 CrossRef CAS.
- J. R. Hurst, J. D. McDonald and G. B. Schuster, J. Am. Chem. Soc., 1982, 104, 2065–2067 CrossRef CAS.
- P. R. Ogilby and C. S. Foote, J. Am. Chem. Soc., 1983, 105, 3423–3430 CrossRef CAS.
- A. A. Krasnovsky Jr, M. E. Bashtanov, N. N. Drozdova, O. A. Yuzhakova and E. A. Luk'yanets, Quantum Electron., 2002, 32, 83–86 CrossRef.
- Y. You, Org. Biomol. Chem., 2018, 16, 4044–4060 RSC.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- H. Kawasaki, S. Kumar, G. Li, C. Zeng, D. R. Kauffman, J. Yoshimoto, Y. Iwasaki and R. Jin, Chem. Mater., 2014, 26, 2777–2788 CrossRef CAS.
- M. Sakamoto, T. Tachikawa, M. Fujitsuka and T. Majima, Langmuir, 2009, 25, 13888–13893 CrossRef CAS PubMed.
- T. Das, P. Ghosh, M. S. Shanavas, A. Maity, S. Mondal and P. Purkayastha, Nanoscale, 2012, 4, 6018–6024 RSC.
- J. Y. Zhao, R. Cui, Z. L. Zhang, M. Zhang, Z. X. Xie and D. W. Pang, Nanoscale, 2014, 6, 13126–13134 RSC.
- R. Vankayala, C. L. Kuo, K. Nuthalapati, C. S. Chiang and K. C. Hwang, Adv. Funct. Mater., 2015, 25, 5934–5945 CrossRef CAS.
- D. Yang, G. Yang, S. Gai, F. He, G. An, Y. Dai, R. Lv and P. Yang, Nanoscale, 2015, 7, 19568–19578 RSC.
- M. Yamamoto, I. Osaka, K. Yamashita, H. Hasegawa, R. Arakawa and H. Kawasaki, J. Lumin., 2016, 180, 315–320 CrossRef CAS.
- M. Yamamoto, K. Shitomi, S. Miyata, H. Miyaji, H. Aota and H. Kawasaki, J. Colloid Interface Sci., 2018, 510, 221–227 CrossRef CAS PubMed.
- S. Miyata, H. Miyaji, H. Kawasaki, M. Yamamoto, E. Nishida, H. Takita, T. Akasaka, N. Ushijima, T. Iwanaga and T. Sugaya, Int. J. Nanomed., 2017, 12, 2703–2716 CrossRef CAS.
- D. Hikosou, S. Saita, S. Miyata, H. Miyaji, T. Furuike, H. Tamura and H. Kawasaki, J. Phys. Chem. C, 2018, 122, 12494–12501 CrossRef CAS.
- R. Ho-Wu, S. H. Yau and T. Goodson III, J. Phys. Chem. B, 2017, 121, 10073–10080 CrossRef CAS PubMed.
- G. Zhang, R. Wang and G. Li, Chin. Chem. Lett., 2018, 29, 687–693 CrossRef CAS.
- J. Zhang, Z. Li, J. Huang, C. Liu, F. Hong, K. Zheng and G. Li, Nanoscale, 2017, 9, 16879–16886 RSC.
- Z. Li, C. Liu, H. Abroshan, D. R. Kauffman and G. Li, ACS Catal., 2017, 7, 3368–3374 CrossRef CAS.
- K. Kawamura, D. Hikosou, A. Inui, K. Yamamoto, J. Yagi, S. Saita and H. Kawasaki, J. Phys. Chem. C, 2019, 123, 26644–26652 CrossRef CAS.
- S. Antonello and F. Maran, Curr. Opin. Electrochem., 2017, 2, 18–25 CrossRef CAS.
- (a) M. Agrachev, S. Antonello, T. Dainese, M. Ruzzi, A. Zoleo, E. Aprà, N. Govind, A. Fortunelli, L. Sementa and F. Maran, ACS Omega, 2017, 2, 2607–2617 CrossRef CAS PubMed; (b) M. Agrachev, S. Antonello, T. Dainese, M. Ruzzi, A. Zoleo, E. Aprà, N. Govind, A. Fortunelli, L. Sementa and F. Maran, Correction to Magnetic Ordering in Gold Nanoclusters, ACS Omega, 2017, 2, 3595 CrossRef CAS PubMed.
- M. Agrachev, M. Ruzzi, A. Venzo and F. Maran, Acc. Chem. Res., 2019, 52, 44–52 CrossRef CAS PubMed.
- J. F. Parker, C. A. Fields-Zinna and R. W. Murray, Acc. Chem. Res., 2010, 43, 1289–1296 CrossRef CAS PubMed.
- X. Kang, H. Chong and M. Zhu, Nanoscale, 2018, 10, 10758–10834 RSC.
- W. Fei, S. Antonello, T. Dainese, A. Dolmella, M. Lahtinen, K. Rissanen, A. Venzo and F. Maran, J. Am. Chem. Soc., 2019, 141, 16033–16045 CrossRef CAS PubMed.
- A. Kawai, M. Mitsui, Y. Kobori and K. Obi, Appl. Magn. Reson., 1997, 12, 405–410 CrossRef CAS.
- C. G. Martinez, S. Jockusch, M. Ruzzi, E. Sartori, A. Moscatelli, N. J. Turro and A. L. Buchachenko, J. Phys. Chem. A, 2005, 109, 10216–10221 CrossRef CAS PubMed.
- C. Corvaja, in Fullerenes: From Synthesis to Optoelectronic Properties, ed. D. M. Guldi and N. Martin, Kluwer Academic Publishers, 2002, pp. 213–236 Search PubMed.
- C. Blättler, F. Jent and H. A. Paul, Chem. Phys. Lett., 1990, 166, 375–380 CrossRef.
- K. M. Salikhov, Yu. N. Molin, R. Z. Sagdeev and A. L. Buchachenko, Spin Polarization and Magnetic Effects in Radical Reactions, Elsevier, Amsterdam, 1984 Search PubMed.
- M. Mitsui, K. Takeda, Y. Kobori, A. Kawai and K. Obi, Chem. Phys. Lett., 1996, 262, 125–130 CrossRef CAS.
- M. Mitsui, K. Takeda, Y. Kobori, A. Kawai and K. Obi, J. Phys. Chem. A, 2004, 108, 1120–1126 CrossRef CAS.
- A. Kawai, T. Okutsu and K. Obi, J. Phys. Chem., 1991, 95, 9130–9134 CrossRef CAS.
- M. De Nardi, S. Antonello, D. Jiang, F. Pan, K. Rissanen, M. Ruzzi, A. Venzo, A. Zoleo and F. Maran, ACS Nano, 2014, 8, 8505–8512 CrossRef CAS PubMed.
- M. Agrachev, S. Antonello, T. Dainese, J. A. Gascón, F. Pan, K. Rissanen, M. Ruzzi, A. Venzo, A. Zoleo and F. Maran, Chem. Sci., 2016, 7, 6910–6918 RSC.
- S. Antonello, T. Dainese, F. Pan, K. Rissanen and F. Maran, J. Am. Chem. Soc., 2017, 139, 4168–4174 CrossRef CAS PubMed.
- A. Venzo, S. Antonello, J. A. Gascón, I. Guryanov, R. D. Leapman, N. V. Perera, A. Sousa, M. Zamuner, A. Zanella and F. Maran, Anal. Chem., 2011, 83, 6355–6362 CrossRef CAS PubMed.
- S. Antonello, M. Hesari, F. Polo and F. Maran, Nanoscale, 2012, 4, 5333–5342 RSC.
- I. Rosenthal, Chemical and Physical Sources of Singlet Oxygen, in Singlet O2, ed. A. A. Frimer, CRC Press, Boca Raton, 1985, vol. I, pp. 13–38 Search PubMed.
- A. Kawai and K. Shibuya, J. Photochem. Photobiol., C, 2006, 7, 89–103 CrossRef CAS.
- M. J. Povich, J. Phys. Chem., 1975, 79, 1106–1109 CrossRef CAS.
- M. Bregnhøj, M. Westberg, F. Jensen and P. R. Ogilby, Phys. Chem. Chem. Phys., 2016, 18, 22946–22961 RSC.
- A. A. Gorman, I. Hamblett, C. Lambert, B. Spencer and M. C. Standen, J. Am. Chem. Soc., 1988, 110, 8053–8059 CrossRef CAS.
- J. Zhang, C. Jiang, J. P. Figueiró Longo, R. B. Azevedo, H. Zhang and L. A. Muehlmann, Acta Pharm. Sin. B, 2018, 8, 137–146 CrossRef PubMed.
- C. Tanielian and C. Wolff, Photochem. Photobiol., 1988, 48, 277–280 CrossRef CAS.
- S. M. Bachilo and R. B. Weisman, J. Phys. Chem. A, 2000, 104, 7711–7714 CrossRef CAS.
- C. Tanielian and C. Wolff, J. Phys. Chem., 1995, 99, 9825–9830 CrossRef CAS.
- M. Pineiro, A. L. Carvalho, M. M. Pereira, A. M. d'A. Rocha Gonsalves, L. G. Arnaut and S. J. Formosinho, Chem.–Eur. J., 1998, 4, 2299–2307 CrossRef CAS.
- C. Ouannès and T. Wilson, J. Am. Chem. Soc., 1968, 90, 6527–6528 CrossRef.
- C. Schweitzer, Z. Mehrdad, F. Shafii and R. Schmidt, Phys. Chem. Chem. Phys., 2001, 3, 3095–3101 RSC.
- E. A. Ogryzlo and C. W. Tang, J. Am. Chem. Soc., 1970, 92, 5034–5036 CrossRef CAS.
- A. P. Darmanyan, W. S. Jenks and P. Jardon, J. Phys. Chem. A, 1998, 102, 7420–7426 CrossRef CAS.
- C. Schweitzer, Z. Mehrdad, F. Shafii and R. Schmidt, J. Phys. Chem. A, 2001, 105, 5310–5316 CrossRef.
- B. F. Minaev, Theor. Exp. Chem., 1984, 20, 199–201 CrossRef.
- S. Antonello, G. Arrigoni, T. Dainese, M. De Nardi, G. Parisio, L. Perotti, A. René, A. Venzo and F. Maran, ACS Nano, 2014, 8, 2788–2795 CrossRef CAS PubMed.
- S. Antonello, T. Dainese, M. De Nardi, L. Perotti and F. Maran, ChemElectroChem, 2016, 3, 1237–1244 CrossRef CAS.
- S. Antonello, A. H. Holm, E. Instuli and F. Maran, J. Am. Chem. Soc., 2007, 129, 9836–9837 CrossRef CAS PubMed.
- S. Wang, Y. Song, S. Jin, X. Liu, J. Zhang, Y. Pei, X. Meng, M. Chen, P. Li and M. Zhu, J. Am. Chem. Soc., 2015, 137, 4018–4021 CrossRef CAS PubMed.
- C. Yao, Y.-j. Lin, J. Yuan, L. Liao, M. Zhu, L.-h. Weng, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 15350–15353 CrossRef CAS PubMed.
- L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514 CrossRef CAS PubMed.
- M. Zhou, C. Yao, M. Y. Sfeir, T. Higaki, Z. Wu and R. Jin, J. Phys. Chem. C, 2018, 122, 13435–13442 CrossRef CAS.
- X. Wen, P. Yu, Y. R. Toh, A. C. Hsu, Y. C. Lee and J. Tang, J. Phys. Chem. C, 2012, 116, 19032–19038 CrossRef CAS.
- R. Castro-Olivares, G. Günter, A. L. Zanocco and E. Lemp, J. Photochem. Photobiol., A, 2009, 207, 160–166 CrossRef CAS.
- I. B. Berlman, Handbook of Fluorescence Spectra of Aromatic Molecules, Academic Press, New York, 1971 Search PubMed.
- J. P. Dinnocenzo, P. B. Merkel and S. Farid, J. Phys. Chem. A, 2017, 121, 7903–7909 CrossRef CAS PubMed.
- A. P. Woodham, G. Meijer and A. Fielicke, Angew. Chem., Int. Ed., 2012, 51, 4444–4447 CrossRef CAS PubMed.
- A. P. Woodham, G. Meijer and A. Fielicke, J. Am. Chem. Soc., 2013, 135, 1727–1730 CrossRef CAS PubMed.
- S. Bhat, R. P. Narayanan, A. Baksi, P. Chakraborty, G. Paramasivam, R. R. J. Methikkalam and A. Nag, J. Phys. Chem. C, 2018, 122, 19455–19462 CrossRef CAS.
- L. D. Zusman, Chem. Phys., 1980, 49, 295–304 CrossRef CAS.
- N. Sutin, Prog. Inorg. Chem., 1983, 30, 441–498 CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- A. B. Meneses, S. Antonello, M.-C. Arévalo, C. C. González, J. Sharma, A. N. Wallette, M. S. Workentin and F. Maran, Chem.–Eur. J., 2007, 13, 7983–7995 CrossRef CAS PubMed.
- S. Antonello, N. V. Perera, M. Ruzzi, J. A. Gascón and F. Maran, J. Am. Chem. Soc., 2013, 135, 15585–15594 CrossRef CAS PubMed.
- A. Ignaczak, W. Schmickler and S. Bartenschlager, J. Electroanal. Chem., 2006, 586, 297–307 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 2nd edn (the “Gold Book”), 1997, online version (2019) created by S. J. Chalk, ISBN 0-9678550-9-8, DOI:10.1351/goldbook.
- C. Schweitzer, Z. Mehrdad, F. Shafii and R. Schmidt, Phys. Chem. Chem. Phys., 2001, 3, 3095–3101 RSC.
- S. Fukuzumi, S. Fujita, T. Suenobu, H. Yamada, H. Imahori, Y. Araki and O. Ito, J. Phys. Chem. A, 2002, 106, 1241–1247 CrossRef CAS.
- B. F. Minaev, Russ. Chem. Rev., 2007, 76, 988–1010 CrossRef.
- S. Farid, J. P. Dinnocenzo, P. B. Merkel, R. H. Young and D. Shukla, J. Am. Chem. Soc., 2011, 133, 4791–4801 CrossRef CAS PubMed.
- O. J. H. Chai, Z. Liu, T. Chen and J. Xie, Nanoscale, 2019, 11, 20437–20448 RSC.
- T. Kawawaki, Y. Negishi and H. Kawasaki, Nanoscale Adv., 2020, 2, 17–36 RSC.
- A. B. Meneses, S. Antonello, M.-C. Arévalo and F. Maran, Electroanal, 2006, 18, 363–370 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Chemicals, determination of relevant kinetic and thermodynamic parameters, further experimental procedures, Table S1 and Fig. S1–S9. See DOI: 10.1039/d0sc00520g |
| ‡ Co-first authors. |
| This journal is © The Royal Society of Chemistry 2020 |