Open Access Article
Open Access ArticleGeometric landscapes for material discovery within energy–structure–function maps†‡
Seyed Mohamad
Moosavi§
 a,
Henglu
Xu§
a,
Linjiang
Chen
b,
Andrew I.
Cooper
a,
Henglu
Xu§
a,
Linjiang
Chen
b,
Andrew I.
Cooper
 b and
Berend
Smit
b and
Berend
Smit
 *a
*a
aLaboratory of Molecular Simulation (LSMO), Institut des Sciences et Ingénierie Chimiques, École Polytechnique Fédérale de Lausanne (EPFL), Rue de l'Industrie 17, CH-1951 Sion, Valais, Switzerland. E-mail: berend.smit@epfl.ch
bLeverhulme Research Centre for Functional Materials Design, Materials Innovation Factory, Department of Chemistry, University of Liverpool, 51 Oxford Street, Liverpool, L7 3NY, UK
First published on 29th April 2020
Abstract
Porous molecular crystals are an emerging class of porous materials formed by crystallisation of molecules with weak intermolecular interactions, which distinguishes them from extended nanoporous materials like metal–organic frameworks (MOFs). To aid discovery of porous molecular crystals for desired applications, energy–structure–function (ESF) maps were developed that combine a priori prediction of both the crystal structure and its functional properties. However, it is a challenge to represent the high-dimensional structural and functional landscapes of an ESF map and to identify energetically favourable and functionally interesting polymorphs among the 1000s to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000s of structures typically on a single ESF map. Here, we introduce geometric landscapes, a representation for ESF maps based on geometric similarity, quantified by persistent homology. We show that this representation allows the exploration of complex ESF maps, automatically pinpointing interesting crystalline phases available to the molecule. Furthermore, we show that geometric landscapes can serve as an accountable descriptor for porous materials to predict their performance for gas adsorption applications. A machine learning model trained using this geometric similarity could reach a remarkable accuracy in predicting the materials' performance for methane storage applications.
000s of structures typically on a single ESF map. Here, we introduce geometric landscapes, a representation for ESF maps based on geometric similarity, quantified by persistent homology. We show that this representation allows the exploration of complex ESF maps, automatically pinpointing interesting crystalline phases available to the molecule. Furthermore, we show that geometric landscapes can serve as an accountable descriptor for porous materials to predict their performance for gas adsorption applications. A machine learning model trained using this geometric similarity could reach a remarkable accuracy in predicting the materials' performance for methane storage applications.
1 Introduction
Design and discovery of porous materials with tailor-made pore sizes, pore shapes, and chemical functionalities is central to a variety of industrial and technological applications, such as gas separation and storage, catalysis, and electronics.1,2 Porous molecular crystals are a class of porous materials formed by crystallisation of molecules with shapes that frustrate close packing and/or that have internal, molecular pores.3,4 Their discrete molecular building block structures give them certain advantages over other extended framework-type or polymeric materials, such as ease of synthesis and applicability where solubility and amorphous porous phases are desired.5,6 Porous molecular crystal materials with high surface areas have been synthesised (to date, up to 3758 m2 g−1),7 some of which show promising performance in applications, including hydrogen isotope separation,8 Xe/Kr separation,9 and molecular separation.10With the significant progress made in fast and accurate in silico prediction of properties and performance of materials,11,12 particularly of porous materials,13–15 computational modelling plays a significant role in material design and discovery. Using computational techniques, one could generate hypothetical materials to explore the potential chemical space beyond the experimentally realised materials, and then perform in silico high-throughput screening of their performance to find the optimal materials for a given application.16–19 Unlike framework-type porous materials, such as metal–organic frameworks (MOFs) and covalent organic frameworks (COFs), which are formed by strong coordination or covalent bonds, porous molecular crystals are formed by the balance of many weak intermolecular interactions, e.g., π–π stacking and hydrogen bonding. As a result, small changes in the molecular structure can drastically change the landscape of possible crystalline packing, leading to different degrees of propensity for polymorphism and materials properties thereby.20 Hypothetical material generation techniques that are widely used for framework materials are not generally applicable to porous molecular crystals. To account for this challenge in design and discovery of porous molecular crystals, Pulido et al.21 proposed the concept of energy–structure–function (ESF) maps, combining crystal structure prediction (CSP) with material property prediction, which represents the possible material properties associated with the molecule. For a known molecule,22 ESF maps revealed new stable polymorphs that were predicted to be promising for different applications before they were targeted for synthesis and measurement in the lab. In this technique, the first step is to generate a series of trial structures using crystal structure prediction techniques, e.g., methods based on mathematical tiling theory,23–25 sampling the conformation space to search for different packing using Monte Carlo techniques26 or quasi-random search,27etc. Next, the relative lattice energies of these in silico generated structures are projected on a representation of the structural landscape to make a crystal energy landscape,28 which is used to guide the search of stable packing of the molecule. For molecules showing a simple structural landscape (e.g., with a pronounced minimum well separated from the bulk of the landscape), a 1-dimensional representation of the landscape, often based on the crystal density,28,29 is sufficient to reveal the stable packing arrangements for the molecule.30 However, porous molecules having an internal cavity or a shape that prevents close packing often give rise to a rich, high-dimensional structural landscapes, with multiple local minima. Some of these minima can be easily hidden in a simple 1-dimensional representation. Hence, it is desirable to project an ESF map onto a more complete representation of the CSP landscape, which closely respects the high-dimensional nature of the ESF map, thus improving its predictive ability in pinpointing crystalline packings for desired materials functions.
Ideally, one would construct a crystal energy landscape by representing the free energy surface of the crystals as a function of thermodynamic variables.28,31,32 However, this becomes challenging and infeasible for large molecules or complex energetics of the systems in presence of solvent molecules.29,30 Therefore, descriptors able to distinguish different crystalline phases are desired for constructing a good representation of the structural landscape. A robust structural descriptor for crystals should be invariant with respect to the choice of crystal lattice vectors, the permutation of atoms in the crystal structure, and rigid motions of the structure such as translation and rotation.33,34 For this purpose of studying porous molecular crystals, a good descriptor should also be invariant to subtle perturbations to the local arrangements of the molecules at their lattice positions. Assuming similar packing leads to similar pore geometries, one can use geometric descriptors to distinguish different molecular packings. Examples of conventional geometric descriptors include crystal density, pore volume, surface area, and pore diameter, all of which satisfy the requirements mentioned above and are cheap to compute; they have been used for representation of structural landscapes.21 However, each of these conventional descriptors describes partial geometric features only and fails to encode the full picture of the pore shapes of porous materials.35,36 Alternatively, one can use persistent homology from mathematics to compute the topological features of shapes.37 Persistent homology is an algebraic tool which describes these topological features with a set of persistent barcodes.38 Persistent homology barcodes provide a quantitative description of the pore shapes, and notably, satisfy the requirements for a geometric representation. While persistent homology was traditionally developed for topological data analysis (TDA),39–41 it has now been extended to a variety of other disciplines, including material sciences.42–45
In this work, we developed a geometric representation based on persistent homology, which allowed us to compute a robust representation of the structural landscapes based on geometric similarity. We show that this representation can be used to automatically explore large databases of porous molecular crystals. This representation has advantages over representations based on a single geometric descriptor in identifying stable crystalline phases, because of its power in encoding the high-dimensional information of an ESF map so as to distinguish structures with unique geometric features not captured by any single geometric descriptor. Moreover, we show that the method offers an explicit structure–function relationship between pore geometries and gas adsorption properties of porous molecular crystals, making it possible to use machine learning to predict materials function on ESF maps with high accuracies.
2 Results
2.1 Geometric landscapes
We start with conceiving a representation for the structural landscapes based on geometric similarity. In such a representation, the structures with similar pore geometry should be mapped close to each other. To formulate this representation, we need a metric to assign similarity between pore shapes. Quantifying this geometric similarity is not trivial as, for example, structures with the same crystal density or largest included sphere could be envisioned with totally different pore shapes.46 Persistent homology, however, allows us to quantify this geometric similarity. Persistent homology can capture the overall similarity of the pore shapes; in contrast to the conventional descriptors, which are more limited. We call such representation of the structural landscape a geometric landscape. The relative lattice energies of the crystals will be projected on this representation to form a crystal energy landscape based on the geometric similarity.To construct the geometric landscapes, we start with identifying the pore structure of the materials. Here, we use a point cloud sampled on the surface of the accessible pores of the material to a probe atom with a van der Waals radius of 1.5 Å.47 The persistent homology barcodes then were computed over filtering topological objects to the size of 8 Å of the constructed Vietoris–Rips complexes48 up to the second dimension for the sampled point cloud (see Fig. 1, Method section, and our previous works35,49 for more details). Each dimension of the barcode captures part of the topological features of the pore shape. The zeroth dimension, which gives the number of connected components, is discarded as it does not contain useful information for our analysis. The first and second dimensions of the barcodes capture the features related to the surface and volume of the pore, respectively. Each geometric barcode records the birth and death of these topological objects, which correspond to the size these features have in space.
The persistent homology calculations map each structure in the database to a high-dimensional topological space. In this space, the pairwise distance between each pair of structures is defined by the distance between their persistent homology barcodes. This pairwise distance corresponds to the geometric similarity between the structures in the high-dimensional space where structures with a large distance are geometrically dissimilar while the structures with a small distance are geometrically similar. The L2 persistence landscape distance50–52 is used to determine the persistent homology barcode distances because of our previous successful experience in assigning pore geometry similarity using this metric.35 To make the final representation, instead of including the entire dataset, consisting of 1000s to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000s crystal structures, in the final representation of the geometric landscape, we first classify the dataset to find unique pore-geometry classes. From each class, we use only a landmark structure as a representative structure, to be included on the final geometric landscape. This method allows applying this analysis to extra-large databases (e.g., for datasets that consider multiple conformers) as instead of representing all data points, only representative, low-energy structures are shown on the geometric landscape while still encompassing all the unique classes of pore shapes. Also, it simplifies the representation of the high-dimensional space to avoid over sampling and representing of populated classes with many structures, yet, very similar geometries. This approach is similar to landmark multidimensional scaling, a widely-used dimensionality reduction methodology in computer science and data analysis.53 To find these representative landmark structures, we perform a Voronoi decomposition of the topological space using the pairwise distances between the barcodes of the materials. To perform this Voronoi decomposition, we select a set of landmark structures covering the topological space with minimum pairwise distance smaller than 10% of the size of the topological space using MaxMin algorithm,54 which ensures the landmarks were distributed homogeneously in the entire topological space (see Method section for details). We assign the remaining structures in the Voronoi cell to their representative landmark structures.
000s crystal structures, in the final representation of the geometric landscape, we first classify the dataset to find unique pore-geometry classes. From each class, we use only a landmark structure as a representative structure, to be included on the final geometric landscape. This method allows applying this analysis to extra-large databases (e.g., for datasets that consider multiple conformers) as instead of representing all data points, only representative, low-energy structures are shown on the geometric landscape while still encompassing all the unique classes of pore shapes. Also, it simplifies the representation of the high-dimensional space to avoid over sampling and representing of populated classes with many structures, yet, very similar geometries. This approach is similar to landmark multidimensional scaling, a widely-used dimensionality reduction methodology in computer science and data analysis.53 To find these representative landmark structures, we perform a Voronoi decomposition of the topological space using the pairwise distances between the barcodes of the materials. To perform this Voronoi decomposition, we select a set of landmark structures covering the topological space with minimum pairwise distance smaller than 10% of the size of the topological space using MaxMin algorithm,54 which ensures the landmarks were distributed homogeneously in the entire topological space (see Method section for details). We assign the remaining structures in the Voronoi cell to their representative landmark structures.
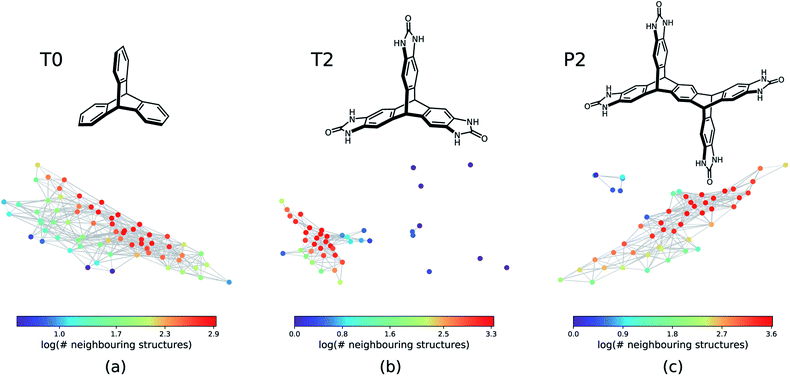
The next step is to apply this technique to generate geometric landscapes for three datasets of crystal structure prediction (CSP) for T0, T2, and P2 molecules (Fig. 2). These molecules possess different directional intermolecular interactions and rigid shapes that promote porosity, and it was shown that they construct multi-minima and complex structural landscapes.21 Our analysis identified 67, 43, and 51 landmark structures for 2072, 3893, and 7860 porous structures in T0, T2, and P2 datasets, respectively. To visualise these geometric landscapes, we use multidimensional scaling (MDS) projection55 of the relative positions of these unique pore geometry classes using the pairwise distance between the landmark structures in the topological space. MDS representations visualise similarity between individuals in a dataset so that points with relatively small pairwise distances in the high dimensional space are mapped close to each other. The MDS representation of the geometric landscapes of the three databases are shown in Fig. 2. In these geometric landscapes, each node, i.e., a Voronoi cell of the topological space, represents a set of geometrically similar materials. Nodes with similar barcodes are mapped close to each other and connected when their pairwise distance in the topological space is below 20% of the size of space. The colour coding indicates the number of structures that are similar to each of the landmark points with a cut-off distance of 15% of the size of the topological space. We observe different landscapes for the molecules in Fig. 2. On the geometric landscape of T0, all the landmark structures are closely located to one another, forming one big cluster, which is in line with its featureless, monotonic energy-density distribution reported previously.21 Similarly, the geometric landscape of P2 shows one cluster of most of the landmark structures, with a smaller cluster located nearby. By contrast, the T2 molecule yields a much more interesting geometric landscape, in which the landmark structures are scattered to a larger extent in the spacing, indicating that these structures have more distinct pore geometries. A proportion of these scattered points corresponds to “spikes” observed in the energy-density landscape for T2,21 though we point out that clusters of similar structures do not have to form such visible “spikes” to be well separated in these geometric projections.
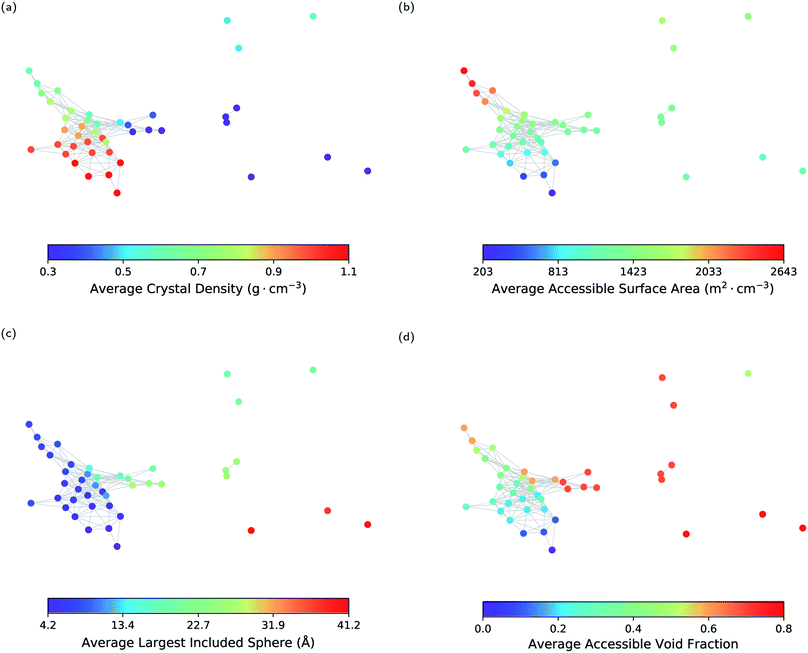
As a first step, we show that geometric landscapes can capture the expected geometric similarity based on the conventional geometric descriptors. Fig. 3 shows that the nodes close to each other have similar values of the conventional descriptors, including crystal density, accessible surface area, largest included sphere and accessible void fraction (see ESI Fig. S1 and S2‡ for the other molecules). In other words, the materials that are measured to be similar in the topological space, indeed have similar conventional descriptors. Furthermore, we can see in Fig. 3 that, for example, there are several landmarks with similar crystal densities (Fig. 3a) but different cavity sizes (Fig. 3c). This shows that the geometric landscapes capture information beyond the conventional descriptors used separately, as these landmarks are distinguished and classified in different geometric classes. Capturing multiple geometrical features by one representation allows for better classification of structures with respect to their pore geometry to represent the full picture of diversity in the pore shapes and geometry of the pores of molecular crystals. If we drew lines from the lowest to the highest value for each conventional descriptor, we would have obtained the 1-D representation of the landscape with respect to the conventional descriptor. In such a 1-D representation, many classes of unique pore geometry will overlay and hence it is difficult to identify. In the geometric landscapes, however, these 1-D representations are embedded into a high-dimensional topological space where all of these unique geometric classes are distinguished from each other.
2.2 Energy-geometry landscapes
Each node of the geometric landscape represents a unique class of pore geometry, and therefore this representation could be used for identifying unique packing classes of the porous molecular crystals. To find these unique packings, we select the structure with the lowest lattice energy for each node in the geometric landscapes as the stable structure of the corresponding geometry class. Using the geometric landscapes, we could identify many unique classes of packing of the three molecules where some of these structures with ordered packing are shown in Fig. 4. These landmark structures exhibit a wide range of pore sizes and shapes, immediately revealing potential targets for experimental efforts. | ||
| Fig. 4 The energy-geometry landscapes of (a) T0, (b) T2, and (c) P2 molecules. The structures with Greek letters are already synthesised in previous works.21,22 The letters used for the other structures are chosen in the basis of their relative lattice energy and names used in the previous works.21 Space-filling representation is used for visualisation of the structures. Carbon, hydrogen, oxygen, and nitrogen atoms are coloured grey, white, red, and blue, respectively. | ||
The stability of these polymorphs could be assessed based on their relative lattice energy compared to the global minimum of the landscape. The energetic differences between the polymorphs originate in different ratios of hydrogen bonding network, π–π stacking, and van der Waals interactions for each packing. We use the T2 molecule to evaluate the potential of geometric landscapes for exploring crystal structure prediction (CSP) databases to find stable polymorphs because of prior experimental realisation of the molecule.21,22 In Fig. 4, we can see that T2-A, T2-δ, T2-γ, T2-α, and T2-β have relatively low lattice energy and, hence, one predicts them to be experimentally accessible. Indeed, four of these materials are among the known experimental polymorphs of the T2 molecule. Therefore, the geometric landscapes could be used to search for stable structures in large CSP databases in one shot.
The other materials with higher relative lattice energies in Fig. 4, yet with unique packings and pore geometries, are potentially interesting because the lattice energy of the porous molecular crystals can be stabilised with proper choice of solvents. Also, previous studies have shown that the lattice energies could vary drastically with dynamics21 and/or presence of solvents,56,57 and therefore one could envision experimental realisation of those materials by solvent stabilisation. However, finding all the experimentally known structures of T2 molecules in the mainly populated cluster can be a sign of difficulty in synthesising the structures in the smaller or isolated clusters (see Fig. 2). For those smaller clusters, as the number of neighbouring structures is very low (see Fig. 2b), the potential well of the landscape is very narrow, and it is unlikely for structures to be trapped in those area of the landscape. This can be explained by the complex architecture of those structures in the small or outlier clusters, e.g., T2-C and T2-H in Fig. 4b, which are more complex assemblies where the T2 molecules assemble to create a hierarchy of pore sizes.
Notably, we see a smaller number of unique ordered packings spotted for the T0 molecule in comparison to T2 and P2 molecules, which implies a comparably simpler landscape of the T0 molecule. This simplicity can be denoted to the lack of hydrogen bonding motifs in T0 molecule. Notably, the only experimentally observed structure for T0 is a densely packed and non-porous structure, where van der Waals interactions are maximised.
2.3 Function-geometry landscapes
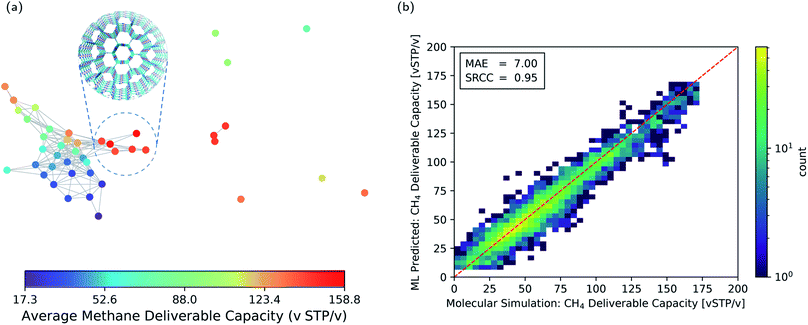
The pore geometry of porous materials can be optimised for a given adsorption application. Here, we show that geometric landscapes can be used for such optimisation. We show this approach for methane storage application, which is an important application of nanoporous materials. The material's performance for this application is assessed by the deliverable capacity, the difference in the gas uptake in a pressure swing adsorption process reported in standard volumetric units (v STP/v). The adsorption and desorption pressure for this process was set to 5.8 bar and 65 bar, respectively, by Advanced Research Project Agency-Energy (ARPA-E).58,59Fig. 5a shows the average methane deliverable capacity of materials in each node of the geometric landscape of the T2 molecule. A good correlation between geometry and performance is observed as materials mapped close to each other have similar deliverable capacity. This analysis shows that the T2-γ structure and the corresponding geometrically similar structures have almost optimal pore shape and size for the methane storage application (Fig. 5a). These materials have one-dimensional channels with a moderate gravimetric surface area but large volumetric pore volume (Fig. 3).
The narrow variation of the materials' performance within each node of the geometric landscape shows a clear correlation between the materials' performance and the geometry of the pores (see ESI Fig. S3‡ for the standard deviation of the materials' performance in each node). This suggests that the geometric landscapes can be used to explore large databases of porous molecular crystals for finding good performing materials. A possible strategy is to combine them with machine learning to filter out the low-performing materials from a large database. In such a scenario,60 instead of performing brute force calculations on the entire database, one carries out calculations only on a subset of structures to obtain enough data, which are used to train the machine learning model.
This machine learning model is then used to identify potentially good performing materials where the expensive calculations are worth performing on them. Since persistent homology analysis gives us a metric of similarity, the natural choice for the machine learning model is a kernel based model.61–63 In such a machine learning model, the predictions rely on the similarity or dissimilarity (distance) of a data point to all the training data in the feature space, in our case the topological space.64 Therefore, the prediction accuracy is higher compared to a method relying only on the nearest neighbor, e.g., the landmarks in Fig. 5a. Here, we use Kernel Ridge Regression (KRR) with combined conventional descriptors and persistent landscape distances (see Method section for details). The machine learning predicted deliverable capacities for 3293 materials in test set are shown and compared to the molecular simulation values in Fig. 5b. The model accuracy for the out of train samples is remarkable with Mean Absolute Error (MAE) of 7.0 (v STP/v) and Spearman Rank Correlation Coefficient (SRCC) of 0.95. This high accuracy of the machine learning model in predicting material properties and their ranking is promising in comparison to the previous studies60,63,65,66 where much larger training sets were used (see ESI Fig. S4‡ for learning curve). The high SRCC suggest that one can safely use the machine learning model to rank materials and do more expensive calculations on the top performing structures. This will drop the computational costs enormously as only 600 datapoints were used for training the model. The high accuracy of the machine learning model is denoted to the importance of pore geometry in the materials' function. Basically, the adsorption properties of porous materials are a function of their chemistry and pore geometry,67 and since the chemistry of the molecule is fixed in each of the CSP databases, the geometric similarity could sort out materials with respect to their function nicely.
3 Discussion
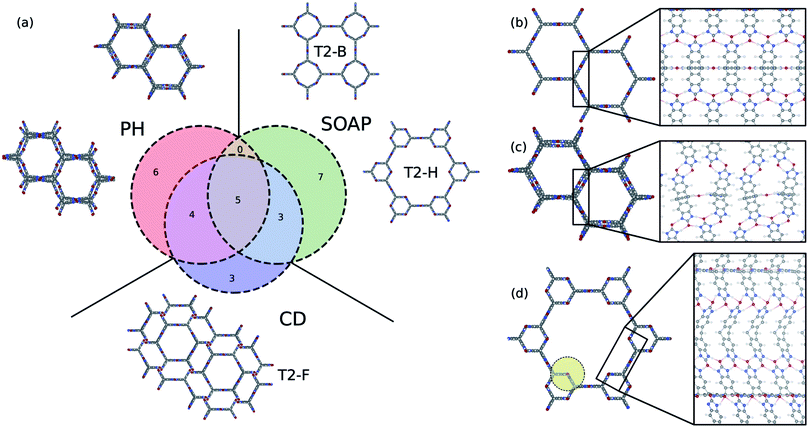
It is instructive to compare the persistent homology approach with other state-of-the-art materials descriptors for porous materials to shine some light on their differences, advantages, and limitations. A wide range of materials descriptors exist that can be used to study porous materials.68 Among them, smooth overlap of atomic positions (SOAP)69 has received special attention; it is widely used to describe atomic environments for machine learning inter-atomic potentials due to its powerful and rich material representation. Applying methods such as regularized entropy match (REMatch) or even simple averaging on the local SOAP descriptor allows the comparison of structures by quantifying their structural similarity.33,34,70 Here, in addition to the comparison with the SOAP method, we compare persistent homology with the conventional geometric descriptors, a four-dimensional vector of the crystal density, surface area, pore volume, and pore size, to further elucidate what is gained using the persistent homology approach.To compare the three methods, we identified the 15 structures from the T2 dataset that were most similar with T2-γ, based on each descriptor. A Venn diagram, which shows the overlap and differences of these sets of structures, is shown in Fig. 6a. All of the methods find the five structures in the dataset that are almost identical to T2-γ. However, each method focuses on different kind of structural similarities, which results in assigning very different structures as similar to the T2-γ (see the structures that are shown in the inset of Fig. 6a). The conventional descriptors (CD) find structures that have very similar pore size and surface area but do not necessarily have the same pore shape (Fig. 6a). By contrast, persistent homology (PH) focuses more on the overall shape of the pore; that is, materials with similar pore shape but slightly different pore sizes and surface areas. On the other hand, the SOAP method is focused more on the similarities of the local environments. For example, two of the packing classes of the T2 molecule that were distinguished using persistent homology (Fig. 4), namely T2-B and T2-H, are found among the most similar structures to T2-γ in SOAP descriptor space (Fig. 6a). In Fig. 6b–d, the local environment of the T2-γ is shown and compared with structures that were found by persistent homology and SOAP to be similar to T2-γ. Although the structure that was found similar by persistent homology has similar pore shape and packing, it has displaced layers of molecules and a broken hydrogen bonding network leading to a very different local environment (Fig. 6c). In contrast, the structure from the SOAP method—that is, the T2-H (Fig. 6d)—has very similar local environment to T2-γ. T2-H has two kind of hydrogen bonding network, one that is exactly the same as the T2-γ and another kind with a rotation around the rod axis. However, T2-H have a very different molecular packing. Indeed, using even a relatively large cutoff for the SOAP descriptors (8.0 Å, which is shown as a yellow circle in Fig. 6d) is not sufficient to capture the overall shape of the large pore of the structure.
This analysis shows that the different approaches and descriptors are encoding different kinds of structural similarities and can hence be seen complementary, and suitable for different applications. For example, SOAP is an elegant machinery to study the potential energy surface of the molecules. The persistent homology method is not sensitive enough to the subtle changes in atomic configurations to be able to map them to potential energy surface. On the other hand, for the cases where long-range distances are involved – for example, where the aim is to classify pore shapes and molecular packing – then we need higher-level descriptors that are invariant to exact lattice arrangement. For such purposes, persistent homology is a suitable choice for encoding geometric similarity.
4 Methods
4.1 Materials
The crystal structure prediction datasets of the molecules and the corresponding lattice energies and adsorption properties were extracted from previous study by Pulido et al.21,71 For each molecule, Pulido et al. initially optimised the molecules at the density functional level of theory with M06-2X exchange–correlation functional72 and 6-311G** basis set. The optimised geometry of each molecule was kept rigid and used for crystal structure generation by performing quasi-random sampling procedure of different symmetry space groups.27 The lattice energy of the generated crystals were minimised with an anisotropic atom–atom potential with specific atomic multipole description of the molecular charge distribution for electrostatic interactions using DMACRYS.73 See Pulido et al.21 for more details.4.2 Persistent barcodes and Voronoi decomposition of the space
We retrieved information of pore accessibility for each structure using Zeo++ (ref. 47) for a probe radius of 1.5 Å and then sampled accessible pores with a fixed number of points per unit accessible surface area. We constructed the Vietoris–Rips complex and generated zero-dimensional (0D), one-dimensional (1D) and two-dimensional (2D) persistence barcodes, up to a cut-off length of 8.0 Å using Ripser.48 To quantise pore shape similarity between two structures in the barcode space, we measured the pairwise distance, by a weighted combination of L2-landscape distance50,51 based on their persistence barcodes (eqn (1)). Λd=1 and Λd=2 are the L2-landscape distances for the first and second dimension of persistent barcodes, respectively.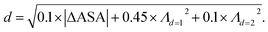 | (1) |
To perform Voronoi decomposition, we selected a set of landmark structures using MaxMin algorithm,53,75 which ensured all landmarks were distributed homogeneously in the entire barcode space. Then we assigned the remaining structures to their closest landmark structures. When applying MaxMin algorithm, we chose the first landmark structure at random, then for selecting a new landmark structure, we took the following steps:
(1) For each structure, calculate its distances to all present landmarks, find the maximal distance, recording as diMax, and the minimum distance, recording as diMin (i for the ith structure);
(2) The new landmark is the structure with the maximal value of diMin. We record the maximal value among all diMax and assigned the size of the barcode space as the Max(dMax) observed in all steps;
(3) Repeat the above steps until Max(dMin) is less than 10% of Max(dMax) to ensure the maximum distance between a structure to its corresponding landmark structure is less than 10% of the maximum pairwise distance in the barcode space (a representative for the size of the barcode space).
4.3 Visualising the pore geometry landscape
Multidimensional scaling (MDS) is a visualisation method based on the pairwise distances, similarity or dissimilarity in a set of objects in a high-dimensional space.55,76 Here, we used metric MDS using the pairwise distances between landmark structures computed using eqn (1). The MDS algorithm aims to preserve the relative distances between data points in the high dimensional space when the points are projected on a 2D plane. The metric for evaluating the consistency between the low dimensional representation and the high dimensional distances is called the stress function eqn (2). This function returns the residual sum of squares of the distances in the HD space to the LD space. The stress function was optimised by the stress majorisation algorithm, which is implemented in scikit-learn, a python machine learning package.77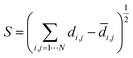 | (2) |
4.4 Machine learning
Kernel Ridge Regression (KRR), a regression model with l2-norm regularisation and kernel trick, was adapted from scikit-learn.77 The kernel distances between structures were determined using a combination of their distance in topological space (TS) and conventional geometric space (CS). The distances in TS were computed using persistent homology and eqn (1). The euclidean distances between the conventional geometric descriptors were used to compute the pairwise distances between structures in CS, using normalized values of largest included sphere, crystal density, void fraction, and accessible surface area. Two radial basis functions (RBF), Gaussian kernel, were used with two independent Gaussian width for the TS and CS. The pairwise distance between data points computed with:| K = λKTS(dTS,σTS) + (1 − λ)KCS(dCS,σCS), | (3) |
| KTS or CS(d,σ) = exp(−σd2). | (4) |
The model was trained using 600 training data using 10-fold cross validation and grid search to find the optimal Gaussian width for each kernel and the regularisation factor. The accuracy of model was found to be highest for λ equal to 0.5.
4.5 SOAP calculations
The SOAP descriptors for each atomic species in the crystal structure were computed with hyperparameters similar to the previous work on zeolites,70i.e., using 12 radial basis functions, 9 spherical harmonics, and Gaussians with width of 0.3. To compare structures we used the distance metric induced by adopting normalized kernel, either the regularized entropy match (REMatch)33 kernel or the average structural kernel. We compared the results for two cut-off of 8.0 and 6.0 Å. All these setting resulted in almost identical set of materials as the most similar structures to T2-γ. All the calculations were done using DScribe78 and atomic simulation environment (ASE)79 packages.5 Conclusions
We introduced a new representation of the structural landscapes for crystal structure prediction (CSP) datasets and energy–structure–function (ESF) maps of porous molecular crystals based on geometric similarity. We showed this technique has advantage over the typical 1-dimensional representation of the landscapes since it captures both local and global geometric similarity of the pore shapes of the materials. The structures that were identified manually in previous works due to their similar conventional descriptors are classified in different geometric classes in the new representation, allowing automatic identification of unique packing of molecules. Moreover, since the chemistry of the building molecules is fixed in a CSP database, this technique could reveal structure–function relationship for gas the adsorption applications of porous molecular crystals.We envision the geometric landscapes to be used to automatically explore CSP databases for finding materials with two features, namely unique packing and high performance. This technique allows exploring large CSP databases to find unique packings which could be subsequently tried to be synthesized experimentally. Besides, instead of performing brute force calculations of a large database of porous materials for a given adsorption application, one can prescreen the database to spot the good performing geometric classes and then do calculations only on those structures that are in an identified good performing geometric class. In this respect, we showed that machine learning could accelerate this procedure even further as geometric landscapes are physically meaningful and machine-understandable18,80 material representation for porous materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the NCCR MARVEL, funded by the Swiss National Science Foundation (SNSF). S. M. M. acknowledges support from SNSF under grant number P1ELP2_184404. H. X. was supported by a MARVEL INSPIRE Potentials Master's Fellowship. Computational resources were provided by the Swiss National Supercomputing Centre (CSCS) under project ID s888. A. I. C. and L. C. gratefully acknowledge the Leverhulme Trust via the Leverhulme Research Centre for Functional Materials Design for funding. S. M. M. thanks Dr Senja Barthel and Kevin M. Jablonka for useful discussions.References
- A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed.
- M. E. Davis, Nature, 2002, 417, 813 CrossRef CAS PubMed.
- T. Hasell and A. I. Cooper, Nat. Rev. Mater., 2016, 1, 16053 CrossRef CAS.
- J. Jones, T. Hasell, X. Wu, J. Bacsa, K. Jelfs, M. Schmidtmann, S. Chong, D. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. Day and A. Cooper, Nature, 2011, 474, 367–371 CrossRef CAS PubMed.
- A. I. Cooper, ACS Cent. Sci., 2017, 3, 544–553 CrossRef CAS PubMed.
- J. Tian, P. K. Thallapally, S. J. Dalgarno, P. B. McGrail and J. L. Atwood, Angew. Chem., Int. Ed., 2009, 48, 5492–5495 CrossRef CAS PubMed.
- G. Zhang, O. Presly, F. White, I. M. Oppel and M. Mastalerz, Angew. Chem., Int. Ed., 2014, 53, 1516–1520 CrossRef CAS PubMed.
- M. Liu, L. Zhang, M. A. Little, V. Kapil, M. Ceriotti, S. Yang, L. Ding, D. L. Holden, R. Balderas-Xicohténcatl, D. He, R. Clowes, S. Y. Chong, G. Schütz, L. Chen, M. Hirscher and A. I. Cooper, Science, 2019, 366, 613–620 CrossRef CAS PubMed.
- L. Chen, P. Reiss, S. Chong, D. Holden, K. Jelfs, T. Hasell, M. Little, A. Kewley, M. Briggs, A. Stephenson, K. Thomas, J. Armstrong, J. Bell, J. Busto, R. Noel, J. Liu, D. Strachan, P. Thallapally and A. Cooper, Nat. Mater., 2014, 13, 954–960 CrossRef CAS PubMed.
- T. Mitra, K. E. Jelfs, M. Schmidtmann, A. Ahmed, S. Y. Chong, D. J. Adams and A. I. Cooper, Nat. Chem., 2013, 5, 276 CrossRef CAS.
- A. Aspuru-Guzik, R. Lindh and M. Reiher, ACS Cent. Sci., 2018, 4, 144–152 CrossRef CAS PubMed.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351(6280), aad3000 CrossRef PubMed.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323 CrossRef CAS PubMed.
- B. Smit and T. L. Maesen, Chem. Rev., 2008, 108, 4125–4184 CrossRef CAS PubMed.
- P. G. Boyd, Y. Lee and B. Smit, Nat. Rev. Mater., 2017, 2, 17037 CrossRef CAS.
- L.-C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem, M. Haranczyk and B. Smit, Nat. Mater., 2012, 11(7), 633–641 CrossRef CAS PubMed.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Energy Environ. Sci., 2016, 9, 3279–3289 RSC.
- L. Turcani, R. L. Greenaway and K. E. Jelfs, Chem. Mater., 2018, 31, 714–727 CrossRef.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gladysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- V. Santolini, M. Miklitz, E. Berardo and K. E. Jelfs, Nanoscale, 2017, 9, 5280–5298 RSC.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543(7647), 657–664 CrossRef CAS PubMed.
- M. Mastalerz and I. M. Oppel, Angew. Chem., Int. Ed., 2012, 51, 5252–5255 CrossRef CAS PubMed.
- O. D. Friedrichs, A. W. Dress, D. H. Huson, J. Klinowski and A. L. Mackay, Nature, 1999, 400, 644–647 CrossRef CAS.
- A. Simperler, M. D. Foster, O. Delgado Friedrichs, R. G. Bell, F. A. Almeida Paz and J. Klinowski, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 263–279 CrossRef PubMed.
- M. D. Foster, O. Delgado Friedrichs, R. G. Bell, F. A. Almeida Paz and J. Klinowski, Angew. Chem., Int. Ed., 2003, 42, 3896–3899 CrossRef CAS PubMed.
- S. Kim, A. M. Orendt, M. B. Ferraro and J. C. Facelli, J. Comput. Chem., 2009, 30, 1973–1985 CrossRef CAS PubMed.
- D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910–924 CrossRef CAS PubMed.
- S. L. Price, Phys. Chem. Chem. Phys., 2008, 10, 1996–2009 RSC.
- E. O. Pyzer-Knapp, H. P. Thompson, F. Schiffmann, K. E. Jelfs, S. Y. Chong, M. A. Little, A. I. Cooper and G. M. Day, Chem. Sci., 2014, 5, 2235–2245 RSC.
- S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- P. M. Piaggi, PhD thesis, École Polytechnique Fédérale de Lausanne (EPFL), 2019.
- P. M. Piaggi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10251–10256 CrossRef CAS PubMed.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Chem. Sci., 2018, 9, 1289–1300 RSC.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, Nat. Commun., 2017, 8, 15396 CrossRef CAS PubMed.
- D. Schwalbe-Koda, Z. Jensen, E. Olivetti and R. Gómez-Bombarelli, Nat. Mater., 2019, 18, 1177–1181 CrossRef CAS PubMed.
- H. Edelsbrunner and J. Harer, Computational topology: an introduction, American Mathematical Soc., 2010 Search PubMed.
- H. Edelsbrunner and J. Harer, Contemporary mathematics, 2008, vol. 453, pp. 257–282 Search PubMed.
- F. Chazal and B. Michel, arXiv preprint arXiv:1710.04019, 2017.
- H. Edelsbrunner, D. Letscher and A. Zomorodian, Proceedings. 41st Annual Symposium on Foundations of Computer Science, 2000, pp. 454–463 Search PubMed.
- A. Zomorodian and G. Carlsson, Discrete Comput. Geom., 2005, 33, 249–274 CrossRef.
- M. Saadatfar, H. Takeuchi, V. Robins, N. Francois and Y. Hiraoka, Nat. Commun., 2017, 8, 15082 CrossRef CAS PubMed.
- Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue and Y. Nishiura, Proc. Natl. Acad. Sci. U. S. A., 2016, 201520877 Search PubMed.
- W. Xu, D. Zhang, P. Lan and Y. Jiao, Int. J. Mech. Sci., 2019, 150, 610–616 CrossRef.
- L. Duponchel, J. Spectr. Imaging, 2018, 7, a1 Search PubMed.
- R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2011, 52, 308–318 CrossRef PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- U. Bauer, Ripser, http://ripser.org, accessed: 2017-08-01 Search PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, J. Chem. Theory Comput., 2018, 14, 4427–4437 CrossRef CAS PubMed.
- P. Bubenik, J. Mach. Learn. Res., 2015, 16, 77–102 Search PubMed.
- P. Bubenik and P. Dłotko, J. Symb. Comput., 2017, 78, 91–114 CrossRef.
- N. Otter, M. A. Porter, U. Tillmann, P. Grindrod and H. A. Harrington, EPJ Data Science, 2017, 6, 17 CrossRef PubMed.
- V. De Silva and J. B. Tenenbaum, Sparse multidimensional scaling using landmark points, technical report, Stanford University, 2004 Search PubMed.
- N. Brown, in Silico Medicinal Chemistry: Computational Methods to Support Drug Design, Royal Society of Chemistry, 2015 Search PubMed.
- I. Borg and P. Groenen, J. Educ. Meas., 2003, 40, 277–280 CrossRef.
- M. K. Dudek and G. M. Day, CrystEngComm, 2019, 21, 2067–2079 RSC.
- D. P. McMahon, A. Stephenson, S. Y. Chong, M. A. Little, J. T. Jones, A. I. Cooper and G. M. Day, Faraday Discuss., 2018, 211, 383–399 RSC.
- T. A. Makal, J.-R. Li, W. Lu and H.-C. Zhou, Chem. Soc. Rev., 2012, 41, 7761–7779 RSC.
- R. W. Howarth, R. Santoro and A. Ingraffea, Clim. Change, 2011, 106, 679 CrossRef CAS.
- M. Fernandez, T. K. Woo, C. E. Wilmer and R. Q. Snurr, J. Phys. Chem. C, 2013, 117, 7681–7689 CrossRef CAS.
- G. Kusano, K. Fukumizu and Y. Hiraoka, J. Mach. Learn. Res., 2017, 18, 6947–6987 Search PubMed.
- C. S. Pun, K. Xia and S. X. Lee, arXiv preprint arXiv:1811.00252, 2018.
- X. Zhang, J. Cui, K. Zhang, J. Wu and Y. Lee, J. Chem. Inf. Model., 2019, 59, 4636–4644 CrossRef CAS PubMed.
- G. James, D. Witten, T. Hastie and R. Tibshirani, An introduction to statistical learning, Springer, 2013, vol. 112 Search PubMed.
- M. Pardakhti, E. Moharreri, D. Wanik, S. L. Suib and R. Srivastava, ACS Comb. Sci., 2017, 19, 640–645 CrossRef CAS PubMed.
- G. S. Fanourgakis, K. Gkagkas, E. Tylianakis, E. Klontzas and G. E. Froudakis, J. Phys. Chem. A, 2019, 6080–6087 CrossRef CAS PubMed.
- T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683–2689 CrossRef PubMed.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, arXiv preprint arXiv:2001.06728, 2020.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- B. A. Helfrecht, R. Semino, G. Pireddu, S. M. Auerbach and M. Ceriotti, J. Chem. Phys., 2019, 151, 154112 CrossRef PubMed.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Additional Computational data (related to “Functional materials discovery using energy–structure–function maps” manuscript), http://eprints.soton.ac.uk/404749/, accessed: 2018-1-1 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- S. L. Price, M. Leslie, G. W. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- D. Ongari, P. G. Boyd, S. Barthel, M. Witman, M. Haranczyk and B. Smit, Langmuir, 2017, 33, 14529–14538 CrossRef CAS PubMed.
- S. M. Moosavi, A. Chidambaram, L. Talirz, M. Haranczyk, K. C. Stylianou and B. Smit, Nat. Commun., 2019, 10, 539 CrossRef CAS PubMed.
- J. D. Carroll and P. Arabie, Annu. Rev. Psychol., 1980, 31, 607–649 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. Sturluson, M. T. Huynh, A. H. York and C. M. Simon, ACS Cent. Sci., 2018, 4, 1663–1676 CrossRef CAS PubMed.
Footnotes |
| † The barcodes, geometric properties and data for all geometric classes are available in “Materials Cloud” viahttps://doi.org/10.24435/materialscloud:2019.0083/v1. |
| ‡ Electronic supplementary information (ESI) available: Geometric landscapes of the molecules and learning curve. See DOI: 10.1039/d0sc00049c |
| § These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |