TinyPols: a family of water-soluble binitroxides tailored for dynamic nuclear polarization enhanced NMR spectroscopy at 18.8 and 21.1 T

Abstract

Dynamic Nuclear Polarization (DNP) has recently emerged as a key method to increase the sensitivity of solid-state NMR spectroscopy under Magic Angle Spinning (MAS). While efficient binitroxide polarizing agents such as AMUPol have been developed for MAS DNP NMR at magnetic fields up to 9.4 T, their performance drops rapidly at higher fields due to the unfavorable field dependence of the cross-effect (CE) mechanism and AMUPol-like radicals were so far disregarded in the context of the development of polarizing agents for very high-field DNP. Here, we introduce a new family of water-soluble binitroxides, dubbed TinyPols, which have a three-bond non-conjugated flexible amine linker allowing sizable couplings between the two unpaired electrons. We show that this adjustment of the linker is crucial and leads to unexpectedly high DNP enhancement factors at 18.8 T and 21.1 T: an improvement of about a factor 2 compared to AMUPol is reported for spinning frequencies ranging from 5 to 40 kHz, with ε_H of up to 90 at 18.8 T and 38 at 21.1 T for the best radical in this series, which are the highest MAS DNP enhancements measured so far in aqueous solutions at these magnetic fields. This work not only breathes a new momentum into the design of binitroxides tailored towards high magnetic fields, but also is expected to push the application frontiers of high-resolution DNP MAS NMR, as demonstrated here on a hybrid mesostructured silica material.

---

Introduction

Over the last two decades, Dynamic Nuclear Polarization (DNP) has developed into an elegant and efficient approach to circumvent the sensitivity limitations of solid-state magic angle spinning (MAS) NMR spectroscopy, opening unprecedented analytical opportunities in materials and life sciences.^1–4 In addition to rapid technological advances in microwave sources and cryogenic probe heads, the introduction of increasingly efficient polarizing agents over the years, from stable free organic radicals⁵ to high spin metal ions,^6–8 has been one of the key factors that contributed to the growing success of modern MAS DNP NMR.

A major milestone was achieved in the early 2000s with the introduction of nitroxide biradicals that provided improved DNP performances over monomeric paramagnetic centres due to relatively strong couplings (∼30 MHz for the dipolar interaction in TOTAPOL⁹) between unpaired electrons being spatially constrained by linkers.^9,10 This magnetic coupling was shown to be essential to achieve efficient electron to nucleus polarization transfer by cross-effect (CE), a mechanism which is particularly operative at high magnetic field. Since then, binitroxides have been extensively studied at 9.4 T and their structure improved by adjusting the length and rigidity of the organic tether to optimize the electron–electron (e–e) coupling and/or the relative orientation of their g-tensors, or by fine tuning their functional groups to modulate their electron relaxation times and/or their solubility.^11–19 This has led to very efficient polarizing agents such as AMUPol¹² or TEKPol¹⁷ that provide enhancement factors of over 250 at 9.4 T and 100 K in variety of glassy matrices. Most applications of DNP MAS NMR are undertaken using these biradicals that remain today the gold standard polarizing agents for hyperpolarized solid-state NMR spectroscopy.

However, the performance of these radicals significantly decreases with increasing magnetic fields. Thus, in a 3.2 mm rotor, the proton enhancement (ε_H) of a frozen solution of 10 mM AMUPol in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) typically drops from 250 at 9.4 T (400 MHz proton frequency) to about 140 at 14.1 T (600 MHz),¹² 48 at 18.8 T (800 MHz) and 20 at 21.1 T (900 MHz, this work). This decrease in enhancement factor is in line with theoretical analysis of CE DNP under MAS, predicting that the probability for three-spin (electron e1–electron e2–nucleus n) crossings driving the DNP polarization transfer when |ω_e1 − ω_e2| = ω_n is fulfilled scales with 1/B₀³.^20,21 The downward field dependence of the whole DNP process is also well reproduced by numerical simulations.^21–24 Several approaches have recently been developed to overcome this unfavorable field dependence.

One solution to achieve high enhancements at very high magnetic fields is to exploit the favorable field dependence of Overhauser Effect (OE) DNP. This mechanism has recently received renewed attention after the discovery that it was active in insulating solids using BDPA (1,3-bisdiphenylene-2-phenylallyl) radicals.^25,26 Enhancements of up to 100 and 70 have been reported in the rigid glassy solvent OTP (ortho-terphenyl), at 18.8 T²⁷ and 21.1 T.²⁸ Magnetization transfer via OE DNP requires however build-up times of several tens of seconds, which partly moderates the overall sensitivity gain. Hybrid biradicals, consisting of a radical with an isotropic g factor tethered to a broad line nitroxide have recently been explored as an alternative strategy to preserve high enhancements at high magnetic field.^29–33 TEMTriPol^29,30 and HyTEiK³² biradicals linking together a nitroxide with a trityl or a BDPA moiety respectively were developed along these lines, yielding enhancement factors at 18.8 T of up to 70 for TEMTriPol in 3.2 mm rotors and 180 for HyTEK2 in 1.3 mm rotors. In both cases, it was observed that these enhancement factors did not decrease with the magnetic field in the same way as is the case for binitroxides, which was rationalized by the presence of a narrow line component for one of the two electrons, associated with strong electron–electron interactions, i.e. strong exchange (J) and dipolar (D) couplings. Dipolar and exchange coupling values of (D = 23 MHz, |J| = 73 MHz) and (D = 28 MHz, 30 < |J| < 70 MHz) were reported for the best performing radicals in the TEMTriPol^29,30 and HyTEK³² series.

While both interactions drive the DNP transfer and contribute to its efficiency, their strength cannot be increased indefinitely. Indeed, the sum of the dipolar and exchange couplings needs to remain smaller than the nuclear Larmor frequency so as to fulfill the CE matching condition. This limitation has been understood since the early days of binitroxide radicals, and at that time, linker lengths and therefore dipolar couplings were optimized to achieve efficient CE DNP transfer at moderate magnetic fields.^10–34 For hybrid TEMTriPols and HyTEKs, it has been shown that a linker length of respectively six and four chemical bonds represented an optimal separation for DNP at 18.8 T, while shorter distances led to lower DNP gains at this field. The detrimental effect of exceedingly strong exchange couplings has also been recently illustrated for diastereoisomers of L-proline-linked trityl-nitroxide biradicals.³⁷ Lately, De Paepe and co-workers have shown that asymmetric biradicals composed of 5 and 6-membered ring nitroxides that have sizeable electron–electron interactions (on the order of 50–70 MHz for both the dipolar and exchange interactions) had advantageous DNP properties. The authors reported DNP gains higher than AMUPOL at 18.8 T, namely ε_H of 27 for the AsymPolPOK radical versus 21 for AMUPol at ∼130 K and 8 kHz MAS rate using 3.2 mm rotors.³⁸

Another adverse feature of AMUPol and TEKPol is the presence of strong depolarization effects^39,40 that manifest themselves as a decrease of the overall contribution of the nuclei to the NMR signal intensity, including in the absence of microwave irradiation. These depolarization effects add up to paramagnetic bleaching and become stronger with faster spinning.^40,41 Numerical studies predict that increasing the probability of adiabatic electron–electron crossings, which can be done by raising their reciprocal magnetic interactions, can attenuate nuclear depolarization.^21–23 It has indeed been experimentally demonstrated that TEMTriPol-1,³⁰ HyTEK2,³² or AsymPolPOK³⁸ radicals, having large J interactions, display reduced or no depolarization losses.

Here, we revisit the structure of six-membered nitroxide ring biradicals and introduce new water-soluble binitroxides, dubbed TinyPols. We show that by reducing the distance between the two unpaired electrons, the unfavorable field dependence is significantly reduced as compared to AMUPol. With the best radical in this series, M-TinyPol, we record DNP enhancement factors as high as 90 and 38 at respectively 18.8 T and 21.1 T in aqueous solutions. As EPR measurements reveal similar J exchange interaction and electron relaxation times for TinyPols and AMUPol, the good performance of TinyPols at high magnetic field is attributed to the effect of a stronger dipolar coupling between the two unpaired electrons. The potential of these radicals is illustrated with the surface structure characterization of a functionalized hybrid silica material.

Results and discussion

TinyPol structures

Recent radical design studies highlighted the critical role of electron–electron couplings in achieving high enhancements at magnetic fields above 9.4 T. In particular, the ratio between ω_H and D + |J| modulates the efficiency of the CE mechanism and the electron–electron distance has to be tailored to the proton Larmor frequency. This has led us to explore binitroxide radicals having a shortened linker length than AMUPol.

Fig. 1 shows the structure of the TinyPol radicals that have been investigated in this study. They all have the same generic chemical structure with a three-bond non-conjugated amine linker and tetrahydropyranyl, methyl-tetrahydropyranyl or cyclohexanol spiranic groups at the α position of the nitroxide moieties. The average distance between the two free electrons (e–e) in TinyPols is estimated to be ca. 10.4 Å, versus 11.6 Å in AMUPol.¹² This distance was evaluated from molecular dynamics simulations from an ensemble of conformations for the TinyPol radical obtained via molecular dynamics simulations (Fig. S11†). The dipolar coupling between the two unpaired electrons was then be calculated with a point dipolar approximation, using the average 〈 1/r³〉 from the molecular dynamics simulation (Fig. S12†), giving 47 MHz for TinyPol, versus 33 MHz for AMUPol. While the reduced distance between the electrons leads to an increase in the magnetic dipolar coupling in the TinyPols, their isotropic J coupling, as defined by the term −JS₁S₂, is expected to be similar to the AMUPol value, i.e. J ≈ −30 MHz. The bulky tetrahydropyranyl, methyl-tetrahydropyranyl and cyclohexanol nitroxide moieties have been chosen in order to preserve long electronic relaxation times as found for PyPol derivatives.^12–14

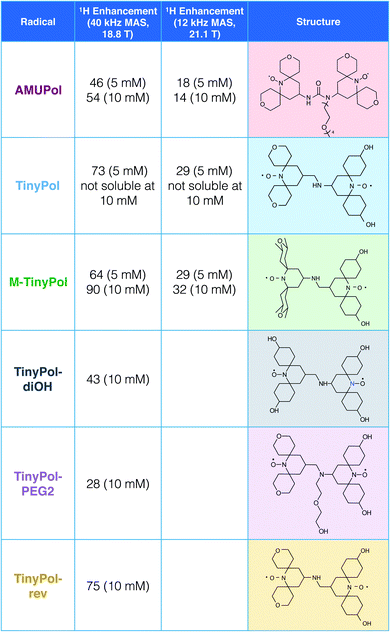Fig. 1 Structures and names of the radicals investigated in this study. Synthetic routes are given in the ESI.† The proton enhancement factors measured in bulk solution of d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) at 18.8 T and 40 kHz MAS frequency are reported at a concentration of 5 and/or 10 mM. The sample temperature has been carefully calibrated at 110 ± 5 K. Experimental details are given in the ESI.†

DNP enhancement factors

The MAS-DNP performance of TinyPols was first measured at 18.8 T for all the radicals in the series and compared with that of AMUPol in water/glycerol solutions. The proton enhancement factors (recorded at a spinning frequency of 40 kHz) are reported in Fig. 1. Apart from TinyPol, they were all measured at a radical concentration of 10 mM, which was found to be optimal (see below). The TinyPol enhancement was measured at 5 mM as this radical could not be solubilized at a higher concentration. M-TinyPol, the best radical in this series, as well as AMUPol, the reference polarizing agent, were both measured at 5 and 10 mM concentration. The enhancements reported here are calculated as the ratio between signal intensity with and without microwave irradiation. While TinyPol–diOH and TinyPol–PEG2 yield modest enhancement values, the three other radicals in the series, namely TinyPol, TinyPol–rev and M-TinyPol, clearly outperform AMUPOL at 18.8 T. At radical concentrations of 5 and 10 mM, the best enhancement factors are obtained with respectively TinyPol (73 versus 46 for AMUPol) and M-TinyPol (90 versus 54 for AMUPol). Given the results of this rapid screening, we focused our investigation on TinyPol and M-TinyPol. In the following we will report detailed measurements conducted at 18.8 and 21.1 T for these two new and highly efficient polarizing agents.

Fig. 2a shows the DNP enhancement factors of 5 mM TinyPol, M-TinyPol and AMUPol solutions in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) at 18.8 T as a function of the MAS frequency. The enhancement curve of AMUPOL is relatively flat over the whole spinning range, reaching a value of 46 at 40 kHz MAS. For both TinyPol and M-TinyPol, we observe a maximum enhancement of 87 and 74 respectively at a spinning frequency of 5 kHz. This enhancement then displays a marked decrease between 5 and 25 kHz, and reaches a plateau at about 73 and 64 at a MAS rate of 40 kHz. At 5 mM biradical concentration TinyPol shows the best enhancement, corresponding to an improvement of around 1.6 with respect to the current standard binitroxide radical AMUPol. While, as mentioned above, TinyPol could not be solubilized at a higher concentration than 5 mM, a concentration series could be measured for M-TinyPol from 5 to 20 mM (Fig. S15†) and a radical concentration of 10 mM was determined to yield the largest DNP enhancement. The corresponding MAS curve measured at 18.8 T is shown in Fig. 2b and compared to values obtained for AMUPol at the same experimental conditions. At a MAS rate of 40 kHz, an enhancement factor of 90 was obtained for 10 mM M-TinyPol, corresponding to an increase by a factor 1.7 when compared to AMUPol. We note in passing that this enhancement is the largest enhancement factor measured for a water-soluble polarizing agent at this magnetic field.

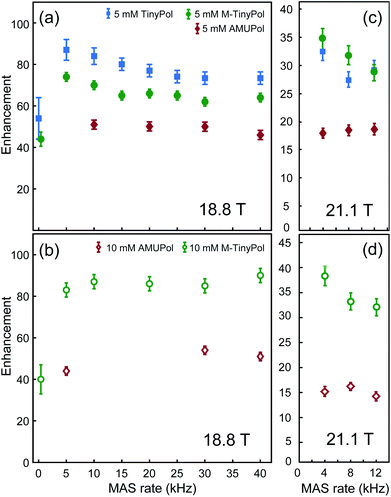Fig. 2 Enhancement factors of AMUPol, TinyPol and M-TinyPol at 5 mM (a and c) and 10 mM (b and d) concentration, measured in bulk solution of d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v), as a function of MAS frequency. ¹H enhancements values measured at 18.8 T (a and b) were obtained from proton NMR spectra, measured in 1.3 mm zirconia rotors at a sample temperature of 110 ± 5 K. ¹H enhancements measured at 21.1 T (c and d) were obtained from carbon-13 cross-polarization spectra, measured in 3.2 mm sapphire rotors at a sample temperature of 115 ± 7 K. Experimental details are given in the ESI.†

The same study has been performed at 21.1 T using a 3.2 mm probe. The data reported in Fig. 2c and d show that TinyPol radicals consistently outperform AMUPol. A maximum enhancement factor of 38 is achieved for M-TinyPol at a concentration of 10 mM and at a spinning frequency of 4 kHz, corresponding to an increase by a factor 2.5 when compared to AMUPol. We attribute this increase in enhancement for TinyPols over AMUPol to increased electron–electron magnetic couplings due to the shorter distance between the two electrons, as evidenced by the electron paramagnetic measurements discussed below. Here we note that the enhancement factors reported here for TinyPols in water solutions are lower than those obtained with the hybrid radicals HyTEKs in organic solvents (up to 180 for HyTEK2 at 40 kHz MAS) (ref).

Contribution factor and overall sensitivity of TinyPol and M-TinyPol

The improvement in enhancement observed from the TinyPol series is very promising. However, as highlighted in the introduction, DNP formulations with binitroxides may be subject to significant signal loss due to the well-documented depolarization effects that accentuate with increasing spinning frequencies. In these conditions the DNP enhancement factor alone is not a realistic indicator of the overall sensitivity gain. For 10 mM AMUPol in glycerol-d₈/D₂O/H₂O, 60 : 30 : 10 (v/v/v), we recently reported that depolarization leads to a continuous signal attenuation which reaches around 50% at 40 kHz MAS and 18.8 T.⁴¹ In the following we consider this effect in order to evaluate the overall sensitivity gain provided by TinyPol radicals. Contribution factors were measured for both TinyPol and M-TinyPol at concentrations of 5 and 10 mM, respectively. These factors were calculated as the ratio of the NMR signal intensity (per unit of mass) of a doped frozen solution divided by the NMR signal intensity (per unit of mass) of the undoped solution, both measured in the absence of microwave irradiations (see eqn (1) in the ESI†). Thus, they report on the ensemble of paramagnetic effects that will lead to a signal loss from the introduction of the radical in the DNP formulation, including depolarization and paramagnetic bleaching effects.

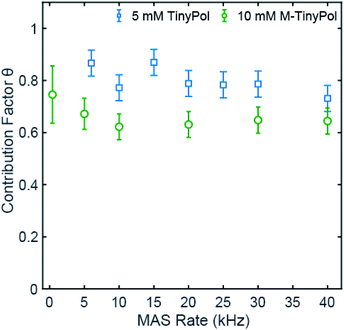
Fig. 3 shows the contribution factor of 5 mM TinyPol and 10 mM M-TinyPol solutions in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) at 18.8 T. For the 5 mM concentration, we observed only a small reduction of the contribution factor over the spinning range and measured a value of 0.73 at 40 kHz MAS that compares with 0.65 for AMUPol measured in this work under the same experimental conditions, using a radical concentration of 5 mM. At a concentration of 10 mM, no appreciable decrease is evident in the 5 to 40 kHz regime, with an average factor of around 0.65. This represents an improvement with respect to AMUPol at this concentration,^40,41 which in turn leads to a significant increase in the overall sensitivity as described below. We note that, as expected, the average value of the contribution factor is lower at a concentration of 10 mM due to enhanced paramagnetic bleaching, while the MAS dependence of the contribution factor suggests that the depolarization effects are quite modest. The reduced depolarization observed for TinyPol radicals is attributed to the strong value of dipolar coupling between the two unpaired electrons, which promotes adiabatic electron–electron spin-exchange crossing events upon MAS, thus limiting the equilibration of polarization between the two electrons.

Fig. 3 Contribution factor of TinyPol (5 mM) and M-TinyPol (10 mM) measured at 18.8 T in a bulk solution of d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v), as a function of MAS frequency. Values are obtained from proton NMR spectra recorded in 1.3 mm zirconia rotors at a sample temperature of 110 ± 5 K.

With the knowledge of the contribution factor and enhancement, we compare in Table 1 the overall DNP sensitivity gain Σ provided by TinyPol, M-TinyPol and AMUPol. This overall sensitivity gain is proportional to the product of the enhancement factor, the contribution factor, and the inverse of the square root of the DNP build-up time (see eqn (2) in the ESI†). The dependence of the DNP build-up times on the MAS frequency is reported in Fig. S16, S17 (18.8 T) and S23, S24 (9.4 T).†

Table 1 Overall sensitivity gains and DNP build-up times of radical solutions in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) for various magnetic fields and concentrations

	9.4 T		18.8 T				21.1 T
MAS rate sample temp.	40 kHz, 110 K		5 kHz, 110 K		40 kHz, 110 K		12 kHz, 115 K
	Σ	T B,ON (s)	Σ	T B,ON (s)	Σ	T B,ON (s)	Σ	T B,ON (s)
a The calculation is done using the contribution factors reported in ref. 41. b The calculation is done using the contribution factor measured for 5 mM AMUPol and 5 mM TinyPol respectively. c The calculation is done using the contribution factor measured for 5 mM AMUPol and 5 mM TinyPol respectively.
5 mM AMUPol	346	7.1	107	15	85	18	29	14.4
5 mM TinyPol	179	11	255	13	158	16	44	13.3
10 mM AMUPol	316	3.8	134	5.0	82^a	10	15^b	10.7
10 mM M-TinyPol	225	4.8	261	8.7	211	13	29^c	7.7

---

These calculations confirm the excellent overall DNP efficiency of TinyPol radicals at magnetic fields of 18.8 T and 21.1 T. In particular M-TinyPol provides an improvement of a factor 2.5 in overall sensitivity gain with respect to AMUPol at 18.8 and 21.1 T (Table 1). Note that we also provide in Fig. S27† a calculation of Boltzmann enhancement factor ε_B for 5 mM TinyPol in a 2 M ¹³C-urea, d₈-glycerol/D₂O/H₂O solution as a function of the MAS frequency in the experimental conditions reported for AsymPolPOK in ref. 38. Under this sample formulation, TinyPol maintains large signal enhancements that are greater than those reported for AsymPolPOK.

Magnetic field dependence of the DNP enhancement

Fig. 4a compares the DNP enhancement (ε_H) provided by AMUPol and TinyPol radicals at 9.4, 18.8 and 21.1 T at both 5 and 10 mM concentrations. We note first that all radicals show a sharp decrease in enhancement when the magnetic field is increased as predicted and experimentally observed for CE DNP with binitroxides. However, this negative field dependence is clearly mitigated for the TinyPol radicals. Thus, at a concentration of 5 mM of TinyPol, the enhancement drops by around 68% when magnetic field is doubled, versus 85% for AMUPol under the same experimental conditions. Similar trends were observed for M-TinyPol at concentrations of 5 and 10 mM. At 9.4 T AMUPol performs significantly better than TinyPol radicals. This trend holds true when overall sensitivity gains S are plotted vs. the magnetic field (Fig. 4b). The benefits of TinyPols at high fields are even more visible in this representation. These observations are in line with the general assumption that there is an optimum value of the electron–electron coupling for efficient DNP transfer that will differ at each magnetic field strength. Here the relatively strong electron–electron dipolar coupling in TinyPols (47 versus 33 MHz for AMUPol) promotes an efficient CE polarization transfer at very high field.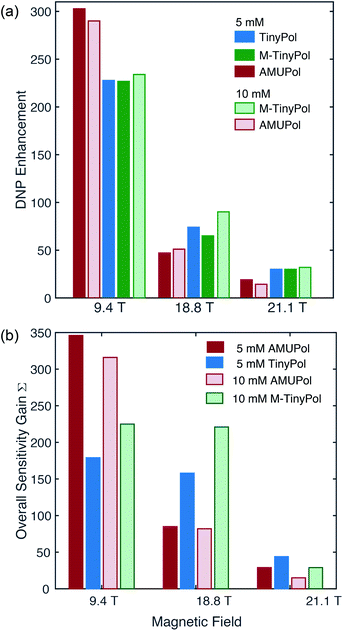

Fig. 4 DNP enhancement factors (a) and overall sensitivity gains (b) of 5 mM and 10 mM TinyPol, M-TinyPol and AMUPol solutions in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) acquired at various magnetic fields. Data recorded at 9.4 T and 18.8 T were acquired in 1.3 mm zirconia rotors at 40 kHz MAS frequency and a sample temperature of ∼110 K. Data recorded at 21.1 T were acquired in 3.2 mm sapphire rotors at 12 kHz MAS frequency and a sample temperature of ∼115 K. The calculation of Σ is given in the ESI.†

Electron spin couplings and relaxation times

Fig. 5a shows the W-band (95 GHz) echo-detected EPR spectra of AMUPol, TinyPol and M-TinyPol radicals recorded at 100 K. The spin lattice relaxation times (T_ir) and the electronic phase memory times (T_M) measured at different field values of the EPR pattern are reported in Fig. 5b and c. The bulky functional groups decorating the nitroxide moieties lead to similar T_ir values for all radicals, ranging between roughly 0.2 and 0.5 ms. The T_M values vary with T_M(AMUPol) > T_M(TinyPol) > T_M(M-TinyPol). The lowest T_m values are observed for M-TinyPol as expected due to the presence of the methyl groups that still undergo rotation at 100 K and induce transverse relaxation. The T_m values are however of the same order of magnitude for the three radicals. Therefore, the electron saturation factor is expected to be fairly similar for the three radicals, and is not the discriminating parameter explaining their different performances. These EPR studies therefore indirectly point out that the main difference between TinyPol radicals and AMUPol reside in their magnetic dipolar coupling strength.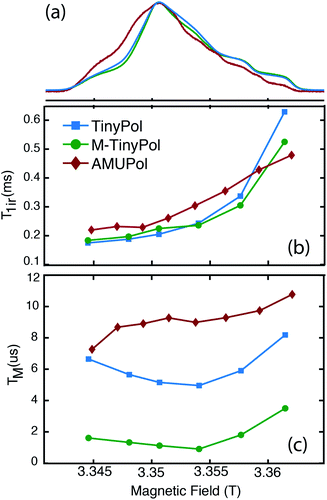

Fig. 5 (Top) W-band (∼94 GHz) echo-detected EPR spectra of 100 μM TinyPol, M-TinyPol and AMUPol solutions in d₈-glycerol/D₂O/H₂O 60/30/10 (v/v/v) recorded at 100 K. (Middle) Electron spin lattice relaxation time (T_1e) and (bottom) electron phase memory time (T_m) measured at various position of the magnetic field. See ESI for Experimental details.†

The solution-state X-band (9.4 GHz) continuous-wave (CW) EPR spectra of the TinyPol radicals are reported in Fig. S25.† They display relatively broad features indicating a modulation of the J coupling by intramolecular motions. As highlighted by Griffin and co-workers⁴² and more recently by Han and co-workers,⁴³ conformational dynamics is the source of the distribution of J coupling in binitroxide polarizing agents. In TinyPols the short linker between the two nitroxide moieties is flexible with internal rotation around the N–CH₂ bond and leads to distribution of rotamers. Molecular dynamics conformational searches were performed for TinyPol, using the AMBER force field in Gromacs (Fig. S11†). The result shows a distribution of electron–electron distances and angles between the two nitroxide groups (Fig. S12 and S13†), with a high occurrence of conformers having an inter-electron distance of around 1 nm, and a relative nitroxide plane orientation in the range of [0, 30°] or [90, 130°]. This translates in a distribution of calculated isotropic J values (Fig. S14†). The solution EPR spectra were thus fitted using three isotropic exchange couplings of different weights (as detailed in Fig. S28,† a three-component fit was needed to reproduce the features of the experimental spectra). With the notable exception of TinyPol–PEG2, three values centred roughly around 0, 30 and 120 MHz were found for all TinyPol radicals (Table S1†).

The differences in the patterns of the EPR spectra among the TinyPols and subsequently in the distribution of exchange coupling values could partly explain the discrepancies in enhancement factors observed within the series (Fig. 1). In particular, we note that the EPR spectrum of TinyPol–PEG2 was fitted using only two J coupling values at around 0 and 120 MHz. This is in contrast with the other radicals that display in addition a contribution at around 30 MHz. This strength of coupling will be particularly effective at high magnetic field.³⁰ The fact that we don't detect this component for TinyPol–PEG2 likely explains the poor DNP performance of this radical. Here we note that the distribution of conformations observed in solution (and therefore of J coupling values) will change at cryogenic temperatures, in a way that will depend on the freezing history of the sample. While the EPR data recorded at room temperature should thus be interpreted with care, they nevertheless provide a useful insight into the range of accessible J coupling for a given polarizing agent.

As mentioned in the introduction, several studies have recently highlighted the importance of sizeable magnetic interactions for efficient DNP at high magnetic field. The significant improvement in DNP performance observed for TinyPol radicals over AMUPol can be rationalized through the theoretical picture developed by Thurber and Tycko²⁰ and later by Mentink-Vigier et al.,²¹ describing cross-effect DNP under MAS as a carousel of separate rotor crossing events that generate spin transitions at avoided energy level crossings. Three avoided crossing drive the DNP magnetization transfer: (i) electron-microwave crossing, when the electron EPR frequency matches the microwave frequency, (ii) three-spin crossing, when the difference of the two electron Larmor frequencies is equal to the nuclear Larmor frequency and (iii) electron–electron crossing when the two electron Larmor frequencies match each other. Analytical calculations under the Landau-Zener theoretical framework show that the probability for the three-spin adiabatic level crossing is proportional to the square of the overall magnetic coupling between the two unpaired electrons in the biradical. As a direct result, increasing the electron–electron dipolar coupling strength—as has been done for TinyPol radicals in comparison with AMUPol—is expected to increase the probability of this three-spin crossing and subsequently the polarization transfer from the electrons to the nuclear spin. Similarly, increased magnetic interactions between electrons favour high adiabaticity at electron–electron crossing and therefore the exchange of polarization. Such an exchange is beneficial to maintain the polarization difference between the lower and the higher frequency electrons, thus improving the DNP process and mitigating depolarization losses. This is what we observe in this study for TinyPol radicals: as their overall electron magnetic interaction is stronger than that of AMUPol, they display not only higher ε_H values but also contribution factors that are less subjected to the effects of fast MAS. These observations are in agreement with previous studies on hybrid radicals and on asymmetric binitroxides.^30–32 We note here that our work further highlights with experimental evidence, not only the critical role of the electron–electron coupling strength in the DNP transfer efficiency, but also the need for optimized electron–electron interactions for each magnetic field, or, in other words, the need for linker structure/length tailored towards a given field value.

DNP SENS on a hybrid mesostructured silica material

Over the last decade, DNP Surface Enhanced NMR Spectroscopy (DNP SENS) has been developed into a powerful and versatile way to investigate surface structure at the molecular level. In particular this approach has proven to be of prime relevance to unravel structure/properties relationships in a large range of challenging chemical systems such as high-performance organometallic heterogeneous catalysts, doped silicon surfaces, functionalized metal–organic frameworks, ligand-capped nanoparticles, cementitious materials, quantum dots or active zeolites.^3–44 Most current applications of DNP SENS are realized using commercial instruments operating at moderate magnetic fields, typically 9.4 T or at 14.1 T. While higher fields would be beneficial in many areas of materials science, very few detailed DNP SENS studies have been reported so far at very high fields above 18.8 T.^45,46 Beyond the scarcity of the instruments, the fact that this methodology relies on sample formulations whose efficiency scales down drastically at high magnetic fields is a strong limitation. Polarizing agents are key elements of these formulations. Here, we report DNP SENS experiments recorded at 18.8 T on a mesoporous silica material, impregnated with an aqueous solution of M-TinyPol. The structure of the material and of the organic fragment distributed within the mesoporous silica network is detailed in Fig. 6a and the synthesis is report in the ESI.† A proton enhancement of 45 was achieved, versus 28 for a sample prepared with a solution of AMUPol under the same experimental conditions of solvent and concentration. Fig. 6b shows the corresponding one-dimensional carbon-13 cross-polarization (CP) and two-dimensional ¹H–¹³C heteronuclear correlation (HETCOR) spectra. The latter displays excellent resolution in the proton chemical shift dimension, as expected at high magnetic field. All the expected ¹H–¹³C correlations could be observed and assigned from this 2D spectrum.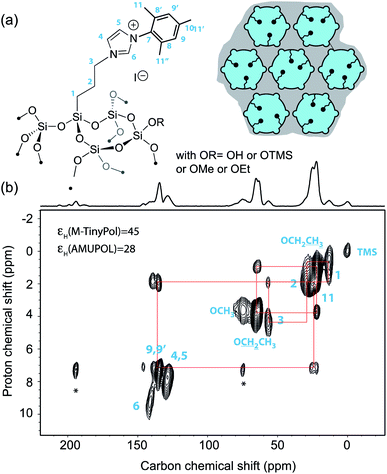

Fig. 6 (a) Structure of the organic imidazolium ligand investigated in this study and schematic representation of the mesoporous silica support [mesopores (6 nm diameter) are shown as circles and micropores (<1 nm diameter) as small half-circles]. Blue color represents the polarizing solution of 10 mM AMUPol or M-TinyPol in H₂O that fills the pores while the gray area represents the silica bulk. (b) Contour plot of a 2D DNP SENS ¹H–¹³C HETCOR spectrum of the surface compound recorded at 18.8 T and 12.5 kHz MAS frequency using a 3.2 mm rotor. The sample was impregnated with a 10 mM solution of TinyPol in H₂O. The contact time was 500 μs. During t₁, eDUMBO homonuclear decoupling was applied.⁴⁷ The one-dimensional carbon-13 cross-polarization spectrum is shown above the 2D map. The red lines show the various correlations.

Conclusions

We have introduced a new series of water-soluble binitroxides dubbed TinyPols tailored for DNP at very high magnetic fields. These radicals have a skeleton similar to that of AMUPol but are designed to have a shorter tether length and therefore smaller electron–electron distance and higher magnetic dipolar interaction. We demonstrated the efficacy of these polarizing agents at 18.8 T and 21.1 T, where TinyPols significantly outperform the reference radical AMUPol. With the best radical in this series, namely M-TinyPol, we report the highest enhancement measured so far in aqueous solution at 18.8 and 21.1 T, of respectively 90 and 38-fold. We note however that the enhancement values at 18.8 T have been obtained in 1.3 mm rotors where the microwave field distribution is more favorable than in 3.2 mm rotors.⁴⁸ Additionally, we have shown that depolarization effects are reduced at fast MAS in these short-linked binitroxides, while the favorable electron relaxation times of AMUPol are preserved.

We believe that this study will give a fresh momentum to AMUPol-like radicals, which were so far disregarded in the context of the development of polarizing agents for very high-field DNP. While the positive effect of reducing the linker length on the electronic couplings and therefore on the enhancement at high field could be expected, such a dramatic improvement in the DNP efficiency was not foreseen.

Since the introduction of bTbK, binitroxides have been designed with a rigid organic tether in order to constrain the orientation of the two nitroxides. Another rather unexpected aspect of this work resides in the experimental observation that the presence of a flexible linker is not a major obstacle to obtain high DNP enhancement factors. While much remains to be understood to depict accurately the ensemble of DNP-active conformers at 100 K in a frozen glassy matrix, our work clearly opens new design perspectives. In particular, the high DNP performances observed for flexible TinyPol and M-TinyPol suggest that at very high field the electron couplings play a more crucial role than the relative nitroxide g-tensor orientation. This establishes priorities in the structural design of new polarizing agents. The next step in the development of efficient bis-nitroxides for high-field MAS DNP will consist in fine tuning the short linker in TinyPol-like radicals, for example by introducing new heteroatoms (in place of current nitrogen and/or carbon atoms) or by adding some conjugation in the backbone to adjust the electron couplings to their Goldilocks values.

As demonstrated in this paper, TinyPol and M-TinyPol provide a 2-fold improvement in the overall sensitivity gain with respect to AMUPol and AsymPolPOK, which translates in a reduction of the experimental time by a factor 4. Applications that are still impractical with current polarizing agents at very high magnetic field due to sensitivity limitation, could now be envisioned. The TinyPols, are stable both in its powder form and in solution, easy to synthesize and manipulate. Therefore, they are expected to open new avenues for the characterization of challenging substrates from materials surfaces to biomolecular assemblies, promoting high-field DNP as a more accessible technique to remove sensitivity and resolution barriers in NMR spectroscopy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from Equipex contracts ANR-10-EQPX-47-01, ANR-15-CE29-0022-01, and ANR-17-CE29-0006-01 are gratefully acknowledged. M. K. gratefully acknowledges financial support from the Deutsche Forschungsgemeinschaft (KA 5221/1-1). M. L. gratefully acknowledges financial support from Fondazione CR Firenze. C. T and M. R. C. thank the European Union’s Horizon 2020 [30] research and innovation program (H-CCAT project) under grant agreement No. 720996. G. S. acknowledges Marie-Skłodowska-Curie Grant 796904.

References

1. Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941.
2. A. J. Rossini, A. Zagdoun, M. Lelli, A. Lesage, C. Copéret and L. Emsley, Acc. Chem. Res., 2013, 46, 1942–1951.
3. P. Berruyer, L. Emsley and A. Lesage, eMagRes, 2018, 7, 93–104.
4. K. Jaudzems, T. Polenova, G. Pintacuda, H. Oschkinat and A. Lesage, J. Struct. Biol., 2018, 206, 90–98.
5. G. Casano, H. Karoui and O. Ouari, eMagRes, 2018, 7, 195–208.
6. B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27190–27204.
7. M. Kaushik, T. Bahrenberg, T. V. Can, M. A. Caporini, R. Silvers, J. Heiliger, A. A. Smith, H. Schwalbe, R. G. Griffin and B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27205–27218.
8. G. Stevanato, D. Kubicki, G. Menzildjian, A. S. Chauvin, K. Keller, M. Yulikov, G. Jeschke, M. Mazzanti and L. Emsley, J. Am. Chem. Soc., 2019, 141, 8746–8751.
9. C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390.
10. K.-N. Hu, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2004, 126, 10844–10845.
11. Y. Matsuki, O. Ouari, J. Herzfeld, P. Tordo and R. G. Griffin, Angew. Chem., Int. Ed., 2009, 121, 5096–5100.
12. C. Sauvée, M. Rosay, G. Casano, F. Aussenac, O. Ouari and P. Tordo, Angew. Chem., Int. Ed. Engl., 2013, 52, 10858–10861.
13. F. A. Perras, R. R. Reinig, I. I. Slowing, A. D. Sadow and M. Pruski, Phys. Chem. Chem. Phys., 2015, 18, 65–69.
14. C. Sauvée, G. Casano, S. Abel, A. Rockenbauer, D. Akhmetzyanov, H. Karoui, D. Siri, F. Aussenac, W. Maas, R. T. Weber, T. Prisner, M. Rosay, P. Tordo and O. Ouari, Chem.–Eur. J., 2016, 22, 5598–5606.
15. D. J. Kubicki, G. Casano, M. Schwarzwälder, S. Abel, C. Sauvée, K. Ganesan, M. Yulikov, A. J. Rossini, G. Jeschke, C. Copéret, A. Lesage, P. Tordo, O. Ouari and L. Emsley, Chem. Sci., 2016, 7, 550–558.
16. A. P. Jagtap, M.-A. Geiger, D. Stöppler, M. Orwick-Rydmark, H. Oschkinat and S. T. Sigurdsson, Chem. Commun., 2016, 52, 7020–7023.
17. A. Zagdoun, G. Casano, O. Ouari, M. Schwaerzwalder, A. J. Rossini, F. Aussenac, M. Yulikov, G. Jeschke, C. Copéret, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2013, 135, 12790–12797.
18. A. Zagdoun, G. Casano, O. Ouari, G. Lapadula, A. J. Rossini, M. Lelli, M. Baffert, D. Gajan, L. Veyre, W. E. Maas, M. Rosay, R. T. Weber, C. Thieuleux, C. Copéret, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2012, 134, 2284–2291.
19. M. Geiger, A. Jagtap, M. Kaushik, H. Sun, D. Stöppler, S. Sigurdsson, B. Corzilius and H. Oschkinat, Chem.–Eur. J., 2018, 24, 13485–13494.
20. K. R. Thurber and R. Tycko, J. Chem. Phys., 2012, 137, 084508.
21. F. Mentink-Vigier, Ü. Akbey, H. Oschkinat, S. Vega and A. Feintuch, J. Magn. Reson., 2015, 258, 102–120.
22. D. Mance, P. Gast, M. Huber, M. Baldus and K. L. Ivanov, J. Chem. Phys., 2015, 142, 234201.
23. F. Mentink-Vigier, S. Vega and G. De Paepe, Phys. Chem. Chem. Phys., 2017, 19, 3506–3522.
24. F. Mentink-Vigier, A.-L. Barra, J. van Tol, S. Hediger, D. Lee and G. De Paepe, Phys. Chem. Chem. Phys., 2019, 17, 33.
25. T. V. Can, M. A. Caporini, F. Mentink-Vigier, B. Corzilius, J. J. Walish, M. Rosay, W. E. Maas, M. Baldus, S. Vega, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2014, 141, 064202.
26. T. V. Can, Q. Z. Ni and R. G. Griffin, J. Magn. Reson., 2015, 253, 23–35.
27. S. R. Chaudhari, D. Wisser, A. C. Pinon, P. Berruyer, D. Gajan, P. Tordo, O. Ouari, C. Reiter, F. Engelke, C. Copéret, M. Lelli, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10609–10612.
28. S. Björgvinsdóttir, B. J. Walder, A. C. Pinon, J. R. Yarava and L. Emsley, J. Magn. Reson., 2018, 288, 69–75.
29. G. Mathies, M. A. Caporini, V. K. Michaelis, Y. Liu, K.-N. Hu, D. Mance, J. L. Zweier, M. Rosay, M. Baldus and R. G. Griffin, Angew. Chem., Int. Ed., 2015, 54, 11770–11774.
30. F. Mentink-Vigier, G. Mathies, Y. Liu, A.-L. Barra, M. A. Caporini, D. Lee, S. Hediger, R. G. Griffin and G. De Paepe, Chem. Sci., 2017, 8, 8150–8163.
31. S. Bothe, J. Nowag, V. Klimavičius, M. Hoffmann, T. I. Troitskaya, E. V. Amosov, V. M. Tormyshev, I. Kirilyuk, A. Taratayko, A. Kuzhelev, D. Parkhomenko, E. Bagryanskaya, T. Gutmann and G. Buntkowsky, J. Phys. Chem. C, 2018, 122, 11422–11432.
32. D. Wisser, G. Karthikeyan, A. Lund, G. Casano, H. Karoui, M. Yulikov, G. Menzildjian, A. C. Pinon, A. Purea, F. Engelke, S. R. Chaudhari, D. Kubicki, A. J. Rossini, I. B. Moroz, D. Gajan, C. Copéret, G. Jeschke, M. Lelli, L. Emsley, A. Lesage and O. Ouari, J. Am. Chem. Soc., 2018, 140, 13340–13349.
33. K. Sato, R. Hirao, I. Timofeev, O. Krumkacheva, E. Zaytseva, O. Rogozhnikova, V. M. Tormyshev, D. Trukhin, E. Bagryanskaya, T. Gutmann, V. Klimavičius, G. Buntkowsky, K. Sugisaki, S. Nakazawa, H. Matsuoka, K. Toyota, D. Shiomi and T. Takui, J. Phys. Chem. A, 2019, 123, 7507–7517.
34. K.-N. Hu, V. S. Bajaj, M. Rosay and R. G. Griffin, J. Chem. Phys., 2007, 126, 044512.
35. C. Ysacco, E. Rizzato, M.-A. Virolleaud, H. Karoui, A. Rockenbauer, F. Le Moigne, D. Siri, O. Ouari, R. G. Griffin and P. Tordo, Phys. Chem. Chem. Phys., 2010, 12, 5841.
36. C. Ysacco, H. Karoui, G. Casano, F. Le Moigne, S. Combes, A. Rockenbauer, M. Rosay, W. Maas, O. Ouari and P. Tordo, Appl. Magn. Reson., 2012, 43, 251–261.
37. W. Zhai, Y. Feng, H. Liu, A. Rockenbauer, D. Mance, S. Li, Y. Song, M. Baldus and Y. Liu, Chem. Sci., 2018, 9, 4381–4391.
38. F. Mentink-Vigier, I. Marin-Montesinos, A. P. Jagtap, T. Halbritter, J. van Tol, S. Hediger, D. Lee, S. T. Sigurdsson and G. De Paepe, J. Am. Chem. Soc., 2018, 140, 11013–11019.
39. K. R. Thurber and R. Tycko, J. Chem. Phys., 2014, 140, 184201.
40. F. Mentink-Vigier, S. Paul, D. Lee, A. Feintuch, S. Hediger, S. Vega and G. De Paepe, Phys. Chem. Chem. Phys., 2015, 17, 21824–21836.
41. S. R. Chaudhari, P. Berruyer, D. Gajan, C. Reiter, F. Engelke, D. L. Silverio, C. Copéret, M. Lelli, A. Lesage and L. Emsley, Phys. Chem. Chem. Phys., 2016, 18, 10616–10622.
42. K.-N. Hu, T. M. Swager and R. G. Griffin, J. Chem. Phys., 2008, 128, 052302.
43. K. Tagami, A. Equbal, I. Kaminker, B. Kirtman and S. Han, Solid State Nucl. Magn. Reson., 2019, 101, 12–20.
44. A. G. M. Rankin, J. Trebosc, F. Pourpoint, J.-P. Amoureux and O. Lafon, Solid State Nucl. Magn. Reson., 2019, 101, 116–143.
45. A. S. L. Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 120–195.
46. I. B. Moroz, A. Lund, M. Kaushik, L. Severy, D. Gajan, A. Fedorov, A. Lesage and C. Copéret, ACS Catal., 2019, 9, 7476–7485.
47. B. Elena, G. De Paepe and L. Emsley, Chem. Phys. Lett., 2004, 398, 532–538.
48. A. Purea, C. Reiter, A. I. Dimitriadis, E. de Rijk, F. Aussenac, I. Sergeyev, M. Rosay and F. Engelke, J. Magn. Reson., 2019, 302, 43–49.

---

Footnote

† Electronic supplementary information (ESI) available: All experimental details such as detailed synthetic procedures, dynamic nuclear polarization enhanced NMR spectroscopy, as well as NMR and EPR data. See DOI: 10.1039/c9sc05384k

---