Open Access Article
Open Access ArticleThe duality of electron localization and covalency in lanthanide and actinide metallocenes†
Danil E.
Smiles
a,
Enrique R.
Batista
 *b,
Corwin H.
Booth
a,
David L.
Clark
b,
Jason M.
Keith
*b,
Corwin H.
Booth
a,
David L.
Clark
b,
Jason M.
Keith
 c,
Stosh A.
Kozimor
c,
Stosh A.
Kozimor
 b,
Richard L.
Martin
b,
Stefan G.
Minasian
b,
Richard L.
Martin
b,
Stefan G.
Minasian
 *a,
David K.
Shuh
*a,
David K.
Shuh
 a,
S. Chantal E.
Stieber
a,
S. Chantal E.
Stieber
 *d and
Tolek
Tyliszczak
a
*d and
Tolek
Tyliszczak
a
aLawrence Berkeley National Laboratory, Berkeley, California 94720, USA. E-mail: sgminasian@lbl.gov
bLos Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: erbatista@lanl.gov
cColgate University, Hamilton, New York 13346, USA
dCalifornia State Polytechnic University, Pomona, California 91768, USA. E-mail: sestieber@cpp.edu
First published on 5th February 2020
Abstract
Previous magnetic, spectroscopic, and theoretical studies of cerocene, Ce(C8H8)2, have provided evidence for non-negligible 4f-electron density on Ce and implied that charge transfer from the ligands occurs as a result of covalent bonding. Strong correlations of the localized 4f-electrons to the delocalized ligand π-system result in emergence of Kondo-like behavior and other quantum chemical phenomena that are rarely observed in molecular systems. In this study, Ce(C8H8)2 is analyzed experimentally using carbon K-edge and cerium M5,4-edge X-ray absorption spectroscopies (XAS), and computationally using configuration interaction (CI) calculations and density functional theory (DFT) as well as time-dependent DFT (TDDFT). Both spectroscopic approaches provide strong evidence for ligand → metal electron transfer as a result of Ce 4f and 5d mixing with the occupied C 2p orbitals of the C8H82− ligands. Specifically, the Ce M5,4-edge XAS and CI calculations show that the contribution of the 4f1, or Ce3+, configuration to the ground state of Ce(C8H8)2 is similar to strongly correlated materials such as CeRh3 and significantly larger than observed for other formally Ce4+ compounds including CeO2 and CeCl62−. Pre-edge features in the experimental and TDDFT-simulated C K-edge XAS provide unequivocal evidence for C 2p and Ce 4f covalent orbital mixing in the δ-antibonding orbitals of e2u symmetry, which are the unoccupied counterparts to the occupied, ligand-based δ-bonding e2u orbitals. The C K-edge peak intensities, which can be compared directly to the C 2p and Ce 4f orbital mixing coefficients determined by DFT, show that covalency in Ce(C8H8)2 is comparable in magnitude to values reported previously for U(C8H8)2. An intuitive model is presented to show how similar covalent contributions to the ground state can have different impacts on the overall stability of f-element metallocenes.
Introduction
Since the discovery of cerocene, Ce(C8H8)2,1,2 a broad debate has ensued regarding the true nature of f-element chemical bonds, the meaning of terms used to describe bonding, and how and when those terms should be used. In the ionic limit, balancing the charges of two dianionic cyclooctatetraene ligands (C8H82−) requires that the cerium atom have a formal +4 charge which leaves the 4f and 5d orbitals unoccupied. This model is supported by a structural analysis of Ce(C8H8)2 and comparison with other lanthanocenes and actinocenes.3–7 The diamagnetic NMR spectrum2,8,9 of Ce(C8H8)2 and similarities between the photoelectron spectra2,10,11 of Ce(C8H8)2 and Th(C8H8)2 seem to support a Ce4+ formulation, although subsequent theoretical analyses12 provide a more nuanced interpretation. In the 1990s, Ce(C8H8)2 was among the first systems to be the focus of computational studies utilizing configuration interaction concepts to account for electron–electron interactions.12–14 These studies find that the ground state electronic configuration of Ce(C8H8)2 is a mixture of two different configurations, and that Ce(C8H8)2 is best approximated as a predominantly Ce3+ (4f1) compound together with two C8H81.5− ligands. The possibility of a multiconfigurational ground state has been explored extensively with theory, and more recent computational studies expand on this interpretation by providing additional strong support for a non-negligible 4f orbital occupation in the ground state of Ce(C8H8)2.15–17 Experimental corroboration has been more difficult to obtain, however, and it is difficult to rationalize the apparent contradictions in between previous measurements9,18–20 which suggest that the 4f-electrons participate in bonding while appearing localized simultaneously. Cerium L3-edge measurements20 of Ce(C8H8)2 provide the only direct experimental evidence of a multiconfigurational ground state, but the spectral interpretations are fraught with controversy.21–24 Taken together, these studies have raised more basic questions regarding whether the concept of a multiconfigurational ground state should apply to all f-element compounds, how it equates to more established models of metal–ligand covalency,25 and how it is manifested by changes in chemical reactivity or magnetic behavior. Although Ce(C8H8)2 is prototypical, such fundamental questions pertain to all formal Ce4+ compounds26–35 and high valent lanthanide compounds,36–41 ytterbium complexes,42–48 and the transuranic actinocenes15,17,49 and have implications throughout the periodic table for the electronic structure models used to describe bonding near the limits of chemically accessible oxidation states.50,51 Improved theoretical models of bonding in these systems are needed to develop new ligands and innovative concepts in lanthanide/actinide separations for nuclear energy.52 Efforts to unravel the complex behavior of correlated electron systems also benefit from investigations of self-contained phenomena in single molecules that can be more precisely characterized using spectroscopy and theory.53–60Our recent work has shown that the metal–ligand covalency and multiconfigurational ground states can be probed experimentally in f-element coordination compounds with X-ray absorption spectroscopy, XAS, at the K-edges for the light atoms directly bound to metal centers (collectively referred to as ligand K-edge XAS).61–64 The spectroscopic technique probes bound state transitions of core 1s electrons localized on the ligands to unoccupied molecular orbitals, which only have intensity if the final state orbitals have ligand np character (n = principal quantum number). Through a combination of ligand K-edge XAS and time-dependent density functional theory (TDDFT) calculations, Solomon and coworkers provided the first demonstrations of this approach as a direct and quantitative probe of electronic structure and covalent bonding in transition metal complexes with M–Cl and M–S bonds.65–68 Recently, the range of ligand chemistries was expanded to include systems incorporating M–O,69–71 M–N,72–74 and M–C bonds.75,76 By acquiring XAS using a scanning transmission X-ray microscope (STXM), we are able to control saturation effects and overcome other challenges with photon attenuation that can preclude measurements with weakly penetrating incident radiation using soft X-rays. Herein, we examine 4f-electron localization in Ce(C8H8)2 using DFT and C K-edge XAS from STXM. Unambiguous evidence for covalent mixing involving the 4f orbitals of e2u symmetry is identified in the experimental spectra with the aid of TDDFT calculations. The results are interpreted in the context of Ce M5,4-edge XAS and multiplet calculations, which also show that Ce(C8H8)2 has significant covalent character owing to ligand-to-metal electron transfer in the ground state. Both molecular orbital theory and configuration interaction models are presented to rationalize these observations relative to earlier work on the actinocenes, and we show how the 4f-electrons can participate in bonding while appearing localized simultaneously.
Results and discussion
Ground state electronic structure and molecular orbital description
A framework for understanding the C K-edge and Ce M5,4-edge spectra of Ce(C8H8)2 can be approximated using molecular orbital (MO) theory following conventions developed for actinide systems, particularly U(C8H8)2.25 In a D8h ligand field, the shape and symmetry of ligand orbitals that are involved in M–C bonding can be estimated from symmetry adapted linear combinations (SALCs) of the sixteen atomic C 2p π orbitals that are perpendicular to the ring planes (C–C π bonding). In this scheme, the centrosymmetric Ce 5d orbitals mix with the C 2p SALCs of a1g (5d-σ), e1g (5d-π), and e2g (5d-δ) symmetry while the Ce 4f orbitals can mix with the a2u (4f-σ), e1u (4f-π), e2u (4f-δ), and e3u (4f-φ) SALCs, which leaves the SALCs of b1g + b2g + e3g symmetries non-bonding. Many previous spectroscopic11,75,77,78 and theoretical10,15–17,49,79,80 studies of f-element metallocenes show that f-orbital mixing is dominated by the δ-bonding MOs of e2u symmetry when compared with the σ, π, and φ-bonding MOs. Mixing in the e2u orbitals in Ce(C8H8)2 is described using the MO model by the linear combination of orbitals as:| Ψ(e2u) = N{4f − λπe2u} | (1) |
| λ = H/[E0(4f) − E0(πe2u)] | (2) |
| ΔE = H2/[E0(4f) − E0(πe2u)] = Hλ | (3) |
Ground state DFT calculations with the B3LYP hybrid functional were conducted on the closed shell configuration to guide assignments of the experimental spectra. The unoccupied orbitals relevant to the C K-edge XAS measurements are summarized in Table 1 and Fig. 1. Similar to results from DFT calculations on Th(C8H8)2 and U(C8H8)2,75 inspection of the Mulliken population analysis for Ce(C8H8)2 in Table 1 shows that the molecular orbitals of e2u (4f-δ) symmetry played a significant role in bonding with the C8H82− ligands, while the orbitals of a2u (4f-σ) and e1u (4f-π) symmetry were best described as metal-based orbitals having negligible C 2p character. In contrast to Th(C8H8)2, where 5f φ-bonding was an important part of the valence electronic structure,75 Ce(C8H8)2 more closely resembled U(C8H8)2 in that the 1e3u and 2e3u orbitals are best described as non-bonding Ce 4f and C 2p based orbitals, respectively.
| Orbital | Energy (eV) | MO (DFT) | |||||
|---|---|---|---|---|---|---|---|
| C 2s | C 2p | M 4f | M 5d | M 6s | M 6p | ||
| a Alpha spin-orbital energies are reported. b The use of a non-orthogonal basis set can cause Mulliken analysis to have nonphysical results such as compositions >100%, or <0.85 The lowest energy MOs are the antibonding LUMO. | |||||||
| 1b2g (Ce–C nb) | 4.57 | 0 | 0.98 | 0 | 0 | 0 | 0 |
| 1b1u (Ce–C nb) | 4.23 | 0 | 0.96 | 0 | 0 | 0 | 0 |
| 2e1g (5d-π) | 2.25 | −0.15 | 0.14 | 0 | 0.63 | 0 | 0 |
| 2e2g (5d-δ) | 1.78 | −0.01 | 0.22 | 0 | 0.76 | 0 | 0 |
| 1e3g (Ce–C nb) | 1.37 | 0 | 0.96 | 0 | 0 | 0 | 0 |
| 2e3u (4f-ϕ) | 1.09 | 0 | 0.89 | 0.07 | 0 | 0 | 0 |
| 2a1g (5d-σ) | −0.82 | 0.02 | 0.02 | 0 | 0.77 | 0.06 | 0 |
| 2e1u (4f-π) | −1.77 | 0 | 0.00 | 0.98 | 0 | 0.01 | 0 |
| 1e3u (4f-ϕ) | −1.84 | 0 | 0.05 | 0.95 | 0 | 0 | 0 |
| 2e2u (4f-δ) | −1.85 | 0 | 0.24 | 0.76 | 0 | 0 | 0 |
| 2a2u (4f-σ) | −2.01 | 0 | 0.02 | 0.98 | 0 | 0 | 0 |
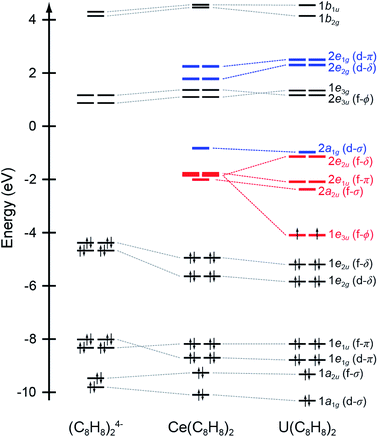 | ||
| Fig. 1 Quantitative molecular orbital diagram showing DFT calculated energies for Ce(C8H8)2 relative to those published previously for U(C8H8)2 and an idealized (C8H8)24− fragment in D4h symmetry.75 Energies for the (C8H8)24− fragment have been shifted by −16.42 eV so that the carbon 1s orbital energies match those of U(C8H8)2. | ||
DFT is advantageous because it describes partial electron delocalization due to covalency associated with specific bonding interactions (e.g., σ, π, δ, φ), which has proven useful for interpretation of ligand K-edge spectra.67,86,87 Results from the hybrid DFT closed-shell singlet approach used here agreed qualitatively with the established descriptions of Ce(C8H8)2 electronic structure from SCF,12,13,88 hybrid DFT,89 and multi-reference calculations,15,17,90 along with related calculations for the actinocenes.75,79,81,90–94 Alternatively, the single determinant MO wavefunction shown in eqn (1) can be reformulated using a configuration interaction (CI) charge transfer model. The CI model accounts for exchange, multiple and core-induced charge transfer interactions, which are typically difficult to incorporate, or not incorporated in MO models. In the CI model where configurations differ by only one electron, the ground state is expressed as
| Ψ = N[|4f0L4〉 + λ|4f1L3〉] | (4) |
A possible concern therefore lies with the closed-shell nature of the DFT solution, which could provide an inaccurate or wholly incorrect formulation of the multiconfigurational ground-state for many-electron lanthanide and actinide systems.100,101 In fact, the hybrid DFT approximation can make direct contact with the multi-configuration representations by examining the B3LYP closed-shell determinant for instabilities. Preliminary calculations, which will be reported separately, indeed reveal a broken-symmetry B3LYP ground state that is nearly degenerate with the closed-shell solution described above. The broken symmetry ground state is an open-shell singlet (an admixture of singlet and triplet states) which couples a Ce 4f electron with a hole on the ligands. When the triplet state is projected from the broken-symmetry determinant, the pure singlet state lies some 0.49 eV below the closed-shell solution,102 and provides additional evidence for an open-shell singlet ground state as inferred above. This simple broken symmetry wavefunction seems to capture much of the multiconfigurational aspects of Ce(C8H8)2 demonstrated in earlier work cited above.
STXM measurements
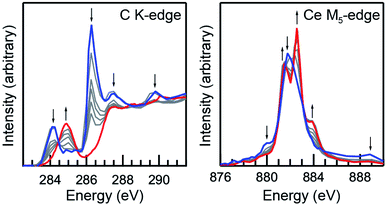
A scanning transmission X-ray microscope (STXM) was utilized to image and obtain C K-edge and Ce M5,4-edge XAS from micron-scale crystals of Ce(C8H8)2.103 This has been demonstrated previously71,75 as an effective approach for minimizing the saturation and self-absorption effects that can plague efforts to obtain spectra using weakly penetrating incident radiation at low photon energies. For samples prepared from finely-divided powders, it was necessary to identify particles that were sufficiently thin104 for transmission XAS measurements and also large enough to provide a suitable signal-to-background ratio. Utilizing methodology developed for the study of group 4 bent metallocene dichlorides, (C5H5)2MCl2 (M = Ti, Zr, Hf)76 and actinocenes (C8H8)2An (An = Th, U),75 small droplets of Ce(C8H8)2 dissolved in toluene were allowed to evaporate on Si3N4 windows in an Ar-filled glovebox to form a large number of small crystallites in a compact area that were suitable for STXM raster scans (Fig. 2).Initially, Ce(C8H8)2 was found to be susceptible to radiation damage during the room-temperature STXM experiments when using standard data acquisition parameters as evidenced by rapid changes in spectral profile and by the emergence of interface distortions in images of the crystallites. To quantify contributions from radiation damage and show a progression from Ce(C8H8)2 to the unidentified product(s) resulting from radiation damage as a function of photon exposure time, short acquisitions of C K-edge and Ce M5-edge spectra were performed in rapid succession over the same sample area (Fig. 3). As described previously for O K-edge measurements on light-sensitive compounds such as potassium permanganate,71 the duration of each individual scan was limited by reducing the number of pixels, the dwell time per pixel, and by using coarse energy step sizes (see Experimental). The product(s) resulting from radiation damage could not be rigorously identified, however, inspection of the Ce M5-edge following repeated scans showed a spectral profile that is characteristic of Ce3+ species. Spectra obtained at the beginning of these experiments (Fig. 3, blue) and before the onset of radiation damage confirm that the C K-edge and Ce M5,4-edge spectra described below are representative of Ce(C8H8)2 with minimal contributions from radiation damage. High quality C K-edge and Ce M5,4-edge XAS were ultimately obtained by averaging datasets from more than 10 independent crystals and by selecting thin crystals (<100 nm) with a large surface area (>4 μm2 with respect to dimensions normal to the beam).
Cerium M5,4-edge XAS
Ce M5,4-edge XAS were obtained and compared with earlier L3-edge XAS studies of Ce(C8H8)2.20,69 The M5,4-edge spectroscopic approach probes electric dipole-allowed 3d104fn → 3d94fn+1 transitions, where n is the number of 4f electrons in the ground state. Because M5,4-edge XAS probes the 4f orbitals directly, it can be advantageous for probing 4f orbital occupation and mixing in systems with multiconfigurational ground states. Fig. 4 compares the background subtracted and normalized Ce M5,4-edge spectra for Ce(C8H8)2 and [Ce(C8H8)2][Li(THF)2] together with selected reference materials CeO2, CeRh3, CeCl62−, and CeCl63−.64,69,105 Each of the spectra are split by approximately 18 eV into a M5-edge (3d5/2 → 4f7/2 and 3d5/2 → 4f5/2) and M4-edge (3d3/2 → 4f5/2) because of the spin–orbit coupling with the core-hole. For CeCl63− and [Ce(C8H8)2][Li(THF)2], both the M5- and M4-edges exhibit energy shifts and fine structure that are characteristic of multiplet splittings observed in the Ce M5,4-edge spectra from other formal Ce3+ compounds.106–109 Likewise, the Ce M5,4-edge spectra for CeCl62−, CeO2, CeRh3,105 and Ce(C8H8)2 consist of main M5 and M4 peaks and weaker “satellite” features at higher energies that are generally consistent with earlier measurements of formal Ce4+ compounds. However, closer inspection of the spectra in Fig. 4 showed that the main M5,4-edge peaks for Ce(C8H8)2 (882.0 and 900.0 eV) and CeRh3 (882.6 and 900.1 eV) were found approximately 1.5 eV lower in energy than observed for CeCl62− (883.7 and 901.6 eV) or CeO2 (883.7 and 901.7 eV). In this regard, the main M5,4-edge energies observed for Ce(C8H8)2 and CeRh3 more closely resemble those of formally Ce3+ compounds including CeCl63− (882.3 and 900.0 eV) and [Ce(C8H8)2][Li(THF)2] (882.4 and 900.2 eV). The similarity between Ce(C8H8)2 and intermetallic compounds105 CeRh3 as well as CeRu2 and CeCo2 could be anticipated given the close correspondence between the L3-edge spectral profiles for those compounds.110,111 It is worth noting that the M5,4-edge XAS of Ce(C8H8)2 also exhibited a 7 eV average separation between the main and satellite features, which is significantly larger than observed for CeO2, CeCl62−, or CeRh3 (4.8, 4.9, and 5.0 eV, respectively).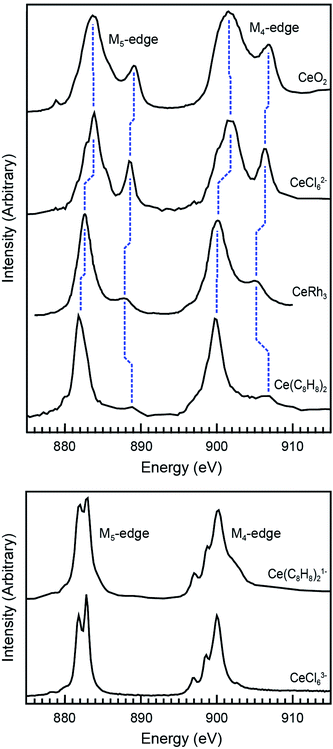 | ||
| Fig. 4 Top panel: Ce M5,4-edge XAS of formal Ce4+ compounds including Ce(C8H8)2 and reference materials CeO2, CeRh3, and (Et4N)2CeCl6. Bottom panel: Ce M5,4-edge XAS of the formal Ce3+ compound [Li(THF)2][Ce(C8H8)2] and reference material (Ph4P)3CeCl6. The data for CeRh3 was reproduced using DigitizeIt from ref. 105, copyright 1985 Elsevier. Data for CeO2 was adapted with permission from ref. 69 copyright 2017 American Chemical Society. Data for (Et4N)2CeCl6 and (Ph4P)3CeCl6 was adapted with permission from ref. 64, copyright 2015 American Chemical Society. | ||
To explore these results further, CI calculations were conducted for Ce(C8H8)2 and [Ce(C8H8)2][Li(THF)2]. The method was employed using the CTM4XAS program, which is a semi-empirical approach developed by de Groot and is based on Cowan's code (Fig. 5 and Table 2).112–114 The CTM4XAS approach provides an accurate calculation of the multiplet states accessible to a free Ce ion while approximating the influence of the ligands by accounting for symmetry and charge transfer. Previous calculations have reproduced the fine structure and satellite features in M5,4-edge spectra of formally tetravalent compounds including CeCl62− and CeO2.64,69,83 This approach has also been applied successfully to model M5,4-edge spectra and to develop quantitative interpretations of charge transfer interactions in the ground state for other transition metal and Ce systems.95,115,116 For [Ce(C8H8)2][Li(THF)2], the M5.4-edge spectrum is reasonably modeled using a simple CeIII atomic multiplet framework accounting for transitions from a 3d104f1 initial state to a 3d94f2 final state. The 4f–4f Slater–Condon Coulomb repulsion (Fff) and 3d spin–orbit coupling (SOC) parameters were reduced to 60% and 98% of atomic Hartree–Fock values, respectively.117 Reduction of the 4f–4f Slater–Condon Coulomb repulsion (Fff) parameter has been applied in previous studies to account for increased Ce3+ bond covalency, and is necessary to accurately model the spectral fine structure. Our previous CI calculations of CeCl63− had a Fff reduction to 79% of atomic values, suggesting that the Ce(C8H8)21− molecule has a higher degree of covalency than CeCl63−.
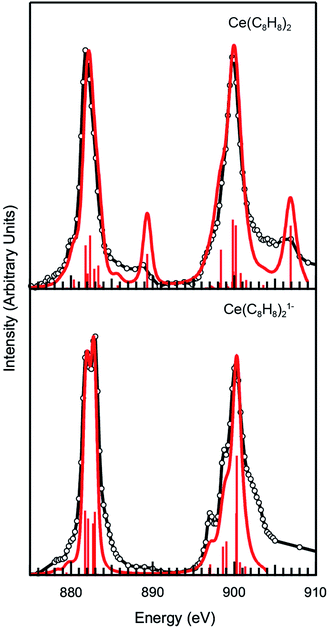 | ||
| Fig. 5 Experimental Ce M5.4-edge spectra (black) and CTM4XAS calculations (red) for Ce(C8H8)2 and [Ce(C8H8)2][Li(THF)2]. | ||
| CeCl62− | CeO2 | Ce(C8H8)2 | |
|---|---|---|---|
| ΔEgs | 2.5 eV | 2.0 eV | −0.1 eV |
| ΔEfs | −1.5 eV | −1.8 eV | −5.0 eV |
| T gs = Tfs | 0.70 | 0.70 | 0.75 |
| 3d104f0 | 75% | 70% | 49% |
3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1 4f1 |
25% | 30% | 51% |
| LMCT calc. | 3.6 eV | 3.2 eV | 2.2 eV |
| LMCT exp. | 3.3 eV | 3.1 eV | 2.1 eV |
For Ce(C8H8)2, a model based on transitions from 3d104f0 to 3d94f1 states does not accurately model the Ce M5.4-edge spectrum, and hence both the initial and final states are described using a charge transfer model. In the charge transfer model, both the initial and final states are defined by two configurations, one of which includes a ligand hole (![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) ) resulting from charge transfer. Thus, the initial state is described by 3d104f0 and 3d10
) resulting from charge transfer. Thus, the initial state is described by 3d104f0 and 3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1 and the final state by 3d94f1 and 3d9
4f1 and the final state by 3d94f1 and 3d9![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f2. These configurations were defined by 4f-4f and 3d-4f Coulomb repulsion, Coulomb exchange and spin–orbit-coupling (SOC) parameters. The interactions of these states were described by the energy separation of the initial (ΔEgs) and final states (ΔEfs) as well as the mixing of each, Tgs and Tfs respectively. As described previously,64 the energy of the lowest LMCT band in the UV/Vis spectrum of Ce(C8H8)2 (2.1 eV)8 was used to provide bounds for these parameters as governed by LMCT ≈ ΔEgs + 2Tgs. In addition, the experimentally observed splitting and intensity ratios between the main and satellite peaks in the M5,4-edge XANES spectra provided limits for the calculations. Fig. 5 and Table 2 show that the calculations for Ce(C8H8)2 were in the closest agreement with these experimental data were defined with ΔEgs = −0.1 eV, ΔEfs = −5.0 eV, and Tgs = Tfs = 0.75, resulting in a ground state that was 49% 3d104f0 and 51% 3d10
4f2. These configurations were defined by 4f-4f and 3d-4f Coulomb repulsion, Coulomb exchange and spin–orbit-coupling (SOC) parameters. The interactions of these states were described by the energy separation of the initial (ΔEgs) and final states (ΔEfs) as well as the mixing of each, Tgs and Tfs respectively. As described previously,64 the energy of the lowest LMCT band in the UV/Vis spectrum of Ce(C8H8)2 (2.1 eV)8 was used to provide bounds for these parameters as governed by LMCT ≈ ΔEgs + 2Tgs. In addition, the experimentally observed splitting and intensity ratios between the main and satellite peaks in the M5,4-edge XANES spectra provided limits for the calculations. Fig. 5 and Table 2 show that the calculations for Ce(C8H8)2 were in the closest agreement with these experimental data were defined with ΔEgs = −0.1 eV, ΔEfs = −5.0 eV, and Tgs = Tfs = 0.75, resulting in a ground state that was 49% 3d104f0 and 51% 3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1, and a calculated LMCT of 2.2 eV. The amount of Ce3+ character (51%) calculated for Ce(C8H8)2 with CTM4XAS is less than the values determined with L3-edge XANES spectroscopy (89%) and multiconfiguration interaction calculations (80%).12,13 Discrepancies with these earlier results, and subtle disagreements with the experimental M-edge spectrum, may reflect the empirical nature of the CTM4XAS calculation. In addition, the CTM4XAS approach cannot shed light on whether the C 2p → Ce 4f LMCT in Ce(C8H8)2 results from simple covalent mixing in the ground state or from coupling of 4f electrons with the ligand π system. However, the results agree qualitatively that the amount C 2p → Ce 4f LMCT in Ce(C8H8)2 exceeds values typically observed for other formal Ce4+ compounds such as CeO2 and CeCl62−. In the case of CeCl62−, a ground state composition containing 25% of the 3d10
4f1, and a calculated LMCT of 2.2 eV. The amount of Ce3+ character (51%) calculated for Ce(C8H8)2 with CTM4XAS is less than the values determined with L3-edge XANES spectroscopy (89%) and multiconfiguration interaction calculations (80%).12,13 Discrepancies with these earlier results, and subtle disagreements with the experimental M-edge spectrum, may reflect the empirical nature of the CTM4XAS calculation. In addition, the CTM4XAS approach cannot shed light on whether the C 2p → Ce 4f LMCT in Ce(C8H8)2 results from simple covalent mixing in the ground state or from coupling of 4f electrons with the ligand π system. However, the results agree qualitatively that the amount C 2p → Ce 4f LMCT in Ce(C8H8)2 exceeds values typically observed for other formal Ce4+ compounds such as CeO2 and CeCl62−. In the case of CeCl62−, a ground state composition containing 25% of the 3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1 configuration was found previously to model the LMCT energy (3.3 eV) as defined by ΔEgs = 2.5 eV, ΔEfs = −1.5 eV, and Tgs = Tfs = 0.70.64 For CeO2, the LMCT energy of 3.1 eV was effectively modeled with a ground state containing 30% of the 3d10
4f1 configuration was found previously to model the LMCT energy (3.3 eV) as defined by ΔEgs = 2.5 eV, ΔEfs = −1.5 eV, and Tgs = Tfs = 0.70.64 For CeO2, the LMCT energy of 3.1 eV was effectively modeled with a ground state containing 30% of the 3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1 configuration as defined by ΔEgs = 2.0 eV, ΔEfs = −1.8 eV, and Tgs = Tfs = 0.70.69 Hence, the CTM4XAS calculations and M5,4-edge XAS reveals a trend towards significantly more Ce3+ (3d10
4f1 configuration as defined by ΔEgs = 2.0 eV, ΔEfs = −1.8 eV, and Tgs = Tfs = 0.70.69 Hence, the CTM4XAS calculations and M5,4-edge XAS reveals a trend towards significantly more Ce3+ (3d10![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f1) character in the ground state of Ce(C8H8)2 (51%) than in CeCl62− (25%) or CeO2 (30%).
4f1) character in the ground state of Ce(C8H8)2 (51%) than in CeCl62− (25%) or CeO2 (30%).
Carbon K-edge XAS
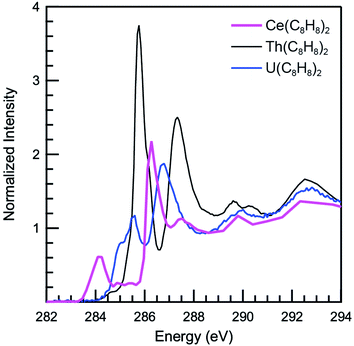
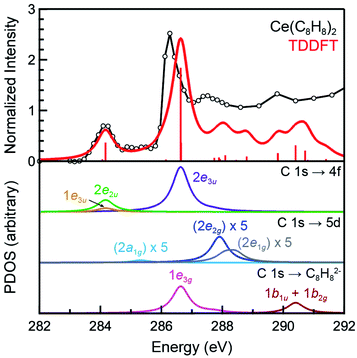
The background subtracted and normalized C K-edge XAS spectrum of Ce(C8H8)2 is shown in Fig. 6 together with previously reported spectra for Th(C8H8)2 and U(C8H8)2.75 Initial evidence for mixing between the Ce 5d and/or 4f orbitals and the C–C π-bonding orbitals of the [(C8H8)2]4− ligand framework is provided by existence of pre-edge features at low energy (283 to 287 eV). Analyzing the first derivative of the experimental spectrum (Fig. S1†) revealed two main features centered at 284.2 eV and 286.7 eV that are analogous to features observed at 1–2 eV higher energies in the C K-edge spectra of Th(C8H8)2 and U(C8H8)2.75 To a first approximation, the shift to lower energies for Ce(C8H8)2 compared to Th(C8H8)2 and U(C8H8)2 is consistent with expectations based on the lower energy of the Ce 5d and 4f orbitals versus 6d and 5f orbitals of Th and U. For additional guidance, energies and oscillator strengths of individual transitions were calculated with TDDFT. Fig. 7 and Table 3 show that the energies calculated by TDDFT correspond well with the experimental data and with the relative energies of orbitals determined from the ground state DFT calculation (Fig. 1). For example, the TDDFT shows a transition from the C 1s orbitals to the antibonding 2e2u (4f-δ) at 284.2 eV, which corresponds to the first low energy feature in the experimental spectrum. At higher energy, the TDDFT shows a second feature at 286.6 eV which includes two overlapping transitions to the antibonding 2e3u (4f-φ) orbitals and the nonbonding 1e3g (Ce–C) orbitals, and corresponds to the second feature in the experimental spectrum. The TDDFT calculated difference in energy between the low and high energy feature is 2.4 eV, which is similar to the gap observed experimentally (2.5 eV) and in the ground state DFT calculation (2.96 eV). In addition, transitions with non-negligible oscillator strength involving the 2e2g (5d-δ) orbitals are calculated at 287.9 eV, which agrees well with a weak intensity feature observed in the experimental spectrum at 287.5 eV near the onset of the edge. Transitions to the antibonding orbitals of 4f-parentage (2a2u, 2e1u, 1e3u) and 5d-parentage (2a1g, 2e1g) are also observed in the TDDFT calculated spectrum (Table 3), however, the calculated oscillator strengths are small and hence these transitions are unresolved in the experimental spectrum.| Final state orbital | Transition energies (eV) | |
|---|---|---|
| XAS | TDDFT | |
| a Experimental values were determined from a plot of the 1st derivative of the spectrum (Fig. S1). Calculated values were taken from TDDFT simulated spectra and shifted by approximately 10 eV (see Experimental). | ||
| 1b1u + 1b2g (Ce–C nb) | 289.0 | 290.4 |
| 2e1g (5d-π) | — | 288.3 |
| 2e2g (5d-δ) | 287.5 | 287.9 |
| 1e3g (Ce–C nb) | 286.7 | 286.6 |
| 2e3u (4f-ϕ) | 286.7 | 286.6 |
| 2a1g (5d-σ) | 285.4 | 285.3 |
| 2e1u (4f-π) | — | 284.3 |
| 1e3u (4f-ϕ) | 284.2 | 284.2 |
| 2e2u (4f-δ) | 284.2 | 284.2 |
| 2a2u (4f-σ) | — | 284.1 |
Evaluation of Ce-(C8H8) bonding and covalency
The C K-edge pre-edge transition intensities are weighted by the amount of C 2p character, and can be used to evaluate C 2p and Ce 4f mixing in specific molecular orbitals. In some cases, quantifying this effect experimentally was challenged by the presence of overlapping transitions. However, clear patterns in the DFT calculations emerge which are supported by qualitative comparisons of the experimental spectra. For example, the C 1s → 2e2g transitions were located at higher energies and unresolved in the experimental spectra; however, the DFT calculations indicate that the composition of the 2e2g (5d-δ) orbitals for Ce(C8H8)2 (22% C 2p and 76% Ce 5d) was effectively the same as reported previously for the 2e2g (6d-δ) orbitals of both Th(C8H8)2 (23% C 2p and 75% Th 6d) and U(C8H8)2 (22% C 2p and 74% U 6d).75 Moving to lower energy, transitions attributable to C 1s → 1e3u were weak and poorly resolved in the experimental and TDDFT calculated spectrum, and the DFT calculations indicate that the 1e3u (5% C 2p, 95% Ce 4f) and 2e3u (89% C 2p, 7% Ce 4f) are best described as non-bonding metal 4f and ligand-based orbitals, respectively. Similar results were reported previously for U(C8H8)2, which had little mixing in the 1e3u (6% C 2p, 94% U 5f) and 2e3u (89% C 2p, 7% U 5f) orbitals. In contrast, evidence for some φ-orbital mixing in the unoccupied valence orbitals was observed for Th(C8H8)2 as shown by intense pre-edge features associated with the bonding 1e3u (33% C 2p, 65% Th 5f) and antibonding 2e3u (49% C 2p, 47% Th 5f) orbitals.At low energy, the C K-edge XAS and TDDFT for Ce(C8H8)2 show a pre-edge feature at 284.2 eV that was attributed to transitions to the unoccupied δ-antibonding orbitals of 2e2u symmetry, and comparison with the TDDFT spectra suggests that the intensity of this feature reflects a significant contribution of C 2p character. Inspection of the ground state DFT calculations confirms this observation by showing that the 2e2u orbitals have 24% C 2p and 76% Ce 4f character. The 2e2u orbitals are the antibonding counterparts to the bonding 1e2u orbitals which are occupied in the ground state and have 72% C 2p and 25% Ce 4f character. The DFT calculated mixing of C 2p character into the 4f orbitals is greater than that determined for the analogous 2e2u (5f-δ) orbitals of Th(C8H8)2 (13% C 2p and 86% Th 5f), and only slightly smaller than the mixing of the 2e2u (5f-δ) orbitals for U(C8H8)2 (28% C 2p and 71% U 5f), such that δ-mixing in the 2e2u orbitals increases in the order Th(C8H8)2 < Ce(C8H8)2 ≈ U(C8H8)2. Because the 2e2u orbitals are the antibonding counterpart to the filled 1e2u orbitals, these results provide new evidence to support earlier theoretical studies15,88 that described how the increase in 4f-electron density in Ce(C8H8)2 results from increased δ-mixing with the C8H82− ligands.
However, a more nuanced picture emerges when considering how changes in the radial extension and energy of atomic f-orbitals Ce4+, Th4+, and U4+ affect the nature of covalent bonding with ligand-based orbitals of e2u symmetry. For example, the decrease in 4th ionization energies (−IE4/4)118 from Th (−7.1 eV) to U (−8.3 eV) and results from several theoretical studies25,84,92,119–121 suggest that moving from Th4+ to U4+ coincides with a decrease in 5f orbital energies. Since the ligand-based orbitals of e2u symmetry are at lower energies, this 5f energy change results in a better energy match (small E0(4f) − E0(πe2u) in eqn (2)) and increased δ-mixing in the 2e2u orbitals for U(C8H8)2. Based on the 4th ionization energy for Ce (−IE4/4 = −9.2 eV),122 the 4f orbitals are an even better energy match for the ligand-based e2u orbitals than anticipated for U(C8H8)2. However, the amount of orbital mixing in Ce(C8H8)2 is slightly less than observed for U(C8H8)2. Hence, the very slight difference in covalency for Ce(C8H8)2 relative to U(C8H8)2 is attributed to the decreased radial extension of the 4f orbitals relative to the 5f orbitals123–126 leading to decreased overlap (smaller H in eqn (2)), which effectively offsets the improved energy match.
The strength of F-orbital bonding
As described above, Ce(C8H8)2 and U(C8H8)2 have qualitatively similar amounts of C 2p mixing with the f-orbitals of e2u symmetry (28% vs. 24% C 2p character, respectively), but different amounts of f-orbital overlap. Consequently, similar amounts of f-orbital mixing does not equate to similar strengths of f-orbital bonding,83,127–137 which highlights the counterintuitive relationship between covalency and stability for f-element molecules.138 Specifically, the decrease in overlap for Ce(C8H8)2 results in a smaller covalent contribution to the bond energy and more localized electrons. This effect is seen clearly upon examination of splittings between the unoccupied f-orbitals in the ground state (2a2u − 2e2u, Fig. 1 and Table 1), which are significant for U(C8H8)2 (1.23 eV) and small for Ce(C8H8)2 (0.16 eV). In a related study, Cl K-edge XAS and DFT results showed that Cl 3p mixing with the 4f/5f-orbitals was of similar magnitude in CeCl62− and UCl62− (15.5 and 22.5% Cl 3p character per bond, respectively) although the two compounds have very different ligand field splitting parameters (θ, t1u − t2u: 0.01 vs. 0.22 eV, respectively).62,64,139,140 The ground state electron density calculations of Kerridge also support this interpretation, showing that the f-electrons are more delocalized for U(C8H8)2 than for Ce(C8H8)2 or transuranic actinocenes.17,49The question of whether f-orbital covalency confers stability to Ce(C8H8)2, Th(C8H8)2, and U(C8H8)2 has also been considered during analyses of their varying physical characteristics and chemical reactivities. For example, the fact that U(C8H8)2 has a low sublimation point, while Th(C8H8)2 and Ce(C8H8)2 do not sublime easily without decomposition, has been partially attributed to the greater strength of 5f orbital bonding in U(C8H8)2.9,141 Following early reports which showed that U(C8H8)2 hydrolyzes slowly at room temperature while Ce(C8H8)2 and Th(C8H8)2 hydrolyze instantaneously,1 Moore and Streitwieser performed a quantitative analysis of hydrolysis reactions for a range of M2(C8H8) and M(C8H8)2 compounds (M = Li, K, Cs and Ce, Th, U).142 In summary, it was hypothesized that under equilibrium conditions slower hydrolysis would result in greater formation of the more conjugated 1,3,5-cyclooctatriene isomer (thermodynamic product) relative to the 1,3,6-cyclooctatriene isomer (kinetic product).143 The opposite effect was observed, such that significant increases in the amount of 1,3,6-C8H10 were observed when varying the metal from Cs to K to Li or from Ce to Th to U (Table 4). Competition experiments with D2O suggested that, for U(C8H8)2 and Li2(C8H8), the rate of protonation of the C8H82− ligands via uncomplexed water molecules slowed, and prior coordination to the metal cation by the water molecule before protonation became competitive. The resultant change in the regiochemistry of protonation explained why U(C8H8)2 and Li2(C8H8) formed more of the 1,3,6-C8H10 isomer, while using other M(C8H8)2 and M(C8H8) complexes or more acidic proton sources increased the relative amount of 1,3,5-C8H10 formation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1,3,5-C8H10 to 1,3,6-C8H10.143
1, 1,3,5-C8H10 to 1,3,6-C8H10.143
Taken together with the spectroscopic and theory results presented above, the work of Moore and Strietweiser suggests that practical hypotheses pertaining to the chemical reactivities of the lanthanides, thorium, uranium, and transuranic actinides can be derived by accounting for differences in d- and f-orbital overlap.144–151 With the exception of Li2(C8H8), formation of the 1,3,6-C8H10 isomer was decreased for all M2(C8H8) relative to M(C8H8)2, which may reflect stabilization of M(C8H8)2 complexes due to mixing with the diffuse 5d- and 6d-orbitals. Similarly, 5f orbital participation in bonding confers stability to U(C8H8)2 because there is a degree of overlap between the U 5f orbitals. Without a similar degree of overlap, 4f-orbital mixing in Ce(C8H8)2 is accompanied by an overall weakening of the complex due to a comparatively large drop in the strength of ionic bonding.62,83,84,127–129
Conclusion
In consideration of the large body of experimental and theoretical work reported previously and cited above, the C K-edge results described herein provide the first direct experimental evidence for covalent mixing between the Ce 4f/5d and the ligand-based C 2p orbitals in Ce(C8H8)2. Ce 5d mixing in Ce(C8H8)2 was greatest for the δ-symmetry e2g orbitals, and ground-state DFT calculations show comparable mixing in the 6d-orbitals of e2g symmetry for both Th(C8H8)2 and U(C8H8)2. The Ce M5,4-edge XAS and CI calculations provide evidence for Ce 4f mixing by showing that contributions of the 4f1L3 configuration (Ce3+) to the ground state of Ce(C8H8)2 are similar to intermetallic compounds such as CeRh3 and significantly larger than observed for other formally Ce4+ compounds including CeO2 and CeCl62−. The ground-state DFT and TDDFT study shows that Ce 4f and C 2p orbital mixing occurs largely in the δ-bonding orbitals of e2u symmetry, and comparisons with earlier DFT and C K-edge studies show that the magnitude of e2u mixing is similar for Ce(C8H8)2 and U(C8H8)2. A simple theoretical framework was provided to rationalize these results, in which covalency in U(C8H8)2 is partially the result of productive overlap between the C 2p and relatively diffuse 5f orbitals. In contrast, metal–ligand overlap decreases with the more contracted 4f orbitals of Ce(C8H8)2, but this is effectively offset by the smaller metal–ligand energy mismatch obtained with the lower energy 4f orbitals. Although covalent orbital mixing was similar for Ce(C8H8)2 and U(C8H8)2, the differences in orbital overlap resulted in a greater covalent contribution to stability for U(C8H8)2 and greater reactivity for Ce(C8H8)2. Taken together, these results show how – in the absence of significant orbital overlap – increases in orbital mixing allow the 4f-electrons in Ce(C8H8)2 to participate in bonding while appearing localized simultaneously. We are currently extending these analyses to the transuranic analogues (C8H8)2An (An = Np, Pu, Am, Cm) to further our understanding of how bonding and electronic structure varies across the f-block elements.Experimental
STXM sample preparation
All manipulations were performed with rigorous exclusion of air and moisture using Schlenk and glovebox techniques under an argon atmosphere. Toluene (Fisher) was distilled from sodium metal and benzophenone prior to use. Ce(C8H8)2 and [Li(THF)2][Ce(C8H8)2] were prepared using the literature procedure.9 To prepare each sample, a small amount (∼1 mg) was dissolved in toluene (1 mL), and an aliquot of the solution (0.5 μL) was transferred to a Si3N4 window (100 nm, Silson) using a micropipette. The toluene was allowed to evaporate over a few seconds, which deposited thin crystallites of the sample on the Si3N4 membrane. After drying for several more minutes, a second window was placed over the sample, sandwiching the crystallites, and the windows were sealed together using Hardman Double/Bubble® epoxy.STXM-XAS measurements and data analysis
The STXM methodology was similar to that discussed previously.64,75,76 Single-energy images and XAS data were acquired using the STXM instruments at the Advanced Light Source-Molecular Environmental Science (ALS-MES) beamline 11.0.2 and at the Canadian Light Source (CLS) spectromicroscopy beamline 10ID-1. The ALS operated in topoff mode (500 mA) and the CLS operated in decay mode (250 to 150 mA). At both facilities, the beamlines operated with ∼0.5 atm He-filled chambers and used elliptically polarizing undulators that delivered photons to entrance slit-less plane-grating monochromators.103 An energy calibration was performed at the C K-edge for CO2 gas (294.95 eV) and at the Ne K-edge for Ne gas (867.30 eV). For these measurements, the X-ray beam was focused with a zone plate onto the sample, and the transmitted photons were detected as function of the energy and sample position. The spot size and spatial resolution were determined from characteristics of the 35 nm zone plate. The energy resolution was estimated at 0.04 eV at the C K-edge and 0.10 at the Ce M-edges, and spectra were collected using circularly polarized radiation to obviate polarization effects. To minimize the impact of radiation damage during spectral acquisitions, individual C K-edge and Ce M5-edge scan times were reduced by limiting the scan range to 50–60 total energy points (130 energy points for full Ce M5,4-edge data), by setting the dwell time to 1 ms per pixel, and by reducing the number of pixels over a target area such that no less than 0.01 μm2 per pixel was achieved. Radiation damage was characterized as shown in Fig. 3 by repeating these scans on the same target area. Spectra that were most representative of undamaged Ce(C8H8)2 were acquired by averaging individual scans obtained from multiple target areas. The C K-edge data were normalized in MATLAB using the MBACK algorithm,152 and by setting the edge jump at 295 eV to an intensity of 1.0. For Ce M5,4-edge data, a line was fit to the pre-edge region below 875 eV and then subtracted from the experimental data to eliminate the background of the spectrum. First-derivative spectra were used as guides to determine the number and position of peaks (see ESI, Fig. S1–S3†).Electronic structure calculations
Ground state electronic structure calculations were performed on Ce(C8H8)2 using B3LYP hybrid DFT,153,154 in the Gaussian 09 code.155 Ce was modeled with the Stuttgart relativistic effective core potential (ecp) and basis set156–158 while C and H were modeled using a Pople style double-ζ 6–31 G(d′,p′) basis set with polarization functions optimized for heavy atoms.159 These functionals and basis sets have demonstrated good agreement between experimental and simulated ligand K-edge XAS spectra for organometallic and inorganic systems.62,75 The molecular orbital composition of Ce(C8H8)2 was obtained by Mulliken population analysis of the individual molecular orbitals.CI calculations
Multiplet calculations were implemented using CTM4XAS, which is a program based on the original code by Cowan112 and further developed by de Groot.113,114 Effects of the crystal field are typically minimal in f-systems, so they were not included,112 and a detailed summary of this method was previously described.64 The [(COT)2Ce]1− configurations were defined by 4f–4f Coulomb repulsion (Fff) reduced to 60% of atomic values, Coulomb 3d-4f repulsion (Ffd) at atomic values, 3d-4f Coulomb exchange (Gfd) at atomic values, and SOC reduced to 98% of atomic values. A Gaussian broadening of 0.25 eV was applied to account for instrumental broadening and Lorentzian broadenings of 0.2 and 0.5 eV were applied to the M5 and M4 edges, respectively. The (COT)2Ce configurations were defined by 4f–4f Coulomb repulsion (Fff) at atomic values, Coulomb 3d-4f repulsion (Ffd) reduced to 63% of atomic values, 3d-4f Coulomb exchange (Gfd) reduced to 90% of atomic values, and SOC reduced to 96% of atomic values. For the 3d94f1 configuration this resulted in values of Ffd = 4.130, Gfd = 4.074, and SOC = 7.144 eV. For the 3d9![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4f2 configuration this resulted in values of Ffd = 3.774, Gfd = 3.653, and SOC = 7.148 eV. Additionally, the parameter space was defined by ΔEgs = −0.1 eV, ΔEfs = −5.0 eV, and Tgs = Tfs = 0.75. A Gaussian broadening of 0.35 eV was applied to account for instrumental broadening and Lorentzian broadenings of 0.3 and 0.6 eV were applied to the M5 and M4 edges, respectively.
4f2 configuration this resulted in values of Ffd = 3.774, Gfd = 3.653, and SOC = 7.148 eV. Additionally, the parameter space was defined by ΔEgs = −0.1 eV, ΔEfs = −5.0 eV, and Tgs = Tfs = 0.75. A Gaussian broadening of 0.35 eV was applied to account for instrumental broadening and Lorentzian broadenings of 0.3 and 0.6 eV were applied to the M5 and M4 edges, respectively.
Simulated C K-Edge spectra
For Ce(C8H8)2, the C K-edge XAS spectra was simulated using TDDFT as described previously.75,76 An energy shift was established to account for the omission of the atomic relaxation associated with the core excitation, relativistic stabilization, and errors associated with the functional. This was achieved by setting the energy of transitions simulated for the antibonding 2e2u (5f-δ) orbitals to be equal to those in the experimental spectra, which resulted in an energy shift of +9.93 eV.Author contributions
Clark, Kozimor, and Shuh oversaw the spectroscopic research, and Minasian conceived of the experiments. Minasian, Shuh and Tyliszczak performed the experiments, and Minasian and Smiles analyzed the data. Batista, Keith, and Martin performed the DFT calculations, and Stieber performed CI calculations. All authors participated in writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Professor Richard Andersen for providing the sample of Ce(C8H8)2. This research was supported equally by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences (CSGB), Heavy Element Chemistry program of the U.S. Department of Energy (DOE) under contract no. DE-AC02-05CH11231 at LBNL (Booth, Minasian, Shuh, Smiles) and by the Director, Office of Science, Office of Basic Energy Sciences, Division of CSGB, Heavy Element Chemistry program of the U.S. DOE at LANL (Batista, Clark, Keith, Kozimor, Martin). Los Alamos National Laboratory is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (contract no. DE-AC52-06NA25396). Stieber acknowledges CPP College of Science, a CSUPERB New Investigator Grant, and NSF XSEDE (CHE160059). STXM research described in this paper was conducted at the Canadian Light Source, which is supported by the Canada Foundation for Innovation, Natural Sciences and Engineering Research Council of Canada, the University of Saskatchewan, the Government of Saskatchewan, Western Economic Diversification Canada, the National Research Council Canada, and the Canadian Institutes of Health Research. Additional STXM research done at ALS beamline 11.0.2 and Tyliszczak were supported by the Director of the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- A. Greco, S. Cesca and G. Bertolini, J. Organomet. Chem., 1976, 113, 321–330 CrossRef.
- A. Streitwieser, S. A. Kinsley, J. T. Rigsbee, I. L. Fragala, E. Ciliberto and N. Rösch, J. Am. Chem. Soc., 1985, 107, 7786–7788 CrossRef.
- K. N. Raymond and C. W. Eigenbrot, Acc. Chem. Res., 1980, 13, 276–283 CrossRef.
- U. Kilimann, R. Herbst-Irmer, D. Stalke and F. T. Edelmann, Angew. Chem., Int. Ed., 1994, 33, 1618–1621 CrossRef.
- T. R. Boussie, D. C. Eisenberg, J. Rigsbee, A. Streitwieser and A. Zalkin, Organometallics, 1991, 10, 1922–1928 CrossRef.
- V. Lorenz, B. M. Schmiege, C. G. Hrib, J. W. Ziller, A. Edelmann, S. Blaurock, W. J. Evans and F. T. Edelmann, J. Am. Chem. Soc., 2011, 133, 1257–1259 CrossRef PubMed.
- K. O. Hodgson and K. N. Raymond, Inorg. Chem., 1972, 11, 3030–3035 CrossRef.
- A. Streitwieser, S. A. Kinsley, C. H. Jenson and J. T. Rigsbee, Organometallics, 2004, 23, 5169–5175 CrossRef.
- M. D. Walter, C. H. Booth, W. W. Lukens and R. A. Andersen, Organometallics, 2009, 28, 698–707 CrossRef.
- J. P. Clark and J. C. Green, J. Chem. Soc., Dalton Trans., 1977, 505–508 RSC.
- J. G. Brennan, J. C. Green and C. M. Redfern, J. Am. Chem. Soc., 1989, 111, 2373–2377 CrossRef.
- M. Dolg, P. Fulde, H. Stoll, H. Preuss, A. Chang and R. M. Pitzer, Chem. Phys., 1995, 195, 71–82 CrossRef.
- M. Dolg, P. Fulde, W. Küchle, C.-S. Neumann and H. Stoll, J. Chem. Phys., 1991, 94, 3011–3017 CrossRef.
- W. J. Liu, M. Dolg and P. Fulde, J. Chem. Phys., 1997, 107, 3584–3591 CrossRef.
- A. Kerridge, R. Coates and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 2896–2905 CrossRef PubMed.
- O. Mooßen and M. Dolg, Chem. Phys. Lett., 2014, 594, 47–50 CrossRef.
- A. Kerridge, Dalton Trans., 2013, 42, 16428–16436 RSC.
- N. M. Edelstein, P. G. Allen, J. J. Bucher, D. K. Shuh, C. D. Sofield, N. Kaltsoyannis, G. H. Maunder, M. R. Russo and A. Sella, J. Am. Chem. Soc., 1996, 118, 13115–13116 CrossRef.
- H.-D. Amberger, H. Reddmann and F. T. Edelmann, J. Organomet. Chem., 2005, 690, 2238–2242 CrossRef.
- C. H. Booth, M. D. Walter, M. Daniel, W. W. Lukens and R. A. Andersen, Phys. Rev. Lett., 2005, 95, 267202 CrossRef PubMed.
- G. Kaindl, G. Schmiester, E. V. Sampathkumaran and P. Wachter, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 10174–10177 CrossRef PubMed.
- T. K. Sham, R. A. Gordon and S. M. Heald, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035113 CrossRef.
- A. Kotani, Mod. Phys. Lett. B, 2013, 27, 1330012 CrossRef.
- J. J. Kas, J. J. Rehr and J. B. Curtis, Phys. Rev. B, 2016, 94 Search PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef.
- A. Kotani, K. O. Kvashnina, S. M. Butorin and P. Glatzel, Eur. Phys. J. B, 2012, 85, 257 CrossRef.
- A. Ashley, G. Balazs, A. Cowley, J. Green, C. H. Booth and D. O'Hare, Chem. Commun., 2007, 1515–1517 RSC.
- M. Coreno, M. de Simone, J. C. Green, N. Kaltsoyannis, N. Narband and A. Sella, Chem. Phys. Lett., 2006, 432, 17–21 CrossRef.
- A. Kerridge and N. Kaltsoyannis, C. R. Chim., 2010, 13, 853–859 CrossRef.
- G. Balazs, F. G. N. Cloke, J. C. Green, R. M. Harker, A. Harrison, P. B. Hitchcock, C. N. Jardine and R. Walton, Organometallics, 2007, 26, 3111–3119 CrossRef.
- D. Werner, G. B. Deacon, P. C. Junk and R. Anwander, Dalton Trans., 2017, 46, 6265–6277 RSC.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2016, 138, 6928–6931 CrossRef.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2017, 139, 2435–2442 CrossRef.
- I. J. Casely, S. T. Liddle, A. J. Blake, C. Wilson and P. L. Arnold, Chem. Commun., 2007, 5037–5039 RSC.
- Y. M. So, Y. Li, K. C. Au-Yeung, G. C. Wang, K. L. Wong, H. H. Y. Sung, P. L. Arnold, I. D. Williams, Z. Y. Lin and W. H. Leung, Inorg. Chem., 2016, 55, 10003–10012 CrossRef PubMed.
- L. Eyring, in Synthesis of Lanthanide and Actinide Compounds, ed. G. Meyer and L. R. Morss, Springer Science, Dordrecht, 1991 Search PubMed.
- B. G. Müller, in Synthesis of Lanthanide and Actinide Compounds, ed. G. Meyer and L. R. Morss, Springer Science, Dordrecht, 1991 Search PubMed.
- Q. N. Zhang, S. X. Hu, H. Qu, J. Su, G. J. Wang, J. B. Lu, M. H. Chen, M. F. Zhou and J. Li, Angew. Chem., Int. Ed., 2016, 55, 6896–6900 CrossRef.
- A. Kovacs, P. D. Dau, J. Marcalo and J. K. Gibson, Inorg. Chem., 2018, 57, 9453–9467 CrossRef.
- N. T. Rice, I. A. Popov, D. R. Russo, J. Bacsa, E. R. Batista, P. Yang, J. Telser and H. S. La Pierre, J. Am. Chem. Soc., 2019, 141, 13222–13233 CrossRef.
- C. T. Palumbo, I. Zivkovic, R. Scopelliti and M. Mazzanti, J. Am. Chem. Soc., 2019, 141, 9827–9831 CrossRef.
- G. Nocton, W. W. Lukens, C. H. Booth, S. S. Rozenel, S. A. Medling, L. Maron and R. A. Andersen, J. Am. Chem. Soc., 2014, 136, 8626–8641 CrossRef PubMed.
- G. Nocton, C. H. Booth, L. Maron and R. A. Andersen, Organometallics, 2013, 32, 5305–5312 CrossRef.
- C. H. Booth, M. D. Walter, D. Kazhdan, Y. J. Hu, W. W. Lukens, E. D. Bauer, L. Maron, O. Eisenstein and R. A. Andersen, J. Am. Chem. Soc., 2009, 131, 6480–6491 CrossRef PubMed.
- C. H. Booth, D. Kazhdan, E. L. Werkema, M. D. Walter, W. W. Lukens, E. D. Bauer, Y. J. Hu, L. Maron, O. Eisenstein, M. Head-Gordon and R. A. Andersen, J. Am. Chem. Soc., 2010, 132, 17537–17549 CrossRef PubMed.
- M. Coreno, M. de Simone, R. Coates, M. S. Denning, R. G. Denning, J. C. Green, C. Hunston, N. Kaltsoyannis and A. Sella, Organometallics, 2010, 29, 4752–4755 CrossRef.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef.
- W. W. Lukens, N. Magnani and C. H. Booth, Inorg. Chem., 2012, 51, 10105–10110 CrossRef CAS.
- A. Kerridge, RSC Adv., 2014, 4, 12078–12086 RSC.
- S.-X. Hu, W.-L. Li, J.-B. Lu, J. L. Bao, H. S. Yu, D. G. Truhlar, J. K. Gibson, J. Marcalo, M. Zhou, S. Riedel, W. H. E. Schwarz and J. Li, Angew. Chem., Int. Ed., 2018, 57, 3242–3245 CrossRef CAS.
- P. T. Wolczanski, Organometallics, 2017, 36, 622–631 CrossRef CAS.
- G. R. Choppin, J. Alloys Compd., 2002, 344, 55–59 CrossRef CAS.
- W. J. Liang, M. P. Shores, M. Bockrath, J. R. Long and H. Park, Nature, 2002, 417, 725–729 CrossRef CAS PubMed.
- J. Park, A. N. Pasupathy, J. I. Goldsmith, C. Chang, Y. Yaish, J. R. Petta, M. Rinkoski, J. P. Sethna, H. D. Abruna, P. L. McEuen and D. C. Ralph, Nature, 2002, 417, 722–725 CrossRef CAS.
- S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711 RSC.
- K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420–1423 CrossRef CAS PubMed.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417 CrossRef CAS PubMed.
- X.-W. Chi, Q.-Y. Wu, J.-H. Lan, C.-Z. Wang, Q. Zhang, Z.-F. Chai and W.-Q. Shi, Organometallics, 2019, 38, 1963–1972 CrossRef CAS.
- C. P. Burns, X. Yang, S. Y. Sung, J. D. Wofford, N. S. Bhuvanesh, M. B. Hall and M. Nippe, Chem. Commun., 2018, 54, 10893–10896 RSC.
- T. P. Latendresse, V. Vieru, B. O. Wilkins, N. S. Bhuvanesh, L. F. Chibotaru and M. Nippe, Angew. Chem., Int. Ed., 2018, 57, 8164–8169 CrossRef CAS PubMed.
- J. N. Cross, J. Su, E. R. Batista, S. K. Cary, W. J. Evans, S. A. Kozimor, V. Mocko, B. L. Scott, B. W. Stein, C. J. Windorff and P. Yang, J. Am. Chem. Soc., 2017, 139, 8667–8677 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, C. N. Christensen, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2012, 134, 5586–5597 CrossRef CAS PubMed.
- S. R. Daly, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor and R. L. Martin, J. Am. Chem. Soc., 2012, 134, 14408–14422 CrossRef CAS PubMed.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef PubMed.
- S. E. Shadle, B. Hedman, K. O. Hodgson and E. I. Solomon, Inorg. Chem., 1994, 33, 4235–4244 CrossRef CAS.
- S. E. Shadle, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1995, 117, 2259–2272 CrossRef CAS.
- S. D. George, P. Brant and E. I. Solomon, J. Am. Chem. Soc., 2005, 127, 667–674 CrossRef PubMed.
- E. I. Solomon, B. Hedman, K. O. Hodgson, A. Dey and R. K. Szilagyi, Coord. Chem. Rev., 2005, 249, 97–129 CrossRef CAS.
- S. G. Minasian, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, W. W. Lukens, R. L. Martin, D. K. Shuh, S. C. E. Stieber, T. Tylisczcak and X. D. Wen, J. Am. Chem. Soc., 2017, 139, 18052–18064 CrossRef CAS PubMed.
- A. B. Altman, J. I. Pacold, J. Wang, W. W. Lukens and S. G. Minasian, Dalton Trans., 2016, 45, 9948–9961 RSC.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, J. A. Bradley, S. R. Daly, S. A. Kozimor, W. W. Lukens, R. L. Martin, D. Nordlund, G. T. Seidler, D. K. Shuh, D. Sokaras, T. Tyliszczak, G. L. Wagner, T.-C. Weng and P. Yang, J. Am. Chem. Soc., 2013, 135, 1864–1871 CrossRef CAS PubMed.
- J. T. Lukens, I. M. DiMucci, T. Kurogi, D. J. Mindiola and K. M. Lancaster, Chem. Sci., 2019, 10, 5044–5055 RSC.
- T. Dumas, D. Guillaumont, C. Fillaux, A. Scheinost, P. Moisy, S. Petit, D. K. Shuh, T. Tyliszczak and C. Den Auwer, Phys. Chem. Chem. Phys., 2016, 18, 2887–2895 RSC.
- C. D. Pemmaraju, R. Copping, S. Wang, M. Janousch, S. J. Teat, T. Tyliszcak, A. Canning, D. K. Shuh and D. Prendergast, Inorg. Chem., 2014, 53, 11415–11425 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351–359 RSC.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, S. A. Kozimor, R. L. Martin, D. K. Shuh, T. Tyliszczak and L. J. Vernon, J. Am. Chem. Soc., 2013, 135, 14731–14740 CrossRef CAS PubMed.
- J. C. Green, Struct. Bonding, 1981, 43, 37–112 CrossRef CAS.
- A. Streitwieser and C. A. Harmon, Inorg. Chem., 1973, 12, 1102–1104 CrossRef CAS.
- J. Li and B. E. Bursten, J. Am. Chem. Soc., 1998, 120, 11456–11466 CrossRef CAS.
- A. H. H. Chang and R. M. Pitzer, J. Am. Chem. Soc., 1989, 111, 2500–2507 CrossRef CAS.
- K. D. Warren, Struct. Bonding, 1977, 33, 97–138 CrossRef CAS.
- J. A. Platts and R. J. Baker, Dalton Trans., 2020, 49, 1077–1088 RSC.
- T. A. Pham, A. B. Altman, S. C. E. Stieber, C. H. Booth, S. A. Kozimor, W. W. Lukens, D. T. Olive, T. Tyliszczak, J. Wang, S. G. Minasian and K. N. Raymond, Inorg. Chem., 2016, 55, 9989–10002 CrossRef CAS PubMed.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- C. J. Cramer, Essentials of Computational Chemistry, Wiley, Chichester, UK, 2nd edn, 2004 Search PubMed.
- S. A. Kozimor, P. Yang, E. R. Batista, K. S. Boland, C. J. Burns, C. N. Christensen, D. L. Clark, S. D. Conradson, P. J. Hay, J. S. Lezama, R. L. Martin, D. E. Schwarz, M. P. Wilkerson and L. E. Wolfsberg, Inorg. Chem., 2008, 47, 5365–5371 CrossRef CAS.
- A. C. Olson, J. M. Keith, E. R. Batista, K. S. Boland, S. R. Daly, S. A. Kozimor, M. M. MacInnes, R. L. Martin and B. L. Scott, Dalton Trans., 2014, 43, 17283–17295 RSC.
- N. Rösch, Inorg. Chim. Acta, 1984, 94, 297–299 CrossRef.
- F. Ferraro, C. A. Barboza and R. Arratia-Pérez, J. Phys. Chem. A, 2012, 116, 4170–4175 CrossRef CAS PubMed.
- E. Solis-Cespedes and D. Paez-Hernandez, Dalton Trans., 2017, 46, 4834–4843 RSC.
- P. M. Boerrigter, E. J. Baerends and J. G. Snijders, Chem. Phys., 1988, 122, 357–374 CrossRef CAS.
- M. Pepper and B. E. Bursten, Chem. Rev., 1991, 91, 719–741 CrossRef CAS.
- M. Koga, W. J. Liu, M. Dolg and P. Fulde, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10648–10654 CrossRef CAS.
- A. Kerridge and N. Kaltsoyannis, J. Phys. Chem. A, 2009, 113, 8737–8745 CrossRef CAS PubMed.
- F. M. F. de Groot, Coord. Chem. Rev., 2005, 249, 31–63 CrossRef CAS.
- B. Vlaisayljevich, P. L. Diaconescu, W. L. Lukens, L. Gagliardi and C. C. Cummins, Organometallics, 2013, 32, 1341–1352 CrossRef.
- C. S. Neumann and P. Fulde, Z. Phys. B: Condens. Matter, 1989, 74, 277–278 CrossRef.
- P. S. Riseborough, Adv. Phys., 2000, 49, 257–320 CrossRef CAS.
- G. Anne, N. S. Vidhyadhiraja and E. L. David, J. Phys.: Condens. Matter, 2007, 19, 106220 CrossRef.
- L. Gagliardi, Int. J. Quantum Chem., 2011, 111, 3302–3306 CrossRef CAS.
- J. L. Jung, M. Atanasov and F. Neese, Inorg. Chem., 2017, 56, 8802–8816 CrossRef CAS PubMed.
- E. R. Batista and R. L. Martin, J. Am. Chem. Soc., 2007, 129, 7224–7225 CrossRef CAS PubMed.
- H. Bluhm, K. Andersson, T. Araki, K. Benzerara, G. E. Brown, J. J. Dynes, S. Ghosal, M. K. Gilles, H. C. Hansen, J. C. Hemminger, A. P. Hitchcock, G. Ketteler, A. L. D. Kilcoyne, E. Kneedler, J. R. Lawrence, G. G. Leppard, J. Majzlam, B. S. Mun, S. C. B. Myneni, A. Nilsson, H. Ogasawara, D. F. Ogletree, K. Pecher, M. Salmeron, D. K. Shuh, B. Tonner, T. Tyliszczak, T. Warwick and T. H. Yoon, J. Electron Spectrosc. Relat. Phenom., 2006, 150, 86–104 CrossRef CAS.
- S. Hanhan, A. M. Smith, M. Obst and A. P. Hitchcock, J. Electron Spectrosc. Relat. Phenom., 2009, 173, 44–49 CrossRef CAS.
- G. Kaindl, G. Kalkowski, W. D. Brewer, E. V. Sampathkumaran, F. Holtzberg and A. S. Vonwittenau, J. Magn. Magn. Mater., 1985, 47–8, 181–189 CrossRef.
- T. Jo and A. Kotani, J. Phys. Soc. Jpn., 1988, 57, 2288–2291 CrossRef CAS.
- G. Kaindl, G. Kalkowski, W. D. Brewer, B. Perscheid and F. Holtzberg, J. Appl. Phys., 1984, 55, 1910–1915 CrossRef CAS.
- B. T. Thole, G. Vanderlaan, J. C. Fuggle, G. A. Sawatzky, R. C. Karnatak and J. M. Esteva, Phys. Rev. B, 1985, 32, 5107–5118 CrossRef CAS PubMed.
- A. Kotani and H. Ogasawara, J. Electron Spectrosc. Relat. Phenom., 1992, 60, 257–299 CrossRef CAS.
- P. Le Fevre, H. Magnan, J. Vogel, V. Formoso, K. Hricovini and D. Chandesris, J. Synchrotron Radiat., 1999, 6, 290–292 CrossRef CAS PubMed.
- H. Ogasawara, A. Kotani, P. Le Fevre, D. Chandesris and H. Magnan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 7970–7975 CrossRef CAS.
- R. D. Cowan, Theory of Atomic Structure and Spectra, University of California Press, 1981 Search PubMed.
- F. M. F. de Groot and A. Kotani, Core Level Spectroscopy of Solids, Taylor and Francis, New York, 2008 Search PubMed.
- E. Stavitski and F. M. F. de Groot, Micron, 2010, 41, 687–694 CrossRef CAS PubMed.
- S. O. Kucheyev, B. J. Clapsaddle, Y. M. Wang, T. van Buuren and A. V. Hamza, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235420 CrossRef.
- S. Turner, S. Lazar, B. Freitag, R. Egoavil, J. Verbeeck, S. Put, Y. Strauven and G. Van Tendeloo, Nanoscale, 2011, 3, 3385–3390 RSC.
- K. O. Hodgson, F. Mares, D. F. Starks and A. Streitwieser, J. Am. Chem. Soc., 1973, 95, 8650–8658 CrossRef CAS.
- X. Y. Cao and M. Dolg, J. Mol. Struct., 2004, 673, 203–209 CrossRef CAS.
- I. D. Prodan, G. E. Scuseria and R. L. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033101 CrossRef.
- M. J. Tassell and N. Kaltsoyannis, Dalton Trans., 2010, 39, 6719–6725 RSC.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
- W. C. Martin, R. Zalubas and L. Hagan, Atomic Energy Levels – The Rare Earth Elements NSRDS-NBS 60, U.S. Department of Commerce, Washington, DC, 1978 Search PubMed.
- H. M. Crosswhite, H. Crosswhite, W. T. Carnall and A. P. Paszek, J. Chem. Phys., 1980, 72, 5103–5117 CrossRef CAS.
- T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565 CrossRef CAS.
- V. Vetere, P. Maldivi and C. Adamo, J. Comput. Chem., 2003, 24, 850–858 CrossRef CAS PubMed.
- M. Atanasov, C. Daul, H. U. Gudel, T. A. Wesolowski and M. Zbiri, Inorg. Chem., 2005, 44, 2954–2963 CrossRef CAS PubMed.
- W. W. Lukens, N. M. Edelstein, N. Magnani, T. W. Hayton, S. Fortier and L. A. Seaman, J. Am. Chem. Soc., 2013, 135, 10742–10754 CrossRef CAS PubMed.
- G. J. P. Deblonde, M. Sturzbecher-Hoehne, P. B. Rupert, D. D. An, M. C. Illy, C. Y. Ralston, J. Brabec, W. A. de Jong, R. K. Strong and R. J. Abergel, Nat. Chem., 2017, 9, 843–849 CrossRef CAS PubMed.
- M. P. Kelley, G. J. P. Deblonde, J. Su, C. H. Booth, R. J. Abergel, E. R. Batista and P. Yang, Inorg. Chem., 2018, 57, 5352–5363 CrossRef CAS PubMed.
- F. Gendron, V. E. Fleischauer, T. J. Duignan, B. L. Scott, M. W. Löble, S. K. Cary, S. A. Kozimor, H. Bolvin, M. L. Neidig and J. Autschbach, Phys. Chem. Chem. Phys., 2017, 19, 17300–17313 RSC.
- A. M. Tondreau, T. J. Duignan, B. W. Stein, V. E. Fleischauer, J. Autschbach, E. R. Batista, J. M. Boncella, M. G. Ferrier, S. A. Kozimor, V. Mocko, M. L. Neidig, S. K. Cary and P. Yang, Inorg. Chem., 2018, 57, 8106–8115 CrossRef CAS PubMed.
- M. B. Jones, A. J. Gaunt, J. C. Gordon, N. Kaltsoyannis, M. P. Neu and B. L. Scott, Chem. Sci., 2013, 4, 1189–1203 RSC.
- D. D. Schnaars, A. J. Gaunt, T. W. Hayton, M. B. Jones, I. Kirker, N. Katsoyannis, I. May, S. D. Reilly, B. L. Scott and G. Wu, Inorg. Chem., 2012, 51, 8557–8566 CrossRef CAS PubMed.
- E. Lu, S. Sajjad, V. E. J. Berryman, A. J. Wooles, N. Kaltsoyannis and S. T. Liddle, Nat. Commun., 2019, 10, 634 CrossRef PubMed.
- J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2018, 140, 17977–17984 CrossRef CAS PubMed.
- H. S. La Pierre and K. Meyer, Inorg. Chem., 2013, 52, 529–539 CrossRef CAS PubMed.
- H. S. La Pierre, M. Rosenzweig, B. Kosog, C. Hauser, F. W. Heinemann, S. T. Liddle and K. Meyer, Chem. Commun., 2015, 51, 16671–16674 RSC.
- N. Barros, D. Maynau, L. Maron, O. Eisenstein, G. Zi and R. A. Andersen, Organometallics, 2007, 26, 5059 CrossRef CAS.
- P. L. Arnold, Z. R. Turner, N. Kaltsoyannis, P. Pelekanaki, R. M. Bellabarba and R. P. Tooze, Chem.–Eur. J., 2010, 16, 9623–9629 CrossRef CAS PubMed.
- M. Gregson, E. Lu, F. Tuna, E. J. L. McInnes, C. Hennig, A. C. Scheinost, J. McMaster, W. Lewis, A. J. Blake, A. Kerridge and S. T. Liddle, Chem. Sci., 2016, 7, 3286–3297 RSC.
- A. Streitwieser and U. Mueller-Westerhoff, J. Am. Chem. Soc., 1968, 90, 7364 CrossRef CAS.
- R. M. Moore, PhD dissertation, University of California, 1985.
- W. R. Roth, Ann. Chem., 1964, 671, 25–31 CAS.
- R. P. Kelly, L. Maron, R. Scopelliti and M. Mazzanti, Angew. Chem., Int. Ed., 2017, 56, 15663–15666 CrossRef CAS PubMed.
- N. H. Anderson, J. Xie, D. Ray, M. Zeller, L. Gagliardi and S. C. Bart, Nat. Chem., 2017, 9, 850–855 CrossRef CAS PubMed.
- M. E. Fieser, C. T. Palumbo, H. S. La Pierre, D. P. Halter, V. K. Voora, J. W. Ziller, F. Furche, K. Meyer and W. J. Evans, Chem. Sci., 2017, 8, 7424–7433 RSC.
- J. Hummer, F. W. Heinemann and K. Meyer, Inorg. Chem., 2017, 56, 3201–3206 CrossRef PubMed.
- S. S. Galley, A. A. Arico, T. H. Lee, X. Y. Deng, Y. X. Yao, J. M. Sperling, V. Proust, J. S. Storbeck, V. Dobrosavljevic, J. N. Neu, T. Siegrist, R. E. Baumbach, T. E. Albrecht-Schmitt, N. Kaltsoyannis and N. Lanata, J. Am. Chem. Soc., 2018, 140, 1674–1685 CrossRef CAS PubMed.
- D. N. Huh, J. W. Ziller and W. J. Evans, Inorg. Chem., 2018, 57, 11809–11814 CrossRef CAS PubMed.
- S. S. Galley, S. A. Pattenaude, C. A. Gaggioli, Y. S. Qiao, J. M. Sperling, M. Zeller, S. Pakhira, J. L. Mendoza-Cortes, E. J. Schelter, T. E. Albrecht-Schmitt, L. Gagliardi and S. C. Bart, J. Am. Chem. Soc., 2019, 141, 2356–2366 CrossRef CAS PubMed.
- Y. S. Qiao and E. J. Schelter, Acc. Chem. Res., 2018, 51, 2926–2936 CrossRef CAS PubMed.
- T. C. Weng, G. S. Waldo and J. E. Penner-Hahn, J. Synchrotron Radiat., 2005, 12, 506–510 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- P. Fuentealba, H. Preuss, H. Stoll and L. Vonszentpaly, Chem. Phys. Lett., 1982, 89, 418–422 CrossRef CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, Mol. Phys., 1991, 74, 1245–1263 CrossRef.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- G. A. Petersson and M. A. Allaham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional plots and tabulated data. See DOI: 10.1039/c9sc06114b |
| This journal is © The Royal Society of Chemistry 2020 |