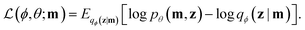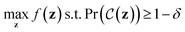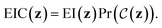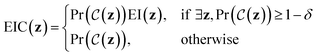Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Constrained Bayesian optimization for automatic chemical design using variational autoencoders†
Ryan-Rhys
Griffiths
 *a and
José Miguel
Hernández-Lobato
*bcd
*a and
José Miguel
Hernández-Lobato
*bcd
aCavendish Laboratory, Department of Physics, University of Cambridge, UK. E-mail: rrg27@cam.ac.uk
bDepartment of Engineering, University of Cambridge, UK. E-mail: jmh233@cam.ac.uk
cAlan Turing Institute, London, UK
dMicrosoft Research, Cambridge, UK
First published on 18th November 2019
Abstract
Automatic Chemical Design is a framework for generating novel molecules with optimized properties. The original scheme, featuring Bayesian optimization over the latent space of a variational autoencoder, suffers from the pathology that it tends to produce invalid molecular structures. First, we demonstrate empirically that this pathology arises when the Bayesian optimization scheme queries latent space points far away from the data on which the variational autoencoder has been trained. Secondly, by reformulating the search procedure as a constrained Bayesian optimization problem, we show that the effects of this pathology can be mitigated, yielding marked improvements in the validity of the generated molecules. We posit that constrained Bayesian optimization is a good approach for solving this kind of training set mismatch in many generative tasks involving Bayesian optimization over the latent space of a variational autoencoder.
Introduction
Machine learning in chemical design has shown promise along a number of fronts. In quantitative structure activity relationship (QSAR) modelling, deep learning models have achieved state-of-the-art results in molecular property prediction1–8 as well as property uncertainty quantification.9–12 Progress is also being made in the interpretability and explainability of machine learning solutions to chemical design, a subfield concerned with extracting chemical insight from learned models.13 The focus of this paper however, will be on molecule generation, leveraging machine learning to propose novel molecules that optimize a target objective.One existing approach for finding molecules that maximize an application-specific metric involves searching a large library of compounds, either physically or virtually.14,15 This has the disadvantage that the search is not open-ended; if the molecule is not contained in the library, the search won't find it.
A second method involves the use of genetic algorithms. In this approach, a known molecule acts as a seed and a local search is performed over a discrete space of molecules. Although these methods have enjoyed success in producing biologically active compounds, an approach featuring a search over an open-ended, continuous space would be beneficial. The use of geometrical cues such as gradients to guide the search in continuous space in conjunction with advances in Bayesian optimization methodologies16,17 could accelerate both drug14,18 and materials19,20 discovery by functioning as a high-throughput virtual screen of unpromising candidates.
Recently, Gómez-Bombarelli et al.21 presented Automatic Chemical Design, a variational autoencoder (VAE) architecture capable of encoding continuous representations of molecules. In continuous latent space, gradient-based optimization is leveraged to find molecules that maximize a design metric.
Although a strong proof of concept, Automatic Chemical Design possesses a deficiency in so far as it fails to generate a high proportion of valid molecular structures. The authors hypothesize21 that molecules selected by Bayesian optimization lie in “dead regions” of the latent space far away from any data that the VAE has seen in training, yielding invalid structures when decoded.
The principle contribution of this paper is to present an approach based on constrained Bayesian optimization that generates a high proportion of valid sequences, thus solving the training set mismatch problem for VAE-based Bayesian optimization schemes.
Methods
SMILES representation
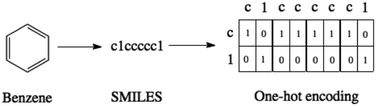
SMILES strings22 are a means of representing molecules as a character sequence. This text-based format facilitates the use of tools from natural language processing for applications such as chemical reaction prediction23–28 and chemical reaction classification.29 To make the SMILES representation compatible with the VAE architecture, the SMILES strings are in turn converted to one-hot vectors indicating the presence or absence of a particular character within a sequence as illustrated in Fig. 1.Variational autoencoders
Variational autoencoders30,31 allow us to map molecules m to and from continuous values z in a latent space. The encoding z is interpreted as a latent variable in a probabilistic generative model over which there is a prior distribution p(z). The probabilistic decoder is defined by the likelihood function pθ(m|z). The posterior distribution pθ(z|m) is interpreted as the probabilistic encoder. The parameters of the likelihood pθ(m|z) as well as the parameters of the approximate posterior distribution qϕ(z|m) are learned by maximizing the evidence lower bound (ELBO)Variational autoencoders have been coupled with recurrent neural networks by ref. 32 to encode sentences into a continuous latent space. This approach is followed for the SMILES format both by ref. 21 and here. The SMILES variational autoencoder, together with our constraint function, is shown in Fig. 2.
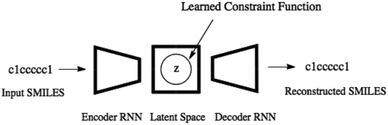 | ||
| Fig. 2 The SMILES variational autoencoder with the learned constraint function illustrated by a circular feasible region in the latent space. | ||
The origin of dead regions in the latent space
The approach introduced in this paper aims to solve the problem of dead regions in the latent space of the VAE. It is first however, important to understand the origin of these dead zones. Three ways in which a dead zone can arise are:(1) Sampling locations that are very unlikely under the prior. This was noted in the original paper on variational autoencoders30 where sampling was adjusted through the inverse conditional distribution function of a Gaussian.
(2) A latent space dimensionality that is artificially high will yield dead zones in the manifold learned during training.33 This has been demonstrated to be the case empirically in ref. 34.
(3) Inhomogenous training data; undersampled regions of the data space are liable to yield gaps in the latent space.
A schematic illustrating sampling from a dead zone, and the associated effect it has on the generated SMILES strings, is given in Fig. 3. In our case, the Bayesian optimization scheme is decoupled from the VAE and hence has no knowledge of the location of the learned manifold. In many instances the explorative behaviour in the acquisition phase of Bayesian optimization will drive the selection of invalid points lying far away from the learned manifold.
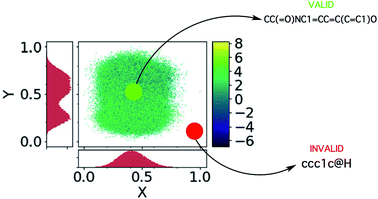 | ||
Fig. 3 The dead zones in the latent space, adapted from ref. 21. The x and y axes are the principle components computed by PCA. The colour bar gives the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value of the encoded latent points and the histograms show the coordinate-projected density of the latent points. One may observe that the encoded molecules are not distributed uniformly across the box constituting the bounds of the latent space. P value of the encoded latent points and the histograms show the coordinate-projected density of the latent points. One may observe that the encoded molecules are not distributed uniformly across the box constituting the bounds of the latent space. | ||
Objective functions for Bayesian optimization of molecules
Bayesian optimization is performed here in the latent space of the variational autoencoder in order to find molecules that score highly under a specified objective function. We assess molecular quality on the following objectives:Jcomplog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) = log P(z) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) − SA(z) − ring-penalty(z), P(z) − SA(z) − ring-penalty(z), |
| JcompQED(z) = QED(z) − SA(z) − ring-penalty(z), |
| JQED(z) = QED(z). |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) is the water–octanol partition coefficient, QED(z) is the quantitative estimate of drug-likeness35 and SA(z) is the synthetic accessibility.36 The ring penalty term is as featured in ref. 21. The “comp” subscript is designed to indicate that the objective function is a composite of standalone metrics.
P(z) is the water–octanol partition coefficient, QED(z) is the quantitative estimate of drug-likeness35 and SA(z) is the synthetic accessibility.36 The ring penalty term is as featured in ref. 21. The “comp” subscript is designed to indicate that the objective function is a composite of standalone metrics.
It is important to note, that the first objective, a common metric of comparison in this area, is misspecified as has been pointed out by ref. 37. From a chemical standpoint it is undesirable to maximize the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score as is being done here. Rather it is preferable to optimize log
P score as is being done here. Rather it is preferable to optimize log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P to be in a range that is in accordance with the Lipinski rule of five.38 We use the penalized log
P to be in a range that is in accordance with the Lipinski rule of five.38 We use the penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective here because regardless of its relevance for chemistry, it serves as a point of comparison against other methods.
P objective here because regardless of its relevance for chemistry, it serves as a point of comparison against other methods.
Constrained Bayesian optimization of molecules
We now describe our extension to the Bayesian optimization procedure followed by ref. 21. Expressed formally, the constrained optimization problem iswhere f(z) is a black-box objective function,
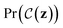 denotes the probability that a Boolean constraint
denotes the probability that a Boolean constraint 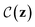 is satisfied and 1 − δ is some user-specified minimum confidence that the constraint is satisfied.39 The constraint is that a latent point must decode successfully a large fraction of the times decoding is attempted. The specific fractions used are provided in the results section. The black-box objective function is noisy because a single latent point may decode to multiple molecules when the model makes a mistake, obtaining different values under the objective. In practice, f(z) is one of the objectives described in Section 2.3.
is satisfied and 1 − δ is some user-specified minimum confidence that the constraint is satisfied.39 The constraint is that a latent point must decode successfully a large fraction of the times decoding is attempted. The specific fractions used are provided in the results section. The black-box objective function is noisy because a single latent point may decode to multiple molecules when the model makes a mistake, obtaining different values under the objective. In practice, f(z) is one of the objectives described in Section 2.3.
Expected improvement with constraints (EIC)
EIC may be thought of as expected improvement (EI),| EI(z) = Ef(z)[max(0,f(z) − η)], |
The incumbent solution η in EI(z), may be set in an analogous way to vanilla expected improvement41 as either:
(1) The best observation in which all constraints are observed to be satisfied.
(2) The minimum of the posterior mean such that all constraints are satisfied.
The latter approach is adopted for the experiments performed in this paper. If at the stage in the Bayesian optimization procedure where a feasible point has yet to be located, the form of acquisition function used is that defined by ref. 41.
Related work
The literature concerning generative models of molecules has exploded since the first work on the topic.21 Current methods feature molecular representations such as SMILES42–54 and graphs55–72 and employ reinforcement learning73–83 as well as generative adversarial networks84 for the generative process. These methods are well-summarized by a number of recent review articles.85–89 In terms of VAE-based approaches, two popular approaches for incorporating property information into the generative process are Bayesian optimization and conditional variational autoencoders (CVAEs).90 When generating molecules using CVAEs, the target data y is embedded into the latent space and conditional sampling is performed47,91 in place of a directed search via Bayesian optimization. In this work we focus solely on VAE-based Bayesian optimization schemes for molecule generation and so we do not benchmark model performance against the aforementioned methods. Principally, we are concerned with highlighting the issue of training set mismatch in VAE-based Bayesian optimizations schemes and demonstrating the superior performance of a constrained Bayesian optimization approach.Results and discussion
Experiment I
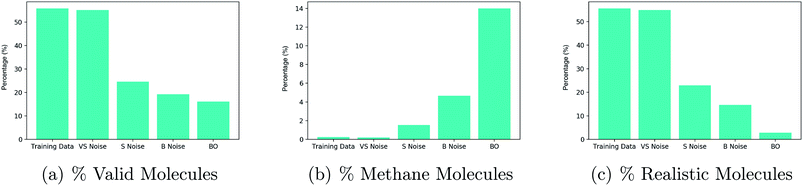
There is a noticeable decrease in the percentage of valid molecules decoded as one moves further away from the training data in latent space. Points collected by Bayesian optimization do the worst in terms of the percentage of valid decodings. This would suggest that these points lie farthest from the training data. The decoder over-generates methane molecules when far away from the data. One hypothesis for why this is the case is that methane is represented as ‘C’ in the SMILES syntax and is by far the most common character. Hence far away from the training data, combinations such as ‘C’ followed by a stop character may have high probability under the distribution over sequences learned by the decoder.
Given that methane has far too low a molecular weight to be a suitable drug candidate, a third plot in Fig. 3(c), shows the percentage of decoded molecules such that the molecules are both valid and have a tangible molecular weight. The definition of a tangible molecular weight was interpreted somewhat arbitrarily as a SMILES length of 5 or greater. Henceforth, molecules that are both valid and have a SMILES length greater than 5 will be referred to as realistic. This definition serves the purpose of determining whether the decoder has been successful or not.
As a result of these diagnostic experiments, it was decided that the criteria for labelling latent points to initialize the binary classification neural network for the constraint would be the following: if the latent point decodes into realistic molecules in more than 20% of decode attempts, it should be classified as realistic and non-realistic otherwise.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 positive class points and 117
440 positive class points and 117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 negative class points. The positive points were obtained by running the training data through the decoder assigning them positive labels if they satisfied the criteria outlined in the previous section. The negative class points were collected by decoding points sampled uniformly at random across the 56 latent dimensions of the design space. Each latent point undergoes 100 decode attempts and the most probable SMILES string is retained. Jcomplog
440 negative class points. The positive points were obtained by running the training data through the decoder assigning them positive labels if they satisfied the criteria outlined in the previous section. The negative class points were collected by decoding points sampled uniformly at random across the 56 latent dimensions of the design space. Each latent point undergoes 100 decode attempts and the most probable SMILES string is retained. Jcomplog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) is the choice of objective function. The raw validity percentages for constrained and unconstrained Bayesian optimization are given in Table 1.
P(z) is the choice of objective function. The raw validity percentages for constrained and unconstrained Bayesian optimization are given in Table 1.
| Run | Baseline | Constrained |
|---|---|---|
| 1 | 29% | 94% |
| 2 | 51% | 97% |
| 3 | 12% | 90% |
| 4 | 37% | 93% |
| 5 | 49% | 86% |
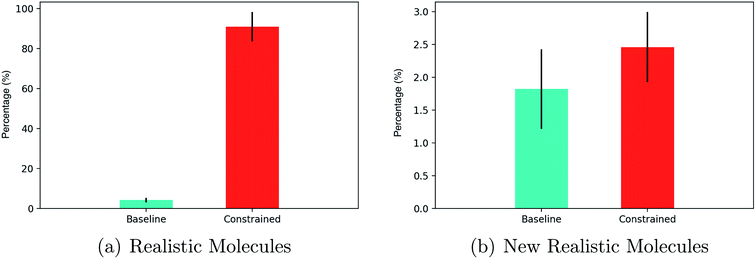
In terms of realistic molecules, the relative performance of constrained Bayesian optimization and unconstrained Bayesian optimization (baseline)21 is compared in Fig. 5(a).
The results show that greater than 80% of the latent points decoded by constrained Bayesian optimization produce realistic molecules compared to less than 5% for unconstrained Bayesian optimization. One must account however, for the fact that the constrained approach may be decoding multiple instances of the same novel molecules. Constrained and unconstrained Bayesian optimization are compared on the metric of the percentage of unique novel molecules produced in Fig. 5(b).
One may observe that constrained Bayesian optimization outperforms unconstrained Bayesian optimization in terms of the generation of unique molecules, but not by a large margin. A manual inspection of the SMILES strings collected by the unconstrained optimization approach showed that there were many strings with lengths marginally larger than the cutoff point, which is suggestive of partially decoded molecules. We run a further test of drug-likeness for the unique novel molecules generated by both methods consisting of passing a number of functional group filters consisting of 8 sets of structural alerts from the ChEMBL database. The alerts consisted of the Pan Assay Interference Compounds (PAINS)96 alert set for nuisance compounds that elude usual reactivity, the NIH MLSMR alert set for excluded functionality filters, the Inpharmatica alert set for unwanted fragments, the Dundee alert set,97 the BMS alert set,98 the Pfizer Lint procedure alert set99 and the Glaxo Wellcome alert set.100 An additional screen dictating that molecules should have a molecular weight between 150–500 daltons was also included. The results are given in Table 2.
| Baseline | Constrained |
|---|---|
| 6.6% | 35.7% |
In the next section we compare the quality of the novel molecules produced as judged by the scores from the black-box objective function.
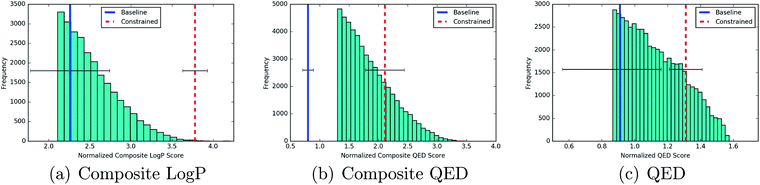
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) objective and over the 90th percentile for the remaining objectives. Table 3 gives the percentile that the averaged score of the new molecules found by each process occupies in the distribution over training set scores. The Jcomplog
P(z) objective and over the 90th percentile for the remaining objectives. Table 3 gives the percentile that the averaged score of the new molecules found by each process occupies in the distribution over training set scores. The Jcomplog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(z) objective is included as a metric for the generative performance of the models. It has been previously noted that it should not be beneficial for the purposes of drug design.
P(z) objective is included as a metric for the generative performance of the models. It has been previously noted that it should not be beneficial for the purposes of drug design.
| Objective | Baseline | Constrained |
|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P composite P composite |
36 ± 14 | 92 ± 4 |
| QED composite | 14 ± 3 | 72 ± 10 |
| QED | 11 ± 2 | 79 ± 4 |
For the penalised log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective function, scores for each run are presented in Table 4. The best score obtained from our constrained Bayesian optimization approach is compared against the scores reported by other methods in Table 5. The best molecule under the penalised log
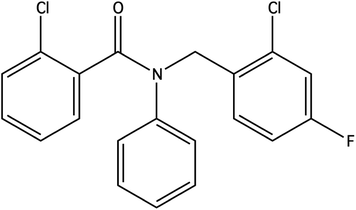
P objective function, scores for each run are presented in Table 4. The best score obtained from our constrained Bayesian optimization approach is compared against the scores reported by other methods in Table 5. The best molecule under the penalised log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective obtained from our method is depicted in Fig. 7.
P objective obtained from our method is depicted in Fig. 7.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective scores with the best score obtained highlighted in bold
P objective scores with the best score obtained highlighted in bold
| Run | Baseline | Constrained |
|---|---|---|
| 1 | 2.02 | 4.01 |
| 2 | 2.81 | 3.86 |
| 3 | 1.45 | 3.62 |
| 4 | 2.56 | 3.82 |
| 5 | 2.47 | 3.63 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P objective function scores against other models. Note that the results are taken from the original works and as such don't constitute a direct performance comparison due to different run configurations
P objective function scores against other models. Note that the results are taken from the original works and as such don't constitute a direct performance comparison due to different run configurations
Experiment II
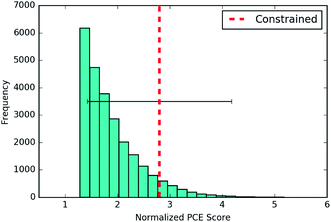
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules drawn at random from the Harvard Clean Energy Project dataset using 512 bit Morgan circular fingerprints101 as input features with bond radius of 2 computed using RDKit.102 While a larger radius may be appropriate for the prediction of PCE in order to represent conjugation, we are only interested in showing how a property predictor might be incorporated into the automatic chemical design framework and not in optimizing that predictor. The network was trained for 25 epochs with the ADAM optimizer103 using black box alpha divergence minimization with an alpha parameter of 5, a learning rate of 0.01, and a batch size of 500. The RMSE on the training set of 200
000 molecules drawn at random from the Harvard Clean Energy Project dataset using 512 bit Morgan circular fingerprints101 as input features with bond radius of 2 computed using RDKit.102 While a larger radius may be appropriate for the prediction of PCE in order to represent conjugation, we are only interested in showing how a property predictor might be incorporated into the automatic chemical design framework and not in optimizing that predictor. The network was trained for 25 epochs with the ADAM optimizer103 using black box alpha divergence minimization with an alpha parameter of 5, a learning rate of 0.01, and a batch size of 500. The RMSE on the training set of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules is 0.681 and the RMSE on the test set of 25
000 molecules is 0.681 and the RMSE on the test set of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules is 0.999.
000 molecules is 0.999.
Concluding remarks
The reformulation of the search procedure in the Automatic Chemical Design model as a constrained Bayesian optimization problem has led to concrete improvements on two fronts:(1) Validity – the number of valid molecules produced by the constrained optimization procedure offers a marked improvement over the original model.
(2) Quality – for five independent train/test splits, the scores of the best molecules generated by the constrained optimization procedure consistently ranked above the 90th percentile of the distribution over training set scores for all objectives considered.
These improvements provide strong evidence that constrained Bayesian optimization is a good solution method for the training set mismatch pathology present in the unconstrained approach for molecule generation. More generally, we foresee that constrained Bayesian optimization is a workable solution to the training set mismatch problem in any VAE-based Bayesian optimization scheme. Our code is made publicly available at https://github.com/Ryan-Rhys/Constrained-Bayesian-Optimisation-for-Automatic-Chemical-Design. Further work could feature improvements to the constraint scheme106–111 as well as extensions to model heteroscedastic noise.112
In terms of objectives for molecule generation, recent work by44,89,91,113,114 has featured a more targeted search for novel compounds. This represents a move towards more industrially-relevant objective functions for Bayesian optimization which should ultimately replace the chemically misspecified objectives, such as the penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P score, identified both here and in ref. 37. In addition, efforts at benchmarking generative models of molecules115,116 should also serve to advance the field. Finally, in terms of improving parallel Bayesian optimization procedures in molecule generation applications one point of consideration is the relative batch size of collected points compared to the dataset size used to initialize the surrogate model. We suspect that in order to gain benefit from sequential sampling the batch size should be on the same order of magnitude as the size of the initialization set as this will induce the uncertainty estimates of the updated surrogate model to change in a tangible manner.
P score, identified both here and in ref. 37. In addition, efforts at benchmarking generative models of molecules115,116 should also serve to advance the field. Finally, in terms of improving parallel Bayesian optimization procedures in molecule generation applications one point of consideration is the relative batch size of collected points compared to the dataset size used to initialize the surrogate model. We suspect that in order to gain benefit from sequential sampling the batch size should be on the same order of magnitude as the size of the initialization set as this will induce the uncertainty estimates of the updated surrogate model to change in a tangible manner.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Jonathan Gordon for useful discussions on the interaction between the Bayesian optimization scheme and the latent space of the variational autoencoder.References
- S. Ryu, J. Lim, S. H. Hong and W. Y. Kim, Deeply learning molecular structure-property relationships using attention-and gate-augmented graph convolutional network, arXiv preprint arXiv:1805.10988, 2018.
- J. Y. Ryu, H. U. Kim and S. Y. Lee, Deep learning improves prediction of drug–drug and drug–food interactions, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4304–E4311 CrossRef CAS.
- L. Turcani, R. L. Greenaway and K. E. Jelfs, Machine Learning for Organic Cage Property Prediction, Chem. Mater., 2018, 31, 714–727 CrossRef.
- S. Dey, H. Luo, A. Fokoue, J. Hu and P. Zhang, Predicting adverse drug reactions through interpretable deep learning framework, BMC Bioinf., 2018, 19, 476 CrossRef CAS PubMed.
- C. W. Coley, R. Barzilay, W. H. Green, T. S. Jaakkola and K. F. Jensen, Convolutional embedding of attributed molecular graphs for physical property prediction, J. Chem. Inf. Model., 2017, 57, 1757–1772 CrossRef CAS PubMed.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, Machine learning for renewable energy materials, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- M. Zeng, J. N. Kumar, Z. Zeng, R. Savitha, V. R. Chandrasekhar and K. Hippalgaonkar, Graph convolutional neural networks for polymers property prediction, arXiv preprint arXiv:1811.06231, 2018.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A graph-convolutional neural network model for the prediction of chemical reactivity, Chem. Sci., 2019, 10, 370–377 RSC.
- I. Cortés-Ciriano and A. Bender, Deep confidence: a computationally efficient framework for calculating reliable prediction errors for deep neural networks, J. Chem. Inf. Model., 2018, 59, 1269–1281 CrossRef PubMed.
- Y. Zhang and A. A. Lee, Bayesian semi-supervised learning for uncertainty-calibrated prediction of molecular properties and active learning, Chem. Sci., 2019 Search PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019 Search PubMed.
- S. Ryu, Y. Kwon and W. Y. Kim, Uncertainty quantification of molecular property prediction with Bayesian neural networks, arXiv preprint arXiv:1903.08375, 2019.
- K. McCloskey, A. Taly, F. Monti, M. P. Brenner and L. J. Colwell, Using attribution to decode binding mechanism in neural network models for chemistry, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11624–11629 CAS.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, What is high-throughput virtual screening? A perspective from organic materials discovery, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS.
- B. Playe, Méthodes d’apprentissage statistique pour le criblage virtuel de médicament, PhD thesis, Paris Sciences et Lettres, 2019.
- J. M. Hernández-Lobato, J. Requeima, E. O. Pyzer-Knapp and A. Aspuru-Guzik, Parallel and distributed Thompson sampling for large-scale accelerated exploration of chemical space, Proceedings of the 34th International Conference on Machine Learning, 2017, vol. 70, pp. 1470–1479 Search PubMed.
- E. Pyzer-Knapp, Bayesian optimization for accelerated drug discovery, IBM J. Res. Dev., 2018, 62, 2–1 Search PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al., Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach, Nat. Mater., 2016, 15, 1120–1127 CrossRef.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. SÃČÂąnchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, The Harvard Clean Energy Project: Large-Scale Computational Screening and Design of Organic Photovoltaics on the World Community Grid, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. R. Seress, C. Roman-Salgado, K. Trepte, S. Atahan-Evrenk and S. Er, et al., Lead candidates for high-performance organic photovoltaics from high-throughput quantum chemistry – the Harvard Clean Energy Project, Energy Environ. Sci., 2014, 7, 698–704 RSC.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4, 268–276 CrossRef.
- D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, ‘Found in Translation’: predicting outcomes of complex organic chemistry reactions using neural sequence-to-sequence models, Chem. Sci., 2018, 9, 6091–6098 RSC.
- W. Jin, C. Coley, R. Barzilay and T. Jaakkola, Predicting Organic Reaction Outcomes with Weisfeiler–Lehman Network, Advances in Neural Information Processing Systems, 2017, pp 2604–2613 Search PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A graph-convolutional neural network model for the prediction of chemical reactivity, Chem. Sci., 2019, 10, 370–377 RSC.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. Bekas and A. A. Lee, Molecular transformer for chemical reaction prediction and uncertainty estimation, arXiv preprint arXiv:1811.02633, 2018.
- J. Bradshaw, M. J. Kusner, B. Paige, M. H. Segler and J. M. Hernández-Lobato, A Generative Model of Electron Paths, International Conference on Learning Representations, 2019 Search PubMed.
- J. Bradshaw, B. Paige, M. J. Kusner, M. H. Segler and J. M. Hernández-Lobato, A Model to Search for Synthesizable Molecules, arXiv preprint arXiv:1906.05221, 2019.
- P. Schwaller, A. C. Vaucher, V. H. Nair and T. Laino, Data-Driven Chemical Reaction Classification with Attention-Based Neural Networks, ChemRxiv, 2019.
- D. P. Kingma and M. Welling, Auto-Encoding Variational Bayes, International Conference on Learning Representations, 2014 Search PubMed.
- D. P. Kingma, S. Mohamed, D. J. Rezende and M. Welling, Semi-supervised learning with deep generative models, Advances in Neural Information Processing Systems, 2014, pp. 3581–3589 Search PubMed.
- S. R. Bowman, L. Vilnis, O. Vinyals, A. M. Dai, R. Józefowicz and S. BengioGenerating Sentences from a Continuous Space, CoNLL, 2015 Search PubMed.
- T. White, Sampling Generative Networks, arXiv preprint arXiv:1609.04468, 2016.
- A. Makhzani, J. Shlens, N. Jaitly, I. Goodfellow and B. Frey, Adversarial autoencoders, arXiv preprint arXiv:1511.05644, 2015.
- R. G. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Quantifying the chemical beauty of drugs, Nat. Chem., 2012, 4, 90–98 CrossRef.
- P. Ertl and A. Schuffenhauer, Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions, J. Cheminf., 2009, 1, 8 Search PubMed.
- R.-R. Griffiths, P. Schwaller and A. Lee, Dataset Bias in the Natural Sciences: A Case Study in Chemical Reaction Prediction and Synthesis Design, ChemRxiv, 2018.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings, Adv. Drug Delivery Rev., 1997, 23, 3–25 CrossRef CAS.
- M. A. Gelbart, J. Snoek and R. P. Adams, Bayesian optimization with unknown constraints, Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence, 2014, pp. 250–259 Search PubMed.
- M. Schonlau, W. J. Welch and D. R. Jones, Global versus local search in constrained optimization of computer models, Lecture Notes - Monograph Series, 1998, pp. 11–25 Search PubMed.
- M. A. Gelbart, Constrained Bayesian Optimization and Applications, PhD thesis, Harvard University, 2015.
- D. Janz, J. van der Westhuizen, B. Paige, M. Kusner and J. M. H. Lobato, Learning a Generative Model for Validity in Complex Discrete Structures, International Conference on Learning Representations, 2018 Search PubMed.
- M. H. Segler, T. Kogej, C. Tyrchan and M. P. Waller, Generating focused molecule libraries for drug discovery with recurrent neural networks, ACS Cent. Sci., 2017 Search PubMed.
- T. Blaschke, M. Olivecrona, O. Engkvist, J. Bajorath and H. Chen, Application of generative autoencoder in de novo molecular design, Mol. Inf., 2017 Search PubMed.
- M. Skalic, J. Jiménez, D. Sabbadin and G. De Fabritiis, Shape-Based Generative Modeling for de Novo Drug Design, J. Chem. Inf. Model., 2019, 59, 1205–1214 CrossRef CAS.
- P. Ertl, R. Lewis, E. J. Martin and V. Polyakov, In silico generation of novel, drug-like chemical matter using the LSTM neural network, arXiv preprint arXiv:1712.07449, Dec 20, 2017.
- J. Lim, S. Ryu, J. W. Kim and W. Y. Kim, Molecular generative model based on conditional variational autoencoder for de novo molecular design, J. Cheminf., 2018, 10, 31 Search PubMed.
- S. Kang and K. Cho, Conditional molecular design with deep generative models, J. Chem. Inf. Model., 2018, 59, 43–52 CrossRef.
- B. Sattarov, I. I. Baskin, D. Horvath, G. Marcou, E. J. Bjerrum and A. Varnek, De Novo Molecular Design by Combining Deep Autoencoder Recurrent Neural Networks with Generative Topographic Mapping, J. Chem. Inf. Model., 2019, 59, 1182–1196 CrossRef CAS.
- A. Gupta, A. T. Müller, B. J. Huisman, J. A. Fuchs, P. Schneider and G. Schneider, Generative recurrent networks for de novo drug design, Mol. Inf., 2018, 37, 1700111 CrossRef.
- S. Harel and K. Radinsky, Prototype-based compound discovery using deep generative models, Mol. Pharm., 2018, 15, 4406–4416 CrossRef CAS.
- N. Yoshikawa, K. Terayama, M. Sumita, T. Homma, K. Oono and K. Tsuda, Population-based de novo molecule generation, using grammatical evolution, Chem. Lett., 2018, 47, 1431–1434 CrossRef CAS.
- E. Bjerrum and B. Sattarov, Improving Chemical Autoencoder Latent Space and Molecular De Novo Generation Diversity with Heteroencoders, Biomolecules, 2018, 8, 131 CrossRef.
- S. Mohammadi, B. O'Dowd, C. Paulitz-Erdmann and L. Görlitz, Penalized Variational Autoencoder for Molecular Design, ChemRxiv, 2019.
- M. Simonovsky and N. Komodakis, GraphVAE: Towards Generation of Small Graphs Using Variational Autoencoders, Artificial Neural Networks and Machine Learning, 2018, pp. 412–422 Search PubMed.
- Y. Li, O. Vinyals, C. Dyer, R. Pascanu and P. Battaglia, Learning deep generative models of graphs, arXiv preprint arXiv:1803.03324, 2018.
- W. Jin, R. Barzilay and T. Jaakkola, Junction Tree Variational Autoencoder for Molecular Graph Generation, International Conference on Machine Learning, 2018, pp 2328–2337 Search PubMed.
- N. De Cao and T. Kipf, MolGAN: An implicit generative model for small molecular graphs, arXiv preprint arXiv:1805.11973, 2018.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, Grammar Variational Autoencoder, International Conference on Machine Learning, 2017, pp. 1945–1954 Search PubMed.
- H. Dai, Y. Tian, B. Dai, S. Skiena and L. Song, Syntax-Directed Variational Autoencoder for Structured Data, International Conference on Learning Representations, 2018 Search PubMed.
- B. Samanta, D. Abir, G. Jana, P. K. Chattaraj, N. Ganguly and M. G. Rodriguez, Nevae: A deep generative model for molecular graphs, Proceedings of the AAAI Conference on Artificial Intelligence, 2019, pp. 1110–1117 Search PubMed.
- Y. Li, L. Zhang and Z. Liu, Multi-objective de novo drug design with conditional graph generative model, J. Cheminf., 2018, 10, 33 Search PubMed.
- H. Kajino, Molecular Hypergraph Grammar with Its Application to Molecular Optimization, International Conference on Machine Learning, 2019, pp. 3183–3191 Search PubMed.
- W. Jin, K. Yang, R. Barzilay and T. Jaakkola, Learning Multimodal Graph-to-Graph Translation for Molecule Optimization, International Conference on Learning Representations, 2019 Search PubMed.
- X. Bresson and T. Laurent, A Two-Step Graph Convolutional Decoder for Molecule Generation, arXiv, abs/1906.03412, 2019.
- J. Lim, S.-Y. Hwang, S. Kim, S. Moon and W. Y. Kim, Scaffold-based molecular design using graph generative model, arXiv preprint arXiv:1905.13639, 2019.
- S. Pölsterl and C. Wachinger, Likelihood-Free Inference and Generation of Molecular Graphs, arXiv preprint arXiv:1905.10310, 2019.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, SELFIES: a robust representation of semantically constrained graphs with an example application in chemistry, arXiv preprint arXiv:1905.13741, 2019.
- Ł. Maziarka, A. Pocha, J. Kaczmarczyk, K. Rataj and M. Warchoł, Mol-CycleGAN-a generative model for molecular optimization, arXiv preprint arXiv:1902.02119, 2019.
- K. Madhawa, K. Ishiguro, K. Nakago and M. Abe, GraphNVP: An Invertible Flow Model for Generating Molecular Graphs, arXiv preprint arXiv:1905.11600, 2019.
- R. D. Shen, Automatic Chemical Design with Molecular Graph Variational Autoencoders, M.Sc. thesis, University of Cambridge, 2018.
- K. Korovina, S. Xu, K. Kandasamy, W. Neiswanger, B. Poczos, J. Schneider and E. P. Xing, ChemBO: Bayesian Optimization of Small Organic Molecules with Synthesizable Recommendations, arXiv e-prints, arXiv:1908.01425, 2019.
- G. L. Guimaraes, B. Sanchez-Lengeling, P. L. C. Farias and A. Aspuru-Guzik, Objective-reinforced generative adversarial networks (ORGAN) for sequence generation models, arXiv preprint arXiv:1705.10843, May 30, 2017.
- Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Optimization of molecules via deep reinforcement learning, Sci. Rep., 2019, 9, 10752 CrossRef.
- E. Putin, A. Asadulaev, Q. Vanhaelen, Y. Ivanenkov, A. V. Aladinskaya, A. Aliper and A. Zhavoronkov, Adversarial threshold neural computer for molecular de novo design, Mol. Pharm., 2018, 15, 4386–4397 CrossRef CAS.
- J. You, B. Liu, Z. Ying, V. Pande and J. Leskovec, Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation, Advances in Neural Information Processing Systems, 2018, vol. 31, pp 6410–6421 Search PubMed.
- E. Putin, A. Asadulaev, Y. Ivanenkov, V. Aladinskiy, B. Sanchez-Lengeling, A. Aspuru-Guzik and A. Zhavoronkov, Reinforced adversarial neural computer for de novo molecular design, J. Chem. Inf. Model., 2018, 58, 1194–1204 CrossRef CAS.
- X. Yang, J. Zhang, K. Yoshizoe, K. Terayama and K. Tsuda, ChemTS: an efficient python library for de novo molecular generation, Sci. Technol. Adv. Mater., 2017, 18, 972–976 CrossRef CAS.
- H. Wei, M. Olarte and G. B. Goh, Multiple-objective Reinforcement Learning for Inverse Design and Identification, 2019 Search PubMed.
- N. Ståhl, G. Falkman, A. Karlsson, G. Mathiason and J. Boström, Deep reinforcement learning for multiparameter optimization in de novo drug design, J. Chem. Inf. Model., 2019 Search PubMed.
- E. Kraev, Grammars and reinforcement learning for molecule optimization, arXiv preprint arXiv:1811.11222, 2018.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de-novo design through deep reinforcement learning, J. Cheminf., 2017, 9, 48 Search PubMed.
- M. Popova, M. Shvets, J. Oliva and O. Isayev, MolecularRNN: Generating realistic molecular graphs with optimized properties, arXiv preprint arXiv:1905.13372, 2019.
- O. Prykhodko, S. Johansson, P.-C. Kotsias, E. J. Bjerrum, O. Engkvist and H. Chen, A de novo molecular generation method using latent vector based generative adversarial network, ChemRxiv, 2019.
- D. Xue, Y. Gong, Z. Yang, G. Chuai, S. Qu, A. Shen, J. Yu and Q. Liu, Advances and challenges in deep generative models for de novo molecule generation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1395 Search PubMed.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, Deep learning for molecular design – a review of the state of the art, Mol. Syst. Des. Eng., 2019, 4, 828–849 RSC.
- D. Schwalbe-Koda and R. Gómez-Bombarelli, Generative Models for Automatic Chemical Design, arXiv preprint arXiv:1907.01632, 2019.
- D. T. Chang, Probabilistic Generative Deep Learning for Molecular Design, arXiv preprint arXiv:1902.05148, 2019.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361, 360–365 CrossRef CAS.
- K. Sohn, H. Lee and X. Yan, Learning structured output representation using deep conditional generative models, Advances in neural information processing systems, 2015, pp 3483–3491 Search PubMed.
- D. Polykovskiy, A. Zhebrak, D. Vetrov, Y. Ivanenkov, V. Aladinskiy, M. Bozdaganyan, P. Mamoshina, A. Aliper, A. Zhavoronkov and A. Kadurin, Entangled Conditional Adversarial Autoencoder for de-novo Drug Discovery, Mol. Pharm., 2018 Search PubMed.
- J. M. Hernández-Lobato, Y. Li, M. Rowland, T. Bui, D. Hernández-Lobato and R. E. Turner, Black-Box Alpha Divergence Minimization, Proceedings of The 33rd International Conference on Machine Learning, New York, New York, USA, 2016, pp 1511–1520 Search PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich and B. Al-Lazikani, ChEMBL: a large-scale bioactivity database for drug discovery, Nucleic Acids Res., 2011, 40, D1100–D1107 CrossRef.
- D. Ginsbourger, R. Le Riche and L. Carraro, A multi-points criterion for deterministic parallel global optimization based on Gaussian processes, HAL preprint hal-00260579, 2008 Search PubMed.
- J. J. Irwin, T. Sterling, M. M. Mysinger, E. S. Bolstad and R. G. Coleman, ZINC: a free tool to discover chemistry for biology, J. Chem. Inf. Model., 2012, 52, 1757–1768 CrossRef CAS.
- J. B. Baell and G. A. Holloway, New substructure filters for removal of pan assay interference compounds (PAINS) from screening libraries and for their exclusion in bioassays, J. Med. Chem., 2010, 53, 2719–2740 CrossRef CAS.
- R. Brenk, A. Schipani, D. James, A. Krasowski, I. H. Gilbert, J. Frearson and P. G. Wyatt, Lessons learnt from assembling screening libraries for drug discovery for neglected diseases, ChemMedChem, 2008, 3, 435–444 CrossRef CAS PubMed.
- B. C. Pearce, M. J. Sofia, A. C. Good, D. M. Drexler and D. A. Stock, An empirical process for the design of high-throughput screening deck filters, J. Chem. Inf. Model., 2006, 46, 1060–1068 CrossRef CAS PubMed.
- J. F. Blake, Identification and evaluation of molecular properties related to preclinical optimization and clinical fate, Med. Chem., 2005, 1, 649–655 CrossRef CAS.
- M. Hann, B. Hudson, X. Lewell, R. Lifely, L. Miller and N. Ramsden, Strategic pooling of compounds for high-throughput screening, J. Chem. Inf. Comput. Sci., 1999, 39, 897–902 CrossRef CAS.
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- G. Landrum, RDKit: open-source cheminformatics software, 2016 Search PubMed.
- D. Kingma and J. Ba, Adam: A method for stochastic optimization, arXiv preprint arXiv:1412.6980, 2014.
- D. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gómez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Convolutional Networks on Graphs for Learning Molecular Fingerprints, Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015, pp 2224–2232 Search PubMed.
- B. Ramsundar, S. M. Kearnes, P. Riley, D. Webster, D. E. Konerding and V. S. Pande, Massively multitask networks for drug discovery, arXiv preprint arXiv:1502.02072, Feb 6, 2015.
- T. Rainforth, T. A. Le, J.-W. van de Meent, M. A. Osborne and F. Wood, Bayesian optimization for probabilistic programs, Advances in Neural Information Processing Systems, 2016, pp 280–288 Search PubMed.
- O. Mahmood and J. M. Hernández-Lobato, A COLD Approach to Generating Optimal Samples, arXiv preprint arXiv:1905.09885, 2019.
- R. Astudillo and P. Frazier, Bayesian Optimization of Composite Functions, International Conference on Machine Learning, 2019, pp 354–363 Search PubMed.
- F. Hase, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, Phoenics: A Bayesian optimizer for chemistry, ACS Cent. Sci., 2018, 4, 1134–1145 CrossRef CAS PubMed.
- R. Moriconi, K. Kumar and M. P. Deisenroth, High-Dimensional Bayesian Optimization with Manifold Gaussian Processes, arXiv preprint arXiv:1902.10675, 2019.
- T. Bartz-Beielstein and M. Zaefferer, Model-based methods for continuous and discrete global optimization, Appl. Soft Comput., 2017, 55, 154–167 CrossRef.
- R.-R. Griffiths, M. Garcia-Ortegon, A. A. Aldrick and A. A. Lee, Achieving Robustness to Aleatoric Uncertainty with Heteroscedastic Bayesian Optimisation, arXiv preprint arXiv:1910.07779, 2019.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz and H. Tribukait, et al., Accelerating the discovery of materials for clean energy in the era of smart automation, Nat. Rev. Mater., 2018, 3 CAS.
- T. Aumentado-Armstrong, Latent Molecular Optimization for Targeted Therapeutic Design, arXiv preprint arXiv:1809.02032, 2018.
- N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, Guacamol: benchmarking models for de novo molecular design, J. Chem. Inf. Model., 2019, 59, 1096–1108 CrossRef CAS.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy and M. Veselov, et al., Molecular Sets (MOSES): A Benchmarking Platform for Molecular Generation Models, arXiv, abs/1811.12823, 2018.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental results validating the algorithm configuration on the toy Branin-Hoo function. See DOI: 10.1039/c9sc04026a |
| This journal is © The Royal Society of Chemistry 2020 |