Open Access Article
Open Access ArticleHow bulky ligands control the chemoselectivity of Pd-catalyzed N-arylation of ammonia†
Seoung-Tae
Kim
 ab,
Suyeon
Kim
ab,
Suyeon
Kim
 ab and
Mu-Hyun
Baik
ab and
Mu-Hyun
Baik
 *ba
*ba
aDepartment of Chemistry, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: mbaik2805@kaist.ac.kr
bCenter for Catalytic Hydrocarbon Functionalizations, Institute for Basic Science (IBS), Daejeon 34141, Republic of Korea
First published on 12th December 2019
Abstract
Steric bulk has been recognized as a central design principle for supporting ligands in the widely utilized Buchwald–Hartwig amination. In a recent example, it was shown that a Pd-catalyst carrying a phosphine ligand can successfully aminate aryl halides using ammonia as the nitrogen source. Interestingly, the chemoselectivity of this reaction was found to depend on the steric demand of the phosphine ligand. Whereas a sterically less demanding phosphine affords diphenylamine as the major product, it was shown that the amination reaction can be stopped after the first amination to give aniline if a sterically more encumbering phosphine ligand is used. Density functional theory calculations were carried out to examine the relationship between the steric demand of the phosphine ligand and the chemoselectivity. It was found that the key feature that leads to the chemoselectivity is the ability of the phosphine ligand to rotate the biaryl moiety of the ligand away from the Pd-center upon amine addition to release some of the steric crowding from the Pd-coordination site.
Introduction
The catalytic formation of C–N bonds is a tremendously important reaction in chemistry and the Pd-catalyzed Buchwald–Hartwig amination is one of the most powerful methods that is used widely in many different applications.1 Among the substrates that may serve as the nitrogen source of the reaction, ammonia is particularly challenging but interesting. Being the simplest of all amines, it is one of the cheapest and most abundant reactants, making it interesting from practical considerations2–5 for large scale synthetic applications. From more fundamental perspectives, using ammonia as a reactant poses several challenges. First, ammonia is an excellent ligand and can form very stable Lewis acid–base adducts with transition metals, which often leads to catalyst deactivation. For ammonia to act as an amine source, one of the N–H bonds must be cleaved during catalytic turnover. The N–H bond energy is ∼107 kcal mol−1 and special provisions must be made to meet this energy demand without making the reaction irreversible. Deprotonation is an obvious strategic alternative to the homolytic N–H bond cleavage, but with the pKa being ∼33, it is not clear at the onset whether this mechanistic pathway offers a decisive advantage.6–8 If the correct conditions were to be found for an efficient reaction that will form a primary arylamine, for instance, it may become difficult to maintain chemoselectivity, as the primary arylamine product should in principle be a better reactant than ammonia. Thus, mixtures of primary and secondary amines are anticipated and engineering chemoselectivity in these reactions becomes a necessary challenge that must be overcome to design a useful synthetic method. Several successful methods for the selective arylation of ammonia using transition metal catalysts have been reported recently.9–14 Buchwald reported an intriguing Pd-catalyzed example using a biaryl phosphine ligand. Interestingly, the chemoselectivity towards the primary or secondary arylamine product was shown to be controlled by the steric demand of the phosphine ligand, as summarized in Scheme 1.15,16 Whereas the sterically less demanding L1 ligand gave only the secondary amine, the chemoselectivity could be completely switched to the primary amine product even at aryl halide concentrations above 0.05 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 by decorating one of the biaryl moieties with Me and OMe functionalities as shown for L3 and L4 in Scheme 1. While the increased conformational rigidity resulting from the 3- and 6-methyl (or methoxy) groups in the biaryl backbone (L2, L3 and L4) was suggested to be a key component for the selectivity inversion,15 the precise mechanism of how the substitution switches the selectivity was unclear. Intuitively, increasing the steric demand of the phosphine ligand to disfavour the binding of the primary amine vs. ammonia is plausible. To obtain a more precise understanding of the features that control the chemoselectivity, we employed quantum chemical molecular modelling methods based on density functional theory (DFT) to construct a full catalytic cycle of the Pd-catalyzed chemoselective arylation reaction.
16 by decorating one of the biaryl moieties with Me and OMe functionalities as shown for L3 and L4 in Scheme 1. While the increased conformational rigidity resulting from the 3- and 6-methyl (or methoxy) groups in the biaryl backbone (L2, L3 and L4) was suggested to be a key component for the selectivity inversion,15 the precise mechanism of how the substitution switches the selectivity was unclear. Intuitively, increasing the steric demand of the phosphine ligand to disfavour the binding of the primary amine vs. ammonia is plausible. To obtain a more precise understanding of the features that control the chemoselectivity, we employed quantum chemical molecular modelling methods based on density functional theory (DFT) to construct a full catalytic cycle of the Pd-catalyzed chemoselective arylation reaction.
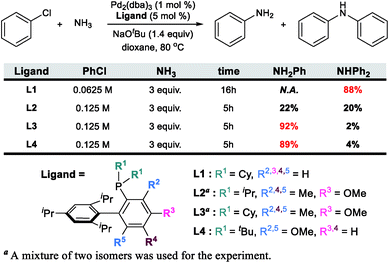 | ||
| Scheme 1 Previous experimental results of N-arylation with four different ligands. The bulkiness of a ligand increases from L1 to L4. | ||
Experimental
Computational details
All density functional theory (DFT) calculations were performed using the Jaguar 9.1 quantum chemistry program.17 Electronic exchange and correlation energy contribution to the total electronic energy was approximated with the B3LYP hybrid functional18,19 along with Grimme's D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 dispersion correction (B3LYP-D3). All intermediate and transition state geometries were optimized with the 6-31G** basis set21–23 for main group atoms. Pd was described by the Los Alamos relativistic effective core potential (ECP)24–26 and its corresponding LACVP basis set. While these basis sets are adequate for obtaining geometries, more reliable energies were obtained from the single point calculations using Dunning's correlation-consistent triple-ζ basis set, cc-pVTZ(-f),27 for main group and larger LACV3P for Pd. The zero-point energy (ZPE), entropic and solvation contributions to the Gibbs energy are obtained at the same level of theory as the geometry optimizations (B3LYP-D3/6-31G**/LACVP). The optimized geometries characterized as the local minima on the potential energy surfaces do not contain any imaginary frequency, while each of the transition states contains one imaginary frequency. The solvation calculations utilized the self-consistent reaction field (SCRF) approach using a standard Poisson–Boltzmann solver28–30 on the gas phase geometry to model the solvation shell of dielectric constant ε = 2.209, which we consider to be an approximate solvation environment offered by the 1,4-dioxane.
20 dispersion correction (B3LYP-D3). All intermediate and transition state geometries were optimized with the 6-31G** basis set21–23 for main group atoms. Pd was described by the Los Alamos relativistic effective core potential (ECP)24–26 and its corresponding LACVP basis set. While these basis sets are adequate for obtaining geometries, more reliable energies were obtained from the single point calculations using Dunning's correlation-consistent triple-ζ basis set, cc-pVTZ(-f),27 for main group and larger LACV3P for Pd. The zero-point energy (ZPE), entropic and solvation contributions to the Gibbs energy are obtained at the same level of theory as the geometry optimizations (B3LYP-D3/6-31G**/LACVP). The optimized geometries characterized as the local minima on the potential energy surfaces do not contain any imaginary frequency, while each of the transition states contains one imaginary frequency. The solvation calculations utilized the self-consistent reaction field (SCRF) approach using a standard Poisson–Boltzmann solver28–30 on the gas phase geometry to model the solvation shell of dielectric constant ε = 2.209, which we consider to be an approximate solvation environment offered by the 1,4-dioxane.
Results and discussion
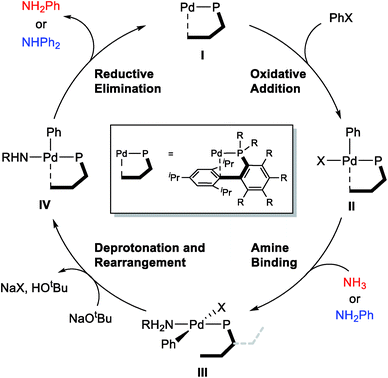
The general mechanism of the Pd-catalyzed Buchwald–Hartwig C–N cross-coupling reaction is well established,31–46 and the main features are summarized in Scheme 2. The catalytic cycle starts with the oxidative addition of the aryl halide substrate to afford intermediate II, which can bind the amine substrate to give a square-planar, 16-electron Pd(II)-intermediate III. The key deprotonation event takes place next with the assistance of an external base, such as NaOtBu, accompanied by the loss of the halide ligand to form a formally under-coordinated Pd-complex where the fourth coordination site is occupied by the aryl moiety of the sterically bulky phosphine ligand. Finally, reductive elimination gives the final amination product and reforms the Pd(0) catalyst.Proximal vs. distal conformation
Given the general pattern of the catalytic cycle, there are several steps where the steric bulk of the ligand can impact the reaction. Before these features are examined in detail, it is helpful to first study the impact of the functionalization on the chemical properties of the phosphine ligand itself. Scheme 1 summarizes the previously reported experimental results for four representative ligands that we studied in detail in this work. One key feature of the phosphine ligands carrying a biaryl appendage is their ability to move the sterically demanding biaryl unit into the coordination site of the Pd-center or move it away when needed. Empirically, it is known that the substitution at the C6 position tends to accelerate the reductive elimination step by increasing the steric congestion (Fig. 1),47 which is easy to understand. It is not clear, however, how the steric congestion may impact the reaction of the primary amine compared to ammonia at this step. In 2007, Buchwald examined how the amine substrate binds to Pd(II),33,48 and suggested that the increased steric demand due to the amine binding may induce the distal-form of the Pd-complex, where the biaryl moiety is rotated away from the Pd-center, as illustrated in Fig. 1. It is plausible to expect that this rotation will be significantly impacted by the presence of the additional R2 substituents on the phosphine-containing aryl ring and also be influenced by the bulkiness of the R1 group on the phosphine. Fig. 1 shows a potential energy surface scan along the Pd–P–C1–C2 dihedral angle, where 19 structures were optimized with a constrained Pd–P–C1–C2 dihedral angle ranging from 0° to 180°. Reaching a geometry that would give the distal-form of L1 is found to be uphill in energy, with the highest energy conformers being in the range of 13 kcal mol−1. Note that the actual rotation barrier is likely to be a few kcal mol−1 higher than what was found for the highest energy conformer.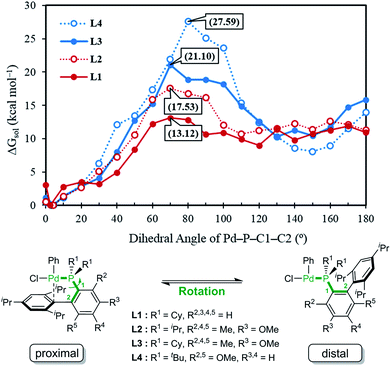 | ||
| Fig. 1 Relative free energy of the oxidative addition Pd-complex vs. varying dihedral angles (Pd–P–C1–C2) depending on the ligand, L1, L2, L3 and L4. | ||
As expected, the ligands that acquire further rigidity via R2 and R5 substitutions demand higher energies to approach the distal-form. Depending on the steric bulkiness of the R1 (iPr = L2, Cy = L3, or tBu = L4) groups, the substitutions increase the energy of the highest conformer to 18, 21 and 28 kcal mol−1, respectively, as shown in Fig. 1. Notably, the ∼3 kcal mol−1 higher energy of L3 over L2 is the result of the rigidity of Cy in L3 over iPr in L2 (see ESI† for details). These energy profiles indicate that the transition to the distal geometry becomes highly improbable for L3 and L4, whereas the (L1/L2)Pd complexes may adopt the distal-form with ease to accommodate amine binding.
Mechanism using L1
Considering the conceptual understanding of how the increased steric demand impedes the rotation of the biaryl functionality, which is key for the switch between the “distal” and “proximal” orientation of the biaryl ligand, the complete reaction mechanism was modelled using the L1 ligand, as shown in Fig. 2. The reaction energy profile for processing ammonia is shown in red, whereas the reaction using aniline as the substrate is given in blue. As discussed above, oxidative addition of phenyl chloride starts the catalytic cycle and the barrier associated with the computed transition state is only 10.1 kcal mol−1, which is consistent with rapid oxidative addition to give the first key intermediate 1A.47 With a less bulky ligand L1, the oxidative addition complex 1A readily rotates the biaryl ring with an estimated barrier of 13 kcal mol−1 and prefers to yield the distal form intermediate 1B rather than 1J which keeps the biaryl position fixed while undergoing rearrangement for the subsequent amine coordination. Since the proximal-conformer 1J located at 12.7 kcal mol−1 has an energy that is comparable to the rotation barrier and the distal-conformer 1B is computed to be 4.4 kcal mol−1 more stable than 1J due to the smaller steric congestion, the reaction will proceed through the distal pathway when L1 is used.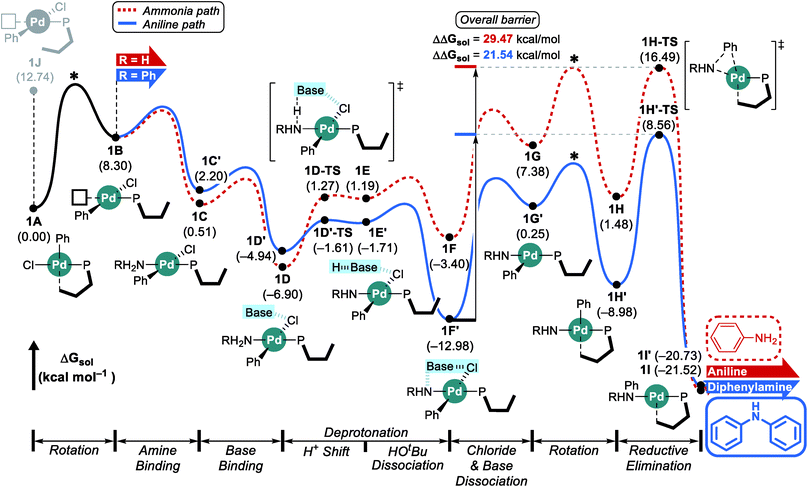 | ||
| Fig. 2 DFT-calculated energy profile for Pd-catalyzed N-arylation with L1. * represents the rotation barrier which is estimated to be over 13 kcal mol−1. | ||
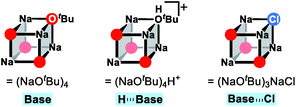
After the ligand rearrangement, the amine/ammonia binding and subsequent deprotonation assisted by NaOtBu push the reaction forward. Note that NaOtBu base is modelled in its tetrameric form considering the non-polar environment of the reaction, as illustrated in Scheme 3.49–51 The tert-butoxide is also examined as an active base but was found to be less probable in this system since this model failed to properly explain the observed chemoselectivity (see ESI† for details).
Since ammonia is the only substrate available at the beginning, the initial reaction follows the pathway shown in red to produce aniline. The binding of ammonia to 1B yields the intermediate 1C that has the same ligand arrangement as the reported crystal structure.33 Next, the NaOtBu base binds to 1C to give intermediate 1D at a free energy of −6.9 kcal mol−1. As discussed above, deprotonation of ammonia is challenging, despite the utility of the strong base NaOtBu, and the deprotonated intermediate 1E is ∼8 kcal mol−1 higher in energy. Dissociation of tert-butanol and extraction of the chloride anion, which becomes incorporated into the NaOtBu tetramer, ensure charge neutrality of this step and result in the intermediate 1F at −3.4 kcal mol−1. Release of the base that carries the chloride anion gives the putative intermediate 1G, which is the 3-coordinate intermediate carrying the aryl and amido groups, in addition to the phosphine ligand. This intermediate is shown in Fig. 2, but is unlikely to exist, as rotation of the biaryl moiety of the phosphine ligand will easily give access to the proximal form to restore the Pd–Cipso interaction and lower the energy of the Pd-complex by ∼6 kcal mol−1 in 1H. The amido-nitrogen can now form a C–N bond in a reductive elimination step. The transition state 1H-TS is found at 16.5 kcal mol−1 resulting in an overall barrier of 23.4 kcal mol−1, ΔrG(1D → 1H-TS), which is reasonable to be overcome under the given experimental conditions.
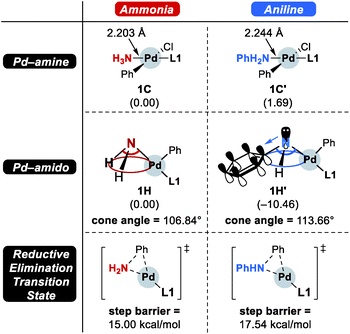
As the catalytic reaction proceeds, aniline and ammonia start to compete as reactants. And our calculations indicate that the binding of aniline is energetically less favoured by 1.7 kcal mol−1 compared to ammonia, which is in good agreement with the intuitive expectation that ammonia should be a better ligand for Pd(II) than aniline. But as demonstrated in a previous study from the Buchwald group, the amine binding preference does not affect the chemoselectivity,48 because this step is associated with very low energies and the amine binding is expected to be fully reversible with little impact on the overall selectivity. Our calculations predict that aniline is much easier to deprotonate and the key intermediate 1F′ is found at a relative energy of −13.0, which is nearly 10 kcal mol−1 lower than its analogue 1F, as illustrated in Fig. 2. Intermediate 1F′ is of utmost importance, as it is the lowest energy intermediate of the whole catalytic cycle. With both aniline and ammonia present in solution, the two reaction pathways are connected through the common intermediate 1B. Thus, intermediate 1F′ formally coexists by establishing an equilibrium with 1Fvia intermediate 1B, where the aniline reactant is exchanged with ammonia. Consequently, the rate determining barriers for both ammonia and aniline reactions must be evaluated from intermediate 1F′. Doing so, our calculations suggest that the overall barrier for reductive elimination using aniline is 21.5 kcal mol−1, ΔrG(1F′ → 1H′-TS), whereas that for ammonia in the presence of aniline becomes 29.5 kcal mol−1, ΔrG(1F′ → 1H-TS), as highlighted in Fig. 2. Therefore, the C–N coupling reaction with L1 is expected to convert aniline that is initially produced to give the diphenylamine product quantitatively, as shown in blue in Fig. 2.
Scheme 4 summarizes the difference of the two substrates that is described in the energy profile. The distinct feature of aniline originates from the interaction between the lone pair of nitrogen and the π-system of its Ph group that lowers its binding affinity and nucleophilicity. The relatively weak binding affinity of aniline gives rise to a Pd–N bond that is 0.041 Å longer and 1.7 kcal mol−1 higher intermediate energy of 1C′ compared to 1C. Whereas the resonance in aniline involving the lone-pair of nitrogen makes 1C′ less stable, this effect facilitates the generation of an amido group where additional lone-pair electrons are formed through deprotonation of the amine substrate. This effect drives the energy to be 10.5 kcal mol−1 lower and the cone angle is wider by 6.82° in 1H′ than in 1H. The difference of nucleophilicity also impacts the reductive elimination step where the amido moiety acts as a nucleophile to form the C–N bond. Our calculations show that the step barrier for reductive elimination in 1H is 2.5 kcal mol−1 lower than that of 1H′, in good agreement with intuitive expectations.
Mechanism using L2
The reaction with the L2 ligand furnishes both aniline and diphenylamine in almost identical amount with 54% conversion over a reaction time of 5 h (Scheme 1),18 while our calculations predict that this reaction should eventually generate diphenylamine dominantly. When interpreting quantum chemically calculated reaction energy profiles, it is important to recognize that the calculated barriers can only give an estimate for the reaction rate. Because it is not possible to reliably estimate the preexponential frequency factor of the Arrhenius equation, it is not possible to reliably represent the reaction rates. Matching experiments to computational models becomes particularly challenging, if the reaction does not convert completely, as is the case here. These limitations notwithstanding, we can still extract some useful information from our calculations using the L2 ligand. Although the functionalization at C3 and C6 positions makes the ligand more sterically bulky and escalates the rotation barrier to over 17 kcal mol−1, the increased steric congestion destabilizes the proximal conformer 2I at the same time and results in a free energy of 17.8 kcal mol−1 (Fig. 3). Thus, as was observed using L1, the distal pathway will also be slightly preferable with the L2 ligand. In addition to the rotation barrier increment, the functionalization accelerates the reductive elimination and therefore, the rotation step becomes the most difficult step in the reaction with L2. From the ground state intermediate 2E′ which has a relative free energy of −11.7 kcal mol−1, the rotation barrier to access 2G is presumably higher than 31 kcal mol−1. Consequently, as the reaction proceeds toward completion and the concentration of ammonia diminishes while that of aniline increases, the aniline pathway shown in blue will be preferred and yield diphenylamine dominantly. Overall, our calculation results predict that diphenylamine should be the major product if the reaction were to be allowed to reach full conversion. Note that the reaction with L1 which gives diphenylamine dominantly ran for 16 h while the reaction with L2 was run only for 5 h (Scheme 1).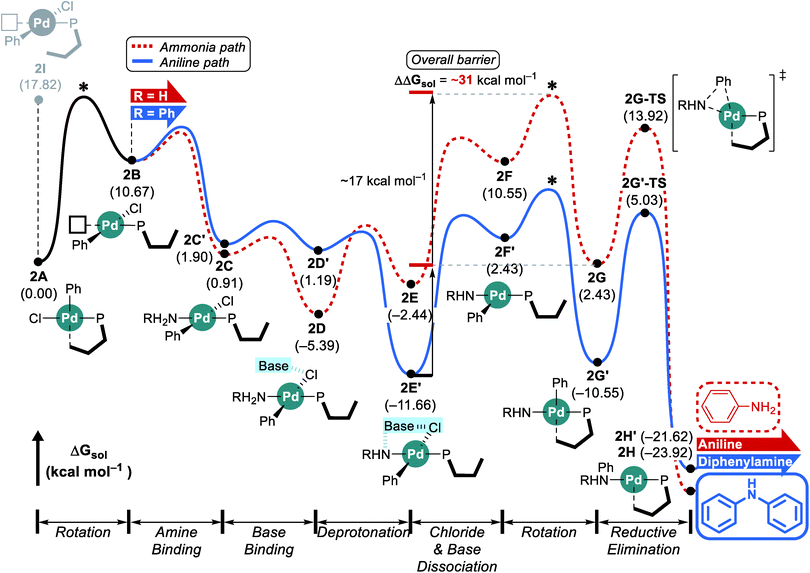 | ||
| Fig. 3 DFT-calculated energy profile for Pd-catalyzed N-arylation with L2. * represents the estimated rotation barrier which is estimated to be over 17 kcal mol−1. | ||
Mechanism using L3
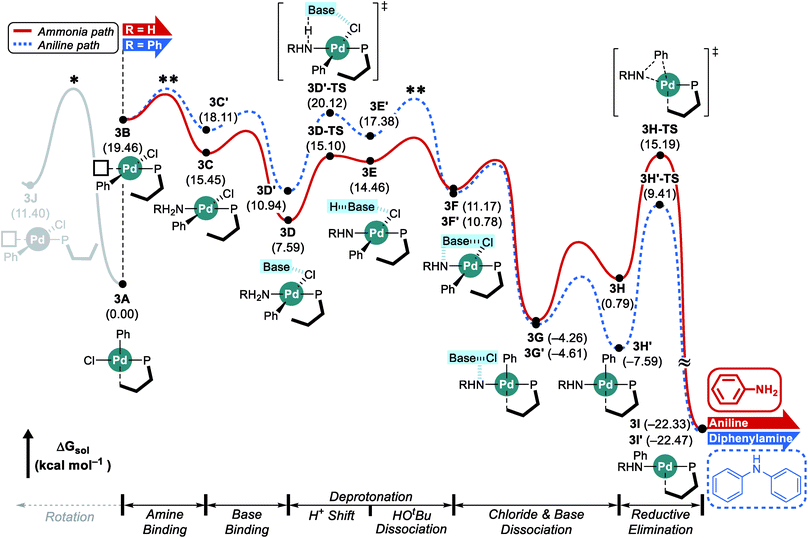
Fig. 4 shows the reaction energy profile of the catalytic reaction with the L3 ligand. In this case, the bulkier alkyl group on the phosphorus further disturbs the rotation in intermediate 3A and the proximal form of L3 is maintained throughout the whole catalytic cycle, as illustrated in Fig. 4. While the distal pathway is also examined as an alternative pathway considering the small energy difference between the proximal intermediate 3B and the estimated rotation barrier, this possibility is discarded since it cannot explain the observed selectivity (see ESI† for details).Once the rearranged intermediate 3B is formed, our proposed mechanism proceeds with the amine binding and subsequent deprotonation without releasing the sterically induced stress based on the proximal orientation of the phosphine ligand. Consequently, the early phase of the catalytic cycle shows much higher, but still accessible intermediate energies. The ammonia adduct 3C is located at 15.5 kcal mol−1 and the subsequent binding of the NaOtBu tetramer affords intermediate 3D at 7.6 kcal mol−1. Deprotonation and chloride extraction ultimately result in the formation of the intermediate 3G at −4.3 kcal mol−1, which can easily undergo reductive elimination via the transition state 3H-TS to produce aniline. Because of the steric crowding associated with the proximal form of the phosphine ligand, this reductive elimination barrier is relatively low and our calculations suggest that the ammonia binding step (3B → 3C) is most difficult in this reaction. As discussed above, we again considered adding an aniline substrate to intermediate 3B instead of ammonia, shown in blue in Fig. 4. With the phosphine ligand locked in the proximal arrangement, the amine adduct 3C′ is found at 18.1 kcal mol−1. The proton shift transition state 3D′-TS requires 20.1 kcal mol−1. Once the intermediate 3H′ is reached, the reductive elimination to form the final product is relatively easy with the transition state 3H′-TS being at 9.4 kcal mol−1. Comparing this reaction energy profile to that discussed for the L1 ligand, significant differences can be identified. The inability to release the steric repulsion encountered in the proximal configuration of the phosphine ligand forces the early phase of the reaction to be higher in energy so that the amine binding step or tert-butanol dissociation step which is part of the deprotonation process could influence the product selectivity. With the amine binding being the rate determining step, this catalytic cycle will provide aniline dominantly because the stronger nucleophilicity of ammonia in addition to the higher concentration of 3 equivalents promotes the generation of 3C over 3C′. Alternatively, the deprotonation could determine the selectivity: unlike in the case of L1, the ammonia substrate is preferred by nearly 5 kcal mol−1 at the proton shift transition states 3D-TS and 3D′-TS. In addition, the intermediate 3E′ is 2.9 kcal mol−1 higher in energy than 3E, leading to a higher probability of tert-butanol dissociation 3E′. While the dissociation barrier could not be explicitly located in the DFT method and thus, we could not compare the dissociation preference quantitatively, it is reasonable to assume that the barrier from 3E′ would be higher by following Hammond's postulate. In conclusion, these reaction energy profiles suggest that as long as ammonia is present, the Pd-catalyst will prefer ammonia over aniline as the reaction substrate.
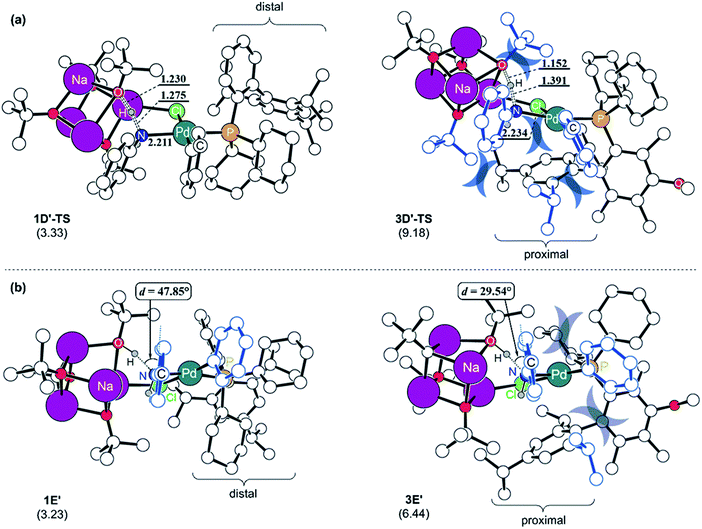
To understand the reason for the arduous aniline deprotonation process in the L3 system, the four structures involved in the proton-shift, 1D′-TS and 1E′ in the L1 system, and 3D′-TS and 3E′ in the L3 system are analysed in greater detail and illustrated in Fig. 5. The shorter O–H and longer N–H distances of 3D′-TS represent a late transition state, whereas the Pd–N bond which is also expected to be shorter according to the reaction progress is 0.023 Å longer and contributes to the higher barrier. The late transition state with respect to the deprotonation trajectory and the elongated Pd–N bond stem from the increased steric clash of the proximal-form. The late transition state is enforced by the bulkiness of the iPr substituent which is incorporated at the para-position of biaryl. This steric bulk determines the aniline-Ph orientation and enhances the repulsive interaction between the Ph and the tert-butoxide moiety in the early phase of the trajectory. Therefore, the saddle point is necessarily pushed to a late phase of the transition where the intense repulsive interaction is resolved to a higher degree. Furthermore, the elongation of the Pd–N bond is governed by the steric bulk of ortho-iPr which distorts the Ph on the Pd towards the Ph of the aniline and increases the repulsive steric interaction between them. As a result, the aniline proton shift barrier becomes 5.9 kcal mol−1 higher in the L3 system. The increased steric clash of the proximal form, especially the distorted Ph on the Pd, makes the intermediate resulting from the proton shift unstable. As shown in Fig. 5b, the proton shift of aniline is 6.4 kcal mol−1 uphill in L3 while that in L1 is only 3.2 kcal mol−1 uphill in energy. The optimized structures of the intermediates 1E′ and 3E′ clearly depict the reason for these energies. As discussed above, the favorable deprotonation property of aniline over ammonia is a result of the π-resonance. In the case of 3E′, this resonance is less likely to be maintained because the dihedral angle between the lone pair of the nitrogen and the Ph-plane of aniline is forced to be only 29.5° due to steric interactions from the Ph moiety on the Pd while 1E′ shows a dihedral angle of 47.8° without that steric demand.
The mechanism using L4 is nearly identical to that of L3 and is not described in detail here, but establishes that the features we describe are generally applicable to different ligand systems.
Conclusions
In conclusion, we studied the mechanism of the Pd-catalyzed N-arylation of ammonia and identified the reasons for the chemoselectivity observed as the nature of the phosphine ligand is varied by functionalization. The chemoselectivity is determined by a synergistic steric effect from the bulkiness of NaOtBu base, which is proposed to exist in a tetrameric form under the given conditions, and the steric demands of the ligands, where the rotation of the biaryl moiety of the phosphine ligand is severely hindered to force the phosphine ligand to maintain a proximal arrangement throughout the entire reaction. If sterically less encumbered ligands are used, the phosphine ligand can easily rotate the biaryl moiety to adopt the distal form, which releases much of the steric crowding that results from the addition of the amine substrate. The chemoselectivity observed for the proposed distal mechanism is ultimately the result of the pKa difference between ammonia and aniline that is expressed in a much easier deprotonation step, resulting in the preferential formation of the diphenylamine product. In the case of the proximal mechanism, the increased steric crowding pushes the early phase of the reaction trajectory towards higher energy and switches the selectivity determining state to the amine binding or the deprotonation process. Ammonia not only has a stronger binding affinity to Pd but also displays an easier proton shift ability due to the reduced steric crowding, which plays a key role in determining the chemoselectivity. Overall, this study offers a precise view on the two distinct reaction channels enabled by the dialkyl biaryl phosphine ligated catalyst and highlights how the bulkiness and rigidity of the ligand determine which channel becomes mechanistically relevant.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MHB acknowledges financial support from the Institute for Basic Science (IBS-R10-A1). We thank Prof. Stephen L. Buchwald and his group for fruitful discussions.Notes and references
- P. Ruiz-Castillo and S. L. Buchwald, Chem. Rev., 2016, 116, 12564–12649 CrossRef CAS PubMed.
- S. Enthaler, ChemSusChem, 2010, 3, 1024–1029 CrossRef CAS PubMed.
- P. T. Anastas and M. M. Kirchhoff, Acc. Chem. Res., 2002, 35, 686–694 CrossRef CAS PubMed.
- M. Appl, Ammonia: Principles and Industrial Practice, Wiley-VCH, Weinheim, 1999 Search PubMed.
- J. I. van der Vlugt, Chem. Soc. Rev., 2010, 39, 2302–2322 RSC.
- D. M. Roundhill, Chem. Rev., 1992, 92, 1–27 CrossRef CAS.
- J. L. Klinkenberg and J. F. Hartwig, Angew. Chem., Int. Ed., 2011, 50, 86–95 CrossRef CAS PubMed.
- J. Zhao, A. S. Goldman and J. F. Hartwig, Science, 2005, 307, 1080–1082 CrossRef CAS PubMed.
- C. Lombardi, J. Day, N. Chandrasoma, D. Mitchell, M. J. Rodriguez, J. L. Farmer and M. G. Organ, Organometallics, 2017, 36, 251–254 CrossRef CAS.
- M. Fan, W. Zhou, Y. Jiang and D. Ma, Org. Lett., 2015, 17, 5934–5937 CrossRef CAS PubMed.
- R. A. Green and J. F. Hartwig, Angew. Chem., Int. Ed., 2015, 127, 3839–3843 CrossRef.
- P. G. Alsabeh, R. J. Lundgren, R. McDonald, C. C. C. Johansson Seechurn, T. J. Colacot and M. Stradiotto, Chem.–Eur. J., 2013, 19, 2131–2141 CrossRef CAS PubMed.
- R. J. Lundgren, B. D. Peters, P. G. Alsabeh and M. Stradiotto, Angew. Chem., Int. Ed., 2010, 49, 4071–4074 CrossRef CAS PubMed.
- G. D. Vo and J. F. Hartwig, J. Am. Chem. Soc., 2009, 131, 11049–11061 CrossRef CAS PubMed.
- C. W. Cheung, D. S. Surry and S. L. Buchwald, Org. Lett., 2013, 15, 3734–3737 CrossRef CAS PubMed.
- D. S. Surry and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 10354–10355 CrossRef CAS PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre and W. A. Lathan, J. Chem. Phys., 1972, 56, 5255–5257 CrossRef CAS.
- V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984 CrossRef CAS.
- P. J. Hay, P. Jeffrey Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. Jeffrey Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay, P. Jeffrey Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard III, J. Am. Chem. Soc., 1994, 116, 11875–11882 CrossRef CAS.
- B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
- W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, J. Chem. Phys., 1970, 52, 2769–2773 CrossRef CAS.
- C. L. McMullin, B. Rühle, M. Besora, A. G. Orpen, J. N. Harvey and N. Fey, J. Mol. Catal. A: Chem., 2010, 324, 48–55 CrossRef CAS.
- B. H. Yang and S. L. Buchwald, J. Organomet. Chem., 1999, 576, 125–146 CrossRef CAS.
- T. E. Barder and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 12003–12010 CrossRef CAS PubMed.
- J. F. Hartwig, S. Richards, D. Barañano and F. Paul, J. Am. Chem. Soc., 1996, 118, 3626–3633 CrossRef CAS.
- S. Shekhar and J. F. Hartwig, Organometallics, 2007, 26, 340–351 CrossRef CAS PubMed.
- T. R. Cundari and J. Deng, J. Phys. Org. Chem., 2005, 18, 417–425 CrossRef CAS.
- F. Barrios-Landeros and J. F. Hartwig, J. Am. Chem. Soc., 2005, 127, 6944–6945 CrossRef CAS PubMed.
- F. Barrios-Landeros, B. P. Carrow and J. F. Hartwig, J. Am. Chem. Soc., 2009, 131, 8141–8154 CrossRef CAS PubMed.
- S. Shekhar, P. Ryberg, J. F. Hartwig, J. S. Mathew, D. G. Blackmond, E. R. Strieter and S. L. Buchwald, J. Am. Chem. Soc., 2006, 128, 3584–3591 CrossRef CAS PubMed.
- J. F. Hartwig, Inorg. Chem., 2007, 46, 1936–1947 CrossRef CAS PubMed.
- M. Ahlquist and P.-O. Norrby, Organometallics, 2007, 26, 550–553 CrossRef CAS.
- Y. Sunesson, E. Limé, S. O. Nilsson Lill, R. E. Meadows and P.-O. Norrby, J. Org. Chem., 2014, 79, 11961–11969 CrossRef CAS PubMed.
- T. Ikawa, T. E. Barder, M. R. Biscoe and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 13001–13007 CrossRef CAS PubMed.
- J. F. Hartwig, Acc. Chem. Res., 1998, 31, 852–860 CrossRef CAS.
- J. P. Wolfe, S. Wagaw, J.-F. Marcoux and S. L. Buchwald, Acc. Chem. Res., 1998, 31, 805–818 CrossRef CAS.
- J. Hartwig, Synlett, 1997, 1997, 329–340 CrossRef.
- D. S. Surry and S. L. Buchwald, Chem. Sci., 2011, 2, 27–50 RSC.
- M. R. Biscoe, T. E. Barder and S. L. Buchwald, Angew. Chem., Int. Ed., 2007, 119, 7370–7373 CrossRef.
- L. M. Jackman and B. C. Lange, J. Am. Chem. Soc., 1981, 103, 4494–4499 CrossRef CAS.
- D. Seebach, Angew. Chem., Int. Ed., 1988, 27, 1624–1654 CrossRef.
- W.-B. Liu, D. P. Schuman, Y.-F. Yang, A. A. Toutov, Y. Liang, H. F. T. Klare, N. Nesnas, M. Oestreich, D. G. Blackmond, S. C. Virgil, S. Banerjee, R. N. Zare, R. H. Grubbs, K. N. Houk and B. M. Stoltz, J. Am. Chem. Soc., 2017, 139, 6867–6879 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates and energies of all computed structures are provided. See DOI: 10.1039/c9sc03095f |
| This journal is © The Royal Society of Chemistry 2020 |