Addressing diversity and inclusion through group comparisons: a primer on measurement invariance testing

Abstract

As the field of chemistry education moves toward greater inclusion and increased participation by underrepresented minorities, standards for investigating the differential impacts and outcomes of learning environments have to be considered. While quantitative methods may not be capable of generating the in-depth nuances of qualitative methods, they can provide meaningful insights when applied at the group level. Thus, when we conduct quantitative studies in which we aim to learn about the similarities or differences of groups within the same learning environment, we must raise our standards of measurement and safeguard against threats to the validity of inferences that might favor one group over another. One way to provide evidence that group comparisons are supported in a quantitative study is by conducting measurement invariance testing. In this manuscript, we explain the basic concepts of measurement invariance testing within a confirmatory factor analysis framework with examples and a step-by-step tutorial. Each of these steps is an opportunity to safeguard against interpretation of group differences that may be artifacts of the assessment instrument functioning rather than true differences between groups. Reflecting on and safeguarding against threats to the validity of the inferences we can draw from group comparisons will aid in providing more accurate information that can be used to transform our chemistry classrooms into more socially inclusive environments. To catalyze this effort, we provide code in the ESI for two different software packages (R and Mplus) so that interested readers can learn to use these methods with the simulated data provided and then apply the methods to their own data. Finally, we present implications and a summary table for researchers, practitioners, journal editors, and reviewers as a reference when conducting, reading, or reviewing quantitative studies in which group comparisons are performed.

---

Introduction

Diversity and inclusion are popular terms in science education at present. In the past few decades, numerous research endeavors have focused on studying diverse populations of students within science, technology, engineering, and mathematics (STEM; e.g., Hong and Page, 2004; Tsui, 2007; Hurtado et al., 2010). Due to a directive to increase minority representation in STEM fields in the United States (Seadler, 2012), colleges and universities have launched initiatives to attract underrepresented minority (URM) students. These initiatives can help to initially increase diversity representation; however, simply admitting students is not enough if they feel unvalued or unwelcome in their college communities (Puritty et al., 2017). Thus, diversity initiatives may fail to retain these students without attention to creating inclusive environments where students of all backgrounds feel they have a voice and that they matter (Puritty et al., 2017). Attaining a diverse STEM workforce, then, means promoting inclusion and social justice in our classrooms and in our research (O’Shea et al., 2016).

Critical Race Theory (CRT) has become a central framework to study issues of inclusion and social justice, particularly for members of marginalized racial groups (Crenshaw, 1995; Solórzano, 1997, 1998; Delgado and Stefanic, 2001; Yosso, 2005; Dixson and Anderson, 2018). Although CRT was born in the legal realm, it has permeated the educational field as well (Crenshaw, 1995; Delgado and Stefanic, 2001). This theory has been linked to five guiding tenets that inform research, curriculum, pedagogy, and policy (Solórzano, 1997; Yosso, 2005). Three of these tenets seem particularly well suited to investigations utilizing quantitative methodology. First, an acknowledgment of the centrality of race and racism in the power relations that underpin society requires that race be explicitly considered rather than ignored in educational research. Second, the de facto existence of ‘dominant ideology’ informed by race and racism requires us to cast aside naive beliefs that research and researchers are neutral and objective (Yosso, 2005) and work to safeguard against systemic biases and the propagation of social inequities in educational research (García et al., 2018; Gillborn et al., 2018). And third, answering CRT's call for a commitment to social justice requires us to privilege research that works to uncover social inequities and moves toward the eradication of racial and other forms of marginalization (Solórzano, 1997). CRT is a framework well equipped to investigate issues of racism and social inequities in educational settings at the individual as well as at the institutional level. For example, Fernández (2002) uses CRT as a framework and takes an individual approach to display a successful educational experience of one immigrant Latino student in a public school in Chicago via qualitative methods. On the other hand, Solórzano and Ornelas (2004) use CRT to investigate the access and availability of Advanced Placement (AP) courses in California high schools and how they affect African American and Latina/o students’ admission to college. This quantitative study exhibits an institutional approach that documents cumulative impacts on individuals and groups of students from minority racial and ethnic populations. Likewise, CRT and quantitative methods can be utilized at the institutional level to investigate achievement gaps in educational systems, providing a wider lens for these investigations (García et al., 2018; López et al., 2018), rather than merely grade comparisons. Whenever possible, studies of this nature benefit from a comprehensive investigation with appropriate categories for investigating achievement gaps, such as race-gender-class intersections (Crenshaw, 1989; Covarrubias, 2011; Covarrubias and Velez, 2013; Litzler et al., 2014; García et al., 2018; Ireland et al., 2018; López et al., 2018) as a movement to achieve a more complete view of the investigation and avoid reproduction of widespread inequities in educational settings (García et al., 2018; Gillborn et al., 2018).

In an effort to combat against racism and other societal inequities, these issues have long been studied with qualitative methodologies (Gillborn et al., 2018; García et al., 2018). Quantitative methods have been criticized for an inability to speak to the details of lived experiences of diverse populations (García et al., 2018) and thus been deemed inappropriate to study these issues in educational settings due to these everyday experiences having deep roots in social relationships (Apple, 2001). Although qualitative methods are more appropriate to capture nuances of societal processes as experienced by individuals, quantitative methods can explore wider structures in which individual and collective experiences are lived, revealing wider structural issues that affect these diverse groups on a larger scale (Gillborn et al., 2018). With this tension between qualitative and quantitative methodologies attending to issues of social inequities, we encourage the use of either or both types of methods when appropriate, following the tenets of CRT. Therefore, in an effort to promote inclusion and equity in our classrooms, appropriate qualitative and quantitative methods can be used in research, with the premise that our methods must be reflexive and safeguarded against systemic racial, ethnic, gender, and other biases favoring the majority groups (Gillborn et al., 2018).

Much of the critique about using quantitative methods to investigate these issues comes from the problem that numbers are positioned as ‘neutral’ and audiences may believe ‘data speaks for itself.’ Critical theorists argue that these claims of neutrality are far from the truth (Gillborn et al., 2018). However, researchers, practitioners, and policy-makers tend to put great emphasis in numbers, as these are the data by which policies are justified and schools and districts are labeled successes or failures (Gillborn et al., 2018). Thus, to rise above these critiques in favor of continuing to use quantitative approaches to investigate social inequities, a process of ongoing self-reflexivity and engagement with historical, social, and political structures of the groups under investigation must be present (García et al., 2018). Additionally, because numbers carry such important consequences, we must use them with caution and systematically interrogate the validity of the inferences we make with these numbers, particularly as it relates to consequential validity (AERA et al., 2014). According to Messick (1995) the social consequences of score interpretation may be positive or negative, intentional or unintentional. Thus, in the interest of advancing inclusion and social justice, researchers must engage in collecting evidence of positive consequences while minimizing adverse effects. As an example of unintentional, negative effect, one could imagine that a subgroup of students misinterprets items on an assessment instrument based on unfamiliar words in the item, which may lead to confounding results in the data for that subgroup. This source of invalidity can potentially lead to erroneous decisions that may have adverse consequences for this subgroup of students (Shephard, 1993; Messick, 1995). Therefore, raising the bar for quantitative methods in our field will require taking steps to safeguard against consequential validity threats that may be present when making group comparisons.

Quantitative standards for group comparisons in CER

In CER, investigations of efforts to broaden participation of diverse student populations have been a focus of multiple studies (i.e., Richards-Babb and Jackson, 2011; Rath et al., 2012; Fink et al., 2018; Stanich et al., 2018; Narawathne, 2019; Shortlidge et al., 2019). Many of these studies have aimed to investigate differential outcomes of URM students by performing group comparisons with various statistical analyses (Rath et al., 2012; Fink et al., 2018; Stanich et al., 2018; Shortlidge et al., 2019). For instance, Fink et al. (2018) proposed a strategy to promote improved general chemistry performance for women and minorities through a growth mindset intervention. The results of the study report higher performance overall favoring the White students; however, post hoc Tukey tests confirmed an intervention effect for minority students, who ultimately earned more than 5 percentage points higher on average in the mindset intervention condition (Fink et al., 2018). Similarly, Stanich et al. (2018) implemented a supplementary instruction (SI) course that aimed to narrow achievement gaps by showing that URM students who participated in the SI course had lower failure rates in general chemistry than URM students who did not take the course. Additionally, this study also aimed to narrow affect gaps by increasing perception of relevance, sense of belonging, and emotional satisfaction toward the subject of chemistry (Stanich et al., 2018). While studies such as these are a positive sign that diversity and inclusion are being taken seriously, there is still work to be done with respect to developing guidelines for quantitative research on these issues.

The next important step in developing research standards is to critically examine the collection, analysis, and representation of quantitative data and results for threats to the validity of inferences when group comparisons are to be made. CER has a long history of assessment design to probe student understanding of concepts taught in the classroom (i.e., Tobin and Capie, 1981; Roadrangka et al., 1983; Loertscher, 2010; Villafañe, et al., 2011; Kendhammer et al., 2013; Wren and Barbera, 2013; Brandriet and Bretz, 2014; Bretz, 2014; Kendhammer and Murphy, 2014; Xu et al., 2016). These, and other, assessment instruments have been used by researchers and practitioners to evaluate the success of classroom interventions and curricular changes. Furthermore, in the last few decades, CER as a field has moved toward an increased interest in affect and motivation in educational settings (Xu et al., 2013; Ferrell and Barbera, 2015; Salta and Koulougliotis, 2015; Ferrell et al., 2016; Liu et al., 2017; Gibbons and Raker, 2018; Gibbons, et al., 2018; Hensen and Barbera, 2019; Rocabado et al., 2019). Thus, assessment instruments may be used in CER to determine research agendas, report findings, evaluate interventions or curricular design and much more.

Given the current interest in measuring affect in the classroom, there is an added concern that many cognitive and emotional factors might have different effects among diverse populations, particularly disfavoring URM groups (Ceci et al., 2009; Villafañe et al., 2014; Rocabado et al., 2019). However, some of the differences noted in these data could be an artifact of the assessment instrument (Jiang et al., 2010); thereby resulting in a potential threat to the validity of the inferences drawn from the instrument-derived data (Arjoon et al., 2013; AERA et al., 2014). Therefore, in the interest of promoting inclusion in the classroom, it is important to know that when an instrument functions well for the whole class, the functionality extends to any subgroups of interest. Nevertheless, simply comparing observed scores for subgroups is not appropriate. As shown by several studies (Kahveci, 2015; Komperda et al., 2018; Montes et al., 2018), differences might arise as artifacts of the instrument functioning and not as differences in understanding, ability, or affect.

Goals of this measurement invariance testing primer

To encourage and support the gathering of evidence to substantiate group comparisons within CER, this manuscript presents the quantitative method of measurement invariance testing for those familiar with factor analysis. A comprehensive review of measurement invariance testing can be found in Vandenberg and Lance (2000). Measurement invariance testing can be used to investigate the degree to which measured student data is represented by the same theoretical model. Prior to introducing the details and meanings of the various levels of measurement invariance testing, we discuss latent variables and data visualization techniques. This introduction provides initial insight into the relations among assessment items as well as providing a basis for understanding the mathematical foundations being tested. We then provide a step-by-step tutorial of measurement invariance testing, discussing what is being tested, how to evaluate if invariance has been achieved, and what (if any) comparisons between groups are supported at each step. Finally, we present a summary of the implications of measurement invariance testing as well as recommendations for researchers, practitioners, reviewers, and journal editors.

Group comparisons on latent constructs

Commonly, the variables of interest in CER are ones that cannot be measured directly, i.e., they are latent traits. Variables such as student self-efficacy, attitude, metacognition, mindset, and understanding of chemistry are all examples of latent traits. Many of these latent traits are multidimensional, that is, they are subdivided into smaller latent units (subconstructs or factors) that make up the latent trait (Brown, 2006, p. 2). To provide an example for our discussion of quantitative data comparison by group, we devised a fictitious assessment instrument to measure the latent trait of ‘perceived relevance’ toward chemistry. Such an instrument might be useful in understanding college students’ perceptions of the field of chemistry. For this fictitious assessment instrument, it could be expected that students’ perceived relevance of chemistry might differ by college major and that a researcher might want to compare data from this instrument by group. While many times the groupings of students we quantitatively investigate are by gender or URM status, these are not the only groupings for which comparisons need to be supported by evidence. For example, with our fictitious instrument the comparison groups could be defined as STEM and non-STEM majors. Other groupings could be first-generation college students or community college transfer students for comparison to students not in these groupings. Whatever the chosen comparison groups are, it is imperative that researchers have a directive to investigate those groups and use an appropriate construct for the comparison.

It is important to note that utilizing assessment instruments that have been developed with a strong theoretical background and which have been investigated for forms of validity and reliability evidence delineated by the Standards for Educational and Psychological Testing (Arjoon et al., 2013; AERA et al., 2014) is imperative to drawing meaningful insights from studies. Following with the example, and assuming that the instrument was created under these conditions, our fictitious assessment instrument is called the Perceived Relevance of Chemistry Questionnaire (PRCQ) and contains three fictitious subconstructs: Importance of Chemistry (IC), Connectedness of Chemistry (CC), and Applications of Chemistry (AC). The fictitious PRCQ is a 12-item instrument with four items per subconstruct. When student responses to these 12 items are examined, the expected pattern of bivariate correlations among responses would be that items aligned with the same subconstruct should have stronger correlations with each other, meaning they are highly associated with each other through an underlying subconstruct, and have weaker correlations with other items aligned with different subconstructs. For comparison purposes then, these item-level patterns need to be consistent within each group.

Group comparisons through data visualization

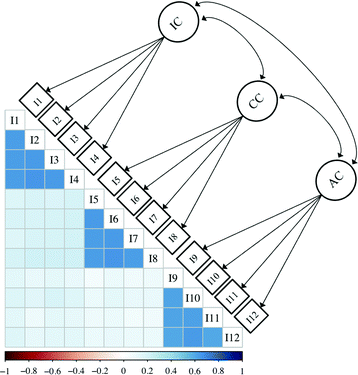
In addition to using descriptive statistics to investigate data patterns, item-level data can be visually inspected using a variety of methods (e.g., box-plots, violin plots, graphs, charts). To demonstrate ways in which to visualize data, we have created simulated PRCQ datasets that highlight several different data patterns across groups (see ESI,† pp. 1–7 for additional details). Item correlation values for one of these datasets are plotted in a correlation heatmap shown in Fig. 1. In this correlation plot the item labels (i.e., I1, I2, etc.) are listed on the diagonal, and the color of each square represents the value for the correlation (i.e., the strength of association) between two items. Pairs of items with stronger correlations are represented with darker squares and pairs of items with weaker correlations are represented with lighter squares. The simulated data used in this example are strongly correlated in four-item sets (I1 to I4, I5 to I8, and I9 to I12); items outside these sets (e.g., I1 and I8) are weakly correlated. As the PRCQ has three subconstructs, another way to represent the relations between the twelve items is with a factor diagram. The intended factor diagram for the 12-item PRCQ instrument has been added above the correlation plot. In a factor diagram each individual item (called an indicator item and represented by a square) is associated with a subconstruct or factor (represented by a circle). Together, these visual representations of the PRCQ data provide initial visual evidence for the presence of the intended factors (i.e., item set groupings).

Fig. 1 A visualization of the lower correlation matrix for the 12-item PRCQ instrument with a factor model overlaid to illustrate how correlations between sets of items implies the presence of an underlying factor structure. We note that, although the covariance matrix is more directly applicable, the correlation matrix is a standardized covariance matrix, and therefore easier to visualize and discuss.

When making measurements that will ultimately be used to compare the outcomes of various groups on an underlying construct (i.e., Importance of Chemistry (IC), Connectedness of Chemistry (CC), and Applications of Chemistry (AC)), it is necessary to provide evidence that the PRCQ instrument is functioning in a similar way for each group being compared. This practice is a way in which the field of CER can meet best practices when making comparisons and provide evidence to support that any differences between the groups’ data are due to true differences in the construct, not a result of systematic bias in the measurement of the construct (Gregorich 2006; Sass 2011). Using our example, as researchers we could be interested in measuring potential differences in the perceived relevance of chemistry (as measured by the PRCQ) between groups. As lower-level chemistry courses serve a range of majors, we could investigate potential differences in perceived relevance between STEM and non-STEM majors, or among multiple groups such as White, African–American, Asian, and Hispanic students. For simplicity in our example, we have simulated response data for a two-group comparison, which will help us visualize the discussion that will proceed. In addition, the data we have simulated is continuous. However, we do understand that much of the data generated in CER is categorical in nature and as such will necessitate a different set of considerations. Thus, we provide explanation and analyses for both continuous and categorical data, in the ESI,† along with code (in R and Mplus) for generating the data visualizations as well as the additional analysis steps described later in this manuscript.

If the aggregated PRCQ data in Fig. 1 were divided by STEM and non-STEM majors, one step towards examining consistent functioning across groups would be to see if the two groups have similar correlation plots. As shown in Fig. 2, when visually comparing the correlation plots by group, it can be seen that they are essentially identical. Ways of testing this similarity statistically will be discussed later.

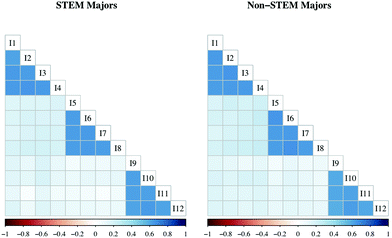Fig. 2 Correlation plots for 12 items with similar strength of association for each item and its intended factor for two subgroups (STEM majors and non-STEM majors) within the data set.

While the situation represented in Fig. 2 is the best possible outcome (i.e., the data are simulated to align with a known factor structure for both groups), it is not always the case that data from students in different groups will show the same strength of association between each item and each intended factor. An example of such a situation is visualized in Fig. 3 where we simulated a difference in strength of association for one item in one group. In this aggregated PRCQ data set (Fig. 3a) we can see inconsistencies around I10, where some correlation boxes are lighter. Although, the overall correlation pattern is consistent (i.e., an instrument that measures three distinct factors as hypothesized for the PRCQ), when we disaggregate the data and view the correlation matrix for each group separately, we observe that I10 has a much lower association with the AC factor for non-STEM majors (Fig. 3c) compared to STEM Majors (Fig. 3b). This group difference would not be obvious when looking at the correlations in the aggregated dataset (Fig. 3a). The situation represented here, dissimilar associations between items and factors across groups, implies that the item is not functioning in similar ways for each group, which could be due to differences in item interpretation for I10. Regardless of the underlying reason, which may never be known for sure, this situation indicates a possible threat to the validity of the potential inferences from the data and needs to be examined more closely to determine whether the data can still be used to compare the groups.

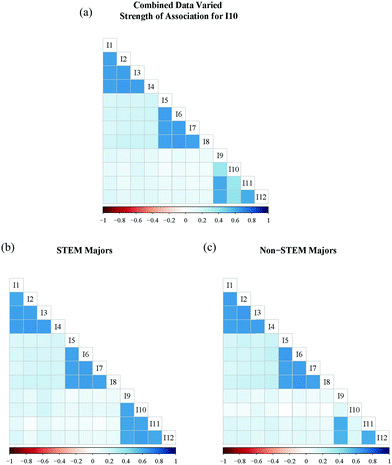Fig. 3 (a) Correlation plot for 12 items with combined dataset; (b) correlation plot with STEM major data; (c) correlation plot with non-STEM major data with I10 correlation lowered.

Another type of measurement difference that could occur between the groups is that an item may not have similar response averages in each group. In the next set of simulated data, the strength of association between all items and their intended factor is equivalent, as in Fig. 3, but the average response for I3 has been modified for the STEM majors group to illustrate this issue. Unlike when the strength of association differed in the previous example, this result is more obviously seen when visualizing the correlations in the aggregated dataset (Fig. 4a) than in the disaggregated sets (Fig. 4b and c).

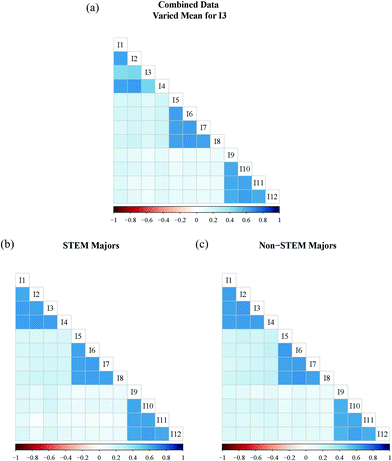Fig. 4 (a) Correlation plot for 12 items with combined dataset; (b) correlation plot of STEM majors with mean of I3 raised; (c) correlation plot of non-STEM majors.

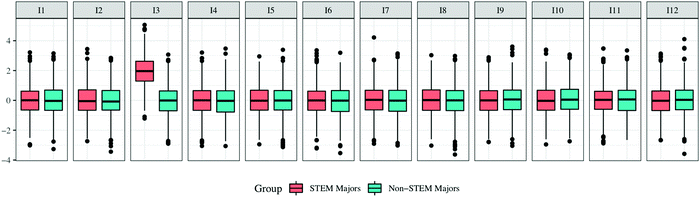
To further visualize the distribution of values for each item within each group, Fig. 5 plots the means for each item in the two groups using a boxplot. It can be clearly seen that the distribution for I3 in the STEM majors group is much different and is shifted to the higher end of the scale. This outcome could occur because there are true differences between the groups or it could be due to improper item functioning for one group. However, a quantitative analysis does not differentiate between these two reasons, thus it is appropriate to further investigate the item functioning when this occurs.

Fig. 5 Boxplot of item means for each group.

The item-level differences noted in Fig. 3–5 may be due to a variety of issues, which would be worth exploring further in order to understand why they occur. However, in considering whether the data can still be used to make comparisons between groups, the degree to which these differences impact the proposed factor structure need to be evaluated using measurement invariance testing. This quantitative method would indicate if the differences pose a potential issue with how the instrument functions for the different groups, potentially limiting the ability to draw valid conclusions about how the underlying factors of interest differ across groups.

Data considerations prior to performing measurement invariance testing

While we have emphasized the importance of visualizing data and have shown various ways it can be useful, we acknowledge that data visualization is insufficient to address the degree to which item-level differences may impact group comparisons, which necessitates more robust investigations using statistical tests. Additionally, and more often than not, many data issues are not easily visualized, but can become evident in statistical analyses. We encourage all researchers to visualize their data and compute descriptive statistics, thereby providing initial insights to the data as well as evidence about the characteristics of the data. Understanding data characteristics will aid the researcher in making other decisions about further analyses, such as which tests are appropriate to run or which estimator is appropriate to use when modeling data.

Different types of data such as categorical or continuous, can be analyzed with measurement invariance testing utilizing appropriate estimators for each type of data. For example, ordinal data (e.g., categorical data from items with a 7-point Likert-type scale) with variance ranging the entire scale is often treated as continuous data and can be estimated with a maximum likelihood estimator (Muthén and Muthén, 2010; Hirschfeld and Von Brachel, 2014). On the other hand, categorical data (e.g., data from a ‘yes or no’ type item or items using fewer than 5 response scale categories) are more appropriately analyzed using a weighted least squares estimator (Muthén and Muthén, 2010; Finney and DiStefano, 2013; Hirschfeld and Von Brachel, 2014; Bowen and Masa, 2015). Ensuring the proper estimator for the data-type is of utmost importance. Violations of normality, independence, and homogeneity are also important to note, and should be handled appropriately. Discussion of estimators and assumptions is beyond the scope of this article; however, we provide a few resource references for interested readers here (Stevens, 2007; Garson, 2012) and in the ESI.†

An additional consideration before conducting measurement invariance testing is statistical power (Cohen, 1988; Hancock and French, 2013). To conduct meaningful statistical analyses, one must ensure an appropriate sample size in order to have enough power to draw meaningful inferences. In measurement invariance testing the interest is in finding no evidence of significant difference between groups, thus, an inappropriate sample size (i.e., too small) can increase the chances of type II error through failing to reject the null hypothesis (of equivalence) when it should have been rejected (Lieber, 1990; Counsell et al., 2019). Recently, work has been done indicating that sample size requirements can be estimated given the number and value of parameters being estimated (Wolf et al., 2013; Mueller and Hancock, 2019).

Confirmatory factor analysis framework

In the previous section we explored visual methods for detecting potential validity threats in our PRCQ data. Though visualizing is an important initial step, more formal statistical methods can and should be employed to evaluate the degree to which differences pose threats to the validity of comparisons. Methods such as Differential Item Functioning have been used to investigate item-level threats in CER (Kendhammer et al., 2013; Kendhammer and Murphy, 2014), however, the purpose of this paper is to explore threats at the construct, or latent variable level. At this level, various frameworks can be used, including Item Response Theory (IRT; Candell and Drasgow, 1988; Mellenbergh, 1989) and factor analysis (Brown, 2006). As factor analysis methods have become commonplace within CER, and IRT is less frequently utilized in our field, this discussion will focus only on evaluating measurement invariance in a factor analysis framework.

Within a Confirmatory Factor Analysis (CFA) framework (Brown, 2006), measurement invariance testing is a technique that can be used to support that the internal structure of an assessment instrument holds for different groups people at one time point (Salta and Koulougliotis, 2015; Bunce et al., 2017; Hensen and Barbera, 2019; Rocabado et al., 2019) or over time in longitudinal studies (Keefer et al., 2013; Hosbein and Barbera, 2020; Rocabado et al., 2019). In the previous section, the idea of internal structure was described in terms of the grouping of items with each other to form an underlying factor of interest (as introduced in Fig. 1). In this section, these associations will be defined more formally using the language of factor analysis.

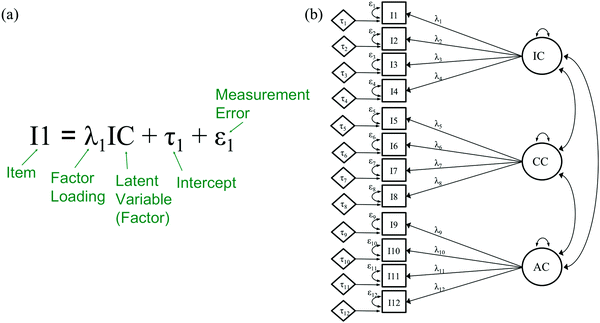
The CFA framework operates under a network of equations, among which, regression equations link items to latent variables (Brown, 2006). Regression or linear equations (see eqn (1)) have several components: a dependent (predicted) variable (y), an independent (predictor) variable (x), the slope of the line (m), the intercept (b), and the measurement error (e).

y = mx + b + e (1)

Translating the regression equation to the language of factor analysis, the predicted variables are the observed variables (i.e., items), the predictor variables are the factors or latent variables, and the slope is the factor loading. In Fig. 6a we write out the regression equation for an item from the PRCQ and in Fig. 6b display the model that underlays the PRCQ using common statistical notations in the CFA framework, which we will use for the remainder of the discussion in this manuscript. In this 12-item (i.e., I1-I12), 3-factor (i.e., IC, CC, AC), model lower-case lambdas (λ) represent the factor loading of each item to its respective factor, lower-case taus (τ) represent the intercept of an item, and lower-case epsilons (ε) represent the measurement error of an item. In addition to these parameters, Fig. 6b shows the covariance between factors (e.g., double headed arrow between IC and CC) and each individual factor variance (e.g., small curved arrow from IC to IC). While these parameters are part of the overall CFA model for the PRCQ, they do not need to be modified when evaluating for measurement invariance.

Fig. 6 (a) Representation of equation components in CFA. Linear equation for I1 and the IC factor with notation and labels corresponding to CFA framework. (b) Factor model displaying the factor analysis notation of the relation between items and their corresponding factors.

Measurement invariance testing within a CFA framework investigates the extent to which the network of equations in a model is similar across group-level data. Therefore, each part of the equation (eqn (1)), for each item is tested for evidence of significant differences across groups, starting with the slopes (loadings), then the intercepts, followed by the measurement error variances. At each stage of measurement invariance testing, evaluation of overall data-model fit occurs.

Data-model fit and fit indices

The primary goal of measurement invariance testing is to examine how well the data collected fit a proposed model of relations among items and factors as described by a set of regression equations. Continuing with the example, we investigate the PRCQ data (by STEM and non-STEM groupings) for item associations based on the proposed (a priori) three-factor model for the PRCQ shown in Fig. 6b. Mapping the data to this proposed model using a maximum likelihood estimator (the default in most software packages and the one that is appropriate for our simulated continuous data), fit indices are generated and are used to evaluate how well the data fit the model. Regardless of the software package used, it is good practice to review several kinds of fit indices that fall in each of these categories: comparative fit, absolute fit, and parsimony correction. The comparative fit indices evaluate the fit of a specified model solution in relation to a baseline model solution. Absolute fit indices assess how reasonable the model fit is based on the null hypothesis that the data fit the model perfectly. Finally, the parsimony correction indices are similar to the absolute fit but include a penalty for poor model parsimony (Brown, 2006).

With these fit index descriptions in mind, we present several suggested cutoff criteria for fit indices that were simulated by Hu and Bentler (1999) using a maximum likelihood estimator. Examples of comparative fit are: the Comparative Fit Index (CFI) and the Tucker-Lewis Index (TLI), both of which have a recommended cutoff of >0.90 as acceptable, but best if >0.95 (Hu and Bentler, 1999). For the absolute fit category, the Chi-square (χ²) test statistic and the standardized root-mean square residual (SRMR) indices can be considered. The χ² is a descriptive index utilized to evaluate how closely the data fit the model. However, this test is highly influenced by sample size, thus additional fit indices must be considered to evaluate appropriate data-model fit (Brown, 2006). Hence the SRMR is a valuable index to add in this category and its cutoff criteria is <0.08 as acceptable (Hu and Bentler, 1999). Finally, for the parsimony correction, the root mean square of approximation (RMSEA) index can be evaluated with acceptable cutoff criteria of <0.06 (Hu and Bentler, 1999). Though these recommended criteria are often considered as firm cutoffs, there are known situations where the strength of the factor loadings can confound interpretation of fit indices (McNeish et al., 2018). Therefore, it is up to the researcher to provide as much evidence as possible to support the acceptability of a proposed factor model. It is also important to note that for categorical data a different estimator should be used, thus model fit indices and cutoff criteria are different from the ones noted here for continuous data and the maximum likelihood estimator. A more thorough description of estimator, model fit indices, and their respective cutoffs for categorical data are provided in the ESI.†

In the following section of this manuscript we present measurement invariance testing as the step-by-step evaluation of a series of nested models. Each step in the evaluation adds a constraint to test whether the groups being compared share a similar measurement model and if comparisons can be supported. Therefore, in addition to evaluating the data-model fit at each step of measurement invariance testing, we also calculate and evaluate the change in data-model fit between nested models. Cheung and Rensvold (1999, 2002) as well as Chen (2007) conducted a series of simulation studies with continuous data to investigate data-model fit criteria, in particular the change in data-model fit at each step of measurement invariance testing. Cheung and Rensvold (2002) focus solely on evaluating the change in Chi-square (Δχ²) between nested models, looking for a nonsignificant value. More recent work finds this practice acceptable (Mueller and Hancock, 2019), as the idea of measurement invariance testing is to find no evidence of significant difference between the models, which provides support for group comparisons. Other researchers, such as Chen (2007) have investigated the change in other fit indices as well, to ensure that there are various indicators that provide further evidence that no significant difference between nested models is observed. Chen (2007) offers a range of values that, based on the simulation studies conducted, offer reasonable cutoff values for the fit indices we have introduced earlier in this section. These values vary by level of invariance being evaluated and therefore will be presented within the appropriate testing step below. However, simulation studies have called into question the exact cutoffs and fit indices to use in the context of invariance testing (Kang et al., 2016) so again the researcher must decide what evidence to present to justify interpretation of models.

Steps of measurement invariance testing

In 1997 Widaman and Reise described 4 steps of measurement invariance testing: configural, metric (weak), scalar (strong), and residual (strict, also known as conservative). In this report we focus on this 4-step method, although there are other methods that utilize additional steps when investigating whether comparisons are supported between groups (for examples see Jöreskog, 1971; Vandenberg and Lance, 2000).

Step 0: establishing baseline model

A preliminary step before conducting measurement invariance testing is to conduct a separate CFA for each group dataset that will be compared. In this step, the CFA is used to investigate that each group's response patterns align with the proposed model to an acceptable level (Gregorich, 2006). The acceptability of the fit between each dataset (i.e., STEM and non-STEM groupings) and the model (Fig. 6) is checked using the fit indices noted earlier. If the data-model fit for either group's data is deemed unacceptable at this stage, measurement invariance testing is not appropriate and comparisons between the groups would not be supported. At this point, the next step would be to conduct an investigation of the reasons for failing to achieve acceptable data-model fit. However, if the data-model fit reached acceptable criteria for each group, then beginning the measurement invariance testing steps is appropriate.

Step 1: configural invariance

Once the independent CFAs for each group are found to have acceptable data-model fit, the first step of measurement invariance testing can begin. In this step, the same model is estimated concurrently for each group, allowing all model parameters to be freely estimated (Gregorich, 2006; Sass, 2011; Putnick and Bornstein, 2016). The point of this unconstrained model is two-fold: (1) to investigate whether items associate with each other in similar ways in all groups (i.e., items belonging to the same factor correlate more highly with each other than to other items); and (2) to establish a baseline of data-model fit, ensuring that subsequent comparisons are conducted utilizing the same network of equations for both groups. This baseline model is called the configural model, as it verifies that the general structure (or configuration) of items and factors is similar across groups. Configural invariance is achieved when this model has acceptable data-model fit values (Hu and Bentler, 1999).

The models in Fig. 7 represent the configural model, for our three-factor PRCQ instrument, for two groups. For discussion purposes, the model parameters for STEM majors (group 1) are labeled with numeric subscripts and those for non-STEM majors (group 2) are labeled with alphabetical subscripts. Take for example the relation between the first factor, IC, and the first item, I1. This relation is symbolized as λ₁ for group 1 and λ_a for group 2. In the configural model, these two relations are free to take on whichever value provides the optimal solution to the system of regression equations.

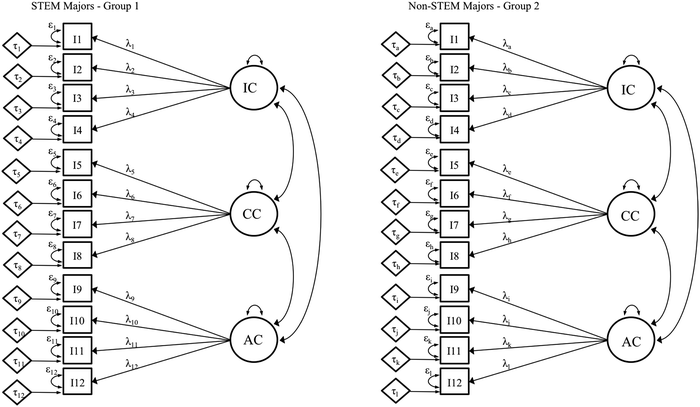Fig. 7 Configural invariance model where all parameters are freely estimated for two groups (STEM and non-STEM majors).

If the configural model fails to reach acceptable levels of fit, the result suggests that the factors are not associated with the same items for both groups (Gregorich, 2006; Putnick and Bornstein, 2016). Therefore, one can question whether the constructs being measured have the same meaning for these groups (Bornstein, 1995; Putnick and Bornstein, 2016). With this outcome, no further invariance testing is advised. However, we encourage researchers to conduct further investigation to find the source of noninvariance between the groups. Modes of investigation could be quantitative in nature, such as inspection of covariance or correlation matrices similar to the visuals we provided earlier (Fig. 1–4). Investigation could also be qualitative in nature, for example conducting cognitive interviews (Willis, 1999) with respondents from both groups to explore the constructs being measured and find the root of the differences between the two groups. These practices can help to ascertain any fundamental differences in construct meaning for different groups, which can provide insight into their lived experiences and interpretation of the construct of study (Komperda et al., 2018).

Step 2: metric invariance (weak)

If a configural model (Fig. 7) is observed to have acceptable data-model fit, the next level of establishing equality between the group-level data can be conducted. This step involves applying the first constraint to the baseline model equations, which establish the linear relationship between items (e.g., I1) and factors (e.g., IC). In the metric model (Fig. 8), also called the weak invariance model (Meredith, 1993), the constraint of equal unstandardized slopes, or factor loadings (λ), is applied (Gregorich, 2006; Sass, 2011; Putnick and Bornstein, 2016; see Fig. 8 where loading subscripts match across groups). That is to say that for STEM majors, the factor loadings are freely estimated, but for non-STEM majors, the loadings are set to be equal to the loadings for STEM majors. At this level of invariance testing, we are exploring whether the strength of associations between the items and the latent variables are similar across groups (Byrne et al., 1989; Gregorich, 2006). To achieve metric invariance, first the fit statistics of the metric model (Fig. 8) are evaluated (Hu and Bentler, 1999), and then they are compared to those of the configural model (Fig. 7). No evidence of significant difference should be observed between the configural and metric models. To evaluate the comparison between configural and metric models, the change in fit indices between levels is established utilizing the guidelines noted earlier. It is important to note that evaluating model fit is pertinent; however, evaluating the change between the models is essential to establishing invariance between groups. Establishing metric invariance implies that the meaning of the factor (in terms of relative weight of items) is similar across groups (Gregorich, 2006). However, this evidence is not enough to make comparisons between groups. At the very least, another level of constraint is needed before group comparisons can be made, as will be summarized in subsequent steps.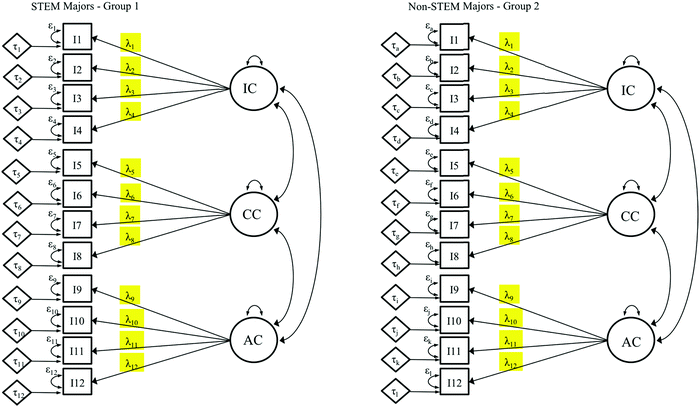

Fig. 8 Metric model where factor loadings (highlighted) are constrained to be equal for both groups. All other parameters (e.g. intercepts and error variances) are freely estimated.

Failure to reach metric invariance suggests that the strength of association between items and the factor to which they belong are different between the groups. The strength of item association with the factor provides meaning to the factor from the perspective of the respondents (Gregorich, 2006). Therefore, if the item-factor associations are significantly different across groups, then the meaning of the underlying factor is different between groups, or the factor loadings are biased (Gregorich, 2006). Generally, when metric invariance is not achieved, there are one or more items with poor loadings for one of the groups compared to the other group. At this juncture, investigation of the item loadings or modification indices generated by the software can provide meaningful insight about the different ways that respondents may associate items to the underlying construct. After evaluation, researchers may choose to release the constraint of equal loadings for the problematic item(s) and run the model again for partial measurement invariance (Byrne et al., 1989; Putnick and Bornstein, 2016). If this release of constraints is undertaken, comparisons between groups are cautioned, particularly for the constructs that involve the problematic items. These items might be the subjects of further investigation as to the alignment between items and underlying constructs for the groups of interest.

Step 3: scalar invariance (strong)

Once metric invariance is established (i.e., no evidence of significant difference is found between the metric and configural models), the next constraint can be applied. The scalar model (Fig. 9), also called the strong (factorial) invariance model (Meredith, 1993), consists of incorporating unstandardized equal intercepts, in addition to equal loadings, across groups in the model (Gregorich, 2006; Sass, 2011; Putnick and Bornstein, 2016). With this addition, the intercepts (τ) are freely estimated for STEM majors, but for non-STEM majors they are set to be equal to the intercepts for STEM majors (see Fig. 9). The purpose of this model is to establish evidence of unbiased estimated factor mean differences between groups (Gregorich, 2006), which implies that factor means encompass all mean differences in the shared variance of the items (Putnick and Bornstein, 2016). Factor means are unbiased because the error terms (ε) are not part of them. This is not true for observed item and observed scale means as they are calculated from the observed item scores that include the associated error terms (Putnick and Bornstein, 2016).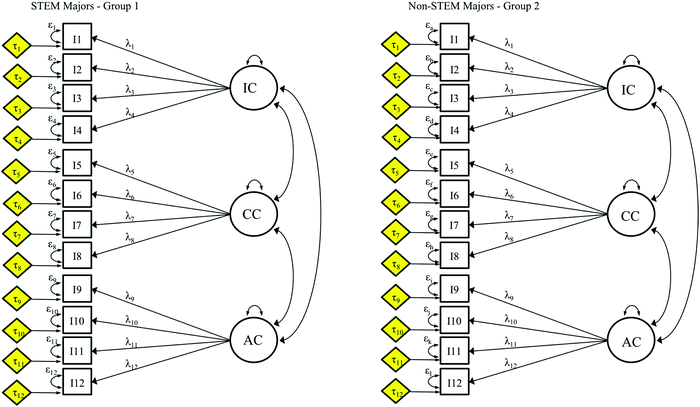

Fig. 9 Scalar model where factor loadings and intercepts (highlighted) are constrained to be equal for both groups. All other parameters, including error variances are freely estimated.

Just as with the metric model, first the scalar data-model fit is evaluated (Hu and Bentler, 1999) and then the fit comparison between, now, the metric (Fig. 8) and scalar (Fig. 9) models utilizing the appropriate values noted earlier. We reiterate that evaluating data-model fit is an important step of measurement invariance; however, essential to providing sufficient evidence for score comparisons is the change in fit statistics from one model to the next.

Once scalar invariance is achieved, the researcher has established evidence to support the comparison of factor means between groups. This evidence helps to rule out that any observed differences arise from variations caused by systematic higher or lower item responses (Gregorich, 2006; Sass, 2011; Putnick and Bornstein, 2016) due to issues like cultural norms.

If the scalar model provides results that are significantly different from the metric model, then scalar invariance has not been achieved and factor mean comparisons between groups are not supported. However, investigation as to the source of mismatch can be conducted. As demonstrated earlier, visualizing the data can be helpful at this juncture. Fig. 5 shows item intercepts displayed as boxplots. Although one can choose to visualize data in various ways, Fig. 5 visually suggests that the intercept for I3 (STEM majors) might be different than the intercept of the same item for the non-STEM majors. As I3 belongs to the IC factor, interpreting the IC factor mean comparisons between groups can be more difficult given this limitation. However, investigation as to the reason for the mismatch between groups is warranted. As previously mentioned, differences in item intercepts can be caused by diverging cultural norms that cause higher or lower item responses in diverse groups (Gregorich, 2006), thus investigating the source of the difference is encouraged. An example of this phenomenon that could cause systematic higher or lower responses is acquiescence bias. For example, one group might not utilize the entire response scale range, rather the response distribution is skewed to either end of the scale or narrowly in the middle.

In this situation, researchers may choose to release the constraint of equal intercepts for I3 only and evaluate the scalar model again. If releasing the constraint for I3 results in scalar model fit that is not significantly different from the metric model, then scalar invariance is established with limitations, sometimes described in terms of partial invariance (Putnick and Bornstein, 2016; Fischer and Karl, 2019). However, if an item loading was not held constant between groups in a previous step of invariance testing then the intercepts must also not be held constant as there is no reason to believe items with two different slopes would be expected to have the same intercepts. There is some evidence that with partial invariance of intercepts comparison of factor means may provide acceptable results (Steinmetz, 2013).

An important distinction at this juncture is that factor means are obtained from the model, not from summing or taking the average of the observed item response values. Factor means are not a ‘set’ number, rather they are a comparison of latent (unobserved) means between two (or more) groups, where one group serves as the reference, taking the value of zero, and the other group or groups is/are compared to the reference. An effect size of the comparison can also be calculated (Hancock, 2001; Bunce et al., 2017). Although this way of making comparisons is not frequently used in CER, the application of this practice is useful. We encourage researchers to work with factor means more often for two main reasons: (1) as explained earlier, factor means are estimated from the model, capture all mean differences in the shared variance of the items in the factor, and are free from error terms (Putnick and Bornstein, 2016). This cannot be said for observed scale scores, meaning composite scores taken directly as an average or sum of the observed variables (i.e., items), since these scores must include the error terms and do not take into account the strength of the association between items and factors. (2) In order to compare observed scale scores, the conservative invariance test, described in the following section, must be achieved. Meaning, it is harder to provide sufficient evidence for observed scale score comparison between groups than it is to compare factor means. Thus, we encourage researchers to utilize factor means as an effective tool for group comparisons as these values are void of error terms and will lead to more accurate interpretations and more meaningful inferences.

Step 4: conservative invariance (strict)

Once scalar invariance is achieved, comparison of factor means between the groups is possible. However, if researchers desire to compare the observed scale scores of each factor; meaning composite scores taken directly as an average or sum of the observed variables (i.e., items), it is advisable to conduct a conservative or strict (Meredith, 1993) invariance test first (Gregorich, 2006; Sass, 2011). The conservative test checks the additional condition that measurement error variances are similar across groups. This is done in the same fashion as the prior models, with the final addition being that the STEM majors’ error variances (ε) are freely estimated and non-STEM majors’ error variances (ε) are constrained to be equal to those of STEM majors (see Fig. 10). At this point, all loadings, intercepts and error variances are fixed to be equal between the groups to be compared. To establish strict invariance, the data-model fit statistics are first evaluated and then compared between the strict (Fig. 10) and scalar (Fig. 9) models and no evidence of significant difference should be found. If strict invariance is established, enough evidence is gathered to warrant observed scale score comparisons between groups (Gregorich, 2006; Sass, 2011). This type of comparison is what most researchers are accustomed to investigating; however, it is important to note that these comparisons require evidence of meeting this highest level of invariance testing. Failure to achieve strict invariance means that observed scale comparisons are not supported. Thus, researchers may investigate scalar invariance (i.e., Step 3) to compare factor scores instead.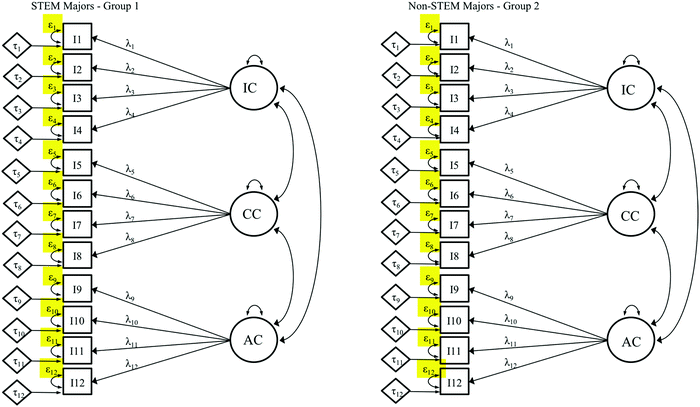

Fig. 10 Conservative (strict) invariance where loadings, intercepts, and error variances are constrained to be equal for both groups.

Based on the four steps described previously, we provide a summary table (Table 1) for readers to reference as they conduct measurement invariance testing in their own studies. This table, while not comprehensive, provides the basic model characteristics, the evidence established, appropriate claims, and supported group comparisons that can be made at each level of invariance testing. This table can also prove useful as reviewers and journal editors review quantitative studies that can benefit from this method to support comparisons between groups or across time.

Table 1 Summary of claims and evidence established at each stage of measurement invariance testing – guide for researchers, practitioners, and reviewers

	Configural	Metric (weak)	Scalar (strong)	Conservative (strict)
Model characteristics	All parameters freely estimated in all groups, no constraints	Factor loadings constrained to be the same for all groups	Factor loadings and item intercepts constrained to be the same for all groups	Factor loadings, item intercepts, and error variances constrained to be the same for all groups
Evidence established	Same number of factors, items associated with the same specific factor for all groups	Evidence in configural plus same strength of association between factors and corresponding items for all groups	Evidence in configural and metric plus same item intercepts for all groups	Evidence in configural, metric, and scalar plus same item error variances for all groups
Appropriate claims	Items are associated with each other and the underlying factors in similar ways	Claims from configural plus meaning of the factor (in terms of relative weight of items) is similar across groups	Claims from configural and metric plus no systematic response biases; differences in factor means are due to a true difference in groups	Claims from configural, metric, and scalar plus no systematic response biases or difference in error between groups; differences in item and scale means are due to a true difference in groups
Supported comparisons between groups	None	None	Factor mean scores (from the model)	Observed scale scores

---

Measurement invariance testing example with simulated data

To illustrate the steps of utilizing measurement invariance testing for determining if, and to what degree, group comparisons can be made, we use the simulated dataset that generated Fig. 4 and 5 to work through an example. The data was simulated to be continuous, therefore the maximum likelihood estimator was used for each model. For each step in the process, the data-model fit results as well as the fit comparisons between models are displayed in Table 2. It is important to note that while fit indices for each model will be calculated and tabulated by the software being used (i.e., R or Mplus, etc.), the change values between models have to be manually calculated with a simple subtraction, with the exception of the p-value associated with the Δχ², which must be retrieved from a χ² table that contains degrees of freedom.

Table 2 Measurement invariance testing for the PRCQ instrument comparing STEM majors and non-STEM majors with simulated data for illustration

Step	Testing level	χ ^2	df	p-Value	CFI	SRMR	RMSEA	Δχ^2	Δdf	p-Value	ΔCFI	ΔSRMR	ΔRMSEA
Note. STEM majors n = 1000. Non-STEM majors n = 1000. Simulated data was used and altered at the scalar level (intercepts) for illustrative purposes; fit indices are from R.
0	Baseline (STEM)	65	51	0.084	0.998	0.021	0.017	—	—	—	—	—	—
0	Baseline (non-STEM)	52	51	0.437	1.000	0.016	0.004	—	—	—	—	—	—
1	Configural	117	102	0.142	0.999	0.018	0.012	—	—	—	—	—	—
2	Metric	120	111	0.245	0.999	0.019	0.009	3	9	0.231	0.000	0.001	0.003
3	Scalar	2268	120	<0.001	0.820	0.191	0.134	2148	9	<0.001	0.179	0.172	0.125

---

At the baseline (Step 0) and configural (Step 1) levels, only the overall data-model fit is investigated. In our PRCQ example, the data at these levels was simulated with essentially perfect data-model fit as noted in Table 2. Perfect fit at these levels is unlikely to happen in a real study; thus, expecting a less-than-perfect fit is reasonable. Therefore, evaluating the data-model fit should follow acceptable guidelines, such as those by Hu and Bentler (1999) used here, or others as appropriate based on the data type. As each of our independent baseline models showed acceptable data-model fit and then the combined configural model showed good data-model fit, we can proceed to the next step of invariance testing.

The metric model data (Step 2) exhibits acceptable data-model fit (see Table 2). Beginning with these metric level indices, we not only evaluate the data-model fit but also compare the fit obtained with the metric model to that of the configural model. First, we evaluate the Δχ² (Cheung and Rensvold, 2002; Mueller and Hancock, 2019) which is a non-significant value, thus providing proof that there is no evidence of significant difference between the models. Then, following the suggestions of Chen (2007), our calculated values of ΔCFI = 0.000, ΔSRMR = 0.001, and ΔRMSEA = 0.003 are within the acceptable change cutoff levels: ΔCFI (<0.01), ΔSRMR (<0.03), and ΔRMSEA (<0.015) to establish metric invariance (Chen, 2007). The comparison between configural and metric models shows that there is no evidence of significant change between these two models, thus metric invariance is achieved based on the comparison and we are warranted in moving to the next step of invariance testing.

For evaluating if scalar invariance is achieved (Step 3), a similar analysis pattern is followed. First, we evaluate the data-model fit. At this point, we observe that the fit indices for the scalar model are no longer within the acceptable ranges (see Table 2). This result is problematic because it is an indication that scalar invariance does not hold for the groups. Further evidence is found when we compare the change in fit indices between the metric and scalar models. Here we observe that our value of Δχ² is significant, and the values for ΔCFI, ΔSRMR, and ΔRMSEA are also not within the recommended fit index cutoffs: ΔCFI (<0.01), ΔSRMR (<0.01), and ΔRMSEA (<0.015) for scalar invariance (Chen, 2007). These additional results confirm that scalar invariance is not reached for these data. As the model at this level is not supported, we do not go on to evaluate the next highest level of invariance (i.e., the strict invariance model at Step 4), as we do not have a supported scalar model to compare it to. However, if the scalar model held and we desired to move on to test for strict invariance, the same guidelines and fit index cutoffs would be used as for scalar invariance (Chen, 2007).

In this simulated data example with the PRCQ, our analysis provided evidence for metric invariance at Step 2 but not for scalar invariance at Step 3. Therefore, these results imply that factor mean comparisons between STEM and non-STEM majors are not supported and should not be performed. Investigating the source of the misfit in the scalar model is warranted. Based on our previous discussion, we know that the I3 intercept is higher for the STEM majors compared to non-STEM majors (see Fig. 4 and 5). At this point, we may choose to qualitatively investigate the difference between these groups for I3. Alternatively, we may choose to release this item's intercept constraint (i.e., allowing the I3 intercept for each group to be freely estimated) and run the scalar model again. If the data-model fit and model comparisons indicate acceptable levels with this modification, partial scalar invariance would be achieved. At this point, we would have limited support for factor mean comparisons. However, we would not be able to make any significant claims, particularly for the IC factor, due to the limitation for I3. Based on this limitation, reflection on the consequences of making factor mean comparisons between these groups and the validity of inferences drawn from these comparisons is crucial. Finally, as we were not able to evaluate for scalar invariance, we have no basis for comparing the observed scale scores of the STEM and non-STEM majors using the PRCQ.

As we have described throughout this manuscript, and shown through the example here, measurement invariance testing provides researchers and practitioners with statistical evidence to support (or in this case, refute) comparisons between the groups evaluated (Sass, 2011). Once it has been established that both groups view the items on an instrument in similar ways (i.e., by establishing a certain level of measurement invariance), the interpretation of results becomes validated. Utilizing measurement invariance testing provides support for meaningful inferences between populations, taking into account response patterns that may arise from a group's background or experiences (Wicherts et al., 2005). Furthermore, providing evidence that the data from an assessment instrument does not have validity threats against a comparison group, such as URMs (Gillborn et al., 2018), provides more confidence in the results obtained and may provide increased support for claims of inclusion for these groups.

Limitations

While we encourage all researchers and practitioners to utilize measurement invariance testing prior to conducting comparisons between groups, we acknowledge there are limitations which may not allow the use of this method. One of these limitations is the sample size required to conduct these model-based tests. Similar to factor analysis techniques, measurement invariance testing requires a large sample size. Although there are no specific rules about the sample size required, some work indicates that sample size requirements can be calculated given the number and value of the parameters being estimated (Wolf et al., 2013; Mueller and Hancock, 2019). However, we encourage researchers to continue investigating newer methods to determine appropriate sample size that may be more suitable for this technique that is specific to the model parameters, the type of data being analyzed, and other characteristics of their study (Wolf et al., 2013). Therefore, when conducting research and comparisons between groups with small samples, the technique presented in this work is not appropriate. Thus, we encourage researchers, practitioners, reviewers and journal editors to consider other methods of reflexivity such as response process evidence and/or content review by culturally-aware experts.

Additionally, researchers should be aware that the fit index cutoffs we have presented in this manuscript both for evaluating data-model fit and for change in model fit indices are suggested values based on simulation studies. While these guidelines are generally accepted within the field of measurement, this is an area of active investigation and these guidelines could evolve in coming years. As we encourage researchers to follow these guidelines, we also encourage a thoughtful evaluation of the data, model, and data-model fit where the suggested guidelines may not apply (Kang et al., 2016; McNeish et al., 2018).

Another limitation of measurement invariance testing is that this technique alone does not inform the exact ways in which groups differ in item and factor interpretation. Although this technique can point to the problematic items and factors that are dissimilar between groups, it cannot provide reasoning for the different meaning of items or factors between groups. This information is best investigated using qualitative methods that can inform the perspective and interpretation from a respondent's point of view.

Finally, as with all statistical inferences, the measurement invariance testing process is built upon a series of assumptions. Without clearly identifying and acknowledging these assumptions, there is little support for the conclusions drawn from invariance testing. Due to the limited focus of this manuscript, only a few of the underlying assumptions for invariance testing were briefly discussed (i.e., theoretical support for the model being tested, quality of data being fit to the model, and acceptability of partial invariance at the metric and scalar stages). However, other assumptions are described more fully in the ESI† and other resources (Bontempo and Hofer, 2007; Hancock et al., 2009; Putnick and Bornstein, 2016; Fischer and Karl, 2019).

Discussion

CER is moving in the direction of greater interest in the differential impacts and outcomes of diverse populations (Rath et al., 2012; Fink et al., 2018; Stanich et al., 2018; Shortlidge et al., 2019). However, efforts to increase diversity by enrolling more URM students are not sustainable unless paired with efforts to increase inclusion and social justice (O’Shea et al., 2016; Puritty et al., 2017). In an effort to ‘re-imagine’ quantitative approaches to better serve social justice initiatives (García et al., 2018) and raise the standards for investigating these issues at different intersections of identity and background (e.g., race and gender; race and math preparation, etc.), we have presented a statistical method which investigates potential validity threats that could arise when analyzing assessment instrument data. Particular focus has been given at each stage of the analysis to explain some issues that could be evidenced if a given model fails to reach acceptable data-model fit criteria. We have included a few examples that could provide readers some ideas to begin their investigation when measurement invariance is not established at a particular level. Suggestions for circumventing some of these difficulties, such as releasing individual item parameters, have also been presented along with their implications. A summary of each stage of testing, along with the supported claims and evidence established is provided in Table 1.

Many recent studies in CER have taken the first step toward raising the research standards by including variables such as gender, race, etc. and appropriate intersections in their studies (Rath et al., 2012; Fink et al., 2018; Stanich et al., 2018; Shortlidge et al., 2019). However, the next step of investigating the validity of the group comparisons was lacking. Therefore, we encourage researchers to investigate their own data, even the data that has already been published, and consider whether the inferences made were valid for the populations being compared. One recent example of this practice is the study conducted by Rocabado et al. (2019), which explored data from a study done in 2016 by Mooring et al. who conducted an evaluation of the attitude impact of an organic chemistry flipped classroom compared to a traditional classroom. The researchers found that the flipped classroom showed significant attitude gains when compared to the traditional classroom (Mooring et al., 2016). Rocabado et al. (2019), not only investigated whether the original comparison was supported, but also studied whether the attitude gains observed extended to the Black female students in the original sample by utilizing measurement invariance testing to support the investigation and comparisons.

Measurement invariance testing provides opportunities to investigate levels of differences that could arise any time group comparisons are to be made. The 4-Step method presented in this primer is not limited to group comparisons by gender, race, or ethnicity only, it includes groups such as those used in this manuscript (i.e., STEM and non-STEM majors) and to same-group analyses in longitudinal comparisons (e.g., pre-post gain). Regardless of how the groups are defined, at the configural model level (Step 1), an acceptable data-model fit suggests that the groups utilize the same network of equations and the basic measurement model (e.g., number of factors present). At this stage, the claim can be made that item associations are similar between groups, as demonstrated by Fig. 2. The configural model provides a lens to observe these item associations when the data is disaggregated by the defined groups. Item correlations might not be similar for all groups and therefore, the configural model might not reach acceptable levels of data-model fit, suggesting group-level differences in the constructs being measured. If this level cannot be achieved, comparisons between groups are not fair due to the difference in constructs. This is an important step in measurement invariance testing, as it provides a strong foundational model on which to base the subsequent tests.

The metric model (Step 2) investigates the strength of the association between factors and their corresponding items (Sass, 2011). The strength of these relations indicates the meaning of the factor (Gregorich, 2006). Therefore, when the metric model fails, it is evidence of differences in factor meaning between the groups, which provides grounds for further investigation. These differences are observed when the entire pattern of item loadings differs between groups. As this result does not indicate why the groups differ in meaning, a thorough investigation of data from items and constructs should be reviewed for validity evidence including aspects of content validity, response process validity, and construct validity, keeping in mind the various groups that could be in the target population. Metric non-invariance may also arise when one or more item loadings on a factor differ greatly between groups (see Fig. 3c), indicating that one group does not associate the item(s) with the construct being measured, while the other group does. For example, in the fictitious Applications of Chemistry (AC) scale, a problematic item might ask about the field of Materials Science. As this field is interdisciplinary between Engineering, Physics, and Chemistry, it is likely that STEM students would have been exposed to examples from the field across many courses. However, non-STEM majors may have never been exposed to the ideas and examples of Material Science and the role Chemistry plays. Therefore, when comparing a group of STEM majors, who are more likely to have been exposed to Materials Science, to a group of non-STEM majors, it is possible that this item functions differently between the groups. The non-STEM majors might not view Material Science as being an application on the AC scale because they have not been introduced to this field and its interconnections. Therefore, when an item cannot be explained by the underlying construct for one group, the meaning of the construct is different between the groups.

The scalar model (Step 3) considers whether item averages within the measurement model are similar across groups. As shown in Fig. 4, item averages may look similar when combined; however, when disaggregated into groups, item means could be different (Fig. 5) leading to the scalar model not reaching acceptable levels of fit. These differences could arise due to acquiescence biases that affect one group and not the other due to cultural norms not shared between groups (Gregorich, 2006). In the fictitious Connectedness of Chemistry (CC) scale, a problematic item might ask about the degree to which chemistry is connected to a specific issue of global warming, say CO₂ emission. One can think that STEM majors might see stronger ties between the issue and chemistry and therefore score higher on this item than a group of non-STEM majors that may not have been exposed to the idea of light-matter interactions. Therefore, if all the STEM majors score this item high (i.e., a 4 or 5 on a 5-point scale) because they have learned about this phenomenon, then the scale is biased for this item between the two groups in this context. If scalar invariance is not achieved, comparisons between groups beyond the metric model level are not warranted. On the other hand, if scalar invariance is reached, estimated factor mean scores can be computed and compared between groups with evidence that differences between groups are not artifacts of the instrument and construct meaning is similar across the groups. However, if a researcher's goal is to compare observed factor scores (e.g., observed item averages), evidence of conservative invariance (Step 4), in which error variances are constrained to be equal between groups, is required (Sass, 2011).

While conducting measurement invariance testing, each stage provides safeguards and reflexivity (Gillborn et al., 2018) about the groups being compared, rendering this quantitative approach suitable for investigating the differential impacts and outcomes of diverse populations and advancing social justice and equity in CER at the institutional level. We encourage all researchers and practitioners not only to investigate the impact of variables such as race/ethnicity and appropriate intersections (e.g., gender status, language status, socioeconomic status) more often in their research and in their classrooms, but also to employ techniques such as measurement invariance testing in order to safeguard against disguising racism and other social injustices and systemic biases when making comparisons between groups (Gillborn et al., 2018; García, López and Vélez, 2018).

Recommendations and implications

Measurement invariance testing provides evidence to support or refute quantitative data any time group comparisons are to be made. Although qualitative methodologies are used more often to investigate individuals’ and groups’ lived experiences, utilizing quantitative methods with reflexivity and safeguards against racial and other biases (Gillborn et al., 2018; García et al., 2018) can enhance research and teaching that aims at studying pedagogies and interventions that benefit URMs in chemistry. This quantitative method is not limited to group comparisons by gender, race, or ethnicity. It includes groups such as those defined by academic major, socioeconomic status, transfer status, or other meaningful categories and also extends to same-group analyses in longitudinal comparisons (e.g., pre-post gain). To make the endeavor of utilizing measurement invariance testing as easy and accessible as possible, we have provided code and ample explanation for two common software programs (R and Mplus) in the ESI.† Although we provided code for these programs, there are a variety of other programs available that support this technique such as SAS, LISREL, EQS, or the AMOS add-in for SPSS. A helpful comparison of software for structural equation modeling with multiple groups can be found in Narayanan (2012).

For researchers and reviewers

Measurement invariance testing is a technique that we encourage all researchers to use when analyzing assessment instrument data for the purpose of group comparison in their studies. Identifying potential validity threats will greatly enhance the interpretation of the results obtained and claims made, as well as further the answer to the call for increased diversity and inclusion. At each specific stage of measurement invariance testing, certain model claims can be supported or refuted, which either provide evidence for group comparison (see Table 1) or inform the subsequent steps to take in the research. Each of the measurement invariance steps is an opportunity to safeguard against observed and unobserved differences between groups that may be artifacts of the assessment instrument. As researchers, it is our duty to ensure that we present results that have the potential of being transformative; thus, working to minimize artifacts of measurement bias in our analyses is imperative to further the field of CER in more inclusive ways.

Likewise, when reviewing articles for publication, reviewers have the responsibility to ensure that the analyses conducted are held to high standards and that the results and implications are supported by sufficient evidence. In this work, we have highlighted the importance of conducting measurement invariance testing when researchers and practitioners utilize assessment instruments of latent traits on which groups will be compared. The results of these comparisons can have important implications and consequences in CER as the field moves toward greater diversity and inclusion. Thus, these comparisons have to be made responsibly to properly address the consequential validity of the inferences drawn from studies where group or longitudinal comparisons are made. Particularly, we advocate for safeguards and reflexivity in research methodology that aims to challenge the idea of neutral and objective research in an effort to work toward the abolition of social inequities (Solórzano, 1997; Yosso, 2005). Therefore, we urge reviewers and journal editors to check the conditions necessary for the comparison of outcomes by group. First, ensuring that researchers provide reason to believe it is valuable to compare the noted groups (i.e., the comparisons are not simply because the demographic data exists) on the variable of interest. Second, that there is reason to believe the construct being compared can be measured appropriately for all groups through establishing the relevant level of measurement invariance. We have shown how measurement invariance testing can provide reflexivity and ample opportunity to check for differences in measurement for groups in studies. Thus, we encourage the use of this method whenever possible.

Often, the comparisons made between groups will be done at the observed scale score level. If this is the ultimate goal of a study, then the researchers and reviewers should be aware that observed score comparisons require meeting strict invariance (the most conservative level of invariance) across all groups. If this strict invariance model provides acceptable data-model fit, then researchers and reviewers have evidence that observed scale scores can be compared between groups. Within this primer on measurement invariance testing, we laid out a step-by-step method, working up to establishing strict invariance. However, it is beneficial to mention that if only the strict invariance test is conducted, the investigation at each stage of measurement invariance testing is not provided and the change in data-model fit from one level to the next is not produced. Although valuable step-by-step information is not obtained when choosing to run only the desired test, this practice is sound. However, if the strict invariance test fails to provide acceptable data-model fit, then researchers may benefit from conducting the lower level tests and investigating the source of measurement non-invariance. Table 1 provides a summary of appropriate claims and comparisons at each level of measurement invariance.

For practitioners

We encourage practitioners to use measurement invariance testing, when possible, in any endeavor to inform their practice where group comparisons with assessment instrument data of latent traits are utilized. Safeguarding against threats to the validity of the inferences drawn from group comparison studies is fundamental to the evaluation and success of inclusive pedagogies in the classroom. We acknowledge that sample size is often a limitation in many studies. Thus we advise practitioners to utilize similar processes of reflexivity to safeguard against threats to the validity of inferences against groups that are appropriate for their sample size, such as cognitive interviews (Willis, 1999). This practice will help to ensure that the investigations conducted across individual and institutional levels remain mindful of the tenets of CRT and move toward, rather than away from, equity. Additionally, we recommend the collaboration between practitioners and researchers in analyzing and interpreting quantitative data, particularly when comparing groups. These collaborations can be fruitful and inform a wider variety of settings in which our studies take place, providing the field of CER a broader and more complete view of the field as it advances toward greater diversity and inclusion.

Lastly, we urge practitioners to review the research literature with a critical lens and hold research findings to a high standard when data is compared by group. Following the steps of measurement invariance testing can inform whether an instrument can be utilized to make meaningful comparisons with diverse groups. For a practical approach, if measurement invariance testing is not feasible, we suggest a careful review of the literature for instruments which have been appropriately tested with diverse populations, to support appropriate data collection and analyses that lead to meaningful conclusions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to thank Gregory R. Hancock, Program Director of Measurement, Statistics and Evaluation and Director of the Center for Integrated Latent Variable Research (CILVR) at the University of Maryland for his thoughtful feedback about measurement invariance. Support was provided to G. A. R. by the National Science Foundation's Florida–Georgia Louis Stokes Alliance for Minority Participation Bridge to the Doctorate award 1612347. This material is also based upon work supported by the National Science Foundation under award 1849473 to J. E. L. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

References

1. AERA, APA and NCME, (2014), Standards for educational and psychological testing, Washington, DC: American Psychological Association.
2. Apple M. W., (2001), Educating the ‘Right’ Way: Markets, Standards, God, and Inequality. New York, NY: RoutledgeFalmer.
3. Arjoon J. A., Xu X. and Lewis J. E., (2013), Understanding the state of the art for measurement in chemistry education research: Examining the psychometric evidence, J. Chem. Educ., 90, 536–545.
4. Bontempo D. E. and Hofer S. M., (2007), Assessing factorial invariance in cross-sectional and longitudinal studies, in Series in positive psychology. Oxford handbook of methods in positive psychology, Ong A. D. and van Dulmen M. H. M. (ed.), Oxford University Press, pp. 153–175.
5. Bornstein M. H., (1995), Form and function: Implications for studies of culture and human development, Cult. Psychol., 1(1), 123–137.
6. Bowen N. K. and Masa R. D., (2015), Conducting measurement invariance tests with ordinal data: A guide for social work researchers, J. Soc. Social Work Res., 6(2), 229–249.
7. Brandriet A. R. and Bretz S. L., (2014), The development of the redox concept inventory as a measure of students’ symbolic and particular redox understandings and confidence, J. Chem. Educ., 91, 1132–1144.
8. Bretz S. L., (2014), Designing assessment tools to measure students’ conceptual knowledge of chemistry, in Tools of Chemistry Education Research, Bunce D. and Cole R. (ed.), ACS Symposium Series.
9. Brown T. A., (2006), Confirmatory Factor Analysis for Applied Research, New York, NY: The Guilford Press.
10. Bunce D. M., Komperda R., Schroeder M. J., Dillner D. K., Lin S., Teichert M. A. and Hartman J. R., (2017), Differential use of study approaches by students of different achievement levels, J. Chem. Educ., 94(10), 1415–1424.
11. Byrne B. M., Shavelson R. J. and Muthén B., (1989), Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance, Psychol. Bull., 105(3), 456–466.
12. Candell G. L. and Drasgow F., (1988), An iterative procedure for linking metrics and assessing item bias in item response theory, Appl. Psychol. Meas., 12(3), 253–260.
13. Ceci S. J., Williams W. M. and Barnett S. M., (2009), Women's underrepresentation in science: Sociocultural and biological considerations, Psychol. Bull., 135(2), 218–261.
14. Chen F. F., (2007), Sensitivity of goodness of fit indexes to lack of measurement invariance, Struct. Equ. Modeling, 14(3), 464–504.
15. Cheung G. W. and Rensvold R. B., (1999), Testing factorial invariance across groups: A reconceptualization and proposed new method, J. Manage., 25(1), 1–27.
16. Cheung G. W. and Rensvold R. B., (2002), Evaluating goodness-of-fit indexes for testing measurement invariance, Struct. Equ. Modeling, 9(2), 233–255.
17. Cohen J., (1988), Statistical power analysis for the behavioral sciences, 2nd edn, Hillsdale, NJ: Lawrence Erlbaum Associates.
18. Counsell A., Cribbie R. A. and Flora D. B., (2019), Evaluating equivalence testing methods for measurement invariance, Multivar. Behav. Res., 55(2), 312–328.
19. Covarrubias A., (2011), Quantitative intersectionality: A critical race analysis of the Chicana/o educational pipeline, J. Latinos Educ., 10(2), 86–105.
20. Covarrubias A. and Velez, V., (2013), Critical race quantitative intersectionality: An antiracists research paradigm that refuses to ‘Let the numbers speak for themselves’, in Dixson A. and Lynn M. (ed.), Handbook of critical race theory in education, New York City: Routledge, pp. 270–285.
21. Crenshaw K., (1989), Demarginalizing the intersection of race and sex: A Black feminist critique of antidiscrimination doctrine, feminist theory and antiracist politics, Univ. Chicago Leg. For., 139–168.
22. Crenshaw K., (1995), Critical race theory: The key writings that formed the movement, New York City: State University of New York Press.
23. Delgado A. and Stefanic J., (2001), Critical race theory: An introduction, New York City: NYU Press.
24. Dixson A. and Anderson C. R., (2018), Where are we? Critical race theory in education 20 years later, Peabody J. Educ., 93(1), 121–131.
25. Fernández L., (2002), Telling stories about school: Using critical race and Latino critical theories to document Latina/Latino education and resistance, Qual. Inq., 8(1), 45–65.
26. Ferrell B. and Barbera J., (2015), Analysis of students’ self-efficacy, interest, and effort beliefs in general chemistry, Chem. Educ. Res. Pract., 16, 318–337.
27. Ferrell B., Phillips M. M. and Barbera J., (2016), Connecting achievement motivation to performance in general chemistry, Chem. Educ. Res. Pract., 17, 1054–1066.
28. Fink A., Cahill M. J., McDaniel M. A., Hoffman A. and Frey R. F., (2018), Improving general chemistry performance through a growth mindset intervention: Selective effects on underrepresented minorities, Chem. Educ. Res. Pract., 19, 783–806.
29. Finney S. J. and DiStefano C., (2013), Non-normal and categorical data in structural equation modeling, in Hancock G. R. and Mueller R. O. (ed.), Structural equation modeling: a second course, Charlotte, NC: Information Age Publishing, pp. 439–492.
30. Fischer R. and Karl J. A., (2019), A primer to (cross-cultural) multi-group invariance testing possibilities in R. Front. Psychol., 10, 1–18.
31. García N. M., López N. and Vélez V. N., (2018), QuantCrit: rectifying quantitative methods through critical race theory, Race Ethn. Educ., 21(2), 149–157.
32. Garson D., (2012), Testing statistical assumptions. Asheboro, NC: Statistical Associates Publishing.
33. Gibbons R. E. and Raker J. R., (2018), Self-beliefs in organic chemistry: Evaluation of a reciprocal causation, cross-lagged model, J. Res. Sci. Teach., 56(5), 598–615.
34. Gibbons R. E., Xu X., Villafañe S. M. and Raker J. R., (2018), Testing a reciprocal causation model between anxiety, enjoyment and academic performance in postsecondary organic chemistry, Educ. Psychol., 38(6), 838–856.
35. Gillborn D., Warmington P. and Demack S., (2018), QuantCrit: education, policy, ‘big data’ and principles for a critical race theory of statistics, Race Ethn. Educ., 21(2), 158–179.
36. Gregorich S. E., (2006), Do self-report instruments allow meaningful comparisons across diverse population groups? Testing measurement invariance using the confirmatory factor analysis framework, Med Care, 44(11 Suppl 3), S78–S94.
37. Hancock G. R., (2001), Effect size, power, and sample size determination for structured means modeling and MIMIC approaches to between-groups hypothesis testing of means on a single latent construct, Psychometrika, 66, 373–388.
38. Hancock G. R. and French B., (2013), Power analysis in covariance structure modeling, in G. R. Hancock and R. O. Mueller (ed.), Structural equation modeling: A second course, 2nd edn, Charlotte, NC: Information Age Publishing, pp. 117–159.
39. Hancock G. R., Stapleton L. M. and Arnold-Berkovits I., (2009), The tenuousness of invariance tests within multisample covariance and mean structure models, in Structural equation modeling in educational research: Concepts and applications, pp. 137–174.
40. Hensen C. and Barbera J. (2019), Assessing affective differences between a virtual general chemistry experiment and a similar hands-on experiment, J. Chem. Educ., 96, 2097–2108.
41. Hirschfeld G. and Von Brachel R., (2014), Multiple-group confirmatory factor analysis in R – A tutorial in measurement invariance with continuous and ordinal, Pract. Assess. Res. Eval., 19(7), 1–11.
42. Hong L. and Page S. E., (2004), Groups of diverse problem solvers can outperform groups of high-ability problem solvers, Proc. Natl. Acad. Sci. U. S. A., 101(46), 16385–16389.
43. Hosbein K. N. and Barbera J., (2020), Development and evaluation of novel science and chemistry identity measures, Chem. Educ. Res. Pract. 10.1039/c9rp00223e.
44. Hu L. T. and Bentler P. M., (1999), Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives, Struct. Equ. Modeling, 6(1), 283–292.
45. Hurtado S., Newman C. B., Tran M. C. and Chang M. J., (2010), Improving the Rate of Success for Underrepresented Racial Minorities in STEM Fields: Insights from a National Project, In New Directions for Institutional Research, no. 148, Wiley Periodicals, Inc.
46. Ireland D. T., Freeman K. E., Winston-Proctor C. E., Delaine K. D., McDonald Lowe S. and Woodson K. M., (2018), (Un)hidden figures: A synthesis of research examining the intersectional experiences of Black women and girls in STEM, Rev. Res. Educ., 42, 226–254.
47. Jiang B., Xu X., García A. and Lewis J. E., (2010), Comparing two tests of formal reasoning in a college chemistry context, Chem. Educ. Res. Pract., 87(12), 1430–1437.
48. Jöreskog K. G. (1971). Simultaneous factor analysis in several populations, Psychometrika, 36, 409–426.
49. Kahveci A., (2015), Assessing high school students’ attitudes toward chemistry with a shortened semantic differential, Chem. Educ. Res. Pract., 16, 283–292.
50. Kang Y., McNeish D. M. and Hancock G. R., (2016), The role of measurement quality on practical guidelines for assessing measurement and structural invariance. Educ. Psychol. Meas., 76(4), 533–561.
51. Keefer K. V., Holden R. R. and Parker J. D. A., (2013), Longitudinal assessment of trait emotional intelligence: Measurement invariance and construct continuity from late childhood to adolescence, Psychol. Assess., 25(4), 1255–1272.
52. Kendhammer L. K. and Murphy K., (2014), General statistical techniques for detecting differential item functioning based on gender subgroups: A comparison of the Mantel–Haenszel procedure, IRT, and logistic regression, in Innovative Uses of Assessments for Teaching and Research ACS Symposium Series, Washington, DC: American Chemical Society.
53. Kendhammer L., Holme T. and Murphy K., (2013), Identifying differential performance in general chemistry: Differential item functioning analysis of ACS general chemistry trial tests, J. Chem. Educ., 90, 846–853.
54. Komperda R., Hosbein K. N. and Barbera J., (2018), Evaluation of the influence of wording changes and course type on motivation instrument functioning in chemistry, Chem. Educ. Res. Pract., 19, 184–198.
55. Lieber R. L., (1990), Statistical significance and statistical power in hypothesis testing, J. Orthop. Res., 8, 304–309.
56. Litzler E., Samuelson C. C. and Lorah J. A., (2014), Breaking it down: Engineering students STEM confidence at the intersection of race/ethnicity and gender, Res. High. Educ., 55, 810–832.
57. Liu Y., Ferrell B., Barbera J. and Lewis J. E., (2017), Development and evaluation of a chemistry-specific version of the academic motivation scale (AMS-Chem), Chem. Educ. Res. Pract., 18, 191–213.
58. Loertscher J., (2010), Using assessment to improve learning in the biochemistry classroom, Biochem. Mol. Biol. Educ., 38 (3), 188–189.
59. López N., Erwin C., Binder M. and Chavez M. J., (2018), Making the invisible visible: Advancing quantitative methods in higher education using Critical Race Theory and intersectionality, Race Ethnic. Educ., 21(2), 180–207.
60. McNeish D., An J. and Hancock G. R., (2018), The thorny relation between measurement quality and fit index cutoffs in latent variable models. J. Pers. Assess., 100(1), 43–52.
61. Mellenbergh G. J., (1989), Item bias and item response theory, Int. J. Educ. Res., 13, 127–143.
62. Meredith W., (1993), Measurement equivalence, factor analysis, and factorial equivalence, Psychometrika, 58, 525–543.
63. Messick S., (1995)., Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning, Am. Psychol., 50(9), 741–749.
64. Montes L. H., Ferreira R. A. and Rodriguez C., (2018), Explaining secondary school students’ attitudes towards chemistry in Chile, Chem. Educ. Res. Pract., 19, 533–542.
65. Mooring S. R., Mitchell C. E. and Burrows N. L., (2016), Evaluation of a flipped, large enrollment organic chemistry course on student attitude and achievement, J. Chem. Educ., 93, 1972–1883.
66. Mueller R. O., Hancock G. R., (2019), Structural Equation Modeling, in Hancock G. R., Stapleton L. M. and Mueller R. O. (ed.), The reviewer's guide to quantitative methods in the social sciences, New York, NY: Routledge, pp. 445–456.
67. Muthén L. K. and Muthén B. O., (2010), Mplus User's Guide, 6th edn, Los Angeles, CA: Muthén and Muthén.
68. Narawathne I. N., (2019), Introducing diversity through an organic approach, J. Chem. Educ., 96(9), 2042–2049.
69. Narayanan A., (2012), A review of eight software packages for structural equation modeling. Am. Stat., 66(2), 129–138.
70. O’Shea S., Lysaght P., Roberts J. and Harwood V., (2016), Shifting the blame in higher education – Social inclusion and deficit discourses, High. Educ. Res. Dev., 35(2), 322–336.
71. Puritty C., Strickland L. R., Alia E., Blonder B., Klein E., Kohl M. T., McGee E., Quintana M., Ridley R. E., Tellman B. and Gerber L. R., (2017), Without inclusion, diversity initiatives may not be enough, Science, 357(6356), 1101–1102.
72. Putnick D. L. and Bornstein M. H., (2016), Measurement invariance conventions and reporting: The state of the art and future directions for psychological research, Dev. Rev., 47, 71–90.
73. Rath K. A., Peterfreund A., Bayliss F., Runquist E. and Simonis U., (2012), Impact of supplemental instruction in entry-level chemistry courses at a midsized public university, J. Chem. Educ., 89, 449–455.
74. Richards-Babb M. and Jackson J. K., (2011), Gendered responses to online homework use in general chemistry, Chem. Educ. Res. Pract., 12, 409–419.
75. Roadrangka V., Yeany R. H. and Padilla M. J., (1983), Paper presented at the annual meeting of the National Association for Research in Science Teaching, Dallas, TX.
76. Rocabado G. A., Kilpatrick N. A., Mooring S. R. and Lewis J. E., (2019), Can we compare attitude scores among diverse populations? An exploration of measurement invariance testing to support valid comparisons between Black female students and their peers in an organic chemistry course, J. Chem. Educ., 96(11), 2371–2382.
77. Salta K. and Koulougliotis D., (2015), Assessing motivation to learn chemistry: Adaptation and validation of Science Motivation Questionnaire II with Greek secondary school students, Chem. Educ. Res. Pract., 16, 237–250.
78. Sass D., (2011), Testing measurement invariance and comparing latent factor means within a confirmatory factor analysis framework, J. Psychoeduc. Assess., 29(4), 347–363.
79. Seadler A., (2012), Obama introduces plan to increase U. S. STEM undergraduates, Earth, 57(6), 27.
80. Shephard L. A., (1993), Evaluating test validity, Am. Educ. Res. Assoc., 19, 405–450.
81. Shortlidge E. E., Rain-Griffith L., Shelby C., Shusterman G. P. and Barbera J., (2019), Despite similar perceptions and attitudes, postbaccalaureate students outperform in introductory biology and chemistry courses, CBE-Life Sci. Educ., 18(3), 1–14.
82. Solórzano D. G., (1997), Images and words that wound: Critical Race Theory, racial stereotyping, and teacher education, Teach. Educ. Quart., 24(3), 5–19.
83. Solórzano D. G., (1998), Critical Race Theory, race and gender microaggressions, and the experiences of Chicana and Chicano scholars, Int. J. Qual. Stud. Educ., 11(1), 121–136.
84. Solórzano D. G. and Ornelas A., (2004), A critical race analysis of Latina/o and African American advanced placement enrollment in public high schools, High School J., 87(3), 15–26.
85. Stanich C. A., Pelch M. A., Theobald E. J. and Freeman S., (2018), A new approach to supplementary instruction narrows achievement and affect gaps for underrepresented minorities, first generation students, and women, Chem. Res. Educ. Pract., 19, 846–866.
86. Steinmetz H., (2013), Analyzing observed composite differences across groups. Methodology, 9(1), 1–12.
87. Stevens J. P., (2007), Intermediate statistics: a modern approach, 3rd edn, New York, NY: Routledge Taylor and Francis Group.
88. Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
89. Tsui L., (2007), Effective strategies to increase diversity in STEM fields: A review of the research literature, J. Negro Educ., 76(4), 555–581.
90. Vandenberg R. J. and Lance C. E., (2000), A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research, Organ. Res. Meth., 2, 4–69.
91. Villafañe S. M., Bailey C. P., Loertscher J., Minderhout V. and Lewis J. E., (2011), Development and analysis of an instrument to assess student understanding of foundational concepts before biochemistry coursework, Biochem. Mol. Biol. Educ., 39(2), 102–109.
92. Villafañe S. M., García C. A. and Lewis J. E., (2014), Exploring diverse students' trends in chemistry self-efficacy throughout a semester of college-level preparatory chemistry, Chem. Educ. Res. Pract., 15(2), 114–127.
93. Wicherts J. M., Nolan C. V. and Heesen D. J., (2005), Stereotype threat and group differences in test performance: A question of measurement invariance, J. Pers. Soc. Psychol., 89(5), 686–716.
94. Widaman K. F. and Reise S. P., (1997), Exploring the measurement invariance of psychological instruments: Applications in the substance use domain, in Bryant K. J., Windle M. E. and West S. G. (ed.), The science of prevention: Methodological advances from alcohol and substance abuse research, Washington, DC: American Psychological Association.
95. Willis G. B., (1999), Cognitive interviewing: A “how to” guide, in Meeting of the American Statistical Association, Research Triangle Institute.
96. Wolf E. J., Harrington K. M., Clark S. L. and Miller M. W., (2013). Sample size requirements for structural equation models: An evaluation of power, bias, and solution propriety, Educ. Psychol., 73(6), 913–934.
97. Wren D. and Barbera J., (2013), Gathering evidence for validity during the design, development, and qualitative evaluation of the thermochemistry concept inventory, J. Chem. Educ., 90, 1590–1601.
98. Xu X., Villafañe S. M. and Lewis J. E., (2013), College students’ attitudes toward chemistry, conceptual knowledge and achievement: structural equation model analysis, Chem. Educ. Res. Pract., 14(2), 188–200.
99. Xu X., Kim E. S. and Lewis J. E., (2016), Sex difference in spatial ability for college students and exploration of measurement invariance, Learn. Individ. Differ., 45, 176–184.
100. Yosso T., (2005), Whose culture has capital? Race Ethnic Educ., 8(1), 69–91.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0rp00025f

---