Open Access Article
Open Access ArticleComputational investigation of Zn-doped and undoped SrEu2Fe2O7 as potential mixed electron and proton conductors
Zongzi Jin a,
Ranran Peng*a,
Yunpeng Xiaa,
Zhenbin Wangb and
Wei Liu*a
a,
Ranran Peng*a,
Yunpeng Xiaa,
Zhenbin Wangb and
Wei Liu*a
aCAS Key Laboratory of Materials for Energy Conversion, Department of Materials Science and Engineering, University of Science and Technology of China, Hefei, 230026, P. R. China. E-mail: pengrr@ustc.edu.cn; wliu@ustc.edu.cn
bDepartment of Physics, Technical University of Denmark, 2800 Kongens Lyngby, Denmark
First published on 2nd November 2020
Abstract
Understanding the electrode properties at the atomistic level is of great benefit to the evaluation of electrode performance and design of better electrode materials in solid oxide fuel cells. In this work, density functional theory (DFT) calculations are employed to investigate the formation and conducting behaviors of oxygen vacancies and proton defects in Ruddlesden–Popper oxide SrEu2Fe2O7 (SEFO), which has been experimentally characterized as a promising cathode. The calculation results suggest both oxygen vacancies and proton defects can be formed in SEFO, and especially, the formation of these defects is largely dependent on oxygen sites in the special crystal structure with alternative stacking of rock-salt layers and double-layered perovskite slabs. The oxygen vacancies within the perovskite slabs have very low formation energies, but demonstrate high energy barriers for migration and low hydration properties; while in the case of those in the rock salt layers, it’s contrary. Interestingly, protons have similar migration abilities in the perovskite slabs and rock salt layers. And therefore, increasing the vacancy concentration of the rock salt layer is beneficial to increase the concentration of proton defects and to improve the proton conductivity. DFT calculations also indicate that substituting Zn for Fe in SEFO can largely depress the oxygen vacancy formation energy, which helps to increase the concentration of both defects. Importantly, the energy barriers for migration of both oxygen ions and protons are barely enhanced, implying a negligible trapping effect of the Zn dopant.
Introduction
To guarantee energy security and solve climate change, developing renewable and sustainable energy conversion devices is regarded as a promising means. Among various energy conversion technologies, solid oxide fuel cells (SOFCs) are one of the most attractive ones because of its high conversion efficiency and low environmental impacts.1 Compared with traditional oxygen-ion conducting ones (O-SOFCs), proton conducting SOFCs (P-SOFCs) based on proton conducting electrolytes are more suitable for operating at low and intermediate temperatures (IT) because of the low energy barriers for proton conduction and proton involved electrode reactions, and thus have attracted more attention recently.2,3 Unfortunately, the lack of proper cathode materials makes P-SOFCs show very a limited advantage on power output over O-SOFCs even at intermediate temperatures.In the cathode of P-SOFC, protons  that are formed at the anode and transferred to the cathode via the electrolyte react with oxygen gas to generate water molecules, which will then be released to the atmosphere, as expressed in the Kröger–Vink notation in eqn (1).
that are formed at the anode and transferred to the cathode via the electrolyte react with oxygen gas to generate water molecules, which will then be released to the atmosphere, as expressed in the Kröger–Vink notation in eqn (1).
 | (1) |
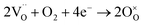 | (2) |
DFT is a powerful tool which can be used to understand the micro-mechanism of SOFC-related electrochemical reactions, and to establish suitable screening and modification schemes to provide directions for the development of electrodes and electrolyte materials.8,9 Many works have suggested that it is useful to investigate the proton conduction in electrolytes and proton/electron mixed conducting cathode materials by revealing the proton uptake and migration energy barriers.10–12
In this work, DFT simulation is used to investigate the possible defects formation and conduction behaviors in ternary double-layered Ruddlesden–Popper phases SrEu2Fe2O7 (SEFO) in which rare earth (Eu) and alkaline earth (Sr) atoms are arranged orderly in the A sites, and the smaller Eu3+ ion prefers the smaller nine-coordinate sites in the rock salt layers rather than the twelve-coordinate sites in the perovskite slabs,13 as shown in Fig. 1a. The special orderly arrangements of the A-site atoms can lead to inhomogeneity in the formation and conduction of defects, and provide more information on exploring novel materials. To further investigate the potential of the SEFO scheme for proton involved reactions, the substitution of Zn for Fe in SEFO is also discussed.
Computational method
Spin-polarized density functional theory (DFT) was employed using the Vienna Ab initio Simulation Package (VASP).14 The electron exchange–correlation functional and the electron–ion interaction were approximated by the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) and projector-augmented wave potentials, respectively.15,16 To correct the large self-interaction error inherent in DFT-GGA for mid-to-late first-row transition metal (TM) oxides, DFT+U methods were used.17 The on-site correction Ueff was applied to Fe, with the effective U values equal to 5.3 eV. The choice of the Ueff value had been used in the Sr3Fe2O7 system.18All calculations used a kinetic energy cutoff of 450 eV for the plane wave basis and Brillouin zone sampling based on the Monkhorst–Pack (MP) scheme.19 A 2 × 2 × 1 G-centered k-point grid was built in 192-atom bulk cells (contains 16 formula units). The electronic energy convergence was set to 10−5 eV, and the residual force on each atom was smaller than 0.05 eV Å−1.
Experimentally, the structure of SEFO was reported as a tetragonal R–P structure in space group P42/mnm with lattice parameters a = 5.507 Å and c = 19.876 Å.20 Along the c-axis, it can be seen to have a stacked structure of strontium oxygen, iron oxygen, europium oxygen, and iron oxygen, as shown in Fig. 1a.
The electronic structural features for each supercell model and magnetic arrangement were analyzed. Topological analysis of the electron density was carried out employing the Bader approach.21
For proton-conducting perovskites, proton defects can form in moist atmosphere, as expressed in eqn (3),
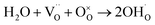 | (3) |
 | (4) |
 is the total energy of the cell containing the oxygen vacancy; E[per] is the total energy of the perfect SEFO and Zn doped SEFO cell; E[O2(g)] is the total energy of the oxygen molecule, but this is problematic since PBE is known to overbind the O2 molecule, so here the E[O2(g)] is calculated by the total energies of atoms and combined with experimental values for the cohesive energies (−5.21 eV) which come from the JANAF thermochemical tables.22 Then, the hydration energy (ΔEhyd) was defined as eqn (5).
is the total energy of the cell containing the oxygen vacancy; E[per] is the total energy of the perfect SEFO and Zn doped SEFO cell; E[O2(g)] is the total energy of the oxygen molecule, but this is problematic since PBE is known to overbind the O2 molecule, so here the E[O2(g)] is calculated by the total energies of atoms and combined with experimental values for the cohesive energies (−5.21 eV) which come from the JANAF thermochemical tables.22 Then, the hydration energy (ΔEhyd) was defined as eqn (5).
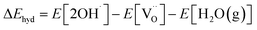 | (5) |
Results and discussion
The confirmation of the magnetic states of oxides helps to accurately evaluate the electronic structure of the system. The SEFO structures with different initial spin moments are constructed, and calculation results suggest that the structure that is antiferromagnetic (AFM, shown in Fig. 1b) has lower energy than that which is ferromagnetic (FM), indicating that the AFM structure is more stable, consistent with the experimental observations.24 Similarly, the SrEu2Fe1.5Zn0.5O7 (SEFZ) that is AFM also demonstrates the most stable configuration, as shown in Fig. 1c.Structural features
Table 1 lists the optimized cell volumes and TM–O bond average lengths. The small overestimation (∼2.6%) of computed cell volumes versus experimental values25 should be ascribed to a well-known shortcoming of the DFT-GGA+U method.| V | Fe–O | Zn–O | |
|---|---|---|---|
| SEFO | 154.675 | 2.022 | None |
| SEFZ | 155.138 | 2.009 | 2.0785 |
Compared with SEFO, the lattice volume of SEFZ expands slightly, which should result from the relatively larger radius of Zn2+. Interestingly, the large Zn2+ ions lead to a longer Zn–O bond, yet simultaneously shorten the Fe–O bond to a certain degree, which may lead to slight distortion of the octahedra and impact the electronic structure of Fe in SEFZ (to be discussed in the next section).
Electronic structure
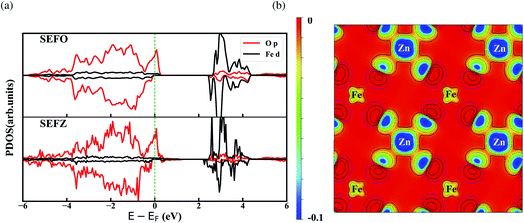
Fig. 2a presents atom and angular-momentum-projected densities of states (PDOS) for SEFO and SEFZ at the PBE+U level of theory. Obviously, SEFO exhibits a typical half-metal state density near the Fermi level. This feature is similar to Sr3Fe2O7. The broad weak hybridized state across the Fermi level due to the overlap between the TMs 3d and O 2p orbitals indicates that electron conduction is possible for SEFO, suggesting that SEFO should have adequate electronic conduction as demanded for an electrode. It should be also noted that the valence band around the Fermi energy level is mainly attributed to the O p band, while the conduction band is mainly from the TMs d band. This highlights the importance of the Fe–O interaction to forming the electronic conductivity. The dominating oxygen character around the Fermi level also suggests that oxygen anions may play a major role in the electron exchange with the reaction intermediates. And for SEFZ, a few 3d electronic states of the Fe which neighbors the Zn in the AB plane appear in the spin-down band gap at 0.35 eV.The 3d magnetic moments and Bader atomic partial charges of the TMs are summarized in Table 2. As expected, the charges of the TMs and O deviate from their respective formal oxidation states because of the mixed ionic–covalent character of the TMs–O bonds, and Zn exhibits a much lower oxidation state than Fe. It should be noted that the Bader charges seem to suggest no significant change before and after substituting Zn in SEFO. Yet, the difference in charge density between SEFZ and SEFO, as shown in Fig. 2b, suggests that Fe in SEFZ exhibits a smaller charge density. The different charge density combined with the variation of the Fe magnetic moment shown in Table 2 jointly indicate that the valence state of Fe in SEFZ is slightly raised. This also explains why the volume expansion of the SEFZ is not as large as expected.
| Bader | Mag | |||
|---|---|---|---|---|
| Fe | Zn | O | Fe | |
| SEFO | 1.765 | None | −1.255 | 4.176 |
| SEFZ | 1.762 | 1.309 | −1.223 | 4.058 |
Formation and migration of oxygen vacancy
Formation energy of oxygen vacancies is a key indicator to evaluate the oxygen vacancy concentration in mixed conducting oxides. The special layered structures of SEFO lead to five distinct oxygen sites, which are labeled OI, OII, OIII, OIV and OV, as shown in Fig. 3a, Here, OI is located in the SrO layer, OII in the EuO layer, and OIII, OIV and OV all in the FeO layer within the slightly tilted octahedra. Fig. 3c shows the formation energies of the oxygen vacancies located at each distinct oxygen site (OI–OV). Among all the five sites, OI has the lowest vacancy formation energy of 1.2 eV, indicating that the oxygen vacancy prefers mostly to be formed at the central site of the pseudo-perovskite slabs. While OII has the highest vacancy formation energy, which makes oxygen vacancies more difficult to be formed than in the rock salt layer. This is similar to that observed in (Sr,La)3Fe2O7−δ, the layered perovskites.26 Such commonality seems to suggest that the difference in the oxygen vacancy formation energies of pseudo-perovskite slabs and the rock salt layer is mainly due to the unique RP layer structure. It should also be noted that oxygen sites in the FeO layer also demonstrate different formation energies, which should be attributed to the slant of the Fe–O octahedra. And the closer the site (OIII) is to the rock salt layer, the larger the formation energy observed.The formation of an oxygen vacancy can be also viewed as a process of the subsequent redistribution of the extra electrons from the oxide ion into the lattice, which in turn impacts the electronic structure. The ability of charge rearrangement may be assessed in two aspects, the number of charge transfer paths and the covalency of the charge transfer paths. It is believed that the main interaction between O atoms and A-position ions is the formation of ionic bonds, while the charge transfer mainly occurs through the TMs–O bonds with covalent bonding components. The oxygen in the rock salt layer can only form one TMs–O bond, while the oxygen in the perovskites layer can form two TMs–O bonds, which benefits the charge rearrangement and thus the low formation energy. Meanwhile, hybridization characteristics between OI and Fe near the Fermi energy level are much larger than between OII and Fe, as shown in Fig. 3d, which favors the charge transfer between OI and Fe, and also depresses the vacancy formation energy. Analysis on both the bonding numbers and the bond hybridization indicates the oxygen site in the rock salt layer should have high vacancy formation energy which should be highly associated with the special layer structure of RP oxides.
Another key factor to determine the oxygen ion conduction is the energy barriers for oxygen ions via oxygen vacancies. Table 3 lists the calculated oxygen vacancy migration barriers in SEFO. Interestingly, for the OI site, the most feasible site to form the oxygen vacancy, the vacancy needs to overcome an energy barrier of at least 0.84 eV to migrate away to other sites, yet only overcome a barrier of 0.53 eV to go back. While for OII, the energy barrier is much lower for the vacancy to migrate away, for which the lowest barrier is only 0.23 eV. These results highly suggest that it is more difficult for an oxygen ion to incorporate into the stable sites for oxygen vacancy. As indicated in Table 3, it can be also found that the minimum energy path (MEP) of vacancy transport is following OII–OV–OII with the barrier of only 0.26 eV, which is much lower than those in many perovskites. Considering both the migration barrier and the defect formation energy, the active energy for oxygen vacancy conduction is about 1.82 eV when the vacancy is following the MEPs.
| Initial | Final | Initial to final | Final to initial | |
|---|---|---|---|---|
| SEFO | OI | OIII | 1 | 0.65 |
| OIV | 0.88 | 0.22 | ||
| OV | 0.84 | 0.53 | ||
| OII | OIII | 0.35 | 0.35 | |
| OIV | 0.55 | 0.68 | ||
| OV | 0.23 | 0.26 | ||
| OV | OIII | 0.78 | 0.74 | |
| OIV | 0.58 | 0.68 | ||
| SEFZ | ObI | OaV | 0.86 | 0.25 |
Similar analysis has also been made on SEFZ. In SEFZ, there are 15 distinct oxygen sites. For simplicity, we only consider the five oxygen sites around the Zn dopant in SEFO (labeled as ObI–ObV) and another five sites (labeled as OaI–OaV) around the Fe ions next to the Zn dopant, as shown in Fig. 3b. Compared with those in SEFO, the vacancy formation energies of the corresponding Fe–O octahedra in SEFZ are all reduced by 0.3–0.4 eV. This indicates that Zn doping has a significant promotion effect on the increase in oxygen vacancy concentration. The effective average Bader charges of SEFO/SEFZ atoms before and after the OI vacancy formation are summarized in Table 4. In SEFO, the formation of an oxygen vacancy at the O1 site slightly reduces the Bader charges of Fe. While in SEFZ, the extra charge left behind by the loss of oxygen atoms is mainly distributed to the oxygen while rarely localized to the iron atoms. This feature of the Fe–O bond is conducive to the formation of vacancies,27 which is favorable for the oxygen exchange and diffusion in the SOFC cathode process. Strikingly, the migration energy barrier for a vacancy to migrate away the Zn dopant (ObI → OaV) hardly changes when compared with the corresponding one in SEFO (OI → OV), implying a negligible trapping effect of the Zn dopant. At the same time the corresponding migration barrier is still smaller than the reported value of BaFeO3.28 Interestingly, the migration energy barriers for a vacancy to migrate toward the Zn dopant (OaV → ObI) is only 0.25 eV, much lower than the one in SEFO (OV → OI), suggesting that the Zn dopant benefits the oxygen migration via vacancies.
| Sr | Eu | Fe | Zn | O | ||
|---|---|---|---|---|---|---|
| SEFO | Free | 1.580 | 1.836 | 1.765 | None | −1.255 |
| Vacancy | 1.580 | 1.831 | 1.759 | None | −1.263 | |
| SEFZ | Free | 1.586 | 1.841 | 1.762 | 1.309 | −1.224 |
| Vacancy | 1.584 | 1.836 | 1.762 | 1.298 | −1.232 | |
Hydration and proton migration
Generally speaking, only a small proportion of vacancies can be hydrated to in mix-conductive perovskite oxides, unlike acceptor-doped proton conductors, such as Y doped BaZrO3.29,30 Therefore, assessing the hydration ability for all oxygen vacancies is of great importance.
in mix-conductive perovskite oxides, unlike acceptor-doped proton conductors, such as Y doped BaZrO3.29,30 Therefore, assessing the hydration ability for all oxygen vacancies is of great importance.
Hydration energies at all five non-equivalent oxygen vacancies in SEFO are evaluated, and in the case of the SEFZ system, only the vacancy sites in the Zn–O octahedra are considered for simplicity. All the calculated hydration energies are shown in Fig. 4a. For SEFO, the oxygen vacancy at the EuO layer demonstrates a good hydration ability with the hydration energy of −1.15 eV, much larger than that at the SrO layer (−0.18 eV). Yet, this value is less negative than Sr3Fe2O7 (−1.44 eV), which may account for the better stability of the SEFO system in moist environments when used as an RSOC air electrode. The other hydration energies are also shown in Fig. 4a. Noticeably, it can be found that the hydration energies of the oxygen sites in both SEFO and SEFZ are greatly dependent on their relative sites instead of the existence of the Zn dopant. That is to say, the Zn dopant has slight impact on the hydration energies of the system, unlike those reported by Zohourian et al. in which the Zn dopant can largely improve the hydration energy of Ba0.5Sr0.5FeO3−δ.31 This may also be rooted in the special layered structure of the SEFO system, which has more free space to relieve the stress caused by the interval proton. Moreover, the better proton accommodation ability of rock-salt layers seems to suggest the universality of double-layered P–R oxides as potential proton involved mixed conducting oxides. Especially, for each oxygen site, the higher the oxygen vacancy formation energy is, the more negative the hydration energy is. This observation clearly indicates the competition between oxygen vacancy and proton defects when exposed to moist conditions. It should also be noticed that although the Zn dopant has less impact on the hydration energy due to the smoothing effect of the layered structure, it can greatly depress the oxygen vacancy formation energy. That means the Zn dopant can largely improve the concentration of proton defects by introducing more oxygen vacancies.
In addition to the hydration energy, the migration energy barriers for protons should also be investigated. As shown in Fig. 4c, migration energy barriers for protons should differ a lot with their locating sites and approaching sites due to the asymmetrical crystal structure. Moreover, unlike the direct migration mechanism of oxygen ions, migration of protons undergoes a hopping mechanism, which includes reorientation (R) and transfer (T) processes. And thus, the migration energy barriers for each proton defect should start from the respective oxygen site, undergoing the reorientation process and/or the transferring process, approaching the other specified oxygen site. It is worth noticing that the stability of the proton of each site has different values rooted in the different orientation states of proton defects relative to neighboring ions and the energies of the most stable proton configurations at the different oxygen sites relative to the 1r configuration are shown in Fig. 4b, which indicates 1r and 2r have better stability than the others. Considering the low stability of protons in the FeO layer and the difficulty to cross to the rock salt layer (as shown in Fig. 4b), we mainly consider the protons located at 1r and 2r to migrate within the SrO and EuO layers here. Table 5 shows the relative hopping styles and barriers for the studied protons. The calculated energy barriers for proton migration are also below 0.5 eV, close to the reported activation energy of proton migration.32 These results indicate great proton diffusion ability in the AB plane. For SEFZ, the proton transfer barriers between 1r ↔ 1r′ and 2r ↔ 2r′ are evaluated. Compared to that in SEFO (as shown in Table 5, 1r-T-1r and 2r-T-2r), the proton transfer in SEFZ is slightly lower, implying a very weak trapping effect in SEFZ due to Zn doping.
| SEFO | [110] | 1r-R-1l | 1l-T-1l | 1l-R-1r | 1r-T-1r |
| 0.43 | 0.43 | 0.21 | 0.1 | ||
| [110] | 2r-R-2l | 2l-T-2l | 2l-R-2r | 2r-T-2r | |
| 0.49 | 0.23 | 0.21 | 0.39 | ||
| SEFZ | [110] | 1r-T-1r′ | 1r′-T-1r | ||
| 0.16 | 0.08 | ||||
| [110] | 2l-T-2l′ | 2l′-T-2l | |||
| 0.20 | 0.26 |
Conclusion
In summary, the formation and migration properties of oxygen vacancies and protons in the SEFO system were investigated by DFT calculations. Compared with the experimental and computational results of Sr3Fe2O7 and BaFeO3, SEFZ has similar oxygen vacancy formation energies and migration potentials, while its more negative hydration energies and lower proton migration potentials indicate its possible proton-conducting ability. Combined with the electronic state density results, we propose that SEFZ has the possibility of oxygen ion–proton–electron triple conductivity.The formation and migration behavior of defects in SEFO are closely related to its unique layer structure. Oxygen vacancies are more difficult to form in the rock salt layer than in the perovskite slab, yet the larger free space in the rock salt layer facilitates the conduction of oxygen vacancies. Moreover, when compared with those in the perovskite slab, the oxygen vacancies in the rock salt layer exhibit very good hydration ability. Great proton migration along the [110] direction with very low energy barriers (0.43 eV) is also confirmed in SEFO.
For Zn-doped SEFO, it was found that the Zn dopant could significantly improve the vacancy concentration by depressing the oxygen vacancy formation energies while hardly impacting the hydration ability, which contributes to the increase in proton concentration. Meanwhile, the Zn dopant demonstrated a trapping effect on the proton conduction. All these imply that SEFZ should have better proton conduction than SEFO because of its higher proton concentration and close migration energy barrier.
Our investigations of SEFO and SEFZ seem to suggest that the fantastic crystal structure of two-layered R–P oxide plays a decisive role in the formation and migration of oxygen vacancies and proton defects. This finding may contribute to the intensive exploration of new proton-involved mixed conductors.
Conflicts of interest
There is no conflict of interest.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 21676261, 51872276, U1632131). The numerical calculations in this paper were done on the supercomputing system in the Supercomputing Center of the University of Science and Technology of China.References
- S. Y. Gómez and D. Hotza, Renewable Sustainable Energy Rev., 2016, 61, 155–174 CrossRef.
- R. J. Gorte, Science, 2015, 349, 1290 CrossRef CAS.
- L. Bi, S. Boulfrad and E. Traversa, Chem. Soc. Rev., 2014, 43, 8255–8270 RSC.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O’Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS.
- Z. Wang, W. Yang, S. P. Shafi, L. Bi, Z. Wang, R. Peng, C. Xia, W. Liu and Y. Lu, J. Mater. Chem. A, 2015, 3, 8405–8412 RSC.
- D. Huan, N. Shi, L. Zhang, W. Tan, Y. Xie, W. Wang, C. Xia, R. Peng and Y. Lu, ACS Appl. Mater. Interfaces, 2018, 10, 1761–1770 CrossRef CAS.
- D. Poetzsch, R. Merkle and J. Maier, Faraday Discuss., 2015, 182, 129–143 RSC.
- A. B. Muñoz-García, A. M. Ritzmann, M. Pavone, J. A. Keith and E. A. Carter, Acc. Chem. Res., 2014, 47, 3340–3348 CrossRef.
- Y. L. Lee, J. Kleis, J. Rossmeisl, S. H. Yang and D. Morgan, Energy Environ. Sci., 2011, 4, 3966–3970 RSC.
- J. A. Dawson, J. A. Miller and I. Tanaka, Chem. Mater., 2015, 27, 901–908 CrossRef CAS.
- Z. Wang, W. Yang, Z. Zhu, R. Peng, X. Wu, C. Xia and Y. Lu, J. Mater. Chem. A, 2014, 2, 16707–16714 RSC.
- A. B. Muñoz-García and M. Pavone, Chem. Mater., 2016, 28, 490–500 CrossRef.
- N. N. M. Gurusinghe, J. De La Figuera, J. F. Marco, M. F. Thomas, F. J. Berry and C. Greaves, Mater. Res. Bull., 2013, 48, 3537–3544 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- S. Dudarev and G. Botton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- W. Tan, D. Huan, W. Yang, N. Shi, W. Wang, R. Peng, X. Wu and Y. Lu, RSC Adv., 2018, 8, 26448–26460 RSC.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- D. Hanžel, Appl. Phys., 1976, 11, 159–162 Search PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS.
- M. W. Chase Jr, C. Davies, J. Downey Jr, D. Frurip, R. McDonald, and A. Syverud, NIST-JANAF Thermochemical Tables, National Institute of Standards and Technology, Gaithersburg, MD, 1986 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- D. Samaras, A. Collomb, J. Joubert and R. Chevalier, Physica B+C, 1977, 86–88, 937–938 CrossRef.
- M. Drofenik, D. Kolar and L. Golič, J. Cryst. Growth, 1973, 20, 75–76 CrossRef CAS.
- I. Kagomiya, K. Jimbo, K. I. Kakimoto, M. Nakayama and O. Masson, Phys. Chem. Chem. Phys., 2014, 16, 10875–10882 RSC.
- A. B. Muñoz-García, D. E. Bugaris, M. Pavone, J. P. Hodges, A. Huq, F. Chen, H. C. Zur Loye and E. A. Carter, J. Am. Chem. Soc., 2012, 134, 6826–6833 CrossRef.
- C. Chen, Z. M. Baiyee and F. Ciucci, Phys. Chem. Chem. Phys., 2015, 17, 24011–24019 RSC.
- D. Poetzsch, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2014, 16, 16446–16453 RSC.
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Proton conducting alkaline earth zirconates and titanates for high drain electrochemical applications, Solid State Ionics, 2001, 295–306 CrossRef CAS.
- R. Zohourian, R. Merkle, G. Raimondi and J. Maier, Adv. Funct. Mater., 2018, 28, 1801241 CrossRef.
- N. Kochetova, I. Animitsa, D. Medvedev, A. Demin and P. Tsiakaras, RSC Adv., 2016, 6, 73222–73268 RSC.
| This journal is © The Royal Society of Chemistry 2020 |