Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Main-group metal cyclophane complexes with high coordination numbers†
Yasir Altaf a,
Muhammad Yarb and
Muhammad Ali Hashmi
a,
Muhammad Yarb and
Muhammad Ali Hashmi *c
*c
aSchool of Chemical and Physical Sciences, Victoria University of Wellington, New Zealand
bDepartment of Chemistry, COMSATS University Islamabad, Abbottabad Campus, KPK 22060, Pakistan
cDepartment of Chemistry, University of Education, Attock Campus, Attock 43600, Pakistan. E-mail: muhammad.hashmi@ue.edu.pk
First published on 20th August 2020
Abstract
Density functional theory calculations using the PBE0-D3BJ hybrid functional have been employed to investigate the complexation of main-group metal-cations with [2.2.2]paracyclophane and deltaphane. Geometry optimization under symmetry constraints was performed to observe the mode of coordination that a metal-cation adopts when it resides inside the cyclophane cavity. Thermodynamic properties were investigated to note the trends of stability along a group of metals. To further investigate the bonding properties, Morokuma–Ziegler energy decomposition analysis, natural bond orbital analysis and Bader's analysis were employed. It was observed that most of the main-group metal complexes with cyclophanes prefer an η6η6η6 coordination mode where the metal-cation sits in the centre of the cyclophane cavity. There is an increased thermodynamic stability in [2.2.2]paracyclophane complexes compared to their deltaphane analogues while the reverse is true regarding the strength of coordination based on interaction energy.
Introduction
Cyclophanes consist of two or more aromatic rings connected through aliphatic bridges, to form a cyclic cavity.1 The aromatic rings are characterized by a planar geometry but the strain imposed by the aliphatic components renders the geometry of the cyclophanes twisted.2There is a growing interest in the donor–acceptor complexes of cyclophanes with metals due to their various applications such as the development of ion-selective electrodes,3 catalysis4 and chelation.5 Metal-chelating agents involving cyclophanes are potential candidates to be used in waste-water treatment since they are known for metal-ion scavenging.3,6 Host molecules undergo conformational changes upon incorporation of the guest species in their macrocyclic cavity and these differences may be observed sometimes through fluorescence. This allows recognition of targetted guest metal-cations.7 Moreover, derivatives of metallacyclophane hosts have been reported as potential candidates for optical biomolecular recognition.8 Luminescent metal-complexes of cyclophanes have been reported to have their potential applications in thin-film nonoporous materials.9 All these applications are due to the potential of the π-rich cyclophane cavity to host electrophilic or cationic guests by making inclusion complexes, despite the fact that some smaller cyclophanes are also known to form exclusion complexes.10
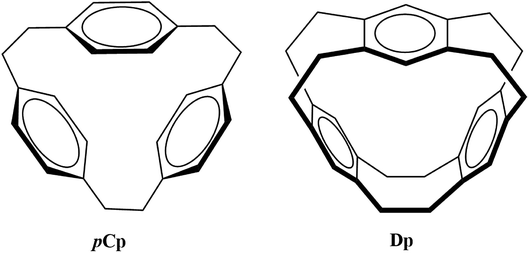
The selectivity and sensitivity of cyclophanes can be improved as evident from the efforts in the past such as derivatization and functionalization using different coordination groups,4,11,12 controlling the size of the cavity to capture guest species13 and replacing the usual phenyl ring with heterocyclic aromatic rings such as imidazolium.14 Owing to the variety of their potential applications, it is important to explore the bonding properties of different possible metallacyclophanes. In the current study, the two cyclophanes [2.2.2]paracyclophane (pCp) and deltaphane (Dp) given in Fig. 1 were selected for this purpose.
pCp was first synthesized by Pierre and co-workers where they called it a π-prismand due to its π-rich prism-shaped cavity15 and demonstrated its complexation with silver triflate. Extending the concept and introducing an increased rigidity compared to that of pCp, Kang et al. reported the synthesis of Dp.16 As the systematic name of the latter i.e. [2,2,2,2,2,2](1,2,4,5)cyclophane suggests, Dp has six ethano bridges compared to three in pCp. pCp and Dp consist of three phenyl rings each bridged through aliphatic chains. However, pCp is more flexible as each aromatic ring is attached to two ethyl bridges unlike its attachment to four in case of Dp.
Due to the presence of phenyl rings, both these molecules contain π-rich cavities that can coordinate to the metal-cations to form stable complexes. It was shown earlier that the silver triflate complex of pCp is much more stable compared to other such complexes with aromatic systems.15 Similarly, the crystal structure of silver triflate complex of Dp was also reported.16 During the same period (mid to late 1980s), Schmidbaur and co-workers reported the groundbreaking complexes of pCp with some of the main-group metals.17–19 Despite these contributions in synthesis of metallacyclophanes of pCp and Dp, a lot of effort is still required to explore the bonding properties of these complexes to make use of these promising π-donating ligands on industrial scale.
In this regard, we previously reported the bonding properties of coinage metal complexes of pCp and Dp.20 Earlier, the groups of Frenking and Castro carried out a computational study on the coordination mode and bonding properties of inclusion complexes of Sn2+ and Ag+ with pCp.21 They further extended the concept to computationally understand the role of formal charge of a cation in π–cation interactions by comparing the complexes of isoelectronic In+ and Cd2+ with pCp.22 In further instances, Castro et al. investigated helicenes23 and Dp24 as potential π-donors to form various π–cation interactions through relativistic DFT approach. A review of the use of relativistic computational tools to study the structural and bonding properties of these π–cation interactions has been published recently25 which shows that different avenues in this field have been opened by the groups of Castro and Frenking over the last few years. The current work is aimed at investigating the coordination and bonding properties of the complexes of group 13 (Ga+, In+ and Tl+), 14 (Ge2+, Sn2+ and Pb2+) and 15 (As3+, Sb3+ and Bi3+) with the π-rich cavity of pCp and Dp using density functional theory (DFT).
Computational details
All calculations related to geometry optimization were performed with the Gaussian 09 suite of programs (Revision D.01).26 The PBE0 hybrid functional27 in conjunction with Grimme's empirical D3 correction with Becke–Johnston damping (D3BJ)28 was used in combination with the def2-TZVP basis-set29 of triple-ζ quality in all these calculations.The optimized structures were further subject to the Morokuma–Ziegler Energy Decomposition Analysis (MZEDA)30 that was carried out with the ADF2014 program.31 The TZ2P (Slater Type Orbital) basis set32 was employed along with the relativistic ZORA Hamiltonian.33,34 MZEDA involves the decomposition of total energy (ΔE) of a molecule as:
| ΔE = (ΔE1 + ΔE2) + ΔEint | (1) |
In eqn (1), ΔEint is the instantaneous interaction between the two molecular fragments and (ΔE1 +ΔE2) is the sum of their individual energies. The above equation implies that ΔEint is the difference between the total energy of a molecule and its fragments. ΔEint can be further subdivided as in eqn (2):
| ΔEint = ΔEPauli + ΔEelstat + ΔEorb | (2) |
Bader's analysis based on quantum theory of atoms in molecules (QTAIM)35 given by Richard Bader was performed using Multiwfn software.36 NBO analysis was carried out with NBO 6.0 program37 as interfaced with Gaussian09.
Molecular graphics were rendered with GaussView 5.0.9.38
Results and discussion
Structural features
In pCp, the C–C bond lengths in bridging ethyl units and that for bridgeheads are 1.54 Å and 1.51 Å compared to the experimental mean bond lengths of 1.43 Å and 1.52 Å respectively. The calculated C–C bond lengths in the phenyl rings are equivalent at 1.39 Å compared to the experimental bond lengths i.e. 1.37 Å. Dp presents a different case with a small variation of bond lengths in phenyl rings. Here, the calculated C–C bond length of the two sides of each phenyl ring attached to ethyl bridges is 1.40 Å compared to its experimental value of 1.390(2) Å while the other four bonds are calculated to be 1.39 Å compared to the experimental 1.387(3) Å bond length.
pCp–Mn+ and Dp–Mn+ complexes
Inclusion complexes of pCp (pCp–Mn+) and Dp (Dp–Mn+) with nine metal-cations of interest were optimized in their D3 and C3 symmetry and confirmed as either minima or transition structures through vibrational analysis. In the former case, the group 13 complexes and pCp–As3+ are C3 symmetric minima while group 14 and the rest of group 15 pCp–Mn+ complexes have D3 symmetry in their ground state structures. In case of group 13 pCp–M+ complexes and pCp–As3+, the D3 symmetry was possible for the transition structures only. The D3 symmetric pCp–Mn+ complexes show η6η6η6 metal–phenyl rings coordination. However, pCp–Ga+ and pCp–As3+ present a case with C3 symmetry showing η6η6η6 coordination while its counterparts i.e. pCp–In+ and pCp–Tl+ exhibit η2η2η2 coordination. As for the Dp complexes, all the nine structures were optimized as minima in C3 as well as D3 symmetry. Dp–Mn+ complexes with C3 show η1η1η1 coordination of a metal ion staying on the top of Dp cavity in each complex. D3 symmetric complexes, on the other hand, exhibit η6η6η6 coordination of the metal-cation present inside the Dp cavity. These results suggest that despite few exceptions, the pCp and Dp complexes of main-group metal-cations under discussion differ from the transition metal complexes where the metal-cation tends to come out of the cavity20,21 preferring peripheral coordination unlike current complexes where central (η6η6η6) coordination is preferred.Some key structural parameters of pCp–Mn+ and Dp–Mn+ of interest are given in Table 1. The experimental evidence is available only for pCp–Ga+, pCp–In+, pCp–Ge2+, pCp–Sn2+ and pCp–As3+ where it can be seen that computational results align well with the experimental ones. However, the distance of metal ion from the center of the pCp cavity in experimental and computational instances differs, which can be attributed to the proximity of corresponding counter anion(s) to the metal cation in experimentally reported complexes. This is in line with the computational findings reported earlier in case of pCp–Sn2+.18 The difference is highly pronounced in case of pCp–As3+ where both the calculated conformations (C3 and D3) exhibit η6η6η6 coordination mode, as mentioned earlier, with As3+ in C3 symmetry displaced by 0.266 Å from the center of the host cavity. On the other hand, the experimentally reported pCp–As3+ shows η2η2η2 coordination where AsCl3 coordinates from the top of the cavity. In addition to pCp–Sn2+, the computational findings for pCp–In+ have also been reported earlier22 which, despite small numerical differences, show a great deal of similarity with the pCp–In+ calculated in our case.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–M denote average metal–carbon distances, distance of metal cation from the center of the cavity, and average distance between C
C–M denote average metal–carbon distances, distance of metal cation from the center of the cavity, and average distance between C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of phenyl rings (upper and lower in pCp–Mn+ and sideways in Dp–Mn+) from metal ion, respectively
C of phenyl rings (upper and lower in pCp–Mn+ and sideways in Dp–Mn+) from metal ion, respectively
| Avg. C–M | Cent–M | Internal Radius | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–M C–M |
||
|---|---|---|---|---|---|
| pCp–Ga+ | C3 | 2.993 | 0.466 | 2.603 | 2.896 |
| D3 | 2.972 | 0.000 | 2.625 | 2.895 | |
| Exp.17 | 2.985 | 0.417 | 2.628 | 2.910 | |
| pCp–In+ | C3 | 3.130 (3.170) | 1.192 (1.698) | 2.644 | 3.052 (3.091) |
| D3 | 3.029 (3.101) | 0.000 (0.000) | 2.689 (2.765) | 2.963 (3.042) | |
| pCp–Tl+ | C3 | 3.144 | 1.351 | 2.640 | 3.066 |
| D3 | 3.040 | 0.000 | 2.701 | 2.976 | |
| pCp–Ge2+ | D3 | 2.843 | 0.000 | 2.476 | 2.746 |
| Exp.18 | 3.062 | 0.994 | 2.449 | 3.017 | |
| pCp–Sn2+ | D3 | 2.952 (2.975) | 0.000 (0.000) | 2.599 (2.595) | 2.872 (2.877) |
| Exp.18 | 2.958 | 0.382 | 2.581 | 2.877 | |
| pCp–Pb2+ | D3 | 2.957 | 0.000 | 2.605 | 2.879 |
| pCp–As3+ | C3 | 2.851 | 0.266 | 2.498 | 2.742 |
| D3 | 2.829 | 0.000 | 2.418 | 2.685 | |
| Exp.19 | 3.458 | 2.799 | 2.578 | 3.390 | |
| pCp–Sb3+ | D3 | 2.866 | 0.000 | 2.498 | 2.769 |
| pCp–Bi3+ | D3 | 2.900 | 0.000 | 2.537 | 2.810 |
| Dp–Ga+ | C3 | 2.637 | 2.354 | 2.365 | 2.744 |
| D3 | 2.836 | 0.000 | 2.467 | ||
| Dp–In+ | C3 | 2.863 | 2.788 | 2.374 | 2.779 |
| D3 | 2.877 | 0.000 | 2.512 | ||
| Dp–Tl+ | C3 | 2.863 | 2.788 | 2.374 | 2.779 |
| D3 | 2.877 | 0.000 | 2.512 | ||
| Dp–Ge2+ | C3 | 2.910 | 2.866 | 2.377 | 2.792 |
| D3 | 2.891 | 0.000 | 2.528 | ||
| Dp–Sn2+ | C3 | 2.526 | 2.219 | 2.345 | 2.732 |
| D3 | 2.823 | 0.000 | 2.449 | ||
| Dp–Pb2+ | C3 | 2.590 | 2.286 | 2.360 | 2.750 |
| D3 | 2.843 | 0.000 | 2.472 | ||
| Dp–As3+ | C3 | 2.206 | 2.060 | 2.230 | 2.658 |
| D3 | 2.724 | 0.000 | 2.343 | ||
| Dp–Sb3+ | C3 | 2.378 | 2.190 | 2.311 | 2.670 |
| D3 | 2.784 | 0.000 | 2.400 | ||
| Dp–Bi3+ | C3 | 2.460 | 2.253 | 2.331 | 2.715 |
| D3 | 2.803 | 0.000 | 2.421 | ||
The structural parameters of C3 and D3 symmetric conformers of pCp–Ga+ are identical except the displacement of Ga+ from the center of the cavity by 0.466 Å in C3 conformer in contrast to its exactly central location in the D3 counterpart. This is supported by identical ΔEint of both the conformers in Table 4. However, in case of pCp–In+ and pCp–Tl+, the metal ion is located significantly further from the center in C3 symmetry while it is exactly in the center in D3 analogue. In both of these complexes, cavity size increases upon inclusion of metal cation for η6η6η6 coordination as evident from internal radius C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–M (Table 1) while it shrinks when the metal cation approaches from the top of the pCp cavity for η2η2η2 interaction. In line with these observations, C3 conformers of pCp–In+ (ΔEint = −51.51 kcal mol−) and pCp–Tl+ (ΔEint = −46.78 kcal mol−) are energetically favourable by −4.73 kcal mol− and −5.2 kcal mol− than their D3 (ΔEint = −46.78 kcal mol− for pCp–In+ and −41.37 kcal mol− for pCp–Tl+) counterparts. Similarly, the D3 symmetric pCp–As3+ is less favourable by 8.47 kcal mol− than its C3 analogue as evidenced by ΔEint (Table 4).
C–M (Table 1) while it shrinks when the metal cation approaches from the top of the pCp cavity for η2η2η2 interaction. In line with these observations, C3 conformers of pCp–In+ (ΔEint = −51.51 kcal mol−) and pCp–Tl+ (ΔEint = −46.78 kcal mol−) are energetically favourable by −4.73 kcal mol− and −5.2 kcal mol− than their D3 (ΔEint = −46.78 kcal mol− for pCp–In+ and −41.37 kcal mol− for pCp–Tl+) counterparts. Similarly, the D3 symmetric pCp–As3+ is less favourable by 8.47 kcal mol− than its C3 analogue as evidenced by ΔEint (Table 4).
| pCp | Dp | pCp | Dp | pCp | Dp | |||
|---|---|---|---|---|---|---|---|---|
| Ga+ | −110.1 | −66.7 | Ge2+ | −304.0 | −284.1 | As3+ | −683.7 | −682.8 |
| In+ | −95.7 | −37.8 | Sn2+ | −259.7 | −227.8 | Sb3+ | −566.7 | −559.0 |
| Tl+ | −92.5 | −30.3 | Pb2+ | −243.9 | −207.5 | Bi3+ | −524.8 | −511.7 |
| Ga | In | Tl | ||||
|---|---|---|---|---|---|---|
| ΔEprep | −3.32 | (−3.09) | 34.55 [10.00] | (−6.80 [4.50]) | 33.72 | (−6.87) |
| ΔEPauli | 66.40 | (61.73) | 89.40 [73.20] | (49.24 [39.10]) | 88.67 | (44.47) |
| ΔEele | −59.47 | (−56.98) | −70.74 [−49.10] | (−49.34 [−31.00]) | −68.25 | (−45.62) |
| 46.1% | (45.8%) | 52.00% [40.80%] | (48.97% [36.90%]) | 52.50% | (50.10%) | |
| ΔEorb | −69.46 | (−67.40) | −65.44 [−71.20] | (−51.42 [−53.10]) | −61.79 | (−45.43) |
| 53.9% | (54.2%) | 48.00% [59.20%] | (51.03% [63.10%]) | 47.5% | (49.9%) | |
| ΔEint | −62.53 | (−62.66) | −46.78 [−58.50] | (−51.51 [−62.00]) | −41.37 | (−46.57) |
| Ge | Sn | Pb | |
|---|---|---|---|
| ΔEprep | −2.66 | −3.77 [2.1] | −3.96 |
| ΔEPauli | 75.88 | 88.57 [86.0] | 96.88 |
| ΔEele | −88.12 | −93.57–66.5 | −96.56 |
| 26.7% | 32.3% [22.4%] | 34.2% | |
| ΔEorb | −242.16 | −205.31 [−229.9] | −193.83 |
| 73.3% | 68.7% [77.6%] | 66.8% | |
| ΔEint | −254.41 | −210.30 [−217.10] | −193.50 |
| As | Sb | Bi | ||
|---|---|---|---|---|
| ΔEprep | −10.29 | (−7.20) | −4.80 | −4.91 |
| ΔEPauli | 78.98 | (130.07) | 103.33 | 106.87 |
| ΔEele | −118.37 | (−132.27) | −127.73 | −129.40 |
| 16.7% | (17.2%) | 20.7% | 22.4% | |
| ΔEorb | −589.09 | (−634.78) | −488.72 | −447.91 |
| 83.3% | (82.8%) | 79.3% | 77.6% | |
| ΔEint | −628.51 | (−636.98) | −512.72 | −470.42 |
In case of Dp–Mn+, all the C3 conformers exhibit η1η1η1 coordination with the metal cation located on the top of the cavity where their D3 analogues are perfectly η6η6η6 coordinated. A comparison of ΔEint (Table 5) shows that in most of the cases, D3 conformers of Dp–Mn+ are energetically favourable compared to their C3 counterparts except Dp–In+, Dp–Tl+ and Dp–As3+ where η1η1η1 coordination is more favourable.
| Ga | In | Tl | ||||
|---|---|---|---|---|---|---|
| ΔEprep | −3.76 | (−6.20) | −4.81 | (−11.67) | −4.78 | (−14.01) |
| ΔEPauli | 105.14 | (72.51) | 149.89 | (57.30) | 149.34 | (51.92) |
| ΔEele | −80.18 | (−48.98) | −102.52 | (−39.82) | −99.57 | (−36.36) |
| 48.4% | (39.3%) | 55.4% | (40.3%) | 55.9% | (41.3%) | |
| ΔEorb | −85.48 | (−75.66) | −82.92 | (−58.98) | −78.54 | (−51.59) |
| 51.6% | (60.7%) | 44.6% | (59.7%) | 44.1% | (58.7%) | |
| ΔEint | −60.52 | (−52.13) | −35.52 | (−41.50) | −28.78 | (−36.03) |
| Ge | Sn | Pb | ||||
|---|---|---|---|---|---|---|
| ΔEprep | −2.10 | (−11.11) | −5.80 | (−9.57) | −8.16 | (−8.98) |
| ΔEPauli | 100.36 | (126.50) | 140.15 | (130.24) | 146.76 | (120.82) |
| ΔEele | −102.48 | (−90.84) | −119.12 | (−94.34) | −121.11 | (−90.38) |
| 27.6% | (24.2%) | 33.4% | (28.6%) | 35.17% | (30.0%) | |
| ΔEorb | −268.68 | (−283.79) | −237.98 | (−235.22) | −223.23 | (−210.59) |
| 72.4% | (75.8%) | 66.6% | (71.4%) | 64.83% | (70.0%) | |
| ΔEint | −270.81 | (−248.13) | −216.92 | (−199.32) | −197.60 | (−180.15) |
| As | Sb | Bi | ||||
|---|---|---|---|---|---|---|
| ΔEprep | −4.48 | (−41.84) | −5.16 | (−28.21) | −6.11 | (−23.29) |
| ΔEPauli | 100.30 | (201.07) | 140.55 | (186.07) | 154.08 | (168.78) |
| ΔEele | −132.95 | (−142.09) | −147.66 | (−140.83) | −152.61 | (−134.77) |
| 17.4% | (16.2%) | 21.6% | (19.7%) | 23.5% | (21.8%) | |
| ΔEorb | −633.37 | (−734.81) | −535.01 | (−575.48) | −496.03 | (−510.29) |
| 82.6% | (83.8%) | 78.4% | (80.3%) | 76.5% | (78.2%) | |
| ΔEint | −666.07 | (−675.84) | −542.09 | (−530.24) | −494.61 | (−476.28) |
Thermodynamic parameters
The trends of thermodynamic stability were established by calculating the enthalpies of reaction for the complexes under discussion given by the reaction as given in eqn (3).| Lg + Mn+ → LgMn+ | (3) |
It can be seen in Table 2 that while moving from left to right in a period, thermodynamic feasibility of pCp or Dp complexes is enhanced as indicated by increasing exothermic enthalpy from group 13 through 14 to 15 in the same period. On the other hand, there is a trend of decreasing thermodynamic feasibility while moving from lighter to heavier elements in a group. These trends can be attributed to the size of ionic radii and formal charges on metal-cations. The smaller the ionic radius (as on the top of a group and the left side of a period), the greater the thermodynamic feasibility of the corresponding complex. Ionic radii of the metal cations under discussion are given in Table 3. Moreover, the role of formal charge has been found crucial in determining the strength of interaction and stability previously in such complexes.22 Upon moving from group 13 to 15 in a period, the formal charge in our case increases from +1 to +3 and so does the exothermic enthalpy of reaction. The trends of thermodynamic feasibility can be correlated with the results obtained from EDA and are discussed in the next section.
Bonding properties
The nature of bonding in the inclusion complexes under discussion was carried out using MZEDA technique, Bader's and NBO analyses. The former decomposes total interaction energy into various energy terms and hence it explains the strength of different interactions. NBO and Bader's analyses predict the type of bonding.Morokuma–Ziegler energy decomposition analysis
The results for MZEDA of pCp–Mn+ complexes are given in Table 4. It is to be noted that ΔEorb indicates the strength of covalent interaction while ΔEele shows the strength of electrostatic attraction. The ratio of ΔEorb to ΔEele explains the relative importance of covalent and ionic interactions i.e. the greater the ratio, the higher the percentage of ΔEorb will be. The total steric repulsion present in a complex is depicted as ΔEPauli. The sum of the above-mentioned three terms accounts for the instantaneous interaction energy ΔEint. However, it is advised in the literature to describe the overall interaction in terms of three separate quantities; ΔEPauli, ΔEele and ΔEorb.43Table 4 shows that in group 13 pCp–M+ complexes, interaction energy is highest on the top of group and lowest in case of pCp–Tl+. This is in line with the trends of enthalpy of reaction (Table 2) that depicts a decrease in thermodynamic feasibility down the group. It can also be argued that increasing cationic radius (Table 3) down the group makes the π-donation from cyclophane cavity to metal less convenient. It can be seen that the C3 symmetric pCp–Ga+ has an η6η6η6 coordination with the three aromatic rings of pCp which facilitates an overall stronger interaction. The metal-cation in pCp–In+ and pCp–Tl+ is located further from the centre of the cavity building an η2η2η2 coordination in each case, thus contributing to a comparatively lower interaction energy.
A deeper insight into the EDA results (Table 4) shows that D3 symmetric η6η6η6 transition structures of group 13 experiences a greater repulsion than their C3 symmetric complexes as indicated by ΔEPauli. This is then compensated by a greater ΔEprep in case of the former compared to the latter. However, both the C3 and D3 conformers of pCp–Ga+ are η6η6η6 with Ga+ locating a little further from the center in C3 symmetric complex while ΔEint is identical for both. Moreover, coordination in pCp–Ga+ is facilitated by a higher percentage of orbital interaction (ΔEorb) than the electrostatic interaction (ΔEele). In case of pCp–In+ and pCp–Tl+, the percentage of ΔEorb is less compared to that in pCp–Ga+ and ΔEele fraction substantially increases which ultimately accounts for a decrease in strength of coordination down the group as suggested by a decreasing ΔEint. The strength of both the attraction terms may be expressed as the ratio of ΔEorb to ΔEele which is 1.2 for pCp–Ga+ while it is 1.0 for each of pCp–In+ and pCp–Tl+. The trends of EDA results for group 14 and 15 are identical to those of group 13.
It is important to note that Table 4 includes EDA results reported earlier for pCp–In+22 and pCp–Sn2+ (ref. 21) calculated at BP86/TZ2P+ level. Although there is difference between the numerical values of those earlier and current studies which may be attributed to the different methodologies (BP86/TZ2P+ earlier versus PBE0/TZ2P current) used in both studies, the trends are identical. For instance, the η2η2η2-coordinated pCp–In+ is favoured compared to its η6η6η6 analogue based on their ΔEint in both the cases. Similarly, ΔEorb is a major attractive term in η6η6η6-coordinated pCp–Sn2+ in earlier and current studies as evidenced by the percentages of their ΔEorb and ΔEele (Table 4).
The trends of EDA in the case of the Dp complexes under discussion (Table 5) are similar to that for pCp complexes. There occurs a decrease in overall interaction energy from top to bottom in a group. However, Dp–In+ and Dp–Tl+ exhibit relatively stronger electrostatic interactions compared to their pCp analogues. This is evident from the ratio of ΔEorb to ΔEele that is 0.8 for both of these complexes while the same is 1.0 for both of their pCp counterparts. All Dp complexes demonstrate the presence of strong coordination as evident from the interaction energy. However, Table 5 shows that ΔEint of D3 symmetric η6η6η6-coordinated Dp–Mn+ complexes is comparatively higher than that of their C3 symmetric η1η1η1-coordinated counterparts. This difference can be correlated to the greater contribution of covalent interactions (ΔEorb) compared to that of electrostatic interactions (ΔEele) in overall ΔEint in case of D3 complexes. On the other hand, C3 symmetric complexes are characterized by higher contribution of ΔEele than that of ΔEorb in the overall ΔEint which causes a comparatively weaker coordination in C3 complexes than their D3 analogues.
It can be deduced from Tables 4 and 5 that on moving from group 13 to 15 in a period, ΔEint increases to a great extent from one metal ion to the next (Table 4). This trend can be attributed to the formal charge of a cation as witnessed previously.22 In our case, the formal charge is +1, +2 and +3 on group 13, 14, and 15 metal ions whereas ΔEint in a period increases in the order of group 13 < group 14 < group 15. Moreover, the percentage of ΔEorb successively increases and that of ΔEele subsequently decreases from left to right in a period. This whole discussion suggests that an increase in formal charge of a metal ion strengthens its coordination with the cyclophane host characterized by an increasing ΔEorb which further accounts for an increase in overall ΔEint along a period.
QTAIM (Bader's) analysis
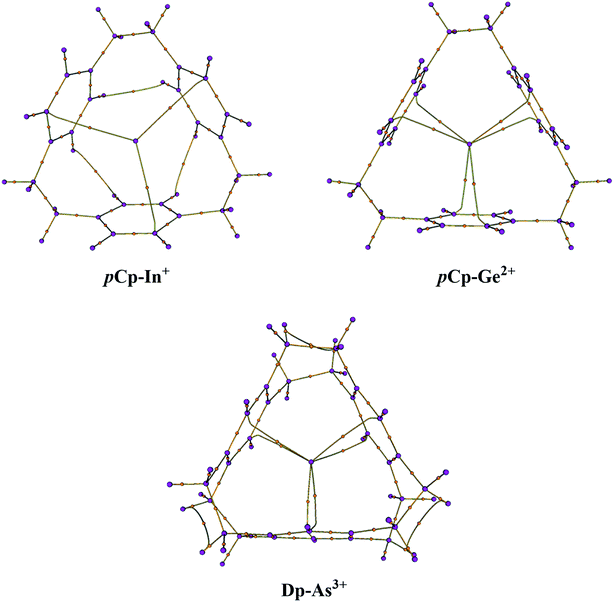
The molecular graphs were extracted from the Bader's analysis results that show the bond paths for all the electron pairs that would be expected for the host molecules i.e. CC and CH bonds. Additionally, there are bond critical paths (BCPs) connecting a metal-cation to the host (Fig. 2). For η2η2η2 complexes i.e. pCp–In+ and pCp–Tl+, there is single BCP between the metal and one carbon atom of each of the aromatic rings toward the surface of the cavity that coordinates with the metal-cation as in the case of pCp–In+ in Fig. 2 where the coordination is on the top of the cavity. For all the pCp and Dp D3 symmetric complexes there are two BCPs connecting the metal from the centre of the cyclophane cavity with two carbon atoms one each on top and bottom sides of the cavity as in the case of pCp–Ge2+ and Dp–As3+ (Fig. 2). The graphs for C3 complexes are similar to each other and same is the case with D3 complexes. This suggests a similar bonding in these complexes.The results for Bader's analysis of all the complexes are given in Table 6 which may be used to classify the types of interaction in these complexes. For that, Popelier has recently devised a mechanism based on electron density (ρ) and its various other functions.44 According to the set of these rules, a small ρ accompanied by a negative Laplacian L (or ∇2ρ > 0 since L = −∇2ρ) usually denotes a depletion of electron density along a BCP and is the characteristic of either closed-shell or donor–acceptor interactions while a small ρ along with L approaching zero indicates a shared interaction. On the other hand, a large electron density and a positive L (or ∇2ρ < 0) shows that electron density is concentrated along a BCP and the interaction will usually be classified as covalent or intermediate. To further confirm the nature of interaction, some additional parameters such as local energy density and the ratio of kinetic energy (G) to ρ are also advised by Popelier.44
| pCp | Dp | |||||||
|---|---|---|---|---|---|---|---|---|
| ρ | L | G/ρ | H | ρ | L | G/ρ | H | |
| Ga+ | 0.017 | 0.036 | 0.572 | −4.0 × 10−4 | 0.024 | 0.046 | 0.574 | −2.1 × 10−3 |
| In+ | 0.016 | 0.032 | 0.545 | −2.0 × 10−4 | 0.023 | 0.057 | 0.634 | −1.6 × 10−3 |
| Tl+ | 0.018 | 0.042 | 0.618 | 3.0 × 10−4 | 0.027 | 0.073 | 0.716 | −1.0 × 10−3 |
| Ge2+ | 0.025 | 0.046 | 0.532 | −1.7 × 10−3 | 0.029 | 0.050 | 0.540 | −2.9 × 10−3 |
| Sn2+ | 0.023 | 0.046 | 0.565 | −1.4 × 10−3 | 0.029 | 0.058 | 0.598 | −2.8 × 10−3 |
| Pb2+ | 0.024 | 0.059 | 0.651 | −7.0 × 10−4 | 0.030 | 0.074 | 0.681 | −1.9 × 10−3 |
| As3+ | 0.055 | 0.045 | 0.428 | −1.2 × 10−2 | 0.034 | 0.056 | 0.519 | −3.6 × 10−3 |
| Sb3+ | 0.030 | 0.050 | 0.524 | −2.8 × 10−3 | 0.034 | 0.057 | 0.542 | −4.2 × 10−3 |
| Bi3+ | 0.028 | 0.060 | 0.588 | −1.9 × 10−3 | 0.034 | 0.072 | 0.625 | −3.4 × 10−3 |
A careful classification based on Table 6 suggests that the complexes under discussion possess shared interactions i.e. electron sharing is enabled between the cyclophane hosts and the cationic guests. These findings are in line with the results of EDA where ΔEorb in most of the cases is a major contributor in total attraction energy compared to ΔEele. All these complexes have a small ρ and its laplacian (L), a G/ρ less than 1 and a negative value of H except pCp–Tl+ that has a positive H suggesting that it has interaction between a shared and a donor–acceptor interaction. The EDA results of pCp–Tl+ support this assumption since ΔEele has a greater percentage than ΔEorb.
Molecular orbital analysis
The electronic structure of the pCp and Dp complexes under consideration was further investigated based on natural population analyses (Table 7). Quantitative molecular orbital (MO) diagrams of pCp–Ga+ (C3 η6η6η6), pCp–In+ (C3 η2η2η2), pCp–Sb3+ (D3 η6η6η6) and Dp–Sn2+ (D3 η6η6η6) are given in Fig. S2 in ESI† to examine bonding and antibonding interactions between the cation and ligand fragments of a complex. The π bonding and antibonding orbitals of a cyclophane ring correspond to those of an aromatic system and have been labelled as π1, π2 and π3. In all the η6η6η6 complexes where the metal cation is centrally located inside the ligand cavity, π1 orbital of the cyclophane ligand coordinates with ns orbital of metal cation (with n = 4, 5, 6 for 4th, 5th and 6th row of elements respectively) giving rise to fully occupied bonding and antibonding π1ns interactions as in Fig. S2(a)† thus not taking part in overall bonding (‘n’ has the value 4, 5, 6 for 4th, 5th, and 6th-row elements respectively). However, np orbital of the metal cation can be bonded to π2 and π3 orbitals of the aromatic system such that pz interacts with π2 based on orientation while π3 has an equal chance of interaction with px and py orbitals of the metal cation. In pCp–In+ and pCp–Tl+ complexes, the bonding scheme is somewhat different as both have η2η2η2 coordination mode. We propose in these two cases that only π2 and π3 of the cyclophane cavity coordinate with ns orbital and one of the np sub-orbitals, respectively leaving behind π1 without any interaction as in Fig. S2(b).† This is also supported by the comparison of the amount of ligand to metal charge transfer (LMCT) in these two complexes (Table 7) with η6η6η6-coordinated pCp–Ga+ where LMCT is double the amount of that in its other two counterparts.| pCp | Dp | ||
|---|---|---|---|
| Ga+ | NC | 0.61 | 0.57 |
| NEC | 4s1.984p0.39 | 4s1.984p0.43 | |
| LMCT | 0.39 | 0.43 | |
| In+ | NC | 0.80 | 0.63 |
| NEC | 5s1.995p0.19 | 5s1.975p0.37 | |
| LMCT | 0.20 | 0.37 | |
| Tl+ | NC | 0.78 | 0.64 |
| NEC | 6s1.986p0.24 | 6s1.986p0.36 | |
| LMCT | 0.22 | 0.36 | |
| Ge2+ | NC | 0.96 | 0.97 |
| NEC | 4s1.994p1.03 | 4s1.984p1.02 | |
| LMCT | 1.04 | 1.03 | |
| Sn2+ | NC | 1.16 | 1.37 |
| NEC | 5s1.995p0.85 | 5s1.985p0.58 | |
| LMCT | 0.84 | 0.63 | |
| Pb2+ | NC | 1.26 | 1.40 |
| NEC | 6s1.996p0.73 | 6s1.986p0.55 | |
| LMCT | 0.74 | 0.60 | |
| As3+ | NC | 0.97 | 0.92 |
| NEC | 4s1.994p2.06 | 4s1.984p2.07 | |
| LMCT | 2.03 | 2.08 | |
| Sb3+ | NC | 1.29 | 1.66 |
| NEC | 5s1.995p1.71 | 5s1.985p1.28 | |
| LMCT | 1.71 | 1.34 | |
| Bi3+ | NC | 1.37 | 1.78 |
| NEC | 6s1.996p1.62 | 6s1.986p1.16 | |
| LMCT | 1.63 | 1.22 | |
It can be seen in Fig. S2(a)† in MO diagram of pCp–Ga+ that π1 of pCp and 4s Ga+ mix to give fully occupied bonding and antibonding MOs where bonding orbital has 15.87% contribution of Ga+ while the remaining 84.13% come from pCp. The contribution of Ga+ in antibonding MO, however, increases to 50.90%. Next, π2 and 4pz mix with a contribution of 6.86% and 83.79% from Ga+ in the resultant bonding and antibonding MOs, respectively. Moreover, π3 mixes equally with 4px and 4py (as discussed above) to give bonding (1.93% from Ga+) and antibonding (60.62% from Ga+) interactions. In contrast, we can observe an overall lesser contribution of 5p orbital of In+ in Fig. S2(b) compared to 4p of Ga+ in (a).† This is in with a higher LMCT in case of η6η6η6-coordinated pCp–Ga+ compared to that in η2η2η2-coordinated pCp–In+ (Table 7). A comparison of (a), (b), (c) and (d) in Fig. S2† suggests that the greater the contribution of p orbital of corresponding metal cation, the larger the LMCT would be.
Comparison of pCp and Dp complexes
pCp and Dp have π-rich cavities and can efficiently host the main-group metal-cations making inclusion complexes with them. However, both possess different structures that cause these π-prismands to behave somewhat differently from each other. Although pCp has a rigid geometry as stated earlier, it is still somewhat flexible due to three ethano-bridges linking the three aromatic rings compared to Dp which has six aliphatic chains bridging the three phenyl rings. It readily undergoes conformational changes and tends to adjust its geometry accordingly to accommodate the metal-cations more conveniently. Hence, the pCp complexes are thermodynamically more feasible compared to the Dp complexes.The comparison is not so simple when it comes to the strength of bonding interaction based on an overall interaction energy. Although, there is no definite trend followed while comparing pCp complexes with their Dp analogues, there are instances where Dp complexes have an increased coordination strength. For example, group 13 pCp–M+ complexes (Table 4) have higher interaction energy than corresponding Dp–M+ complexes (Table 5) which follows the same trend as in their thermodynamic feasibility (Table 2). However, the interaction energy in case of most of the group 14 and 15 pCp–Mn+ is lower than their Dp analogues. This anomaly can be attributed to the collective effects of ΔEorb and ΔEprep. As a general trend, ΔEorb is greater while ΔEprep is smaller for Dp–Mn+ complexes compared to pCp–Mn+ complexes.
Conclusion
Quantum chemical calculations were employed to investigate the pCp and Dp complexes of main-group metals. Geometry optimization under symmetry constraints shows that an η6η6η6 mode of coordination is preferred in most of the cases. These complexes present excellent examples of host–guest interactions unlike the previously reported transition metal complexes of cyclophanes where a metal-cation takes peripheral position on top of the cavity. Most of the complexes are minima in D3 symmetry whereas group 13 pCp–M+ and pCp–As3+ have only C3 symmetric minima. MZEDA shows based on an overall interaction energy that all the complexes of interest bear strong metal–cyclophane coordination. The thermodynamic stability of pCp complexes is higher than their Dp analogues which is as expected due the more flexible and “adjustable” structure of pCp compared to Dp. However, the trends of coordination strength in both the cases are mixed. For example, group 13 pCp complexes have higher interaction energy than their Dp counterparts (a trend that is in line with their thermodynamic stability) while the majority of the rest of Dp complexes have an increased coordination strength compared to the corresponding pCp complexes (thus opposing the trend of thermodynamic stability). This can be correlated with the fact that generally ΔEprep is lower and ΔEorb is higher for Dp–Mn+ complexes than corresponding pCp–Mn+ except group 13 complexes which result in an overall higher ΔEint for Dp–Mn+ than pCp–Mn+ of group 14 and 15. NBO analysis provided the basis for explaining in detail the electronic structure of complexes. Different parameters of Bader's analysis suggest the shared nature of M–C interactions in all these complexes except pCp–Tl+ that has a donor–acceptor type of interaction.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors thank Dr Matthias Lein, Professor Martyn P. Coles, Dr Ralf Tonner, Dr Khurshid Ayub and Dr Julia Schaht for useful discussions. One of the authors (Yasir Altaf) acknowledges Victoria Doctoral Scholarship to pursue this research. Additional computer time was provided by the Victoria University of Wellington High Performance Computer Facilities Raapoi and Heisenberg.References
- P. M. Keehn and S. M. Rosenfeld, Cyclophanes, Academic Press, New York, 1983, vol. I and II Search PubMed.
- F. N. Diedrich, Cyclophanes, Royal Society of Chemistry, Cambridge, 1991 Search PubMed.
- J. Gross, G. Harder, A. Siepen, J. Harren, F. Vögtle, H. Stephan, K. Gloe, B. Ahlers, K. Cammann and K. Rissanen, Concave hydrocarbons, Chem.–Eur. J., 1996, 2, 1585–1595 CrossRef CAS.
- Y. Murakami, Functionalized cyclophanes as catalysts and enzyme models, Cyclophanes II, Berlin, Heidelberg, 1983; pp. 107–155 Search PubMed.
- J. C. Garrison, R. S. Simons, W. G. Kofron, C. A. Tessier and W. J. Youngs, Synthesis and structural characterization of a silver complex of a mixed-donor N-heterocyclic carbene linked cyclophane, ChemComm, 2001, 1780–1781 RSC.
- T. Seppälä, E. Wegelius and K. Rissanen, [2.2.2]m, p, p-and [2.2.2]m, m, p-Cyclophane-Ag-triflate: new π-prismand complexes, New J. Chem., 1998, 22, 789–791 RSC.
- B. Valeur and I. Leray, Design principles of fluorescent molecular sensors for cation recognition, Coord. Chem. Rev., 2000, 205, 3–40 CrossRef CAS.
- D. Ramaiah, P. P. Neelakandan, A. K. Nair and R. R. Avirah, Functional cyclophanes: Promising hosts for optical biomolecular recognition, Chem. Soc. Rev., 2010, 39, 4158–4168 RSC.
- R. V. Slone, K. D. Benkstein, S. Bélanger, J. T. Hupp, I. A. Guzei and A. L. Rheingold, Luminescent transition-metal-containing cyclophanes (“molecular squares”): covalent self-assembly, host-guest studies and preliminary nanoporous materials applications, Coord. Chem. Rev., 1998, 171, 221–243 CrossRef CAS.
- H. Schmidbaur, W. Bublak, B. Huber, G. Reber and G. Müller, Coordination-Polymeric Paracyclophane Complexes of Copper and Silver, Angew. Chem., Int. Ed. Engl., 1986, 25, 1089–1090 CrossRef.
- M. B. Inoue, P. Oram, G. Andreu-de Riquer, M. Inoue, P. Borbat, A. Raitsimring and Q. Fernando, Transition Metal Complexes of 12-and 13-Membered Functionalized Macrocycles, Dioxotetraazacycloalkanediacetates, Inorg. Chem., 1995, 34, 3528–3535 CrossRef CAS.
- M. B. Inoue, I. C. Muñoz, L. Machi, M. Inoue and Q. Fernando, Structural and spectroscopic studies of binuclear Cu2+ and Co2+ complexes with an amide-based naphthalenophane, Inorg. Chim. Acta, 2000, 311, 50–56 CrossRef CAS.
- P. Saarenketo, R. Suontamo, T. Jödicke and K. Rissanen, Ab Initio MO Study of Silver Ion Complexation in [2.2.2] Cyclophane π-Prismands, Organometallics, 2000, 19, 2346–2353 CrossRef CAS.
- E. Alcalde, C. Ayala, I. Dinarès, N. Mesquida and F. Sánchez-Ferrando, Novel [1n]-meta-Heterophane Frameworks with a Bis-Betaine Nature, J. Org. Chem., 2001, 66, 2281–2290 CrossRef CAS PubMed.
- J. L. Pierre, P. Baret, P. Chautemps and M. Armand, [2.2.2]paracyclophane, a novel type of metal cation complexing agent (. pi.-prismand), J. Am. Chem. Soc., 1981, 103, 2986–2988 CrossRef CAS.
- H. C. Kang, A. Hanson, B. Eaton and V. Boekelheide, [26](1, 2, 4, 5) Cyclophane (deltaphane) and related compounds. Simultaneous. pi.-electron interaction among three benzene rings, J. Am. Chem. Soc., 1985, 107, 1979–1985 CrossRef CAS.
- H. Schmidbaur, R. Hager, B. Huber and G. Müller, Arene Complexes with Weak Interactions: A Macrocyclic Tris(arene) Complex of Gallium(I) with η18 Coordination, Angew. Chem., Int. Ed. Engl., 1987, 26, 338–340 CrossRef.
- T. Probst, O. Steigelmann, J. Riede and H. Schmidbaur, GeII and SnII Complexes of [2.2.2]Paracyclophane with Threefold Internal η6 Coordination, Angew. Chem., Int. Ed. Engl., 1990, 29, 1397–1398 CrossRef.
- T. Probst, O. Steigelmann, J. Riede and H. Schmidbaur, Arsen (III)-, Antimon (III)-und Bismuth (III)-halogenid-Komplexe des [2.2. 2] Paracyclophans: Vom lockeren van-der-Waals-Addukt zu stark gerichteten π-Komplexen mit zwei-und dreifacher externer η6-Koordination, Chem. Ber., 1991, 124, 1089–1093 CrossRef CAS.
- Z. X. Wong and M. Lein, Guest-Host Interaction of Coinage Metals in π-Rich Cavities, Aust. J. Chem., 2016, 69, 969–974 CrossRef CAS.
- C. O. Ulloa, M. Ponce-Vargas, R. de Mattos Piccoli, G. F. Caramori, G. Frenking and A. Munoz-Castro, [2.2.2]Paracyclophane, preference for η6 or η18 coordination mode including Ag(I) and Sn(II): a survey into the cation-π interaction nature through relativistic DFT calculations, RSC Adv., 2015, 5, 7803–7811 RSC.
- A. O. Ortolan, G. F. Caramori, G. Frenking and A. Muñoz-Castro, Role of the cation formal charge in cation-π interaction. A survey involving the [2.2.2]paracyclophane host from relativistic DFT calculations, New J. Chem., 2015, 39, 9963–9968 RSC.
- A. O. Ortolan, G. F. Caramori, R. L. T. Parreira and A. Muñoz-Castro, Helicenes as Molecular Tweezers in the Formation of Cation-π Complexes. Bonding and Circular Dichroism Properties from Relativistic DFT Calculations, ChemPhysChem, 2018, 19, 2321–2330 CrossRef CAS PubMed.
- A. O. Ortolan, N. D. Charistos, R. Guajardo-Maturana, C. O. Ulloa, G. F. Caramori, R. L. T. Parreira and A. Muñoz-Castro, On the cation-π capabilities of small all sp2-carbon host structures. Evaluation of [6.8]3cyclacene from relativistic DFT calculations, Int. J. Quantum Chem., 2019, 119, e25811 CrossRef.
- D. Macleod-Carey, G. F. Caramori, R. Guajardo-Maturana, D. Paez-Hernandez, A. Muñoz-Castro and R. Arratia-Perez, Advances in bonding and properties of inorganic systems from relativistic calculations in Latin America, Int. J. Quantum Chem., 2019, 119, e25777 CrossRef.
- M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized gradient approximation made simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS; (c) C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169 CrossRef CAS.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–2465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- (a) K. Kitaura and K. Morokuma, A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS; (b) T. Ziegler and A. Rauk, A theoretical study of the ethylene-metal bond in complexes between copper(1+), silver(1+), gold(1+), platinum(0) or platinum(2+) and ethylene, based on the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1558–1565 CrossRef CAS; (c) T. Ziegler and A. Rauk, Carbon monoxide, carbon monosulfide, molecular nitrogen, phosphorus trifluoride, and methyl isocyanide as sigma donors and pi acceptors. A theoretical study by the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS; (d) F. M. Bickelhaupt and E. J. Baerends, in Rev. Comput. Chem., ed. K. B. Lipkowitz and D. B. Boyd, Wiley, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Towards an order-N DFT method, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed; (c) E. Baerends, et al., ADF2014. SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com/, 2014 Search PubMed.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1-118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- R. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Clarendon Press, 1990 Search PubMed.
- T. Lu and F. M. Chen, A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- R. Dennington, T. Keith and J. Millam, GaussView Version 5.0.9, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- C. Cohen-Addad, P. Baret, P. Chautemps and J.-L. Pierre, Structures cristallines du [2.2.2]paracyclophane (I) (C24H24) et de son complexe avec le perchlorate d’argent (II) (C24H24.AgClO4), Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 1346–1349 CrossRef.
- L. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell university press Ithaca, NY, 1960, vol. 260 Search PubMed.
- L. H. Ahrens, The use of ionization potentials Part 1. Ionic radii of the elements, Geochim. Cosmochim. Acta, 1952, 2, 155–169 CrossRef CAS.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- P. L. A. Popelier, The Chemical Bond: Fundamental Aspects of Chemical Bonding, John Wiley & Sons, Ltd, 2014, ch. 8, pp. 271–308 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05303a |
| This journal is © The Royal Society of Chemistry 2020 |