Open Access Article
Open Access ArticleInfluence of Ch substitution on structural, electronic, and thermoelectric properties of layered oxychalcogenides (La0.5Bi0.5O)CuCh (Ch = S, Se, Te): a new insight from first principles
Shibghatullah Muhammady ,
Rena Widita and
Yudi Darma
,
Rena Widita and
Yudi Darma *
*
Department of Physics, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, Ganesha 10, Bandung, 40132, Indonesia. E-mail: yudi@fi.itb.ac.id
First published on 22nd July 2020
Abstract
We study the structural, electronic, and thermoelectric properties of p-type layered oxychalcogenides (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) from first principles. Ch substitution from S to Te enhances the local-symmetry distortions (LSDs) in CuCh4 and OLa2Bi2 tetrahedra, where the LSD in OLa2Bi2 is more pronounced. The LSD in CuCh4 tetrahedra comes from the possible pseudo-Jahn–Teller effect, indicated by the degeneracy-lifted t2g and eg states of Cu 3d10 orbital. The Ch substitution decreases bandgap from 0.529, 0.256 (Γ → 0.4Δ), to 0.094 eV (Z → 0.4Δ), for Ch = S, Se, Te, respectively, implying the increasing carrier concentration and electrical conductivity. The split-off energy at Z and Γ points are also increased by the substitution. The valence band shows deep O 2p states in the electron-confining [LaBiO2]2+ layers, which is essential for thermoelectricity. (La0.5Bi0.5O)CuTe provides the largest thermoelectric power from the Seebeck coefficient and the carriers concentration, which mainly come from Te 5px/py, Cu 3dzx, and Cu 3dzy states. The valence band shows the partial hybridization of t2g and Chp states, implied by the presence of nonbonding valence t2g states. This study provides new insights, which predict experimental results and are essential for novel functional device applications.
1. Introduction
Renewable energy sources are globally researched but maximizing their energy efficiency is challenging. Moreover, energy waste as thermal energy cannot be avoided in energy conversion processes. This condition leads to an increase in energy consumption. For the utilization of the energy waste, the thermal energy can be recovered and provide clean energy using the thermoelectric effect, which generates electric power from temperature (T, in K) gradient.1–5 The thermoelectric effect is measured by the figure of merit (ZT) formulated by
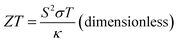 | (1) |
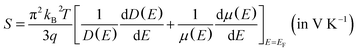 | (2) |
The superlattice structures are promising in generating the thermoelectric effect. The p-type Bi2Te3/Sb2Te3 superlattice structure shows the high thermoelectric power with ZT up to 2.4 at room temperature (RT), which is the result of the optimum control of electrons and phonons.10 The similar superlattice structure, accompanied by n-type δ-doped Bi2Te3−xSex in the superlattice thermoelectric modules, show the high cooling fluxes, which is potentially useful for modern device applications.11 Furthermore, the hybrid inorganic–organic superlattice is promising for the flexible thin-film thermoelectric material.12 Moreover, the natural superlattice (SnS)1.2(TiS2)2 has its thermoelectric performance improved in the in-plane direction. Moreover, σ along the in-plane is higher than that of the cross-plane directions, showing the anisotropic behavior. On the other hand, the lattice κ of this system is low because of the phonon scattering in the modulating periodic layers.13
The layered oxychalcogenides (RO)TmCh (R = La, Ce, Nd, Pr, Bi; Tm = Cu, Ag; and Ch = S, Se, Te) are the p-type semiconductors. The systems provide potential applications in thermoelectrics and optoelectronics14 and are considered as the natural superlattice systems consisting of the insulating oxide and conducting chalcogenide layers.15–17 The systems have (LaO)AgS-type crystal structure with the space group of P4/nmm (no. 129), in which Ag (O) is tetrahedrally surrounded by S (La) atoms.18,19 For example, the layered oxychalcogenides (LaO)CuCh show the wide bandgap (Eg) of 2.3 to 3.1 eV by substituting Ch from Te to S, providing potential applications in optoelectronics.20–25 Also, the excitonic emission at RT has been observed.26 Our previous report has shown that the dielectric constant (ε0), the optical dichroism, and the plasmonic states of (LaO)CuCh systems can be tuned by the Ch substitution.27 However, despite possessing the natural superlattice structure, (LaO)CuCh systems exhibit the low σ, indicating that these systems are not suitable for the thermoelectric application.25
Regarding the layered oxychalcogenides, (BiO)CuCh (Ch = Se, Te) are more suitable for the thermoelectric application. (BiO)CuSe show ZT of 0.50 at 923 K, while (BiO)CuTe show ZT of 0.42 and 0.66 at 373 and 673 K, respectively.6,15 From the experimental and first-principles perspectives, our previous report shows that, in spite of having the lower S than that of (BiO)CuSe system, (BiO)CuTe system provides the larger thermoelectric power due to the high σ and the metallic behavior. Intriguingly, Sr2+ and Ca2+ doping at Bi site and Ba doping modulation can enhance ZT of (BiO)CuSe system.28–31 The previous report shows that La doping in (BiO)CuSe increases both σ and κ but decreases S as the La doping concentration (x) increases, leading to the maximum ZT of 0.74 at 923 K for x = 0.08. The increase of σ is induced by the significant increase of μ.32 It has also been shown that the increasing x from 0.02 to 0.06 enhances σ and n but reduces μ at high T. It is suggested that the increase of n is induced by the presence of Bi vacancies due to the doping.33 On the other hand, the other report shows the increment of μ due to the increasing x.34 However, doping (BiO)CuTe system for tuning the thermoelectric performance is still a few. For example, the enhancement of the thermoelectric power factor of 16% by Bi addition in (BiO)CuTe system at 723 K has previously been reported.35 Moreover, structural properties and contributions of orbital states toward the thermoelectric properties of doped (BiO)CuCh are still yet to be explored.
In this paper, we investigate structural, electronic, and thermoelectric properties of layered oxychalcogenides (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems calculated by first principles. As the small x tunes the thermoelectricity of La-doped (BiO)CuSe,32,33 we are interested in the possible role of the same portion of La and Bi elements in inducing new structural, electronic, and thermoelectric properties of (La0.5Bi0.5O)CuCh. The results are comprehensively discussed to investigate the effect of Ch substitution on the properties, which are compared to that of (LaO)CuCh and (BiO)CuCh systems. The structural properties were fully optimized to obtain their most stable condition, followed by calculations of band structure, total density of states (TDOS), and projected density of states (TDOS). This study reveals the local-symmetry distortion (LSD) at CuCh4 and OLa2Bi2 tetrahedra, as well as the effect of Ch substitution on both electronic and thermoelectric properties.
2. Computational methodology
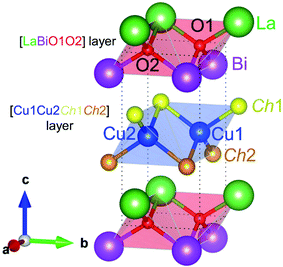
The structural and electronic properties of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems (space group: P4/nmm)18,19 were calculated using Quantum-ESPRESSO package code.36,37 Fig. 1 shows the crystal structure model of (La0.5Bi0.5O)CuCh unit cell. In the unit cell, the system consists of [LaBiO1O2]2+ and [Cu1Cu2Ch1Ch2]2− layers showing CuiCh12Ch22 (i = 1, 2) and OkLa2Bi2 (k = 1, 2) tetrahedra. Ch1 and Ch2 element are also denoted by Chj (j = 1, 2). Table 1 summarizes the initial structural parameters based on that of (LaO)CuCh.38 The use of i, j, and k is due to the structural symmetry distortion with the presence of two different layers, that are La and Bi layers. The term ‘distortion’ refers to the fact that the top and the bottom sides of [Cu1Cu2Ch1Ch2]2− layers are located between different La and Bi layers, leading to the decrease of the structural symmetry degree. The structural symmetry distortion will be later discussed in Results and discussions.| Initial lattice parameter (Å) | (La0.5Bi0.5O)CuS | (La0.5Bi0.5O)CuSe | (La0.5Bi0.5O)CuTe | |
|---|---|---|---|---|
| a | 3.9938 | 4.0670 | 4.1808 | |
| c | 8.5215 | 8.8006 | 9.3441 | |
| Atoms (site symmetry symbol) | Initial atomic positions | |||
| Cui: Cu1 (xCu, −yCu, zCu), Cu2 (−yCu, xCu, zCu) (2b) | (xCu, yCu, zCu) | (1/4, 1/4, 1/2) | (1/4, 1/4, 1/2) | (1/4, 1/4, 1/2) |
| Ok: O1 (xO, −yO, zO), O2 (−yO, xO, zO) (2a) | (xO, yO, zO) | (1/4, 1/4, 0) | (1/4, 1/4, 0) | (1/4, 1/4, 0) |
| La (xLa, xLa, zLa), Bi −(xBi, xBi, zBi) (2c) | (xLa = xBi, zLa = zBi) | (1/4, 0.14763) | (1/4, 0.13963) | (1/4, 0.1267) |
| Chj: Ch1 (xCh1, xCh1, zCh1), Ch2 −(xCh2, xCh2, zCh2) (2c) | (xCh1 = xCh2, zCh1 = zCh2) | (1/4, 0.6623) | (1/4, 0.6698) | (1/4, 0.6754) |
The calculation employs the plane-wave method within the generalized gradient approximation (GGA), which includes the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functionals.39 The previous reports have successfully carried out this method for various systems.40,41 The norm-conserving pseudopotential methods are used to approach all-electron potentials. For Cui, Chj, and Ok atoms, the Troullier–Martins (TM) method42–44 are used, while for La and Bi atoms, the Goedecker–Hartwigsen–Hutter–Teter (GHHT) method45,46 are used. Note that we use the different pseudopotential methods since this technique can minimize deviations between experimental and calculated structural properties. This technique has been used in our previous report in investigating the structural and electronic properties of (LaO)ZnPn (Pn = P, As, Sb) systems.47 The calculation is initiated by the full structural optimization by means of the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method48–51 with threshold force of ∼0.03 eV Å−1. The corresponding command is variable-cell relaxation (vc-relax). Notably, the BFGS method is suitable for large molecular systems.52 Using this method, the optimized lattice parameters of several systems53–56 are comparable with that of the corresponding experimental results. Hence, this method is also suitable for small systems. The Broyden mixing method57 was used for the corresponding self-consistent field (SCF) calculation. The SCF calculation employed threshold and cut-off kinetic energies of ∼3.0 and ∼1088 eV, respectively, as well as k-point mesh of and 9 × 9 × 4. The SCF calculation was followed by the band structure calculation. A k-point path of Γ–X–R–Z–Γ–M–A–Z is used in the corresponding Brillouin zone. In the whole paper, visualizations of all crystal structures and calculations of LSD parameters are performed using VESTA.58 Any term of ‘Ch substitution’ refers to the Ch substitution from S to Te.
3. Results and discussion
3.1. Structural properties
Table 2 presents the calculated structural parameters of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems compared with that of the previous experimental reports of (LaO)CuCh and (BiO)CuCh systems.38 The structural parameters include the lattice parameters a and c. We use a general term Δη to represent Δa and Δc, which is the difference percentage between calculated data (ηcalc) and experimental results (ηexp). This term is expressed as| Δη = [(ηcalc/ηexp) − 1] × 100% (dimensionless). | (3) |
| Parameter | (La0.5Bi0.5O)CuS | (La0.5Bi0.5O)CuSe | (La0.5Bi0.5O)CuTe | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Calc | Exp1 | Exp2 | Calc | Exp1 | Exp2 | Calc | Exp1 | Exp2 | ||
| a (Å) | 3.9699 | 3.9938(2) | 3.8691(1) | 4.0413 | 4.0670(1) | 3.9287(1) | 4.1442 | 4.1808(2) | 4.0411(2) | |
| c (Å) | 8.5791 | 8.5215(4) | 8.5602(4) | 8.9197 | 8.8006(8) | 8.9291(2) | 9.4662 | 9.3441(8) | 9.5237(5) | |
| Δa (%) | — | −0.5981 | 2.6056 | — | −0.6329 | 2.8651 | — | −0.8746 | 2.5522 | |
| Δc (%) | — | 0.6759 | 0.2207 | — | 1.3532 | −0.1054 | — | 1.3072 | −0.6033 | |
| Vcell (Å3) | 135.2083 | 135.9217 | 128.1456 | 145.6745 | 145.5662 | 137.8178 | 162.5799 | 163.3264 | 155.5267 | |
| Cu1 (xCu, −yCu, zCu) | xCu | 0.2477 | 1/4 | 0.2481 | 1/4 | 0.2502 | 1/4 | |||
| Cu2 (−yCu, xCu, zCu) | yCu | 0.2481 | 1/4 | 0.2480 | 1/4 | 0.2501 | 1/4 | |||
| zCu | 0.5016 | 1/2 | 0.4987 | 1/2 | 0.4988 | 1/2 | ||||
| O1 (xO, −yO, zO) | xO | 0.2500 | 1/4 | 0.2500 | 1/4 | 0.2502 | 1/4 | |||
| O2 (−yO, xO, zO) | yO | 0.2502 | 1/4 | 0.2503 | 1/4 | 0.2503 | 1/4 | |||
| zO | −0.0014 | 0 | 0.0000 | 0 | 0.0004 | 0 | ||||
| La (xLa, xLa, zLa) | xLa | 0.2497 | 1/4 | — | 0.2496 | 1/4 | — | 0.2499 | 1/4 | — |
| zLa | 0.1566 | 0.14763(7) | — | 0.1458 | 0.13963(6) | — | 0.1280 | 0.1267(1) | — | |
| Bi −(xBi, xBi, zBi) | xBi | 0.2501 | — | 1/4 | 0.2497 | — | 1/4 | 0.2501 | — | 1/4 |
| zBi | 0.1415 | — | 0.14829(5) | 0.1347 | — | 0.14020(4) | 0.1264 | — | 0.12733(9) | |
| Ch1 (xCh1, xCh1, zCh1) | xCh1 | 0.2512 | 1/4 | 1/4 | 0.2510 | 1/4 | 1/4 | 0.2500 | 1/4 | 1/4 |
| zCh1 | 0.6567 | 0.6623(1) | 0.6710(2) | 0.6684 | 0.6698(1) | 0.6758(1) | 0.6771 | 0.6754(1) | 0.6810(1) | |
| Ch2 −(xCh2, xCh2, zCh2) | xCh2 | 0.2505 | 1/4 | 1/4 | 0.2507 | 1/4 | 1/4 | 0.2499 | 1/4 | 1/4 |
| zCh2 | 0.6722 | 0.6623(1) | 0.6710(2) | 0.6768 | 0.6698(1) | 0.6758(1) | 0.6772 | 0.6754(1) | 0.6810(1) | |
The terms Δa and Δc represent the percentages of the differences between the calculated and experimental a and c, respectively. The calculated a and c are increased by the Ch substitution, as also observed in the experimental for both (LaO)CuCh and (BiO)CuCh systems. This increase is due to the different effective ionic radii of S2−, Se2−, and Te2−, i.e., 1.84, 1.98, and 2.21 Å.59 Furthermore, the previous experimental results show that both a and c are dependent on La and Bi, summarized in Fig. 2. The calculated results show that a is smaller than that of (LaO)CuCh and larger than that of (BiO)CuCh systems. On the other hand, the calculated c is larger than that of (LaO)CuCh and larger than that of (BiO)CuCh systems. However, (La0.5Bi0.5O)CuS shows that both a and c are larger than that of the experiments. This result indicates that the co-existence of La and Bi significantly influences both a and c. Moreover, in each (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuTe systems, the calculated cell volumes (Vcell) are between those of both (LaO)CuCh and (BiO)CuCh (Ch = S, Te) systems, while Vcell of (La0.5Bi0.5O)CuSe system is larger than those of both systems.
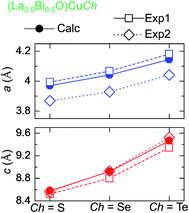 | ||
| Fig. 2 Trend of lattice parameters of for (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems different Ch from calculation (Calc) and experiments of (LaO)CuCh (Exp1) and (BiO)CuCh (Exp2). | ||
Each system reveals the structural symmetry distortion, indicated by the fact that the change of atomic positions is no longer only possessed by both zLa and zCh. Instead, all the atoms shift their coordinate components (x, y, z) from the experimental coordinates. The atomic positions of Ok and Cui slightly shift from 2a and 2b sites, respectively, within the P4/nmm space group. In (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuSe systems, both xCu and yCu are lower than 1/4, while (La0.5Bi0.5O)CuS system shows the opposite result. Moreover, (La0.5Bi0.5O)CuS system shows that zCu is higher than 1/2, which is in contrast with that of the other systems. Regarding Ok atom, for all the systems, xO and yO are slightly higher than 1/4. (La0.5Bi0.5O)CuS shows that zO is slightly higher (lower) than 1/2, while (La0.5Bi0.5O)CuTe system shows that zO is slightly lower than 1/2. On the other hand, (La0.5Bi0.5O)CuSe system does not show any zO shift.
The calculation shows that the atomic positions La, Bi, and Chj shift from their 2c sites. xLa and xBi are lower than 1/4, except xBi for (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuTe systems. On the other hand, xCh1 and xCh2 are higher than 1/4, except xTe2. Furthermore, zLa is higher than that of (LaO)CuCh, while zBi is lower than that of (BiO)CuCh systems. For (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuSe systems, zCh1 is lower than that of both (LaO)CuCh and (BiO)CuCh systems, while zCh2 shows the opposite result. These results provide LSD in CuiCh12Ch22 and OkLa2Bi2 tetrahedra.
The LSD parameters60,61 are to describe the LSD in CuiCh12Ch22 and OkLa2Bi2 tetrahedra. First, the mean quadratic elongation (λtet) is expressed as
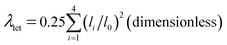 | (4) |
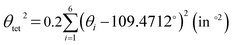 | (5) |
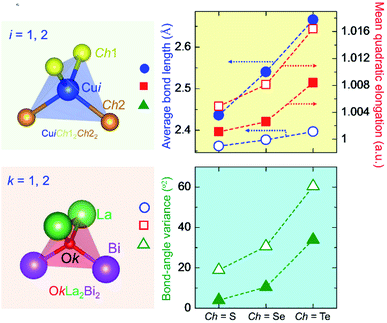
Table 3 summarizes the average bond length (lav) and the LSD parameters of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems. For all the systems, the Ch substitution increases lav, λtet, and θtet2 for both calculated and experimental results.38 The calculated lav of both CuiCh12Ch22 and OkLa2Bi2 tetrahedra are higher than that of both (LaO)CuCh and (BiO)CuCh systems, except lav of OkLa2Bi2 tetrahedra in (La0.5Bi0.5O)CuTe system, which is lower than that of (LaO)CuCh system. Furthermore, both λtet and θtet2 of CuiCh12Ch22 tetrahedra are higher than that of (LaO)CuCh but lower than that of (BiO)CuChsystems. In contrast, both λtet and θtet2 of OkLa2Bi2 tetrahedra are lower than that of (LaO)CuCh but higher than that of (BiO)CuCh systems. This result shows the co-existence of La and Bi ions significantly influences the local-symmetry distortion, compared to those of both (LaO)CuCh and (BiO)CuCh systems. For comparing the LSD among the systems, we summarize the LSD parameters from the calculation in Fig. 3. We find that lav of CuiCh12Ch22 tetrahedra are higher than that of OkLa2Bi2 tetrahedra. Intriguingly, the increases of lav of both CuiCh12Ch22 and OkLa2Bi2 tetrahedra are almost linear with respect to the Ch substitution, where CuiCh12Ch22 tetrahedra show the larger lav gradient. On the other hand, λtet and θtet2 of OkLa2Bi2 are higher than that of CuiCh12Ch22 tetrahedra. Concerning the Ch substitution, λtet and θtet2 increments of OkLa2Bi2 are also higher than that of CuiCh12Ch22 tetrahedra. This result indicates that the LSD of OkLa2Bi2 is more sensitive to the Ch substitution than that of CuiCh12Ch22 tetrahedra. Notably, the LSD of both tetrahedra is induced by the aspiration of the insulating and conducting layers to fit each other on the interface between them. Furthermore, the LSD of CuiCh12Ch22 tetrahedra cannot be provoked by the Jahn–Teller (JT) effect which the fully-occupied Cu 3d orbital cannot possess. We suggest that this LSD is induced by the pseudo-JT effect (PJTE)63 in CuiCh12Ch22 tetrahedra, which will be discussed later.
| Tetrahedra | lav (Å) | λtet | θtet2 (°2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Calc | Exp1 | Exp2 | Calc | Exp1 | Exp2 | Calc | Exp1 | Exp2 | |
| (La0.5Bi0.5O)CuS | |||||||||
| CuiS12S22 | 2.4362 | 2.4291 | 2.4259 | 1.0011 | 1.0002 | 1.0021 | 4.0014 | 0.7452 | 8.2968 |
| OkLa2Bi2 | 2.3619 | 2.3601 | 2.3138 | 1.0049 | 1.0058 | 1.0024 | 18.9186 | 21.9534 | 9.4120 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| (La0.5Bi0.5O)CuSe | |||||||||
| CuiSe12Se22 | 2.5403 | 2.5235 | 2.5145 | 1.0026 | 1.0007 | 1.0068 | 10.4807 | 2.6446 | 27.7188 |
| OkLa2Bi2 | 2.3770 | 2.3760 | 2.3293 | 1.0081 | 1.0106 | 1.0047 | 30.6467 | 39.6827 | 17.9075 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| (La0.5Bi0.5O)CuTe | |||||||||
| CuiTe12Te22 | 2.6656 | 2.6563 | 2.6560 | 1.0084 | 1.0049 | 1.0164 | 33.9264 | 19.5995 | 67.0207 |
| OkLa2Bi2 | 2.3967 | 2.4024 | 2.3565 | 1.0164 | 1.0209 | 1.0116 | 60.4193 | 76.1717 | 43.0506 |
3.2. Band structures
The left panels of Fig. 4 present the band structures of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems (range: −2.8 ≤ (E − EF) ≤ 2.8 eV), zoomed in the right panels (range: −1.0 ≤ (E − EF) ≤ 1.0 eV). EF is the Fermi energy level. We find that all the systems are semiconductors, indicated by the presence of Eg. The Ch substitution decreases Eg. The band structures pattern is also modified by the Ch substitution. Fig. 4(d) and (e) show that (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuSe systems have the indirect Eg of 0.529 and 0.256 eV (Γ → 0.4Δ), respectively. The term 0.4Δ denotes the path connecting 0.4Γ to Z points. These Eg are lower than that of both (LaO)CuCh (1.67 and 1.44 eV for Ch = S and Se, respectively)27 and (BiO)CuCh systems (0.68 and 0.40 eV for Ch = S and Se, respectively)64 within the GGA. Furthermore, (La0.5Bi0.5O)CuTe system exhibits the indirect Eg of 0.094 eV (Z → 0.4Δ), which is lower than that of (LaO)CuTe system27 and shows the different behaviors with that of the metallic (BiO)CuTe system.64 However, this Eg is close to that of (LaO)CuTe system by including the on-site Coulomb repulsion (U) and spin–orbit coupling (SOC) corrections.65 We suggest that the decrease Eg corresponds to the increase of the lattice parameters as Ch is substituted from S to Te. The increase of the lattice parameters enlengthens the interatomic distances, leaving binding forces valence electrons and the corresponding parent ions reduced. Thus, the valence electrons are easier to move freely and induce the increase of n and σ. This suggestion assumes that Eg is roughly inversely proportional to n.66 Hence, the decrease of Eg may indirectly be correlated with the ionic radii of Ch2− ions.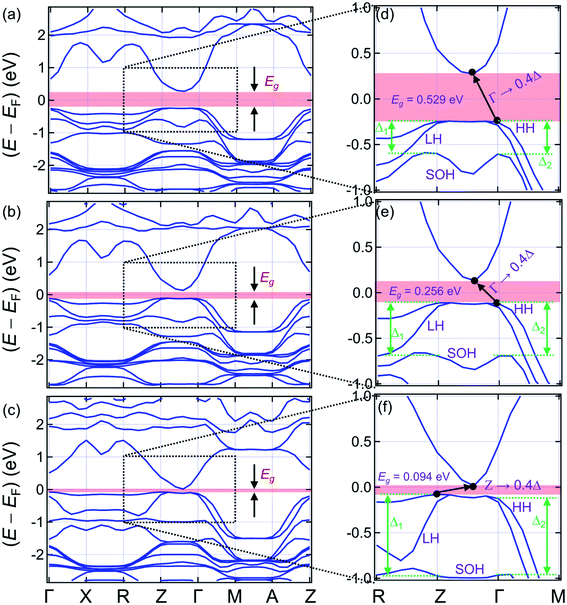 | ||
| Fig. 4 Band structures of (a) (La0.5Bi0.5O)CuS, (b) (La0.5Bi0.5O)CuSe, and (c) (La0.5Bi0.5O)CuTe systems. (d–f) The right panels show zoomed band structures in the range of −1.0 < EF < 1.0 eV. | ||
Experimental Eg of all the systems might be higher than that of the present work because of the limitation of the GGA, usually underestimating Eg in the exact Kohn–Sham band structures.67 Furthermore, including U in the calculation might also provide a closer Eg to that of the possible experimental result. However, U is not suitable to be included in a closed-shell system, where its valence orbitals are in the full occupation or empty.68 Here, (La0.5Bi0.5O)CuCh systems are closed-shell systems. The ionic electronic configurations in (La0.5Bi0.5O)CuCh systems are La3+: [Xe], Bi3+: [Xe] 4f145d106s2, O2−: [He] 2s22p6, Cu+: [Ar] 3d10, S2−: [Ne] 3s23p6, Se2−: [Ar] 3d104s24p6, and Te2−: [Kr] 4d105s25p6.69 Also, the exchange–correlation term in Cu 3d orbital cannot be fully described by U.65,70 The use of hybrid-functional71–75 or GW approximations76 might induce the wider Eg than that of the GGA. However, both of them usually overestimate Eg of semiconductors.77–79 Furthermore, the Hartree–Fock (HF) exchange in the hybrid-functional approximations can lead to the d-element exchange splitting overestimation.73,80 These explanation encourages us to keep the GGA method without U correction, thus, indicates that the calculated properties are sufficient to predict experimental electronic properties.
The valence band (VB) structures of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) show the tuning of heavy hole (HH), light hole (LH), and split-off hole (SOH) states due to the Ch substitution. We are interested in the k-path of R–Z–Γ–M to observe this tuning since this path is near the Eg transition. Along R–Z path, HH and LH states are separated, followed by SOH. The energy separation between HH and LH states is increased by the Ch substitution, while the energy level of SOH state is pushed down. The increasing separation between HH and LH states is shown by the decrease and increase of steepness of HH and LH states, respectively. Along Z–Γ path, the HH and LH coincide from 0.8Δ to 0.2Δ points. The SOH state shows a valley in the middle of this path, as its energy level is also pushed down by the Ch substitution. Along Γ–M path, the HH and LH states are separated with the lower separation that that of R–Z path. However, this separation is not sensitive to the Ch substitution. On the other hand, the energy level of the SOH state is also sensitively pushed down. We are interested in the shifts of HH, LH, and SOH states at Z and Γ points. By substituting Ch from S to Se, HH, LH, and SOH states show shifts of 137, 122, and −99 meV, respectively, at Z point. At Γ points, HH, LH, and SOH states show shifts of 131, 124, and −88 meV, respectively. By substituting Ch from Se to Te, HH, LH, and SOH states show shifts of 33, −12, and −279 meV, respectively, at Z point. At Γ points, HH, LH, and SOH states show shifts of 0, 3, and −272 meV, respectively. It is indicated that the energy levels of HH and LH states are more sensitive to the Ch substitution from S to Se than that of the SOH state. On the other hand, the energy level of SOH is sensitive to the Ch substitution from Se to Te, while the energy levels of HH and LH are in contrast. This result leads to a shift of split-off energy (Δl) (l = 1, 2) of each system, defined as the energy separation between the HH and SOH states. Table 4 presents the split-off energy (Δl, l = 1, 2) of the systems. The term Δ1 and Δ2 are located at Z and Γ points, respectively. The difference between Δ1 and Δ2 are defined as δ12. For all the systems, we find the result of Δ1 > Δ2, leading to the positive δ12. Interestingly, the Ch substitution increases both Δl and δ12. This result shows the significant role of the Ch substitution in tuning the band structures.
| System | Split-off energy (Δl) (in meV) | δ12 = Δ1 − Δ2 | |
|---|---|---|---|
| Δ1 (Z point) | Δ2 (Γ point) | ||
| (La0.5Bi0.5O)CuS | 350 | 349 | 1 |
| (La0.5Bi0.5O)CuSe | 586 | 569 | 17 |
| (La0.5Bi0.5O)CuTe | 897 | 841 | 56 |
3.3. Density of states
Fig. 5 presents the TDOS of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems (range: −8.5 ≤ (E − EF) ≤ 5.0 eV). The TDOS shows the decrease of VB width due to the Ch substitution. We find the VB widths of 6.17, 6.00, and 5.98 eV in (La0.5Bi0.5O)CuS, (La0.5Bi0.5O)CuSe, and (La0.5Bi0.5O)CuTe systems, respectively. Hence, the Ch substitution slightly enhances the energy localization of VB. The VB can be divided into four levels, i.e., lower bonding, upper bonding, nonbonding, and antibonding levels, as summarized in Table 5. Theoretically, a VB consists of bonding, nonbonding, and antibonding levels. In this work, the four divisions are only to differ between the two peaks of bonding levels. The Ch substitution decreases the lower bonding level and nonbonding level widths but increases the antibonding level width. On the other hand, regarding the upper bonding level, (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuSe systems show the lowest and highest level widths, respectively. Furthermore, the Ch substitution decreases the conduction band (CB) width. We find the CB widths of 4.60, 4.34, and 3.91 eV in (La0.5Bi0.5O)CuS, (La0.5Bi0.5O)CuSe, and (La0.5Bi0.5O)CuTe systems, respectively, indicating the enhancement of energy localization of CB.| System | Division level (level width) (in eV) | |||
|---|---|---|---|---|
| Lower bonding | Upper bonding | Nonbonding | Antibonding | |
| (La0.5Bi0.5O)CuS | −6.28 to −4.58 (1.70) | −4.58 to −3.16 (1.42) | −3.16 to −1.42 (1.74) | −1.42 to −0.21 (1.21) |
| (La0.5Bi0.5O)CuSe | −6.09 to −4.50 (1.59) | −4.50 to −2.59 (1.91) | −2.59 to −1.35 (1.24) | −1.35 to −0.09 (1.26) |
| (La0.5Bi0.5O)CuTe | −6.00 to −4.45 (1.55) | −4.45 to −2.67 (1.78) | −2.67 to −1.66 (1.01) | −1.66 to −0.01 (1.65) |
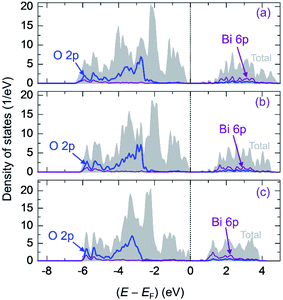
Fig. 5 also presents the PDOS of O 2p and Bi 6p states (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems. O 2p states of O1 and O2 have the same DOS shape, thus, O 2p states are mentioned without assigning k. We calculate DOS centroids (Ecentroid) for analyzing the PDOS using the expression81–83
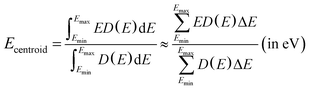 | (6) |
Regarding the thermoelectricity, from eqn (2), we predict S using the term −(dD(E)/dE) calculated at E ∼ EF. In the present work, the term −(dD(E)/dE) corresponds to hole as carriers for E < EF. The minus (−) sign is used since E below EF is converted to binding energy, which is represented with the plus sign, as previously shown in the photoemission spectra.64 Furthermore, we also calculate n(E) expressed as
| n(E) = D(E)f(E) (a.u.) | (7) |
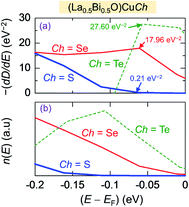 | ||
| Fig. 6 (a) First derivative of total density of states −(dD(E)/dE) and (b) carriers concentration n(E) of (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems as functions of energy (E). | ||
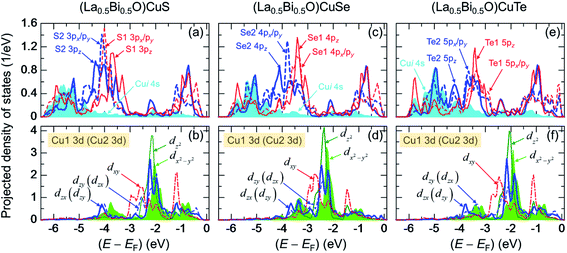
Fig. 7 presents PDOS of Cui 4s, sub-Chj np (px, py, pz), and sub-Cui 3d states in (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) systems. This figure shows the details of orbital contributions to the lower bonding, upper bonding, nonbonding, and antibonding levels in the VB. Notably, the degeneracy-lifted Chj np and Cui 3d orbitals may be induced by the PJTE63 in the fully-occupied Cui 3d orbital, related to the LSD in CuiCh12Ch22 tetrahedra. Notably, the tetrahedral-type crystal would allow the splitting of d orbital into 3-fold degenerate Cu 3d-t2g (dzx, dzy, dxy) and 2-fold degenerate Cu 3d-eg states (dx2−y2, dz2). In the present work, each Cu 3d-t2g and Cu 3d-eg states split into the different energy levels. Even, dzx and dzy states have the different PDOS profile, implying that Cu 3d orbital no longer degenerates. Hence, the PJTE induces the LSD and totally lifts the degeneracy of Cui 3d orbital. We find that Chj npx/py states mainly contribute S and n(E), followed by Cu 3dzx and Cu dzy states.
The lower bonding level is contributed by Cui 4s and Chj np states. Based on the theoretical picture, Cu+ 4s orbital should be empty. However, top panels for all the systems show the presence of Cui 4s (PDOS of Cu1 4s = PDOS of Cu2 4s) states in the VB. This result can be induced by the hybridization between Cui 4s and Chj np orbitals. Furthermore, the energy level of this hybridization slightly increases due to the Ch substitution, indicated by the increase of the energy levels of both orbitals. Furthermore, we find that the DOS profiles of Ch1 np and Ch2 np states are different. The different profiles are induced by structural symmetry distortion and the fact that Ch1 and Ch2 are close to the different La and Bi layers, leading to different chemical bonding between Bi–Ch1 and La–Ch2 bonds. In the lower bonding level, the energy levels of Ch2 np states are higher than that of Ch1 np states. We find the two highest peaks of Ch1 npz and Ch2 npz states in all the systems, alongside Se2 4px/py peak in (La0.5Bi0.5O)CuSe system. This result indicates that the hybridization between Cui 4s and Chj np along c-axis direction is stronger than that of ab-plane direction.
The upper bonding level is contributed by Cui 3d and Chj np states. In (La0.5Bi0.5O)CuS system, S1 3px/py and S2 3px/py peaks, located at around −4.0 and −4.1 eV, respectively, are the highest peaks among the sub-Chj np states, as presented in Fig. 7(a). At the same energy levels, we find the degeneracy-lifted Cu13dzx and Cu13dzy peaks, as well as the degeneracy-lifted Cu23dzx and Cu23dzy peaks, as shown in Fig. 7(b). This result implies that the upper bonding is more pronounced along ab-plane direction. However, in (La0.5Bi0.5O)CuSe system, Se1 4pz peak, located at around −3.4, is the highest peak among the sub-Chj np states, followed by Se2 4px/py located at −3.8 eV, as depicted in Fig. 7(c). From Fig. 7(d), at both −3.4 and −3.8 eV, there appear Cui3dz2 and Cu13dzx (Cu23dzy) states, respectively, indicating the slightly more pronounced upper bonding along c-axis direction. On the other hand, in (La0.5Bi0.5O)CuTe system, Te1 5pz peak at −3.4 eV is the highest peak among the sub-Chj np states, as shown in Fig. 7(e). Fig. 7(f) shows Cui3dx2−y2 and Cu13dzy (Cu23dzx) peaks at the same energy level with that of Te1 5pz states. This result indicates that Te1 5pz states experience the strongest hybridization with Cui 3d states compared to the other sub-Tej np states. We highlight for all the systems that Cui 3d-t2g states strongly hybridize with Chj np states and also show the larger contribution in the upper bonding level than that of Cui 3d-eg states.
The nonbonding level is mainly contributed by the localized Cui 3d-eg states (Cui3dx2−y2 and Cui3dz2) based on Fig. 7. As the state with the highest peak, Cui3dz2 states are localized at −2.1, −2.4, and −2.1 eV in (La0.5Bi0.5O)CuS, (La0.5Bi0.5O)CuSe, and (La0.5Bi0.5O)CuTe systems, respectively. From Fig. 7(d), (La0.5Bi0.5O)CuSe system shows the highest peak of Cui3dx2−y2 states among all the systems. However, the nonbonding level shows the presence of Cu13dzx (Cu23dzy) and Cu13dzy (Cu23dzx), indicating that Cui 3d-t2g states partially hybridize with Chj np states. This result is different from the previous suggestion that Cu and Ch ions are bound either along zx, zy, or xy planes.38 For all the systems, Ch2 npz also slightly contribute to the nonbonding level, followed by Ch1 npz states. Additionally, the contribution of Ch1 npz states is increased by the Ch substitution.
The antibonding level is contributed by Cui 3d and Chj np states. Based on the bottom panels of Fig. 7, all the systems show the highest peaks of Cui3dx2−y2 states, located at around −1.2, −1.4, and 1.1 eV in (La0.5Bi0.5O)CuS, (La0.5Bi0.5O)CuSe, and (La0.5Bi0.5O)CuTe systems, respectively. This highest peaks are followed by Cui3dz2 peaks located at the close energy levels to those of Cui3dx2−y2 states. Regarding Chj, all the systems show the highest peaks of Ch1 npz and Ch2 npz states, located at around −0.9 eV based on the top panels of Fig. 7. In (La0.5Bi0.5O)CuS system, we find two high peaks of S1 3px/py and S2 3px/py states, which are located at −0.4 and −1.2 eV, respectively. In (La0.5Bi0.5O)CuSe and (La0.5Bi0.5O)CuTe systems, the highest Se1 4px/py (Te1 5px/py) and Se2 4px/py (Te2 5px/py) peaks are located at −0.3 (−0.1) and −1.1 (−1.2) eV, respectively. This result indicates that the antibonding is more pronounced along ab-plane direction. We also highlight for all the systems that Cui 3d-t2g states strongly hybridize with Chj np states and also show the larger contribution in the antibonding level than that of Cui 3d-eg states.
4. Conclusions
The structural and electronic properties of the layered oxychalcogenides (La0.5Bi0.5O)CuCh (Ch = S, Se, Te) have been investigated based on the first principles. From the structural properties, the LSDs in CuiCh12Ch22 and OkLa2Bi2 tetrahedra are increased by the Ch substitution, in which the LSD in OkLa2Bi2 is stronger than that of CuCh4 tetrahedra. The possible PJTE in the fully-occupied Cui 3d orbital is suggested to be responsible for inducing the LSD in CuiCh12Ch22 tetrahedra and to lift the degeneracy level of t2g and eg states. From the electronic properties, all the systems are semiconductors. (La0.5Bi0.5O)CuS and (La0.5Bi0.5O)CuSe exhibit the indirect Eg (Γ → 0.4Δ) of 0.529 and 0.256 eV, respectively. On the other hand, (La0.5Bi0.5O)CuTe exhibits the indirect Eg (Z → 0.4Δ) of 0.094 eV. The Ch substitution also increases the split-off energies at Z and Γ points. In the valence band, O 2p states are located at the deep energy levels, leading to the electron-confinement between the insulating [LaBiO2]2+ layers. This result is crucial for thermoelectricity, where (La0.5Bi0.5O)CuTe may provide the largest thermoelectricity by comparing S and n(E), mainly contributed by Te 5px/py, Cu 3dzx, and Cu 3dzy states. Alongside being located at the bonding and antibonding level, t2g states are also located at the nonbonding level, leading to the partial hybridization of t2g and Ch p orbitals. The result provides new insights and finding, which open experimental works.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Ministry of Research and Technology (MORT)/The National Agency for Research and Innovation (NARI) of the Republic of Indonesia 2020 research program.References
- M. H. Elsheikh, D. A. Shnawah, M. F. M. Sabri, S. B. M. Said, M. H. Hassan, M. B. A. Bashir and M. Mohamad, Renewable Sustainable Energy Rev., 2014, 30, 337–355 CrossRef.
- C. Forman, I. K. Muritala, R. Pardemann and B. Meyer, Renewable Sustainable Energy Rev., 2016, 57, 1568–1579 CrossRef.
- H. Jouhara, N. Khordehgah, S. Almahmoud, B. Delpech, A. Chauhan and S. A. Tassou, Therm. Sci. Eng. Prog., 2018, 6, 268–289 CrossRef.
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- G. A. Slack, in Solid State Physics, Elsevier, 1979, vol. 34, pp. 1–71 Search PubMed.
- P. Vaqueiro, G. Guélou, M. Stec, E. Guilmeau and A. V. Powell, J. Mater. Chem. A, 2013, 1, 520–523 RSC.
- M. Cutler and N. F. Mott, Phys. Rev., 1969, 181, 1336–1340 CrossRef CAS.
- W. Liu, X. Tan, K. Yin, H. Liu, X. Tang, J. Shi, Q. Zhang and C. Uher, Phys. Rev. Lett., 2012, 108, 166601 CrossRef PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2011, 7, 105–114 CrossRef PubMed.
- R. Venkatasubramanian, E. Siivola, T. Colpitts and B. O'Quinn, Nature, 2001, 413, 597–602 CrossRef CAS PubMed.
- G. Bulman, P. Barletta, J. Lewis, N. Baldasaro, M. Manno, A. Bar-Cohen and B. Yang, Nat. Commun., 2016, 7, 10302 CrossRef CAS PubMed.
- C. Wan, R. Tian, M. Kondou, R. Yang, P. Zong and K. Koumoto, Nat. Commun., 2017, 8, 1024 CrossRef PubMed.
- C. Wan, Y. Wang, N. Wang, W. Norimatsu, M. Kusunoki and K. Koumoto, J. Electron. Mater., 2011, 40, 1271–1280 CrossRef CAS.
- S. D. Luu and P. Vaqueiro, Semicond. Sci. Technol., 2014, 29, 064002 CrossRef.
- Y. Liu, L.-D. Zhao, Y. Liu, J. Lan, W. Xu, F. Li, B.-P. Zhang, D. Berardan, N. Dragoe and Y.-H. Lin, J. Am. Chem. Soc., 2011, 133, 20112–20115 CrossRef CAS PubMed.
- H. Hiramatsu, K. Ueda, K. Takafuji, H. Ohta, M. Hirano, T. Kamiya and H. Hosono, Appl. Phys. A, 2004, 79, 1521–1523 CrossRef CAS.
- Y. Zhou and L. D. Zhao, Adv. Mater., 2017, 29, 1702676 CrossRef PubMed.
- M. Palazzi, C. Carcaly and J. Flahaut, J. Solid State Chem., 1980, 35, 150–155 CrossRef CAS.
- M. Palazzi and S. Jaulmes, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 1337–1339 CrossRef.
- K. Ueda, S. Inoue, S. Hirose, H. Kawazoe and H. Hosono, Appl. Phys. Lett., 2000, 77, 2701–2703 CrossRef CAS.
- S.-i. Inoue, K. Ueda, H. Hosono and N. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245211 CrossRef.
- K. Ueda, S. Inoue, H. Hosono, N. Sarukura and M. Hirano, Appl. Phys. Lett., 2001, 78, 2333–2335 CrossRef CAS.
- K. Ueda and H. Hosono, J. Appl. Phys., 2002, 91, 4768–4770 CrossRef CAS.
- Y. Ohki, K. Takase, Y. Takahashi, Y. Takano and K. Sekizawa, J. Alloys Compd., 2006, 408–412, 98–100 CrossRef CAS.
- Y. Ohki, S. Komatsuzaki, Y. Takahashi, K. Takase, Y. Takano and K. Sekizawa, AIP Conf. Proc., 2006, 850, 1309–1310 CrossRef CAS.
- Y. Takano, C. Ogawa, Y. Miyahara, H. Ozaki and K. Sekizawa, J. Alloys Compd., 1997, 249, 221–223 CrossRef CAS.
- S. Muhammady, I. M. Sutjahja, A. Rusydi, T. Winata, K. Takase and Y. Darma, Jpn. J. Appl. Phys., 2017, 56, 121201 CrossRef.
- F. Li, T.-R. Wei, F. Kang and J.-F. Li, J. Mater. Chem. A, 2013, 1, 11942–11949 RSC.
- L. D. Zhao, D. Berardan, Y. L. Pei, C. Byl, L. Pinsard-Gaudart and N. Dragoe, Appl. Phys. Lett., 2010, 97, 092118 CrossRef.
- X. Zhang, C. Chang, Y. Zhou and L.-D. Zhao, Materials, 2017, 10, 198 CrossRef PubMed.
- Y.-L. Pei, H. Wu, D. Wu, F. Zheng and J. He, J. Am. Chem. Soc., 2014, 136, 13902–13908 CrossRef CAS PubMed.
- Y. Liu, J. Ding, B. Xu, J. Lan, Y. Zheng, B. Zhan, B. Zhang, Y. Lin and C. Nan, Appl. Phys. Lett., 2015, 106, 233903 CrossRef.
- D. S. Pankratova, A. P. Novitskii, K. V. Kuskov, I. A. Sergienko, D. V. Leybo, A. T. Burkov, P. P. Konstantinov and V. V. Khovaylo, Semiconductors, 2019, 53, 624–627 CrossRef CAS.
- H. Wang, S. Li, Y. Liu, J. Ding, Y.-H. Lin, H. Xu, B. Xu and C.-W. Nan, Sci. Rep., 2016, 6, 24620 CrossRef CAS PubMed.
- H.-C. Chang, H.-J. You, R. Sankar, Y.-J. Yang, L.-C. Chen and K.-H. Chen, Ceram. Int., 2019, 45, 9254–9259 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. d. Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- H. Hiramatsu, H. Yanagi, T. Kamiya, K. Ueda, M. Hirano and H. Hosono, Chem. Mater., 2008, 20, 326–334 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Muhammady, Y. Kurniawan, M. A. K. Purbayanto and Y. Darma, Mater. Res. Express, 2018, 5, 066303 CrossRef.
- S. Muhammady, E. Nurfani, R. Kurniawan, I. M. Sutjahja, T. Winata and Y. Darma, Mater. Res. Express, 2017, 4, 024002 CrossRef.
- N. Troullier and J. L. Martins, Solid State Commun., 1990, 74, 613–616 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8861–8869 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- S. Muhammady, A. S. Erlyanti, R. Widita and Y. Darma, Int. J. Quantum Chem., 2020, 120, e26090 CAS.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- J. D. Head and M. C. Zerner, Chem. Phys. Lett., 1985, 122, 264–270 CrossRef CAS.
- Y. Jiang-Ni, Z. Zhi-Yong, Y. Jun-Feng and D. Zhou-Hu, Chin. Phys. B, 2010, 19, 017101 CrossRef.
- C. J. Fennie and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 184111 CrossRef.
- G. Wu, S. K. Zheng, P. Wu, J. Su and L. Liu, Solid State Commun., 2013, 163, 7–10 CrossRef CAS.
- R. Chowdhury, S. Adhikari and P. Rees, Phys. B: Condens. Matter, 2010, 405, 4763–4767 CrossRef CAS.
- C. G. Broyden, Math. Comput., 1965, 19, 577–593 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. E. Fleet, Mineral. Mag., 1976, 40, 531–533 CrossRef.
- R. Freitag and J. Conradie, J. Chem. Educ., 2013, 90, 1692–1696 CrossRef CAS.
- W. E. Brittin, J. Chem. Educ., 1945, 22, 145 CrossRef CAS.
- R. G. Pearson, J. Mol. Struct.: THEOCHEM, 1983, 103, 25–34 CrossRef.
- S. Muhammady, Y. Kurniawan, S. Ishiwata, A. Rousuli, T. Nagasaki, S. Nakamura, H. Sato, A. Higashiya, A. Yamasaki, Y. Hara, A. Rusydi, K. Takase and Y. Darma, Inorg. Chem., 2018, 57, 10214–10223 CrossRef CAS PubMed.
- D. Zou, S. Xie, Y. Liu, J. Lin and J. Li, J. Mater. Chem. A, 2013, 1, 8888–8896 RSC.
- B. Feng, G. Li, Y. Hou, C. Zhang, C. Jiang, J. Hu, Q. Xiang, Y. Li, Z. He and X. a. Fan, J. Alloys Compd., 2017, 712, 386–393 CrossRef CAS.
- J. P. Perdew, Int. J. Quantum Chem., 1985, 28, 497–523 CrossRef.
- H.-Y. Lee and J. Robertson, J. Appl. Phys., 2013, 113, 213706 CrossRef.
- T. L. Brown, H. E. LeMay, B. E. Bursten and L. S. Brunauer, Chemistry: The Central Science, Prentice Hall Englewood Cliffs, New Jersey, 1994 Search PubMed.
- Y. Zhang, X. Yuan, X. Sun, B.-C. Shih, P. Zhang and W. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075127 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 125, 249901 CrossRef.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796–A823 CrossRef.
- W.-D. Schöne and A. G. Eguiluz, Phys. Rev. Lett., 1998, 81, 1662–1665 CrossRef.
- J. L. F. Da Silva, M. V. Ganduglia-Pirovano, J. Sauer, V. Bayer and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045121 CrossRef.
- S. Das, G. Shi, N. Sanders and E. Kioupakis, Chem. Mater., 2018, 30, 7124–7129 CrossRef CAS.
- M. Marsman, J. Paier, A. Stroppa and G. Kresse, J. Phys.: Condens. Matter, 2008, 20, 064201 CrossRef CAS PubMed.
- J. Stewart, Calculus, Thomson Brooke/Cole, Ontario, 6 edn, 2009 Search PubMed.
- P. Oelhafen, E. Hauser, H.-J. Güntherodt and K. H. Bennemann, Phys. Rev. Lett., 1979, 43, 1134–1137 CrossRef CAS.
- H. M. Meyer III, D. M. Hill, J. H. Weaver, D. L. Nelson and C. F. Gallo, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7144–7147 CrossRef PubMed.
- K. Pal, S. Anand and U. V. Waghmare, J. Mater. Chem. C, 2015, 3, 12130–12139 RSC.
| This journal is © The Royal Society of Chemistry 2020 |