Open Access Article
Open Access ArticlePredicting reactivity for bioorthogonal cycloadditions involving nitrones†
Masaya Nakajima *a,
Didier A. Bilodeaub and
John Paul Pezacki
*a,
Didier A. Bilodeaub and
John Paul Pezacki *b
*b
aGraduate School of Pharmaceutical Sciences, Chiba University, 1-8-1 Inohana, Chuo-ku, Chiba 260-8675, Japan. E-mail: m.nakajima@chiba-u.jp
bDepartment of Chemistry and Biomolecular Sciences, University of Ottawa, 150 Louis-Pasteur, Ottawa, Ontario K1N 6N5, Canada. E-mail: john.pezacki@uottawa.ca
First published on 13th August 2020
Abstract
Nitrones are useful dipoles in both synthesis and in bioorthogonal transformations to report on biological phenomena. In bioorthogonal reactions, nitrones are both small and relatively easy to incorporate into biomolecules, while providing versatility in their ability to harbor different substituents that tune their reactivity. Herein, we examine the reactivities of some common and useful nitrone cycloadditions using density functional theory (DFT) and the distortion/interaction (D/I) model. The data show that relative reactivities can be predicted using these approaches, and useful insights gained further enchancing reactivities of both nitrones and their dipolarophile reaction partners. We find that D/I is a useful guide to understanding and predicting reactivities of cycloadditions involving nitrones.
Bioorthogonal chemistry provides important methods for creating covalent chemical linkages to enable the study of biological processes inside cells that are otherwise difficult to examine.1–6 A number of bioorthogonal reactions have been developed and are now used as techniques to efficiently, selectively and covalently link two reactive groups.7–14 In addition to bioorthogonality, the ability to react with high specificity within biological environments, as well as fast reaction kinetics are highly sought after, as they allow for the utility of chemistry at low concentrations needed for in vivo applications. Reactions involving nitrone dipoles are amongst the fastest bioorthogonal chemical reactions. These include strain-promoted alkyne–nitrone cycloadditions (SPANC) as well as trans-cyclooctene–nitrone ligations that occur selectively and with high reaction velocities.15–23 Furthermore, nitrones provide an added level of versatility in that their reactivity can be tuned stereoelectronically, through substituent effects on both the nitrone nitrogen atom and on the adjacent carbon atoms. This tuneability has enabled duplex labelling experiments with different nitrone–alkyne pairs. However, to take full advantage of this tuneability theoretical modelling is needed.
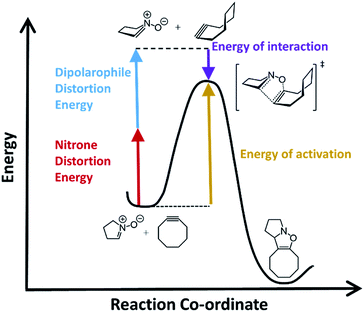
Computational chemistry has proven to be an invaluable tool in studying bioorthogonal reaction mechanisms and allowing for multiplex labelling experiments.24–33 Recent work by Liang and Houk as well as others, have demonstrated that density functional theory (DFT) calculations combined with distortion/interactions (D/I) models can be useful and even predictive of relative reactivities of different reactants in bioorthogonal reactions.34 The D/I theory purports that when molecules react, they must first distort from their equilibrium geometries and that this energetic requirement is counterbalanced by a gain in energy of interactions between the distorted geometries.35,36 Fig. 1 shows a general example for how this would apply to SPANC reactions. When the nitrone functional group is contained within a ring, generally we have observed faster reaction kinetics that are commensurate with very high stabilities towards hydrolysis.37 However, the requirement for nitrone distortion is expected to be significant, thus making these reactions ideally suited for study by DFT and D/I.
In order to assess the ability of DFT and D/I to predict reactivities of nitrone-based cycloaddition chemistry, we modelled 12 commonly used nitrone–dipolarophile reactions using Gaussian 16, and M06-2X functionals with 6-31G* basis set.38–41 We also calculated the D/I energies shown in Fig. 1 for these archetypical reactions. Single point energies were then calculated in acetonitrile (see ESI for calculated values†) and in methanol solvent (Table 1) in order to account for solvent effects on the relative energies and transitions states. The data is summarized in Table 1.
| a Geometry optimizations were carried out at the M06-2X level of theory with the 6-31G(d) basis set. Solvent effects in methanol were evaluated at the M06-2X/6-311++G(d,p) level at 298.15 K with a self-consistent reaction field (SCRF) using the SMD model on the gas-phase-optimized structures. Dis_nitrone is the distortion energy for the nitrones shown, dis_dipolarophile is the distortion energy for the different dipolarophiles shown, dis_total refers to the total distortion energy, and int represents the interaction energy for the given reaction. The C–O and C–C bond distances are for the bond lengths at the transition states for the bonds forming in the reactions. The bond angles represent those in the illustration above the table. Rate constants were measured previously.17,23,42,43 |
|---|
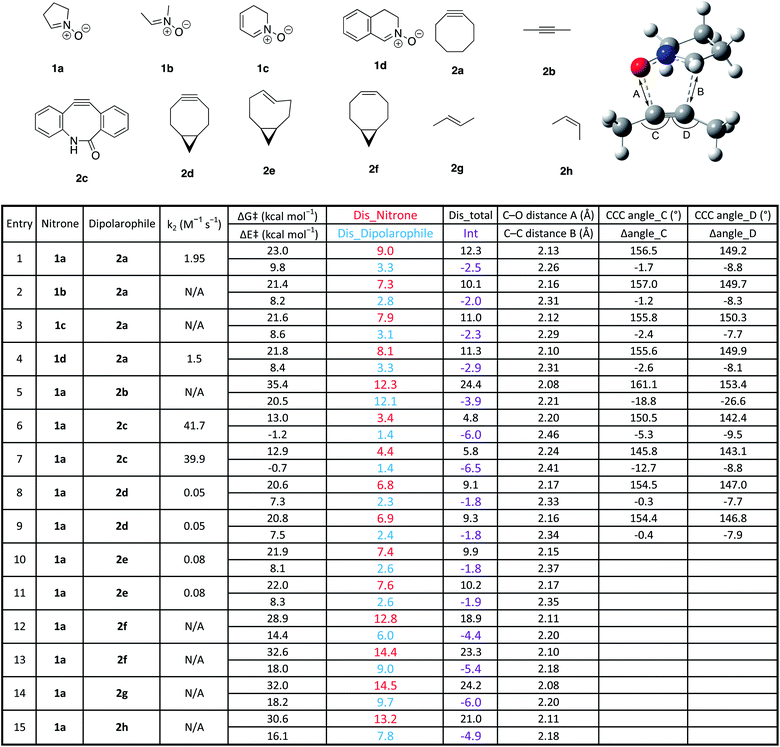 |
First, we used cyclooctyne 2a for dipolarophile and compared the differences in reactivity with four kinds of nitrone (Table 1 entries 1–4). The activation energy was within the range of 21.4–23.0 kcal mol−1, and 1b gave the smallest value. Distortion energy of nitrones also had the smallest value for 1b, suggesting that 1b had the least steric hindrance (entry 2). In addition, 1a, which contains a relatively large amount of sp3 carbons, has the highest distortion energy, and 1d, which includes a relatively large amount of sp2 carbons and conjugated aromatic ring, has the highest interaction energy (entries 1 and 4).
Next, using 1a for the nitrone reactant, we compared four alkynes (Table 1, entries 1, 5–9). We determined that the maximum activation energy of 35.4 kcal mol−1 was obtained in 2-butyne (2b), for which the structure is not distorted and is linear (entry 5). It can be seen that the distortion energy of dipolarophile is as large as 12.1 kcal mol−1; the Me-CC bond angle of alkyne in the transition state is distorted by −18.9° and −26.7°, respectively. In addition, because the atomic distance of the newly formed C–C and C–O bond in the transition state is shorter, deformation also occurs in the nitrone, and the value of distortion energy becomes large. Thus, according to Hammond postulate, the reaction of unstrained 2b has a late transition state and shows large activation energy.
The benzannulated cyclooctyne 2c showed the smallest activation energy (entries 6 and 7). Interestingly, in both regioisomers, the distortion of the bond angles of the alkyne in the transition state are −5.4° and −9.5°, or −12.8° and 8.8°, respectively, which is larger than that of cyclooctyne 2a (entry 1). However, the distortion energies of 2c in the transition state are 1.60 and 1.89 kcal mol−1, which are the smallest of all. Therefore, for 2c, it was revealed that the distortion of the CCC bond angle had no significant effect on the energy change at the transition state.
For bicyclononyne 2d, both diastereomers gave similar results (entries 8 and 9). Distortion energies of both nitrone and dipolarophile were smaller than that of cyclooctyne, probably because of the conformational restriction introduced by the fused cyclopropane ring. Finally, the calculation was performed using cycloalkenes as well as linear alkenes and a linear alkyne as dipolarophiles (entries 10–15). The results showed that in the strained trans-cyclooctene (TCO), the activation barrier and distortion energy were smaller than that of the cylcooctyne, indicating that the reaction proceeds by early transition state. On the other hand, unstrained olefins, cis-cyclooctene and trans/cis-butene, show large activation energy and distortion energy, implying the late transition states and energetically unfavourable reactions relative to the other dipolarophiles studied.
As had been observed previously, we also found that the relative contribution of alkyne or alkene distortion energy was directly proportional to the spontaneity of the reactions.42 In Fig. 2A, we plotted the bond length of the newly forming C–C and C–O bonds in the transitions states for the cycloaddition reactions against the nitrone distortion energies. We observed that the nitrone distortion energies increase as the transition state position moves towards the products of the reaction. The longer bond lengths represent earlier transition states according to the Hammond postulate.
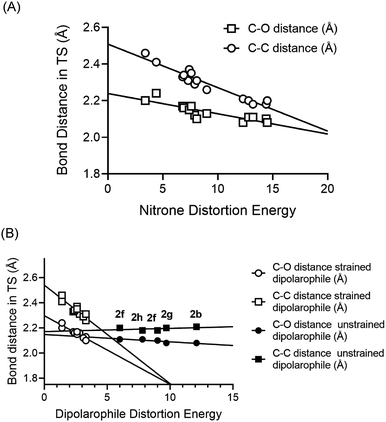 | ||
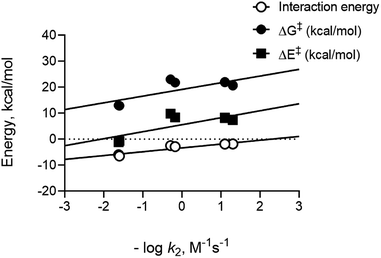
| Fig. 2 (A) Plots of C–C and C–O bond distances in the computed transition states vs. the distortion energy of the nitrones from the different entries from Table 1. (B) Plots of C–C and C–O bond distances in the computed transition states vs. the distortion energy of the dipolarophiles from the different entries from Table 1. In this case two different trend lines were observed, a relatively flat trendline for the unstrained alkenes and alkynes and a steeper dependency for the strained cyclooctynes and TCO. | ||
For the distortion energies of the dipolarophiles, two distinct trends were observed. In Fig. 2B we plotted the bond length of the newly forming C–C and C–O bonds in the transitions states for the cycloaddition reactions against the dipolarophile distortion energies. Here we observed that unstrained dipolarophiles 2b, 2f–h all displayed differences in distortion energies that were not dependent on the position of the transition state. However, the strained cyclooctynes and TCO both displayed strong correlation between distortion energies and the position of the transition state.
For SPANC reactions we clearly observe an important dependence on overall barrier for reactions towards both distortion energies of alkyne and nitrone. For cyclooctynes that are already more strained and distorted in the ground state, these effects are magnified, as is the case for entries 6 and 7, and to a lesser extent entry 8 as compared with entries 1–4.
Recently we have reported that nitrones will react with different trans-cyclooctenes (TCO) in TCO–nitrone ligation reactions.23 While these reactions are somewhat slower than their tetrazine counterparts, they still represent useful chemical transformations with utility in bioorthogonal applications and give other applications to TCOs when tetrazine reactions are not possible. Here our analyses show that strained TCO (s-TCO) has little requirement for distortion prior to reaching the transition state with nitrone reaction partners and that nitrone reaction partners also do not need to achieve significant distortion in the transition state, Table 1, entries 10 and 11 as compared with entries 12–15. The relative contributions are comparable with the reactions of the same nitrone with bicyclononyne (BCN). When comparing results for cis-cyclooctene and acyclic alkenes and their reactions with nitrones, both barriers for reactions and distortion energies increase dramatically, as expected. Generally speaking, cis-alkenes should be slightly more reactive in reactions with dipoles, with exception to s-TCO where strain energy and distortion greatly outweigh steric approach control. Again, DFT and D/I provide a useful framework for predicting the reactions of different nitrones with TCOs.
To compare calculated energies with experimental data, we used rate constant data previously measured for entries where numbers were available.17,23,42,43 Since rate constants are related to reaction barriers through transition state theory, we plotted the negative log of the bimolecular rate constants versus calculated parameters. Importantly, distortion energies calculated for nitrones and dipolarophiles do not readily predict the trend in reactivities that we observe experimentally. Rather, we only see the interaction energies for the different reactions follow a linear trend demonstrating a linear free energy relationship between these computed energies and experimental data, see Fig. 3. Good correlation for interactions energies suggest that they play an important role in defining the relative barrier heights for the reaction. The overall observed correlation suggests that the D/I model accurately predicts the relative reactivities for nitrone cycloadditions in solution, thus confirming the applicability of D/I theory with respect to predicting reactivity trends for both SPANC and TCO–nitrone ligation reactions.
Conclusions
We have examined the reactivities of some common and useful nitrone cycloadditions using density functional theory (DFT) and applied the distortion/interaction model. Our results show that these methods predict relative reactivities as compared with experimental results. Nitrone distortion energies appear to follow a trend that reflects their relative contribution to the overall transition state structure. Interestingly, the total interaction energies for the different reactions modeled to play a dominant role in affecting relative barrier heights for reactions involving both strained alkynes and trans-cyclooctenes. The relative magnitudes of the interaction energies appear to predict the relative reactivity and trends in reactivities. In summary, we have found that D/I theory can explain experimental trends in reactivity for cycloadditions involving nitrones and provide a convenient tool to predict reactivity that is useful in planning and experimental design. Future studies will focus on computations involving other nitrone cycloaddition reactions, as well as studying the potential for other mutually orthogonal reactions for multiplex labelling experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Natural Sciences and Engineering Council of Canada (NSERC) for financial support for this project, in the form of a discovery grant to J.P. Pezacki. Numerical calculations were carried out on the SR24000 computer at the Institute of Management and Information Technologies, Chiba University.Notes and references
- D. M. Patterson, L. A. Nazarova and J. A. Prescher, ACS Chem. Biol., 2014, 9, 592–605 CrossRef CAS PubMed.
- E. M. Sletten and C. R. Bertozzi, Angew. Chem., Int. Ed., 2009, 48, 6974–6998 CAS.
- C. S. Mckay and M. G. Finn, Chem. Biol., 2014, 21, 1075–1101 CAS.
- A. F. L. Schneider and C. P. R. Hackenberger, Curr. Opin. Biotechnol., 2017, 48, 61–68 CrossRef CAS PubMed.
- G. Liu, E. A. Wold and J. Zhou, Curr. Top. Med. Chem., 2019, 19, 892–897 CAS.
- A. Godinat, A. A. Bazhin and E. A. Goun, Drug Discovery Today, 2018, 23, 1584–1590 CrossRef CAS PubMed.
- E. M. Sletten and C. R. Bertozzi, Acc. Chem. Res., 2011, 44, 666–676 CrossRef CAS PubMed.
- A. Vázquez, R. Dzijak, M. Dračínský, R. Rampmaier, S. J. Siegl and M. Vrabel, Angew. Chem., Int. Ed., 2017, 56, 1334–1337 Search PubMed.
- B. Akgun, C. Li, Y. Hao, G. Lambkin, R. Derda and D. G. Hall, J. Am. Chem. Soc., 2017, 139, 14285–14291 CrossRef CAS PubMed.
- A. Mamot, P. J. Sikorski, M. Warminski, J. Kowalska and J. Jemielity, Angew. Chem., Int. Ed., 2017, 129, 15834–15838 CrossRef.
- C. P. Ramil, M. Dong, P. An, T. M. Lewandowski, Z. Yu, L. J. Miller and Q. Lin, J. Am. Chem. Soc., 2017, 139, 13376–13386 CrossRef CAS PubMed.
- T. S. Tang, H. Liu and K. K. Lo, Chem. - Eur. J., 2016, 22, 9649–9659 CrossRef CAS PubMed.
- R. D. Row and J. A. Prescher, Acc. Chem. Res., 2018, 51, 1073–1081 CrossRef CAS PubMed.
- S. Ghiassian, L. Yu, P. Gobbo, A. Nazemi, T. Romagnoli, W. Luo, L. G. Luyt and M. S. Workentin, ACS Omega, 2019, 4, 19106–19115 CrossRef CAS PubMed.
- D. A. Mackenzie, A. R. Sherratt, M. Chigrinova, L. L. W. Cheung and J. P. Pezacki, Curr. Opin. Chem. Biol., 2014, 21, 81–88 CrossRef CAS PubMed.
- D. A. Mackenzie and J. P. Pezacki, Can. J. Chem., 2014, 92, 337–340 CrossRef CAS.
- C. S. Mckay, J. A. Blake, J. Cheng, C. Danielson and J. P. Pezacki, Chem. Commun., 2011, 47, 10040–10042 CAS.
- A. R. Sherratt, M. Chigrinova, D. A. Mackenzie, N. K. Rastogi, M. T. M. Ouattara, A. T. Pezacki and J. P. Pezacki, Bioconjugate Chem., 2016, 27, 1222–1226 CrossRef CAS PubMed.
- D. A. Mackenzie, A. R. Sherratt, M. Chigrinova, A. J. Kell and J. P. Pezacki, Chem. Commun., 2015, 51, 12501–12504 CAS.
- M. Colombo, S. Sommaruga, S. Mazzucchelli, L. Polito, P. Verderio, P. Galeffi, F. Corsi, P. Tortora and D. Prosperi, Angew. Chem., Int. Ed., 2012, 51, 496–499 CrossRef CAS PubMed.
- P. N. Gunawardene, W. Luo, A. M. Polgar, J. F. Corrigan and M. S. Workentin, Org. Lett., 2019, 21, 5547–5551 CrossRef CAS PubMed.
- W. Luo, J. Luo, V. V. Popik and M. S. Workentin, Bioconjugate Chem., 2019, 30, 1140–1149 CAS.
- K. D. Margison, D. A. Bilodeau, F. Mahmoudi and J. P. Pezacki, ChemBioChem, 2020, 21, 948–951 CrossRef CAS PubMed.
- Y. Liang, J. L. MacKey, S. A. Lopez, F. Liu and K. N. Houk, J. Am. Chem. Soc., 2012, 134, 17904–17907 CrossRef CAS PubMed.
- C. G. Gordon, J. L. MacKey, J. C. Jewett, E. M. Sletten, K. N. Houk and C. R. Bertozzi, J. Am. Chem. Soc., 2012, 134, 9199–9208 CAS.
- P. An, T. M. Lewandowski, T. G. Erbay, P. Liu and Q. Lin, J. Am. Chem. Soc., 2018, 140, 4860–4868 CrossRef CAS PubMed.
- D. N. Kamber, Y. Liang, R. J. Blizzard, F. Liu, R. A. Mehl, K. N. Houk and J. A. Prescher, J. Am. Chem. Soc., 2015, 137, 8388–8391 CrossRef CAS PubMed.
- M. K. Narayanam, Y. Liang, K. N. Houk and J. M. Murphy, Chem. Sci., 2016, 7, 1257–1261 RSC.
- Y. Fang, H. Zhang, Z. Huang, S. L. Scinto, J. C. Yang, C. W. Am Ende, O. Dmitrenko, D. S. Johnson and J. M. Fox, Chem. Sci., 2018, 9, 1953–1963 RSC.
- W. D. Lambert, S. L. Scinto, O. Dmitrenko, S. J. Boyd, R. Magboo, R. A. Mehl, J. W. Chin, J. M. Fox and S. Wallace, Org. Biomol. Chem., 2017, 15, 6640–6644 RSC.
- H. Tao, F. Liu, R. Zeng, Z. Shao, L. Zou, Y. Cao, J. M. Murphy, K. N. Houk and Y. Liang, Chem. Commun., 2018, 54, 5082–5085 RSC.
- T. Bettens, M. Alonso, P. Geerlings and F. De Proft, Chem. Sci., 2020, 11, 1431–1439 RSC.
- J. G. de la Concepción, M. Ávalos, P. Cintas and J. L. Jiménez, Chem. - Eur. J., 2018, 24, 7507–7512 CrossRef PubMed.
- F. Liu, Y. Liang and K. N. Houk, Acc. Chem. Res., 2017, 50, 2297–2308 CrossRef CAS PubMed.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS PubMed.
- C. S. McKay, J. A. Blake, J. Cheng, D. C. Danielson and J. P. Pezacki, Chem. Commun., 2011, 47, 10040–10042 RSC.
- R. A. Miranda-Quintana, M. M. González, D. Hernández-Castillo, L. A. Montero-Cabrera, P. W. Ayers and C. Morell, J. Mol. Model., 2017, 23, 1–15 CrossRef CAS PubMed.
- A. I. Adjieufack, I. M. Ndassa, J. K. Mbadcam, M. Ríos-Gutiérrez and L. R. Domingo, Theor. Chem. Acc., 2017, 136, 1–12 Search PubMed.
- R. Herrera, A. Nagarajan, M. A. Morales, F. Méndez, H. A. Jiménez-Vázquez, L. G. Zepeda, J. Tamariz and J. Tamariz, J. Org. Chem., 2001, 66, 1252–1263 CrossRef CAS PubMed.
- E. A. Boafo, K. Darko, B. A. Afriyie, R. Tia and E. Adei, J. Mol. Graphics Modell., 2018, 81, 1–13 CrossRef CAS PubMed.
- C. S. Mckay, M. Chigrinova, J. A. Blake and J. P. Pezacki, Org. Biomol. Chem., 2012, 10, 3066–3070 RSC.
- C. S. McKay, J. Moran and J. P. Pezacki, Chem. Commun., 2010, 46, 931–933 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05092j |
| This journal is © The Royal Society of Chemistry 2020 |