Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A thermodynamic and kinetic study of the antioxidant activity of natural hydroanthraquinones†
Quan V. Vo *a,
Nguyen Minh Thong
*a,
Nguyen Minh Thong *b,
Trinh Le Huyen
*b,
Trinh Le Huyen cd,
Pham Cam Nam
cd,
Pham Cam Nam d,
Nguyen Minh Tam
d,
Nguyen Minh Tam *ef,
Nguyen Thi Hoag and
Adam Mechler
*ef,
Nguyen Thi Hoag and
Adam Mechler h
h
aInstitute of Research and Development, Duy Tan University, Danang 550000, Vietnam. E-mail: vovanquan2@duytan.edu.vn
bThe University of Danang, Campus in Kon Tum, 704 Phan Dinh Phung, Kon Tum, Vietnam. E-mail: nmthong@kontum.udn.vn
cDepartment of Applied Chemistry, National Chiao Tung University, Hsinchu 30010, Taiwan
dDepartment of Chemical Engineering, The University of Danang, University of Science and Technology, Danang 550000, Vietnam
eComputational Chemistry Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: nguyenminhtam@tdtu.edu.vn
fFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
gAcademic Affairs, The University of Danang-University of Technology and Education, 48 Cao Thang, Da Nang 550000, Vietnam
hDepartment of Chemistry and Physics, La Trobe University, Victoria 3086, Australia
First published on 27th May 2020
Abstract
Novel hydroanthraquinones isolated from marine algal-derived endophytic fungus Talaromyces islandicus EN-501 exhibited promising antioxidant properties in preliminary studies, raising the prospect of adapting these compounds for therapeutic use in diseases caused by oxidative stress. For medicinal applications it is beneficial to develop a full understanding of the antioxidant activity of these compounds. In this study, the hydroperoxide radical scavenging activity of five natural hydroanthraquinones was evaluated by kinetic and thermodynamic calculations. The results showed that the radical scavenging of these hydroanthraquinones in the gas phase and in lipid solvents was defined by the formal hydrogen transfer mechanism, that for the polar environments was decided by the sequential proton loss electron transfer pathway. The hydroanthraquinones exhibited good hydroperoxide scavenging activity in both polar and non-polar media. The overall rate constant values for the radical scavenging reaction were in the range of 3.42 × 101 to 2.60 × 105 M−1 s−1 and 3.80 × 106 to 5.87 × 107 M−1 s−1 in pentyl ethanoate and water solvents, respectively. Thus the activity of 8-hydroxyconiothyrinone B (1) is about 2.6 and 444.6 times higher than that of Trolox in the studied solvents, identifying 8-hydroxyconiothyrinone B as a promising antioxidant.
1. Introduction
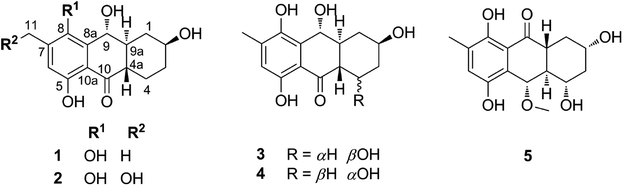
In recent trends of drug discovery emphasis has returned to finding bioactive natural products. In nature, marine-derived fungi are known as good sources of hydroanthraquinones whose pharmacological properties have proven beneficial for the treatment of diseases caused by oxidative stress.1–4 Recently, five new hydroanthraquinone derivatives from marine algal-derived endophytic fungus Talaromyces islandicus EN-501 were isolated and evaluated for biological activity.3 The compounds were identified as 8-hydroxyconiothyrinone B (1), 8,11-dihydroxyconiothyrinone B (2), 4-(R)-8-dihydroxyconiothyrinone B (3), 4-(S)-8-dihydroxyconiothyrinone B (4), and 4-(S)-8-dihydroxy-10-O-methyldendryol E (5) (Fig. 1). Experimental studies for their antioxidant properties suggested good activity,3 warranting a theoretical investigation of the free radical scavenging activity of these compounds that has not been explored thus far.The relationship between the structural characteristics and the activity of antioxidant compounds can be elucidated based on three main mechanistic pathways of radical scavenging.5–8 One of these is the formal hydrogen transfer (FHT) mechanism where the main step is the dissociation of a hydrogen atom from the antioxidant molecule; therefore this mechanism is defined energetically by the bond dissociation enthalpy (BDE). The second common mechanism is the single electron transfer-proton transfer (SET-PT) that is defined by two thermodynamic parameters: ionization energy (IE) (for the electron transfer step) and proton dissociation enthalpy (PDE) (proton transfer from the ionized molecule). The third common mechanism is sequential proton loss electron transfer (SPLET) where the first step is proton dissociation, characterized energetically by proton affinity (PA) and electron transfer enthalpy (ETE) which is the logical next step in the mechanism (Table S1, ESI†).
During the recent years, along with outstanding developments of computing power, the predictive power of computational methods has also increased dramatically, in silico study becoming a useful tool for exploring the radical scavenging activity of the potential antioxidant compounds. The computational methods in quantum chemistry provide reasonably accurate information but save time and money compared to experimental methods.9–13 Based on a program of evaluating the antioxidant potential of natural products,10,11,14,15 this study was carried out to attain three essential goals: (1) establish the most likely mechanism by thermodynamic investigation of the antioxidant activity of hydroanthraquinones through three mechanisms involving SPLET, SETPT, and FHT;15,16 (2) approximate radical scavenger activity by performing kinetic evaluation of the HOO˙ scavenging reaction of hydroanthraquinones in the gas phase as well as in physiological environments; and (3) explain the results by analysis of the relationship between environments and molecular structures with the antioxidant activity and oxidation resistance of hydroanthraquinone derivatives.
2. Computational methods
Thermochemical properties (i.e. BDE, IE and PA) and kinetic parameters (activation energies ΔG≠ (kcal mol−1), tunneling corrections (κ) and rate constant (k)) in the gas phase as well as physiological environments (water for the aqueous solution and pentyl ethanoate for lipid medium) of the compounds were computed at the M06-2X/6-311++G(d,p) level of theory. This method is proven to be highly accurate for computing both thermodynamic and kinetic parameters with low errors compared to more complex methods (i.e. G3(MP2)-RAD) or experimental data.10,17–20 The kinetic calculations were computed following the quantum mechanics based test for overall free radical scavenging activity (QM-ORSA) protocol with the solvation model density (SMD) method that has been widely used for evaluating the radical scavenging activity of antioxidants due to low errors compared with experimental data (kcalc/kexp ratio = 1–2.9).9,10,21,22The rate constant (k) was calculated by using the conventional transition state theory (TST) and 1M standard state as:23–27
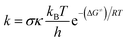 | (1) |
The Marcus theory was used to estimate the reaction barriers of SET reactions.31–34 The free energy of reaction ΔG≠ for the SET pathway was computed following the eqn (2) and (3).
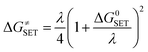 | (2) |
| λ ≈ ΔESET − ΔG0SET | (3) |
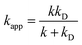 | (4) |
| kD = 4πRABDABNA | (5) |
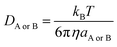 | (6) |
η is the viscosity of the solvents (i.e. η(pentyl ethanoate) = 8.62 × 10−4 Pa s and η(H2O) = 8.91 × 10−4 Pa s) and a is the radius of the solute.
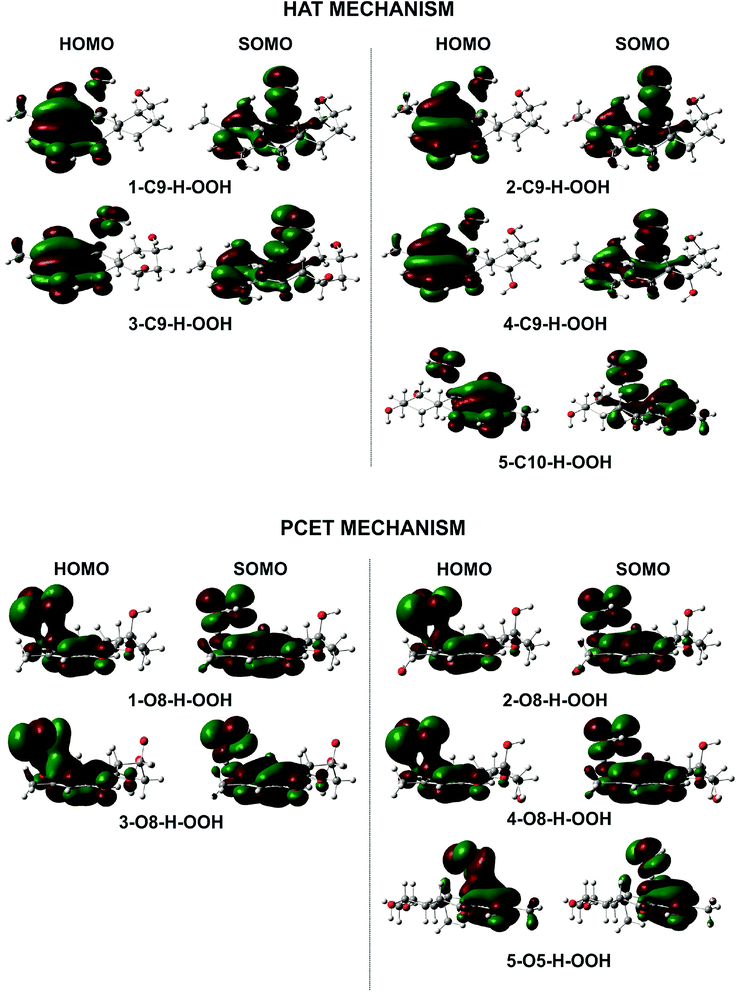
The Okuno42 and Benson corrections were used to reduced over-penalizing entropy losses in solution.9,43–45 For the species that have multiple conformers, all of these were investigated and the conformer with the lowest electronic energy was included in the analysis.11,46 All transition states were characterized by the existence of only one single imaginary frequency. Intrinsic coordinate calculations (IRCs) were performed to ensure that each transition state is corrected.22 The calculations were performed with the Gaussian 09 suite of programs,47 and the Eyringpy code48,49 depending on the particular problem. The shape of frontier molecular orbitals (HOMO and SOMO) in transition states that were visualized by using the GaussView 05 software was analyzed to distinguish between HAT and PCET mechanisms.
3. Results and discussions
3.1. Thermodynamic study
Initially, the antioxidant activity was evaluated by calculating the thermochemical parameters (BDEs, PAs and IEs) that define affinity for the three main mechanisms including FHT, SETPT and SPLET, respectively (Table S1, ESI†).15,16 Thus thermochemical characteristics in the gas phase of all of possible X–H (X = C, O) bonds were firstly screened by using DFT calculation at the M06-2X/6-31G level (Table S2, ESI†); the X–H (X = C, O) bonds with the lowest BDEs or PAs were then computed at the higher level M06-2X/6-311++G(d,p). The results are shown in Table 1.As shown in Table 1, the BDE(O–H) values are in the range of 76.8 to 88.6 kcal mol−1, whereas those for C–H bonds are 76.2–84.8 kcal mol−1. In the antioxidant activity of 5 following the FHT mechanism the C10–H and O5–H bonds were dominant, while for compound 1, 2, 3 and 4 the lowest BDEs were observed at the O8–H bond and C9–H bond (at about 76–79 kcal mol−1). Thus in gas phase these compounds appear to be potent radical scavengers according to the FHT pathway.
The computed PA and IE values are in the gas phase were in the range of 313.8 to 331.8 kcal mol−1 and 172.7 to 180.3 kcal mol−1, respectively. It was found that compound 2 has the lowest PA and IE values (PA = 313.8 and IE = 172.7 kcal mol−1), thus the radical scavenging of this compound may be followed the SETPT and SPLET pathways in the gas phase.
To investigate the favored antioxidant mechanism of the studied compounds, the free energy (ΔGo) of the first step for the HOO˙ scavenging of the hydroanthraquinones following each mechanism were calculated in vacuum and shown in Table S3, ESI.† The results show that only FHT mechanism yields negative ΔGo, whereas the reactions following the SETPT and SPLET mechanisms are not spontaneous. Hence, the FHT pathway is suggested to be the main antiradical mechanism for the neutral hydroanthraquinones in the gas phase.
3.2. Kinetic study
| Reactions | ΔG≠ | κ | kEck |
|---|---|---|---|
| 1–O8–H + HOO˙ | 8.5 | 20.9 | 7.23 × 107 |
| 1–C9–H + HOO˙ | 12.2 | 68.4 | 5.18 × 105 |
| 2–O8–H + HOO˙ | 11.0 | 19.4 | 1.02 × 106 |
| 2–C9–H + HOO˙ | 14.4 | 68.2 | 1.14 × 104 |
| 3–O8–H + HOO˙ | 9.3 | 14.1 | 1.33 × 107 |
| 3–C9–H + HOO˙ | 10.4 | 65.7 | 1.07 × 107 |
| 4–O8–H + HOO˙ | 9.8 | 23.6 | 1.02 × 107 |
| 4–C9–H + HOO˙ | 11.4 | 63.6 | 1.69 × 106 |
| 5–O5–H + HOO˙ | 15.7 | 14.4 | 2.89 × 102 |
| 5–C10–H + HOO˙ | 16.2 | 160.0 | 1.39 × 103 |
| Trolox + HOO˙ | 9.7 | 36.7 | 1.87 × 107 |
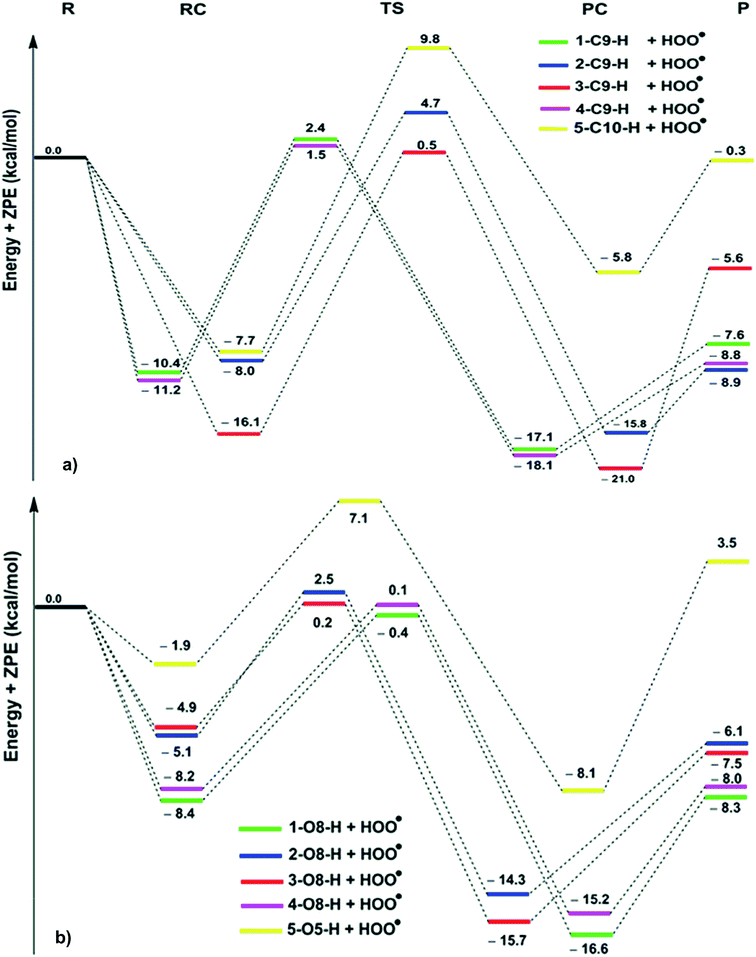 | ||
| Fig. 2 PES for the reactions of the hydroanthraquinones with HOO˙ in the gas phase ((a) C–H; (b) O–H; R: reagent, RC: pre-complex; TS: transition state; PC: post-complex; P: products). | ||
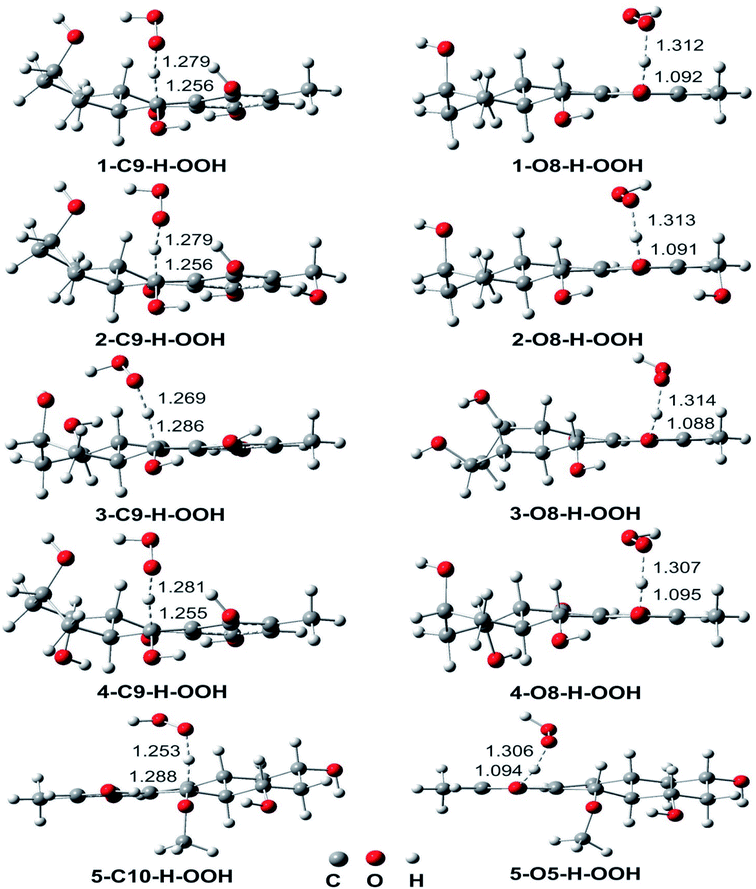 | ||
| Fig. 3 Optimized geometries of TSS between the studied compounds and HOO˙ radical in the gas phase following the FHT mechanism. | ||
The reaction proceeds via reaction complexes (RC) that are energetically more stable than the reactants: about 7.7–16.1 kcal mol−1 for the H-abstraction of the C–H bonds and 1.9–8.4 kcal mol−1 for the H-abstraction of the O–H bonds. After that, the reactions can proceed to transition states (TS) from the RC by FHT process; TSs have higher energy barriers than RC: around 12.0–17.0 kcal mol−1 in the case of (C–H) and 5.1–9.0 kcal mol−1 at (O–H). The energy barrier of the reaction path via C–H positions is higher than that in case of O–H positions at an average by 6.9 kcal mol−1. The lowest TS energy (−0.4 kcal mol−1) was observed at the HOO˙ antiradical of the 1–O8–H bond that correlates with the lowest calculated BDE value of O–H bonds (BDE(1–O8–H) = 76.8 kcal mol−1). Comparing the energy barriers of the transition states of the reaction pathways at both C–H and O–H positions of hydroanthraquinones, one can make a conclusion that the reaction at the O–H bond is energetically preferred over the C–H bond.
As shown in Table 2, the rate constants for the hydroanthraquinones + HOO˙ reactions in the gas phase are in the range of 2.89 × 102 to 7.23 × 107 M−1 s−1, while the ΔG≠ values for these processes are from 8.5 to 16.2 kcal mol−1. The tunneling corrections (κ) for the HOO˙ radical scavenging of the O–H bonds (14.1–23.6) are lower than those of the C–H bonds (63.6–160.0). Based on the calculated data, among the studied compounds the HOO˙ scavenging activity of 1 is the fastest with kEck = 7.23 × 107 M−1 s−1; it is nearly four times higher than that of Trolox (kEck = 1.87 × 107 M−1 s−1). The compounds 3 and 4 also exhibit an excellent hydroperoxyl radical scavenging (kEck = ∼107 M−1 s−1), whereas that for compound 5 is the lowest with kEck = ∼103 M−1 s−1. This result is in good agreement with the obtained BDE values in the thermodynamic evaluation. Thus compounds 1, 3 and 4 are promising scavengers in the gas phase.
The effect of the explicit presence of a solvent, i.e. water, molecule on the radical scavenging of the most active antioxidant (compound 1) was also investigated given the potential influence of hydrogen bonding on the proton dissociation process (Table S4 and Fig. S1, ESI†). The presence of the H2O molecule in the reaction can have a substantial effect on the rate constant of the HOO˙ radical scavenging reaction of 1. For examples, the 1–O8–H(H2O) + ˙OOH and 1–O8–H(H2O) + ˙OOH(H2O) reactions in the gas phase have rate constants kEck = 5.06 × 105 and 2.89 × 106 M−1 s−1, respectively, compared with kEck = 7.23 × 107 M−1 s−1 for the 1–O8–H + ˙OOH reaction. This is contrary to the intuition that H-bonding to water should promote bond dissociation, and is the result of explicit inclusion of a water molecule. In an environment where there is competition for hydrogen bonding this effect might be less pronounced.
To gain further into the mechanism of the H-abstraction of the O–H and C–H bonds, frontier molecular orbital (FMO) analysis of the transition states was performed and the results are shown in Fig. 4.50,51 There is an overlap in the highest occupied molecular orbital (HOMO) density surfaces between delocalized π-orbitals of the rings and a lone pair on the central peroxyl oxygen of the hydroperoxyl radical in case of the TSs that were formed by H-abstraction from the O8(5)H bond. This overlap allows electron transfer between the two in the TS structures. Moreover, the singly-occupied molecular orbitals (SOMO) of transition states involve p type orbitals, which are orthogonal to the transition vector. That suggests that the reaction between the studied compounds and HOO˙ in position O5, and O8 occurs via the proton coupled electron transfer (PCET) mechanism.10,52 On the other hand a significant atomic orbital density oriented along the C⋯H⋯O transition vector is observed in the SOMO density surfaces of the TSs formed by H-abstraction of the C9(10)–H bond. It means that the single entity (H˙) is transferred along the line connecting the C9(10) and O centers, which corresponds to hydrogen atom transfer (HAT) mechanism.52,53 Thus the FMO analysis shows that the HOO˙ radical scavenging of C9(10)–H bond follows the HAT mechanism, whereas the PCET pathway is favored at the O8(5)–H bonds. This may explain the higher rare constants for the H-abstraction from the O–H bonds compared to the C–H bonds despite of the lower BDE values at the C9–H (compound 2 and 4) and C10–H (compound 5) bonds compared to the O–H bonds of these compounds.
Acid–base equilibria. Previous studied showed that the antioxidant activity should be evaluated in physiological environments that provides more accurate data that correlates well with experimental results.9,10 Thus in this section the antioxidant activity of the hydroanthraquinones was investigated against HOO˙ radical in aqueous solution (water, pH = 7.4) and lipid environment (pentyl ethanoate) that mimic the polar and nonpolar environments in the human body.9–11,15,46 To determine the structure of the studied compounds in the aqueous solution, knowing protonation state is important. The pKa (negative logarithm of the acid dissociation constant) values and the molar fractions of five hydroanthraquinones were computed by using the model reaction (7) and eqn (8) following the literature9,54–56 and are shown in Table 3.
| HA + Ref− → A− + HRef | (7) |
pKa = ΔGs/RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) + pKa(HRef) ln(10) + pKa(HRef)
| (8) |
| Comp. | OH position | pKa | fprotonated(HA) | fdeprotonated(A−) |
|---|---|---|---|---|
| 1 | O8–H | 8.57 | 0.937 | 0.063 |
| 2 | O8–H | 8.24 | 0.874 | 0.126 |
| 3 | O8–H | 8.50 | 0.926 | 0.074 |
| 4 | O8–H | 8.50 | 0.926 | 0.074 |
| 5 | O5–H | 8.69 | 0.951 | 0.049 |
As can be seen from Table 3, the calculated pKa values are from 8.24 to 8.69. The fprotonated(HA) values are in the range of 0.874 to 0.951, whereas those for the fdeprotonated(A−) are in the range of 0.049 to 0.126. Thus in the water solvent (pH = 7.4), the hydroanthraquinones exist in both anionic and neutral states and these states were both included in the further study.
Kinetic study. As shown in thermodynamic section, the HOO˙ antiradical activity of the hydroanthraquinones in the gas phase was decided by the FHT mechanism, which is a good indication for the dominant HOO˙ radical scavenging pathway in the nonpolar medium. In the polar environment the HOO˙ radical scavenging is, however, affected by interaction with water that leads to concurrent pathways following the FHT mechanism (for the neutral states) and SET mechanism (for the anionic states).15 Therefore, the overall rate constants (koverall) i.e. the total of all rate constants of the studied mechanistic pathways9 were calculated according to the eqn (9) and (10). The branching ratios (Γ) that characterize the contribution of each reactions mechanism or pathways in the overall rate constant9,10 were computed following the eqn (11). The obtained results are shown in Table 4.
| Comp. | Pentyl ethanoate | Water | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mechanism | ΔG≠ | kapp | Γ | ΔG≠ | kapp | f | kfa | Γ | |||
| a kf = f × kapp. | |||||||||||
| 1 | SET | 5.1 | 9.30 × 108 | 0.063 | 5.86 × 107 | 99.7 | |||||
| FHT | O8 | 12.2 | 2.60 × 105 | 100.0 | 13.4 | 1.70 × 105 | 0.937 | 1.59 × 105 | 0.3 | ||
| koverall | 2.60 × 105 | 5.87 × 107 | |||||||||
| 2 | SET | 7.2 | 3.00 × 107 | 0.126 | 3.78 × 106 | 99.4 | |||||
| FHT | O8 | 14.9 | 1.90 × 103 | 100.0 | 14.5 | 2.50 × 104 | 0.874 | 2.19 × 104 | 0.6 | ||
| koverall | 1.90 × 103 | 3.80 × 106 | |||||||||
| 3 | SET | 5.4 | 6.60 × 108 | 0.074 | 4.88 × 107 | 100 | |||||
| FHT | O8 | 13.5 | 4.80 × 104 | 83.0 | 14.1 | 4.80 × 104 | 0.926 | 4.44 × 104 | 0.1 | ||
| C9 | 15.1 | 7.00 × 103 | 17.0 | 15.5 | 7.00 × 103 | 6.48 × 104 | 0.0 | ||||
| koverall | 2.89 × 104 | 4.89 × 107 | |||||||||
| 4 | SET | 5.6 | 4.70 × 108 | 0.074 | 3.48 × 107 | 99.8 | |||||
| FHT | O8 | 13.4 | 3.90 × 104 | 99.2 | 14.3 | 6.60 × 104 | 0.926 | 6.11 × 104 | 0.2 | ||
| C9 | 16.7 | 3.10 × 102 | 0.8 | 16.4 | 7.60 × 102 | 7.04 × 102 | 0.0 | ||||
| koverall | 3.93 × 104 | 3.48 × 107 | |||||||||
| 5 | SET | 5.2 | 9.20 × 108 | 0.049 | 4.51 × 107 | 100.0 | |||||
| FHT | O5 | 18.1 | 2.70 × 101 | 100.0 | 17.3 | 4.55 × 102 | 0.951 | 4.32 × 102 | 0.0 | ||
| C10 | 19.5 | 7.20 | 26.7 | 18.6 | 2.40 × 101 | 2.28 × 101 | 0.0 | ||||
| koverall | 3.42 × 101 | 4.51 × 107 | |||||||||
| Trolox | 12.6 | 1.00 × 105 | 11.7 | 1.30 × 105 | |||||||
Rate constant in lipid medium:
| koverall = ∑kFHTapp(X–H) | (9) |
Rate constant in aqueous medium:
| koverall = fA−kSETapp(A−) + fHAkFHTapp(HA) = kSETf(A−) + kFHTf(HA) | (10) |
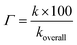 | (11) |
As shown in Table 4, the HOO˙ radical scavenging activity of the hydroanthraquinones is more than 200 times higher in water than in pentyl ethanoate solvent. The koverall values in the nonpolar environment are defined by the FHT pathway of the O–H bonds (Γ = 83−100%) and are in the range of 3.42 × 101 to 2.60 × 105 M−1 s−1, whereas those for the polar solvent is decided by the SET mechanism (Γ = 99.4–100.0%, koverall = 3.80 × 106 to 5.87 × 107 M−1 s−1). This result suggests that the SET mechanism plays a deciding role in the antioxidant activity of the hydroanthraquinones in polar environments. The highest overall rate constant was observed at compound 1 with koverall = 2.60 × 105 M−1 s−1 and 5.87 × 107 M−1 s−1 in polar and non-polar media, respectively. The compounds 3 and 4 also exhibit excellent HOO˙ radical scavenging with koverall = 2.89 × 104 and 3.93 × 104 M−1 s−1 in lipid medium and 4.89 × 107 and 3.48 × 107 M−1 s−1 in the aqueous solution, respectively. Compound 5 exhibits the lowest radical scavenging in lipid medium (koverall = 3.42 × 101 M−1 s−1), however this value in the polar environment is the second highest with koverall = 4.51 × 107 M−1 s−1. Comparing the obtained results with Trolox (koverall = 1.00 × 105 and 1.30 × 105 M−1 s−1 in pentyl ethanoate and water, respectively, Table 4) the studied compounds exhibit higher HOO˙ radical scavenging than the reference compound Trolox in the aqueous solution. The HOO˙ radical scavenging of 1 is about 2.6 and 444.6 times higher than that of Trolox in the nonpolar and polar environments, respectively. Hence, 1 is the most potential antioxidant in physiological environments. This is in good agreement with the experimental data of the DPPH and ABTS testing.58
4. Conclusions
The hydroperoxide radical scavenging activity of five natural hydroanthraquinones was evaluated by thermodynamic and kinetic calculations. The results showed that the formal hydrogen transfer pathway is the main mechanism for the antiradical activity of these hydroanthraquinones in nonpolar environments. It was found that the H-abstraction of O8–H bond plays a deciding role in the antioxidant activity of the studied compounds. However, the SET mechanism is favored in polar environment. It is important to notice that most of the studied compounds exhibit excellent HOO˙ scavenging activity in both polar and non-polar environments. In particular the HOO˙ radical scavenging of 1 is about 2.6 and 444.6 times higher than that of Trolox in the studied solvents. Hence, compound 1 is a potent antioxidant in physiological environments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2018.42.References
- M. Isaka, P. Chinthanom, P. Rachtawee, K. Srichomthong, P. Srikitikulchai, P. Kongsaeree and S. Prabpai, J. Antibiot., 2015, 68, 334–338 CrossRef CAS PubMed.
- J. Kornsakulkarn, W. Choowong, P. Rachtawee, N. Boonyuen, S. Kongthong, M. Isaka and C. Thongpanchang, Phytochem. Lett., 2018, 24, 46–50 CrossRef CAS.
- H. L. Li, X. M. Li, X. Li, C. Y. Wang, H. Liu, M. U. Kassack, L. H. Meng and B. G. Wang, J. Nat. Prod., 2017, 80, 162–168 CrossRef CAS PubMed.
- T. Shi, X.-M. Hou, Z.-Y. Li, F. Cao, Y.-H. Zhang, J.-Y. Yu, D.-L. Zhao, C.-L. Shao and C.-Y. Wang, RSC Adv., 2018, 8, 27596–27601 RSC.
- M. Leopoldini, N. Russo and M. Toscano, Food Chem., 2011, 125, 288–306 CrossRef CAS.
- J. S. Wright, E. R. Johnson and G. A. DiLabio, J. Am. Chem. Soc., 2001, 123, 1173–1183 CrossRef CAS PubMed.
- N. Nenadis and M. Z. Tsimidou, Phytochem. Lett., 2012, 48, 538–543 CAS.
- N. M. Thong, D. T. Quang, N. H. T. Bui, D. Q. Dao and P. C. Nam, Chem. Phys. Lett., 2015, 625, 30–35 CrossRef.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef.
- Q. V. Vo and A. Mechler, J. Chem. Inf. Model., 2020, 60, 316–321 CrossRef CAS PubMed.
- A. Bagno, F. Rastrelli and G. Saielli, Chem.–Eur. J., 2006, 12, 5514–5525 CrossRef CAS PubMed.
- G. Saielli, Molecules, 2020, 25, 2085 CrossRef PubMed.
- Q. V. Vo, P. C. Nam, M. V. Bay, N. M. Thong, N. D. Cuong and A. Mechler, Sci. Rep., 2018, 8, 12361 CrossRef PubMed.
- Q. V. Vo, P. C. Nam, M. Van Bay, N. M. Thong and A. Mechler, RSC Adv., 2019, 9, 42020–42028 RSC.
- K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 40, 2103–2110 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 1095–1099 CrossRef CAS PubMed.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed.
- Q. V. Vo, M. V. Bay, P. C. Nam and A. Mechler, J. Phys. Chem. B, 2019, 123, 7777–7784 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 CrossRef.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
- Y. Lu, A. Wang, P. Shi and H. Zhang, PLoS One, 2017, 12, e0169773 CrossRef PubMed.
- Y. Lu, A. Wang, P. Shi, H. Zhang and Z. Li, PLoS One, 2015, 10, e0133259 CrossRef PubMed.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver, Y. Luo, J. R. Pladziewicz, L. K. Ausman, T. L. Jentzsch and J. J. O'Konek, J. Phys. Chem. A, 2006, 110, 11665–11676 CrossRef CAS PubMed.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 17, 549–560 CrossRef CAS.
- G. G. Stokes, Mathematical and Physical Papers, University Press, Cambridge, 1905 Search PubMed.
- Y. Okuno, Chem.–Eur. J., 1997, 3, 212–218 CrossRef CAS PubMed.
- S. Benson, The foundations of chemical kinetics, Malabar, Florida, 1982 Search PubMed.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, J. Phys. Chem. B, 2011, 115, 12234–12246 CrossRef CAS PubMed.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682–3689 RSC.
- Q. V. Vo, T. V. Gon, M. V. Bay and A. Mechler, J. Phys. Chem. B, 2019, 123, 10672–10679 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed.
- G. A. DiLabio and E. R. Johnson, J. Am. Chem. Soc., 2007, 129, 6199–6203 CrossRef CAS PubMed.
- L. Muñoz-Rugeles, A. Galano and J. Raúl Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2017, 19, 6969–6972 RSC.
- J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS PubMed.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Phys. Chem. A, 2011, 115, 2367–2377 CrossRef CAS PubMed.
- A. M. Rebollar-Zepeda, T. Campos-Hernández, M. T. Ramírez-Silva, A. Rojas-Hernández and A. Galano, J. Chem. Theory Comput., 2011, 7, 2528–2538 CrossRef CAS PubMed.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- J. R. Pliego Jr, Chem. Phys. Lett., 2003, 367, 145–149 CrossRef.
- J. Torres-Lapasió, M. Garcia-Alvarez-Coque, E. Bosch and M. Rosés, J. Chromatogr. A, 2005, 1089, 170–186 CrossRef PubMed.
- H.-L. Li, X.-M. Li, X. Li, C.-Y. Wang, H. Liu, M. U. Kassack, L.-H. Meng and B.-G. Wang, J. Nat. Prod., 2016, 80, 162–168 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04013d |
| This journal is © The Royal Society of Chemistry 2020 |