Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The antioxidant activity of natural diterpenes: theoretical insights†
Quan V. Vo *ab,
Nguyen Minh Tam
*ab,
Nguyen Minh Tam *cd,
Le Trung Hieue,
Mai Van Bayf,
Nguyen Minh Thong
*cd,
Le Trung Hieue,
Mai Van Bayf,
Nguyen Minh Thong g,
Trinh Le Huyen
g,
Trinh Le Huyen hi,
Nguyen Thi Hoaj and
Adam Mechler
hi,
Nguyen Thi Hoaj and
Adam Mechler k
k
aInstitute of Research and Development, Duy Tan University, Danang 550000, Vietnam. E-mail: vovanquan2@duytan.edu.vn
bFaculty of Chemical Technology - Environment, The University of Danang-University of Technology and Education, Danang 550000, Vietnam. E-mail: vvquan@ute.udn.vn
cComputational Chemistry Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: nguyenminhtam@tdtu.edu.vn
dFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
eUniversity of Sciences-Hue University, Hue 530000, Vietnam
fDepartment of Chemistry, The University of Danang-, University of Science and Education, Danang 550000, Vietnam
gThe University of Danang, Campus in Kon Tum, 704 Phan Dinh Phung, Kon Tum 580000, Vietnam
hDepartment of Applied Chemistry, National Chiao Tung University, Hsinchu 30010, Taiwan
iDepartment of Chemical Engineering, The University of Danang-University of Science and Technology, Danang 550000, Vietnam
jAcademic Affairs, The University of Danang-University of Technology and Education, Danang 550000, Vietnam
kDepartment of Chemistry and Physics, La Trobe University, Victoria 3086, Australia
First published on 16th April 2020
Abstract
Diterpenes that were isolated from Crossopetalum gaumeri (Loes.) Lundell (Celastraceae) plants are reported to exhibit a range of biological activities, in particular as radical scavengers. Thus further insight into the antioxidant activity of diterpenes in physiological environments is much needed but not studied yet. In this study, the antioxidant activity of nine natural diterpenes was evaluated using kinetic and thermodynamic calculations. It was found that the sequential proton loss electron transfer (SPLET) mechanism is favored in polar environments, whereas formal hydrogen transfer (FHT) is the main pathway for the radical scavenging of these diterpenes in the gas phase as well as in lipid media. The rate constants for the HOO˙ radical scavenging of these compounds in the gas phase, polar and nonpolar solvents are in the range of 2.29 × 10−2 to 4.58 × 107, 9.74 × 10−3 to 1.67 × 108 and 3.54 × 10−5 to 1.31 × 105 M−1 s−1, respectively. 7-Deoxynimbidiol (6), exhibits the highest HOO˙ radical scavenging with koverall = 1.69 × 108 M−1 s−1 and 9.10 × 104 M−1 s−1 in water and pentyl ethanoate solvents, respectively, that is about 1300 times higher than that of Trolox in polar environments. It is thus a promising natural antioxidant in physiological environments.
1. Introduction
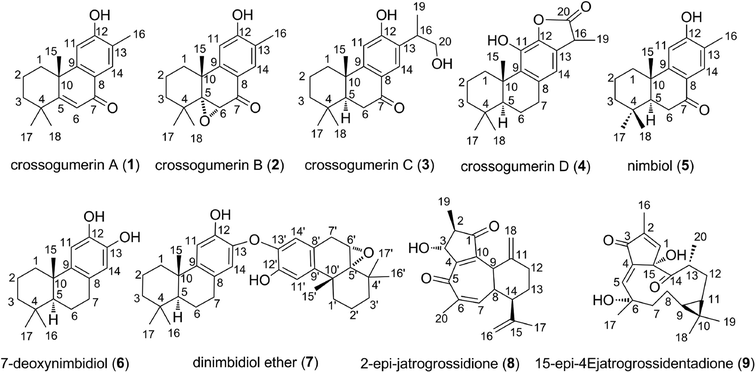
Diterpenes are natural products based on a podocarpane skeleton. These compounds are isolated from Crossopetalum gaumeri (Loes.) Lundell (Celastraceae) plants.1 Diterpenes and derivatives have great therapeutic potential.2,3 They exhibit a broad spectrum of biological activities including antimicrobial, antiviral, anti-inflammatory, and antitumor effects.4 Classes of diterpenes possessing high bio-activity include crossogumerins A–D (1–4), nimbiol (5), 7-deoxynimbidiol (6), dinimbidiol ether (7), 2-epi-jatrogrossidione (8), and 15-epi-4Ejatrogrossidentadione (9) (Fig. 1). Compounds 1–5 exhibit cytotoxicity against both HeLa (carcinoma of the cervix) and Hep-2 (lung carcinoma) human tumor cells lines, whereas compounds 2 and 5 exhibit strong activity against HeLa cells with low IC50 values (IC50 = 3.1 and 8.1 μM, respectively).5 Compound 6 showed good analgesic and anti-inflammatory activities, inhibiting the pain induced by PGE2 and reducing edema.6 Remarkably, the compounds 2-epi-jatrogrossidione (8) and 15-epi-4Ejatrogrossidentadione (9) exhibit potential antimicrobial activity against Bacillus subtilis.1Experimental studies of the antioxidant properties of diterpenes revealed good activity,1,6,7 warranting a theoretical investigation of the free radical scavenging mechanism of these compounds. The antioxidant activity of some diterpenes including ferruginol, hinokiol and sugiol was evaluated theoretically by using the Density Functional Theory (DFT) method. It was showed that ferruginol and hinokiol could exhibit higher antioxidant activity than butylated hydroxytoluene (BHT).8 However the activity has not been fully explored thus far. Previous works demonstrated that quantum chemistry calculations offer an effective and elegant way to study the mechanism and kinetics of radical reactions, evaluating the antioxidant capacity of organic compounds at the molecular level in both gas phase and physiological environments.8–16 Thus a thermodynamic and kinetic study in the radical scavenging activity of the natural diterpenes is crucial to glean a better understanding of their radical scavenging activity.
This study is thus aimed to (1) investigate the thermodynamics of the antioxidant activity of diterpenes through three mechanisms: formal hydrogen transfer (FHT), sequential electron transfer proton transfer (SETPT), or sequential proton loss electron transfer (SPLET); (2) kinetically evaluate the HOO˙ radical scavenging capacity of diterpenes in gas phase and physiological environments; and (3) analyze the effects of solvent environments and molecular structures on the antioxidant activity and oxidation resistance of diterpene derivatives.
2. Computational methods
In this study, the thermochemical properties: bond dissociation energies (BDEs), ionization energies (IEs), and proton affinities (PAs) of all compounds were determined in the gas phase following the well-established (RO)B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) calculating model.12,17–22 The kinetic study in the gas phase and physiological environments, including water for polar environment and pentyl ethanoate for non-polar environment with the solvation model density (SMD), was performed according to the quantum mechanics based test for overall free radical scavenging activity (QM-ORSA) protocol10,23,24 using the M06-2X/6-31+G(d,p) and M06-2X/6-311++G(d,p)9,25–27 levels and the Eyringpy code.28,29 The use of different functionals for thermochemistry and kinetics to enhance accuracy of the calculations was established and justified before.11,13 Rate constant (k) was computed following the transition state theory and 1 M standard state at 298.15 K according to the eqn (1) (details method in the Table S5, ESI†):24,30–34
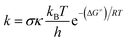 | (1) |
The overall rate constant (koverall), and branching ratios (Γ) were computed following the QM-ORSA model.10 All of the calculations were performed with the Gaussian 16 suite of programs.38
3. Results and discussions
3.1. Thermodynamic study
According to previous studies, the antioxidant activity may follow either of three main mechanisms including FHT, SETPT or SPLET. Thermodynamically each of these are characterized by corresponding thermochemical parameters: BDEs, PAs, and IEs, respectively.11,13,19,39 While the actual values of these parameters may vary in solvent environments, the overall characteristics of the compounds established in the gas phase are normally transferable to different environments. Thus, in the initial step, the thermochemical characteristics of possible X–H (X = C, O) bonds were screened in the gas phase by using DFT calculation at the B3LYP/3-21G level (Table S1, ESI†). The lowest PA and BDE values were then calculated at higher level ROB3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p)11,19 and these results are presented in Table 1.| Comp. | Positions | BDE | PA | IE |
|---|---|---|---|---|
| 1 | O12–H | 85.3 | 307.2 | 156.0 |
| 2 | O12–H | 85.4 | 305.1 | 156.3 |
| 3 | O12–H | 87.6 | 293.6 | 143.0 |
| 4 | C16–H | 74.6 | 146.7 | |
| O11–H | 84.0 | 306.0 | 146.7 | |
| 5 | O12–H | 85.6 | 304.5 | 155.6 |
| 6 | O12–H | 74.7 | 311.0 | 140.9 |
| O13–H | 75.2 | 310.7 | ||
| 7 | O12–H | 83.0 | 273.4 | 111.2 |
| 8 | C3–H | 74.8 | 161.2 | |
| C9–H | 351.6 | |||
| 9 | C13–H | 88.7 | 162.0 | |
| C16–H | 356.2 |
It was found that the BDE values were in the range of 74.6 to 88.7 kcal mol−1. The radical scavenging of compounds 1, 2, 3, 5, 6, and 7 following FHT mechanism was defined by the O12(13)–H bonds, while the lowest BDE values of the rest compounds were observed at C–H bonds. Due to the lowest BDE(O–H) values were detected at the O12(13)–H bonds of the compound 6 (BDE = 74.7 and 75.2 kcal mol−1, respectively), this diterpene compound can be considered a promising radical scavenger following the FHT mechanism.
The calculated PA values of the studied compounds were in the range of 273.4–356.2 kcal mol−1 and the calculated IEs for the diterpenes were 111.2–162.0 kcal mol−1. Compound 7 has the lowest PA and IE values at 273.4 kcal mol−1 and 111.2 kcal mol−1, respectively, whereas those for 9 are highest at 356.2 kcal mol−1 and 162.0 kcal mol−1, respectively. Hence, the SETPT and SPLET mechanisms may be feasible for compound 7 in the gas phase.
The investigation of the free energy change (ΔGo) of the first step for the HOO˙ scavenging of the diterpenes (Table S2, ESI†) in the gas phase indicated that the SETPT and SPLET mechanisms are not spontaneous (ΔGo > 0); the FHT mechanism, however, is supported by the negative ΔGo. Thus the FHT mechanism appears to be the main radical scavenging pathway for the studied diterpenes in the gas phase.
3.2. Kinetic study
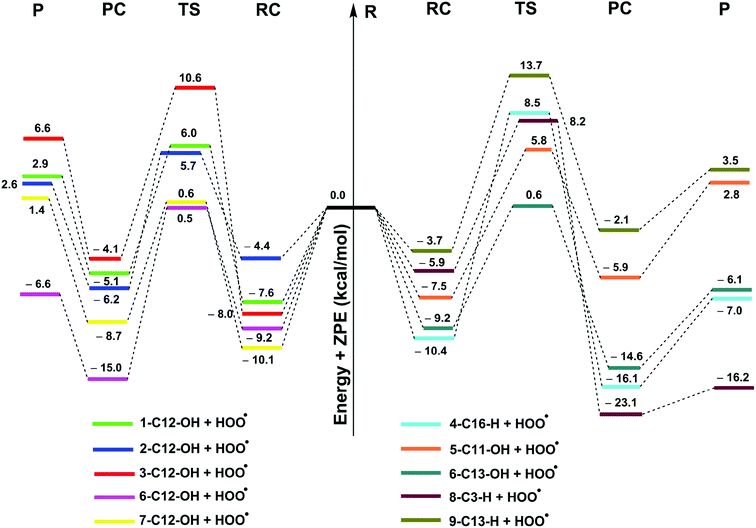 | ||
| Fig. 2 PES for the reactions of studied compounds with HOO˙ in the gas phase (reagent, RC: pre-complex; TS: transition state; PC: post-complex; P: products). | ||
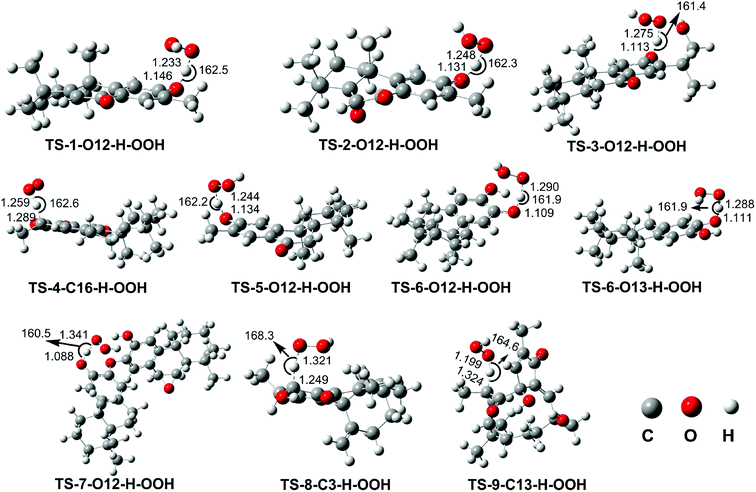 | ||
| Fig. 3 Optimized geometries TSs following the FHT mechanism between the studied compounds and HOO˙ radical in the gas phase. | ||
| Reactions | ΔG≠ | κ | kEck |
|---|---|---|---|
| 1–O12–H + HOO˙ | 14.2 | 210.7 | 5.18 × 104 |
| 2–O12–H + HOO˙ | 14.3 | 144.4 | 2.77 × 104 |
| 3–O12–H + HOO˙ | 19.4 | 16.9 | 6.63 × 10−1 |
| 4–C16–H + HOO˙ | 17.3 | 226.3 | 3.14 × 102 |
| 5–O12–H + HOO˙ | 14.3 | 231.1 | 4.70 × 104 |
| 6–O12–H + HOO˙ | 9.3 | 50.0 | 4.58 × 107 |
| 6–O13–H + HOO˙ | 9.6 | 62.6 | 3.55 × 107 |
| 7–O12–H + HOO˙ | 11.2 | 51.2 | 3.92 × 106 |
| 8–C3–H + HOO˙ | 17.4 | 17.9 | 2.11 × 101 |
| 9–C13–H + HOO˙ | 23.0 | 247.9 | 2.29 × 10−2 |
As shown in Fig. 2, the reaction proceeds via the pathway:
| R → RC → TS → PC → P |
The RCs are energetically more stable than the reactants in the range of 2.1–23.1 kcal mol−1. After the formation of RC, the reactions can proceed to transition states (TS) by formal hydrogen transfer process with the reaction barriers in the range of 9.7–18.9 kcal mol−1 and then form the products after pass though the post-complexes. The H-abstraction of the 6–O12–H and 6–O13–H bonds is easier than those of the other compounds with the lowest reaction barriers (9.7 and 9.8 kcal mol−1, respectively). This suggests that the compound 6 is the best potential HOO˙ radical scavenger of all of the studied compounds.
As shown in Table 2, the reaction barriers for the HOO˙ scavenging of the diterpenes in the gas phase at 298.15 K are in the range of 9.3–23.0 kcal mol−1, while the rate constant values for these reactions are in the range of 2.29 × 10−2 to 4.58 × 107 M−1 s−1 and the tunneling corrections (κ) for the H-abstraction of the X–H bonds are 16.9–247.9. The HOO˙ scavenging of 3, 8, and 9 are the lowest with kEck = 10−2 to 101 M−1 s−1. However, the compounds 1, 2, 4, 5, and 7 exhibit a moderate HOO˙ radical scavenging activity with kEck = 102 to 106 M−1 s−1. It is important to note that the highest rate constants are observed at the reactions of 6 + HOO˙ with kEck = 4.58 × 107 and 3.55 × 107 M−1 s−1 for the H-abstraction of 6–O12–H and 6–O13–H, respectively. This result correlates well with the obtained BDE values in the thermodynamic investigation (BDE(O12–H) = 74.7 kcal mol−1, BDE(O13–H) = 75.2 kcal mol−1). The compound 6 is thus predicted as the most active antioxidant among all of the studied diterpenes in the gas phase.
Acid–base equilibria. The investigation of radical scavenging in physiological environments provides the most accurate data of antioxidant activity.10 Therefore in this section the antioxidant activity of the diterpenes was evaluated against HOO˙ radical in physiological environments (water at pH = 7.4 for aqueous solution and pentyl ethanoate for lipid medium). As shown in the thermodynamic section, the lowest PA values for the compounds 8 and 9 were observed at the C–H bonds that have low pKa (pKa < 12) values. Consequently, these compounds were ignored in the acid–base equilibria calculations due to the neutral state at pH = 7.4. The pKa values of seven diterpenes (1–7) were calculated using the model reaction (2) below, following the literature.40 The calculated pKa values and the molar fractions (f) that were computed following the literature10 are presented in Table 3:
| HA + Ref− → A− + HRef | (2) |
| Comp. | OH position | pKa | fprotonated (HA) | fdeprotonated (A−) |
|---|---|---|---|---|
| 1 | O12–H | 8.30 | 0.888 | 0.112 |
| 2 | O12–H | 8.52 | 0.929 | 0.071 |
| 3 | O12–H | 8.20 | 0.863 | 0.137 |
| 4 | O11–H | 8.58 | 0.938 | 0.062 |
| 5 | O12–H | 8.55 | 0.934 | 0.066 |
| 6 | O13–H | 8.98 | 0.974 | 0.026 |
| 7 | O12–H | 7.77 | 0.701 | 0.299 |
The value of pKa was defined by eqn (3):40–42
pKa = ΔGs/RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) + pKa(HRef) ln(10) + pKa(HRef)
| (3) |
As shown in the Table 3, the calculated pKa values are in the range of 7.77 to 8.98. The fprotonated (HA) and fdeprotonated (A−) are in the range of 0.701 to 0.974 and 0.026 to 0.299, respectively. Thus in the aqueous solution at pH = 7.4, the diterpenes 1–7 exist at both neutral and anion states, whereas 8 and 9 exist at neutral states and these states have been used for further study.
Kinetic study. From the thermodynamics section, the FHT mechanism defined the HOO˙ radical scavenging of the studied compounds in the gas phase. The FHT mechanism is thus a favorable pathway for the HOO˙ radical scavenging in the lipid solvent. However, in the aqueous solution, the diterpenes exist at both anion and neutral states, so the HOO˙ radical scavenging of diterpenes can follow both the FHT and SET mechanisms. Calculations of the Gibbs free energy change of the reactions of neutral diterpenes with HOO˙ radical following the SET mechanism yielded positive values in both water and lipid media (Table S3, ESI†) thus these reactions are not spontaneous. Hence, the HOO˙ radical scavenging in the physiological environments is calculated via the SET mechanism for the anion states and the FHT mechanism for the neutral states.27 The overall rate constants (koverall) were calculated according to the eqn (4) and (5) and the obtained results are shown in Table 4.
| Comp. | Mechanism | Pentyl ethanoate | Water | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔG≠ | kapp | Γ | ΔG≠ | kapp | f | kfa | Γ | |||
| a kf = fkapp. | ||||||||||
| 1 | SET | 9.9 | 3.60 × 105 | 0.112 | 4.03 × 104 | 100.0 | ||||
| HAT | O12 | 19.4 | 1.27 | 100.0 | 18.9 | 1.89 × 101 | 0.888 | 1.68 × 101 | 0.0 | |
| koverall | 1.27 | 4.03 × 104 | ||||||||
| 2 | SET | 10.5 | 1.30 × 105 | 0.071 | 9.23 × 103 | 99.7 | ||||
| HAT | O12 | 17.9 | 1.82 × 101 | 100.0 | 18.7 | 2.64 × 101 | 0.929 | 2.45 × 101 | 0.3 | |
| koverall | 1.82 × 101 | 9.25 × 103 | ||||||||
| 3 | SET | 12 | 1.10 × 104 | 0.137 | 1.51 × 103 | 99.7 | ||||
| HAT | O12 | 22.8 | 6.40 × 10−3 | 100.0 | 19.8 | 5.33 | 0.863 | 4.60 | 0.3 | |
| koverall | 6.40 × 10−3 | 1.51 × 103 | ||||||||
| 4 | SET | 5.3 | 7.90 × 108 | 0.062 | 4.90 × 107 | 100.0 | ||||
| HAT | C16 | 20.5 | 1.10 | 100.0 | 18.8 | 4.70 × 101 | 0.938 | 4.41 × 101 | 0.0 | |
| koverall | 1.10 | 4.90 × 107 | ||||||||
| 5 | SET | 10 | 3.00 × 105 | 0.066 | 1.98 × 104 | 99.9 | ||||
| HAT | O11 | 17.8 | 2.39 × 101 | 100.0 | 19.1 | 1.37 × 101 | 0.934 | 1.28 × 101 | 0.1 | |
| koverall | 2.39 × 101 | 1.98 × 104 | ||||||||
| 6 | SET | 3.2 | 6.40 × 109 | 0.026 | 1.66 × 108 | 99.9 | ||||
| HAT | O12 | 12.9 | 7.70 × 104 | 58.8 | 13.6 | 1.20 × 105 | 0.974 | 1.17 × 105 | 0.1 | |
| C13 | 13.3 | 5.40 × 104 | 41.2 | 14.4 | 6.70 × 104 | 6.53 × 104 | 0.0 | |||
| koverall | 1.31 × 105 | 1.67 × 108 | ||||||||
| 7 | SET | 11.2 | 3.92 × 104 | 0.299 | 1.17 × 104 | 100.0 | ||||
| HAT | O12 | 14.3 | 1.48 × 104 | 100.0 | 15.5 | 2.07 × 103 | 0.701 | 1.45 × 103 | 0.0 | |
| koverall | 1.48 × 104 | 1.32 × 104 | ||||||||
| 8 | SET | |||||||||
| HAT | C3 | 20.3 | 2.80 × 10−1 | 100.0 | 19.2 | 3.00 | 1 | 3.00 | 100.0 | |
| koverall | 2.80 × 10−1 | 3.00 | ||||||||
| 9 | SET | |||||||||
| HAT | C13 | 26.2 | 3.54 × 10−5 | 100.0 | 23.6 | 9.74 × 10−3 | 1 | 9.74 × 10−3 | 100.0 | |
| koverall | 3.54 × 10−5 | 9.74 × 10−3 | ||||||||
In lipid media:
| koverall = ∑kFHTapp (X–H) | (4) |
In the aqueous solution:
| koverall = fA−kSETapp (A−) + fHAkFHTapp (HA) = kSETf (A−) + kFHTf (HA) | (5) |
As can be seen in Table 4, the overall rate constants for the HOO˙ radical scavenging of the diterpenes in the lipid medium are in the range of 3.54 × 10−5 to 1.31 × 105 M−1 s−1, whereas those for the aqueous solution are much higher at koverall = 9.74 × 10−3 to 1.67 × 108 M−1 s−1. The koverall values in the lipid solvent are defined by the H-abstraction of the X–H bonds (Γ ∼ 100%), while the SET mechanism is the main pathway for the HOO˙ radical scavenging in the aqueous solution (Γ = 99.7–100.0%). The compounds 8 and 9 exhibit low HOO˙ radical scavenging activity in both water and pentyl ethanoate solvents with koverall < 101 that can be ascribed to the absence of phenolic system in these compounds. The compounds 1, 2, 3, 5, and 7 exhibit moderate HOO˙ radical scavenging activity in the aqueous solution (koverall ∼ 103 to 104). Interestingly, the HOO˙ scavenging activity of compound 4 in the polar solvent is about 107 times higher than that in the nonpolar solvent. Thus 4 has the second largest overall rate constant in the aqueous solution. The highest overall rate constant was calculated for compound 6 with koverall = 1.31 × 105 M−1 s−1 and 1.67 × 108 M−1 s−1 in non-polar and polar media, respectively.
To gain more accurate values, the M06-2X/6-311++G(d,p) level of theory was used, which is currently among best methods to compute accurate kinetic parameters.9,27 At this level of theory the most active compound 6 was analyzed and the obtained results are presented in Table 5. It was found that the HOO˙ radical scavenging of 6 in water (koverall = 1.69 × 108 M−1 s−1) is about 1857 times higher than that (koverall = 9.40 × 104 M−1 s−1) in pentyl ethanoate solvent. Moreover, in comparison with a typical natural antioxidant-Trolox (koverall = 1.00 × 105 and 1.30 × 105 M−1 s−1 in pentyl ethanoate and water, respectively), compound 6 exhibits similar HOO˙ radical scavenging activity in the lipid medium. However, the HOO˙ radical scavenging of 6 is about 1300 times higher than that of Trolox, and 13 times higher than that of trans-resveratrol13 in the polar environment. Hence, 6 is a promising antioxidant in polar environments.
4. Conclusions
This study was carried out to evaluate the antioxidant activity of nine natural diterpenes by kinetic and thermodynamic calculations. It was found that the FHT mechanism is the main pathway for the radical scavenging of these diterpenes in the gas phase and in lipid environment, whereas the SET mechanism is favored in polar environment. The kinetic calculations showed that the rate constant values for the HOO˙ radical scavenging of these compounds in the gas phase, polar and nonpolar solvents are in the range of 2.29 × 10−2 to 4.58 × 107 M−1 s−1, 9.74 × 10−3 to 1.67 × 108 M−1 s−1 and 3.54 × 10−5 to 1.31 × 105 M−1 s−1, respectively. The compounds 8 and 9 exhibited low radical scavenging activity due to the absence of phenolic system, whereas the phenolic compound 6 is predicted to be the most potent HOO˙ radical scavenger in all of the studied compounds with koverall = 1.69 × 108 M−1 s−1 (in water) and 9.10 × 104 M−1 s−1 (in pentyl ethanoate solvent). Thus, compound 6 becomes one of the most potent antioxidant in polar physiological environments due to its HOO˙ radical scavenging is about 1300 and 13 times higher than those of Trolox and trans-resveratrol, respectively.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2018.308.References
- G. I. Hernández-Bolio, J. A. Ruiz-Vargas and L. M. Peña-Rodríguez, J. Nat. Prod., 2019, 82, 647–656 CrossRef PubMed
.
- S. Hortelano, Inflammation Allergy: Drug Targets, 2009, 8, 28–39 CrossRef PubMed
.
- N. Gurusamy, I. Lekli, S. Mukherjee, D. Ray, M. K. Ahsan, M. Gherghiceanu, L. M. Popescu and D. K. Das, Cardiovasc. Res., 2010, 86, 103–112 CrossRef CAS PubMed
.
- M. Pal, T. Mishra, A. Kumar and S. K. Tewari, Pharm. Chem. J., 2016, 50, 558–567 CrossRef CAS
.
- G. Miron-Lopez, I. L. Bazzocchi, I. A. Jimenez-Diaz, L. M. Moujir, R. Quijano-Quiñones, L. Quijano and G. J. Mena-Rejon, Bioorg. Med. Chem. Lett., 2014, 24, 2105–2109 CrossRef CAS PubMed
.
- H. E. Zapata-Estrella, A. D. Sánchez-Pardenilla, K. García-Sosa, F. Escalante-Erosa, F. de Campos-Buzzi, N. L. Meira-Quintão, V. Cechinel-Filho and L. M. Peña-Rodríguez, Nat. Prod. Commun., 2014, 9, 1934578X1400900925 CrossRef
.
- K. García-Sosa, R. Aldana-Pérez, R. V. E. Moo, P. Simá-Polanco and L. M. Peña-Rodríguez, Nat. Prod. Commun., 2017, 12, 1934578X1701200903 CrossRef
.
- A. Stobiecka, Food Biophys., 2019, 14, 1–12 CrossRef
.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum Chem., 2019, 119, e25665 CrossRef
.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed
.
- Q. V. Vo and A. Mechler, J. Chem. Inf. Model., 2020, 60, 316–321 CrossRef CAS PubMed
.
- Q. V. Vo, P. C. Nam, M. V. Bay, N. M. Thong, N. D. Cuong and A. Mechler, Sci. Rep., 2018, 8, 12361 CrossRef PubMed
.
- Q. V. Vo, P. C. Nam, M. Van Bay, N. M. Thong and A. Mechler, RSC Adv., 2019, 9, 42020–42028 RSC
.
- T. C. Ngo, D. Q. Dao, N. M. Thong and P. C. Nam, RSC Adv., 2016, 6, 30824–30834 RSC
.
- E. Alvareda, P. A. Denis, F. Iribarne and M. Paulino, Comput. Theor. Chem., 2016, 1091, 18–23 CrossRef CAS
.
- P. A. Denis, J. Phys. Chem. C, 2013, 117, 3895–3902 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P.-C. Nam, M. T. Nguyen and A. K. Chandra, J. Phys. Chem. A, 2005, 109, 10342–10347 CrossRef CAS PubMed
.
- J. S. Wright, E. R. Johnson and G. A. DiLabio, J. Am. Chem. Soc., 2001, 123, 1173–1183 CrossRef CAS PubMed
.
- G. DiLabio, D. Pratt, A. LoFaro and J. S. Wright, J. Phys. Chem. A, 1999, 103, 1653–1661 CrossRef CAS
.
- A. K. Chandra and T. Uchimaru, J. Phys. Chem. A, 2000, 104, 9244–9249 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- J. R. l. Alvarez-Idaboy and A. Galano, J. Phys. Chem. B, 2012, 116, 9316–9325 CrossRef CAS PubMed
.
- Q. V. Vo, M. V. Bay, P. C. Nam and A. Mechler, J. Phys. Chem. B, 2019, 123, 7777–7784 CrossRef CAS PubMed
.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed
.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed
.
- M. Carreon-Gonzalez, A. Vivier-Bunge and J. R. Alvarez-Idaboy, J. Comput. Chem., 2019, 40, 2103–2110 CrossRef CAS PubMed
.
- E. Dzib, J. L. Cabellos, F. Ortíz-Chi, S. Pan, A. Galano and G. Merino, Int. J. Quantum Chem., 2019, 119, e25686 CrossRef
.
- E. Dzib, J. L. Cabellos, F. Ortiz-Chi, S. Pan, A. Galano and G. Merino, Eyringpy 1.0.2, Cinvestav, Mérida, Yucatán, 2018 Search PubMed
.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC
.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS
.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS
.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823–1835 CrossRef CAS
.
- E. Vélez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971–977 CrossRef
.
- E. Pollak and P. Pechukas, J. Am. Chem. Soc., 1978, 100, 2984–2991 CrossRef CAS
.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed
.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. P. Jr, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed
.
- A. M. Rebollar-Zepeda, T. Campos-Hernández, M. T. Ramírez-Silva, A. Rojas-Hernández and A. Galano, J. Chem. Theory Comput., 2011, 7, 2528–2538 CrossRef CAS PubMed
.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed
.
- J. R. Pliego Jr, Chem. Phys. Lett., 2003, 367, 145–149 CrossRef
.
- J. Torres-Lapasió, M. Garcia-Alvarez-Coque, E. Bosch and M. Rosés, J. Chromatogr., 2005, 1089, 170–186 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02681f |
| This journal is © The Royal Society of Chemistry 2020 |