Open Access Article
Open Access ArticleModifying structural polymorphs and tuning electronic properties in pressure-stabilized binary Ir–Sb phases
Siyuan Liua,
Dan Zhou*bc,
Manai Cuia,
Jing Xua,
Xuejiao Maa,
Yuheng Chenga,
Zhexue Jin*d and
Yanhui Liu *a
*a
aDepartment of Physics, College of Science, Yanbian University, Yanji 133000, China. E-mail: yhliu@ybu.edu.cn
bSchool of Science, Changchun University of Science and Technology, Changchun 130000, China. E-mail: zhoudan777@aliyun.com
cDepartment of Materials Science, State Key Laboratory of Superhard Materials, Key Laboratory of Automobile Materials of MOE, Jilin University, Changchun 130000, China
dDepartment of Computer Science, College of Engineering, Yanbian University, Yanji 133000, China. E-mail: jinzhexue@ybu.edu.cn
First published on 20th May 2020
Abstract
The search for novel structures and chemical stoichiometry of binary Ir–Sb compounds is of great importance in view of their catalytic applications. Based on the results of swarm structure searching technique combined with density functional theory, we proposed the hitherto unknown Ir–Sb phase diagram in a wide pressure range with various chemical compositions. Besides two ambient pressure phases of IrSb3-Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and IrSb2-P21/c, five novel phases of IrSb-C2/c, IrSb-P
and IrSb2-P21/c, five novel phases of IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , IrSb2-P
, IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, IrSb2-I4/mmm and Ir2Sb-Pmmn were identified at high pressures. The phonon dispersion curves reveal that these phases are all dynamically stable. The calculated electronic results show that a mixed behavior of covalent, ionic and metallic bonds simultaneously exits in these novel phases. A pressure-induced electronic topological transition in Ir2Sb-Pmmn phase occurs according to the theoretical electronic band structures, while is not shown in other stoichiometries of the Ir–Sb system. Our work provides a potential opportunity for experimental synthesis of crystal structures with different chemical stoichiometries of the binary Ir–Sb system.
21m, IrSb2-I4/mmm and Ir2Sb-Pmmn were identified at high pressures. The phonon dispersion curves reveal that these phases are all dynamically stable. The calculated electronic results show that a mixed behavior of covalent, ionic and metallic bonds simultaneously exits in these novel phases. A pressure-induced electronic topological transition in Ir2Sb-Pmmn phase occurs according to the theoretical electronic band structures, while is not shown in other stoichiometries of the Ir–Sb system. Our work provides a potential opportunity for experimental synthesis of crystal structures with different chemical stoichiometries of the binary Ir–Sb system.
Introduction
Transition-metal compounds have aroused a great deal of interest from researchers due to their fundamental physics and as potential candidates for thermoelectric energy converters.1–4 Binary transition-metal antimonides are considered as important functional materials exhibiting a range of potential applications for superconductivity and as lithium ion battery anode materials.5–7 However, it is still a major challenge to experimentally synthesize transition-metal antimonides with novel structures and chemical stoichiometry in general under ambient conditions, because of the requirement for high temperatures and multi-step reactions under vacuum.8,9 Fortunately, recent studies experimental synthesis has made several successes to synthesize several transition-metal antimonides, e.g., arsenopyrite-type structure of CoSb2,10,11 skutterudite-type structure of CoSb3,12,13 nickel arsenide-type structure of NiSb and CoSb,14,15 marcasite-type structure of NiSb2,16 and anti-PbCl-type structure of Cu2Sb.17High temperature phase diagram of intermetallic compounds Ir–Sb was reported in the 1950s based on metallographic, thermal and X-ray analyses.18 The melting points were determined from cooling curves of alloys prepared from chemically pure components. Hexagonal NiAs-type IrSb was obtained according to metallographic observations of alloys after annealing 1500 K.19 The melting point of IrSb2 is higher than 1050 K, while IrSb3 forms by a peritectic reaction of 1126 K.20 Moreover, pressure induced irreversible isosymmetric transition of IrSb3 by the X-ray diffraction up to 43 GPa have been reported.21,22 Because of its relatively opened structure, it is expected to exhibit interesting behavior under high pressure. This void space can be filled with different atoms such as La or Ge to obtain the related family of compounds called filled skutterudites or stuffed skutterudites.23 Filled skutterudite compounds have been considered as potential candidates for thermoelectric applications.24,25 Interestingly, it could be interpreted as a pressure-induced self-insertion reaction which could be effectively improved the thermoelectric properties.
Utilizing the first-principle calculations combined with Boltzmann transport equation (BTE) and semiclassical analysis, high figure of merit zTs of 1.45 are obtained in n-type doped IrSb3 at higher pressure.26 These studies show that pressure plays a powerful role to tune the thermoelectric properties.27 Thus, it is necessary to systematically investigate the crystal structure with various iridium antimonies stoichiometry and explore the corresponding bonding characterizes under high pressure.
In this paper, we have explored the binary Ir–Sb phase diagram via a first-principles swarm-intelligence structure search and established a comprehensive understanding of the evolution of its crystal structures at 0–100 GPa. In addition to reproducing the known IrSb-P63/mmc, IrSb2-P21/c and IrSb3-Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , the five novel high-pressure phases of Ir2Sb-Pmmn, IrSb-C2/c, IrSb-P
, the five novel high-pressure phases of Ir2Sb-Pmmn, IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , IrSb2-P
, IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m and IrSb2-I4/mmm become energetically stable at 4.2 GPa, 16.4 GPa, 76.5 GPa, 45 GPa and 59.2 GPa, respectively. The electronic properties have been comprehensively investigated.28,29 Interestingly, pressure-driven evolution of the electronic topology transitions in IrSb2-P4/nmm phase has been confirmed. Furthermore, the pressure-induced different bonding characters are shown in these antimonies. Our result represents a significant step toward understanding the structural and electrical behavior of the binary Ir–Sb system under extreme condition.
21m and IrSb2-I4/mmm become energetically stable at 4.2 GPa, 16.4 GPa, 76.5 GPa, 45 GPa and 59.2 GPa, respectively. The electronic properties have been comprehensively investigated.28,29 Interestingly, pressure-driven evolution of the electronic topology transitions in IrSb2-P4/nmm phase has been confirmed. Furthermore, the pressure-induced different bonding characters are shown in these antimonies. Our result represents a significant step toward understanding the structural and electrical behavior of the binary Ir–Sb system under extreme condition.
Results and discussion
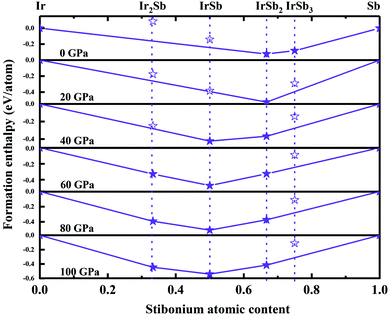
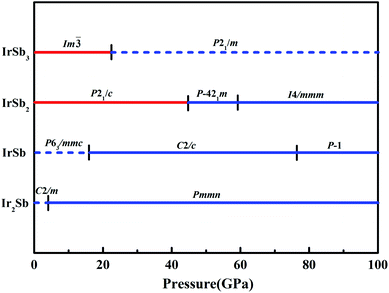
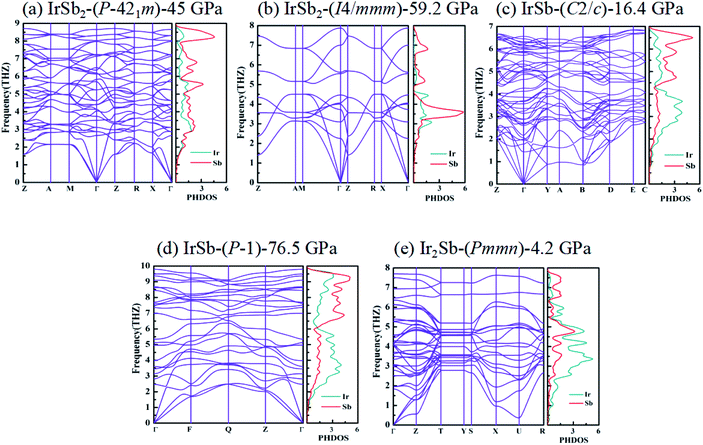
We have performed systematic structure prediction for Ir–Sb system by variable-cell simulation with cell sizes of 1–4 formula units (f.u.) at 0–100 GPa. The crystal structure with the lowest energy was predicted under different pressures, and the enthalpies formation of ΔHf for the iridium antimonies stoichiometry can be obtained in the structure search at varying pressures, as shown in Fig. 1. The relative thermodynamic stability of different Ir–Sb compounds with respect to elemental solids Ir and Sb is calculated according to the following equation: ΔHf(IrxSby) = [H(IrxSby) − xH(Ir) − yH(Sb)]/(x + y). In the formula, H(IrxSby) represents the enthalpy of the structure in the range of stable pressure, and H(Ir) and H(Sb) represent the enthalpy of the Ir atom and the Sb atom at the corresponding pressure. Then, we construct the convex hull data for Ir–Sb system at each pressure. Solid star indicates thermodynamically stable phases and the unstable or meta-stable phases are expressed by hollow star.The built pressure-composition phase diagram of the Ir–Sb system is shown in Fig. 2, with the stable structures identified using colors and space groups. At ambient pressure, the already known stoichiometries of IrSb3-Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and IrSb2-P21/c are well-reproduced in our structural search calculations in Fig. 3(a) and (b). However, it is to be found that experimental phase of the ground state IrSb (space group P63/mmc) tend to decompose into IrSb2 phase in our pressure-composition phase diagram. Moreover, the optimized crystal parameters of IrSb2 (space group P21/c) are a = 6.734 Å, b = 6.675 Å, c = 6.831 Å in good well with the experimental values of a = 6.600 Å, b = 6.500 Å, c = 6.700 Å, and that of in IrSb (space group P63/mmc) are a = b = 4.082 Å, c = 5.634 Å also consistent with the experimental values of a = b = 3.978 Å, c = 5.521 Å,6–8 validating that our adopted structure searching method and PBE functional are applicable to the Ir–Sb system. No imaginary frequency is observed throughout the whole Brillouin zone, which indicates that the five novel phases are dynamically stable in the pressure region from this study, as shown in Fig. 4. The five novel phases of IrSb2-P
and IrSb2-P21/c are well-reproduced in our structural search calculations in Fig. 3(a) and (b). However, it is to be found that experimental phase of the ground state IrSb (space group P63/mmc) tend to decompose into IrSb2 phase in our pressure-composition phase diagram. Moreover, the optimized crystal parameters of IrSb2 (space group P21/c) are a = 6.734 Å, b = 6.675 Å, c = 6.831 Å in good well with the experimental values of a = 6.600 Å, b = 6.500 Å, c = 6.700 Å, and that of in IrSb (space group P63/mmc) are a = b = 4.082 Å, c = 5.634 Å also consistent with the experimental values of a = b = 3.978 Å, c = 5.521 Å,6–8 validating that our adopted structure searching method and PBE functional are applicable to the Ir–Sb system. No imaginary frequency is observed throughout the whole Brillouin zone, which indicates that the five novel phases are dynamically stable in the pressure region from this study, as shown in Fig. 4. The five novel phases of IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P
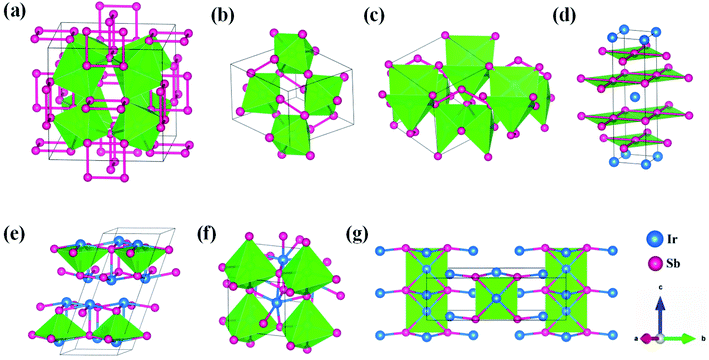
21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and Ir2Sb-Pmmn are stable shown in Fig. 3(c)–(g) under high pressure and the crystal structure and physical properties of these structures will be examined in detail next. IrSb3 is crystalized in a skutterudite-type structure, which can be also considered as a body centered cubic structure with a space group of Im
and Ir2Sb-Pmmn are stable shown in Fig. 3(c)–(g) under high pressure and the crystal structure and physical properties of these structures will be examined in detail next. IrSb3 is crystalized in a skutterudite-type structure, which can be also considered as a body centered cubic structure with a space group of Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) in Fig. 3(a). The antimonies atoms form planer, rectangular Sb4 square with Sb–Sb distance of 3.033 Å. High-pressure calculations shows that the cubic IrSb3-Im
in Fig. 3(a). The antimonies atoms form planer, rectangular Sb4 square with Sb–Sb distance of 3.033 Å. High-pressure calculations shows that the cubic IrSb3-Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) will be stability up to 22.2 GPa.
will be stability up to 22.2 GPa.
At ambient pressure, the IrSb2-P21/c has a monoclinic symmetry in Fig. 3(b). Four Ir atoms and eight Sb atoms occupy the Wyckoff 4e site in the unit cell, respectively. In this structure, each Ir atom is coordinated to six Sb atoms in an octahedron environment, connected by an antimony bridge. The bond length of Ir–Sb and Sb–Sb is 2.688 and 2.902 Å, respectively. At 45 GPa, the simulated IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m phase becomes more favorable, which has a tetragonal primitive symmetry with lattice parameters of a = b = 5.854 Å, and c = 6.196 Å in Fig. 3(c). In this case of the IrSb2-P
21m phase becomes more favorable, which has a tetragonal primitive symmetry with lattice parameters of a = b = 5.854 Å, and c = 6.196 Å in Fig. 3(c). In this case of the IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m phase, four Ir atoms occupy the wyckoff 4e site and six Sb atoms lie in 4e, 2a, and 2c sites in the unit cell, respectively. Each Ir atom is coordinated to five Sb atoms formed a quadrangular pyramid. Interestingly, the antimony atoms consist of Sb3 unites with the Sb–Sb distance of 2.782 Å, which join the neighbor six quadrangular together. In the IrSb2-I4/mmm phase, it has a tetragonal primitive symmetry, its equilibrium lattice parameters are a = b = 2.955 Å, and c = 11.218 Å at 59.2 GPa in Fig. 3(d). Two Ir atoms occupy the Wyckoff 2a site and four Sb atoms lie in 4e site in the unit cell. The IrSb2-I4/mmm phase consists of alternate Ir and Sb layers atoms, with the Sb–Sb distance of 2.955 Å in the square layer, which is larger than that of 2.782 Å in IrSb2-P
21m phase, four Ir atoms occupy the wyckoff 4e site and six Sb atoms lie in 4e, 2a, and 2c sites in the unit cell, respectively. Each Ir atom is coordinated to five Sb atoms formed a quadrangular pyramid. Interestingly, the antimony atoms consist of Sb3 unites with the Sb–Sb distance of 2.782 Å, which join the neighbor six quadrangular together. In the IrSb2-I4/mmm phase, it has a tetragonal primitive symmetry, its equilibrium lattice parameters are a = b = 2.955 Å, and c = 11.218 Å at 59.2 GPa in Fig. 3(d). Two Ir atoms occupy the Wyckoff 2a site and four Sb atoms lie in 4e site in the unit cell. The IrSb2-I4/mmm phase consists of alternate Ir and Sb layers atoms, with the Sb–Sb distance of 2.955 Å in the square layer, which is larger than that of 2.782 Å in IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m.
21m.
The optimized structure of IrSb-C2/c has a monoclinic structure at 16.4 GPa. At pressure of 76.5 GPa, the IrSb-C2/c transforms into an anorthic IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structure. In the IrSb-C2/c phase, with lattice parameters of a = 11.207 Å, b = 5.326 Å, and c = 5.061 Å, and α = γ = 90.0°, β = 110.7° at 16.4 GPa in Fig. 3(e). Eight Ir atoms occupy the Wyckoff 8f site and eight Sb atoms lie in the 8f site in the unit cell. Each Ir atom is coordinated to five Sb atoms to form an octahedron in a unit cell. In the IrSb-P
structure. In the IrSb-C2/c phase, with lattice parameters of a = 11.207 Å, b = 5.326 Å, and c = 5.061 Å, and α = γ = 90.0°, β = 110.7° at 16.4 GPa in Fig. 3(e). Eight Ir atoms occupy the Wyckoff 8f site and eight Sb atoms lie in the 8f site in the unit cell. Each Ir atom is coordinated to five Sb atoms to form an octahedron in a unit cell. In the IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase, it belongs to a triclinic system, with lattice parameters of a = 4.812 Å, b = 5.034 Å, and c = 5.033 Å, and α = 98.8°, β = 99.6°, γ = 92.1° at 76.5 GPa in Fig. 3(f). Four Ir atoms occupy the Wyckoff 2i site and four Sb atoms lie in the 2i site in the unit cell. Each Ir atom is coordinated to six Sb atoms to form an octahedral structure in a unit cell. The optimized structure of Ir2Sb-Pmmn has a tetragonal structure at 4.2 GPa. In this structure, lattice parameters are a = 3.874 Å, b = 12.479 Å, and c = 4.183 Å at 4.2 GPa in Fig. 3(g). Eight Ir atoms occupy the Wyckoff 2a, 2b and 4e sites and four Sb atoms lie in the 4e site in the unit cell. Each Ir atom has adopted the four nearest neighboring Sb atoms forming planar structure. The refined cation–anion bond length is 2.740 Å. The current theoretical phonon dispersion curves and phonon density of states (PHDOS) have evidence of the absence of any imaginary dynamical vibration in the whole Brillouin zone for the novel five structures, as shown in Fig. 4.
phase, it belongs to a triclinic system, with lattice parameters of a = 4.812 Å, b = 5.034 Å, and c = 5.033 Å, and α = 98.8°, β = 99.6°, γ = 92.1° at 76.5 GPa in Fig. 3(f). Four Ir atoms occupy the Wyckoff 2i site and four Sb atoms lie in the 2i site in the unit cell. Each Ir atom is coordinated to six Sb atoms to form an octahedral structure in a unit cell. The optimized structure of Ir2Sb-Pmmn has a tetragonal structure at 4.2 GPa. In this structure, lattice parameters are a = 3.874 Å, b = 12.479 Å, and c = 4.183 Å at 4.2 GPa in Fig. 3(g). Eight Ir atoms occupy the Wyckoff 2a, 2b and 4e sites and four Sb atoms lie in the 4e site in the unit cell. Each Ir atom has adopted the four nearest neighboring Sb atoms forming planar structure. The refined cation–anion bond length is 2.740 Å. The current theoretical phonon dispersion curves and phonon density of states (PHDOS) have evidence of the absence of any imaginary dynamical vibration in the whole Brillouin zone for the novel five structures, as shown in Fig. 4.
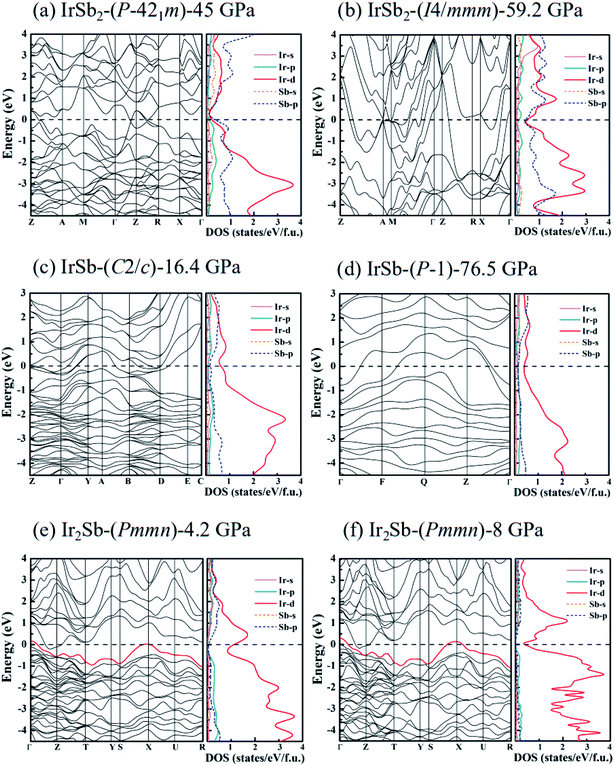
To study the chemical bonding and electronic properties of the five novel phases of IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P
21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and Ir2Sb-Pmmn, we have calculated the energy band structure, projected density of states (PDOS) and the electron localization function. As shown in the calculated PDOS (Fig. 5(a)–(e)), several electric bands cross the Fermi energy along high-symmetry directions in these structures. The results show the metallic characters for the five novel phases. Moreover, PDOS raises overlap between Sb 5p and Ir 5d orbitals below the Fermi level, indicating charge transfer from Sb 2p to Ir 5d. The electrons transferred are responsible for the relatively low difference of electronegativity of antimony (2.05) and iridium (2.20). The presence of strong Ir 5d component above the Fermi level indicates the depletion of 5d electrons in Ir atoms. This is further supported by the formation of Ir–Sb ionic bond by the electron localization function (ELF) analysis in Fig. 6(a)–(e).
and Ir2Sb-Pmmn, we have calculated the energy band structure, projected density of states (PDOS) and the electron localization function. As shown in the calculated PDOS (Fig. 5(a)–(e)), several electric bands cross the Fermi energy along high-symmetry directions in these structures. The results show the metallic characters for the five novel phases. Moreover, PDOS raises overlap between Sb 5p and Ir 5d orbitals below the Fermi level, indicating charge transfer from Sb 2p to Ir 5d. The electrons transferred are responsible for the relatively low difference of electronegativity of antimony (2.05) and iridium (2.20). The presence of strong Ir 5d component above the Fermi level indicates the depletion of 5d electrons in Ir atoms. This is further supported by the formation of Ir–Sb ionic bond by the electron localization function (ELF) analysis in Fig. 6(a)–(e).
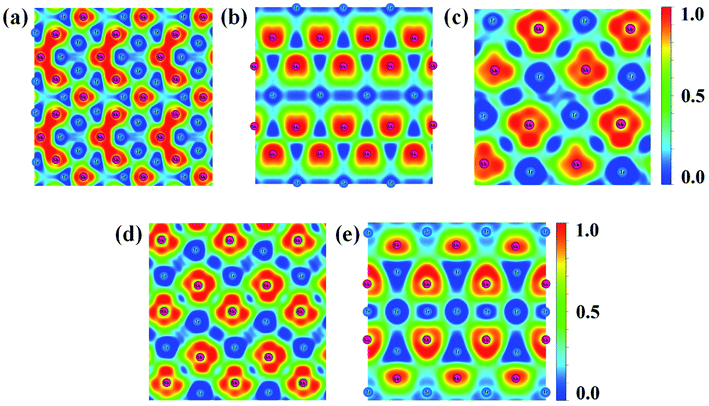 | ||
Fig. 6 Contours of the ELF for the structures of (a) IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, (b) IrSb2-I4/mmm, (c) IrSb-C2/c, (d) IrSb-P 21m, (b) IrSb2-I4/mmm, (c) IrSb-C2/c, (d) IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , and (e) Ir2Sb-Pmmn with isosurface of 0.8. , and (e) Ir2Sb-Pmmn with isosurface of 0.8. | ||
A metallic Ir–Ir behavior can be observed near 0.5 ELF value. Moreover, the ELF appears Sb trimers in IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m is illustrated in Fig. 6(a).30 The strong electron localization between Sb–Sb trimers indicates that the strong Sb–Sb covalent bonds bridged the Ir–Sb unites. The lack of electron density between Ir and Sb atom suggests extremely weak interactions between metal atoms in IrSb2-I4/mmm (Fig. 6(b)). In Fig. 6(c)–(e), the information of Ir–Sb ionic bond and the electron localization around Sb atoms are shown in the ELF analysis.
21m is illustrated in Fig. 6(a).30 The strong electron localization between Sb–Sb trimers indicates that the strong Sb–Sb covalent bonds bridged the Ir–Sb unites. The lack of electron density between Ir and Sb atom suggests extremely weak interactions between metal atoms in IrSb2-I4/mmm (Fig. 6(b)). In Fig. 6(c)–(e), the information of Ir–Sb ionic bond and the electron localization around Sb atoms are shown in the ELF analysis.
We employ the Bader charge analysis, which provides a description of electron transfer, to quantify the amount of charge belonging to each atom at different stoichiometries.31 The calculated charge amounts are 9.88 (4.56), 9.64 (4.68), 9.66 (4.34), 9.69 (4.30) and 9.43 (4.10) electron for Ir (Sb) in IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P
21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and Ir2Sb-Pmmn phases, respectively. This results reveal that the charge states of Ir and Sb atoms change with pressure-induced transition and a peculiar reverse electron donation from Sb to Ir atoms. Accordingly, in Ir–Sb system, the bond between Ir and Sb atom shows evident ionic character and a little covalent bond exists between Ir and Sb atoms at the same time.
and Ir2Sb-Pmmn phases, respectively. This results reveal that the charge states of Ir and Sb atoms change with pressure-induced transition and a peculiar reverse electron donation from Sb to Ir atoms. Accordingly, in Ir–Sb system, the bond between Ir and Sb atom shows evident ionic character and a little covalent bond exists between Ir and Sb atoms at the same time.
It is worth noting that an electronic topological transition can occur at doping, high pressure, temperature or other external reagents alter the Fermi surface of an electronic system that has significant impacts on the corresponding physical and chemical properties.32,33 Therefore, we have checked the potential pressure-induced electronic topological transition in Ir2Sb-Pmmn. As shown in Fig. 5(e), it is found that there is no band near the X point at 4.2 GPa. As the pressure increases, the band moves down and approaches to the Fermi level at point X. Fig. 5(f) clearly shows that the red band along S–X–U is not fully occupied at 8 GPa and will form a hole pocket near the Fermi surface. Current theoretical predictions suggest that an electronic topological transition occurs in the Ir2Sb-Pmmn structure.
In summary, the unbiased structure searching and density functional theory calculations are performed to explore the pressure-stabilized phases of Ir–Sb compounds under high pressure with a wide range of concentrations. Five novel phases of IrSb2-P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P
21m, IrSb2-I4/mmm, IrSb-C2/c, IrSb-P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and Ir2Sb-Pmmn were identified at high pressure. The theoretical phonon dispersion curves suggest that all these phases are dynamical stable. The calculated electronic band structures and density of states suggest that they are metallic. A pressure-induced electronic topological transition has been found in an Ir2Sb phase. Accordingly, the electronic bonding states show evident covalent character in all of these five novel phases. The Bader charge analysis reveals that prominent electrons transfer from Ir to Sb atom in these novel phases are responsible for the ionic bonding feature of these compounds. The present findings establish the pressure-composition phase diagram of Ir–Sb system and corresponding electronic properties, which offer guidance for further fundamental understanding and experimental synthesis.
and Ir2Sb-Pmmn were identified at high pressure. The theoretical phonon dispersion curves suggest that all these phases are dynamical stable. The calculated electronic band structures and density of states suggest that they are metallic. A pressure-induced electronic topological transition has been found in an Ir2Sb phase. Accordingly, the electronic bonding states show evident covalent character in all of these five novel phases. The Bader charge analysis reveals that prominent electrons transfer from Ir to Sb atom in these novel phases are responsible for the ionic bonding feature of these compounds. The present findings establish the pressure-composition phase diagram of Ir–Sb system and corresponding electronic properties, which offer guidance for further fundamental understanding and experimental synthesis.
Methods
Structure prediction
Crystal structure prediction was performed at pressures of 0–100 GPa via an unbiased swarm intelligence based CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method,34–36 which was designed to search for the most stable or metastable structures of given compounds.37–41First-principles calculations
Structural optimizations, electronic structure and phonon calculations, and molecular dynamics were performed in the framework of density functional theory (DFT). The generalized gradient approximation (GGA) expressed by the Perdew–Burke–Ernzerhof (PBE) functional42 as implemented in the Vienna Ab initio Simulation Package (VASP)43,44 was adopted. The electron–ion interaction was described by the projector augmented-wave potentials, with 5d76s2 and 5s25p3 configurations treated as valence electrons for Ir and Sb atoms are, respectively. The cutoff energy of 600 eV and Monkhorst–Pack scheme with a k-point grid of 2π × 0.03 Å−1 were adopted to obtain converged total energies (∼1 meV per atom).45,46 Phonon dispersions were calculated using the supercell approach as implemented in PHONOPY code with a displacement of 0.01 Å for all calculation. 2 × 2 × 2, 4 × 4 × 1, 1 × 2 × 2, 2 × 2 × 2, and 3 × 1 × 3 supercells were found to be large enough for obtaining the converged dynamical matrixes for the P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m, I4/mmm, C2/c, P
21m, I4/mmm, C2/c, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , and Pmmn structures, respectively.47 For both heavy elements of Ir and antimony-containing systems relativistic shifts in the electron's atomic energy levels play a significant role.48 Therefore, the spin orbital coupling (SOC) effect has been considered for the calculations of electronic band structures.
, and Pmmn structures, respectively.47 For both heavy elements of Ir and antimony-containing systems relativistic shifts in the electron's atomic energy levels play a significant role.48 Therefore, the spin orbital coupling (SOC) effect has been considered for the calculations of electronic band structures.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
Y. L. designed the research, S. L., D. Z. and Z. J. performed the calculations, Y. L., S. L., D. Z. and Z. J. analyzed the results and wrote the manuscript. All authors contributed to the discussions.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
This work was supported by the Natural Science Foundation of China (11764043, 11704044, 11504007, and 11404035) and the Natural Science Foundation of Jilin Province, Science and Technology Development Project under No. 20180101226JC.References
- S. T. Oyama, J. Solid State Chem., 1992, 96, 442–445 CrossRef CAS.
- G. D. Mahan, B. C. Sales and J. W. Sharp, Phys. Today, 1997, 50, 42–47 CrossRef CAS.
- F. J. DiSalvo, Science, 1999, 285, 703–706 CrossRef CAS PubMed.
- T. Caillat, A. Borshchevsky and J. P. Fleurial, AIP Conf. Proc., 1993, 271, 771–776 CrossRef CAS.
- G. A. Slack and V. G. Tsoukala, J. Appl. Phys., 1994, 76, 1665–1671 CrossRef CAS.
- N. N. Zhuravlev, G. S. Zhdanov and R. N. Kuz'min, Kristallografiya, 1960, 5, 553–562 Search PubMed.
- A. Kjekshus and T. Rakke, Acta Chem. Scand., Ser. A, 1977, 31, 517–529 CrossRef CAS.
- A. Kjekshus, Acta Chem. Scand., 1961, 15, 678–681 CrossRef CAS.
- F. Hulliger, Helv. Phys. Acta, 1961, 34, 782–786 CAS.
- G. S. Zhdanov and R. N. Kuz'min, Kristallografiya, 1961, 6, 872–881 CAS.
- T. Siegrist and F. Hulliger, J. Solid State Chem., 1986, 63, 23–30 CrossRef CAS.
- N. N. Zhuravlev and G. S. Zhdanov, Kristallografiya, 1956, 1, 509–513 CAS.
- K. Koga, K. Akai, K. Oshiro and M. Matsuura, 20th ICT, 2001, pp. 105–108 Search PubMed.
- U. Furst and F. Halla, Z. Phys. Chem., 1938, 40, 285–307 Search PubMed.
- T. Chen, J. C. Mikkelsen and G. B. Charlan, J. Cryst. Growth, 1978, 43, 5–12 CrossRef CAS.
- A. Kjekshus, T. Rakke and A. F. Andresen, Acta Chem. Scand., 1974, 28, 996–1000 CrossRef.
- M. Blander, G. Hagg and A. Westgren, Arkiv for kemi mineralogi och geologi B, 1935, 12, 1–6 Search PubMed.
- R. N. Kuz'min, G. S. Zhdanov and N. N. Zhuravlev, Kristallografiya, 1957, 2, 48–50 Search PubMed.
- R. N. Kuz'min, Kristallografiya, 1958, 3, 366–367 Search PubMed.
- H. Okamoto, J. Phase Equilib., 1994, 15, 640–642 CrossRef CAS.
- T. Caillat, A. Borschevsky and J. P. Fleurial, J. Alloys Compd., 1993, 199, 207–210 CrossRef CAS.
- H. Okamoto, J. Phase Equilib., 1994, 15, 567–568 CrossRef.
- S. W. Kim, Y. Kimura and Y. Mishima, J. Electron. Mater., 2004, 33, 1156–1160 CrossRef CAS.
- G. S. Nolas, D. T. Morelli and T. M. Tritt, Annu. Rev. Mater. Sci., 1999, 29, 89–116 CrossRef CAS.
- G. Chen, M. S. Dresselhaus, G. Dresselhaus, J. P. Fleurial and T. Caillat, Int. Mater. Rev., 2003, 48, 45–66 CrossRef CAS.
- X. X. Yang, Z. H. Dai, Y. C. Zhao, W. C. Niu, J. Y. Liu and S. Meng, Phys. Chem. Chem. Phys., 2019, 21, 851–858 RSC.
- S. Y. Lin, M. L. Xu, J. Hao, X. L. Wang, M. Wu, J. M. Shi, W. W. Cui, D. Liu, W. W. Lei and Y. W. Li, J. Mater. Chem. C, 2019, 7, 4527–4532 RSC.
- C. Wang, Y. X. Liu, X. Chen, P. Lv, H. R. Sun and X. B. Liu, Chin. Phys. Lett., 2020, 37, 026201–026205 CrossRef.
- S. Q. Jiang, X. Yang, X. L. Huang, Y. P. Huang, X. Li and T. Cui, Chin. Phys. Lett., 2020, 37, 016302–016306 Search PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- D. Zhou, Q. Li, Y. M. Ma, Q. L. Cui and C. F. Chen, J. Phys. Chem. C, 2013, 117, 12266–12271 CrossRef CAS.
- X. J. Ma, X. Li, D. Zhou, J. Xu, W. Q. Gao and Y. H. Liu, J. Alloys Compd., 2019, 791, 1257–1262 CrossRef CAS.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116–094124 CrossRef.
- H. Wang, Y. C. Wang, J. Lv, Q. Li, L. J. Zhang and Y. M. Ma, Comput. Mater. Sci., 2016, 112, 406–415 CrossRef CAS.
- C. Y. Zhu, X. Qu, M. Zhang, J. Y. Wang, Q. Li, Y. Geng, Y. M. Ma and Z. M. Su, J. Mater. Chem. A, 2019, 7, 13356–13363 RSC.
- G. T. Zhang, R. Gao, Y. R. Zhao, T. T. Bai and Y. F. Hu, J. Alloys Compd., 2017, 723, 802–810 CrossRef CAS.
- X. Q. Song, K. T. Yin, Y. C. Wang, A. Hermann, H. Y. Liu, J. Lv, Q. Li, C. F. Chen and Y. M. Ma, J. Phys. Chem. Lett., 2019, 10, 2761–2766 CrossRef CAS PubMed.
- Q. Li, D. Zhou, W. T. Zheng, Y. M. Ma and C. F. Chen, Phys. Rev. Lett., 2013, 110, 136403–136407 CrossRef PubMed.
- D. Zhou, Q. Li, W. T. Zheng, Y. M. Ma and C. F. Chen, Phys. Chem. Chem. Phys., 2017, 19, 4560–4566 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafnerr, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Hafnerr, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- D. Thirumalai, R. W. Hall and B. J. Berne, J. Chem. Phys., 1984, 81, 2523–2527 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106–134115 CrossRef.
- G. Y. Gao, R. Hoffmann, N. W. Ashcroft, H. Y. Liu, A. Bergara and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 184104–184117 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |