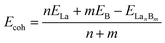Perfect cubic La-doped boron clusters La₆&[La@B₂₄]^+/0 as the embryos of low-dimensional lanthanide boride nanomaterials

Abstract

La-doped boron nanoclusters have received considerable attention due to their unique structures and bonding. Inspired by recent experimental observations of the inverse sandwich D_8h La₂B₈ (1) and triple-decker C_2v La₃B₁₄⁻ (2) and based on extensive global searches and first-principles theory investigations, we present herein the possibility of the perfect cubic La-doped boron clusters O_h La₆&[La@B₂₄]⁺ (3, ¹A_1g) and O_h La₆&[La@B₂₄] (4, ²A_2g) which appear to be the embryos of the metallic one-dimensional La₁₀B₃₂ (5) nanowire, two-dimensional La₃B₁₀ (6) nanosheet, and three-dimensional LaB₆ (7) nanocrystal, facilitating a bottom-up approach to build cubic lanthanide boride nanostructures from gas-phase clusters. Detailed molecular orbital and bonding analyses indicate that effective (d–p)σ, (d–p)π and (d–p)δ covalent coordination interactions exist in La₆&[La@B₂₄]^+/0 (3/4) clusters, while the 1D La₁₀B₃₂ (5), 2D La₃B₁₀ (6), and 3D LaB₆ (7) crystals exhibit mainly electrostatic interactions between the trivalent La centers and cubic B₂₄ frameworks, with weak but discernible coordination contributions from La (5d) ← B (2p) back-donations. The IR and Raman spectra of La₆&[La@B₂₄]^+/0 (3/4) and band structures of La₁₀B₃₂ (5) and La₃B₁₀ (6) are computationally simulated to facilitate their future characterizations.

---

1. Introduction

As a prototypical electron-deficient element next to carbon in the periodical table, boron has a rich chemistry characterized with delocalized multicenter-two-electron (mc-2e) bonds in both bulk allotropes and polyhedral molecules.¹ Boron-based materials have found wide applications in field emissions, supercapacitors, optical absorptions, photodetectors, and etc.^2–6 A bottom-up approach has received considerable attention in the past two decades to investigate the structural transitions from small boron nanoclusters to boron nanomaterials. Persistent joint photoelectron spectroscopy (PES) and first-principles theory investigations in the past two decades by Wang and coworkers have unveiled an unexpectedly rich landscape for size-selected boron clusters from planar or quasi-planar B_n^−/0 (n = 3–38, 41 and 42) to cage-like borospherenes D_2d B₄₀^−/0 and C₃/C₂ B₃₉⁻. Multiple low-lying isomers appear to compete and coexist in most gas-phase boron B_n^−/0 clusters, starting from n = 7.^7–10 Ion-mobility measurements in combination with density functional theory (DFT) calculations, on the other hand, have shown that boron cluster monocations (B_n⁺) possess double-ring tubular structures in the size range between n = 16–25,¹¹ unveiling another structural domain for boron nanoclusters. Transition-metal-doping has proven to induce dramatic structural and bonding pattern changes to boron clusters. Typical examples include the transition-metal-centered monocyclic boron wheel clusters M@B_n (Co@B₈⁻, Ru@B₉⁻, and Ta@B₁₀⁻) with the maximum planar coordination number of CN = 10 and transition-metal-centered boron double-ring tubular clusters M@B_n⁻ (Co@B₁₆⁻, Rh@B₁₈⁻, and Ta@B₂₀⁻) with the record tubular coordination number of CN = 20 known in experiments.^12–18 A family of inverse sandwich di-lanthanide boron complexes D_7h La₂B₇⁻, D_8h La₂B₈ (1), and D_9h La₂B₉⁻ with a perfect B_n ring (n = 7, 8, 9) sandwiched between two La atoms were observed in 2018 in PES measurements.^19,20 The first inverse triple-decker di-lanthanide boron cluster C_2v La₃B₁₄⁻ (2) was discovered in 2019 in a joint experimental and theoretical investigation²¹ in which two conjoined La₂B₈ (1) inverse sandwiches share a B–B edge and a La vertex in the titled La–B₈–La–B₈–La motif. Boron clusters as typical Wankel motor molecules with fluxional bonds also exhibit structural fluxionalities where metal dopants play an important role.^22–25 Our group very recently predicted the possibility of the inverse sandwich double-ring tubular molecular rotor C_2h La₂&[B₂@B₁₈] which possesses the smallest core–shell structure reported in boron clusters.²⁶

Bulk lanthanide hexaboride LaB₆ (7) has been widely used as cathode materials due to its numerous excellent properties such as low work function, ultrahigh hardness, high chemical inertness, and high melting point.^27–30 It possesses a typical cubic CaB₆-type lattice (Pm3̄m, O_h¹) characterized with a 3D network constituted of B₆ octahedrons, with the interstitial locations filled by trivalent La atoms.³¹ Interestingly, each unit cell in LaB₆ (7) contains a B₂₄ cubic framework which possesses six equivalent B₈ rings on the surface sharing twelve B–B dumb-bells on the edges, with each B₈ ring sandwiched between two neighboring La atoms. The strong structural similarity between the gas-phase inverse sandwich La₂B₈ (1) complex and cubic three-dimensional (3D) LaB₆ (7) crystal has been previously noticed.³¹ LaB₆ nanowires in cubic LaB₆ (7) lattice were also recently confirmed to be active electrochemical materials for supercapacitors.³² However, a cubic embryo of the LaB₆ (7) lattice still remains unknown to date in a bottom-up approach starting from gas-phase clusters. Such a cubic embryo may also be used to form one-dimensional (1D) lanthanide boride nanowires and two-dimensional (2D) lanthanide boride nanosheets.

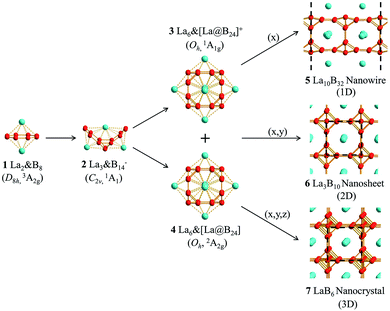
Keep the inspiration in mind and based on extensive global minimum (GM) searches and first-principles theory calculations, we predict herein the highly stable perfect cubic La-doped boron clusters O_h La₆&[La@B₂₄]⁺ (3, ¹A_1g) and O_h La₆&[La@B₂₄] (4, ²A_2g) which consist of six equivalent La₂B₈ (1) inverse sandwiches embedded in a cube sharing one La atom at center. More interestingly, La₆&[La@B₂₄]^+/0 (3/4) clusters with a B₂₄ framework turn out to be the cubic embryos of the metallic 1D La₁₀B₃₂ (5) nanowire, 2D La₃B₁₀ (6) nanosheet, and 3D LaB₆ (7) nanocrystal in a bottom-up approach. The newly obtained ferromagnetic 1D La₁₀B₃₂ (5) and nonmagnetic 2D La₃B₁₀ (6) are expected to serve as efficient electronical and optical nanomaterials.

2. Theoretical procedure

Extensive GM searches were performed on La₇B₂₄⁺ monocation using the TGmin2 code³³ at the DFT level, in combination with manual structural constructions based on the experimentally observed La₂B₈ (1) and La₃B₁₄⁻ (2). Over 3000 trial structures were explored in both singlet and triplet states at PBE/TZVP. The low-lying isomers were then fully optimized at the PBE0 (ref. 34) and TPSSh³⁵ levels with the 6-311+G* basis set³⁶ for B and Stuttgart relativistic small-core pseudopotential for La^37,38 using the Gaussian 09 program suite.³⁹ Low-lying isomers of the open-shell neutral La₇B₂₄ were obtained from the corresponding lowest-lying structures of La₇B₂₄⁺.

The GM search on 1D La₁₀B₃₂ (5) was performed with the EOU program developed by our group.⁴⁰ A GM search based on the PSO technique implemented in the widely used Particle Swarm Optimization (CALYPSO)⁴¹ package was executed for 2D La₃B₁₀ (6). The calculations on 1D La₁₀B₃₂ (5), 2D La₃B₁₀ (6), and 3D LaB₆ (7) nanostructures were performed using the Vienna ab initio simulation package (VASP),^42,43 within the framework of projector augmented wave (PAW) pseudopotential method^44,45 and PBE generalized gradient approximation (GGA).^46,47 The Coulomb-corrected local spin-density approximation (LSDA+U) was utilized for both structural relaxation and static calculation (U = 5 eV).^31,48 The cutoff energy of the plane wave basis is set to 500 eV. Atomic structures are fully relaxed using the conjugate gradient method until the maximum force on each atom was less than 0.01 eV Å⁻¹ and the energy precision was set to 10⁻⁵ eV. Chemical bonding analyses were performed for La₆&[La@B₂₄]⁺ (3) using the adaptive natural density partitioning (AdNDP) approach at the PBE0 level^49,50 and for 3D LaB₆ (7) crystal utilizing the solid-state AdNDP (SSAdNDP) method.^51,52 Natural bonding orbital (NBO) analyses were performed on La₇B₂₄⁺ (3) using the NBO 6.0 program.⁵³ Born–Oppenheimer molecular dynamics (BOMD) simulations were performed on La₇B₂₄⁺ (3) for 30 ps at 300 K and 1000 K using the CP2K software package.⁵⁴

3. Results and discussions

3.1 Structures and stabilities

Starting from the experimentally observed C_2v La₃B₁₄⁻ (2) which possesses a tilted La–B₈–La–B₈–La inverse triple-decker structure with two conjoined B₈ rings sharing a B–B dumb-bell, we manually constructed the perfect cubic hepta-lanthanide-doped boron clusters O_h La₆&[La@B₂₄]⁺ (3, ¹A_1g) and O_h La₆&[La@B₂₄] (4, ²A_2g) from two C_2v La₃B₁₄⁻ (2) clusters which share two B–B dumb-bells on the edges and one La atom at the center, with two extra La atoms added on the top and bottom, respectively. With one La atom endohedrally coordinated at the center (@) and six La atoms exohedrally coordinated on the surface (&), O_h La₆&[La@B₂₄]^+/0 (3/4) can be viewed as consisting of six equivalent La₂B₈ (1) inverse sandwiches embedded in a cube sharing twelve B–B dumb-bells on the edges and one La vertex at the center. Interestingly and encouragingly, as shown in Fig. S1 and S2,† extensive GM searches strongly suggest that the highly stable perfect cubic La₆&[La@B₂₄]⁺ (3) and La₆&[La@B₂₄] (4) with a B₂₄ framework be the well-defined GMs of the systems with the lowest vibrational frequencies of 111 cm⁻¹ and 112 cm⁻¹, respectively. La₆&[La@B₂₄]^+/0 (3/4) possess the optimized La–B distances of r_La–B = 2.94/2.95 Å between the central La atom and its cubic B₂₄ ligand and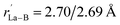 between the surface La atoms and their neighboring B₈ ligands on the surface, with the B–B distances of r_B–B = 1.67/1.67 Å within the B–B dumb-bells on the edges and 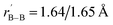within the B₃ triangles at the corners. The large HOMO–LUMO gap of ΔE_gap = 2.35 eV calculated for La₆&[La@B₂₄]⁺ (3) well supports its high chemical stability. As shown in Fig. S1,† its second lowest-lying triplet C₁ La₆&[La@B₂₄]⁺ (³A) which is slightly distorted (with r_La–B = 2.93–2.95 Å and ) due to Jahn–Teller effect lies 1.30 and 1.36 eV higher than the O_h GM in energy at PBE0 and TPSSH levels, respectively. Both the distorted cubic quintet and heptet isomers with the relative energies of 2.50 eV and 3.53 eV at PBE0, respectively, appear to be much less stable (Fig. S1†). Extensive molecular dynamics simulations indicate that La₆&[La@B₂₄]⁺ (3) is also highly dynamically stable, with the calculated average root-mean-square-deviations of RMSD = 0.12 Å and maximum bond length deviations of MAXD = 0.38 Å at 1000 K. Similar situation exists in La₆&[La@B₂₄] (4). La₆&[La@B₂₄]^+/0 (3/4) are therefore the well-defined deep-lying GMs of the systems highly stable both thermodynamically and dynamically.

We initially constructed a 1D La₅B₁₆ nanowire (P4/mmm) (Fig. S3†) by extending the finite La₆&[La@B₂₄]^+/0 (3/4) clusters periodically in one direction (x), resulting in a 1D nanowire with one small imaginary phonon frequency at 49i cm⁻¹. This imaginary phonon frequency corresponds to a typical Peierls phase transition which leads to the slightly more stable 1D La₁₀B₃₂ nanowire (5, P4/mmm) (by 0.07 eV) when the unit cell is doubled in size, with the two La atoms inside slightly off-centered by 0.22 Å (Fig. 1). Similarly, 2D La₃B₁₀ (6) (P4/mmm) and 3D LaB₆ (7) (Pm3̄m) networks can be obtained by expanding La₆&[La@B₂₄]^+/0 (3/4) periodically in (x, y) and (x, y, z) directions, respectively (Fig. 1). The 1D (5), 2D (6), and 3D (7) networks possess the optimized lattice parameters of a = 8.66 Å, a = b = 4.17 Å and a = b = c = 4.16 Å at PBE level, respectively. Our calculated lattice parameters and La–B distance (r_La–B = 3.06 Å) for 3D LaB₆ (7) agree well with the corresponding experimentally measured values of a = b = c = 4.16 Å and r_La–B = 3.05 Å.³¹ The newly obtained 2D La₃B₁₀ (6) possesses the optimized La–B distances of r_La–B(x) = r_La–B(y) = 3.05 Å and r_La–B(z) = 3.07 Å between the central La atom and its B₂₄ cubic ligand. Similar La–B distances exist in 1D La₁₀B₃₂ (5). These La–B distances turn out to be slightly longer than the corresponding La–B coordination bond lengths of r_La–B = 2.94/2.95 Å in La₆&[La@B₂₄]^+/0 (3/4) clusters. Interestingly, as shown in Fig. S4 and S5,† 1D La₁₀B₃₂ (5) has the lowest cohesive energy among the 1D structures obtained via extensive EOU global searches, while La₃B₁₀ (6) is the lowest-lying structure in all the 2D La₃B₁₀ conformations probed by extensive PSO global searches, with the second lowest-lying 1D and 2D structures lying 3.13 eV and 1.88 eV higher in cohesive energy per unit cell than La₁₀B₃₂ (5) and La₃B₁₀ (6), respectively. 1D La₁₀B₃₂ (5) and 2D La₃B₁₀ (6) are thus strongly favored in thermodynamics compared with their other low-lying counterparts.

Fig. 1 Optimized structures of inverse sandwich D_8h La₂&B₈ (1), inverse triple-decker C_2v La₃@B₁₄⁻ (2), cubic O_h La₆&[La@B₂₄]⁺ (3), cubic O_h La₆&[La@B₂₄] (4), 1D La₁₀B₃₂ nanowire (5), 2D La₃B₁₀ nanosheet (6), and 3D LaB₆ nanocrystal (7).

To evaluate the relative stability of 1D La₁₀B₃₂ (5), 2D La₃B₁₀ (6), and 3D LaB₆ (7) networks, we computed their average cohesive energy per atom

where E_La, E_B, and E_LanBm are the total energies of a single La atom, a single B atom, and a unit cell of the La_nB_m lattices and n and m are the numbers of La and B atoms, respectively. La₁₀B₃₂ (5), La₃B₁₀ (6), and LaB₆ (7) appear to have the calculated cohesive energies of E_coh = 6.33, 6.50 and 6.95 eV per atom, respectively. These values appear to be systematically higher than the corresponding cohesive energy per atom of E_coh = 5.65 eV calculated for neutral embryo La₆&[La@B₂₄] (4).

3.2 Electronic structures and bonding patterns

The high stabilities of these cubic lanthanide boride nanostructures can be traced back to their unique electronic structures and bonding patterns. Detailed NBO analyses on closed-shell La₆&[La@B₂₄]⁺ (3) show that the central La atom possesses the natural atomic charge of q_La = −0.50|e|, electronic configuration of La[Xe]4f^0.185d^3.046s^0.24, and total Wiberg bond order of WBI_La = 5.26, while the six surface La atoms have the natural atomic charge of q_La = +1.43|e|, electronic configuration of La[Xe]4f^0.155d^1.416s^0.10, and total Wiberg bond order of WBI_La = 2.86. Obviously, both the central and surface La atoms in La₆&[La@B₂₄]⁺ (3) donate their 6s² electrons almost completely to the B₂₄ cubic ligand and there exists an effective La 5d ← B 2p back-donation from the cubic B₂₄ ligand to the central La atom. Especially, the central La atom with the 5d occupation of 5d^3.04 has a much higher total La–B coordination bond order (5.26) than that of the partially coordinated surface La atoms (2.86) with the 5d occupation of 5d^1.41. Obvious La–B coordination interaction with the average La–B bond order of WBI_La–B = 0.22 exists between the central La and its 24 equivalent B ligands in La₆&[La@B₂₄]⁺ (3). The La coordination centers in inverse sandwich La₂&B₈ (1) and La₃@B₁₄⁻ (2) possess the net atomic charges of q_La = +1.29, +1.39/1.17|e|, electronic configurations of La[Xe]4f^0.175d^1.496s^0.10, La[Xe]4f^0.13/0.165d^1.37/1.636s^0.11/0.11, and total Wiberg bond orders of WBI_La = 2.87, 2.88/3.08, repectively, similar to the situation in the six surface La atoms in La₆&[La@B₂₄]⁺ (3). Detailed molecular orbital (MO) analyses indicate that all the occupied orbitals of the closed-shell La₆&[La@B₂₄]⁺ (3) are effective bonding MOs, while its lowest unoccupied MO (LUMO, (a_2g)) is basically an anti-bonding orbital mainly originated from the 5d atomic orbitals of the six surface La atoms (Fig. S6†). With a valence electron occupying the non-degenerate LUMO (a_2g) of La₆&[La@B₂₄]⁺ (3), neutral La₆&[La@B₂₄] (4) possesses a singly occupied highest occupied MO (SOMO (a_2g)). Such an electron occupation helps maintain the O_h symmetry of the open-shell neutral which possesses the same geometry as La₆&[La@B₂₄]⁺ (3).

To better understand the bonding nature and stabilization mechanism, we performed a detailed AdNDP bonding analysis on the closed-shell La₆&[La@B₂₄]⁺ (3) which recovers both the localized and delocalized bonds of the system. As clearly indicated in Fig. 2a, La₆&[La@B₂₄]⁺ (3) possesses 12 equivalent 2c-2e B–B σ bonds on twelve B–B dumb-bells with the occupation number of ON = 1.78|e| and 8 equivalent 3c-2e σ bonds over eight B₃ triangles at the corners of the cube with ON = 1.83|e|, forming the σ-skeleton on the cubic B₂₄ ligand. The remaining 26 delocalized bonds are mainly responsible for the La–B coordination interactions in the complex, including 6 10c-2e B₈(σ)–La₂(d_σ) bonds, 12 10c-2e B₈(σ)–La₂(d_π) bonds, and 6 10c-2e B₈(π)–La₂(d_δ) bonds with ON = 1.72–1.90|e| on six equivalent conjoined La₂B₈ (1) inverse sandwiches embedded in the cube and 2 31c-2e B₂₄(π)–La₇(d_σ) bonds totally delocalized over the whole molecule with ON = 2.00|e| (Fig. 2a, see Fig. S7† for more details). Overall, cubic La₆&[La@B₂₄]⁺ (3) has similar (d–p)σ, (d–p)π, and (d–p)δ coordination interactions with that of observed inverse sandwich La₂B₈ (1) and triple-decker La₃B₁₄⁻ (2).^19–21 The bonding pattern presented above provides further evidence that all the occupied MOs of La₆&[La@B₂₄]⁺ (3) are intrinsically bonding MOs (Fig. S6†), while all its antibonding MOs remain empty. Such a unique electron occupation renders an exceptionally high stability to the monocation.

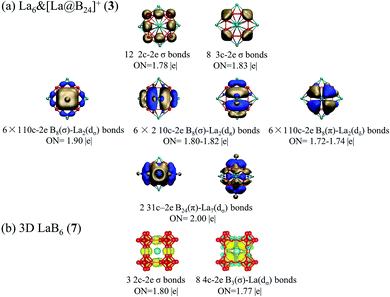Fig. 2 AdNDP bonding patterns of (a) La₆&[La@B₂₄]⁺ (3) cluster and (b) 3D LaB₆ (7) crystal, with the occupation numbers (ONs) indicated. Each 10c-2e B₈–La₂ bond in the second row represents six equivalent La–B₈–La coordination bonds, as detailed in the ESI in Fig. S7.†

We also performed a detailed SSAdNDP analysis on the periodical 3D LaB₆ (7) cubic lattice in Fig. 2b. There are 3 equivalent 2c-2e B–B σ bonds on three B–B dumb-bells in the cubic unit cell with ON = 1.80|e| which correspond to the 12 2c-2e B–B σ bonds on the B₂₄ ligand in La₆&[La@B₂₄]⁺ (3). The remaining 8 equivalent 4c-2c B₃(σ)–La(d_σ) bonds between the central La atom and the eight B₃ triangles at the corners with ON = 1.77|e| represent mainly electrostatic interactions between the trivalent La center and B₂₄ cubic framework, with weak but discernible coordination contributions from La (5d) ← B (2p) back-donations (Fig. 2b). Similar bonding patterns exist in 1D La₁₀B₃₂ (5) and 2D La₃B₁₀ (6). Detailed Bader charge analyses⁵⁵ indicate that the central La atom in LaB₆ (7) carries the net atomic charges of q_La = +1.71|e|, with its B neighbors possessing the average atomic charge of q_B = −0.29|e|. The formation of rare earth (RE) boride crystals REB₆ in infinite lattices involve an obvious electron transfer from the trivalent RE centers to the boron sublattice. 1D (5), 2D (6), and 3D (7) nanocrystals with the elongated La–B distances of r_La–B(z) = 3.05–3.07 Å possess obviously weaker La–B covalent coordination interactions than that in La₆&[La@B₂₄]^+/0 (3/4) clusters which have the La–B coordination distances of r_La–B = 2.94–2.95 Å. The size of the trivalent RE atoms, rather than their electron configuration, is the main factor responsible for their boride structures.⁵⁶

The calculated band structures and corresponding projected density of states (PDOS) of 1D La₁₀B₃₂ (5) and 2D La₃B₁₀ (6) nanostructures are depicted in Fig. 3. Notably, these nanostructures all appear to be metallic in nature. Both 2p orbitals from B atoms and 5d orbitals from La centers contribute to the calculated PDOS near the Fermi level, with La-5d orbitals making major contributions to the PDOS above the Fermi level, while B-2p orbitals dominating the PDOS below the Fermi level. Both spin unpolarized and spin-polarized computations were carried out to determine the ground states for these nanomaterials during the structural optimizations. 1D La₁₀B₃₂ (5) network turned out to be a ferromagnetic metal with the total magnetic moment of 2.03 μ_B per unit cell which mainly originates from the surface La atoms (with each surface La carrying the magnetic moment of 0.12 μ_B, while each central La carrying the magnetic moment of only 0.008 μ_B). In contrast, both 2D La₃B₁₀ (6) and 3D LaB₆ (7) are nonmagnetic in nature with the calculated magnetic moments of zero.

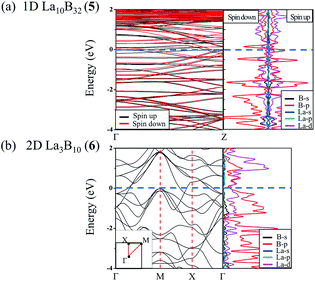Fig. 3 Calculated band structures and projected densities of states (PDOS) of (a) 1D La₁₀B₃₂ (5) and (b) 2D La₃B₁₀ (6) using the PBE functional.

3.3 Simulated IR and Raman spectra of the La₆&[La@B₂₄]⁺ embryo

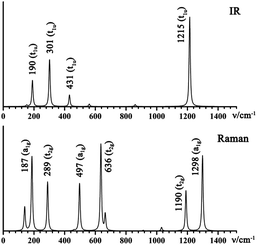
Infrared photodissociation (IR-PD) in combination with first-principles theory calculations has proven to be a powerful means to characterize novel gas-phase clusters.^57,58 We computationally simulate the IR and Raman spectra of the closed-shell La₆&[La@B₂₄]⁺ (3) in Fig. 4a to facilitate its future experimental characterizations. The high-symmetry O_h La₆&[La@B₂₄]⁺ possesses relatively simple vibrational spectra, with sharp asymmetrical IR vibrations at 190 (t_1u), 301 (t_1u), 431 (t_1u), and 1215 (t_1u) cm⁻¹ and symmetrical Raman features at 187 (a_1g), 289 (t_2g), 497 (a_1g), 636 (t_2g), 1190 (t_2g) and 1298 (a_1g) cm⁻¹, respectively. The strong Raman peaks at 187 cm⁻¹ and 497 cm⁻¹ mainly represent the typical radial breathing modes (RBMs) (a_1g) of the six evenly distributed surface La atoms and the B₂₄ cubic framework, respectively. Such RBM spectral features can be used to characterize hollow boron structures.⁵⁹ As shown in Fig. S8,† similar but slightly more complicated IR and Raman spectra are obtained for the open-shell neutral La₆&[La@B₂₄] (4).

Fig. 4 Simulated IR and Raman spectra of O_h La₆&[La@B₂₄]⁺ (3) at PBE0/6-311+G(d) level.

4. Conclusions

Based on extensive GM searches and first-principles theory calculations, we have predicted in this work the highly stable perfect cubic O_h La₆&[La@B₂₄]^+/0 (3/4) which are the embryos of the metallic 1D La₁₀B₃₂ (5) nanowire, 2D La₃B₁₀ (6) nanosheet, and 3D LaB₆ (7) nanocrystal, building a bridge between gas-phase lanthanide boride clusters and their low-dimensional nanomaterials. La₆&[La@B₂₄]^+/4 (3/4) clusters and 1D (5), 2D (6), and 3D (7) nanocrystals exhibit strong similarities in structures, with the periodical nanostructures possessing obviously weaker La (5d) ← B (2p) back-donations than their cubic embryos. Using the commercially available 3D LaB₆ (7) as target, it is possible to synthesize the newly predicted 0D (3/4), 1D (5), and 2D (6) nanomaterials by laser ablations, chemical vaporizations, or arc-discharges. The construction strategy demonstrated in this work may be applicable to the design of more rare-earth boride nanomaterials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (21720102006 to S.-D. Li, 11504213 to Y.-W. Mu, and 21803037 to W.-Y. Zan).

Notes and references

1. F. A. Cotton, G. Wilkinson, C. A. Murrillo and M. Bochmann, Advanced Inorganic Chemistry, Wiley, New York, 6th edn, 1999.
2. J. Q. Xu, G. H. Hou, H. Q. Li, T. Y. Zhai, B. P. Dong, H. L. Yan, Y. R. Wang, B. H. Yu, Y. Bando and D. Golberg, NPG Asia Mater., 2013, 5, e53.
3. A. Sussardi, T. Tanaka, A. U. Khan, L. Schlapbach and T. Mori, J. Materiomics, 2015, 1, 196.
4. G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506.
5. S. Carenco, D. Portehault, C. Boissière, N. Mézailles and C. Sanchez, Chem. Rev., 2013, 113, 7981.
6. Y. Tian, Z. k. Guo, T. Zhang, H. J. Lin, Z. J. Li, J. Chen, S. Z. Deng and F. Liu, Nanomaterials, 2019, 9, 538.
7. Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754.
8. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727.
9. H. Bai, T. T. Chen, Q. Chen, X. Y. Zhao, Y. Y. Zhang, W. J. Chen, W. L. Li, L. F. Cheung, B. Bai, J. Cavanagh, W. Huang, S. D Li, J. Li and L. S. Wang, Nanoscale, 2019, 11, 23286.
10. T. Jian, X. N. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550.
11. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503.
12. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165.
13. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101.
14. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350.
15. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
16. T. Jian, W. L. Li, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Chem. Sci., 2016, 7, 7020.
17. W. L. Li, T. Jian, X. Chen, H. R. Li, T. T. Chen, X. M. Luo, S. D. Li, J. Li and L. S. Wang, Chem. Commun., 2017, 53, 1587.
18. T. Heine and G. Merino, Angew. Chem., Int. Ed., 2012, 51, 4275.
19. W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972.
20. T. T. Chen, W. L. Li, J. Li and L. S. Wang, Chem. Sci., 2019, 10, 2534.
21. T. T. Chen, W. L. Li, W. J. Chen, J. Li and L. S. Wang, Chem. Commun., 2019, 55, 7864.
22. S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732.
23. L. Liu, D. Moreno, E. Osorio, A. C. Castro, S. Pan, P. K. Chattaraj, T. Heinea and G. Merino, RSC Adv., 2016, 6, 27177.
24. G. Martínez-Guajardo, J. L. Cabellos, A. Díaz-Celaya, S. Pan, R. Islas, P. K. Chattaraj, T. Heine and G. Merino, Sci. Rep., 2015, 5, 11287.
25. M. Yan, H. R. Li, X. Y. Zhao, X. Q. Lu, Y. W. Mu, H. G. Lu and S. D. Li, J. Comput. Chem., 2019, 40, 966.
26. X. Q. Lu, Q. Chen, X. X. Tian, Y. W. Mu, H. G. Lu and S. D. Li, Nanoscale, 2019, 11, 21311.
27. C. H. Chen, T. Aizawa, N. Iyi, A. Sato and S. Otani, J. Alloys Compd., 2004, 366, L6.
28. H. Zhang, J. Tang, J. S. Yuan, J. Ma, N. Shinya, K. Nakajima, H. Murakami, T. Ohkubo and L. C. Qin, Nano Lett., 2010, 10, 3539.
29. S. S. Ordanyan, S. V. Vikhman, D. D. Nesmelov, D. P. Danilovich and I. B. Panteleev, Adv. Sci. Technol., 2014, 89, 47.
30. H. Zhang, J. Tang, L. Zhang, B. An and L. C. Qin, Appl. Phys. Lett., 2008, 92, 173121.
31. W. L. Li, C. Ertural, D. Bogdanovski, J. Li and R. Dronskowski, Inorg. Chem., 2018, 57, 12999.
32. Q. Xue, Y. Tian, S. Z. Deng, Y. Huang, M. S. Zhu, Z. X. Pei, H. F. Li, F. Liu and C. Y. Zhi, Mater. Today Energy, 2018, 10, 28.
33. X. Chen, Y. F. Zhao, Y. Y. Zhang and J. Li, J. Comput. Chem., 2019, 40, 1105.
34. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
35. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
36. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
37. D. Feller, J. Comput. Chem., 1996, 17, 1571.
38. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045.
39. M. J. Frisch, et al., Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009.
40. F.-W. Mu, A global search code based on exhaustible operations of units, 2020, to be published.
41. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
42. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
44. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
45. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
48. V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929.
49. N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590.
50. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580.
51. B. D. Dunnington and J. R. Schmidt, J. Chem. Theory Comput., 2012, 8, 1902.
52. T. R. Galeev, B. D. Dunnington, J. R. Schmidt and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2013, 15, 5022.
53. P. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, 2013.
54. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103.
55. G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354.
56. J. Etourneau and P. Hagenmuller, Philos. Mag. B, 1985, 52, 589.
57. G. Wang, M. Zhou, J. T. Goettel, G. J. Schrobilgen, J. Su, J. Li, T. Schloder and S. Riedel, Nature, 2014, 514, 475.
58. M. R. Fagiani, X. W. Song, P. Petkov, S. Debnath, S. Gewinner, W. Schcllkopf, T. Heine, A. Fielicke and K. R. Asmis, Angew. Chem., Int. Ed., 2016, 56, 501.
59. D. Ciuparu, R. F. Klie, Y. M. Zhu and L. Pfefferle, J. Phys. Chem. B, 2004, 108, 39.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01616k

---