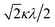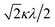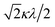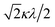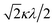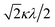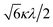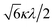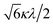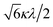Open Access Article
Open Access ArticleDetailed magnetic analysis and successful deep-neural-network-based conformational prediction for [VO(dmso)5][BPh4]2†
Hiroshi Sakiyama *a,
Takaaki Abikoa,
Kosuke Yoshidaa,
Kaoru Shomuraa,
Ryoji Mitsuhashi
*a,
Takaaki Abikoa,
Kosuke Yoshidaa,
Kaoru Shomuraa,
Ryoji Mitsuhashi b,
Yoshiki Koyamac,
Masahiro Mikuriya
b,
Yoshiki Koyamac,
Masahiro Mikuriya c,
Masayuki Koikawa
c,
Masayuki Koikawa d and
Minoru Mitsumi
d and
Minoru Mitsumi e
e
aDepartment of Science, Faculty of Science, Yamagata University, 1-4-12 Kojirakawa, Yamagata 990-8560, Japan. E-mail: saki@sci.kj.yamagata-u.ac.jp; Tel: +81 23 628 4601
bInstitute of Liberal Arts and Science, Kanazawa University, Kakuma, Kanazawa 920-1192, Japan
cDepartment of Applied Chemistry for Environment, School of Science and Technology, Kwansei Gakuin University, Gakuen 2-1, Sanda 669-1337, Japan
dDepartment of Chemistry and Applied Chemistry, Graduate School of Science and Engineering, Saga University, 1 Honjo-machi, Saga, Saga 840-8502, Japan
eDepartment of Chemistry, Okayama University of Science, 1-1 Ridaicho, Kita-ku, Okayama, Okayama 700-0005, Japan
First published on 6th March 2020
Abstract
Pentakis(dimethylsulfoxide-κO)oxidovanadium(IV) bis(tetraphenylborate), [VO(dmso)5][BPh4]2 (dmso: dimethylsulfoxide), was synthesized, and its pseudo-C4 VO6 coordination geometry was revealed by a single-crystal X-ray method. A novel equation set was obtained for magnetic susceptibility and magnetization of the d1 complexes, considering the axial distortion and the spin–orbit coupling for the 2D free-ion term. The equation set enabled magnetic simulation for significantly symmetry-lowered d1 complexes to obtain the anisotropic g-values and also the excitation energies. In addition, conformational prediction was conducted, using the enumeration results on the basis of the group theory. The dominant conformers were predicted on the basis of the density functional theory (DFT) method, and especially, the conformer in the crystal was successfully predicted by a deep neural network method.
Introduction
Magnetic susceptibility and magnetization are fundamental physicochemical properties that need to be interpreted based on an appropriate theoretical model. Magnetic data, however, are sometimes too difficult to be simulated, especially when the orbital angular momentum remains unquenched. In the case of metal complexes of cubic symmetry, the orbital angular momentum remains when the ground term belongs to the T irreducible representation. The magnetic theory was established for the T-ground-term complexes;1–3 however, it doesn't work well when the distortion from the cubic symmetry is large. To solve this problem, the most important thing is to consider the excited terms that will influence when the symmetry is lowered. In this study, a new theoretical equation set was obtained for the simplest T-term, 2T2 term, considering also the excited 2E term. The theoretical equation set is expected to work universally for any degree of distortion. Deriving such theoretical equations, considering the excited term, is expected to enable the magnetic analysis for all metal complexes in the future, clarifying the ground states experimentally.Octahedral metal complexes with the T-term ground state are expected to exhibit significant magnetic anisotropy originate from small distortion, due to the spin–orbit coupling. On the other hand, too large distortion causes a split of the T-term to afford a non-T-term ground state, diminishing the significant magnetic anisotropy. The novel magnetic equation set, derived in this study, can be universally used for both large and small distortion for the 2T2-ground-term complexes. Moreover, the novel equation set can relate the magnetic data, the electron spin resonance (ESR) data, and the electronic spectral data.
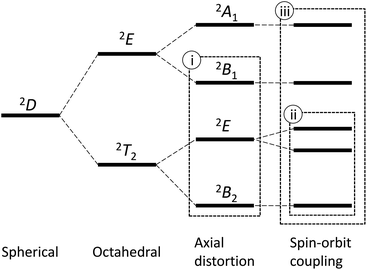
An octahedral vanadium(IV) complex is the simplest example of the T-ground-term complex, possessing the d1 electronic configuration. The 2D free-ion term splits into the ground 2T2 state and the excited 2E state in the O symmetry; however, the further splitting caused by the tetragonal distortion changes the ground state to the non-T-term ground state, 2B2, in the C4 symmetry (Fig. 1).4 In this case, since the orbital angular momentum is almost quenched, the first-order spin–orbit coupling is neglected and only the admixing effect by the second-order spin–orbit coupling is considered.4,5 Hereafter, we refer this approximation as method (i). This method is valid only when the first-order orbital angular momentum is practically quenched due to the large distortion.
On the other hand, when the distortion from the regular octahedron is not so large, the conventional T-term theory1–3,5 is valid. In this case, since the orbital angular momentum remains unquenched, the first-order spin–orbit coupling plays an important role. Hereafter, we refer this as method (ii). This method considers the first-order spin–orbit coupling of the states originated from the 2T2 state, but the higher states from the 2E state are not considered. Thus, the method (ii) is valid only when the admixing of the higher states can be neglected. So far, these two methods have been applied for axially distorted octahedral d1 systems.5
In this study, in order to solve the problems of the limitation in the above two methods, new method (iii) is derived, considering both the first-order and the second-order spin–orbit coupling effects for all the states derived from the 2D free-ion term by symmetry-lowering. In addition, structure and magnetic properties are investigated for a newly prepared pentakis(dimethylsulfoxide-κO)oxidovanadium(IV) complex, [VO(dmso)5][BPh4]2 (1) (dmso: dimethylsulfoxide), in order to evaluate the three methods.
Another topic of this study is predicting the structure of flexible metal complexes. Even a simple [VO(dmso)5]2+ type complex cation has more than 8000 conformers6 with respect to the rotations around V–O(dmso) and O–S bonds. In such a case, as we conducted previously for [Mg(dmso)6]2+ complex cation,7 one of the reliable methods in predicting structures is a conformational analysis considering all the possible conformers. In this study, conformational analysis was conducted, using the enumeration result7 on the basis of the group theory, in order to find which conformers are stable. Moreover, conformational prediction was conducted by also a machine learning technique in artificial intelligence with a deep neural network model.8
Results and discussion
Synthesis and characterization of 1
An oxidovanadium(IV) complex, [VO(dmso)5][BPh4]2 (1), was newly synthesized from oxidovanadium(IV) sulfate and sodium tetraphenylborate in dmso solution. Synthetic details are described in Experimental section. The compound is stable in dmso solution, and can be recrystalized from dmso/2-propanol. Complex 1 was characterized by infrared spectra and elemental analysis. If the IR spectra of 1 are compared with its derivatives, [Mg(dmso)6][BPh4]2,7 [Co(dmso)6][BPh4]2,9 and [Zn(dmso)6][BPh4]2,10 the band at around 983 cm−1 is unique, and it can be reasonably assigned to the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band (1000–970 cm−1).11 The band at around 952 cm−1 is common to the other derivatives, and can be assigned to the S
O stretching band (1000–970 cm−1).11 The band at around 952 cm−1 is common to the other derivatives, and can be assigned to the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band of the dmso-κO ligand (∼950 cm−1).12 The intense bands at around 735 and 708 cm−1 are assigned to tetraphenylborate anion.
O stretching band of the dmso-κO ligand (∼950 cm−1).12 The intense bands at around 735 and 708 cm−1 are assigned to tetraphenylborate anion.
Crystal structure of 1
Crystallographic data are summarized in Table 1, and the structure of the complex cation, [VO(dmso)5]2+, is shown in Fig. 2. The compound consists of the complex cations and the tetraphenylborate anions in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio. In the complex cation, the oxido and five dmso ligands coordinate to the central vanadium(IV) ion through the oxygen atoms, forming an octahedral VO6 coordination geometry.
2 molar ratio. In the complex cation, the oxido and five dmso ligands coordinate to the central vanadium(IV) ion through the oxygen atoms, forming an octahedral VO6 coordination geometry.
| a R1 = Σ||Fo| − |Fc||/Σ|Fo|.b wR2 = [Σ(w(Fo2 − Fc2)2)/Σw(Fo2)2]1/2. | |
|---|---|
| Empirical formula | C58H70B2O6S5V |
| Formula weight | 1096.00 |
| Crystal system | Monoclinic |
| Space group | P21/c |
| a/Å | 11.7605(7) |
| b/Å | 12.7062(8) |
| c/Å | 37.334(2) |
| β/° | 91.0600(10) |
| V/Å3 | 5578.0(6) |
| Z | 4 |
| Crystal dimensions/mm | 0.38 × 0.26 × 0.24 |
| T/K | 90 |
| λ/Å | 0.71073 |
| ρcalcd/g cm−3 | 1.305 |
| μ/mm−1 | 0.414 |
| F(000) | 2316 |
| 2θmax/° | 57.1 |
| No. of reflections measured | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 379 379 |
| No. of independent reflections | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 (rint = 0.0541) 561 (rint = 0.0541) |
| Data/restraints/parameters | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561/4/668 561/4/668 |
| R1a (I > 2.00σ(I)) | 0.0544 |
| wR2b (all reflections) | 0.1289 |
| Goodness of fit indicator | 1.027 |
| Highest peak, deepest hole/e Å−3 | 0.450, −0.376 |
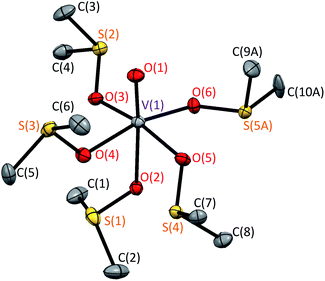 | ||
| Fig. 2 Crystal structure of [VO(dmso)5]2+ in 1 at 90 K. Hydrogen atoms and disordered minor structure are omitted for clarity. | ||
Although the disorder was observed around one of the dmso moieties [S(5A), C(9A), C(10A)], we will discuss only the main structure, because the occupancy of the minor structure is small [0.146(2)]. (Note: alert B in checkCIF is due to the missing hydrogen atoms that could not be handled well in the disordered minor moiety.) Selected bond distances and angles are summarized in Table 2. The V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance was found to be 1.5974(18) Å, and this is normal for the octahedral oxidovanadium(IV) complexes [1.57–1.61 Å].13 The equatorial V–O distances fall in the range of 2.0009(17)–2.0270(18) Å, which is shorter than the axial V–O distance of 2.1841(17) Å. These distances are also normal for the octahedral oxidovanadium(IV) complexes [1.99–2.03 Å for equatorial V–O and 2.16–2.24 Å for axial V–O].13 The central VO6S5 unit was found to take the defect S6 symmetry (conformer L5-B35*6), which was thought to be stable. In the related [Co(dmso)6]2+ and [Zn(dmso)6]2+ complex cations, the S6 symmetry was found for the MO6S6 unit [M = Mg(II), Co(II), and Zn(II)].7,9,10
O bond distance was found to be 1.5974(18) Å, and this is normal for the octahedral oxidovanadium(IV) complexes [1.57–1.61 Å].13 The equatorial V–O distances fall in the range of 2.0009(17)–2.0270(18) Å, which is shorter than the axial V–O distance of 2.1841(17) Å. These distances are also normal for the octahedral oxidovanadium(IV) complexes [1.99–2.03 Å for equatorial V–O and 2.16–2.24 Å for axial V–O].13 The central VO6S5 unit was found to take the defect S6 symmetry (conformer L5-B35*6), which was thought to be stable. In the related [Co(dmso)6]2+ and [Zn(dmso)6]2+ complex cations, the S6 symmetry was found for the MO6S6 unit [M = Mg(II), Co(II), and Zn(II)].7,9,10
| Atom–atom | Distance/Å | Atom–atom | Distance/Å |
|---|---|---|---|
| V(1)–O(1) | 1.5974(18) | V(1)–O(2) | 2.1841(17) |
| V(1)–O(3) | 2.0160(18) | V(1)–O(4) | 2.0270(18) |
| V(1)–O(5) | 2.0195(18) | V(1)–O(6) | 2.0009(17) |
| Atom–atom–atom | Angle/° | Atom–atom–atom | Angle/° |
|---|---|---|---|
| O(1)–V(1)–O(2) | 174.40(8) | O(1)–V(1)–O(3) | 97.06(8) |
| O(1)–V(1)–O(4) | 95.89(8) | O(1)–V(1)–O(5) | 97.58(8) |
| O(1)–V(1)–O(6) | 99.72(8) | O(2)–V(1)–O(3) | 83.78(7) |
| O(2)–V(1)–O(4) | 78.56(7) | O(2)–V(1)–O(5) | 81.77(7) |
| O(2)–V(1)–O(6) | 85.81(7) | O(3)–V(1)–O(4) | 90.45(7) |
| O(3)–V(1)–O(5) | 165.32(7) | O(3)–V(1)–O(6) | 89.10(7) |
| O(4)–V(1)–O(5) | 89.21(7) | O(4)–V(1)–O(6) | 164.32(7) |
| O(5)–V(1)–O(6) | 87.28(7) |
Comparing the structure of 1 with its perchlorate derivative, [VO(dmso)5][ClO4]2 (2),13 the conformations of the cations are different from each other with respect to the orientation of the terminal methyl groups, although the central VO6S5 units have the same defect S6 symmetry. In 2, oxido oxygen is hydrogen-bonded to a dmso methyl group of the adjacent complex cation, forming a one-dimensional chain structure of the complex cations, while the cation is isolated from the others in 1. This structural difference is thought to be one of the reasons of the conformational difference between 1 and 2.
Theory
Here we extend the conventional T-term theory1–3,5 by considering also the excited E-term. We start with the conventional Hamiltonian, H = Vdis + κλL·S + β[κLu + ge Su]·Hu (u = x, y, z), for a slightly distorted octahedral structure with the d1 electronic configuration, where Δ is the axial splitting parameter, κ is the orbital reduction factor, λ is the spin–orbit coupling parameter, and Vdis = Δ(2/3 − Lz2/3).14 It should be emphasized that not only the Hamiltonian but also the basis set is important. Now we introduce the following basis set (eqn (1)) for the d1 electronic configuration, using the |ML, MS〉 functions (ML = 0, ±1, ±2 and MS = ±1/2). The functions ψ+1, ψ+2, ψ+3, ψ+4, and ψ+5 correspond to −idxyα,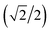 {−idyzα − dxzα},
{−idyzα − dxzα}, 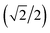 {–idyzα + dxzα}, dx2−y2α, and dz2α, respectively, and the functions ψ−1, ψ−2, ψ−3, ψ−4, and ψ−5 correspond to idxyβ,
{–idyzα + dxzα}, dx2−y2α, and dz2α, respectively, and the functions ψ−1, ψ−2, ψ−3, ψ−4, and ψ−5 correspond to idxyβ, 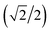 {−idyzβ + dxzβ},
{−idyzβ + dxzβ}, 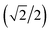 {−idyzβ − dxzβ}, dx2−y2β, and dz2β, respectively, where α and β correspond to up and down spins, respectively.
{−idyzβ − dxzβ}, dx2−y2β, and dz2β, respectively, where α and β correspond to up and down spins, respectively.
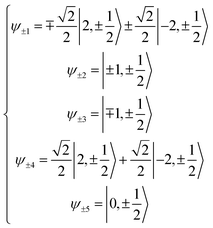 | (1) |
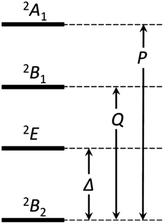
If the 2E term is included to the matrix for the 2T2 term, the secular matrix for the 2D term is obtained as shown in Table 4. The parameters Q and P represent the energy separations from 2B2 to 2B1 and from 2B2 to 2A1, respectively (Fig. 3).
Now, the basis set is converted to a new basis set (eqn (2)), then the secular matrix for the 2D term can be modified as shown in Table 5.
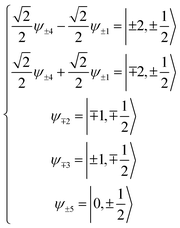 | (2) |
By solving the resulting secular matrix, the zero-field energies, E(0)n, and the first- and second-order Zeeman coefficients, E(1)n,z, E(1)n,x, E(2)n,z, and E(2)n,x, can be obtained (n = ±1, ±2, ±3, ±4, ±5). Fortunately, the matrix can be solved parametrically as closed forms, and the exact solution can be obtained. The resulting equations are included in ESI.† As well as the zero-field energies and the Zeeman coefficients, the anisotropic g-values can be expressed (eqn (3)), using only three parameters, the orbital reduction factor κ, the parameter v [v = Δ/(κλ)], and the parameter q [q = Q/(κλ)].
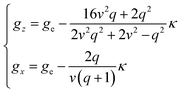 | (3) |
Electron spin resonance (ESR) and magnetic properties
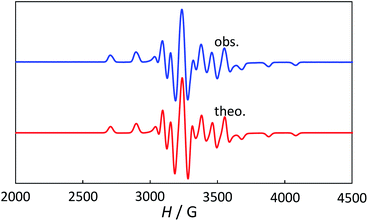
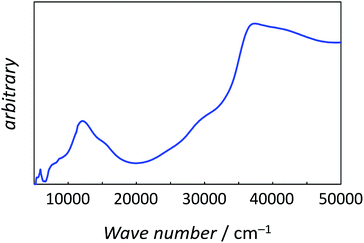
The powder electron spin resonance (ESR) spectra were measured at room temperature and at liquid nitrogen temperature (Fig. 4). The spectra were essentially the same at both temperatures, showing axial pattern. From the simulation, the g-values were obtained as gz = 1.933 and gx = 1.974 at liquid nitrogen temperature. These values are close to those for the [VO(H2O)5]2+ complex (gz = 1.933 and gx = 1.981), which were thoroughly discussed by Figgis and Hitchman.15 They considered the ligand-field splitting under C4v symmetry and the admixing from the excited 2B1 and 2E states to the ground B2 state. From the powder electronic spectra, the transition energies for 2B2 → 2E (Δ) and 2B2 → 2B1 (Q) transitions were estimated as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 16
000 cm−1 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively for the [VO(H2O)5]2+ complex.4 Using the following approximation, the κ2λ value was estimated as 141 cm−1, where κ and λ are the orbital reduction factor and the spin–orbit coupling parameter, respectively.
000 cm−1, respectively for the [VO(H2O)5]2+ complex.4 Using the following approximation, the κ2λ value was estimated as 141 cm−1, where κ and λ are the orbital reduction factor and the spin–orbit coupling parameter, respectively.
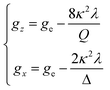 | (4) |
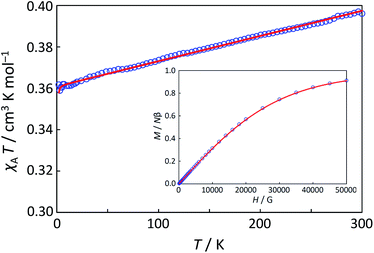
Magnetic susceptibility (χA) was measured in the temperature range of 2–300 K, and the χAT versus T plot is shown in Fig. 5. The observed χAT value at 300 K (0.396 cm3 K mol−1) was close to the spin-only value (0.375 cm3 K mol−1) for the S = 1/2 spin state. When lowering the temperature, the observed χT value linearly decreased to 2 K (0.360 cm3 K mol−1 at 2 K). The saturation behaviour of the magnetization (Fig. 5, insertion) is consistent with the S = 1/2 ground state. For the magnetic data analysis, the symmetry was assumed to be axial because the ESR showed an axial pattern. The magnetic susceptibility data were analysed by the magnetic susceptibility equation (eqn (5)), including the newly derived zero-field energies and Zeeman coefficients in the Theory section above. For the magnetization, the powder average is calculated using the expanded equation16 (eqn (6) and (7)) for the axial symmetry (n = ±1, ±2, ±3, ±4, ±5; m = 90), although the Brillouin function equation14 is also valid for 1 with the averaged g-value, due to the small g-anisotropy.
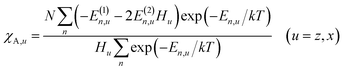 | (5) |
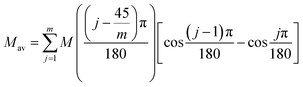 | (6) |
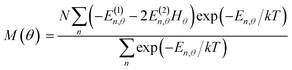 | (7) |
The best-fitting parameter set was obtained as (λ, κ, Δ, Q, TIP) = (250 cm−1, 0.76, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, 16
000 cm−1, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, 80 × 10−6 cm3 K mol−1) with good discrepancy factors (Rχ = 6.2 ×10−5 and RχT = 8.2 ×10−6). The obtained λ value is consistent with the expected spin–orbit coupling parameter for vanadium(IV) ion (250 cm−1).15 The obtained κ value is smaller than the free-ion value, but it is normal because of the π orbital contribution. The obtained Δ and Q values, corresponding to the 2B2 → 2E and 2B2 → 2B1 separations, respectively, are concordance with the electronic spectra (Fig. 6). The P value, corresponding to the 2B2 → 2A1 separation, could not be determined from the magnetic data fitting. From the obtained parameters, the anisotropic g-values were calculated, using eqn (3). The calculated g-values were gz = 1.930 and gx = 1.977, which were in good agreement with the observed ESR result. Consequently, the magnetic analysis by method (iii) was successfully conducted to simulate the magnetic data, the electron spin resonance (ESR) data, and the electronic spectral data.
000 cm−1, 80 × 10−6 cm3 K mol−1) with good discrepancy factors (Rχ = 6.2 ×10−5 and RχT = 8.2 ×10−6). The obtained λ value is consistent with the expected spin–orbit coupling parameter for vanadium(IV) ion (250 cm−1).15 The obtained κ value is smaller than the free-ion value, but it is normal because of the π orbital contribution. The obtained Δ and Q values, corresponding to the 2B2 → 2E and 2B2 → 2B1 separations, respectively, are concordance with the electronic spectra (Fig. 6). The P value, corresponding to the 2B2 → 2A1 separation, could not be determined from the magnetic data fitting. From the obtained parameters, the anisotropic g-values were calculated, using eqn (3). The calculated g-values were gz = 1.930 and gx = 1.977, which were in good agreement with the observed ESR result. Consequently, the magnetic analysis by method (iii) was successfully conducted to simulate the magnetic data, the electron spin resonance (ESR) data, and the electronic spectral data.
The conventional magnetic analysis by method (i) was also successfully conducted to simulate the magnetic data with the parameters (giso, TIP) = (1.96, 125 × 10−6 cm3 K mol−1) with good discrepancy factors (Rχ = 2.3 ×10−5 and RχT = 9.8 ×10−6). The obtained isotropic g-value (giso = 1.96) was consistent with the averaged g-value (gav = 1.962) obtained by method (iii); however, the further analysis was unable to determine the anisotropic g-values by method (i).
The magnetic analysis by method (ii), considering the T-term, was also conducted, and the magnetic data seemed to be simulated with the parameters (λ, κ, Δ) = (83 cm−1, 0.85, 2150 cm−1) with good discrepancy factors (Rχ = 4.3 ×10−5 and RχT = 6.3 ×10−6). However, the Δ value obtained by method (ii) was not consistent with the electronic spectra. Worse, the calculated anisotropic g-values (gz = 1.999, gx = 1.946, gav = 1.964) by method (ii) were completely different from the ESR data except for the averaged value.
In conclusion, in the case of the [VO(dmso)5][BPh4]2 complex (1), the octahedral coordination geometry was significantly symmetry-lowered by the oxido ligand. Thus, the T-term based analysis [method(ii)] was no longer useful, because the excited E-term was completely neglected in this method. Conventional spin-only method [method(i)] worked well to obtain reasonable isotropic g-value, because the orbital angular momentum was practically quenched. The novel method [method (iii)], considering both the T-term and the excited E-term, worked quite well to obtain the consistent anisotropic g-values and also the excitation energies for 1. Method (iii) is of course effective not only for the large distortion case, but also the small distortion case. Moreover, the method is expected to be effective for the intermediate case and to be able to be expanded for the symmetries that are not subgroups of octahedral symmetry.
Conformational analysis for [VO(dmso)5]2+ complex cation
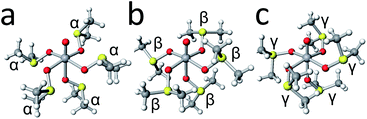
A lot of conformers are possible for the octahedral pentakis-dmso oxidovanadium(IV) complex cation, because it is flexible with respect to the rotation around the V–O(dmso) and O–S bonds. Therefore, in order to find which conformers are stable, conformational analysis was conducted for the [VO(dmso)5]2+ complex cation. Enumeration of this type of conformers was previously conducted on the basis of group theory,6 and the result was described using the conformer codes. Since the defect S6 conformation is stable for the central VO6S5 unit and only this conformation is practically possible, 243 conformers, possessing the defect-S6-VO6S5 unit (code name: L5-B35), were considered in conformational analysis.The resulting top six conformers and typical conformers are listed in Table 6. When we previously conducted the conformational analysis of the [Mg(dmso)6]2+ complex cation,7 the three typical dmso-arms are named as α, β, and γ. The nature of the each arm conformation is as follows. The α-arm conformation is generally suitable for reducing the inter-ligand steric repulsions, and is often found in related dmso complexes, [Zn(dmso)6][ClO4]2, [Mn(dmso)6]I2, [Fe(dmso)6][SnCl6]2, [Co(dmso)6][SnCl6]2, and [Ni(dmso)6][SnCl6]2;17 the β-arm conformation is less suitable in reducing the inter-ligand steric repulsions, but is possible to be stabilized to some extent by CH⋯π interaction with surroundings; the γ-arm conformation is not suitable in reducing the inter-ligand steric repulsions, but is suitable for reducing the size of the complex cation.7 In the case of the present [VO(dmso)5]2+ complex cation, three typical conformers possessing α5-, β5-, and γ5-arms are shown in Fig. 7. As expected, the α5 conformer is the most stable among them, while the γ5 conformer is the most unstable. Judging from the energy differences between conformers (Table 6) and the thermal energy value (kT = 0.60 kcal mol−1 at 300 K), several conformers, are thought to be mixed in solution.
| Conformera | Point group | Armsb | ΔEc |
|---|---|---|---|
| a Conformer codes are listed in Table S1.b Counterclockwise order in Fig. 7.c Energy difference (kcal mol−1). | |||
| L5-B35-123 | C1 | αααβα | 0.00 |
| L5-B35-126 | C1 | ααββα | 0.06 |
| L5-B35-162 | C1 | ααβαβ | 0.29 |
| L5-B35-135 | C1 | ααβαα | 0.31 |
| L5-B35-132 | C1 | ααααα | 0.51 |
| L5-B35-153 | C1 | ααβββ | 1.05 |
| L5-B35-233 | C1 | βββββ | 4.67 |
| L5-B35-1 | C1 | γγγγγ | 13.45 |
The crystal structure of [VO(dmso)5]2+ and several stable conformers are shown in Fig. 8. It is noted that the crystal structure (Fig. 8a) is the mirror image of that in Fig. 2. Judging from the energy differences, conformer L5-B35-123 possessing αααβα-arms and conformer L5-B35-126 possessing ααββα-arms are the dominant species in solution.
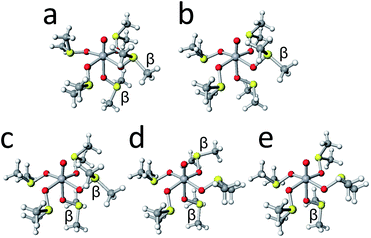 | ||
| Fig. 8 The crystal structures of [VO(dmso)5]2+ cation (a) and the structures of conformers L5-B35-123 (b), L5-B35-126 (c), L5-B35-162 (d), and L5-B35-135 (e). | ||
Conformational prediction by deep neural network method
In this study, conformational prediction for the [VO(dmso)5]2+ complex cation was conducted by also a machine learning technique in artificial intelligence with a deep neural network model,8 trained on a magnesium derivative data. Previously, we conducted conformational analysis of [Mg(dmso)6]2+ complex cation, considering 130 conformers possessing the S6–MgO6S6 cores.7 By learning the resulting structure-energy pairs, a trained neural-network-model was successfully constructed. This model can successfully indicate whether the conformation is energetically stable with a five-point scale for [Mg(dmso)6]2+. Prediction for the present [VO(dmso)5]2+ complex cation became possible by adding a scaling factor to input data and a processing program for output data. As the result, the most probable conformer was predicted as L5-B35-126, and all of the 243 conformers were categorized in a five-point scale (A: the most probable 25 conformers; B: 66 conformers; C: 91 conformers; D: 47 conformers; E: 14 conformers). The predicted conformer L5-B35-126 was incidentally the conformer found in the crystal structure. The top six conformers discussed in the above section were included in the most probable category A. Therefore, the 243 candidates of the conformers were successfully narrowed down to one tenth. Generally, full conformation search with structure optimization calculation is a time-consuming task. Therefore, narrowing down candidates by machine learning is expected to be useful in timesaving in future structural prediction. It should be also emphasized that the prediction by machine learning completes at once, using unoptimized structures immediately generated on the basis of the group theory, as long as the trained model exists. Anyhow, the deep neural net work model, trained on the more symmetric [Mg(dmso)6]2+ data, was found to be quite useful in predicting the conformer of symmetry-lowered [VO(dmso)5]2+.Experimental
Materials and methods
All the chemicals were commercial products and were used as supplied. Elemental analyses (C, H, and N) were obtained at the Elemental Analysis Service Centre of Kyushu University. IR spectra were recorded on a JASCO FT/IR-4100 FT-IR spectrometer. Magnetic susceptibility measurements were made on a Quantum Design MPMS-XL5 susceptometer with scan rates of 1 K min−1 for 2–20 K and 2 K min−1 for 20–300 K at 5 kOe. The isothermal magnetization was measured on a Quantum Design MPMS-XL5 susceptometer at 2 K in an applied field up to 50 kOe. The magnetic correction for the sample holder was performed by measurement for the empty polyethylene film inside a plastic straw. The susceptibilities were corrected for the diamagnetism of the constituent atoms using Pascal's constants. X-band ESR spectra were recorded at room temperature (rt) and 77 K on JEOL JES-TE300 ESR spectrometer. Experimental conditions: ν = 9.44790 (rt) and 9.19431 (77 K) GHz; microwave power = 4.0 mW; modulation frequency = 100 kHz; modulation width = 10.0 G. The powder electronic spectra were recorded on Shimadzu UV-3100 spectrometer that was equipped with an integrating sphere in the 200–2000 nm region.Synthetic procedures
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) /cm−1] using a KBr disk: 3055–2985, 2915, 1580, 1478, 1424, 1319, 1135, 1032, 983, 952, 931, 749, 735, 708, 612.
/cm−1] using a KBr disk: 3055–2985, 2915, 1580, 1478, 1424, 1319, 1135, 1032, 983, 952, 931, 749, 735, 708, 612.Crystallography
Single-crystals suitable for X-ray analysis were obtained by slow diffusion of 2-propanol to a dmso solution of 1. Single-crystal diffraction data were measured on a Bruker Smart APEX CCD diffractometer. The structure was solved by intrinsic phasing methods and expanded using Fourier techniques. The non-hydrogen atoms were refined anisotropically except for the disordered minor dmso domain, and hydrogen atoms were refined using the riding model. In the minor domain, hydrogen atoms were not considered because the hydrogen atoms in the major domain failed to converge. The final cycle of full-matrix least squares refinement on F2 was let to satisfactory converge with R1 = 0.0544 [I > 2σ(I)]. Final R(F), wR(F2), and goodness of fit agreement factors, as well as details on data collection and analysis are in Table 1.Computations
Magnetic analyses and magnetic simulation were conducted using MagSaki(VIV)0.1.1 and MagSaki(B)0.7.4 programs of MagSaki series. ESR simulation was conducted using “Hyperfine Spectrum” program with the spin Hamiltonian, Hs = βBgS + SAI.18 DFT computations were performed using GAMESS program19 on FUJITSU PRIMERGY CX400 (TATARA computer) at Kyushu University. Structural optimizations were performed with LC-BOP/6-31G.20Deep neural network method
Machine learning and conformational prediction using deep neural network models were conducted by Keras21 and TensorFlow22 under Jupyter23 and Anaconda24 on a Windows 8 computer. A deep neural network was adopted as a model, and supervised learning was performed to classify conformer structures into five classes of energy. For the learning, the previously obtained 130 optimized structures of [Mg(dmso)6]2+ conformers and energy values were used. The 130 data were increased to 390 by symmetry operations (C3 and C32). For each structure, 216 S⋯H distances were extracted, obtaining a 216-dimensional feature vector, and the resulting 216 × 390 tensor was prepared as input data. This input data was split into training and test data in a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. In the model, the ReLU function22 was used for the activation function of the hidden layer, and the softmax function22 was used for the output layer. Finally, a four-layer model with 128 units was adopted as the minimum model. To avoid overfitting, the training was rounded up in 2000 cycles before the scores (accuracy and loss) worsened. As the result, eight weight tensors were successfully obtained for the [Mg(dmso)6]2+ conformers. To predict the [VO(dmso)5]2+ conformers, the trained [Mg(dmso)6]2+ model was used with an additional scaling factor for input and summing program for output. Without the scaling factor, the output values showed no difference in conformers; however, the scaling factor was found to change the magnitude in the output without changing the order of the conformers. By controlling the scaling factor, the program can be used for both most probable structure prediction and energy classification. Instead of the lacking S⋯H distances in the [VO(dmso)5]2+ conformer, extremely large values were used in the input, assuming fictitious atoms at infinite distance. In this way, the effects of fictitious atoms can be eliminated. Initial structures of the conformers were generated by ConfDatMaker software.25
3 ratio. In the model, the ReLU function22 was used for the activation function of the hidden layer, and the softmax function22 was used for the output layer. Finally, a four-layer model with 128 units was adopted as the minimum model. To avoid overfitting, the training was rounded up in 2000 cycles before the scores (accuracy and loss) worsened. As the result, eight weight tensors were successfully obtained for the [Mg(dmso)6]2+ conformers. To predict the [VO(dmso)5]2+ conformers, the trained [Mg(dmso)6]2+ model was used with an additional scaling factor for input and summing program for output. Without the scaling factor, the output values showed no difference in conformers; however, the scaling factor was found to change the magnitude in the output without changing the order of the conformers. By controlling the scaling factor, the program can be used for both most probable structure prediction and energy classification. Instead of the lacking S⋯H distances in the [VO(dmso)5]2+ conformer, extremely large values were used in the input, assuming fictitious atoms at infinite distance. In this way, the effects of fictitious atoms can be eliminated. Initial structures of the conformers were generated by ConfDatMaker software.25
Conclusions
In this study, a universal magnetic equation set was newly obtained for metal complexes with d1 electronic configuration, considering the axial ligand-field splitting and the spin–orbit coupling to the 2D free-ion term. The magnetic analysis using the equation set was successfully conducted for a newly prepared oxidovanadium(IV) complex, [VO(dmso)5][BPh4]2 (1), to obtain the anisotropic g-values and the excitation energies reasonably. The equation set was found to be universally useful for octahedral metal complexes with large and small distortion, and the method was expected to be expanded for the symmetries that are not subgroups of octahedral symmetry. The single-crystal X-ray method revealed that the complex cation, [VO(dmso)5]2+, in 1 was found to take conformer L5-B35-126 by a single-crystal X-ray method. The DFT-based conformational analysis predicted two dominant conformers, L5-B35-123 and L5-B35-126, in dmso solution. The deep-neural-network-based conformational prediction was also conducted and conformer L5-B35-126 was successfully predicted for the [VO(dmso)5]2+ complex cation, using the deep neural network model, trained on the more symmetric [Mg(dmso)6]2+ derivative data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Japan society for the promotion of science (JSPS) KAKENHI Grant Number 15K05445. Financial support by Yamagata University is also acknowledged. HS thanks Dr Motohisa Fukuda at Yamagata University for his valuable advice.References
- B. N. Figgis, Trans. Faraday Soc., 1961, 57, 198 RSC.
- B. N. Figgis, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1966, 1411 RSC; B. N. Figgis, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1967, 442 RSC; B. N. Figgis, M. Gerloch, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1968, 2086 RSC.
- F. E. Mabbs and D. J. Machin, Magnetism and Transition Metal Complexes, Chapman and Hall, 1973 Search PubMed.
- C. J. Ballhausen and H. B. Gray, Inorg. Chem., 1962, 1, 111 CrossRef CAS; D. J. Robbins, M. J. Stillman and A. J. Thomson, J. Chem. Soc., Dalton Trans., 1974, 813 RSC.
- D. J. Machin and K. S. Murray, J. Chem. Soc. A, 1967, 1330 RSC.
- H. Sakiyama and K. Waki, J. Math. Chem., 2017, 55, 1360 CrossRef CAS.
- H. Sakiyama, K. Shomura, M. Ito, K. Waki and M. Yamasaki, Dalton Trans., 2019, 48, 10174 RSC.
- J. Schmidhuber, Neural Networks, 2015, vol. 61, p. 85 Search PubMed; I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- H. Sakiyama, R. Sudo, T. Abiko, D. Yoshioka, R. Mitsuhashi, M. Omote, M. Mikuriya, M. Yoshitake and M. Koikawa, Dalton Trans., 2017, 46, 16306 RSC; R. Sudo, D. Yoshioka, M. Mikuriya and H. Sakiyama, X-Ray Struct. Anal. Online, 2012, 28, 71 CrossRef CAS.
- H. Sakiyama, T. Abiko, M. Ito, R. Mitsuhashi, M. Mikuriya, K. Waki and T. Usuki, Polyhedron, 2019, 158, 494 CrossRef CAS; H. Sakiyama, T. Abiko, M. Ito, R. Mitsuhashi, M. Mikuriya and K. Waki, Polyhedron, 2016, 119, 512 CrossRef.
- A. L. Doadrio, J. Sotelo and A. Fernández-Ruano, Quim. Nova, 2002, 25, 525 CrossRef CAS.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds: Part B: Applications in Coordination, Organometallic, and Bioinorganic Chemistry, John Wiley & Sons, Inc., 2008 Search PubMed.
- J. Krakowiak, D. Lundberg and I. Persson, Inorg. Chem., 2012, 51, 9598 CrossRef CAS PubMed.
- O. Kahn, Molecular Magnetism, VCH, 1993 Search PubMed.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and its Application, Wiley-VCH, 2000 Search PubMed.
- H. Sakiyama, Magnetochemistry, 2019, 5, 17 CrossRef CAS.
- I. Persson, Acta Chem. Scand., Ser. A, 1982, 36, 7 CrossRef CAS; A. P. White, K. N. Robertson, T. S. Cameron, B. V. Liengme, D. B. Leznoff, S. Trudel and M. A. S. Aquino, Can. J. Chem., 2007, 85, 372 CrossRef; M. A. Haque, B. Davaasuren, A. Rothenberger and T. Wu, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2016, 72, 1791 CrossRef.
- W. R. Hagen, Biomolecular EPR Spectroscopy, CRC, 2009 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS; M. S. Gordon and M. W. Schmidt, Advances in Electronic Structure Theory, Elsevier, 2005 Search PubMed.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425 CrossRef CAS.
- Keras, 2018, https://keras.io/2.0 Search PubMed.
- TensorFlow, 2018, https://www.tensorflow.org/ Search PubMed.
- Project Jupyter, 2018, https://jupyter.org/ Search PubMed.
- Anaconda, 2018, https://www.anaconda.com/ Search PubMed.
- H. Sakiyama, J. Comput. Chem. Jpn. Int. Ed., 2018, 4, 2018-0013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Magnetic equations and conformer codes (Fig. S1 and Table S1). CCDC 1978109. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra00854k |
| This journal is © The Royal Society of Chemistry 2020 |