Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical and experimental study on the electronic and optical properties of K0.5Rb0.5Pb2Br5: a promising laser host material
Tuan V. Vu *ab,
A. A. Lavrentyevc,
B. V. Gabreliand,
Dat D. Vo*ab,
Hien D. Tonge,
N. M. Denysyukf,
L. I. Isaenko
*ab,
A. A. Lavrentyevc,
B. V. Gabreliand,
Dat D. Vo*ab,
Hien D. Tonge,
N. M. Denysyukf,
L. I. Isaenko gh,
A. Y. Tarasovagh and
O. Y. Khyzhun
gh,
A. Y. Tarasovagh and
O. Y. Khyzhun *f
*f
aDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: vuvantuan@tdtu.edu.vn; voduydat@tdtu.edu.vn
bFaculty of Electrical & Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cDepartment of Electrical Engineering and Electronics, Don State Technical University, 1 Gagarin Square, 344010 Rostov-on-Don, Russian Federation
dDepartment of Computational Technique and Automated System Software, Don State Technical University, 1 Gagarin Square, 344010 Rostov-on-Don, Russian Federation
eFaculty of Engineering, Vietnamese German University, Binh Duong, Vietnam
fFrantsevych Institute for Problems of Materials Science, National Academy of Sciences of Ukraine, 3 Krzhyzhanivsky Street, 03142 Kyiv, Ukraine. E-mail: khyzhun@ipms.kiev.ua
gNovosibirsk State University, 630090 Novosibirsk, Russian Federation
hV. S. Sobolev Institute of Geology and Mineralogy, SB RAS, 630090 Novosibirsk, Russian Federation
First published on 17th March 2020
Abstract
The data on the electronic structure and optical properties of bromide K0.5Rb0.5Pb2Br5 achieved by first-principle calculations and verified by X-ray spectroscopy measurements are reported. The kinetic energy, the Coulomb potential induced by the exchange hole, spin-orbital effects, and Coulomb repulsion were taken into account by applying the Tran and Blaha modified Becke–Johnson function (TB-mBJ), Hubbard U parameter, and spin-orbital coupling effect (SOC) in the TB-mBJ + U + SOC technique. The band gap was for the first time defined to be 3.23 eV. The partial density of state (PDOS) curves of K0.5Rb0.5Pb2Br5 agree well with XES K Ll and Br Kβ2, and XPS spectra. The valence band (VB) is characterized by the Pb-5d3/2 and Pb-5d5/2 sub-states locating in the vicinities of −20 eV and −18 eV, respectively. The VB middle part is mainly formed by K-3p, Rb-4p and Br-4s states, in which the separation of Rb-4p3/2 and Rb-4p1/2 was also observed. The strong hybridization of Br-p and Pb-s/p states near −6.5 eV reveals a major covalent part in the Br–Pb bonding. With a large band gap of 3.23 eV, and the remarkably high possibility of inter-band transition in energy ranges of 4–7 eV, and 10–12 eV, the bromide K0.5Rb0.5Pb2Br5 is expected to be a very promising active host material for core valence luminescence and mid-infrared rare-earth doped laser materials. The anisotropy of optical properties in K0.5Rb0.5Pb2Br5 is not significant, and it occurs at the extrema in the optical spectra. The absorption coefficient α(ω) is in the order of magnitude of 106 cm−1 for an energy range of 5–25 eV.
1 Introduction
Laser materials have been studied for many years due to their applications in many areas requiring high technologies such as global communication, medicine, diagnostic analysis, sensors, security, and defense.1–3 As a result of this long process of research and development, a variety of laser materials has been discovered which can be divided into solid, liquid, gas, and plasma groups.4 Among these, the solid-state lasers appear to be more advantageous for commercial manufacturing and practical usages where the compactness and simplicity of maintenance are required. For the last two decades, rare earth-doped borates and halides have been intensively studied and developed as they possess outstanding properties including good physical and chemical stability, high optical quality, large dimension, and moisture resistance.5,6 Recently, increasing attention has been paid to the rare-earth doped double halides as they can operate in the mid-IR range.7 Especially, the active crystal hosts with general formula APb2B5 (A = K, Rb; and B = Cl, Br) are of great interest owing to their low phonon energy of about 140 cm−1 which inhibits the non-radiative transition rate and increases the quantum yield.8–13 Rubidium- and potassium-bearing lead bromides, RbPb2Br5 (RPB) and KPb2Br5 (KPB), can be considered representative laser materials in this group because they are non-hygroscopic and they can readily incorporate with rare-earth (RE) ions.12–17 Thus, the composition of these laser materials can be varied for a wider range of applications. However, there are still challenges to be resolved before applying these materials in practical uses. The KPB compounds are reported to be thermal unstable,15,18,19 in which the phase-transition causes isotropy breaking to form light scattering centers. Thus, the emission generation is reduced due to optical losses. Meanwhile, the RPB compounds undergo no phase -transition even at melting point.19 The drawback of RPB compounds is that RE ion concentration in the crystals is an order of magnitude lower than in KPB crystals. To combine the positive properties of both compounds, KPB and RPB, many experiments have been made to define the best value of x in KxRb1−xPb2Br5 materials.20–22 It was experimentally found that the K0.5Rb0.5Pb2Br5 compound contains sufficient RE ion concentration for a high emission rate. At the same time, the phase-transition of this material occurs only at the melting point.22 This result indicates that K0.5Rb0.5Pb2Br5 appears to be a very promising laser material which is suitable for commercial manufacturing and practical uses. For this purpose, the XPS spectrum of K0.5Rb0.5Pb2Br5 was reported,22 and its thermal expansion was also studied.23To our knowledge, there is no theoretical study on the electronic structure of K0.5Rb0.5Pb2Br5, which is, in fact, very necessary for understanding the inter-band transition of optical electrons in the process of amplification and generation of radiation, or the effect of valence electrons on phonon energy via electron–phonon coupling.24 Among the optical properties of K0.5Rb0.5Pb2Br5 only the absorption edge was reported.22 Although the absorption edge of RPB compounds is observed to depend on the polarization,13,22 it has not been studied for the case of K0.5Rb0.5Pb2Br5. It is worth mentioning that the polarization of optical properties, and photoelectron distribution can influence the cross section, and laser–material interaction, meanwhile the laser writing is affected by light polarization.25,26 This quaternary bromide was not studied also employing the method of X-ray emission spectroscopy (XES) providing information on the partial densities of states of a solid. To overcome the above drawbacks, in this paper, a theoretical study on the electronic and optical properties of K0.5Rb0.5Pb2Br5 is presented.
Recently, the density functional theory (DFT) has been successfully performed to study many systems including monolayers, nanoribbons, and bulks.27–32 The DFT calculations can be used to not only validate experimental results but also to give insight to the electronic, and optical properties of a semiconductor.27 In current study, the DFT calculations were performed by applying augmented plane-wave method (APW)33,34 in the framework of Kohn–Sham equations.35 Because K0.5Rb0.5Pb2Br5 is a semiconductor with excited processes, both generalized gradient approximation of Perdew, Burke, and Ernzerhof (GGA-PBE)36 and Tran and Blaha modified Becke–Johnson (TB-mBJ) functional37,38 were used to simulate the exchange–correlation interaction to evaluate the effect of kinetic energy as well as exchange interaction of exciting hole on the electronic structure. The spin-orbital coupling (SOC) effect,39 and the Hubbard parameter U40,41 were also employed in the calculations as they play a very important role in a system with heavy elements likes Pb.42–51
2 Computational details
As the crystal structure of K0.5Rb0.5Pb2Br5 has not been available in any published studies, the simulation was based on the monoclinic structure of KPb2Br5, as shown in Fig. 1(a), with space group P21/c and lattice parameters a = 9.314 Å, b = 8.412 Å, c = 13.053 Å and β = 90.097°.22 The equilibrium structure of K0.5Rb0.5Pb2Br5 was obtained by optimizing a 1 × 1 × 2 supercell of KPb2Br5 structure, in which one K atom was replaced by one Rb atom as shown in Fig. 1(b).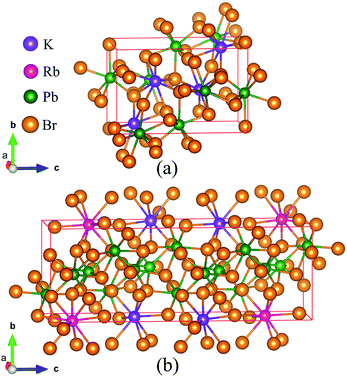 | ||
| Fig. 1 (a) KPb2Br5 crystal structure and (b) supercell of 1 × 1 × 2 used for optimization of K0.5Rb0.5Pb2Br5 structure. | ||
The optimized structure of K0.5Rb0.5Pb2Br5 was used for calculating the electronic properties, in which the density functional theory as implemented in WIEN2k codes52 was used. The full potential of the current system was simulated by applying Muffin-tin (MT) model and the augmented plane wave plus local-orbital (APW + lo) method,34,53 where the potential does not depend on shape-approximation. The Muffin-tin sphere radius (RMT) of 2.5 a.u. was used for K, Rb, Pb and Br elements. The Fourier series were applied to expand the charge density with Gmax = 14 (a.u.)−1, while the wavefunctions were expanded within Brillouin zone involving 1000 k-points with the maximum angular momentum lmax = 10, and RMTminkmax = 8. The exchange–correlation interaction was modeled by GGA-PBE36 and TB-mBJ37,38 methods with and without SOC39 and Hubbard U parameters. The Hubbard U parameter of 0.43 Ry was chosen for 5d states of Pb, 3p states of K and 4p states of Rb because such an approach was proven to give reliable theoretical results.40,41 The self-consistent process was converged when the difference in charge density is less than 10−4 Ry.
3 Experimental
In the present XES experiments, we use the optical quality K0.5Rb0.5Pb2Br5 crystal synthesized as described in detail in ref. 22 and cut at the (001) plane. Its XPS spectrum of valence electrons was measured as reported elsewhere.22 The X-ray emission Br Kβ2 spectrum (MII,III → K transition) yielding information on the energy distribution of bromine 4p electronic states was measured using a DRS-2M spectrograph equipped with a quartz crystal as dispersion element (the (0001) reflecting plane bent according to Johann technique) and the spectrum was excited employing a BKhV-7 X-ray tube (Au anode). The spectrograph resolution, ΔEmin, in the energy range corresponding to the region which covers the Br Kβ2 spectrum measured in the third reflection order was better than 0.25 eV and the operation regimes of the BKhV-7 X-ray tube were follows: accelerating voltage 45.5 kV and anode current 69.0 mA. The XES K Ll spectrum arising due to the LIII → MI transition and representing information on the energy distribution of potassium 4s electronic states was acquired in the second order of reflection with spectrometer energy resolution better than 0.3 eV using an RSM-500 spectrometer supplied with a diffraction grating (600 groves per 1 mm and curvature radius equal to 6026 mm). Operation regimes of an electron gun when acquiring the XES K Ll spectrum were the following: accelerating voltage 5.3 kV and anode current 5.7 mA.4 Results and discussion
4.1 Electronic structure of K0.5Rb0.5Pb2Br5
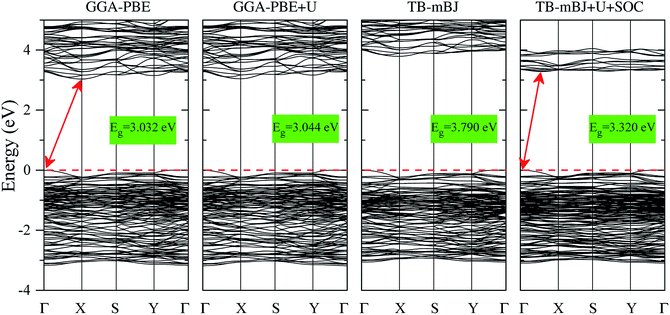
The electronic structures of K0.5Rb0.5Pb2Br5 obtained by GGA-PBE, GGA-PBE + U, TB-mBJ, and TB-mBJ + U + SOC, Fig. 2, are very different from each other. Thus, the valence band XPS spectrum of this compound22 is presented in Fig. 2 for finding the best correspondence of the theoretical results to the experiment. In general, the surface Fermi level of XPS spectra is higher than the valence band maximum.54 Therefore, the calculated total DOS was scaled by setting the top of valence band to zero energy level, and the XPS spectrum of valence electrons was shifted to ensure that the energy positions of the maxima on the curve of total density of states correspond to the positions of the main maxima (and “shoulders”) on the experimental X-ray photoelectron spectrum.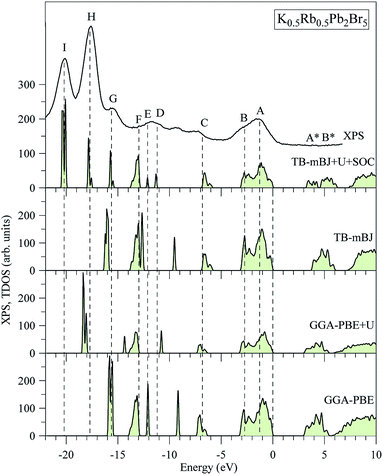 | ||
| Fig. 2 Total DOS of K0.5Rb0.5Pb2Br5 computed by employing the GGA-PBE, GGA-PBE + U, MBJ, and TB-mBJ + U + SOC techniques in comparison with the XPS spectrum of valence electrons of K0.5Rb0.5Pb2Br5 crystal.22 The Fermi level was shifted to zero energy level, while the XPS spectrum was shifted to the common energy scale of total DOS. | ||
As it was reported in the work of Tarasova et al.,22 the band gap of KPb2Br5 is about 3.46 eV, while the band gap of RbPb2Br5 is 3.42 eV or 3.47 eV depending on the polarization. Because the band gap of K0.5Rb0.5Pb2Br5 is currently not available in published papers, it is considered to be some value between 3.42 and 3.47 eV. Based on this estimation, the GGA-PBE band gap is significantly smaller than the experimental values.22 It is widely accepted that GGA-PBE methods cause an over-delocalization of occupied states shifting the valence band to higher energy level, so the band gap is reduced. To compensate this effect, the Hubbard U parameter was introduced to GGA-PBE + U method. As a result, the valence band (VB) lower part is shifted to lower energy level by about 2 eV, as shown in Fig. 2. At the same time, the VB upper part is slightly moved, so the band gap is improved by only 0.012 eV. Taking into account the kinetic energy, and the Coulomb potential induced by the exchange hole in the TB-mBJ method,55 the K0.5Rb0.5Pb2Br5 band gap is increased by 0.758 eV in comparison with the GGA-PBE band gap. However, the electronic structure of K0.5Rb0.5Pb2Br5 is comparable with the XPS spectrum only when both U and SOC parameters were included in the TB-mBJ + U + SOC method. The TB-mBJ + U + SOC band gap is about 0.1 eV smaller than the smallest band gap of RbPb2Br5, however the separation of Pb-5d3/2 and Pb-5d5/2 is observed, and most of the main peaks (and shoulders) of the XPS spectrum are well reproduced. Since the TB-mBJ + U + SOC method reproduces the reliable electronic structure of K0.5Rb0.5Pb2Br5 in comparison with experimental data, it was used for studying further properties of this compound.
The partial DOS curves of K0.5Rb0.5Pb2Br5 in Fig. 3 show that the Pb-5d3/2 and Pb-5d5/2 sub-states are located in the vicinities of −20 eV and −18 eV, respectively. The middle part of the VB is mainly formed by K-3p, Rb-4p, Br-4s states, in which the separation of Rb-4p3/2 and Rb-4p1/2 was also observed. The hybridization of Br-p and Pb-s/p states results in significant states contributions at −6.5 eV, and also near the valence band maximum (VBM). This reveals a major covalent part in the Br–Pb bonding. Contributions of the electronic states associated with potassium and rubidium are minor in the upper VB range as Fig. 3 demonstrates, however the present calculations predict some contributions of K-4s and Rb-5s states in the energy region between peculiarities A and B of the XPS spectrum of valence electrons of K0.5Rb0.5Pb2Br5. The conduction band minimum (CBM) is dominated by Pb-p and Br-p states, the upper parts are formed by Rb-s and K-s states.
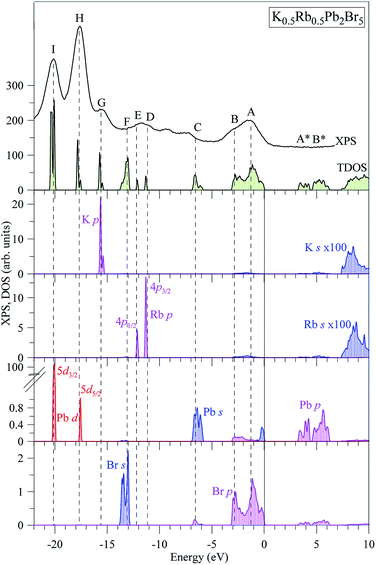 | ||
| Fig. 3 Total DOS and main partial densities of K0.5Rb0.5Pb2Br5 (computed by employing TB-mBJ + U + SOC method) in comparison with the XPS spectrum of valence electrons of K0.5Rb0.5Pb2Br5 crystal.22 The Fermi level was shifted to zero energy level, while the XPS spectrum was shifted to the common energy scale of total DOS. | ||
In spite of the fact that contributions of K-4s states are minor in the VB range of K0.5Rb0.5Pb2Br5 as the data of the TB-mBJ + U + SOC calculations predict (Fig. 3), we were able to measure the energy distribution of these states experimentally. Results of comparison of the XES K Ll spectrum presenting energy distribution of K-4s states together with the Br Kβ2 spectrum bringing information on Br-4p electronic states, the main contributors to the valence band of K0.5Rb0.5Pb2Br5 in accordance with the present DFT calculations (Fig. 3), as well as the XPS spectrum of valence electrons of the bromide under discussion are presented in Fig. 4. Such a comparison of the XES and XPS spectra allows for statement that, the present experimental data yield that the maximum of the Br Kβ2 band is positioned in the vicinity of the maximum A of the XPS spectrum and reveals a significant input of Br-4p states in the vicinity of the peculiarity B, being in excellent agreement with partial Br-4p DOS curve shown in Fig. 3. Similar energy distribution of Br-4p states was found earlier to be characteristic of Pb- and Br-bearing counterparts APb2Br5 (A = K, Rb, Tl).46,47,56 Furthermore, the maximum of the K Ll band is located in the energy region between features A and B of the XPS spectrum (provided that a general energy scale is used for comparison of XES and XPS spectra), again agreeing with the TB-mBJ + U + SOC calculations of K0.5Rb0.5Pb2Br5. Therefore, the present TB-mBJ + U + SOC calculations with respect to main peculiarities of contributions of Br-4p and K-4s electronic states in the K0.5Rb0.5Pb2Br5 VB are fairly supported by XES and XPS experiments as comparison of Fig. 3 and 4 indicates. Certainly, some contributions of valence Pb-s and Pb-p states should come in the valence band of K0.5Rb0.5Pb2Br5 as visible from Fig. 3. Available database literature on X-ray emission lines and bands of chemical elements57–60 brings no information on the existence of XES spectra representing energy distribution of valence Pb-s and Pb-p states. Since lead is a heavy element, its outer (valence) states X-ray emission spectra should involve transitions of electrons in the VB levels (P orbitals) to vacancies in nearby inner core-levels (N or O orbitals) and such transitions should correspond to photons in ultra-soft X-ray range as it is reported to be characteristic of 5d-metal compounds.60–63 Probably, possibilities of synchrotron radiation should be used as it is proved to be sufficient in the case of compounds based on 5d-metals.63,64 This problem looks worth to be a task of special research because available experimental ability does not give us possibility to check experimentally the energy distribution of those states in the case of studying the valence band occupation in the bromide under discussion. Furthermore, the present DFT calculations yield that Rb-5s states should give minor contributions to the K0.5Rb0.5Pb2Br5 VB in the same energy region as K-4s electronic states bring. To probe Rb-5s states, X-ray emission spectrum should involve electron transitions from the OI energy level to the inner MII,III or NII,III levels.63 However, the existence of such XES spectra has not been reported yet.60,63,65 Therefore, we leave this task for future research.
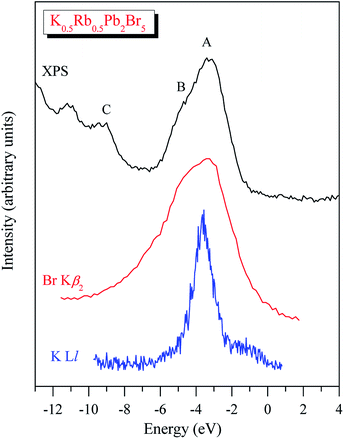 | ||
| Fig. 4 XPS spectrum of valence electrons of K0.5Rb0.5Pb2Br5 matched on a general energy scale with XES K Ll and Br Kβ2 spectra of this crystal. | ||
The band structures shown in Fig. 5 signify that K0.5Rb0.5Pb2Br5 is an indirect semiconductor with the VBM positioned at Γ-point and the CBM located near X-point. So, it requires less phonon for the momentum conversion in the electron–hole recombination process. While the Hubbard U parameter causes the minor effect on the band structure obtained by GGA-PBE and GGA-PBE + U methods, the exchange hole effect included in the TB-mBJ method induces a significant rise of unoccupied states widening the band gap. When introducing both U and SOC parameters in the TB-mBJ + U + SOC method, the CBM is slightly relocated from X-point and the unoccupied states in the conduction band are remarkably shifted down to lower energy levels which narrow band gap of K0.5Rb0.5Pb2Br5 to 3.320 eV.
 | ||
| Fig. 5 Band structures of K0.5Rb0.5Pb2Br5 calculated by GGA-PBE, TB-mBJ, GGA-PBE + U, and TB-mBJ + U + SOC techniques (the Fermi level is set to be at zero). | ||
4.2 Optical properties of K0.5Rb0.5Pb2Br5
The optical properties of K0.5Rb0.5Pb2Br5 can be obtained based on TB-mBJ + U + SOC calculations of the wave function |knp〉 and eigenvalue energy Ekn in a unit-cell volume V with crystal momentum k and spin σ. Then, the real ε1(ω) and imaginary ε2(ω) parts of the dielectric function ε(ω) can be calculated following Kramers–Kronig relations:66
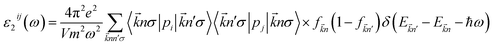 | (1) |
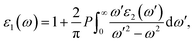 | (2) |
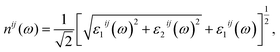 | (3) |
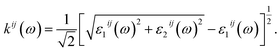 | (4) |
Finally, the adsorption coefficient α(ω), optical reflectance R(ω), and the energy loss spectrum L(ω) were calculated:
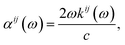 | (5) |
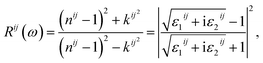 | (6) |
 | (7) |
It is shown in Fig. 6(a) that the polarization of ε1(ω) function is only recognizable at the extrema of its spectrum. The reflectivity of K0.5Rb0.5Pb2Br5 is high at about 4 eV, where ε1(ω) functions reach their maximum values. The polarization is also remarkable in the vicinity of 5 eV, where the permittivity along the y/z-directions is higher than along the x-direction. In the energy range of 5–7 eV, there is sharp decrease of ε1(ω) functions to negative values resulting in the damping of electromagnetic (EM) wave and a reverse polarization where the intensity of ε1xx(ω) is higher than the ones of ε1yy(ω) and ε1zz(ω). For energy level higher than 7 eV, the polarization becomes minor, and the ε1(ω) functions sharply increase to the third highest peak followed by weak response to the incident EM wave with little fluctuation.
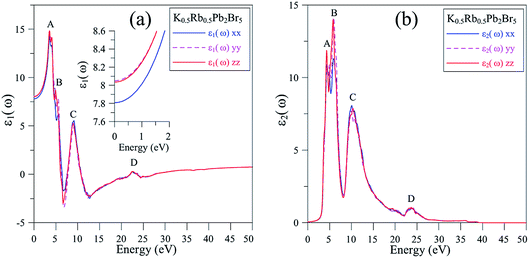 | ||
| Fig. 6 (a) Real and (b) imaginary components of dielectric function ε(ω) of K0.5Rb0.5Pb2Br5 (calculated with TB-mBJ + U + SOC). | ||
The inter-band transition of electron in K0.5Rb0.5Pb2Br5 is featured by the ε2(ω) spectrum in Fig. 6(b), where remarkable phonon absorption is recognized at the energy level of about 5 eV corresponding to the first ε2(ω) extremum. The polarization of ε2(ω) is observed in the energy range of 5–6 eV, where ε2yy(ω) and ε2zz(ω) are higher than ε2xx(ω). At 6 eV, ε2(ω) functions reach the highest value with strongest polarization, before a sharp decrease to the negative concave down point at 8 eV. For energy level higher than 8 eV, the ε2(ω) functions rise up again to the third highest peak at 11 eV where the reverse polarization occurs. The inter-band transition of electron is expected to be at highest rate in the energy range of 4–7 eV. This range can be narrowed by doping with rare-earth ions, as in the cases of rare-earth doped KPb2Br5, and RbPb2Br5,13,68,69 making the rare-earth doped K0.5Rb0.5Pb2Br5 be one of the most promising laser materials operating in the mid-infrared energy range. The second highest extremum of ε2(ω) is found in the vicinity of 10–12 eV. This signifies a remarkably high inter-band transition between valence core levels near −6.5 eV to the conduction band, which is an advantage for core valence luminescence induced by impurities in such halides with large band gap like K0.5Rb0.5Pb2Br5.70–73
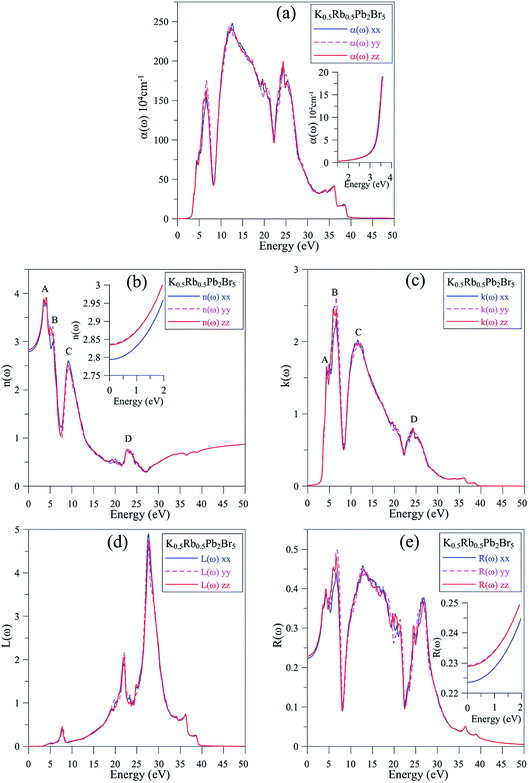
In Fig. 7(a), the absorption edge of K0.5Rb0.5Pb2Br5 is positioned near 3.5 eV indicating the transparency of this compound for EM wave with wave-length longer than 354 nm. For the energy range of 5–25 eV, the absorption coefficient α(ω) can reach the order of magnitude of 106 cm−1 at 7 eV, 12 eV, and 24 eV where significant polarization is also observed. In the vicinity of 7 eV, the αyy(ω) and αzz(ω) functions are higher than αxx(ω), then the first reverse polarization occurs at the concave down point at 8 eV, and the polarization changes again at concave down point at 22 eV. The extremum of α(ω) at a very high energy level of 24 eV can be explained by the inter-band transition between the Pb-5d3/2 and Pb-5d5/2 sub-states and the unoccupied states in the conduction band.
The reflectivity R(ω) of K0.5Rb0.5Pb2Br5 plotted in Fig. 7(e) is characterized by the rate of 40–50%. The reflectivity R(ω) is anisotropic in the vicinities of 5 eV, 13 eV, and 27 eV. The reverse polarization is observed at concave down points at 8 eV, and 22 eV. For the energy level lower than 3.5 eV, the absorption coefficient α(ω) is almost zero, so the reflectivity may origin from the oscillations of the polarization of atoms. At the energy level ranging from 4 eV to 27 eV, the reflectivity R(ω) increases significantly together with the increase of α(ω), but not at the same rate. The refractive index n(ω), the extinction coefficient k(ω), and the energy loss L(ω) were calculated and presented in Fig. 7(b)–(d).
Fig. 7(b) and (c) show good relationship of shapes between n(ω) and k(ω) with ε1(ω) and ε2(ω), respectively. The n(ω), spectrum starts at static value of about 2.8, with the difference due to polarization of about 0.05, indicating the existence of birefringence in K0.5Rb0.5Pb2Br5. The n(ω) spectrum increases to the highest peaks of 3.8–3.9 at energy range of 3–5 eV. This causes the largest change in the velocity of EM wave with wave-length of 348–413 nm in the K0.5Rb0.5Pb2Br5 compound. The reverse polarization is found at the concave down point at 5.5 eV, then, at 10 eV n(ω), it reaches its highest peak where nxx(ω) is higher than nyy(ω) and nzz(ω). The extinction coefficient k(ω) is remarkable in the energy range of 5–14 eV with the highest peak at 6 eV, the attenuation decreases gradually for energies higher 15 eV. The loss energy L(ω) shown in Fig. 7(d) is very small for energy level lower than 28 eV which is opposite to behavior of the absorption coefficient α(ω) in Fig. 7(a), this signifies a minor thermalization owing to the sub-band transition of the electron in the conduction band. However, in the vicinity of 28 eV both L(ω) and α(ω) reach their high peaks because of strong interaction of atoms and photons of these energies.
5 Conclusion
The electronic structure and optical properties of K0.5Rb0.5Pb2Br5 semiconductor were studied by applying the first-principle calculation within Kohn–Sham framework. The GGA-PBE and TB-mBJ methods with and without Hubbard U and SOC parameters were employed to investigate the electronic structure of K0.5Rb0.5Pb2Br5 under the effects of kinetic energy, Coulomb potential induced by exchange hole, and spin-orbital interaction. It was found that the TB-mBJ + U + SOC method well reproduces electronic structure of K0.5Rb0.5Pb2Br5 in comparison with XPS spectrum.The band gap of K0.5Rb0.5Pb2Br5 was determined for the first time to be indirect, and the theoretically predicted value is of 3.32 eV. The Pb-5d3/2 and Pb-5d5/2 sub-states are located in vicinities of −20 eV and −18 eV, respectively. The middle part of the valence band is mainly formed by K-3p, Rb-4p, Br-4s states, in which the separation of Rb-4p3/2 and Rb-4p1/2 was also observed. The valence band maximum (VBM) is mostly composed of hybridization of Br-p and Pb-s/p states. While the conduction band minimum (CBM) is dominated by Pb-p and Br-p states, the upper part is constructed by Rb-s and K-s states. The TB-mBJ + U + SOC calculations concerning main peculiarities of contributions of Br-4p and K-4s electronic states in the K0.5Rb0.5Pb2Br5 VB are fairly supported by XES and XPS experiments.
The reflectivity of K0.5Rb0.5Pb2Br5 is high for photons with energies of about 4 eV. In the energy range from 5 eV to 7 eV, the ε1(ω) functions undergo a sharp decrease to negative values resulting in the damping of electromagnetic wave and a reverse polarization where the intensity of ε1xx(ω) is higher than the ones of ε1yy(ω) and ε1zz(ω). For energy level higher than 7 eV, K0.5Rb0.5Pb2Br5 weakly responds to the incident electromagnetic wave. The phonon absorption is remarkable at 5 eV. The polarization of ε2(ω) is observed in the energy range from 5 eV to 6 eV, where ε2yy(ω) and ε2zz(ω) are higher than ε2xx(ω). At 6 eV, ε2(ω) functions reach the highest value with strongest polarization. The reverse polarization occurs at 8 eV. The inter-band transition of electron is expected to be at highest rate in the energy range from 4 eV to 7 eV. This range can be narrowed by doping with rare-earth ions, making the rare-earth doped K0.5Rb0.5Pb2Br5 be one of the most promising laser materials operating in the mid-infrared energy range. The second highest extremum of ε2(ω) is found in the vicinity of 10–12 eV. This signifies a remarkably high inter-band transition between valence core levels near −6.5 eV to the conduction band, which is an advantage for core valence luminescence induced by impurities.
The K0.5Rb0.5Pb2Br5 compound is transparent for electromagnetic wave with wave-length longer than 354 nm. For the energy range from 5 eV to 25 eV, the absorption coefficient α(ω) can reach the order of magnitude of 106 cm−1 with three main extrema at 7 eV, 12 eV, and 24 eV where significant polarization is also observed. The reverse polarization occurs at the concave down points at 8 eV, and 22 eV. K0.5Rb0.5Pb2Br5 reveals significant birefringence at energy levels in the vicinity of 5 eV. Electromagnetic waves with wave-length in the interval from 348 nm to 413 nm undergo a remarkable change of velocity in the K0.5Rb0.5Pb2Br5 compound. The extinction coefficient k(ω) is remarkable in the energy range from 5 eV to 14 eV with the highest peak at 6 eV, the attenuation decreases gradually for energies higher 15 eV. For energy levels lower than 28 eV, minor thermalization may happen owing to the sub-band transition of the electron in the conduction band. However, in the vicinity of 28 eV both L(ω) and α(ω) reach their high peaks because of the strong interaction of atoms and photons of these energies. Generally, the fact that the polarization of optical properties occurs at the extrema in the optical spectra. Despite that fact that the polarization is minor in most of the cases, it is necessary to be taken into account when using K0.5Rb0.5Pb2Br5 as an active host for laser materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2018.334. The present work was supported also by the Russian Foundation for Basic Research (grant no. 19-42-540012).References
- M. Bertolotti and R. Roy, Am. J. Phys., 1985, 53, 507–508 CrossRef.
- M. C. Cassidy, A. Bruno, S. Rubbert, M. Irfan, J. Kammhuber, R. N. Schouten, A. R. Akhmerov and L. P. Kouwenhoven, Science, 2017, 355, 939 CrossRef CAS PubMed.
- T. H. Maiman, Nature, 1960, 187, 493–494 CrossRef.
- V. Lupei, in Laser Materials: Relationship Between Materials and Laser Properties, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, Oxford, 2001, pp. 4416–4423 Search PubMed.
- C. Tu and Y. Wang, in The Recent Development of Rare Earth-Doped Borate Laser Crystals, ed. A. Al-Khursan, IntechOpen, 2012, pp. 63–118 Search PubMed.
- M. Velázquez, A. Ferrier, J.-L. Doualan and R. Moncorgé, in Rare-earth-doped low phonon energy halide crystals for mid-infrared laser sources, ed. A. Al-Khursan, IntechOpen, 2012, pp. 119–142 Search PubMed.
- L. Isaenko, A. Yelisseyev, A. Tkachuk, S. Ivanova, S. Vatnik, A. Merkulov, S. Payne, R. Page and M. Nostrand, Mater. Sci. Eng., B, 2001, 81, 188–190 CrossRef.
- A. Ferrier, M. Velázquez, J.-L. Doualan and R. Moncorgé, J. Lumin., 2009, 129, 1905–1907 CrossRef CAS.
- L. Isaenko, A. Yelisseyev, A. Tkachuk and S. Ivanova, in New Monocrystals with Low Phonon Energy for Mid-IR Lasers, ed. M. Ebrahim-Zadeh and I. T. Sorokina, Springer Netherlands, Dordrecht, 2008, pp. 3–65 Search PubMed.
- O. Y. Khyzhun, V. L. Bekenev, N. M. Denysyuk, O. V. Parasyuk and A. O. Fedorchuk, J. Alloys Compd., 2014, 582, 802–809 CrossRef CAS.
- A. G. Okhrimchuk, V. K. Mezentsev, N. V. Lichkova and V. N. Zagorodnev, Opt. Mater., 2015, 43, 1–5 CrossRef CAS.
- K. Rademaker, E. Heumann, G. Huber, S. A. Payne, W. F. Krupke, L. I. Isaenko and A. Burger, Opt. Lett., 2005, 30, 729–731 CrossRef CAS PubMed.
- K. Rademaker, W. F. Krupke, R. H. Page, S. A. Payne, K. Petermann, G. Huber, A. P. Yelisseyev, L. I. Isaenko, U. N. Roy, A. Burger, K. C. Mandal and K. Nitsch, J. Opt. Soc. Am. B, 2004, 21, 2117–2129 CrossRef CAS.
- R. Balda, J. Fernández, A. Mendioroz, M. Voda and M. Al-Saleh, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 165101 CrossRef.
- L. I. Isaenko, S. V. Melnikova, A. A. Merkulov, V. M. Pashkov and A. Y. Tarasova, Phys. Solid State, 2009, 51, 589–592 CrossRef CAS.
- V. A. Pustovarov, I. N. Ogorodnikov, N. S. Kuzmina, A. A. Smirnov and A. P. Yelisseyev, Phys. Solid State, 2005, 47, 1570–1572 CrossRef CAS.
- A. M. Tkachuk, S. Ivanova, L. I. Isaenko, A. P. Yelisseyev, S. Payne, R. Solarz, R. Page and M. Nostrand, Opt. Spectrosc., 2002, 92, 83–94 CrossRef CAS.
- S. V. Melnikova, L. I. Isaenko, V. M. Pashkov and I. V. Pevnev, Phys. Solid State, 2005, 47, 332–336 CrossRef CAS.
- V. B. Shirokov, Y. I. Yuzyuk, B. Dkhil and V. V. Lemanov, Phys. Solid State, 2008, 50, 928–936 CrossRef CAS.
- L. I. Isaenko, A. A. Merkulov, S. V. Melnikova, V. M. Pashkov and A. Y. Tarasova, Cryst. Growth Des., 2009, 9, 2248–2251 CrossRef CAS.
- N. V. Lichkova, V. N. Zagorodnev, A. G. Okhrimchuk, L. N. Butvina, D. V. Irzhak and V. K. Karandashev, Inorg. Mater., 2014, 50, 197–204 CrossRef CAS.
- A. Y. Tarasova, L. I. Isaenko, V. G. Kesler, V. M. Pashkov, A. P. Yelisseyev, N. M. Denysyuk and O. Y. Khyzhun, J. Phys. Chem. Solids, 2012, 73, 674–682 CrossRef CAS.
- L. I. Isaenko, A. A. Merkulov, A. Y. Tarasova, V. M. Pashkov and V. A. Drebushchak, J. Therm. Anal. Calorim., 2009, 95, 323–325 CrossRef CAS.
- R. Heid, in Density Functional Perturbation Theory and Electron Phonon Coupling, ed. E. Pavarini, E. Koch and U. Schollwöck, Forschungszentrum Jülich, 2013, vol. 3 Search PubMed.
- M. Gecevičius, M. Beresna, J. Zhang, W. Yang, H. Takebe and P. G. Kazansky, Opt. Express, 2013, 21, 3959–3968 CrossRef PubMed.
- G. Huber, W. W. Krühler, W. Bludau and H. G. Danielmeyer, J. Appl. Phys., 1975, 46, 3580–3584 CrossRef CAS.
- N. Pandey, A. Kumar and S. Chakrabarti, RSC Adv., 2019, 9, 29556–29565 RSC.
- N. Pandey, A. Kumar and S. Chakrabarti, ACS Appl. Mater. Interfaces, 2019, 11, 39248–39253 CrossRef CAS PubMed.
- N. Pandey, A. Kumar and S. Chakrabarti, Appl. Surf. Sci., 2020, 504, 144411 CrossRef CAS.
- N. Pandey, A. Kumar and S. Chakrabarti, J. Magn. Magn. Mater., 2020, 497, 166073 CrossRef.
- T. V. Vu, N. V. Hieu, L. T. P. Thao, N. N. Hieu, H. V. Phuc, H. D. Bui, M. Idrees, B. Amin, L. M. Duc and C. V. Nguyen, Phys. Chem. Chem. Phys., 2019, 21, 22140–22148 RSC.
- T. V. Vu, N. V. Hieu, H. V. Phuc, N. N. Hieu, H. Bui, M. Idrees, B. Amin and C. V. Nguyen, Appl. Surf. Sci., 2020, 507, 145036 CrossRef CAS.
- G. K. H. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195134 CrossRef.
- K. Schwarz, P. Blaha and G. K. H. Madsen, Comput. Phys. Commun., 2002, 147, 71–76 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155109 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107–3114 CrossRef CAS.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929–16934 CrossRef CAS PubMed.
- P. Novák, F. Boucher, P. Gressier, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 235114 CrossRef.
- M. J. Verstraete, M. Torrent, F. Jollet, G. Zérah and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045119 CrossRef.
- M. Kopciuszyński, M. Krawiec, R. Zdyb and M. Jałochowski, Sci. Rep., 2017, 7, 46215 CrossRef PubMed.
- C. I. Oprea, Z. Rinkevicius, O. Vahtras, H. Ågren and K. Ruud, J. Chem. Phys., 2005, 123, 014101 CrossRef PubMed.
- A. Hermann, J. Furthmüller, H. W. Gäggeler and P. Schwerdtfeger, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155116 CrossRef.
- A. A. Lavrentyev, B. V. Gabrelian, V. T. Vu, N. M. Denysyuk, P. N. Shkumat, A. Y. Tarasova, L. I. Isaenko and O. Y. Khyzhun, J. Phys. Chem. Solids, 2016, 91, 25–33 CrossRef CAS.
- A. A. Lavrentyev, B. V. Gabrelian, V. T. Vu, N. M. Denysyuk, P. N. Shkumat, A. Y. Tarasova, L. I. Isaenko and O. Y. Khyzhun, Opt. Mater., 2016, 53, 64–72 CrossRef CAS.
- T. V. Vu, A. A. Lavrentyev, B. V. Gabrelian, L. N. Ananchenko, O. V. Parasyuk, O. Karaim and O. Y. Khyzhun, J. Mater. Sci.: Mater. Electron., 2018, 29, 16088–16100 CrossRef CAS.
- T. V. Vu, A. A. Lavrentyev, B. V. Gabrelian, V. A. Ocheretova, O. V. Parasyuk and O. Y. Khyzhun, Mater. Chem. Phys., 2018, 208, 268–280 CrossRef CAS.
- T. V. Vu, A. A. Lavrentyev, B. V. Gabrelian, H. D. Tong, O. V. Parasyuk and O. Y. Khyzhun, Computational Condensed Matter, 2019, 21, e00392 CrossRef.
- T. V. Vu, A. Lavrentyev, B. Gabrelian, D. D. Vo, K. D. Pham, N. Denysyuk, L. Isaenko, A. Tarasova and O. Khyzhun, Opt. Mater., 2020, 102, 109793 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowski, F. Tran and L. D. Marks, WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, ed. K. Schwarz, Techn. Universität Wien, Austria, 2018, ISBN 3-9501031-1-2 Search PubMed.
- W. Kohn, A. D. Becke and R. G. Parr, J. Chem. Phys., 1996, 100, 12974–12980 CrossRef CAS.
- P. D. C. King, T. D. Veal, C. F. McConville, F. Fuchs, J. Furthmüller, F. Bechstedt, J. Schörmann, D. J. As, K. Lischka, H. Lu and W. J. Schaff, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115213 CrossRef.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- O. Y. Khyzhun, V. L. Bekenev, N. M. Denysyuk, I. V. Kityk, P. Rakus, A. O. Fedorchuk, S. P. Danylchuk and O. V. Parasyuk, Opt. Mater., 2013, 36, 251–258 CrossRef CAS.
- J. A. Bearden, Rev. Mod. Phys., 1967, 39, 78–124 CrossRef CAS.
- T. P. Schreiber and A. M. Wims, X-Ray Spectrom., 1982, 11, 42–45 CrossRef CAS.
- D. Cullen, J. Hubbell and L. Kissel, EPDL97: The evaluated photo data library ’97 version, Lawrence Livermore National Laboratory, Report UCRL-50400, 1997, vol. 6, rev. 5 Search PubMed.
- M. Blokhin and I. Shweizer, X-ray Spectroscopy Handbook, 1982 Search PubMed.
- A. Lukirskii, I. Brytov and V. Fomichev, Sov. Phys. Solid State, 1966, 8, 72–75 Search PubMed.
- A. McAlister, R. Dobbyn, J. Cuthile and M. Williams, Soft X-Ray Emission Spectra of Metallic Solids: Critical Review of Selected Systems and Annotated Spectral Index, Nat. Bur. Stand. (U.S.), Spec. Publ., 1974, vol. 369 Search PubMed.
- A. Meisel, G. Leonhardt and R. Sargan, X-Ray Spectra and Chemical Binding, Springer-Verlag, Berlin/Heidelberg, 1989, p. 419 Search PubMed.
- E. Z. Kurmaev, A. Moewes, Z. V. Pchelkina, I. A. Nekrasov, A. A. Rempel and D. L. Ederer, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 073108 CrossRef.
- X-Ray Absorption and X-Ray Emission Spectroscopy - Theory and Applications, ed. J. A. van Bokhoven and C. Lamberti, John Wiley & Sons Ltd, Chichester, United Kingdom, 2016 Search PubMed.
- F. Wooten, Optical Properties of Solids, Academic Press, New York, 1972 Search PubMed.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- U. Hömmerich, E. Brown, P. Amedzake, S. B. Trivedi and J. M. Zavada, J. Appl. Phys., 2006, 100, 113507 CrossRef.
- A. G. Bluiett, D. Peele, K. Norman, E. Brown, U. Hömmerich, S. B. Trivedi and J. M. Zavada, Opt. Mater., 2011, 33, 985–988 CrossRef CAS.
- A. S. Voloshinovskii, V. B. Mikhailik and P. A. Rodnyi, Radiat. Meas., 1995, 24, 383–385 CrossRef CAS.
- P. A. Rodnyi, Radiat. Meas., 2004, 38, 343–352 CrossRef CAS.
- Y. Chornodolskyy, G. Stryganyuk, S. Syrotyuk, A. Voloshinovskii and P. Rodnyi, J. Phys.: Condens. Matter, 2007, 19, 476211 CrossRef.
- G. Shwetha and V. Kanchana, J. Phys.: Condens. Matter, 2019, 31, 115501 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |