Open Access Article
Open Access ArticleRotational excitation of C2(X1Σg+) by para- and ortho-H2
Faouzi Najar *ab and
Yulia Kalugina
*ab and
Yulia Kalugina cd
cd
aLaboratoire de Spectroscopie Atomique, Moléculaire et Application, Faculté des Sciences, Université Tunis el Manar, Tunis 2092, Tunisia. E-mail: faouzi.najar@ipeit.rnu.tn
bInstitut Préparatoire aux Etudes d’Ingénieurs de Tunis, Université de Tunis, Tunis 1007, Tunisia
cInstitute of Spectroscopy RAS, Fizicheskaya Str. 5, 108840 Troitsk, Moscow, Russia
dDepartment of Optics and Spectroscopy, Tomsk State University, 36 Lenin Ave., Tomsk 634050, Russia
First published on 27th February 2020
Abstract
A new four dimensional (4D) potential energy surface for the C2(X1Σg+)–H2 van der Waals system is generated. The potential was obtained from a multi-reference internally contracted configuration-interaction method including the Davidson correction (MRCI+Q). The four atoms were described using the augmented correlation-consistent quadruple zeta (aug-cc-pVQZ) basis sets. Both molecules were treated as rigid rotors. Close-coupling calculations of the inelastic integral cross sections of C2 in collisions with para-H2(jH2 = 0) and ortho-H2(jH2 = 1) were also carried out at low energies. After Boltzmann thermal averaging, rate coefficients were obtained for temperatures ranging from 5 to 100 K. The rate coefficients for collisions with ortho-H2 are significantly larger than the rate coefficients for collisions with para-H2.
1 Introduction
The C2 molecule is one of the best known constituents of the interstellar medium. It was first detected by Souza and Lutz.1 Subsequently, many absorption lines have been detected in the near-infrared region for the A1Πu–X1Σg+ Phillips system,2–8 and in the UV region for the D1Σu–X1Σg+ Mulliken system9 and the F1Πu–X1Σg+ band.10,11 The C2 molecule is used as a diagnostic probe of the physical condition in diffuse molecular clouds. The populations of its rotational levels are determined by competition between collisional excitation and radiative excitation through absorption into excited electronic states followed by fluorescence to various vibrational levels of X1Σg+.2 The analysis of rotationally excited C2 provides useful information about the density of collision partners, the kinetic temperature and the strength of the radiation field permeating the gas.12 In order to perform a more accurate analysis of C2 excitation, rotational rate coefficients of C2 excited by its principal interstellar collisional partner, H2, are required. In ref. 13, the full dimensional PES was calculated by the CCSD(T)-F12a/cc-pCVTZ-F12 method. However, we suppose that there is a lack of static correlation because of the multi configurational character of the PES for interacting C2 and H2. In this paper, we present a new complete four dimensional (4D) PES for the ground electronic state of the C2–H2 collisional system calculated at the MRCI+Q level. Then, this accurate PES was used to perform rotational excitation of C2 with both para-H2 and ortho-H2.The activation energy of the C2 + H2 ⇌ C2H + H reaction being about 900 cm−1,14 inelastic cross sections of C2 in collisions with H2(jH2 = 0) and H2(jH2 = 1) are reported for total energies of up to 1000 cm−1 for the first 9 even rotational levels, yielding converged rate coefficients up to 100 K.
Excitation rate coefficients of C2 excited by para-H2(jH2 = 0) were provided by Najar et al.15 In this study, the PES was derived by averaging only over three specific H2 orientations. These calculations gave a first estimate of C2–para-H2 collisional rate coefficients. However, rotational excitation rate coefficients for C2 in collision with ortho-H2 are also needed for a complete description of C2 excitation.16
The paper is organized as follows: Section 2 describes the calculation of the potential energy surface, Section 3 contains a concise description of the scattering calculations, and in Section 4, we present and discuss our results.
2 Potential energy surface
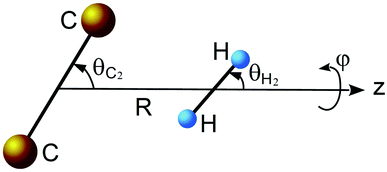
As mentioned in previous work,17 the ground electronic state of the C2–H2 system is described by two dominant configurations. Because of this multi configurational character, the potential energy surface (PES) of this van der Waals complex was accomplished by first performing full valence complete active space (CASSCF) calculations18,19 followed by multi-reference internally contracted configuration-interaction (MRCI) calculations,20,21 including all single and double excitations from the CASSCF reference function. The contributions of higher-order excitations were estimated using the normalized multi-reference Davidson correction.22,23 In the CASSCF-MRCI calculations, the active space is defined by distributing 10 electrons in 10 molecular orbitals. The 1s2 orbitals of the carbon atoms were kept frozen. To achieve a good description of weak interactions, the calculations were performed using a rather large aVQZ basis set of Dunning.24–26 All ab initio calculations were carried out using the MOLPRO program package.27The body-fixed coordinate system presented in Fig. 1 was used. The center of the coordinates is placed in the middle of the bond of the C2 molecule. Vector R is directed along the z-axis and connects the C2 and H2 centers of mass. The rotation of the C2 molecule is defined by angle θC2 and the rotation of the H2 molecule is defined by angle θH2, while ϕ is the dihedral angle.
The ab initio calculations were performed using the approximation of rigid interacting molecules with the H2 bond length corresponding to the ground vibrational state: rH–H = 1.449 Bohr.28 For C2, we used the experimental equilibrium distance rC–C = 2.348 Bohr,29 which differs by less than 1% from the calculated value obtained by averaging over the ν = 0 wavefunction. We note that employing state-averaged geometries is a reliable approximation for including zero-point vibrational effects within a rigid-rotor PES.30–32
In order to determine the interaction potential V(R,θC2,θH2,ϕ), the basis set superposition error (BSSE) was corrected for all geometries with the Boys and Bernardi counterpoise scheme:33
| V(R,θC2,θH2,ϕ) = EC2–H2(R,θC2,θH2,ϕ) − EC2(R,θC2,θH2,ϕ) − EH2(R,θC2,θH2,ϕ) | (1) |
At each point R the calculations were carried out for 122 angular orientations with θC2 varying from 0° to 180°, θH2 varying from 0° to 90°, and ϕ varying from 0° to 90°. R-distances were varied from 4.8 to 20 Bohr, giving 29 grid points.
For the solution of the close-coupling scattering equations, it is most convenient to expand the interaction potential V(R,θC2,θH2,ϕ) into the angular functions at each value of R. For the scattering of two linear rigid rotors, we used the expansion of Green:34
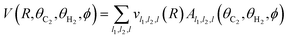 | (2) |
The basis functions Al1,l2,l(θC2,θH2,ϕ) are products of the associated Legendre polynomials Plm:
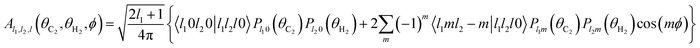 | (3) |
To obtain the expansion described above, at each point of the radial grid R we fitted the ab initio points to expression (2) using a linear least squares method, with lmax1 = 6 and lmax2 = 4. The choice of such expansion parameters limits the results to a total of 28 radial expansion coefficients vl1,l2,l(R). The root-mean-square error (rmse) of the fits in the long and (attractive) medium range was of the order of 10−3 to 10−2 cm−1. The medium repulsive wall (energies of the order of 102 to 103 cm−1) was reproduced with rmse of 1–10 cm−1.
Each radial coefficient was interpolated using cubic splines for 4.8 < R ≤ 16a0. For R > 16a0 the energy (not the coefficients) was extrapolated using the c5/R5 + c6/R6 functional form based on its values at R = 16a0 and R = 18a0. For R < 4.8a0 the energy was extrapolated using the functional form A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(BR) based on its values at R = 4.8a0 and R = 5a0. Thus, our PES covers the whole range of R. However, we suggest to use it in the range from 3.0 to 100a0.
exp(BR) based on its values at R = 4.8a0 and R = 5a0. Thus, our PES covers the whole range of R. However, we suggest to use it in the range from 3.0 to 100a0.
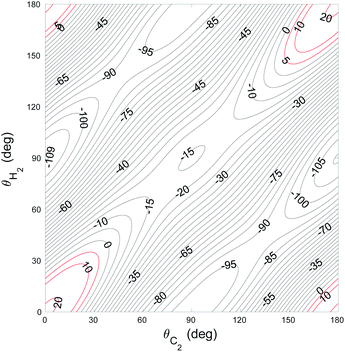
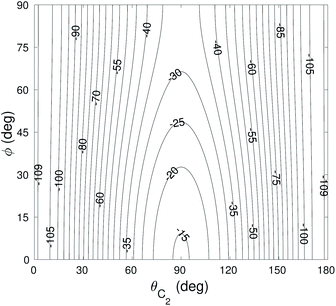
The global minimum of the 4D PES corresponds to a T-shaped structure with θC2 = 0°, θH2 = 90°, ϕ = 0° and R = 6.92a0 with V = −109.22 cm−1. In Fig. 2–4 we present the contour plots of the interaction energy surface for fixed equilibrium parameters. It is seen that there is a weak anisotropy of the PES for the Jacoby angle ϕ and a strong anisotropy for the angle θC2. The local minimum of the PES occurs for another T-shaped structure with θC2 = 90°, θH2 = 0°, ϕ = 0° and R = 6.70a0. The interaction energy at this point is V = −101.63 cm−1.
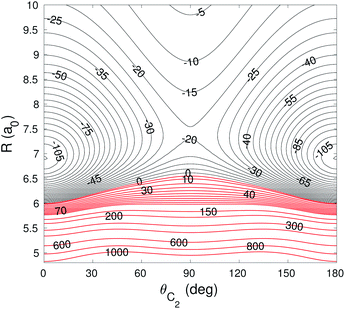 | ||
| Fig. 4 Contour plot of the cut of the 4D PES for fixed θH2 = 90° and ϕ = 0°. Energy is in cm−1. Red contour lines represent repulsive interaction energies. | ||
3 Scattering study of excitation of C2 by para- and ortho-H2
In the present work, we consider collisions of 12C2 with para- and ortho-H2. Only even rotational levels j were considered here because, in homonuclear molecules with zero nuclear spins like C2, rotational levels with odd values are not allowed. On the other hand, the H2 molecule can exist in two forms denoted para- and ortho-H2. In the former, the nuclear spins of the hydrogen atoms are opposed resulting in total I = 0, whereas, in the latter, the nuclear spins are aligned and I = 1. As the nuclear wavefunction must be asymmetric, in para-H2, only even rotational states, jH2 = 0, 2,… are allowed, and in ortho-H2, only odd values, jH2 = 1, 3,… are allowed.Full close-coupling calculations35 were carried out for total energies up to 1000 cm−1, using C2 and H2 as rigid rotors with rotational and centrifugal distortion constants BC2 = 1.820 cm−1 and DC2 = 6.92 × 10−6 cm−1 (ref. 36), and BH2 = 60.853 cm−1 and DH2 = 3.3 × 10−6 cm−1,29 respectively. Transitions among C2 rotational levels up to j = 16 were computed for collisions involving para-H2(jH2 = 0) and ortho-H2(jH2 = 1). For convergence of the cross sections, the rotational states jH2 = 0, 2 and jH2 = 1, 3 were included in the rotational basis sets for para- and ortho-H2, respectively. The inclusion of the jH2 = 4 channel in para-H2 affects the cross sections by less than 1 percent. For the C2 molecule, the rotational basis set was extended up to jmax = 24 at the largest total energy considered (1000 cm−1). The coupled scattering equations were solved by the MOLSCAT code37 using the propagator of Manolopoulos.38 For the C2–H2 system the reduced mass is μ = 1.8597 amu. The integration parameters were chosen to ensure convergence of the cross sections in this range. The minimum and maximum integration distances chosen were Rmin = 3 Bohr and Rmax = 50 Bohr, respectively. The maximum value of the total angular momentum J used in the calculations was chosen according to a convergence criterion of 0.01 Å2. The energy grid was adjusted to describe all the details of the resonances of the inelastic cross sections. The thermal rate coefficients at temperature T are obtained by averaging the rotational inelastic cross sections, σj→j′, over a Boltzmann distribution of collision energy Ec:
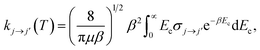 | (4) |
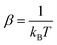 , where kB is the Boltzmann constant.
, where kB is the Boltzmann constant.
4 Results
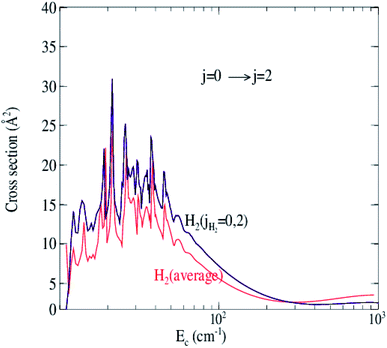
First we compare the σ0→2 cross sections for the excitation of C2 with para-H2(jH2 = 0, 2) calculated with the 4D PES and including jH2 = 0, 2 in the rotational basis set of H2 with the cross sections for the excitation of C2 with para-H2 calculated previously by Najar et al.15 with a 2D effective PES averaged over three specific H2 orientations using equal weights of 1/3 for the three geometries considered. As we can see in Fig. 5, the two cross sections are close, having the same form of resonances with a shift and small difference in amplitudes. The difference is appreciable at high energies, approaching 35 percent. To understand where the difference comes from, we present in Table 1 cross sections at different energies for C2-paraH2 calculations with a PES averaged over 3 orientations, C2-paraH2 4D PES calculations with just the basis jH2 = 0 and C2-paraH2 4D PES calculations with the rotational basis involving jH2 = 0 and jH2 = 2 levels (jH2 = 0, 2). We note that at low energies the major difference (∼15%) is due to lack of anisotropy in the PES averaged over 3 orientations. At high energies the inaccuracies of the PES have only a minor influence on the cross sections, and the differences stem mainly from neglect of the jH2 = 2 rotational state. This result was also confirmed by Lique et al.39 in the SiS–H2 system.| Energy (cm−1) | 2D effective PES | 4D PES, jH2 = 0 | 4D PES, jH2 = 0, 2 |
|---|---|---|---|
| 50 | 11.249 | 13.307 | 14.160 |
| 100 | 5.613 | 6.580 | 7.087 |
| 300 | 2.622 | 2.650 | 2.515 |
| 500 | 2.978 | 2.819 | 2.379 |
| 1000 | 3.540 | 3.298 | 2.567 |
Fig. 6 shows the collision energy dependence of the 0 → 2 inelastic integral cross sections of C2 in collision with para-H2(jH2 = 0) (including jH2 = 0, 2) and ortho-H2(jH2 = 1) (including jH2 = 1, 3). The figure illustrates many resonances in the cross sections for collision energies below 100 cm−1, which are a consequence of the temporary trapping of the H2 molecule in the attractive potential well, involving the formation of quasi-bound states of the van der Waals C2–H2 complex. We note a difference in amplitude and shape of the resonances between the two cross sections. The collisions with ortho-H2 are more strongly inelastic. This is expected because, unlike with ortho-H2, the long-range interactions with para-H2(jH2 = 0) do not involve the permanent quadrupole moment of the H2 molecule; only induction and dispersion forces participate.40 This behavior was also found in H2–H2 (ref. 41) and SO2–H2 (ref. 42) collisions.
 | ||
| Fig. 6 Cross sections for rotational excitation of C2 by para-H2(jH2 = 0, 2) and ortho-H2(jH2 = 1, 3) for the 0 → 2 transition as a function of collision energy. | ||
Rate coefficients for rotational excitation of C2 by para-H2(jH2 = 0) and ortho-H2(jH2 = 1) have been computed from cross sections generated from the grid of collision energies. The representative variation with temperature is illustrated in Fig. 7. The curves in Fig. 7 and the results in Table 2 show that the rates for ortho-H2(jH2 = 1) are significantly larger by a factor of 5 on average. This result, also found previously for some systems like CO–H2,43 H2O–H2 (ref. 44) and SiS–H2,45 confirms the expectation that ortho-H2(jH2 = 1) is a more efficient perturbant than para-H2(jH2 = 0).
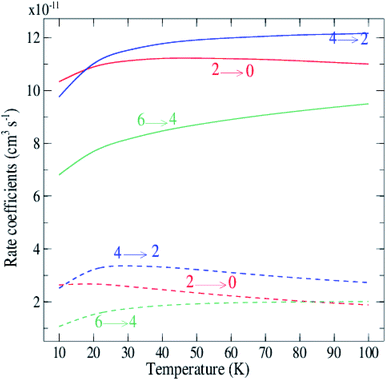 | ||
| Fig. 7 Temperature dependence of rotational de-excitation rate coefficients of C2 excited by H2 for Δj = 2 transitions. Dashed lines: para-H2(jH2 = 0); solid lines: ortho-H2(jH2 = 1). | ||
| Transition | Para-H2 | Ortho-H2 |
|---|---|---|
| 2 → 0 | 0.234(-10) | 1.122(-10) |
| 0.188(-10) | 1.100(-10) | |
| 4 → 2 | 0.322(-10) | 1.191(-10) |
| 0.273(-10) | 1.216(-10) | |
| 6 → 4 | 0.192(-10) | 0.870(-10) |
| 0.201(-10) | 0.949(-10) | |
| 8 → 6 | 0.110(-10) | 0.610(-10) |
| 0.141(-10) | 0.704(-10) |
In the paper of Lavendy et al.,46 for construction of the PES the authors considered only 5 relative orientations of C2 and H2 for each R value. Later, Phillips47 used this PES to compute the rate coefficients using the close-coupling approach. In our previous work,15 we constructed a 2D PES based on nearly 900 ab initio points. For each (R,θ) we considered 3 angular orientations of the H2 molecule, the energies of which were then averaged. In that work,15 we compared our collision rates for C2–para-H2(jH2 = 0) to those of Phillips47 for the temperature range T < 100 K. We found that the rates calculated by Phillips are greater by a factor of 5. This difference is due to the fact that the interaction potential used by Phillips overestimates the anisotropy of the potential. In addition, Phillips found that para-H2(jH2 = 0) and ortho-H2(jH2 = 1) are nearly identical colliders, which doesn’t agree with our findings that there is a notable difference. This can also be explained by the fact that the potential of Phillips based on the ab initio energies of Lavendy et al. was constructed by neglecting the terms responsible for the quadrupole–quadrupole interactions.
5 Conclusions
We have applied full close-coupling calculations to investigate rotational excitation in the C2 molecule for collisions involving para-H2(jH2 = 0) and ortho-H2(jH2 = 1). The calculations are performed using a highly accurate 4D potential energy surface. The inclusion of jH2 = 2 in the rotational basis set of H2 makes an appreciable contribution at high energies to the para-H2 cross sections, approaching 35 percent. Rate coefficients for transitions among the levels of C2 up to j = 16 were determined for the range of temperatures 5 ≤ T ≤ 100 K. Rate coefficients with ortho-H2 are larger by a factor of 5 on average than rate coefficients with para-H2.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. K. acknowledges financial support from the Russian Science Foundation through grant no. 17-12-01395 and grant 8.1.03.2017, and ‘The Tomsk State University competitiveness improvement programme’.Notes and references
- S. P. Souza and B. L. Lutz, Astrophys. J., 1977, 216, L49 CrossRef CAS.
- F. H. Chaffee, B. L. Lutz, J. H. Black, P. A. Vanden Bout and R. L. Snell, Astrophys. J., 1980, 236, 474 CrossRef CAS.
- L. M. Hobbs and B. Cambell, Astrophys. J., 1982, 254, 108 CrossRef CAS.
- A. C. Danks and D. L. Lambert, Astron. Astrophys., 1983, 124, 188 CAS.
- E. F. van Dishoeck and J. H. Black, Astrophys. J., 1989, 340, 273 CrossRef CAS.
- S. R. Federman, C. J. Strom and D. L. Lambert, et al., Astrophys. J., 1994, 424, 772 CrossRef CAS.
- P. Sonnentrucker, D. E. Welty, J. A. Thorburn and D. G. York, Astrophys. J., Suppl. Ser., 2007, 168, 58 CrossRef CAS.
- M. Kaźmierczak, M. R. Schmidt, A. Bondar and J. Krelowski, Mon. Not. R. Astron. Soc., 2010, 402, 2548 CrossRef.
- T. P. Snow, Astrophys. J., 1978, 220, L93 CrossRef CAS.
- D. J. Lien, Astrophys. J., 1984, 287, L95 CrossRef CAS.
- D. L. Lambert, Y. Sheffer and S. R. Federman, Astrophys. J., 1995, 438, 740 CrossRef CAS.
- E. F. van Dishoeck and J. H. Black, Astrophys. J., 1982, 258, 533 CrossRef CAS.
- H. Han, A. Li and H. Guo, J. Chem. Phys., 2014, 141, 244312 CrossRef PubMed.
- N. Masakazu, M. Akira and M. Akira, J. Phys. Chem. A, 2009, 113, 8963 CrossRef PubMed.
- F. Najar, D. Ben Abdallah, N. Jaidane, Z. Ben Lakhdar, G. Chambaud and M. Hochlaf, J. Chem. Phys., 2009, 130, 204305 CrossRef CAS PubMed.
- R. C. Hupe, Y. Sheffer and S. R. Federman, Astrophys. J., 2012, 761(1), 38 CrossRef.
- F. Najar, D. Ben Abdallah, N. Jaidane and Z. Ben Lakhdar, Chem. Phys. Lett., 2008, 460, 31 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- E. R. Davidson and D. W. Silver, Chem. Phys. Lett., 1977, 52, 403 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, et al., MOLPRO, version 2010.1, a package of ab initio program, 2010, http://www.molpro.net Search PubMed.
- M. P. Hodges, R. J. Wheatley, G. K. Schenter and A. H. Harvey, J. Chem. Phys., 2004, 120, 710 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- P. Valiron, M. Wernli, A. Faure, L. Wiesenfeld, C. Rist, S. Kedzuch and J. Noga, J. Chem. Phys., 2008, 129, 134306 CrossRef PubMed.
- Y. Scribano, A. Faure and L. Wiesenfeld, J. Chem. Phys., 2010, 133, 231105 CrossRef PubMed.
- A. Faure, P. Jankowski, T. Stoecklin and K. Szalewicz, Sci. Rep., 2016, 6, 28449 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- S. Green, J. Chem. Phys., 1975, 62, 2271 CrossRef CAS.
- A. M. Arthurs and A. Dalgarno, Proc. R. Soc. A., 1960, 256, 540 Search PubMed.
- M. Martin, J. Photochem. Photobiol., A, 1992, 66, 263 CrossRef CAS.
- J. M. Hutson and S. Green, MOLSCAT Computer Code, version 14,Distributed by Collaborative Computational Project No. 6 of the Engineering and Physical Sciences Research Council, UK, 1994 Search PubMed.
- D. E. Manolopoulos, J. Chem. Phys., 1986, 85, 6425 CrossRef CAS.
- F. Lique, R. Tobola and J. Klos, et al., Astron. Astrophys., 2008, 478, 567 CrossRef.
- D. R. Flower, J. M. Launay, E. Kochanski and J. Prissette, Chem. Phys., 1979, 37, 355 CrossRef CAS.
- G. Danby, D. R. Flower and T. S. Monteiro, Mon. Not. R. Astron. Soc., 1987, 226, 739 CrossRef CAS.
- J. Cernicharo, A. Spielfiedel and C. Balança, et al., Astron. Astrophys., 2011, 531, A103 CrossRef.
- A. R. Offer, M. C. van Hemert and E. F. van Dishoeck, J. Chem. Phys., 1994, 100, 362 CrossRef CAS.
- M. Wernli, P. Valiron, A. Faure, L. Wiesenfeld, P. Jankowski and K. Szalewicz, Astron. Astrophys., 2006, 446, 367 CrossRef CAS.
- J. Klos and F. Lique, Mon. Not. R. Astron. Soc., 2008, 390, 239 CrossRef CAS.
- H. Lavendy, J. M. Robbe, G. Chambaud, B. Levy and E. Roueff, Astron. Astrophys., 1991, 251, 365 CAS.
- T. R. Phillips, Mon. Not. R. Astron. Soc., 1994, 271, 827 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |