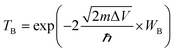First principles study of Schottky barriers at Ga₂O₃(100)/metal interfaces

Abstract

A low Schottky barrier height (SBH) of metal–semiconductor contact is essential for achieving high performance electronic devices. Based on first principles calculations, we have comprehensively investigated the interfacial properties of β-Ga₂O₃ (100) with different metals including Mg, Ni, Cu, Pd and Pt. SBHs have been calculated via layered partial density of states (PDOS) and validated by visual wavefunctions. The results surprisingly show that Mg contact possesses the lowest SBH of 0.23 eV, while other SBHs range from 1.06 eV for Ni, 1.17 eV for Pd and 1.27 eV for Cu to 1.39 eV for Pt. This shows that SBHs of β-Ga₂O₃ are not fully dependent on metal work functions due to a Fermi level pinning effect. The tunneling barrier was also calculated via electrostatic potential with a 72.85% tunneling probability of the Mg/Ga₂O₃ interface. The present study will provide an insight into characteristics of Ga₂O₃/metal interfaces and give guidance for metal choice for Ga₂O₃ electronic devices.

---

1 Introduction

As a fourth generation wide band gap semiconductor material, gallium oxide (Ga₂O₃) is getting more and more attention due to its excellent properties and wide potential applications in the fields of power devices and optoelectronic devices.^1–3 There exist five crystalline phases, namely α, β, γ, δ, and ε, among which the β-phase is the most stable phase. β-Ga₂O₃ with a wide band gap (∼4.9 eV) possesses a high critical breakdown field (E_c) of 8 MV cm⁻¹,^4,5 resulting in a huge Baliga figure-of-merit (BFOM) of more than 3000 which is far better than other wide band gap semiconductors such as GaN and SiC.^6,7 In addition, large-size single-crystal β-Ga₂O₃ substrates can be synthesized through conventional melt growth methods, including Edge-defined Film-fed Growth (EFG).^8,9

It is known that the contact properties between metal and semiconductor can greatly impact the performance of electronic devices. Generally, different metals contact with a semiconductor would form an energy barrier at the interface, which is called Schottky barrier (SB) and responsible for current transport.¹⁰ A low SBH can induce a low contact resistance which is of great significance for interfacial electron transfer and besides reduce devices' power consumption.¹¹

Relevant experiments of Ga₂O₃ SB have been conducted in previous studies. Some researchers have observed that SBHs varied with different metal contacts by using IPE measurements,¹² ranging from 1.27 eV for Pd, 1.54 eV for Ni, 1.58 eV for Pt and 1.71 eV for Au. It seems that the dependence of the SBH on metal work function is not obvious for metal/β-Ga₂O₃ (010) interface. In the same year, Yao's group reported Schottky diodes concerning β-Ga₂O₃ with five metals (W, Cu, Ni, Ir and Pt).¹³ SBHs were in the range of 1.0–1.3 eV and 1.6–2.0 eV by performing respectively current–voltage (I–V) and capacitance–voltage (C–V) measurements, which showed little dependence on the metal work functions. However, research on the SBH of metal/β-Ga₂O₃ (100) interface is limited. Nowadays, theoretical calculation based on first principles is allowed to simulate more kinds of metal contacts, which furthermore helps to explore the regularity of SBHs between interfaces under a same condition without being affected by experimental environment. Moreover, to the best of our knowledge, theoretical study of SBHs on Ga₂O₃/metal interface is very limited, probably due to the complexity of Ga₂O₃ interfacial configurations or the interference of metal-induced gap states (MIGS). SBH is usually affected by interfacial structures, surface states, defects, work functions and so on.¹⁴ It is necessary to obtain accurate SBHs without the interference of MIGS¹⁵ and evaluate its properties.

In present paper, we provide a theoretical study of the contacts between β-Ga₂O₃ (100) and a series of common metals (Mg, Cu, Pd, Ni, Pt) by performing first principles calculations. The hybrid functional method of Heyd, Scuseria and Ernzerhof (HSE06) was used to describe the electronic structure of the contacts which had been proven to show a better agreement with the experimental results than LDA or GGA methods.^16,17 To obtain an explicit SBH, we use layer-resolved PDOS to display a clear semiconductor band gap combined with the visual wavefunctions to show the influence of MIGS. Finally, our theoretical results are in good agreement with the experimental observations.

2 Computational methods

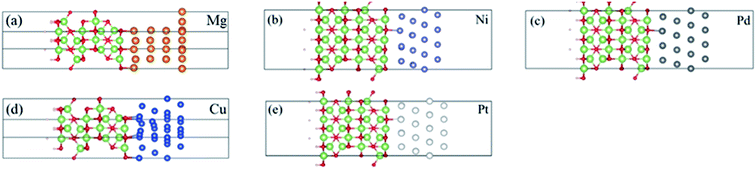
In our study, we have chosen the (100) face of β-Ga₂O₃ in the calculation, which has been proven to be a stable face by previous DFT studies.¹⁸ We do have considered the possibility of using other planes, for example, (010) and (2̄01). In contrast, the (100) plane is nonpolar¹⁸ and shows good convergence. Furthermore, experiment¹⁹ showed that the dependence on different planes is not very notable. Therefore, we construct interfaces with ten-layer (100) oriented β-Ga₂O₃ and four-layer metal atoms. For Ni, Pd, Cu and Pt metals, which are all with face-centered cubic structures, (111) face is the natural growth face and the most commonly used one in the experiment and first principles calculations.^20–22 While Mg metal has a hexagonal close packed structure, (0001) face is the most commonly used.²³ A vacuum layer of 15 Å is set to ensure decoupling between neighboring slabs. In our models, the lattice constant of Ga₂O₃ slab was fixed while the lattice constants of metals were adjusted in order to accommodate reliable prediction on the band gap of Ga₂O₃, which furthermore predicts reliable SBH. The corresponding lattice constant mismatches range from 2.9% to 8.6%, as given in Table 1. A convergence test with respect to the thickness of both the metal and the Ga₂O₃ has been conducted. During relaxation of the configurations, we allowed the six layers of Ga₂O₃ atoms near the interface and metal atoms to interact. The dangling bonds on the Ga₂O₃ surface were passivated by hydrogen atoms (see Fig. 1) to reduce the effect of surface states, which is a very commonly used method to treat semiconducting surfaces in first principles studies.^24–26 The pseudopotential hydrogen of 0.33 was used, according to the amount of lacked electron calculated by charge conservation for the dangling bonds of both Ga and O atoms on this Ga₂O₃ surface. The hydrogen atoms were also relaxed in the optimization process.

Table 1 Calculated interfacial properties of β-Ga₂O₃/metal interfaces: W_M is the calculated work function for a clean metal surface. The corresponding lattice mismatches are given. The equilibrium distance d_s-m is the minimum interatomic distance after optimization. E_b is the binding energy per interfacial Ga atom. N_atoms is the total number atoms of interfacial model. Φ_t and Φ_e are SBHs obtained in our calculations and experimental measurements, respectively

Metal	WM (eV)	Mismatch (%)	ds-m (Å)	Eb (eV)	Natoms	Φt (eV)	Φe (eV)
Mg	3.81	3.0	2.10	0.47	60	0.23 (n)	0.1 (ref. 32)
Ni	4.49	8.6	2.13	0.54	98	1.06 (n)	0.97–1.55 (ref. 12, 19 and 13)
Pd	5.83	3.2	2.28	0.40	98	1.17 (n)	1.01–1.29 (ref. 12 and 19)
Cu	5.20	3.0	2.10	0.37	72	1.27 (n)	1.13–1.36 (ref. 13 and 33)
Pt	5.73	2.9	2.28	0.13	98	1.39 (n)	1.05–1.58 (ref. 12 and 13)

---

Fig. 1 Side view of the optimized structures for (a) Ga₂O₃/Mg (b) Ga₂O₃/Ni (c) Ga₂O₃/Pd (d) Ga₂O₃/Cu and (e) Ga₂O₃/Pt interfaces. The rectangle plotted in black line shows the crystal lattice. The green, red, and pink balls respectively represent Ga, O, and H atoms.

All calculations, including geometry optimization and electronic structure calculation, were performed with the Norm-Conserving Pseudopotential (NCPP) implemented in the plane-wave package PWmat code^27,28 which has been proven to be an accurate and efficient package to calculate large semiconducting systems.²⁹ The Perdew–Berk–Ernzerhof (PBE) exchange-correlation functional was used^30,31 to optimize the structure with a plane wave energy cutoff of 60 Ryd. The Monkhorst–Pack k-point mesh was set to 3 × 2 × 1 for the model of 98 atoms, and the force threshold was set to 0.02 eV Å⁻¹. The convergence tolerance of energy is 1 × 10⁻⁵ eV. HSE06 hybrid functional was used to calculate the electronic structure with a mixing parameter of 0.34. We yielded a band gap of 4.9 eV for β-Ga₂O₃ bulk, which shows a good agreement with the experimental value.¹

3 Results and discussions

3.1. Geometry and stability of β-Ga₂O₃/metal interfaces

The optimized configurations of Ga₂O₃ (100)/metal contacts are shown in Fig. 1. All systems have achieved convergence criteria. The interlayer distances (d_s-m), determined by minimizing the total energy, are 2.10 Å, 2.13 Å, 2.28 Å, 2.10 Å and 2.28 Å for Mg/Ga₂O₃, Ni/Ga₂O₃, Pd/Ga₂O₃, Cu/Ga₂O₃ and Pt/Ga₂O₃ interfaces, respectively. Mg/Ga₂O₃ and Cu/Ga₂O₃ contacts show small interfacial equilibrium distance of 2.10 Å. While Pd/Ga₂O₃ and Pt/Ga₂O₃ interfaces reveal an interfacial spacing more than 2.2 Å which indicate a physical combination. In order to evaluate the stability of the contact structure, we calculated the binding energy of the Ga₂O₃/metal interfaces, as collected in Table 1. The binding energy (E_b) per interface Ga or O atom is defined as:

E_b = (E_Ga2O3 + E_M − E_Ga2O3−M)/N

where E_Ga2O3, E_M and E_Ga2O3−M are respectively the relaxed total energies for the passivated Ga₂O₃ surface, the clean metal surface and the combined system, and N is the number of interfacial Ga or O atoms. From Table 1, we can see that positive binding energies indicate stable contacts for all the five interfaces. Among them, Mg and Ni exhibit stronger binding energies with Ga₂O₃. However, the E_b comparison between these two contacts is not straightforward due to their different stacking ways in the interfacial structures, as described before. Of all systems, we can see that O ions nearby the interface are more likely to be close to metal atoms than Ga ions, showing a more active property. Moderate binding energies of 0.40 and 0.37 eV have been found for Pd and Cu contacts respectively. Pt shows very weak adhesion on Ga₂O₃ with the smallest binding energy of only 0.13 eV. It is also found that larger binding energies usually result in smaller d_s-m.

3.2 Electronic properties

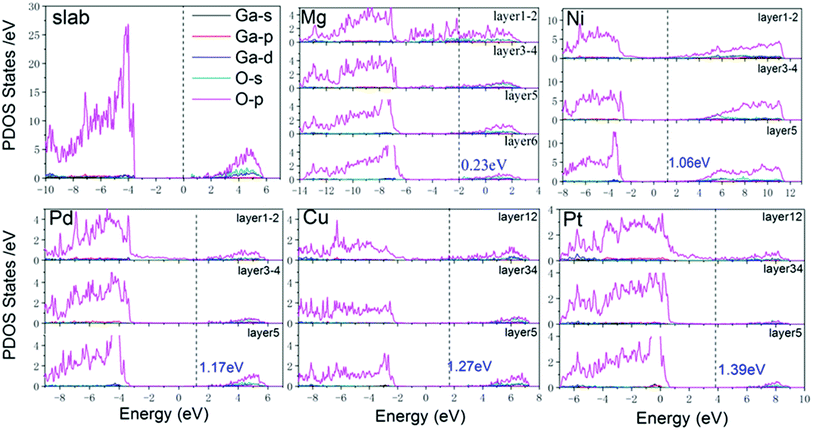
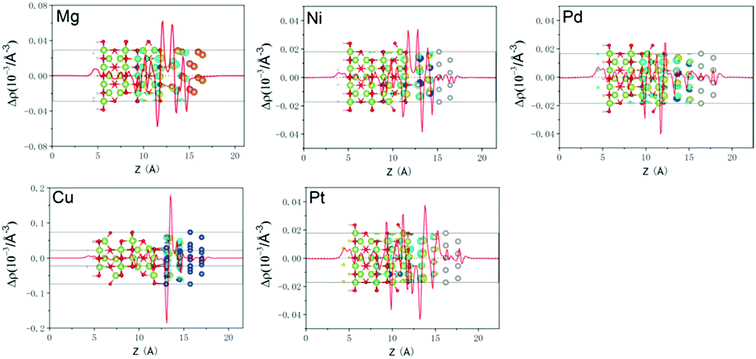
To analyze the electrical properties of Ga₂O₃/metal contacts, the layer-resolved PDOS are displayed in Fig. 2. The Fermi level is marked by a vertical dashed line, and the Ga₂O₃ PDOS of layer 1–2, layer 3–4, and layer 5 near the interface are clearly shown in the figure. For comparison, the PDOS of freestanding Ga₂O₃ is also shown in the first diagram of Fig. 2. It shows a 4.0 eV band gap of Ga₂O₃ surface smaller than the bulk, which is consistent with previous finding, that generally the band gap of semiconducting slab is reduced relative to the bulk due to the effect of surface states.³⁴ The valence band maximum (VBM) consists of O-p states predominantly together with minor Ga components, whereas the conduction band minimum (CBM) is characterized by a combined contribution of O-s states, Ga-s states and O-p states, which are consistent with previous researches.^35,36 For the layer 1–2 of all interfacial systems, PDOS show obvious MIGS with continuous and minute states that exist in the band gap of Ga₂O₃. MIGS belong to semiconductor intrinsic surface states, which are also called interface states, will decay gradually away from the interface.^37–39 In the Fig. 2, we can see that interface states significantly reduce in the 3–4 layers, which furthermore almost disappear in the 5^th layer of all contacts. Moreover, the band gap of Ga₂O₃ is becoming more unambiguous as the interface states fade away. Particularly, Mg interface appears obviously sharp peaks in the band gap of 1–2 layered PDOS due to the interfacial atomic orbital hybridization and strong interaction between the interfaces, which indicate a chemical binding. Therefore, we have shown the layer-6 atomic PDOS of Ga₂O₃/Mg interface. The magnitude of the SBH depends on the position of the Fermi level at the interface.⁴⁰ As we can easily see that the five contacts are all n-type SB according to the position of Fermi level. However, it is hard to derive exact SBH from undetermined CBM. Therefore, visual wavefunctions were used to validate the SBHs as follows.

Fig. 2 Layer-resolved partial density of states (PDOS) (DOS on specified atoms and orbitals) of freestanding β-Ga₂O₃ slab and Ga₂O₃ on Mg, Ni, Pd, Cu, and Pt surfaces, respectively. The vertical dashed line is Fermi level. Layer1–2, layer3–4 and layer5 denote the number of Ga₂O₃ layers near the interface. Blue values denote SBHs acquired from the fifth layer of PDOS and tested by wavefunctions.

In order to further understand the charge transfer and charge distribution between Ga₂O₃ and metal after interface formation, we explored the charge density difference in the direction perpendicular to the interface. For quantitative analysis, the plane-averaged charge density difference perpendicularly to the interface is also calculated, as shown in Fig. 3 with red curves. The charge density difference is defined as:

Δρ(z) = ρ_Ga2O3−M(z) − ρ_Ga2O3(z) − ρ_M(z)

where ρ_Ga2O3−M, ρ_Ga2O3 and ρ_M are the charge densities of Ga₂O₃–metal system, the Ga₂O₃ slab and metal slab, respectively. It is noted that charge accumulation concentrates on interfacial region for all systems. The plane-averaged charge density difference shows that the peak values of Cu and Mg contacts are larger than Pt, Pd and Ni systems at the interfaces. Correspondingly, Mg system possesses the strongest interfacial interaction, as we have previously described. As for Cu contact, charge accumulation is more concentrated at the interface with a high peak value. For other systems, the curves oscillate or disperse due to the effects of interface states.

Fig. 3 Charge density difference and planar-averaged electron density difference Δρ(z) for Ga₂O₃–Mg, Ni, Pd, Cu and Pt systems. The yellow and blue color isosurfaces correspond to the accumulation and depletion of electrons (ρ = 1 × 10⁻³ e Å⁻³), respectively.

3.3. Schottky barrier and tunneling barrier at Ga₂O₃–metal contacts

SB plays a key role in the metal–semiconductor interface research, which can primarily influence the electron transport in device. The SBH can be acquired from the difference between Fermi level of interfacial systems and identifiable CBM/VBM of Ga₂O₃. The CBM of Ga₂O₃ derived from the 5^th layered PDOS is uncertain, therefore, we furthermore analyzed their wavefunctions to confirm. Wave functions of Ga₂O₃/Mg and Ga₂O₃/Cu systems have been used as two examples in Fig. 4, where some representative eigen values were selected to plot visual wavefunctions according to the PDOS of Cu and Mg systems in Fig. 2.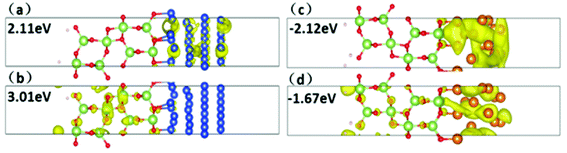

Fig. 4 Visual wavefunction of Ga₂O₃/Cu at (a) 2.11 eV (b) 3.01 eV and Ga₂O₃/Mg at (c) −2.12 eV (d) −1.67 eV. Yellow areas denote wavefunction distribution.

Through the distribution of wavefunctions marked by yellow, it is feasible to recognize the local wavefunction and continuous wavefunction. MIGS are reflected in Fig. 4(a) and (c) in which wavefunctions cover all metal atoms and local Ga₂O₃ interfacial atoms, with 2.11 eV and −2.12 eV energy eigenvalues corresponding to the energy of semiconducting band gap in the PDOS of Ga₂O₃/Cu and Ga₂O₃/Mg, respectively. We had tested different eigenvalues which near the corresponding band edge of Ga₂O₃, until wavefunctions wrap all Ga₂O₃ atoms as displayed in Fig. 4(b) and (d). In this way, the CBM values were found similar to the 5^th layered PDOS of the two contacts. By this approach, accurate electron SBHs of all contacts have been determined to be respectively 0.23 eV, 1.06 eV, 1.17 eV, 1.27 eV and 1.39 eV for Ga₂O₃/Mg, Ga₂O₃/Ni, Ga₂O₃/Pd, Ga₂O₃/Cu and Ga₂O₃/Pt without interference of interface states. Besides, in Fig. 4(c) we can see wavefunctions obviously cover in Ga₂O₃/Mg interfacial region which indicates a strong interaction between the contacts. While energy reaches −1.67 eV, wavefunctions start distributing on both Ga₂O₃ and metal atoms which can be interpreted by the coupling effect of the two slabs, as shown in Fig. 4(d).

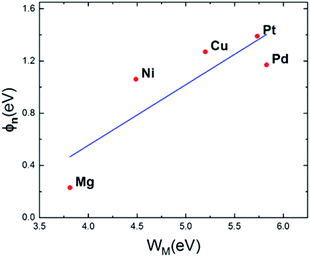
The metal work functions using strain calculated by DFT method^41,42 are collected in Table 1. Fig. 5 visualizes the relationship between metal work functions and SBHs. The slope of the blue fit line is approximately 0.40 which shows a little dependence of SBH on metal work functions. It does not conform to Schottky–Mott behavior⁴³ of Ga₂O₃ semiconductor, since a certain density of interface states can pin the Fermi level inside the semiconducting bandgap. Among them Mg contact possesses the smallest SBH just below the CBM, which derives from both low metal work function and strong interaction between interfaces. However, due to Fermi level pinning,⁴⁴ SB does not vanish.

Fig. 5 Calculated Schottky barrier heights vs. metal work functions.

The tunneling barrier is another figure to assess the contact performance, which can be calculated by using the average electrostatic potentials of interfacial systems as shown in Fig. 6, in which the Fermi level is marked with red dashed line. The electrostatic potential above Fermi level at the interface is regarded as tunneling barrier which is marked with red rectangle.⁴⁵ The height and half-width of the rectangle are expressed as the height (ΔV) and width (W_B) of tunneling barrier, respectively.⁴⁶ We can see that among five metals, Mg contact has the least ΔV and notably small W_B, indicating higher electron transfer efficiency. It is noted that the coordinate scale in Pd and Pt systems is larger than Mg and Ni systems. They show higher ΔV than other metal contacts in Fig. 6, which indicate low tunneling probabilities. These results were summarized in Table 2. And the tunneling probability (T_B) from metals to Ga₂O₃ can be calculated by the following formula:

where m is the effective mass of a free electron and ħ is the reduced Plank's constant. The results of T_B are 72.85%, 41.70%, 42.84%, 37.31% and 29.60% for Mg, Ni, Cu, Pd and Pt contacts, respectively. Apparently, Mg contact shares the highest tunneling probability which is significant for tunneling transmission. While Pt contact has the least probability among the five contacts, which is consistent with the SBHs results. The SBH of Cu system is larger than Ni and Pd contacts. However, Cu system possesses a little higher tunneling probability than Ni and Pd contacts probably due to a closer interfacial equilibrium distance for Ga₂O₃/Cu interface which is beneficial for electron injection.

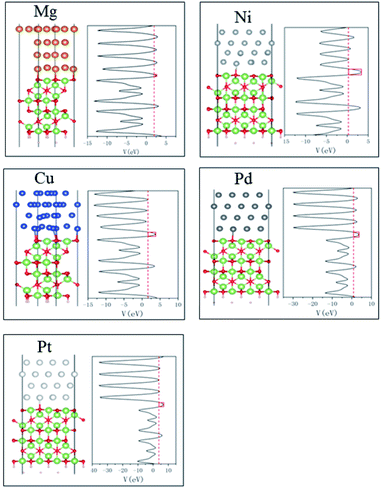Fig. 6 Side view of optimized structures and average electrostatic potential along the direction normal to the metal/Ga₂O₃ interfaces.

Table 2 Tunneling barrier height ΔV, wide W_B and probabilities (T_B) through Ga₂O₃/metal contacts

	ΔV (eV)	WB (Å)	TB (%)
Mg	0.78	0.15	72.85
Ni	2.14	0.25	41.70
Cu	2.01	0.25	42.84
Pd	2.72	0.25	37.31
Pt	2.88	0.3	29.60

---

4 Conclusion

In summary, we provide the first systematic research on the interfacial SBHs of Ga₂O₃ with Mg, Ni, Pd, Cu and Pt metals. We draw a conclusion that among the five interfaces Ga₂O₃/Mg contact possesses the least SBH which indicates an excellent electron transport property. Besides, SBHs of Ga₂O₃ are not distinctly regulated by metal work functions due to Fermi level pinning. Visual wavefunctions were plotted to give a clear interpretation of the MIGS and confirm the value of SBHs. In the meanwhile, the results provide an insight into the interfacial characteristics of Ga₂O₃ in contact with metals, which will give useful guidance for the selection of metal in β-Ga₂O₃ electronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the National Nature Science Foundation of China (Grant No. 21573129 and 21403300). The authors also acknowledge a generous grant of computer time from the Institute of Semiconductors in Beijing.

References

1. K. Matsuzaki, H. Hiramatsu, K. Nomura, H. Yanagi, T. Kamiya, M. Hirano and H. Hosono, Thin Solid Films, 2006, 496, 37–41.
2. M. Higashiwaki, K. Sasaki, T. Kamimura, M. Hoi Wong, D. Krishnamurthy, A. Kuramata, T. Masui and S. Yamakoshi, Appl. Phys. Lett., 2013, 103, 123511.
3. M. H. Wong, K. Sasaki, A. Kuramata, S. Yamakoshi and M. Higashiwaki, IEEE Electron Device Lett., 2016, 37, 212–215.
4. H. H. Tippins, Phys. Rev., 1965, 140, A316–A319.
5. M. Orita, H. Ohta, M. Hirano and H. Hosono, Appl. Phys. Lett., 2000, 77, 4166–4168.
6. M. Higashiwaki, K. Sasaki, A. Kuramata, T. Masui and S. Yamakoshi, Appl. Phys. Lett., 2012, 100, 13504.
7. M. Higashiwaki, K. Sasaki, A. Kuramata, T. Masui and S. Yamakoshi, Phys. Status Solidi A, 2014, 211, 21–26.
8. H. Aida, K. Nishiguchi, H. Takeda, N. Aota, K. Sunakawa and Y. Yaguchi, Jpn. J. Appl. Phys., 2008, 47, 8506–8509.
9. E. G. Víllora, K. Shimamura, Y. Yoshikawa, K. Aoki and N. Ichinose, J. Cryst. Growth, 2004, 270, 420–426.
10. C. Funck and S. Menzel, AIP Adv., 2019, 9, 45116.
11. S. Ghosh, R. Raveendran, A. Saeki, S. Seki, M. Namboothiry and A. Ajayaghosh, Acs Appl. Mater. Inter., 2019, 11, 1088–1095.
12. E. Farzana, Z. Zhang, P. K. Paul, A. R. Arehart and S. A. Ringel, Appl. Phys. Lett., 2017, 110, 202102.
13. Y. Yao, R. Gangireddy, J. Kim, K. K. Das, R. F. Davis and L. M. Porter, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2017, 35, 3D–113D.
14. X. Ma, X. Wu, Y. Wang and Y. Dai, Phys. Chem. Chem. Phys., 2017, 19, 18750–18756.
15. M. C. Toroker, D. K. Kanan, N. Alidoust, L. Y. Isseroff, P. Liao and E. A. Carter, Phys. Chem. Chem. Phys., 2011, 13, 16644–16654.
16. A. Alkauskas, P. Broqvist, F. Devynck and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 106802.
17. B. R. Tuttle, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125322.
18. V. M. Bermudez, Chem. Phys., 2006, 323, 193–203.
19. M. E. Ingebrigtsen, L. Vines, G. Alfieri, A. Mihaila, U. Badstübner, B. G. Svensson and A. Kuznetsov, Mater. Sci. Forum, 2017, 897, 755–758.
20. H. Zhong, R. Quhe, Y. Wang, Z. Ni, M. Ye, Z. Song, Y. Pan, J. Yang, L. Yang, M. Lei, J. Shi and J. Lu, Sci. Rep., 2016, 6, 21786.
21. A. Mahmoud, P. Deleuze and C. Dupont, J. Chem. Phys., 2018, 148, 204701.
22. R. Sun, G. Yang, F. Wang, G. Chu, N. Lu and X. Shen, Mater. Sci. Semicond. Process., 2018, 84, 64–70.
23. T. Vegge, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 35412.
24. J. A. Steckel, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155406.
25. S. Tanaka, T. Tamura, K. Okazaki, S. Ishibashi and M. Kohyama, Phys. Status Solidi C, 2007, 4, 2972–2976.
26. Y. Liu, F. Liu, R. Wang, J. Luo, X. Jiang, R. Huang, S. Li and L. Wang, Phys. Rev. Appl., 2019, 12, 64012.
27. W. Jia, Z. Cao, L. Wang, J. Fu, X. Chi, W. Gao and L. Wang, Comput. Phys. Commun., 2013, 184, 9–18.
28. W. Jia, J. Fu, Z. Cao, L. Wang, X. Chi, W. Gao and L. Wang, J. Comput. Phys., 2013, 251, 102–115.
29. Y. Liu, F. Zheng, X. Jiang, J. Luo, S. Li and L. Wang, Phys. Rev. Appl., 2019, 11, 44058.
30. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 121104.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. J. Shi, X. Xia, Q. Abbas, J. Liu, H. Zhang, Y. Liu and H. Liang, J. Semicond., 2019, 40, 12805.
33. D. Splith, S. Müller, F. Schmidt, H. von Wenckstern, J. J. van Rensburg, W. E. Meyer and M. Grundmann, Phys. Status Solidi A, 2014, 211, 40–47.
34. X. Zhou, E. J. M. Hensen, R. A. van Santen and C. Li, Chem. - Eur. J., 2014, 20, 6915–6926.
35. Y. Li, C. Yang, L. Wu and R. Zhang, Mod. Phys. Lett. B, 2017, 31, 1750172.
36. K. Yamaguchi, Solid State Commun., 2004, 131, 739–744.
37. J. Chen, Z. Zhang, Y. Guo and J. Robertson, Microelectron. Eng., 2019, 216, 111056.
38. J. Goniakowski and C. Noguera, Interface Sci., 2004, 12, 93–103.
39. M. Farmanbar and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 161304.
40. N. R. D'Amico, G. Cantele, C. A. Perroni and D. Ninno, J. Phys.: Condens. Matter, 2015, 27, 15006.
41. N. E. Singh-Miller and N. N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235407.
42. X. Ma, Y. Dai, L. Yu and B. Huang, Nanoscale, 2016, 8, 1352–1359.
43. J. R. Lince, D. J. Carr E and P. D. Fleischauer, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 1647–1656.
44. C. Gong, L. Colombo, R. M. Wallace and K. Cho, Nano Lett., 2014, 14, 1714.
45. G. Lee, S. Kim, S. Jhi and H. Lee, Nat. Commun., 2015, 6, 6181.
46. Y. Wang, R. X. Yang, R. Quhe, H. Zhong, L. Cong, M. Ye, Z. Ni, Z. Song, J. Yang, J. Shi, J. Li and J. Lu, Nanoscale, 2016, 8, 1179–1191.

---