Open Access Article
Open Access ArticleDual responsive PMEEECL–PAE block copolymers: a computational self-assembly and doxorubicin uptake study†
Amin Koochakiab,
Mohammad Reza Moghbeli*a,
Sousa Javan Nikkhaha,
Alessandro Ianiro bc and
Remco Tuinier
bc and
Remco Tuinier *bc
*bc
aSmart Polymers and Nanocomposites Research Group, School of Chemical Engineering, Iran University of Science and Technology, Tehran 16846-13114, Iran. E-mail: mr_moghbeli@iust.ac.ir
bLaboratory of Physical Chemistry, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: r.tuinier@tue.nl
cInstitute for Complex Molecular Systems, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands
First published on 20th January 2020
Abstract
The self-assembly behaviour of dual-responsive block copolymers and their ability to solubilize the anticancer drug doxorubicin (DOX) has been investigated using all-atom molecular dynamics (MD) simulations, MARTINI coarse-grained (CG) force field simulation and Scheutjens–Fleer self-consistent field (SCF) computations. These diblock copolymers, composed of poly{γ-2-[2-(2-methoxyethoxy)ethoxy]ethoxy-ε-caprolactone} (PMEEECL) and poly(β-amino ester) (PAE) are dual-responsive: the PMEEECL block is thermoresponsive (becomes insoluble above a certain temperature), while the PAE block is pH-responsive (becomes soluble below a certain pH). Three MEEECL20–AEM compositions with M = 5, 10, and 15, have been studied. All-atom MD simulations have been performed to calculate the coil-to-globule transition temperature (Tcg) of these copolymers and finding appropriate CG mapping for both PMEEECL–PAE and DOX. The output of the MARTINI CG simulations is in agreement with SCF predictions. The results show that DOX is solubilized with high efficiency (75–80%) at different concentrations inside the PMEEECL–PAE micelles, although, interestingly, the loading efficiency is reduced by increasing the drug concentration. The non-bonded interaction energy and the RDF between DOX and water beads confirm this result. Finally, MD simulations and SCF computations reveal that the responsive behaviour of PMEEECL–PAE self-assembled structures take place at temperature and pH ranges appropriate for drug delivery.
1. Introduction
The self-assembly of amphiphilic block copolymers in water results in different types of supramolecular structures, such as spherical micelles, cylindrical micelles and vesicles, depending on the chemical composition and relative mass of the blocks.1 These self-assembled structures are composed of an insoluble core made of the hydrophobic blocks, surrounded by a hydrophilic corona which provide stability in solution.2,3 Bio-compatible and bio-degradable amphiphilic block copolymers have attracted the attention of researchers for their potential use in bio-applications such as drug delivery.4,5 In fact, the core of the assemblies can be used to encapsulate drug while the corona can provide protection against immune recognition (opsonization).6–8 Recently, it was demonstrated that block copolymers which can respond to external stimuli such as temperature and pH are efficacious for drug delivery applications,9–12 as tumor tissues are warmer9,13 and more acidic14,15 than normal ones.Thermoresponsive polymers show a change in solubility upon changing temperature. Differently, pH-responsive polymers undergo a hydrophilic to hydrophobic transition upon changing pH due to charge effect.16 These two types of responsive polymers can be combined into block copolymers where the solubility of each block can be controlled independently. This gives rise to a dual-responsive self-assembly behaviour which can be exploited to release drugs in a controlled fashion.17,18 For instance, a slow drug release can be achieved when both blocks are in a hydrophobic state resulting in a compact self-assembled structure,19 while an instantaneous release can be obtained if both blocks becomes soluble and the self-assembled structures fall apart.20
In this in silico study we designed a new class of dual-responsive block copolymers and we computationally investigated their self-assembly behaviour and their ability to solubilize the anticancer drug doxorubicin (DOX). As corona-forming block the thermoresponsive poly{γ-2-[2-(2-methoxyethoxy)ethoxy]ethoxy-3-caprolactone} (PMEEECL) has been selected.21 This polymer is soluble at room temperature but becomes insoluble above the so-called coil-to-globule transition temperature Tcg (i.e. the temperature that marks the transition from swollen to collapsed state of the polymer). This kind of phase behaviour is named lower critical solution temperature (LCST) and is usually observed in solutions containing hydrophilic polymers which interact with water via hydrogen bonds.9 Differently from the widely used poly(N-isopropylacrylamide) (PNIPAM),13 PMEEECL is fully biocompatible.22 Cheng et al.22 copolymerized PMEEECL with poly(γ-octyloxy-ε-caprolactone) (PMEEECL-b-POCTCL) by ring-opening polymerization. Although the obtained block copolymers showed a low cytotoxicity and a Tcg around 38 °C, the loading efficiency of doxorubicin (DOX) was not sufficiently high due to the characteristics of the core-forming blocks. Min et al.23 prepared micelles from block copolymers using the pH-responsive biodegradable poly(β-amino ester) (PAE) as core-forming block for the delivery of camptothecin (CPT) and observed a significant increase in therapeutic efficacy with minimum side effects using these micelles containing CPT. Moreover, the appropriate loading efficiency around 96% and 82% was observed with this block copolymer when CPT was fed as the ratio of 5 wt% and 10 wt% to polymeric micelles, respectively. Therefore, PAE has been selected as core-forming block in this study. On the basis of these results one could expect that block copolymers made of PMEEECL and PAE (PMEEECL–PAE) exhibit the desired dual-responsive behaviour combined with a high drug loading ability.
A step-by-step approach has been followed to study the self-assembly behaviour of PMEEECL–PAE, their dual-responsivity and their uptake of DOX. Based on previous investigations24,25 MEEECL20 has been chosen as hydrophilic block. Scheutjens–Fleer self-consistent field (SCF) computations,26,27 which are suitable to perform systematic investigations due to low computational cost,28 have been used to determine the equilibrium morphology of MEEECL20–AEM self-assembled structures as a function of the hydrophobic block length M. Based on the SCF results, three PMEEECL20–PAEM (M = 5, 10, and 15) compositions, forming, respectively, spherical micelles, cylindrical micelles and vesicles (or flat bilayers) have been selected. All atom molecular dynamics (MD) simulations have been performed on these copolymers to compute the value of Tcg as a function of the PAE block length. Subsequently, MARTINI coarse-grained (CG) force field simulations29,30 have been used to study the self-assembly behaviour of the copolymers, particularly the structure and the equilibrium morphology of the resulting assemblies. These computational methods have been previously used to study block copolymer self-assembly providing good agreement with experimental results.31–34 It is best suited to study macromolecular aggregates because the coarse-graining allows describing the system with less degrees of freedom, making the simulation much faster than all-atom MD. The encapsulation of DOX within PMEEECL20–PAE5 spherical micelles at different DOX concentrations has been investigated by MARTINI CG force field simulations. Finally, the effect of temperature and pH on the self-assembled structure was studied by MARTINI CG force field and SCF theory, respectively. The results obtained with the different methods were in good agreement and showed the great potential of PMEEECL–PAE block copolymer for drug delivery applications. To our knowledge, such a combination of computational techniques has not yet been used to study dual-response block copolymers.
2. Methods
2.1. MD simulation
Both all-atom and MARTINI CG MD simulations were performed by LAMMPS35 under isothermal–isobaric NPT (constant pressure P, temperature T and number of particles in the box N) conditions. Details of the simulations are provided in Table S1.† Moreover, by using the Nose–Hoover algorithm the temperature and pressure were controlled with a coupling time of 0.1 ps and a coupling time of 1 ps, respectively. To calculate the solvent access surface area (SASA), the radial distribution function (RDF) between the PMEEECL20–PAEM amphiphilic block copolymer and hydrogen atoms of water molecules as well as the snapshots of simulation systems for both all-atom MD and MARTINI CG force field simulations, Visual Molecular Dynamic (VMD) package36 was used.Below, a detailed description of the applied simulation protocols and the performed data analysis is reported.
To study the thermoresponsive behaviour of the copolymers and identify the Tcg, the radius of gyration of the blocks (Rg), the SASA, the non-bonded interaction energy between block copolymer and solvent molecules and the RDF between the oxygen of PMEEECL block and hydrogen of water molecules were calculated from the simulation results.
The temperature dependence of Rg of PMEEECL was fitted by the Boltzmann sigmoid function:41
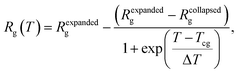 | (1) |
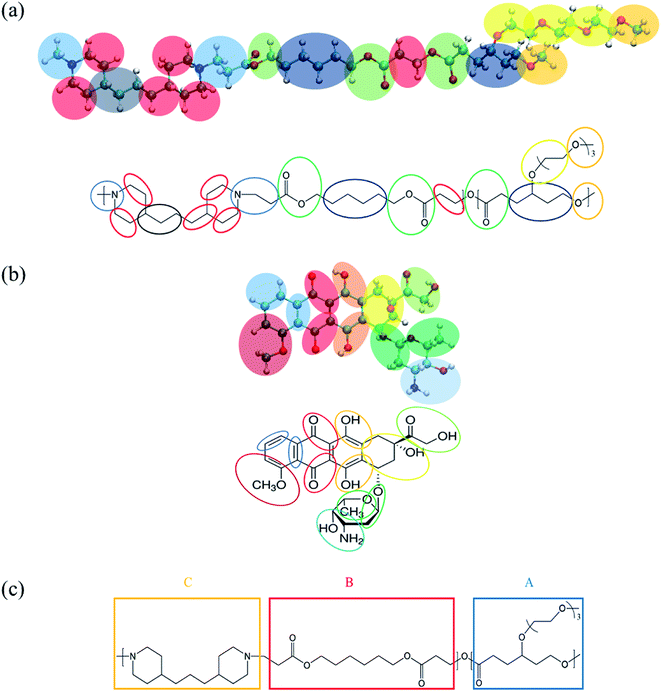 | ||
| Fig. 1 MARTINI coarse-grained (CG) mapping for (a) a PMEEECL–PAE block copolymer, (b) DOX used for MARTINI CG force field simulations and (c) SCF coarse-graining of PMEEECL–PAE block copolymers. | ||
The evaluation of the order parameter Pmicelle (Fig. S3†), was monitored to set an appropriate simulation timed. It has been defined as 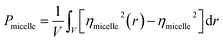 where ηmicelle is the micelle dimensionless density (volume fraction) and has been calculated by the volume average of the difference between local and overall density squared.45 Between 400 ns and 600 ns the value of Pmicelle changed hardly varied, so a simulation time of 600 ns was set. The self-assembled structural properties of block copolymer such as total radius of the micelle Rmicelle and core size Rcore were calculated using the following equations:46
where ηmicelle is the micelle dimensionless density (volume fraction) and has been calculated by the volume average of the difference between local and overall density squared.45 Between 400 ns and 600 ns the value of Pmicelle changed hardly varied, so a simulation time of 600 ns was set. The self-assembled structural properties of block copolymer such as total radius of the micelle Rmicelle and core size Rcore were calculated using the following equations:46
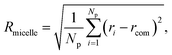 | (2) |
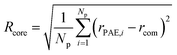 | (3) |
To quantify the loading efficiency (LE) and capacity (LC) of DOX into the PMEEECL–PAE self-assembled structures the following equations have been used:
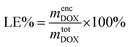 | (4) |
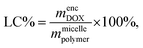 | (5) |
The diffusion coefficient of DOX beads (DDOX) was calculated from the mean square displacement (MSD) as follows:47,48
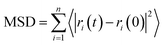 | (6) |
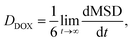 | (7) |
All the computations were performed in the presence of a fixed amount of monovalent salt in the lattice to adjust the ionic strength. To this end the volume fraction of the cations (I+) in the lattice is set to ϕ+ = 0.03, while the anions (I−) are used as charge neutralizers, meaning that their volume fraction (ϕ−) is automatically adjusted to achieve the overall charge neutrality of the lattice. Both cations and anions are set to occupy single lattice sites.
The acid–base reactions of water and the pH responsive C group are modelled as chemical equilibria by specifying the reaction acid dissociation constants pKSCFa. In the SCF procedure these constants depend on the lattice constant, and can be determined from the experimental pKa values:
| pKSCFa = pKa − log10[10−24λ3Nav] | (8) |
In the computations we used pKSCFaW = 15.35 and pKSCFaC = 9.5, the latter estimated from literature values.52 Since two potentially charged groups are present on each PAE monomer, the protonation of C is modelled according to the equilibrium:
| C + 2W+ ⇌ C2+ + 2W | (9) |
It should be noted that this simple description was interpreted to align with the coarse-grained model description. The short-range interactions are modelled via a set of Flory–Huggins interaction parameters χij (Table S2†). For the interactions between A, B, C, and W the χij values where estimated from the Hansen solubility parameters53 obtained via the group contribution method.54 All other interaction parameters were set to 0.
3. Results and discussion
3.1. Preferred morphology of PMEEECL20–PAEM
SCF computations have been performed first to determine the preferred morphology of PMEEECL20–PAEM self-assembled structures at pH = 7 and room temperature as a function of the PAE block length 2 < M < 20. For each copolymer the equilibrium value of the critical aggregation concentration, ϕbulk, have been computed in each of the three lattice geometries. For details about this procedure we refer to previous literature.26,28,55 The preferred geometry is the one associated with the lowest ϕbulk value, since the free energy of micelle formation ΔGmic is related with ϕbulk via the relation ΔGmic = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
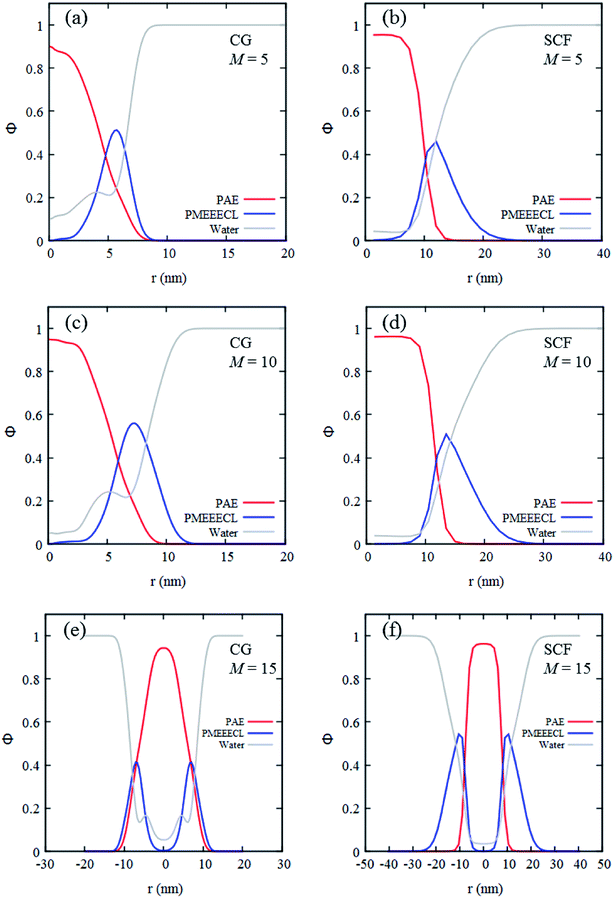
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕbulk.56 The results indicate that at neutral pH and at room temperature PMEEECL20–PAEM block copolymers in water assemble into spherical micelles for M ≤ 6, into cylindrical micelles for 7 ≤ M ≤ 12 and into vesicles or flat bilayers for M ≥ 13. Based on these results three copolymer compositions (M = 5, 10, 15) assembling in three different geometries, have been selected for in-depth studies.
ϕbulk.56 The results indicate that at neutral pH and at room temperature PMEEECL20–PAEM block copolymers in water assemble into spherical micelles for M ≤ 6, into cylindrical micelles for 7 ≤ M ≤ 12 and into vesicles or flat bilayers for M ≥ 13. Based on these results three copolymer compositions (M = 5, 10, 15) assembling in three different geometries, have been selected for in-depth studies.
3.2. Effect of hydrophobic block on Tcg
The typical signature of the Tcg is a large drop in the polymer size, expressed via the value of Rg, which is due to a collapse of the chains. By fitting the Rg values obtained from the simulation results with a Boltzmann sigmoid function (see eqn (1))41 (see Fig. 2a and Table S3†) Tcg values = 312, 302 and 298 K with 2.5 K error bars estimated from the figure have been found for PMEEECL block in PMEEECL20–PAE5, PMEEECL20–PAE10, and PMEEECL20–PAE15, respectively. The value of Tcg decreases with increasing hydrophobic PAE block length. Tcg as a function of (Fig. 2b and Table S4†) of the PMEEECL mass fraction f can be reasonably described using Tcg = 26.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(f) + 318.96. Hence, the thermoresponsive behaviour of the copolymer can be controlled by adjusting the PAE block length. It should be noted that no observable size change was detected for the PAE blocks because it is not a thermosensitive polymer (see Table S3†).
ln(f) + 318.96. Hence, the thermoresponsive behaviour of the copolymer can be controlled by adjusting the PAE block length. It should be noted that no observable size change was detected for the PAE blocks because it is not a thermosensitive polymer (see Table S3†).
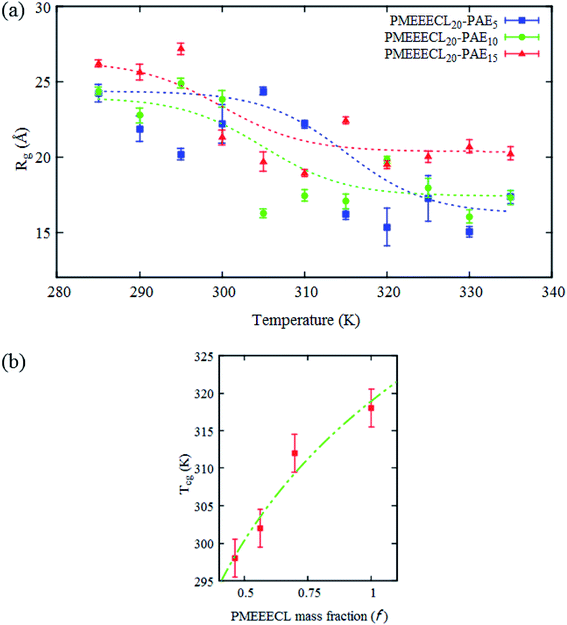 | ||
Fig. 2 (a) All-atom MD simulations results for the radius of gyration (Rg) for the hydrophilic (PMEEECL) part of PMEEECL20–PAEM block copolymer with M = 5, 10, and 15 as a function of temperature. The dotted curve is a fit using eqn (1). (b) Coil-to-globule transition temperature (Tcg) of PMEEECL in the block copolymer as a function of PMEEECL mass fraction. For f = 1 the Tcg has been derived from ref. 24. The dot-dashed curve follows Tcg = 26.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(f) + 318.96. ln(f) + 318.96. | ||
To gain better understanding on the coil-to-globule transition behaviour of PMEEECL20–PAEM block copolymers, the non-bonded interaction energies (including van der Waals and electrostatic energies) between the copolymer blocks and the solvent as well as the solvent accessible surface area (SASA) have been calculated (Fig. S4†). These parameters describe the affinity between blocks and solvent molecules which enable to quantify the transition behaviour of the blocks. For instance, SASA is related to the surface area of PMEEECL20–PAEM block copolymers which is accessible to the water molecules. It can be calculated by extending the van der Waals radius for each atom by 1.4 Å. A reduction of the SASA value implies a reduction of the access surface area for water molecules along the PMEEECL chain. Therefore, in agreement with the temperature-dependence of Rg, the non-bonded interaction energies and SASA values of PMEEECL decreased significantly, indicating a reduction in the affinity between the water molecules and PMEEECL. This corresponds to the observed trends in Tcg.
Coil-to-globule transition behaviour can also be observed in the radial distribution function (RDF) of the hydrogen atom of water with respect to the PMEEECL oxygen atoms (Fig. S5†), which have been computed at two different temperatures, 285 K (hydrophilic state) and 335 K (hydrophobic state). These RDFs describe the probability to find water hydrogens at a certain distance from the PMEEECL oxygen atoms, hence they are related with the PMEEECL-water hydrogen bonding probability. A substantial in the RDF in proximity to the oxygen atoms can be observed above Tcg (Fig. S5†), testifying that the hydrophilic–hydrophobic transition is caused by a temperature-induced dehydration, in agreement with previous literature on LCST polymers.57 Unlike the PMEEECL block, the RDF of centre of mass (COM) of PAE block and hydrogen of water molecules (Fig. S6†) shows no reduction upon increasing the temperature which is in agreement with previous results.
3.3. Self-assembly of PMEEECL20–PAEM
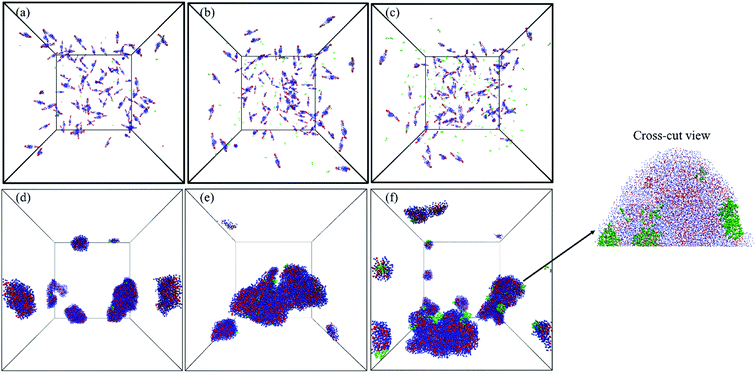
Once the relation between Tcg and the PAE block length was established, the self-assembly behaviour of the three selected copolymers, PMEEECL20–PAE5, PMEEECL20–PAE10, and PMEEECL20–PAE15, at 300 K has been investigated by MARTINI CG force field simulations (Fig. 3). In Fig. 3 the self-assembly process is depicted with a series of snapshot after different simulation times where the water beads are removed for clarity. Initially, 200 PMEEECL20–PAEM chains were randomly placed in the simulation box with 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water beads with an approximate concentration of 8 wt%, 10 wt%, and 12 wt% for M = 5, 10, and 15, respectively. After 200 ns of simulation time the onset of self-assembly could be observed and by further increasing the simulation time the self-assembled structure where formed. These remained stable and did not coalesce for the last 100 ns of simulation. In addition, by increasing the PAE block length, the self-assembly process speeds up, as shown by the evolution of the order parameter (Fig. S3†). Details of the spherical and cylindrical and bilayer morphologies are presented in the fifth column of Fig. 3 for more clarification. The quantitative description of the self-assembly behaviour, i.e. the number of cluster, as a function of simulation time for spherical morphology is plotted in Fig. S7† which reveals two spherical micelles remain after a simulation time of 600 ns. It follows in agreement with the SCF predictions, that PMEEECL20–PAE5 forms small spherical micelles, PMEEECL20–PAE10 forms cylindrical micelles and PMEEECL20–PAE15 forms bilayer structures.
000 water beads with an approximate concentration of 8 wt%, 10 wt%, and 12 wt% for M = 5, 10, and 15, respectively. After 200 ns of simulation time the onset of self-assembly could be observed and by further increasing the simulation time the self-assembled structure where formed. These remained stable and did not coalesce for the last 100 ns of simulation. In addition, by increasing the PAE block length, the self-assembly process speeds up, as shown by the evolution of the order parameter (Fig. S3†). Details of the spherical and cylindrical and bilayer morphologies are presented in the fifth column of Fig. 3 for more clarification. The quantitative description of the self-assembly behaviour, i.e. the number of cluster, as a function of simulation time for spherical morphology is plotted in Fig. S7† which reveals two spherical micelles remain after a simulation time of 600 ns. It follows in agreement with the SCF predictions, that PMEEECL20–PAE5 forms small spherical micelles, PMEEECL20–PAE10 forms cylindrical micelles and PMEEECL20–PAE15 forms bilayer structures.
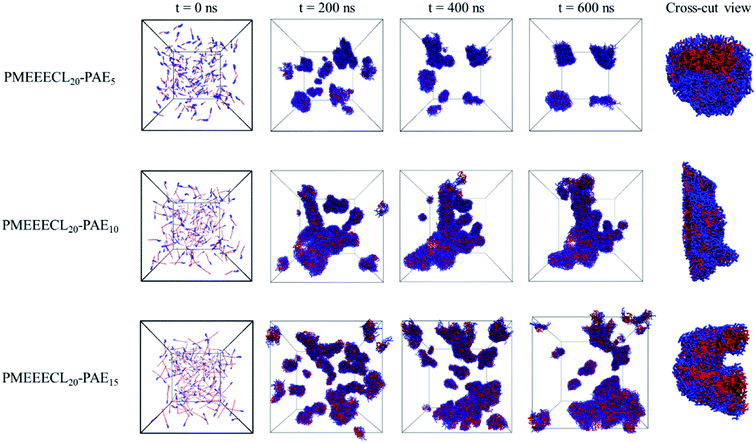 | ||
| Fig. 3 Snapshot series from micellization of PMEEECL20–PAEM with M = 5, 10, and 15. Water beads are removed for clarity and blue and red beads show PMEEECL and PAE beads, respectively. | ||
The self-assembly of the three copolymers have also been studied with SCF theory which, similarly to the CG MARTINI method, enables to generate radial concentration profiles (Fig. 4). These profiles describe the spatial distribution of the components as a function of the distance from the centre of the self-assembled structures. For both methods at room temperature and neutral pH the concentration profiles predict the self-assembled structures to be composed of a dehydrated core (only 5–10% water present) rich in PAE, surrounded by a hydrated corona rich in PMEEECL.
These regions are separated by an interface which appears more diffuse in the CG MARTINI simulations (Fig. 4). This difference is probably caused by three main factors. Firstly, the interaction potentials used in the CG MARTINI method are softer. Secondly, the interaction parameters used in the two methods are different. Thirdly, in the SCF computations the concentration profiles are directly calculated optimizing the free-energy and assuming perfect geometries while in the CG MARTINI simulations they are calculated from the beads distribution in space. The CG MARTINI self-assembled structures appear quite irregular in shape and exhibit areas where the lyophobic core is directly in contact with the solvent. When performing a radial average such irregularities result in an apparently larger interface between the lyophilic and lyophobic domains, which explains the jumps observed in the CG MARTINI water concentration profile at the interface between the two blocks. The SCF computations predict bigger sizes for the assemblies (as can be observed in the concentration profiles in Fig. 4) but this difference is simply due to the different coarse-graining procedures applied, which does not fully reflect the size, the steric hindrance and the flexibility of the copolymer chains. Overall, it may be concluded that the SCF predictions and computer simulation results are in qualitative and semi-quantitative agreement.
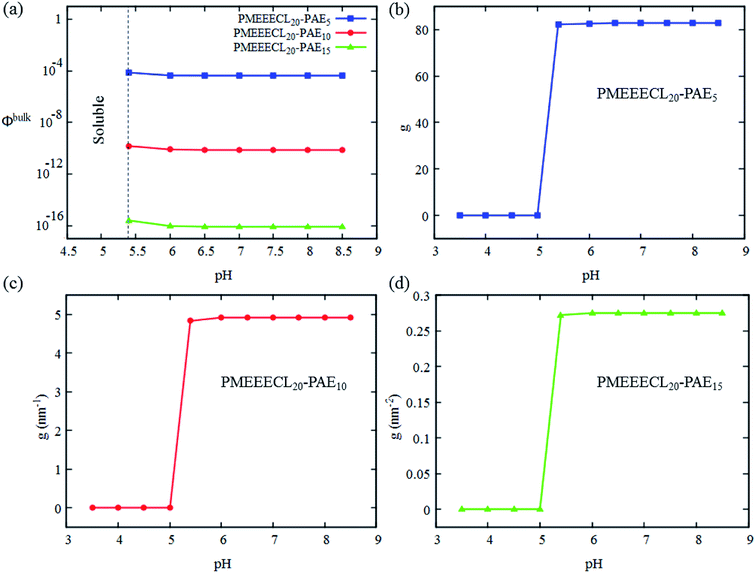
3.4. Response to stimuli
3.5. DOX encapsulation
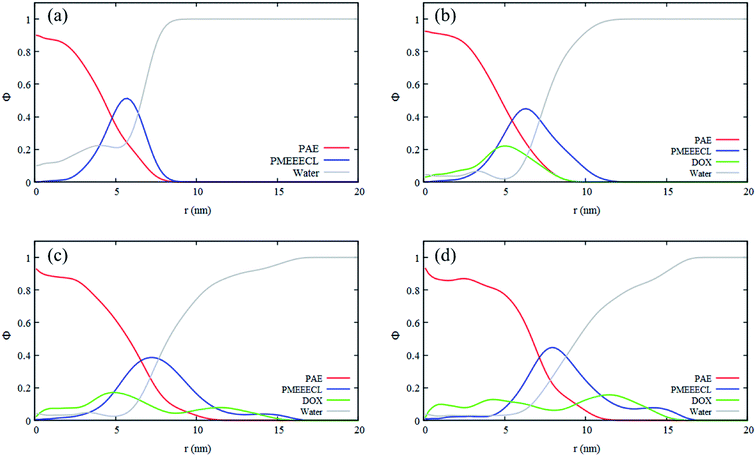
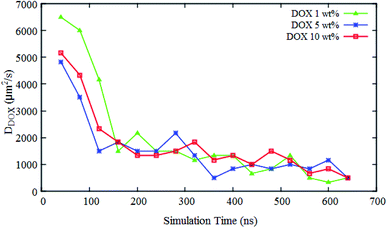
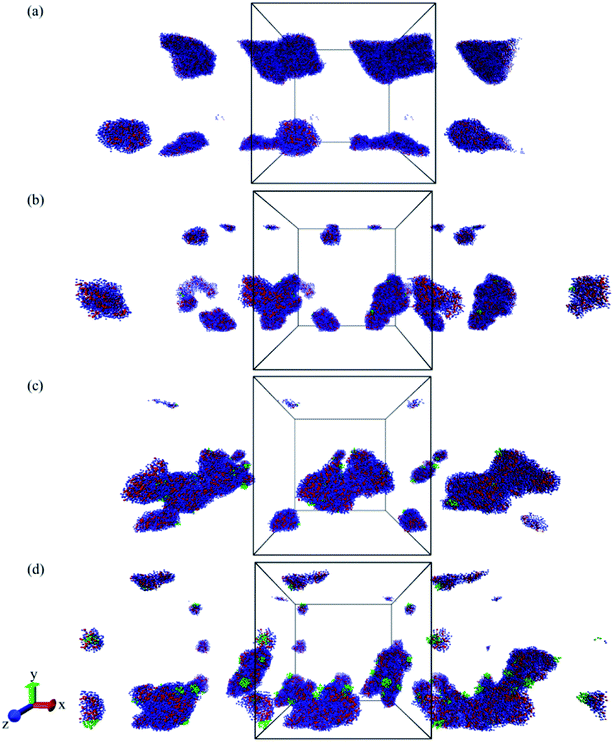
As mentioned in the introduction section, 310–315 K would be an appropriate range of the coil-to-globule transition temperature Tcg for the amphiphilic block copolymer for drug delivery applications.13 By using all-atom MD simulations, Tcg of PMEEECL20–PAEM with M = 5, 10, and 15 was calculated and the appropriate amphiphilic block copolymer for drug delivery application was found to be PMEEECL20–PAE5 with 312 ± 2.5 K for. These block copolymers self-assemble into a spherical morphology based on both SCF computations and CG simulations. The spherical geometry is an appropriate morphology for particles moving through a body environment. Transport of for instance cylindrical micelles for instance is easily hampered due to their significant lengths, and also vesicles are typically big. Therefore, PMEEECL20–PAE5 block copolymers with a radius R close to 7 nm have been selected to study the solubilisation of doxorubicin at 300 K at three DOX concentrations (1 wt%, 5 wt%, and 10 wt%; here the wt% is the amount with respect to the total amount of PMEEECL20–PAE5) with CG MARTINI force field simulations. We note that, since only two spherical micelles appear in the simulation box (see Fig. 3), the aggregation number and size computed from the simulations are approximate. The CG MARTINI concentration profiles (Fig. 6) enable to visualize the spatial distribution of DOX within the micelles and how this is affected by the DOX concentration. At 1 wt%, DOX is mainly located at the interface between the micelle's core and corona (Fig. 6a). With increasing DOX concentration the location of DOX beads shifts from the interface of core and corona towards the corona section (Fig. 6b). Still, for 10 wt% (Fig. 6c) there are some DOX beads at the external layer of micelle, although the core encapsulation dominates in comparison to 1 wt% and 5 wt% which can be occurred at guest, i.e. DOX, concentrations higher than the solubility.58 It should be also noted that by increasing the DOX concentration the size of micelle is increased.The self-diffusion coefficient of DOX (DDOX) was computed from the mean-square displacements (MSD) determined using the CG simulations. The MSDs were converted to the D values by using eqn (6) and (7) and plotted in Fig. 7 for three DOX concentrations. Prior to self-assembly, DDOX lies in range ∼4800–6500 μm2 s−1 but after 600 ns of simulation, when the micelles were formed and DOX is solubilized, the drug diffusivity decreases about one order of magnitude to ∼500 μm2 s−1. This can be explained by the fact that the DOX beads first diffuse as individual beads, whereas they diffuse together with the block copolymer micelle after encapsulation. A series of snapshots from the first and last part of the simulations are provided in Fig. 8 (for full movies refer to ESI Videos S1–S3†). It can be observed that the DOX beads move from the solution to the micelles as the micelles form.
The DOX loading efficiency, defined as the ratio between loaded in the core and at the interface of core and corona of the micelle with respect to the total amount of DOX (see Methods) was approximately 80%, 78%, and 75% when DOX was fed as the ratio of 1 wt%, 5 wt%, and 10 wt% to block copolymers, respectively, after 600 ns of simulation time. This small decrease in the solubilization might be related to the reduction of micelle capacity by increasing the concentration of DOX. As can be observed, see Fig. 8, all DOX beads were captured by micelles at the three different concentrations studied. This implies that the non-loaded DOX molecules reside in the corona of the micelles. The presence of DOX resulted in an increase in the final number of micelles. Hence the average aggregation number, i.e. the number of block copolymer chains added to the simulation box divided by the number of micelles, reduced from 26.25 to 15 by increasing the DOX concentration from 1 wt% to 10 wt%, respectively. This is caused by the interfacial adsorption of DOX, which reduces the interfacial tension of the core. This effect was predicted theoretically and verified experimentally previously.58 Its effect can be seen for example in Fig. 9: in absence of DOX only two spherical micelles were found, but by adding DOX at three different concentrations more stable micelles with the same simulation time were observed, which corresponds to theoretical predictions and experimental observations.58
4. Conclusions
In this work, a dual-responsive PMEEECL–PAE block copolymer was designed in silico and the self-assembly behaviour of these polymers was studied with a combination of all-atom molecular dynamics (MD) simulations, MARTINI coarse-grained (CG) force field simulation and Scheutjens–Fleer self-consistent field (SCF) computations. The results reveal that the PMEEECL blocks are thermoresponsive, and become insoluble above a certain temperature, of which the value can be tuned by varying the copolymer composition via the PMEEECL mass fraction f. Upon decreasing f, spherical micelles, cylindrical micelles and bilayer self-assembled structures can be obtained. These self-assembled structures are also pH sensitive, and disassemble at pH < 5.4 due to PAE protonation. Responsivity at this pH range is ideal for drug delivery applications. Finally, it is demonstrated that spherical MEEECL20–AE5 micelles can solubilize the anticancer drug doxorubicin (DOX) with high efficiency (75–80%) at different concentrations. The solubilisation occurs via interfacial adsorption of DOX at the micelle core–corona interface at low DOX concentration. Upon increasing the DOX concentration the preferred DOX accumulation location shifts from the interface towards the corona area. The results provided by this unique combination of computational techniques show that PMEEECL–PAE block copolymers are great candidates for stimuli controlled drug delivery applications.Conflicts of interest
There are no conflicts to declare.References
- Y. Mai and A. Eisenberg, Self-assembly of block copolymers, Chem. Soc. Rev., 2012, 41, 5969–5985, 10.1039/C2CS35115C.
- Y. Tang, S. Y. Liu, S. P. Armes and N. C. Billingham, Solubilization and controlled release of a hydrophobic drug using novel micelle-forming ABC triblock copolymers, Biomacromolecules, 2003, 4, 1636–1645, DOI:10.1021/bm030026t.
- R. D. Wesley, C. A. Dreiss, T. Cosgrove, S. P. Armes, W. Bank, L. Thompson, F. L. Baines and N. C. Billingham, Structure of a hydrophilic–hydrophobic block copolymer and its interactions with salt and an anionic surfactant, Langmuir, 2005, 21, 4856–4861, DOI:10.1021/la046830y.
- H. Oliveira, E. Pérez-Andrés, J. Thevenot, O. Sandre, E. Berra and S. Lecommandoux, Magnetic field triggered drug release from polymersomes for cancer therapeutics, J. Controlled Release, 2013, 169, 165–170, DOI:10.1016/j.jconrel.2013.01.013.
- G. Liu, S. Ma, S. Li, R. Cheng, F. Meng, H. Liu and Z. Zhong, The highly efficient delivery of exogenous proteins into cells mediated by biodegradable chimaeric polymersomes, Biomaterials, 2010, 31, 7575–7585, DOI:10.1016/j.biomaterials.2010.06.021.
- Y. H. Bae and K. Park, Targeted drug delivery to tumors: myths, reality and possibility, J. Controlled Release, 2011, 153, 198–205, DOI:10.1016/j.jconrel.2011.06.001.
- G. T. Chang, T. Y. Ci, L. Yu and J. D. Ding, Enhancement of the fraction of the active form of an antitumor drug topotecan via an injectable hydrogel, J. Controlled Release, 2011, 156, 21–27, DOI:10.1016/j.jconrel.2011.07.008.
- Z. P. Zhang and S. S. Feng, The drug encapsulation efficiency, in vitro drug release, cellular uptake and cytotoxicity of paclitaxel-loaded poly(lactide)-tocopheryl polyethylene glycol succinate nanoparticles, Biomaterials, 2006, 27, 4025–4033, DOI:10.1016/j.biomaterials.2006.03.006.
- A. Gandhi, A. Paul, S. O. Sen and K. K. Sen, Studies on thermoresponsive polymers: phase behaviour, drug delivery and biomedical applications, Asian J. Pharm. Sci., 2015, 10, 99–107, DOI:10.1016/j.ajps.2014.08.010.
- E. S. Lee, K. T. Oh, D. Kim, Y. S. Youn and Y. H. Bae, Tumor pH-responsive flower-like micelles of poly(L-lactic acid)-b-poly (ethylene glycol)-b-poly(L-histidine), J. Controlled Release, 2007, 123, 19–26, DOI:10.1016/j.jconrel.2007.08.006.
- V. S. Miguel, A. J. Limer, D. M. Haddleton, F. Catalina and C. Peinado, Biodegradable and thermoresponsive micelles of triblock copolymers based on 2-(N,N-dimethylamino)ethyl methacrylate and e-caprolactone for controlled drug delivery, Eur. Polym. J., 2008, 44, 3853–3863, DOI:10.1016/j.eurpolymj.2008.07.056.
- S. Q. Liu, N. Wiradharma, S. J. Gao, Y. W. Tong and Y. Y. Yang, Bio-functional micelles self-assembled from a folate-conjugated block copolymer for targeted intracellular delivery of anticancer drugs, Biomaterials, 2007, 28, 1423–1433, DOI:10.1016/j.biomaterials.2006.11.013.
- N. Kamaly, B. Yameen, J. Wu and O. C. Farokhzad, Degradable controlled-release polymers and polymeric nanoparticles: mechanisms of controlling drug release, Chem. Rev., 2016, 116, 2602–2663, DOI:10.1021/acs.chemrev.5b00346.
- D. J. Adams, M. L. Wahl, J. L. Flowers, B. Sen, M. Colvin, M. W. Dewhirst, G. Manikumar and M. C. Wani, Camptothecin analogs with enhanced activity against human breast cancer cells. II. Impact of the tumor pH gradient, Cancer Chemother. Pharmacol., 2006, 57, 145–154, DOI:10.1007/s00280-005-0008-5.
- D. J. Adams and L. R. Morgan, Tumor physiology and charge dynamics of anticancer drugs: implications for camptothecin-based drug development, Curr. Med. Chem., 2011, 18, 1367–1372, DOI:10.2174/092986711795029609.
- Z. Luo, Y. Li, B. Wang and J. Jiang, pH-sensitive vesicles formed by amphiphilic grafted copolymers with tunable membrane permeability for drug loading/release: a multiscale simulation study, Macromolecules, 2016, 49, 6084–6094, DOI:10.1021/acs.macromol.6b01211.
- H. Wei, X. Z. Zhang, H. Cheng, W. Q. Chen, S. X. Cheng and R. X. Zhuo, Self-assembled thermo- and pH-responsive micelles of poly(10-undecenoic acid-b-N-isopropylacrylamide) for drug delivery, J. Controlled Release, 2006, 116, 266–274, DOI:10.1016/j.jconrel.2006.08.018.
- R. S. Kalhapure and J. Renukuntla, Thermo- and pH dual responsive polymeric micelles and nanoparticles, Chem.-Biol. Interact., 2018, 295, 20–37, DOI:10.1016/j.cbi.2018.07.016.
- Á. González García, A. Ianiro and R. Tuinier, On the colloidal stability of spherical copolymeric micelles, ACS Omega, 2018, 3, 17976–17985, DOI:10.1021/acsomega.8b02548.
- J. Sankaranarayanan, E. A. Mahmoud, G. Kim, J. M. Morachis and A. Almutairi, Multiresponse strategies to modulate burst degradation and release from nanoparticles, ACS Nano, 2010, 4, 5930–5936, DOI:10.1021/nn100968e.
- J. Hao, J. Servello, P. Sista, M. C. Biewer and M. C. Stefan, Temperature-sensitive aliphatic polyesters: synthesis and characterization of γ-substituted caprolactone monomers and polymers, J. Mater. Chem., 2011, 21, 10623–10628, 10.1039/C1JM11288K.
- Y. Cheng, J. Hao, L. A. Lee, M. C. Biewer, Q. Wang and M. C. Stefan, Thermally controlled release of anticancer drug from self-assembled γ-substituted amphiphilic poly(ε-caprolactone) micellar nanoparticles, Biomacromolecules, 2012, 13, 2163–2173, DOI:10.1021/bm300823y.
- K. H. Min, J. H. Kim, S. M. Bae, H. Shin, M. S. Kim, S. Park, H. Lee, R. W. Park, I. S. Kim, K. Kim, I. C. Kwon, S. Y. Jeong and D. S. Lee, Tumoral acidic pH-responsive MPEG-poly(β-amino ester) polymeric micelles for cancer targeting therapy, J. Controlled Release, 2010, 144, 259–266, DOI:10.1016/j.jconrel.2010.02.024.
- A. Koochaki, M. R. Moghbeli and S. Javan Nikkhah, Coil-to-globule transition of thermo-responsive γ-substituted poly (ε-caprolactone) in water: a molecular dynamics simulation study, Curr. Appl. Phys., 2018, 18, 1313–1319, DOI:10.1016/j.cap.2018.07.011.
- A. Koochaki, M. R. Moghbeli and S. Javan Nikkhah, Effect of γ-substituted poly(ε-caprolactone) chain length on its coil-to-globule transition temperature in water: a molecular dynamics simulation study, Chem. Phys., 2019, 527, 110506, DOI:10.1016/j.chemphys.2019.110506.
- G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Springer, Netherlands, 1998 Search PubMed.
- P. N. Hurter, J. M. H. M. Scheutjens and T. A. Hatton, Molecular modeling of micelle formation and solubilization in block copolymer micelles. 1. A self-consistent mean-field lattice theory, Macromolecules, 1993, 26, 5592–5601, DOI:10.1021/ma00073a010.
- A. Ianiro, J. Patterson, Á. González García, M. M. J. van Rijt, M. M. R. M. Hendrix, N. A. J. M. Sommerdijk, I. K. Voets, A. C. C. Esteves and R. Tuinier, A roadmap for poly(ethylene oxide)-block-poly-ε-caprolactone self-assembly in water: prediction, synthesis, and characterization, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 330–339, DOI:10.1002/polb.24545.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI force field: coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111, 7812–7824, DOI:10.1021/jp071097f.
- S. J. Marrink, A. H. de Vries and A. E. Mark, Coarse grained model for semiquantitative lipid simulations, J. Phys. Chem. B, 2004, 108, 750–760, DOI:10.1021/jp036508g.
- S. M. Loverde, M. L. Klein and D. E. Discher, Nanoparticle shape improves delivery: rational coarse grain molecular dynamics (rCG-MD) of taxol in worm-like PEG-PCL micelles, Adv. Mater., 2012, 24, 3823–3830, DOI:10.1002/adma.201103192.
- D. J. Beltran-Villegas, M. G. Wessels, J. Y. Lee, Y. Song, K. L. Wooley, D. J. Pochan and A. Jayaraman, Computational Reverse-Engineering Analysis for Scattering Experiments on Amphiphilic Block Polymer Solutions, J. Am. Chem. Soc., 2019, 141, 14916–14930, DOI:10.1021/jacs.9b08028.
- Z. Li and E. E. Dormidontova, Kinetics of Diblock Copolymer Micellization by Dissipative Particle Dynamics, Macromolecules, 2010, 43, 3521–3531, DOI:10.1021/ma902860j.
- A. Prhashanna and S. Bor Chen, Chain exchange kinetics between linear ABA-type triblock copolymer micelles, Polymer, 2017, 118, 22–29, DOI:10.1016/j.polymer.2017.04.049.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38, DOI:10.1016/0263-7855(96)00018-5.
- W. L. Jorgensen and J. Tirado-Rives, The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin, J. Am. Chem. Soc., 1988, 110, 1657–1666, DOI:10.1021/ja00214a001.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Definition and testing of the GROMOS force-field versions 54A7 and 54B7, Eur. Biophys. J., 2011, 40, 843–856, DOI:10.1007/s00249-011-0700-9.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926, DOI:10.1063/1.445869.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Taylor & Francis, Inc., 1988 Search PubMed.
- D. J. Finney, Bioassay and the practice of statistical inference, International Statistical Review/Revue Internationale de Statistique, 1979, 47, 1–12, DOI:10.2307/1403201.
- T. E. de Oliveira, C. M. Marques and P. A. Netz, Molecular dynamics study of the LCST transition in aqueous poly(N-n-propylacrylamide), Phys. Chem. Chem. Phys., 2018, 20, 10100–10107, 10.1039/C8CP00481A.
- S. Nawaz and P. Carbone, Coarse-Graining Poly(ethylene oxide)–Poly(propylene oxide)–Poly(ethylene oxide) (PEO–PPO–PEO) Block Copolymers Using the MARTINI Force Field, J. Phys. Chem. B, 2014, 118, 1648–1659, DOI:10.1021/jp4092249.
- L. Qiu, J. Liu, R. Alessandri, X. Qiu, M. Koopmans, R. W. A. Havenith, S. J. Marrink, R. C. Chiechi, L. J. A. Koster and J. C. Hummelen, Enhancing doping efficiency by improving host-dopant miscibility for fullerene-based n-type thermoelectrics, J. Mater. Chem. A, 2017, 5, 21234, 10.1039/c7ta06609k.
- D. Mu, X.-R. Huang, Z.-Y. Lu and C.-C. Sun, Computer simulation study on the compatibility of poly(ethylene oxide)/poly(methyl methacrylate) blends, Chem. Phys., 2008, 348, 122–129, DOI:10.1016/j.chemphys.2008.03.015.
- R. Mackenzie, J. Booth, C. Alexander, M. C. Garnett and C. A. Laughton, Multiscale modeling of drug-polymer nanoparticle assembly identifies parameters influencing drug encapsulation efficiency, J. Chem. Theory Comput., 2015, 11, 2705–2713, DOI:10.1021/ct501152a.
- Y. Chen, Q. L. Liu, A. M. Zhu, Q. G. Zhang and J. Y. Wu, Molecular simulation of CO2/CH4 permeabilities in polyamide–imide isomers, J. Membr. Sci., 2010, 348, 204–212, DOI:10.1016/j.memsci.2009.11.002.
- S. Rasouli, M. R. Moghbeli and S. J. Nikkhah, A comprehensive molecular dynamics study of a single polystyrene chain in a good solvent, Curr. Appl. Phys., 2018, 18, 68–78, DOI:10.1016/j.cap.2017.10.010.
- The SCF code was provided by F. A. M. Leermakers and developed by F. A. M. Leermakers and J. van Male from Wageningen University, The Netherlands.
- F. A. M. Leermakers, J. C. Eriksson and J. Lyklema, Association colloids and their equilibrium modelling, in Fundamentals of Interface and Colloid Science, ed. J. Lyklema, 2005, vol. 5, pp. 4.1–4.123, DOI:10.1016/S1874-5679(05)80008-X.
- Y. Lauw, F. A. M. Leermakers and M. A. Cohen Stuart, Self-consistent-field analysis of the micellization of carboxy-modified poly(ethylene oxide)–poly(propylene oxide)–poly(ethylene oxide) triblock copolymers, J. Phys. Chem. B, 2006, 110, 465–477, DOI:10.1021/jp053795a.
- A. V. Rayer, K. Z. Sumon, L. Jaffari and A. Henni, Dissociation constants (pKa) of tertiary and cyclic amines: structural and temperature dependences, J. Chem. Eng. Data, 2014, 59, 3805–3813, DOI:10.1021/je500680q.
- E. Stefanis and C. Panayiotou, Prediction of hansen solubility parameters with a new group-contribution method, Int. J. Thermophys., 2008, 29, 568–585, DOI:10.1007/s10765-008-0415-z.
- T. Lindvig, M. L. Michelsen and G. M. Kontogeorgis, A Flory–Huggins model based on the Hansen solubility parameters, Fluid Phase Equilib., 2002, 203, 247–260, DOI:10.1016/S0378-3812(02)00184-X.
- J. G. J. L. Lebouille, F. A. M. Leermakers, M. A. Cohen Stuart and R. Tuinier, Design of block-copolymer-based micelles for active and passive targeting, Phys. Rev. E, 2016, 94, 042503, DOI:10.1103/PhysRevE.94.042503.
- H. J. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, FRG, 2003 Search PubMed.
- T. E. De Oliveira, D. Mukherji, K. Kremer and P. A. Netz, Effects of stereochemistry and copolymerization on the LCST of PNIPAm, J. Chem. Phys., 2017, 146, 034904, DOI:10.1063/1.4974165.
- A. Ianiro, Á. González García, S. Wijker, J. P. Patterson, A. C. C. Esteves and R. Tuinier, Controlling the spatial distribution of solubilized compounds within copolymer micelles, Langmuir, 2019, 35, 4776–4786, DOI:10.1021/acs.langmuir.9b00180.
Footnote |
| † Electronic supplementary information (ESI) available: Computer simulations (Table S1), Flory–Huggins interaction parameters (Table S2), radii of gyration of PMEEECL and PAE parts of block copolymer (Table S3), the hydrophilic mass fraction dependency of coil-to-globule transition temperature of PMEEECL in block copolymers (Table S4), the bond and angle distribution of PMEEECL, PAE (Fig. S1), and DOX (Fig. S2), the simulation time-dependency of micelle order parameter (Fig. S3), solvent access surface area as a function of interaction energy for both PMEEECL and PAE blocks (Fig. S4), the RDF of PMEEECL block and water molecules (Fig. S5), the RDF of PAE block and water molecules (Fig. S6), the number of cluster for spherical micelles as a function of simulation time (Fig. S7), and the RDF of PMEEECL beads and water beads as a function of temperature (Fig. S8). Additionally, see Videos S1–S3 which show the encapsulation process of DOX into spherical micelle composed of PMEEECL20–PAE5 when it was fed as the ratio of 1 wt%, 5 wt%, and 10 wt% to block copolymers. See DOI: 10.1039/c9ra09066e |
| This journal is © The Royal Society of Chemistry 2020 |