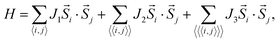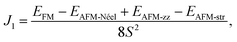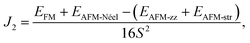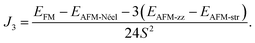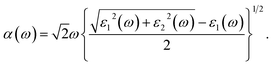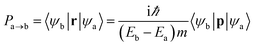Electronic, magnetic and optical properties of MnPX₃ (X = S, Se) monolayers with and without chalcogen defects: a first-principles study

Abstract

Based on density functional theory (DFT), we performed first-principles studies on the electronic structure, magnetic state and optical properties of two-dimensional (2D) transition-metal phosphorous trichalcogenides MnPX₃ (X = S and Se). The calculated interlayer cleavage energies of the MnPX₃ monolayers indicate the energetic possibility to be exfoliated from the bulk phase, with good dynamical stability confirmed by the absence of imaginary contributions in the phonon spectra. The MnPX₃ monolayers are both Néel antiferromagnetic (AFM) semiconductors with direct band gaps falling into the visible optical spectrum. Magnetic interaction parameters were extracted within the Heisenberg model to investigate the origin of the AFM state. Three in-plane magnetic exchange parameters play an important role in the robust AFM configuration of Mn ions. The Néel temperatures (T_N) were estimated by means of Monte Carlo simulations, obtaining theoretical T_N values of 103 K and 80 K for 2D MnPS₃ and MnPSe₃, respectively. With high spin state Mn ions arranged in honeycomb lattices, the spin-degenerated band structures exhibit valley polarisation and were investigated in different biaxial in-plain strains, considering the spin-orbital coupling (SOC). 2D MnPX₃ monolayers show excellent performance in terms of the optical properties, and the absorption spectra were discussed in detail to find the transition mechanism. Different amounts and configurations of chalcogen vacancies were introduced into the MnPX₃ monolayers, and it was found that the electronic structures are heavily affected depending on the vacancy geometric structure, leading to different magnetic state and absorption spectra of defected MnPX₃ systems.

---

1 Introduction

Two-dimensional (2D) van der Waals materials have been recently extensively explored,^1–5 owing to their unique electronic structures and interesting physical and chemical properties, since the first experiments on the demonstration of the extraordinary transport properties of graphene.^6,7 For several decades, the family of 2D crystals has grown considerably with new additions such as boron nitride (BN),⁸ black phosphorus (BP)⁹ and transition metal dichalcogenides (TMDs).¹⁰ Recently, a series of 2D transition metal trichalcogenides (TMTs) MPX₃ (M = V, Cr, Mn, Fe, Co, Ni and Zn; X = Se and Se) has gained many investigations over their synthesis and optical and electrical properties connected with weak interlayer van der Waals interactions.^11–17 Bulk 3D MPX₃ compounds can be prepared via chemical vapour deposition (CVD)¹⁴ and chemical vapour transport (CVT)¹⁸ methods with high crystal quality. By mechanical exfoliation and chemical intercalation, the 2D monolayers of MPX₃ can be obtained with intermediate band gaps ranging from 1.3 eV to 3.5 eV,¹⁸ making them the ideal candidates for exfoliated 2D magnets and indicating their enhanced light absorption efficiency.^18,19 DFT calculations predict that 2D MPX₃ monolayers exhibit a large variety of magnetic behaviours, including ferromagnetic (FM) metal, antiferromagnetic (AFM) semiconductors and nonmagnetic (NM) insulators or metals, which can be effectively modulated via doping or lattice strain effects.²⁰ These various magnetic functionalities of 2D MPX₃ can be employed for low dimensional spintronic and magnetoelectronic applications. The wide range of band gaps indicate that 2D MPX₃ compounds can also be considered as promising candidates for optoelectronic and clean energy generation and related water splitting applications.^21,22

Among the 2D MPX₃ family, AFM phase MnPX₃ compounds are the most interesting and widely focused materials due to the prediction of some exciting properties, such as visible-light catalytic activity,²³ the possibility of use in valleytronics,²⁴ doping-induced half-metallicity,²⁵ etc. Their magnetic structure and spin ordering and control through doping and strain effects have been theoretically investigated.^25–27 Notably, considering the treatment of spin-orbital coupling, 2D MnPX₃ monolayers have been predicted with a spontaneous valley polarisation with degenerate spins.²⁴ The magnetic behaviour and valley polarisation of 2D MnPX₃ monolayers can be controlled by transition metal substitutions and electronic coupling via heterostructures, resulting in FM, half-metallic and bipolar magnetic semiconductors.^28–30 These strategies offers a practical avenue for exploring novel valleytronic devices which can be fabricated from 2D MnPX₃ monolayers.

It is well know that defects (dopants, vacancies, interstitial atoms, etc.) play a significant role in tailoring of 2D materials and controllable modifications can lead to drastic changes of their electronic, magnetic, optical and transport properties. Although many density functional theory (DFT) calculations have been carried out on the electronic and magnetic properties, the optical properties of 2D MnPX₃ and the influence of chalcogen vacancies in these materials has been rarely investigated. Herein, we present an explicit investigation of the electronic structure of MnPX₃ monolayers in order to gain insight into the magnetic and optical properties in detail. The influence of chalcogen vacancies on the electronic structure and magnetic and optical properties are also systemically studied and discussed in this work.

2 Computational details

Spin-polarised DFT calculations based on plane-wave basis sets of 500 eV cutoff energy were performed with the Vienna ab initio simulation package (VASP).^31–33 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional³⁴ was employed. The electron–ion interaction was described within the projector augmented wave (PAW) method³⁵ with Mn (3p, 3d, 4s), P (3s, 3p), S (3s, 3p) and Se (4s, 4p) states treated as valence states. The Brillouin-zone integration was performed on Γ-centred symmetry reduced Monkhorst–Pack meshes using a Gaussian smearing with σ = 0.05 eV, except for the calculation of total energies and densities of states (DOSs). For those calculations, the tetrahedron method with Blöchl corrections³⁶ was employed. The 12 × 12 × 4 and 24 × 24 × 1 k-meshes were used for the studies of bulk and monolayer MnPX₃, respectively, and the 12 × 12 × 1 k-mesh was used for the 2 × 2 × 1 supercells consisting of 4-fold unit monolayers in case of vacancy studies. In the case of 2D MnPX₃, to ensure decoupling between periodically repeated layers, a vacuum space of 20 Å was used. The convergence criteria for energy and force were set to 10⁻⁶ eV and 0.005 eV Å⁻¹, respectively.

The PBE + U scheme³⁷ was adopted to properly describe the strongly correlated system of Mn 3d orbitals with the effective on-site Coulomb interaction parameter U = 5 eV.^24,38 The HSE06 hybrid functional³⁹ was also used for some systems with a 12 × 12 × 1 k-mesh in order to get more accurate band gaps. Dispersion interactions were considered adding a 1/r⁶ atom–atom term as parameterised by Grimme (“D2” parameterisation).⁴⁰

The single layer lattice dynamical stability was determined using the first principles phonon calculations code PHONOPY⁴¹ applying the finite displacement method⁴² within PBE + U. These phonon calculations were performed in 4 × 4 × 1 supercells and very tight convergence criteria of 10⁻⁸ eV for energy and 0.1 meV Å⁻¹ for force were used with a 6 × 6 × 1 k-mesh. Monte-Carlo simulations were performed within the Metropolis algorithm⁴³ to estimate the T_N value, using periodic boundary conditions with a series of superlattices containing different amounts of magnetic sites. The optical spectra were calculated from the frequency dependent dielectric matrix after the electronic ground state had been determined.⁴⁴ The PYPROCAR code was used to plot the spin-textures.⁴⁵ Crystal structures and charge densities were visualised by VESTA.⁴⁶

3 Results and discussions

3.1 Electronic and magnetic structure of 3D MnPX₃

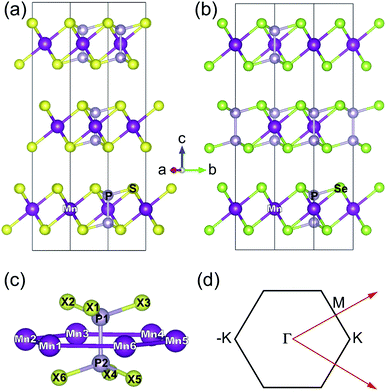
The three-dimensional (3D) bulk MnPS₃ crystallises in the C2/m space group,⁴⁷ while MnPSe₃ in R3̄.⁴⁸ Both of them can be represented in hexagonal unit cells as shown in Fig. 1(a) and (b), respectively (for details, see ESI,† Structural data for bulk MnPS₃ and Structural data for bulk MnPSe₃). Every unit cell contains three MnPX₃ single layers which have D_3d symmetry, despite the different 3D bulk space groups. The 2D MPX₃ layer is composed of two Mn²⁺ ions which form a hexagonal honeycomb lattice and one [P₂X₆]⁴⁻ bipyramid built from a P–P dimer connected with two sulphur/selenium trimers. The P–P dimer locates vertically across the centre of each honeycomb plane, with an in-plane twist of 60° between the top and bottom trimers as shown in Fig. 1(c). The lattice parameters a = b and c of 3D MnPX₃ were fully relaxed in NM, FM and AFM magnetic states and they are listed in Table 1 with the respective total and relative energies. The energy difference ΔE = E^AFM − E^FM is −164 meV for 3D MnPS₃ and −110 meV for 3D MnPSe₃, demonstrating that MnPX₃ bulk prefers the AFM state rather than the FM state. In particular, the NM states of 3D MnPX₃ crystals show much higher energies than that of the AFM one (ΔE > 25 eV), revealing that the NM state is strongly unfavourable in energy. The AFM ground state lattice parameters are in a good agreement with the experimental values.^47,48 Clearly, each lattice parameter and monolayer thickness d of MnPSe₃ are larger than the corresponding values of MnPS₃, caused by a larger ion radius of selenium compared to that of sulphur.

Fig. 1 Crystal structures of (a) 3D MnPS₃ and (b) 3D MnPSe₃. (c) Structure of the Mn-ion honeycomb lattice and centering [P₂X₆] bipyramid. (d) Sketch of the 2D Brillouin zone for the 2D hexagonal lattice with high symmetry k-points labeled.

Table 1 Relative to the lowest energy values (ΔE, in eV) as well as lattice parameters (in Å) for 3D MnPX₃ (X = S, Se) in different magnetic states obtained with PBE + U + D2

X	State	ΔE	a	c	d	Mn–X	Mn–Mn
a Ref. 47.b Ref. 48.
S	NM	25.582	5.789	18.991	3.065	2.44	3.34
	FM	0.165	6.070	19.899	3.314	2.63	3.50
	AFM	0	6.064	19.893	3.313	2.62	3.51
	Expt^a		6.077	20.388
Se	NM	26.201	6.144	19.286	3.379	2.56	3.55
	FM	0.113	6.303	20.086	3.491	2.76	3.69
	AFM	0	6.398	20.082	3.487	2.76	3.69
	Expt^b		6.387	19.996

---

An interesting magnetic property for the bulk state is the interlayer magnetic coupling between monolayers in the unit cell. The energy differences between different inter-layer magnetic coupling ΔE_int = E^AFM_int − E^FM_int are 0.5 meV and −0.27 meV for bulk MnPS₃ and MnPSe₃, respectively. Consequently, the FM inter-layer coupling is preferred for bulk MnPS₃, but AFM is preferred for bulk MnPSe₃. The different signs of ΔE_int can be attributed to the different monolayer arrangement for the two bulks in different space groups. The small ΔE_int is due to the large distance of about 7 Å between adjacent Mn honeycomb layers, and the neighbouring chalcogen atoms cannot act as a media bridge to mediate the long-range superexchange interactions across the large van der Waals gap, thus, the total energy is not sensitive to the inter-layer magnetic coupling, as in FePS₃.⁴⁹

Now the electronic structure of 3D MnPX₃ is briefly discussed. The band structure and DOS obtained by the PBE + U method are shown in Fig. 2(a, b) and (c, d) for 3D MnPS₃ and MnPSe₃, respectively. The band structures are spin-degenerated in the AFM state, showing similar features for both bulk MnPX₃ materials. The upper valence bands (VBs) at E − E_F > −1.0 eV are mainly formed by S/Se p and partly by Mn 3d orbitals; the lower conduction bands (CBs), at E − E_F < 3.5 eV for 3D MnPS₃ and E − E_F < 2.5 eV for MnPSe₃, are mostly composed of S/Se p and the partial contributions from P p orbitals are almost equal to that of the Mn 3d states. The band gaps and the magnetic moments of Mn ions were extracted and are listed in Table 2. The GGA-PBE results give indirect band gaps of 1.31 eV for 3D MnPS₃ and 1.08 eV for 3D MnPS₃, respectively. As is well known, the GGA approximation usually underestimates the semiconductor band gap, thus, the PBE + U and HSE06 methods were further used to evaluate the band structure and resulting direct band gaps at the K point of the Brillouin Zone (BZ). The band gaps obtained by the PBE + U method are 2.37 eV for bulk MnPS₃ and 1.81 eV for bulk MnPSe₃. Moreover, the HSE06 functional predicts more accurate band gaps for the bulk systems with values of 3.08 eV and 2.50 eV for MnPS₃ and MnPSe₃, which shows good agreement with the experimental values of 3.0 eV and 2.5 eV,¹⁸ respectively. The magnetic moments of Mn ions calculated with the PBE + U method are 4.60 μ_B for both 3D MnPS₃ and MnPSe₃ (Table 2) and they are larger than that obtained with other functionals. These calculated values are in good agreement with the one obtained in the neutron diffraction experiments: 4.40 μ_B⁵⁰ for MnPS₃ and 4.74 μ_B⁴⁸ for MnPSe₃, revealing the high spin state of Mn²⁺ ions.

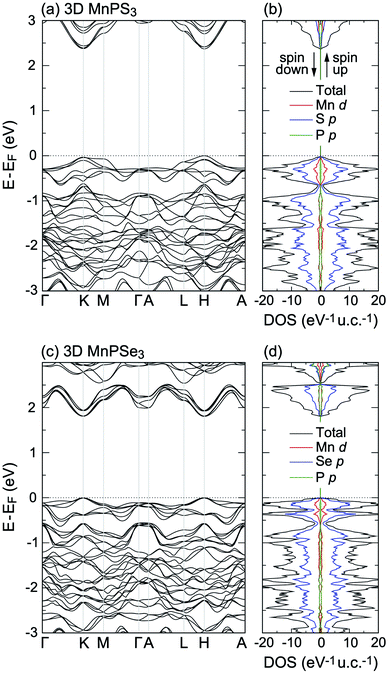Fig. 2 Band structures and total and partial DOS of (a and b) 3D MnPS₃ and (c and d) 3D MnPSe₃, obtained with PBE + U.

Table 2 Band gaps (E_g, in eV) and Mn magnetic moments (M, in μ_B) obtained with different methods for 2D and 3D MnPX₃ systems. The available experimental values for band gaps are placed in parenthesis

System	PBE		PBE + U		HSE06
	Eg	M	Eg	M	Eg	M
a Indirect.b Ref. 18.
3D MnPS3	1.31^a	4.24	2.37	4.60	3.08 (3.0^b)	4.48
2D MnPS3	1.49	4.25	2.50	4.59	3.25	4.49
3D MnPSe3	1.08^a	4.25	1.81	4.58	2.50 (2.5^b)	4.50
2D MnPSe3	1.17	4.26	1.84	4.59	2.56	4.50

---

3.2 Exfoliation energy and dynamical stability of 2D MnPX₃

In order to evaluate the possibility of 2D MnPX₃ monolayer mechanical exfoliation from the bulk, the cleavage energy was calculated by E_cl = (E_(d0→∞) − E₀)/A, where A is the in-plane area and d₀ is the van der Waals gap of bulk crystals. The theoretical value of E_cl is 0.12 J m⁻² for MnPS₃ and 0.23 J m⁻² for MnPSe₃. The two E_cl values are smaller than the experimentally estimated cleavage energy in graphite (0.37 J m⁻²),⁵¹ indicating that the exfoliation of bulk MnPX₃ is feasible in experiments. The E_cl = 0.23 J m⁻² value for MnPSe₃ is consistent with the previous theoretical results of 0.24 J m⁻²,⁵² whereas the E_cl = 0.12 J m⁻² value for MnPS₃ is much lower than the previous calculated value about of 0.26 J m⁻².¹⁸ In other words, the E_cl value for MnPS₃ is approximately twice smaller than the value calculated for MnPSe₃ as can be explained by two factors. The dominant one is that the Se ions offer larger van der Waals force than the S ions, and it can be also confirmed by the comparison between the E_cl values for FePS₃ (0.27 J m⁻²) and R3̄ FePSe₃ (0.38 J m⁻²).¹⁸ The second one is the different monolayer arrangement in the bulks between two bulk MnPX₃ compounds and can be proved by the E_cl value of 0.16 J m⁻² for fully relaxed MnPS₃ in the R3̄ space group and 0.21 J m⁻² for MnPSe₃ in the C2/m space group.

To estimate the dynamical stability of MnPX₃ monolayers, the phonon spectra were calculated within the finite displacement method and the respective phonon dispersions are presented in Fig. 3 along the high-symmetry directions of the hexagonal BZ. Importantly, no imaginary modes in the phonon dispersions are observed, confirming the dynamical stability of 2D MnPX₃, thus, they can be isolated in the experiments as freestanding layers. According to the phonon DOS given in right-hand side of the figure, the low frequency phonon bands below 8 THz for MnPX₃ are dominated by Mn–S/Se interactions, whereas the middle and high frequency branches above 8 THz originate from the internal molecular vibrations of the [P₂X₆] group, consistent with the previous results.⁵³ According to the fact that the radius and mass of selenium atoms are larger compared to that of sulphur, and that the bond length of Mn–Se is longer than that of Mn–S, the phonon bands of MnPSe₃ are shifted to lower frequencies compared to those of MnPS₃.

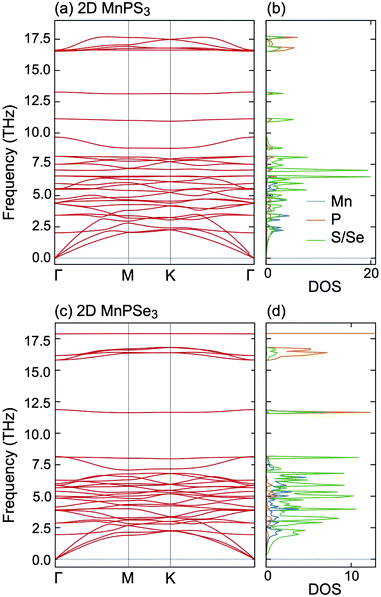Fig. 3 Phonon dispersion spectra and the corresponding DOS for (a and b) 2D MnPS₃ and (c and d) 2D MnPSe₃.

3.3 Magnetic properties of 2D MnPX₃

Four possible magnetic configurations were investigated to evaluate the ground state of 2D MnPX₃ monolayers. The different spin configurations are FM, AFM-Néel, AFM-zig-zag and AFM-stripy (ESI, Fig. S1†). To extract the total energies of different magnetic structures, we used four ordered spin states defined using a 2 × 1 × 1 supercell. The total energies of different spin configurations and the relative energy differences with respect to the AFM-Néel configuration calculated within the PBE + U method are listed in Table 3. It can be seen that the lowest total energy is the AFM-Néel state for the 2D MnPX₃ monolayer. In addition, NM configurations were also calculated, showing NM MnPX₃ monolayers are in a semi-metallic state. Similar to that of 3D bulk unit systems, the NM state of 2D MnPX₃ monolayers also shows much larger energies compared to the AFM ground state by 8.78 eV for MnPS₃ and by 8.87 eV for MnPSe₃, demonstrating that the MnPX₃ monolayers persist with AFM magnetism similar to the 3D bulk system. Accordingly, the Mn ions magnetic moments of 2D MnPX₃ are comparable to values for the 3D bulk state, listed in Table 2. Therefore one can conclude that 2D MnPX₃ is a robust intrinsic AFM monolayer.

Table 3 Total energy (E_tot, in eV) and relative to the lowest energy (ΔE, in meV) values for 2D MnPX₃ in the different magnetic states obtained for a 2 × 1 × 1 supercell with PBE + U. Calculated and available experimental values for T_N (in K) are given in the last column

Monolayer	Energy	FM	AFM-Néel	AFM-zigzag	AFM-stripy	TN
a Ref. 54.b Ref. 48.
MnPS3	Etot	−112.316	−112.423	−112.375	−112.377	103 (calc.)
	ΔE	107.14	0	48.07	46.51	115 (expt.^a)
MnPSe3	Etot	−104.620	−104.697	−104.666	−104.659	80 (calc.)
	ΔE	77.18	0	31.23	37.53	74 (expt.^b)

---

To extract the exchange interaction parameters between Mn ions spins, the Heisenberg Hamiltonian was considered

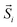where is the total spin magnetic moment of the atomic site and i, J_ij are the exchange coupling parameters between two local spins. Considering one central Mn atom interacting with three nearest neighbouring (NN, J₁), six next-nearest neighbouring (2NN, J₂), and three third-nearest neighbouring (3NN, J₃) Mn atoms. Here, the long-range magnetic exchange parameters (J) can be obtained by²⁶


where S is the calculated magnetic moment of the Mn ion and E_FM, E_AFM-Néel, E_AFM-zz and E_AFM-str are the total energies in FM, AFM-Néel, AFM-zigzag and AFM-stripy magnetic configurations, respectively.

Using the presented results one gets J₁ = 0.65 meV, J₂ = 0.037 meV and J₃ = 0.20 meV for 2D MnPS₃ and J₁ = 0.47 meV, J₂ = 0.03 meV and J₃ = 0.19 meV for 2D MnPSe₃, which are in excellent agreement with the results from previous studies.²⁶ With all positive exchange parameters J, these results indicate that both MnPS₃ and MnPSe₃ monolayers are in a robust AFM-Néel phase. The significant exchange interaction values indicate that the 2NN J₂ and 3NN J₃ exchange couplings make important contributions to the ground magnetic state, besides NN J₁. The NN exchange J₁ state comes from the competition between NN Mn–Mn direct exchange and Mn–X–Mn superexchange. The direct Mn–Mn interaction is always AFM according to the d orbital overlaps, while the Mn–X–Mn superexchange is always FM due to the Mn–X–Mn angle which is close to 90° (84.26° for MnPS₃ and 84.03° for MnPSe₃), as can be understandable from the well-known Goodenough–Kanamori–Anderson (GKA) rules.^55–57 Because of the high spin Mn²⁺ d⁵ state and the short Mn–Mn distance (3.51 Å for MnPS₃ and 3.69 Å for MnPSe₃), the AFM direct exchange wins the competition and dominates the value of J₁. The 2NN J₂ and 3NN J₃ exchange coupling parameters can be considered as super–superexchange interactions mediated by Mn–X⋯X–Mn bridges, and the strong hybridisation between X np orbitals and Mn 3d orbitals (see below) resulting in AFM interactions. According to the monolayer geometry, J₃ involves a Mn–X1⋯X3–Mn bridge with two X ions located in the same chalcogen sub-layer and it is stronger than J₂ with Mn–X1⋯X5–Mn with X ions located in separate sub-layers. In general, the AFM-Néel ground state is mostly from strong AFM direct exchanges between the Mn²⁺ ions for monolayer MnPX₃.

On basis of the Ising model, Monte Carlo simulations with periodic boundary conditions were performed to estimate the Néel temperatures of MnPX₃ monolayers. The three exchange parameters J₁, J₂ and J₃ were used in a series of superlattices L × L (L = 16, 32, 64) containing a large amount of magnetic sites to accurately evaluate the value. Upon the heat capacity C_v(T) = (〈E²〉 − 〈E〉²)/k_BT² reaching the equilibrium state at a given temperature, the T_N value can be extracted from the peak of the specific heat profile. The specific heat capacites per spin as a function of temperature are plotted in Fig. 4. From the simulated C_v(T) curves, one can find the peak ascent steepening as the lattice size increases. The accurately estimated T_N value is 103 K for 2D MnPS₃ and 80 K for 2D MnPSe₃, which is in excellent agreement with the experimental values of 100 K (ref. 54) evaluated from the susceptibility data for MnPS₃ and 74 K (ref. 48) revealed by neutron diffraction experiments for MnPSe₃ in the bulk phase.

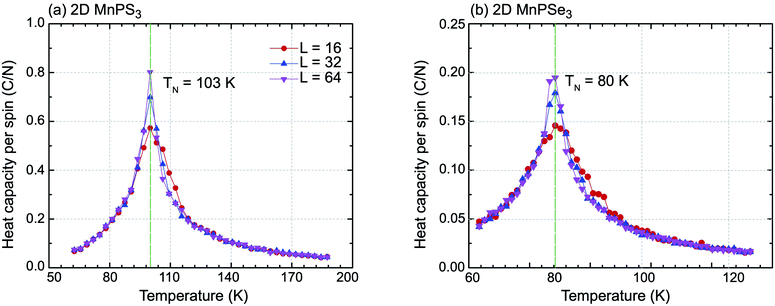Fig. 4 Specific heat capacity with respect to temperature for (a) 2D MnPS₃ and (b) 2D MnPSe₃ for different lattice sizes used in the Monte Carlo simulations.

3.4 Electronic structures of 2D MnPX₃

Having studied the magnetic ground state, the electronic properties of 2D MPX₃ were investigated. The band structures calculated by PBE + U and the HSE06 method are presented in Fig. 5(a) and (b) for 2D MnPS₃ and MnPSe₃, respectively. As expected, both monolayers demonstrate semiconductor behaviour. The band gaps calculated by different functionals are given in Table 2. With a value of 3.25 eV for 2D MnPS₃ and 2.56 eV for 2D MnPSe₃ obtained by HSE06 functional, the gap is little larger than the corresponding value of the 3D bulk due to the quantum confinement effect when going from 3D to 2D. For 2D systems, the pure PBE functional gives direct band gaps at K point in a contrast to the other considered approaches (PBE + U and HSE06). As a consequence, 2D MPX₃ can act as good candidates for 2D magnet semiconductors with a localised magnetic moment on the Mn ions.

Fig. 5 PBE + U calculated band structures of (a) 2D MnPS₃ and (b) 2D MnPSe₃, compared with those obtained with the HSE06 functional. The lower panels are the corresponding square of transition dipole moment matrix.

The upper VBs (above −0.5 eV) are composed of two bands, obtained by PBE + U, which almost overlap those of the HSE06 results. The other HSE06 VBs move towards a lower energy range compared to those of the PBE + U bands. One can see that the HSE06 CBs all move up to a higher energy range compared to that of the PBE + U bands, thus the HSE06 band gaps show the best consistency with the experimental values. However, the band dispersion of HSE06 is almost similar to that of PBE + U, that is to say, the main characters of the band structures are almost correctly described by the PBE + U method. Therefore, we focused on the total DOS and partial DOS of 2D MnPX₃ obtained within the PBE + U method.

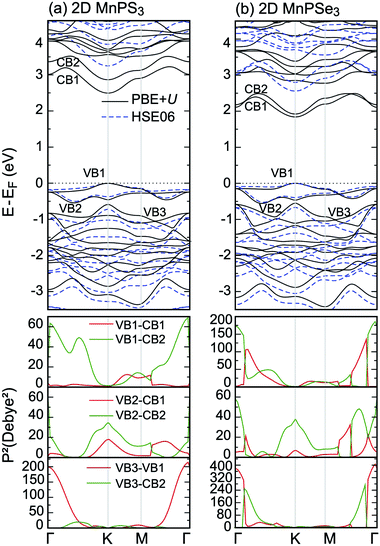
The total DOS and partial DOS are shown in Fig. 6: (a) for MnPS₃ and (e) 2D MnPSe₃, respectively. Due to the AFM ground state, the DOS is identical for spin up and spin down channels. Since the trigonal anti-prismatic MnX₆ octahedron is under D_3d symmetry in both monolayers, the Mn 3d orbitals can be decomposed into a single a₁ (d_z²) orbital and two 2-fold degenerate e₁ (d_xz, d_yz) and e₂ (d_xy, d_x²−y²) orbitals. The five d electrons occupy only one spin channel, leading to the high spin state of Mn ions, due to the strong crystal field effect. The top of the valence band VB is mainly dominated by the hybridisation between Mn d–e₁, S/Se p_x and p_y orbitals, as shown in Fig. 6(b, c) and (f, g). Moreover, the strong hybridisation between Mn d–e₁, e₂ orbitals and S/Se p_x, p_y orbitals can be clearly seen in the whole energy range, confirming the superexchange interactions between the Mn d orbitals mediated by the S/Se p orbitals. The bottom of the conduction band CB is derived from Mn d–e₁, e₂, S/Se p_x, p_y and P p, s orbitals. Compared with that of 2D MnPS₃, the contributions from the P s orbitals to the two lower CBs are stronger than those of P p states for 2D MnPSe₃, as shown in Fig. 6(d) and (h), respectively. Clearly, a 0.25 eV sub-gap appears at 2.6 eV in CBs for MnPSe₃ above the two lower CBs. In addition, from −0.5 eV to the Fermi level of the upper VBs, the hybridisation effect between Mn 3d and S p orbitals of 2D MnPS₃, as reflected by one main sharp peak, is stronger than that of 2D MnPSe₃ where two main sharp peaks are observed, resulting in more localised electron properties for MnPS₃ than that for MnPSe₃.

Fig. 6 Total and partial DOS states of (a-d) 2D MnPS₃ and (e-h) 2D MnPSe₃ obtained with PBE + U.

The different electronic structures of MnPX₃ monolayers can be attributed to two factors: (i) the stronger crystal field effect in MnS₆ octahedrons compared to that of MnSe₆ due to the larger atomic radius and bond lengths of Se ions compared to those of S ions, as listed in Table 1; (ii) S ions have stronger electronegativity than Se ions, thus, the onsite energy of Se p and s orbitals is closer to that of Mn d states compared to the S ions. As a consequence, the d–p hybridisation in MnPS₃ is stronger than that of MnPSe₃, resulting in the larger band gap and more itinerant electrons of MnPS₃ compared to those of MnPSe₃. Moreover, the two factors can lead to stronger Mn–X⋯X–Mn mediated super–superexchange interactions in MnPS₃ compared to those in MnPSe₃, which can clarify that MnPS₃ has higher a T_N value than MnPSe₃.

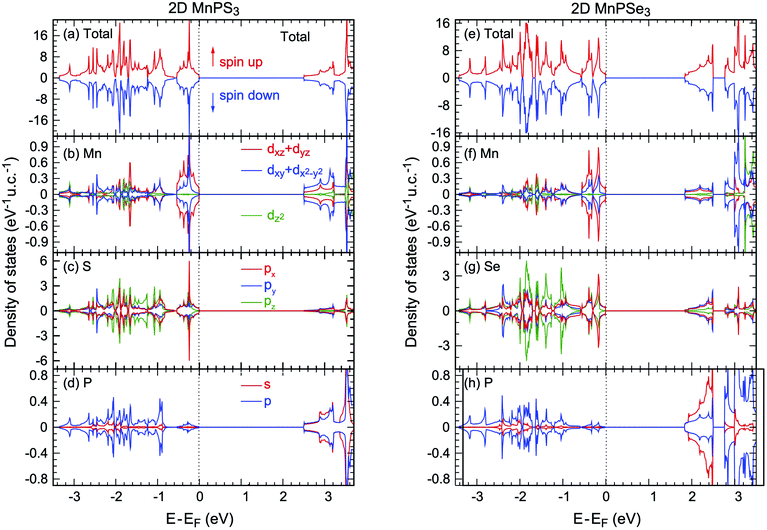
As a Néel AFM semiconductor is constructed with a honeycomb lattice, a spontaneous valley polarisation along with degenerate spins can be realised in 2D MnPX₃ monolayers.²⁴ In order to study the valley polarisation, 2D MnPX₃ band structures were further investigated taking into account the spin-orbital coupling (SOC) (Fig. S2 in ESI†). The valley polarisation of 2D MnPSe₃ is more significant than that of 2D MnPS₃ (discussed below), herein we only present the band structure of the MnPSe₃ monolayer with SOC taken into account (Fig. 7(a)). The respective valley polarisation can be estimated by the energy differences between the uppermost VB and lowest CB at the K and −K points of the BZ, defined as Δ^CB/VB_val = E^CB/VB_K − E^CB/VB_−K. The spontaneous valley degeneracy splittings of about Δ^CB/VB_val = 7/−3 meV for MnPS₃ and 20/−35 meV for MnPSe₃ appear for the uppermost VB band and lowest CB bands, respectively, which are consistent with previous studies.^24,30 Due to the valley polarisation, the band gap slightly reduces to 2.49 eV for 2D MnPS₃ and 1.80 eV for 2D MnPSe₃, but remains direct at the K point. Caused by the SOC effect, the upper VBs show large energy-splittings of about 0.2 eV at the Γ point, compared to those of PBE + U bands, which demonstrate the twofold energy-degeneracy for the occupied VBs. Except for the Γ point, the SOC band dispersion shows similar features as that of PBE + U with small energy shifts along the high symmetry k-path. Due to the time-reversal symmetry, the total magnetic moments are 0 μ_B for any direction spin components for both 2D MnPX₃ monolayers, as demonstrated by the SOC bands which do not show any spin-splitting in the momentum space.

Fig. 7 (a) Band structure of 2D MnPSe₃ calculated with and without SOC within the PBE + U method. The schematic diagram of bands at the K and −K valleys is presented on the right-hand side of (a). (b) The effect of in-plane bi-axial strain to valley polarisation Δ^CB/VB_val at the K and −K points.

Here, we also studied the effect of the biaxial in-plane strain in the MnPSe₃ monolayer on the valley polarisation. The results of Δ^VB_val and Δ^CB_val with respect to the strain are plotted in Fig. 7(b) with positive and negative strains representing tensile and compressive effects, respectively. The tensile strain will enlarge the Mn–Mn bonds length while the compressive effect will enlarge the d–d direct AFM interactions. It is found that the tensile strains reduce valley polarisation Δ^VB_val, whereas the compressive strains slightly increase the value. For Δ^CB_val, both tensile and compressive strains reduce the absolute value, and interestingly the tensile strain will change the Δ^CB_val sign from negative to positive. As a result, the SOC band gap remains direct character under compressive strain but changes to indirect feature under tensile effect (uppermost VB at K point band and lowest CB at −K point). The strain effect to the band gap of SOC can be evaluated as ΔE_g = E_g(K) − E_g(−K) = |Δ^CB_val| + |Δ^VB_val|. The estimated maximum value of ΔE_g is 55 meV in the equilibrium state. That is to say, the valley polarisation of pristine MnPSe₃ monolayers is most easily to be detected in experiment without in-plane strain which offers an undesirable influence on the valley polarisation.

3.5 Optical properties of 2D MnPX₃

Besides the interesting magnetic properties, the 2D MnPX₃ monolayers also show significant optical performance with band gaps in the fundamental range. The linear optical properties can be obtained from the frequency-dependent complex dielectric function as ε(ω) = ε₁(ω) + iε₂(ω), where ε₁(ω) and ε₂(ω) are the real and imaginary parts, respectively, of the dielectric function at the photon energy ω.⁴⁴ To describe the decay of light intensity spreading in unit distance in medium, the absorption coefficient α(ω) can be calculated from the dielectric function as^23,58

Since the point group of the Néel AFM state is D_3d, 2D MnPX₃ monolayers process inversion symmetry which will introduce parity–forbidden transitions between VBs and CBs.⁵⁹ In order to investigate the effect of symmetry-induced parity–forbidden transitions to the optical absorption properties, the transition dipole moment (TDM) defined by the electric dipole moment were calculated. For a single, non-relativistic particle of mass m, the TDM can be denoted in terms of the momentum operator p,⁶⁰

TDM P_a→b means a transition where a single charged particle changes from initial state |ψ_a〉 in an occupied band to final state |ψ_b〉 in an empty band with energy E_a and E_b at its position r. In general, the sum of the square of TDM (P² in unit of Debye²) implies the transition probabilities between the initial and final states.

It is well known that the optical properties strongly depend on the band structures. As mentioned above, the band structures obtained by the PBE + U method show the main features as those of the HSE06 functional. Herein, we paid our attentions to the optical properties of 2D MnPX₃ evaluated by the PBE + U method. The lower panels of Fig. 5(a) and (b) show the curves for P² with transitions from VB(1,2,3) to CB(1,2) (VB1 means the top VB and VB2 the second top VB, etc.; see upper panels of Fig. 5) along the high symmetry k-path according to the band structures. The absorption coefficient spectra α(ω) in a wide energy range are presented in Fig. 8 (a) for 2D MnPS₃ and (b) for 2D MnPSe₃.

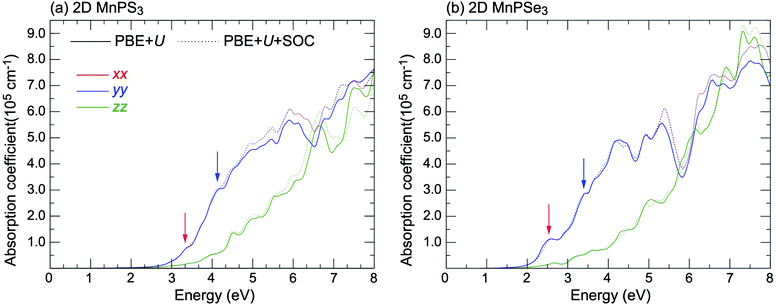Fig. 8 The absorption spectra of (a) 2D MnPS₃ and (b) 2D MnPSe₃ considered with and without a SOC effect within the PBE + U method.

The curves of α(ω) for the two MnPX₃ monolayers demonstrate some similar character in the whole energy range due to their similar band structures. All the spectra exhibit anisotropic character between in-plane xx (yy) components and out-plane zz components, corresponding to the 2D monolayer anisotropy. The threshold energy of the absorption spectra occurs at around 2.50 eV and 1.84 eV for 2D MnPS₃ and 2D MnPSe₃, respectively, according to their direct band gaps as fundamental absorption edge. However, the P² spectra shows a zero value at the K point, it means a forbidden transition between the direct band edge. Additionally, the value of the P² spectra between VB1 and CB1 is not very large, especially for 2D MnPS₃, therefore, the absorption coefficient starts to increase very slowly at the fundamental band gap threshold. Nevertheless, with a higher energy phonon incidence, the α(ω) spectra increases sharply when the associated matrix elements are large and the transitions are allowed. For instance, around the Γ point, P² spectra show the largest values for transitions from VB3 to VB1, and the α(ω) spectra increase rapidly around the corresponding energy of about 3.8 eV for 2D MnPS₃ while a sharp peak at 2.6 eV for 2D MnPSe₃ is shown. According to the different band gaps, it is evident that the P² spectra of 2D MnPSe₃ show much larger values than those of MnPS₃ in the corresponding transitions and k points (Fig. 8). For example, with 3.2 eV photon induced, the absorption coefficient α(ω) shows a value of 2 × 10⁵ cm⁻¹ for 2D MnPSe₃, which is four times larger than 0.5 × 10⁵ cm⁻¹ for 2D MnPS₃. As a consequence, the 2D MnPSe₃ monolayer is a stronger absorption efficiency material than 2D MnPS₃, especially in the fundamental optical range.

The α(ω) spectra of these two compounds were further calculated taking into account SOC (see Fig. 8) and the obtained curves demonstrate the similar features as the spectra calculated on the basis of the initial PBE + U approach. In the low energy range under ∼5.0 eV, the absorption spectra calculated with PBE + U + SOC and PBE + U almost overlap each other, while showing some difference above ∼5.0 eV. Noticeably, the peaks marked by red and blue arrows at 2.6 eV and 3.4 eV reduce apparently with comparison to the PBE + U spectra for MnPSe₃ SOC-α(ω), this is owing to the large energy-splitting for the SOC-VBs at the Γ point, leading to the descending of transition probabilities. Accordingly, the SOC bands of 2D MnPS₃ do not show apparent energy-splitting at the Γ point (Fig. 7 and ESI, Fig. S2†), and the peaks marked by arrows at 3.4 eV and 4.2 eV do not exhibit much difference between SOC-α(ω) and PBE + U-α(ω) spectra. In addition, the marked peak at 2.6 eV for 2D MnPSe₃ can be attributed to the electron transitions between the two highest bands of VBs and two lowest bands of CBs, and it is followed by a down-step absorption caused by the 0.25 eV sub-gap between 2.5 eV and 2.75 eV in the CBs. Meanwhile, the marked peak at 3.4 eV is followed by an up-step for α_xx(ω) of MnPS₃, and it can be attributed to the low DOS for the unoccupied orbitals between 3.2 eV and 3.4 eV.

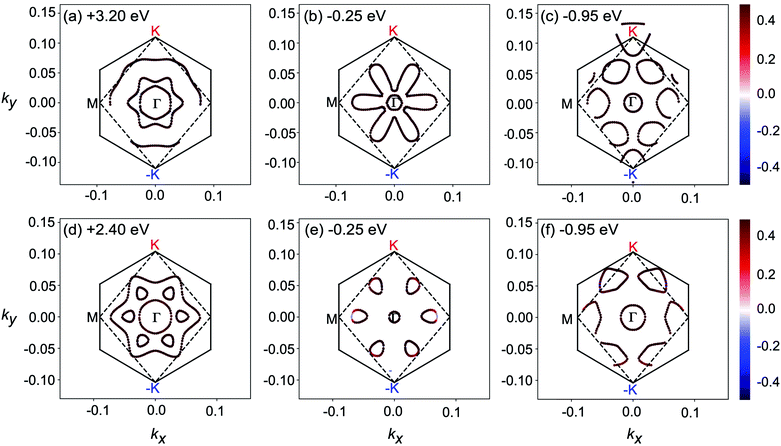
To further explore the underlying electron transition mechanism of 2D MnPX₃, the k_x–k_y constant energy cuts of spin-textures were extracted from the calculated band structures as shown in Fig. 9 (the chosen energies for the cuts are marked for every panel and the energy differences between the low and high values are almost equal to the energy of the typical peaks in the absorption spectra mentioned above). All spin-textures are spin degenerated, caused by the robust intrinsic AFM state for both studied materials. Most importantly, the spin-textures show various circles, indicating the existence of electron pockets in the energy space for 2D MnPX₃, which will benefit the electron transitions. For simplicity, we discussed the spin-textures of MnPSe₃ monolayers to explore the transition possess. For 2D MnPSe₃, the centre electron pocket at the Γ point belongs to VB1 at −0.25 eV, the six pockets located along the Γ–M path belong to VB2 at −0.25 eV and VB3 at −0.95 eV, whereas the empty pockets at +2.4 eV belong to both CB1 and CB2. Particularly, the six unoccupied pockets connected together as a whole big pocket for CB2. As shown in Fig. 5, the P_VB2–CB2² spectrum exhibits a maximum peak at the Γ point, the P_VB2–CB1² and P_VB2–CB2² present some extreme values along the Γ–M path. Moreover, both P_VB3–CB1² and P_VB3–CB2² show much larger values along the Γ–M path. The combination of the abundant electron pockets and large value of P² is advantageous to the electron transitions between the occupied VBs and empty CBs, leading to the marked peaks for the absorption coefficient of 2D MnPSe₃ as discussed. According to the similar spin-textures, this mechanism can also be applied for the description of the electron transitions in 2D MnPS₃. The optical absorption and electronic structures indicate that 2D MnPX₃ monolayers would exhibit good performance for photocatalytic water splitting as shown in the previous study.²³

Fig. 9 Spin textures of 2D MnPS₃ (a–c) and 2D MnPSe₃ (d–f) shown in the k_x–k_y plane cantered at the Γ point at different energies E − E_F. The projection of the spin on the z axis from negative to positive is colour coded with the blue-red scale. The solid line hexagonal is the BZ and the broken line is the edge of spin-textures.

3.6 Vacancy defects in 2D MnPX₃

The effect of sulphur and selenium vacancies on the magnetic and optical properties of 2D MnPX₃ is also investigated. In all considered vacancy systems, a 2 × 2 × 1 supercell was built to avoid the interaction between two defects or defect-pairs with the distance more than 10 Å. Three different amounts and geometric configurations of defects are discussed (Fig. 10): (a) one vacancy at the X1 site, named as V_S@1L or V_Se@1L with a defect concentration about 4.2%; (b) two neighbouring vacancies at sites X2 and X3 of the same chalcogen sub-layer named as V_S2@1L or V_Se2@1L with a concentration about 8.3%; (c) two neighbouring vacancies at sites X1 and X4 of different chalcogen sub-layers named V_S2@2L or V_Se2@2L (see Fig. 10(c)). The S/Se vacancy formation energy was calculated to evaluate the energetic stability:⁶¹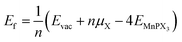 , where n is the defect number and E_vac and E_MnPX3 are the energies of relaxed vacancy system and pristine cell, respectively. The chemical potential energy is calculated from the most stable state of chalcogen crystal, as μ_S = −4.13 eV with the P2/c space group and μ_Se = −3.50 eV with the P2₁/c space group. The vacancy formation energies are presented in Table 4. All E_f values for S/Se vacancies are small, which implies easy defect formation in experiments. According to the different electronegativity of sulphur and selenium, it is found that E_f(V_S) > E_f(V_Se) in the corresponding systems, and E_f(V_X2@1L) > E_f(V_X2@2L) with the same defect account, revealing that the Se vacancy is more energetically favourable to produce than the S one, whereas a pair of vacancies is energetically unfavourable to produce in the same layer as V_X2@1L rather than in the different layers as V_X2@2L.

Fig. 10 MnPX₃ monolayer in the polyhedral representation to illustrate different vacancy configurations: (a) V_X@1L, (b) V_X2@1L and (c) V_X2@2L. Dotted circles indicate the respective chalcogen vacancies.

Table 4 Formation energy (E_f, in eV), Mn ion magnetic moments (orbital and total, M, in μ_B) and band gaps (E_g, in eV) for spin up/down electrons obtained for different defected 2D MnPX₃ systems with PBE + U

Vacancy	Ef	MMn1/MMn6	MMn2/MMn5	MMn3/MMn4	Ms/Mp/Md	Mtot	E^upg/E^downg
VS@1L	1.41	−4.584/4.583	4.583/−4.583	−4.587/4.587	−0.001/0.003/−0.001	0.001	2.39/2.38
VS2@1L	1.65	−4.584/4.584	4.593/−4.592	−4.587/4.586	−0.001/0.003/0.000	0.002	1.62/1.63
VS2@2L	1.47	−4.587/4.587	4.579/−4.579	−4.587/4.587	0.000/0.000/0.000	0.000	2.26/2.26
VSe@1L	1.18	−4.588/4.588	4.583/−4.583	−4.588/4.587	−0.001/0.003/−0.001	0.001	1.79/1.79
VSe2@1L	1.50	−4.586/4.586	4.596/−4.595	−4.593/4.592	−0.001/0.003/0.000	0.002	1.26/1.26
VSe2@2L	1.26	−4.593/4.593	4.579/−4.579	−4.593/4.593	0.000/0.000/0.000	0.000	1.75/1.75

---

The magnetic moments M of different Mn ions, and total M of s, p or d orbitals are listed in Table 4 for 2D vacancy MnPX₃ systems. Upon the vacancy defects induced, the 1X@1L and 2X@1L defect systems are all driven into a ferrimagnetic state with tiny net M_total values of about 0.001 μ_B and 0.002 μ_B, respectively, whereas the 2X@2L vacancy systems remain in an AFM state without a net magnetic moment. The different magnetic properties can result from the changed system symmetry of vacancy systems. All the vacancy systems have a bilateral-symmetry axis along the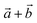 direction, while the 2X@2L system has one more inversion symmetry in the same direction. Accordingly, the Mn honeycomb lattice in a defect supercell shows some deformations with different M values for each Mn ion, as listed in Table 4. The total magnetic moments derived from different orbitals are also presented, and it should be noted that the net magnetic moment is dominated by the S/Se p orbitals around defects. However, with such a slight net M_total, the influence of chalcogen defects on the 2D MnPX₃ monolayer can be almost neglected. In other words, the negligible M_total of vacancy MnPX₃ further demonstrate the strong AFM interactions between the Mn ions in the honeycomb lattice.

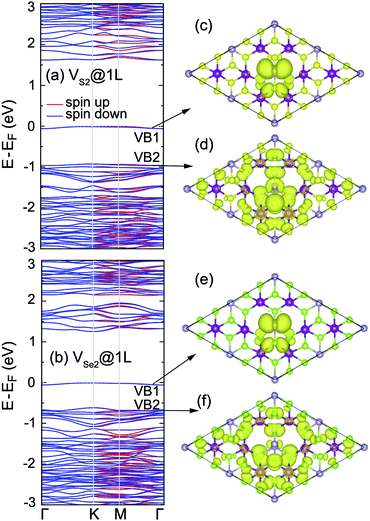
In order to seek the influence of chalcogen vacancies on the electronic properties of the 2D MnPX₃, band structure, total and partial DOS of different defect-derived systems were then calculated (see ESI, Fig. S3†). According to the crystal symmetry change and net magnetic moment, the bands show a small spin-split along the K–M–Γ path, but remain spin degenerate along the Γ–K path for V_X@1L and V_X2@1L systems, while the band structures remain spin degenerate along the whole high-symmetry k-paths for V_X2@2L systems. Strikingly, there is no isolated defect state generated within the band gap in the band structure for V_X@1L and V_X2@2L derived systems, but such a state appears in the band structure of the V_X2@1L vacancy system (Fig. 11). These defect states appear as flat bands and they are mostly derived from the chalcogen and phosphorus p orbitals, as shown in the partial DOS. Herein, the partial charge density plots of VB1 and VB2 are illustrated in Fig. 11(c) and (d) for V_S2@1L and Fig. 11(e) and (f) for V_Se2@1L, respectively. As the chalcogen vacancy pair locates at X2 and X3 sites, the charge distribution mostly concentrates at neighbouring P1 and X1 ions, and partly at X5 and X6 sites for the mid-gap bands, all displaying p-like features, confirming the p orbital contribution to the defect state. For the VB2 states, the electron distributions locate at vacancy-neighbouring ions more than on the other ions, revealing that there are some defect states locating just under the Fermi level. Due to the defect states, the band gaps of vacancy systems are smaller than those of pristine monolayers, as listed in Table 4.

Fig. 11 Band structures of (a) 2D MnPS₃ V_S2@1L and (b) 2D MnPSe₃ V_S2@1L defect systems obtained with PBE + U. Partial charge densities (iso-surface value = 2 × 10⁻³e Å⁻³) obtained for VB1 and VB2 of (c and d) 2D MnPS₃ V_S2@1L and (e and f) 2D MnPSe₃ V_S2@1L defect systems, respectively.

Without mid-gap bands generated, the uppermost VBs apparently show some flat band behaviours for V_X@1L and V_X2@2L monolayers, as shown for their band structures (ESI, Fig. S3†). It also can be further confirmed by the partial electron distribution which localises around the vacancies (ESI, Fig. S4†). As a consequence, the defect states are mainly located just under the Fermi level for the vacancy MnPX₃ system without a mid-gap state. From comparison, the defect states of the 2D MnPS₃ vacancy monolayer are more localised than those of the corresponding 2D MnPSe₃ monolayer. Due to the defect states, the band gaps of vacancy systems are smaller than those of pristine monolayers, as listed in Table 4.

Vacancy defects strongly influence the optical properties of the host material. Herein, the absorption spectra of defected MnPX₃ monolayers were investigated and the xx components of α(ω) are plotted in Fig. 12. The α(ω)_xx spectra of vacancy systems show similar characteristics compared to those of pristine monolayers in the whole energy range except for the new defect-related peaks. The extreme values of absorption spectra alternate between the different systems with the continuous incident photon energy, revealing almost equal absorption efficiency for both pristine and defected systems. Some new features for the absorption spectra of vacancy systems should be noticed. Caused by the reduced band gaps, the α(ω) spectra threshold shifts to lower energy for the vacancy systems, compared with the α(ω)_xx spectra of pristine monolayers. Particularly, a significant defect-peak appears at 1.70 eV for V_S2@1L and 1.40 eV for V_Se2@1L system, attributed to the direct transitions between the VB1 states to the lower part of the CBs of these n-type semiconductors. Similarly, the defect induced peaks in the energy range from 2.5 (2.0) eV to 3.0 (2.5) eV for MnPS₃ (MnPSe₃) vacancy systems also show significant width, although the defect states form flat bands under the Fermi level for V_X@1L and V_X2@2L systems. The SOC effect on the absorption spectra were also considered in the vacancy systems. For simplicity, only the xx component α(ω) spectra of V_X2@1L systems are presented. As with that of pristine monolayers, the SOC-α(ω) spectra also show more smoothly than that of thr PBE + U-α(ω) spectra. Absorption spectra usually can be used as criteria to assess the crystal quality of the monolayers. Here, only the V_X2@1L vacancy can be easily assessed with a new peak within the band gap for the absorption spectra. In addition, both V_X@1L and V_X2@1L vacancies could be probed by circularly polarised light due to the spin-splittings, as determined by the different transition dipole moments which show large splits between the spin up and spin down channels (Fig. 13). However, the V_X2@2L defects cannot be easily detected because of the absence of both in-gap absorption peak and spin-splittings. From the discussion above, some further theoretical and experimental studies on the chalcogen vacancy defects should be carried out, such as circular polarisation, bound exciton and net magnetic detection, to identify the defect states and influence on the optical and magnetic properties of 2D MnPX₃ monolayers.

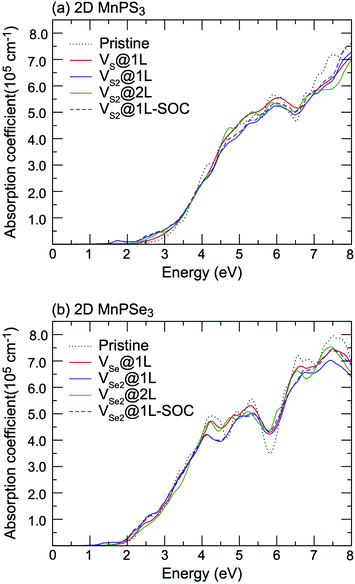Fig. 12 The xx component of the absorption coefficient α(ω) as a function of energy for pristine and defected (a) 2D MnPS₃ and (b) 2D MnPSe₃ systems.

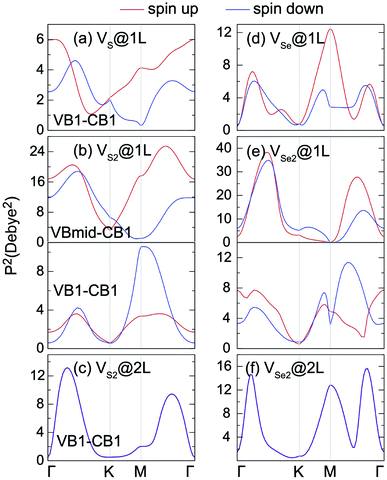Fig. 13 The square of transition dipole moment matrix for 2D MnPS₃ (left panels) and 2D MnPSe₃ (right panels) defected systems.

4 Conclusions

A systematic first-principles study on the electronic, magnetic and optical properties of 2D transition-metal phosphorous trichalcogenide MnPX₃ (X = S, Se) was carried out based on density functional theory. The bulk MnPS₃ in the C2/m space group and MnPSe₃ in the R3̄ space group show AFM semiconductor behaviour with a direct band gap. For both materials, the monolayer form is energetically favourable and these layers can be exfoliated from the bulk phase with small cleavage energies, 0.12 J m⁻² for MnPS₃ and 0.23 J m⁻² for MnPSe₃, which are much lower than the 0.37 J m⁻² of graphite. Confirmed by the phonon spectrum with no imaginary dispersion, MnPX₃ monolayers show a good dynamical stability. The 2D MnPX₃ monolayers are Néel AFM semiconductors with a direct band gap value of 2.37 eV (PBE + U) or 3.08 eV (HSE06) for 2D MnPS₃ and 1.84 eV (PBE + U) or 2.56 eV (HSE06) for 2D MnPSe₃ at the K point, in excellent agreement with the experimental data. The NN, 2NN and 3NN exchange parameters are all positive, revealing the AFM-Néel ground state of 2D MnPX₃. Using periodic boundary conditions, Monte Carlo simulations gave theoretical T_N values of 103 K and 80 K for 2D MnPS₃ and MnPSe₃, respectively. With high spin state Mn ions arranged in a honeycomb lattice, 2D MnPX₃ shows valley polarisation with spin-degeneracy in the band structure if the spin-orbital coupling is considered. Moreover, in-plane strain offers an undesirable effect for the valley polarisation. With direct band gaps falling into the visible optical spectrum, MnPX₃ monolayers have good performance for optical absorption which were investigated based on the electronic structures and transition dipole moment matrix. The influence of single and a pair of chalcogen vacancies on the electronic, magnetic and optical properties of MnPX₃ were also investigated, and the effect is strongly correlated with the vacancy structure configurations. Two vacancies in the same chalcogen sublayer will introduce mid-gap state and spin-splitting, whereas two vacancies in different chalcogen sublayers show no mid-gap states and no spin-splitting. From the absorption spectra of vacancy systems, it is proposed that optical absorption spectra cannot be used as an ideal criteria to determine the crystal quality of the 2D MnPX₃ monolayers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 21973059). Y. J. thanks the support from the Natural Science Foundation of Hubei Province (Grant No. 2018CFB724) and from the Education Department (Grant No. D20171803). E. V. thanks the support by the Ministry of Education and Science of Russian Federation within the framework of the State Assignment for Research, Grants no. 4.6759.2017/8.9.

References

1. A. Geim, Science, 2009, 324, 1530–1534.
2. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutierrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926.
3. A. K. Geim and I. V. Grigorieva, Nature, 2014, 499, 419–425.
4. G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano, V. R. Cooper, L. Liang, S. G. Louie, E. Ringe, W. Zhou, S. S. Kim, R. R. Naik, B. G. Sumpter, H. Terrones, F. Xia, Y. Wang, J. Zhu, D. Akinwande, N. Alem, J. A. Schuller, R. E. Schaak, M. Terrones and J. A. Robinson, ACS Nano, 2015, 9, 11509–11539.
5. Z. Lin, Y. Lei, S. Subramanian, N. Briggs, Y. Wang, C.-L. Lo, E. Yalon, D. Lloyd, S. Wu, K. Koski, R. Clark, S. Das, R. M. Wallace, T. Kuech, J. S. Bunch, X. Li, Z. Chen, E. Pop, V. H. Crespi, J. A. Robinson and M. Terrones, APL Mater., 2018, 6, 080701–080721.
6. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
7. K. Novoselov, Rev. Mod. Phys., 2011, 83, 837–849.
8. K. Zhang, Y. Feng, F. Wang, Z. Yang and J. Wang, J. Mater. Chem. C, 2017, 5, 11992–12022.
9. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
10. G. H. Han, D. L. Duong, D. H. Keum, S. J. Yun and Y. H. Lee, Chem. Rev., 2018, 118, 6297–6336.
11. C.-T. Kuo, M. Neumann, K. Balamurugan, H. J. Park, S. Kang, H. W. Shiu, J. H. Kang, B. H. Hong, M. Han, T. W. Noh and J.-G. Park, Sci. Rep., 2016, 6, 20904.
12. S. Lee, K.-Y. Choi, S. Lee, B. H. Park and J.-G. Park, APL Mater., 2016, 4, 086108.
13. M. A. Susner, M. Chyasnavichyus, M. A. McGuire, P. Ganesh and P. Maksymovych, Adv. Mater., 2017, 29, 1602852.
14. F. Wang, T. A. Shifa, P. Yu, P. He, Y. Liu, F. Wang, Z. Wang, X. Zhan, X. Lou, F. Xia and J. He, Adv. Funct. Mater., 2018, 28, 1802151.
15. R. N. Jenjeti, R. Kumar, M. P. Austeria and S. Sampath, Sci. Rep., 2018, 8, 8586.
16. S. Y. Kim, T. Y. Kim, L. J. Sandilands, S. Sinn, M.-C. Lee, J. Son, S. Lee, K.-Y. Choi, W. Kim, B.-G. Park, C. Jeon, H.-D. Kim, C.-H. Park, J.-G. Park, S. J. Moon and T. W. Noh, Phys. Rev. Lett., 2018, 120, 136402.
17. R. Gusmão, Z. Sofer, D. Sedmidubský, S. Huber and M. Pumera, ACS Catal., 2017, 7, 8159–8170.
18. K.-z. Du, X.-z. Wang, Y. Liu, P. Hu, M. I. B. Utama, C. K. Gan, Q. Xiong and C. Kloc, ACS Nano, 2016, 10, 1738–1743.
19. D. Mukherjee, P. M. Austeria and S. Sampath, ACS Energy Lett., 2016, 1, 367–372.
20. B. L. Chittari, Y. Park, D. Lee, M. Han, A. H. MacDonald, E. Hwang and J. Jung, Phys. Rev. B, 2016, 94, 184428.
21. J. Chu, F. Wang, L. Yin, L. Lei, C. Yan, F. Wang, Y. Wen, Z. Wang, C. Jiang, L. Feng, J. Xiong, Y. Li and J. He, Adv. Funct. Mater., 2017, 27, 1701342.
22. C.-F. Du, Q. Liang, R. Dangol, J. Zhao, H. Ren, S. Madhavi and Q. Yan, Nano-Micro Lett., 2018, 10, 67.
23. X. Zhang, X. Zhao, D. Wu, Y. Jing and Z. Zhou, Adv. Sci., 2016, 3, 1600062.
24. X. Li, T. Cao, Q. Niu, J. Shi and J. Feng, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3738–3742.
25. X. Li, X. Wu and J. Yang, J. Am. Chem. Soc., 2014, 136, 11065–11069.
26. N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425.
27. Q. Pei, X.-C. Wang, J.-J. Zou and W.-B. Mi, Front. Phys., 2018, 13, 666.
28. L. Zhong, X. Chen and J. Qi, Phys. Chem. Chem. Phys., 2017, 19, 15388–15393.
29. Q. Pei, Y. Song, X. Wang, J. Zou and W. Mi, Sci. Rep., 2017, 7, 9504.
30. Q. Pei and M. Wenbo, Phys. Rev. Appl., 2019, 11, 014011.
31. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257.
32. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
34. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
36. P. E. Blöchl, O. Jepsen and O. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
37. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
38. C. Franchini, R. Podloucky, J. Paier, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 2573.
39. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
40. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
41. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
42. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
43. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092.
44. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmuller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 764.
45. U. Herath, P. Tavadze, X. He, E. Bousquet, S. Singh, F. Muñoz and A. H. Romero, 2019, arXiv:1906.11387.
46. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
47. G. Ouvrard, R. Brec and J. Rouxel, Mater. Res. Bull., 1985, 20, 1181–1189.
48. A. Wiedenmann, J. Rossat-Mignod, A. Louisy, R. Brec and J. Rouxe, Solid State Commun., 1981, 40, 1067–1072.
49. X. Wang, K. Du, Y. Y. F. Liu, P. Hu, J. Zhang, Q. Zhang, M. H. S. Owen, X. Lu, C. K. Gan, P. Sengupta, C. Kloc and Q. Xiong, 2D Materials, 2016, 3, 1–9.
50. K. Kurosawa, S. Saito and Y. Yamaguchi, J. Phys. Soc. Jpn., 1983, 52, 3919–3926.
51. R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406.
52. X. Li, X. Wu and J. Yang, J. Am. Chem. Soc., 2014, 136, 11065–11069.
53. A. Hashemi, H.-P. Komsa, M. Puska and A. V. Krasheninnikov, J. Phys. Chem. C, 2017, 121, 27207–27217.
54. C. C. Mayorga-Martinez, Z. Sofer, D. Sedmidubský, Š. Huber, A. Y. S. Eng and M. Pumera, ACS Appl. Mater. Interfaces, 2017, 9, 12563–12573.
55. J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 1955, 100, 564–573.
56. J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23.
57. P. W. Anderson, Phys. Rev., 1959, 115, 2–13.
58. V. Wang, W. Xiao, D. M. Ma, R. J. Liu and C. M. Yang, J. Appl. Phys., 2014, 115, 043708.
59. W. Meng, X. Wang, Z. Xiao, J. Wang, D. B. Mitzi and Y. Yan, J. Phys. Chem. Lett., 2017, 8, 2999–3007.
60. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, 2019, arXiv:1908.08269.
61. R. Ovcharenko, E. Voloshina and J. Sauer, Phys. Chem. Chem. Phys., 2016, 18, 25560–25568.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra09030d

---