Open Access Article
Open Access ArticleAtmospheric implication of synergy in methanesulfonic acid–base trimers: a theoretical investigation†
Dongping Chen,
Weina Wang,
Danfeng Li and
Wenliang Wang *
*
School of Chemistry and Chemical Engineering, Shaanxi Normal University, Xi'an 710119, P. R. China. E-mail: wlwang@snnu.edu.cn; Tel: +86-29-81530815
First published on 31st January 2020
Abstract
Synergy between molecules is ubiquitous in atmospheric clusters and significantly affects new particle formation (NPF). Herein, the effects of the synergy between base molecules on the stability and evaporation of MSA–X–Y (MSA = methanesulfonic acid; X, Y = ammonia (A), methylamine (M), or dimethylamine (D)) trimers were investigated via density functional theory (DFT) and the atmospheric clusters dynamic code (ACDC) method. The results show that proton transfer from MSA to X is exothermal and barrierless due to the synergy between X and Y molecules in MSA–X–Y trimers compared with MSA-X dimers. Cyclic hydrogen bonds are a typical characteristic of the stable trimers. Topological analysis using atoms in molecules (AIM) theory indicates that the electron density (ρ) and Laplacian of the electron density (∇2ρ) at the bond critical points (BCPs) in the trimers exceed the standard range of hydrogen bonds. The affinity for attaching a Y molecule to the MSA–X dimers and the substitution of Y1 (Y = A and MA) by Y2 (Y2 = MA and DMA) in the MSA–X–Y trimers are thermodynamically spontaneous. In addition, the cyclic stabilization energy of the MSA–X–Y trimers increased as the alkalinities of X and Y increased. The total evaporation rate of the trimers decreased as the alkalinities of X and Y increased. Low temperature and high pressure significantly facilitate the formation of trimers. It is further confirmed that synergy plays an important role in atmospheric NPF events.
1. Introduction
Atmospheric aerosols have significant influences on air quality, atmospheric circulation, and human health by directly changing solar radiation and indirectly serving as cloud condensation nuclei (CCN).1–3 New particle formation (NPF) frequently occurs in different areas, from coastland to inland, and contributes more than half of the CCN in the atmosphere.4–9 Increasing studies of NPF have been launched to explore its initial mechanisms; however, there are still many uncertainties regarding the nucleation species that contribute to NPF at the molecular level.10,11 As one of the important sources of atmospheric NPF, neutral homogeneous nucleation plays a primary role in the tropospheric budgets of atmospheric gases and is a current focus in atmospheric chemistry.12 Hydrogen bonding and electrostatic interactions are considered to be primarily responsible for homogeneous cluster formation.13–15 However, the influence of the interaction between the different species on the stability of the clusters is still unclear.Methanesulfonic acid (MSA, CH3SO3H) is regarded as an important oxidation product of dimethylsulfide (DMS, CH3SCH3) released from the sea.16 The concentration of gaseous MSA is typically in the range of 105 to 107 molecules per cm3 in the atmosphere, which is approximately 10% to 100% of the gaseous SA in coastal regions.17 Its atmospheric lifetime is long, and it cannot be easily decomposed by photolysis in the typical atmospheric environment.18 Although MSA is a potential candidate for NPF, its mechanism of particle formation is ambiguous. Recently, NPF involving MSA and ammonia (A, NH3), methylamine (M, CH3NH2), or dimethylamine (D, CH3NHCH3) was investigated experimentally by the Finlayson-Pitts group using a special flow system.19–23 Their results showed that MSA and A, M, or D easily form atmospheric aerosol particles under ambient conditions with medium or high humidity, where A, M, and D show different dependencies on the concentration of the MSA precursor. However, the micro-mechanism of formation of MSA-based clusters remains unresolved at the molecular level.
Recently, Glasoe et al. found experimentally that there is an increase in particle formation when ammonia is combined with single-digit part per trillion (ppt) levels of amines; this is called synergy.24 Synergy between molecules is ubiquitous in atmospheric NPF; it significantly affects the structure, thermodynamic properties, and formation of the initial atmospheric clusters. Ammonia and methylamine together can significantly enhance the stability of small SA-based clusters due to synergy, according to a theoretical investigation.12 Recently, the results of a theoretical investigation showed that MSA can act as a nucleation center in NPF through strong noncovalent interactions with other precursors.18 The results of theoretical calculations by Miao et al. indicate that amines can form more stable clusters with MSA− than with A.25 Theoretical research shows that methyl hydrogen sulfate (MHS)-based and MSA-based trimers are more thermodynamically favorable and may participate in atmospheric NPF due to synergy between the base molecules.26,27 To our knowledge, the effects of synergy between basic molecules on the binding energy and stability of the initial clusters involving MSA is still unclear at the molecular level, especially for MSA–base–base trimers. In this work, the hydrogen bonding, thermodynamic properties, evaporation, and atmospheric relevance of MSA–X–Y (X, Y = A, M, and D) trimers have been investigated using DFT theoretical methods and ACDC kinetics simulations.
2. Computational details
Due to its efficiency and convenience, the global minimum sampling technique is widely used to search for the global-minimum structures of atmospheric clusters. In this work, this method was used to locate the global minima of the MSA–X dimers and MSA–X–Y trimers. A detailed flowchart and relevant descriptions are presented in Fig. S1 and Section 1 in the ESI,† respectively. Four density functional theory (DFT) methods, i.e. B3LYP-D3, M06-2X, PW91PW91, and ωB97X-D, were utilized to perform structural optimization, frequency analysis, and thermochemical calculations for all the stable clusters in conjunction with the aug-cc-pVTZ basis set for C, H, N and O atoms (aug-cc-pV(T+d)Z for S atom)28–32 (see Section 2 in the ESI†). The binding energies (BEs) were corrected with zero-point vibrational energy (ZPVE), and the thermodynamic properties of the clusters were investigated by the supermolecular approach (see Section 3 in the ESI†). In addition, the benchmark results show that the structural parameters optimized by the B3LYP-D3 method are reliable (see Fig. S2 in the ESI†). Therefore, in this work, all structural parameters of the MSA-based clusters were obtained by the B3LYP-D3 method.Atoms in molecules (AIM) theory33 and the noncovalent interaction (NCI) index34 are widely used to characterize noncovalent interactions.12,25,35,36 The change in the atomic charge (q) at H atom was obtained by natural bond orbital theory (NBO)37(see Section 4 in the ESI†). All wavefunctions of the electron structures for the dimers and trimers were obtained at the B3LYP-D3/aug-cc-pVTZ level. In addition, the total evaporation rates of the MSA–X–Y trimers were obtained through ACDC simulations in MATLAB-R2013a38–40 (see Section 5 and eqn (1)–(4) in the ESI†). In addition, under thermodynamic equilibrium conditions, the [MSA–X–Y]/[MSA–X] ratios were calculated through the complex concentration relationship dominated by the law of conservation of mass (see Section 6 and eqn (5) and (6) in the ESI†).Topology analyses of AIM and NCI were performed using the Multiwfn41 and VMD42 programs. Theoretical calculations were performed using the ABCluster,43,44 MOPAC45 and GAUSSIAN 09 (ref. 46) programs.
3. Results and discussion
3.1. Structure analysis
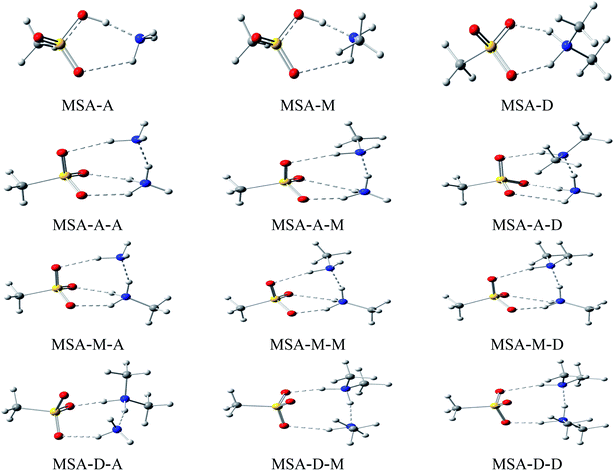
Herein, the lowest energy configurations of 12 dimers (MSA–A, MSA–M, MSA–D, A–A, A–M, A–D, M–A, M–M, M–D, D–A, D–M, and D–D) and 9 heterotrimers (MSA–A–A, MSA–A–M, MSA–A–D, MSA–M–A, MSA–M–M, MSA–M–D, MSA–D–A, MSA–D–M, and MSA–D–D) were searched and optimized, as shown in Fig. 1. For all MSA-based clusters, the ring structures were formed by multiple hydrogen bonds between electronegative atoms (O and N) and electropositive atoms (H). In the cyclic clusters, each monomer acts as both a receptor and donor. The “MSA–X” (X = A, M, and D) notation represents two interactions: H–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S of MSA with the N atom of X and N–H of X with S
S of MSA with the N atom of X and N–H of X with S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of MSA, respectively. The notation of the “MSA–X–Y” (X, Y = A, M, and D) trimer denotes three interactions: SO–H⋯N, N–H⋯N, and N–H⋯O
O of MSA, respectively. The notation of the “MSA–X–Y” (X, Y = A, M, and D) trimer denotes three interactions: SO–H⋯N, N–H⋯N, and N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S in MSA and X, X and Y, and Y and S
S in MSA and X, X and Y, and Y and S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in MSA, respectively. The stability of the cyclic clusters is stronger than that of the linear clusters due to multiple hydrogen bonds. Therefore, the stable cyclic clusters are discussed in this work; the MSA-free homodimers and other high energy structures of the MSA-based clusters are presented in Fig. S3 and S4.†
O in MSA, respectively. The stability of the cyclic clusters is stronger than that of the linear clusters due to multiple hydrogen bonds. Therefore, the stable cyclic clusters are discussed in this work; the MSA-free homodimers and other high energy structures of the MSA-based clusters are presented in Fig. S3 and S4.†
Corresponding key geometric information for these stable cyclic clusters is shown in Table 1. Generally, cyclic structures formed by SO–H⋯N, N–H⋯N, and N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S hydrogen bonds are a typical characteristic of stable MSA-based clusters. The six-membered and eight-membered rings are formed by multiple hydrogen bonds in MSA–X (X = A, M, and D) dimers and MSA–D–Y (Y = A, M, and D) trimers, respectively; however, one six- and one eight-membered ring do coexist in the MSA–A–Y (Y = A, M, and D) and MSA–M–Y (Y = A, M, and D) trimers. Herein, to compare the structural parameters of the dimers and trimers, the configuration of the trimers (such as MSA–A–A) can be divided into two corresponding dimers (such as MSA–A and A–A). The synergy between X and Y has a significant influence on the length and strength of the relevant hydrogen bonds in MSA–X–Y cyclic trimers compared with MSA–X dimers. The length of the SO–H⋯N hydrogen bond is 1.611 Å in MSA–A, which is 0.571, 0.554, and 0.548 Å longer than its counterparts in the MSA–A–A (1.040 Å), MSA–A–M (1.063 Å), and MSA–A–D (1.057 Å) trimers, respectively. The main point to take away here is that the short lengths of the bonds in the trimers indicate that the proton has been completely transferred from MSA to the A molecule. The change of length for the N–H⋯N hydrogen bond is similar to that of N–H⋯S
S hydrogen bonds are a typical characteristic of stable MSA-based clusters. The six-membered and eight-membered rings are formed by multiple hydrogen bonds in MSA–X (X = A, M, and D) dimers and MSA–D–Y (Y = A, M, and D) trimers, respectively; however, one six- and one eight-membered ring do coexist in the MSA–A–Y (Y = A, M, and D) and MSA–M–Y (Y = A, M, and D) trimers. Herein, to compare the structural parameters of the dimers and trimers, the configuration of the trimers (such as MSA–A–A) can be divided into two corresponding dimers (such as MSA–A and A–A). The synergy between X and Y has a significant influence on the length and strength of the relevant hydrogen bonds in MSA–X–Y cyclic trimers compared with MSA–X dimers. The length of the SO–H⋯N hydrogen bond is 1.611 Å in MSA–A, which is 0.571, 0.554, and 0.548 Å longer than its counterparts in the MSA–A–A (1.040 Å), MSA–A–M (1.063 Å), and MSA–A–D (1.057 Å) trimers, respectively. The main point to take away here is that the short lengths of the bonds in the trimers indicate that the proton has been completely transferred from MSA to the A molecule. The change of length for the N–H⋯N hydrogen bond is similar to that of N–H⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. The lengths of the N–H⋯N hydrogen bonds are 1.760, 1.671, and 1.597 Å in the MSA–A–A, MSA–A–M, and MSA–A–D trimers, respectively. By comparing the lengths of the hydrogen bonds of the trimers with those in the corresponding dimers, the results show that the lengths of the hydrogen bonds in the trimers are 0.503, 0.542, and 0.599 Å shorter than those in the corresponding dimers (A–A, 2.263 Å, A–M, 2.213 Å, and A–D, 2.196 Å, see Table S1†), respectively. Similar phenomena occur in other trimers, such as MSA–M–Y and MSA–D–Y trimers. The length of a hydrogen bond is a common indicator to evaluate its strength. The synergy between X and Y bases shortens the lengths of the hydrogen bonds in these trimers. The non-covalent interactions in the trimers are stronger than those in their corresponding dimers, and the synergy increases with increasing alkalinity of X and Y. From Table 1, the results show that the effects of synergy on the three types of hydrogen bonds are different due to steric hindrance of the trimers. A trimer is more advantageous than a dimer to function as a nucleus of aerosol particles in atmospheric NPF.
O. The lengths of the N–H⋯N hydrogen bonds are 1.760, 1.671, and 1.597 Å in the MSA–A–A, MSA–A–M, and MSA–A–D trimers, respectively. By comparing the lengths of the hydrogen bonds of the trimers with those in the corresponding dimers, the results show that the lengths of the hydrogen bonds in the trimers are 0.503, 0.542, and 0.599 Å shorter than those in the corresponding dimers (A–A, 2.263 Å, A–M, 2.213 Å, and A–D, 2.196 Å, see Table S1†), respectively. Similar phenomena occur in other trimers, such as MSA–M–Y and MSA–D–Y trimers. The length of a hydrogen bond is a common indicator to evaluate its strength. The synergy between X and Y bases shortens the lengths of the hydrogen bonds in these trimers. The non-covalent interactions in the trimers are stronger than those in their corresponding dimers, and the synergy increases with increasing alkalinity of X and Y. From Table 1, the results show that the effects of synergy on the three types of hydrogen bonds are different due to steric hindrance of the trimers. A trimer is more advantageous than a dimer to function as a nucleus of aerosol particles in atmospheric NPF.
| Trimer | SO–H⋯N | N–H⋯N | N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Rb | ΔRc | θd | Rb | ΔRc | θd | Rb | ΔRc | θd | |
| a Bond length (R), change of bond length (ΔR) and bond angle (θ) in the clusters.b Inter-molecular hydrogen bond distance.c ΔR = RN/O–H (dimer/trimer) − RN/O–H (monomer).d Inter-molecular hydrogen bond angle. | |||||||||
| MSA–A | 1.611 | 0.065 | 171.6 | — | — | — | 2.345 | 0.003 | 119.8 |
| MSA–M | 1.502 | 0.102 | 171.8 | — | — | — | 2.487 | 0.003 | 107.9 |
| MSA–D | 1.672 | 0.705 | 146.9 | — | — | — | 1.672 | 0.044 | 146.9 |
| MSA–A–A | 1.040 | 0.857 | 138.0 | 1.760 | 0.053 | 159.9 | 1.986 | 0.013 | 163.1 |
| MSA–A–M | 1.063 | 0.672 | 156.0 | 1.671 | 0.076 | 164.2 | 2.017 | 0.011 | 153.4 |
| MSA–A–D | 1.057 | 0.700 | 155.4 | 1.597 | 0.102 | 167.3 | 1.960 | 0.013 | 159.3 |
| MSA–M–A | 1.038 | 0.871 | 139.2 | 1.796 | 0.046 | 161.0 | 1.986 | 0.013 | 163.8 |
| MSA–M–M | 1.053 | 0.723 | 153.8 | 1.721 | 0.062 | 164.8 | 2.026 | 0.010 | 153.0 |
| MSA–M–D | 1.052 | 0.725 | 154.7 | 1.680 | 0.074 | 167.7 | 1.982 | 0.011 | 158.9 |
| MSA–D–A | 1.063 | 0.639 | 169.6 | 2.024 | 0.049 | 150.7 | 1.767 | 0.010 | 154.2 |
| MSA–D–M | 1.061 | 0.651 | 169.1 | 1.726 | 0.060 | 170.8 | 1.992 | 0.011 | 157.0 |
| MSA–D–D | 1.058 | 0.662 | 168.2 | 1.696 | 0.068 | 172.4 | 1.966 | 0.011 | 160.7 |
3.2. AIM and CT analysis
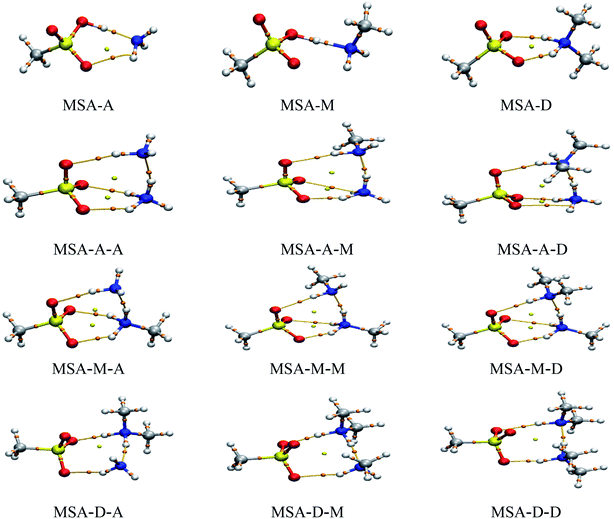
AIM theory is widely used to reveal the physical nature of noncovalent interactions.34,47 Therefore, the noncovalent interactions in these clusters were assessed qualitatively and quantitatively by topological analysis. The values of the electron density (ρ(r)) and the Laplace of the electron density (∇2ρ(r)) at bond critical points (BCPs) are presented in Table 2. In addition, the ginger and yellow balls in Fig. 2 refer to the BCPs and ring critical points (RCPs), respectively. The results show that the values of ρ(r) and ∇2ρ(r) were obviously changed by the strong synergy between the X and Y molecules. For ρ(r) and ∇2ρ(r) on the SO–H⋯N hydrogen bonds in these trimers, the values range from 0.0122 to 0.3433 a.u. and from −1.8668 to −1.6348 a.u., respectively. As a result, most of these values are beyond the scope of the criteria of hydrogen bonds (ρ(r), 0.002 to 0.040 a.u.; ∇2ρ(r), 0.014 to 0.139 a.u.) due to the acid–base reaction.48 The value of ∇2ρ is usually used to determine the type of noncovalent interaction. A negative (∇2ρ(r) < 0) or positive (∇2ρ(r) > 0) value indicates a shared-shell or closed-shell interaction in these clusters, respectively. Similar to the SO–H⋯N hydrogen bonds, for ρ(r) and ∇2ρ(r) on the N–H⋯N hydrogen bonds, the values range from 0.0510 to 0.0780 a.u. and from 0.0230 to 0.0693 a.u., respectively. For the N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S hydrogen bonds, the values range from 0.0232 to 0.0589 a.u. and from 0.0777 to 0.1090 a.u., respectively. These results show that the SO–H⋯N hydrogen bond is the strongest in the MSA–X–Y trimers, followed by N–H⋯N and N–H⋯O
S hydrogen bonds, the values range from 0.0232 to 0.0589 a.u. and from 0.0777 to 0.1090 a.u., respectively. These results show that the SO–H⋯N hydrogen bond is the strongest in the MSA–X–Y trimers, followed by N–H⋯N and N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S. For the MSA–X–Y trimers, the proton transfer from MSA to X (X = A, M, or D) is exothermal and barrierless due to the strong synergy between X and Y. In addition, the results of the NCI analysis (see Fig. S5;† the value of the isosurface for RDG is equal to 0.3 a.u.) are consistent with the conclusions of the AIM analysis.
S. For the MSA–X–Y trimers, the proton transfer from MSA to X (X = A, M, or D) is exothermal and barrierless due to the strong synergy between X and Y. In addition, the results of the NCI analysis (see Fig. S5;† the value of the isosurface for RDG is equal to 0.3 a.u.) are consistent with the conclusions of the AIM analysis.
| Complex | SO–H⋯N | N–H⋯N | N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Δq(H)b | ρ(r) | ∇2ρ(r) | Δq(H)b | ρ(r) | ∇2ρ(r) | Δq(H)b | ρ(r) | ∇2ρ(r) | |
| a ρ(r) and ∇2ρ at the BCPs in the MSA–X and MSA–X–Y complexes except for MSA–M dimer.b Δq(H) = q(H)dimer/trimer − q(H)monomer. | |||||||||
| MSA–A | −0.002 | 0.0695 | 0.0428 | — | — | — | 0.050 | 0.0122 | 0.0497 |
| MSA–M | −0.019 | 0.0931 | −0.0055 | — | — | — | 0.045 | — | — |
| MSA–D | −0.037 | 0.3130 | −1.1763 | — | — | — | 0.141 | 0.0536 | 0.0417 |
| MSA–A–A | −0.047 | 0.3206 | −1.8512 | 0.093 | 0.0510 | 0.0657 | 0.064 | 0.0243 | 0.0797 |
| MSA–A–M | −0.047 | 0.2997 | −1.6858 | 0.086 | 0.0643 | 0.0481 | 0.068 | 0.0232 | 0.0787 |
| MSA–A–D | −0.048 | 0.3046 | −1.7255 | 0.077 | 0.0780 | 0.0232 | 0.092 | 0.0267 | 0.0854 |
| MSA–M–A | −0.050 | 0.3262 | −1.8613 | 0.102 | 0.0471 | 0.0693 | 0.064 | 0.0242 | 0.0797 |
| MSA–M–M | −0.046 | 0.3123 | −1.7700 | 0.099 | 0.0573 | 0.0587 | 0.067 | 0.0227 | 0.0777 |
| MSA–M–D | −0.047 | 0.3130 | −1.7751 | 0.094 | 0.0642 | 0.0483 | 0.088 | 0.0253 | 0.0827 |
| MSA–D–A | −0.044 | 0.3058 | −1.7160 | 0.126 | 0.0502 | 0.0669 | 0.063 | 0.0226 | 0.0776 |
| MSA–D–M | −0.045 | 0.3083 | −1.7362 | 0.120 | 0.0569 | 0.0592 | 0.069 | 0.0244 | 0.0816 |
| MSA–D–D | −0.045 | 0.3433 | −1.8668 | 0.120 | 0.0621 | 0.0519 | 0.087 | 0.0589 | 0.1090 |
Charge transfer (CT) from an acceptor to a donor is also a common phenomenon in the formation of atmospheric clusters.49 The values of Δq(H) on the H atom in the hydrogen bonds for all the trimers are presented in Table 2. The values for q(H) of the SO–H⋯N hydrogen bonds range from −0.050 to −0.002 a.u., while the Δq(H) values for N–H⋯N and N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S range from 0.077 to 0.126 a.u. and from 0.050 to 0.141 a.u., respectively. For the MSA–X–Y trimers, CT from the acceptor to the donor significantly promotes electron delocalization between the three different hydrogen bonds due to the synergy of X and Y, which is very beneficial for stabilizing MSA–X–Y atmospheric clusters. From Table 2, the results indicate that CT from MSA to X in SO–H⋯N hydrogen bonds is favored over that from Y to X in N–H⋯N and from O
S range from 0.077 to 0.126 a.u. and from 0.050 to 0.141 a.u., respectively. For the MSA–X–Y trimers, CT from the acceptor to the donor significantly promotes electron delocalization between the three different hydrogen bonds due to the synergy of X and Y, which is very beneficial for stabilizing MSA–X–Y atmospheric clusters. From Table 2, the results indicate that CT from MSA to X in SO–H⋯N hydrogen bonds is favored over that from Y to X in N–H⋯N and from O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S to Y in N–H⋯O
S to Y in N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S. This is consistent with the conclusions of the previous analyses by the AIM and NCI methods. In addition, the distance between a BCP and an RCP is generally used to assess the relative strengths of hydrogen bonds in cyclic clusters.50 The distances between the BCP and RCP for the MSA–X–Y trimers are presented in Table 3. The distance between the BCP of the SO–H⋯N hydrogen bond and the RCP is far longer than those between the BCPs of the other hydrogen bonds and the RCP; this indicates that SO–H⋯N is the strongest hydrogen bond in the MSA–X–Y trimers.
S. This is consistent with the conclusions of the previous analyses by the AIM and NCI methods. In addition, the distance between a BCP and an RCP is generally used to assess the relative strengths of hydrogen bonds in cyclic clusters.50 The distances between the BCP and RCP for the MSA–X–Y trimers are presented in Table 3. The distance between the BCP of the SO–H⋯N hydrogen bond and the RCP is far longer than those between the BCPs of the other hydrogen bonds and the RCP; this indicates that SO–H⋯N is the strongest hydrogen bond in the MSA–X–Y trimers.
| Complex | SO–H⋯N | N–H⋯N | N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
|---|---|---|---|
| a The distances between the BCP and RCP in the MSA–X and MSA–X–Y complexes except for MSA–M dimer. | |||
| MSA–A | 1.0745 | — | 0.5081 |
| MSA–M | — | — | — |
| MSA–D | 1.1083 | — | 0.9198 |
| MSA–A–A | 1.6909 | 1.3626 | 1.3388 |
| MSA–A–M | 1.7170 | 1.4220 | 1.2913 |
| MSA–A–D | 1.7265 | 1.4343 | 1.2816 |
| MSA–M–A | 1.6916 | 1.3639 | 1.3355 |
| MSA–M–M | 1.7260 | 1.4009 | 1.2907 |
| MSA–M–D | 1.7376 | 1.4091 | 1.2797 |
| MSA–D–A | 1.6840 | 1.6680 | 1.2127 |
| MSA–D–M | 1.5795 | 1.3985 | 1.3155 |
| MSA–D–D | 1.5864 | 1.4141 | 1.3071 |
3.3. Interaction energy
BEs and thermodynamic properties are usually used to evaluate the stability and volatility of atmospheric clusters. Proton transfer induced by the acid–base reaction is regarded as one of the fundamental driving forces for the formation of aerosol particles. Herein, the average values of the BEs, ΔH298 Kθ and ΔG298 Kθ for all clusters, which were obtained by four DFT methods at 298.15 K and 1 atm, are summarized in Tables S2–S5† and are compared with some published data (see Table S6†). The results show that the synergy between base molecules has a significant influence on the BE, ΔH298 Kθ and ΔG298 Kθ values of the MSA–X–Y trimers. In these trimers, barrier-free proton transfer can be induced by synergy between the X and Y molecules. The synergistic effect observed in the experiment can also be attributed to kinetics, and the kinetic rate will be at the kinetic limit when the synergy between X and Y is very strong.24 Herein, the BEs are −56.49 kJ mol−1, −69.01 kJ mol−1 and −77.26 kJ mol−1 for MSA–A, MSA–M, and MSA–D, respectively (see Table S6†). The MSA–X–Y trimers were formed via attaching a Y (Y = A, MA, and DMA) monomer to the MSA–X (X = A, MA, and DMA) dimers.The affinity of a Y (Y = A, MA, and DMA) molecule to the MSA–X (X = A, MA, and DMA) dimers was investigated in this section. Table 4 presents the BEs and the changes in the enthalpy and Gibbs free energy for the reactions where a Y molecule is added to an MSA–X dimer. According to the values of ΔBE, the attachment of Y to all the MSA–X dimers is favorable, and the affinity of Y increases as the alkalinity of Y increases. The affinity of Y (Y = A, MA, and DMA) to the MSA–D (−12.2 to −17.9 kJ mol−1) dimer is much higher than that to MSA–M (−4.18 to −13.2 kJ mol−1) but lower than that to MSA–A (−15.7 to −28.9 kJ mol−1); the difference is determined by the alkalinities of X and Y. In addition, the affinity is affected by steric hindrance in the trimers.
| X | Y | MSA–X + Y ↔ MSA–X–Y | ||
|---|---|---|---|---|
| ΔBEsb | ΔΔH298 Kθ | ΔΔG298 Kθ | ||
| a The results are the means obtained from four DFT levels (in kJ mol−1).b BEs corrected with ZPVE, ΔBEs = BEs(MSA–X–Y) − BEs(MSA–X). | ||||
| A | A | −40.5 | −45.3 | −15.7 |
| M | −50.0 | −52.2 | −21.8 | |
| D | −58.0 | −59.0 | −28.9 | |
| MA | A | −47.6 | −51.5 | −4.18 |
| M | −56.9 | −58.2 | −10.2 | |
| D | −60.0 | −60.0 | −13.2 | |
| DMA | A | −53.4 | −55.5 | −12.2 |
| M | −62.0 | −62.3 | −15.7 | |
| D | −65.6 | −64.9 | −17.9 | |
Generally, cyclic trimers can be considered as the association of two relevant dimers. The additional stabilization energy for the trimers induced by the cyclic structure greatly enhances the stability of the trimers. For example, MSA–A–A can be regarded as one cluster consisting of two dimers: MSA–A and A–A. The ΔBEs were calculated to be −96.99, −56.49, and −7.66 kJ mol−1 for MSA–A–A, MSA–A, and A–A, respectively (see Tables 5 and S7†). For the MSA–A–A trimer, the total value of ΔBE for MSA–A and A–A is only −64.15 kJ mol−1; this shows that the additional stabilization energy induced by the synergy of two ammonia molecules reaches 32.8 kJ mol−1 in the MSA–A–A trimer. A similar tendency exists in the other clusters (see Table 5). The additional stabilization energy of cyclic trimers is beneficial to the formation of the initial clusters. In addition, a conclusion can be easily drawn that the effects of synergy on the ΔBE increased as the alkalinity of the bases increased. The main reason for the above results is the difference in the alkalinities of the basic acceptors. It is well known that among these three base acceptors, D is the most basic, followed by M and A.
| MSA–X | X–Y | MSA–X–Y | ΔBEsb | ΔΔH298 Kθ | ΔΔG298 Kθ |
|---|---|---|---|---|---|
| a The results are the means obtained from four DFT levels (in kJ mol−1).b BEs corrected with ZPVE, ΔBEs = BEs(MSA–X–Y) − BEs(MSA–X) − BEs(X–Y). | |||||
| MSA–A | A–A | MSA–A–A | −32.8 | −37.6 | −13.7 |
| MSA–A | A–M | MSA–A–M | −40.1 | −42.5 | −22.3 |
| MSA–A | A–D | MSA–A–D | −46.7 | −47.9 | −28.9 |
| MSA–M | M–A | MSA–M–A | −37.6 | −41.6 | −23.1 |
| MSA–M | M–M | MSA–M–M | −45.0 | −47.4 | −30.5 |
| MSA–M | M–D | MSA–M–D | −46.9 | −48.5 | −33.4 |
| MSA–D | D–A | MSA–D–A | −42.1 | −45.3 | −27.9 |
| MSA–D | D–M | MSA–D–M | −48.1 | −50.3 | −34.8 |
| MSA–D | D–D | MSA–D–D | −50.7 | −51.6 | −36.8 |
The BEs and the changes in the enthalpy and Gibbs free energy for the substitution of Y1 (Y1 = A/M) by Y2 (Y2 = M/D) in the MSA–X–Y trimers are presented in Table 6. As shown in Table 6, the substitution of A or M by M or D molecule is more favorable in the corresponding trimers because the alkalinities of M and D are stronger than that of A. In other words, the MSA–X–M and MSA–X–D trimers are more stable than the MSA–X–A trimer. When the difference in alkalinity between X and Y is large, the significance of the synergistic effect on the substitution is greater. Recently, it was further confirmed that base displacement on the cluster surface is both thermodynamically and kinetically favorable by the experiments and computations reported by Bzdek et al.51
| X | Y1 | Y2 | MSA–X–Y1 + Y2 ↔ MSA–X–Y2 + Y1 | ||
|---|---|---|---|---|---|
| ΔBEsb | ΔΔH298 Kθ | ΔΔG298 Kθ | |||
| a The results are the means obtained from four DFT levels (in kJ mol−1).b BEs corrected with ZPVE, ΔBEs = BEs(MSA–X–Y2) − BEs(MSA–X–Y1). | |||||
| A | A | DMA | −17.5 | −13.7 | −13.2 |
| A | MA | −9.5 | −6.9 | −6.2 | |
| MA | DMA | −8.0 | −6.8 | −7.0 | |
| MA | A | DMA | −12.4 | −8.5 | −9.0 |
| A | MA | −9.3 | −6.7 | −6.0 | |
| MA | DMA | −3.1 | −1.8 | −3.0 | |
| DMA | A | DMA | −12.2 | −9.4 | −5.7 |
| A | MA | −8.6 | −6.9 | −3.4 | |
| MA | DMA | −3.6 | −2.6 | −2.2 | |
In addition, the values of ΔΔG298 Kθ for the clusters are presented in Tables 4–6 and S6–S8;† these values are negative for the processes of attachment and substitution. The results show that the addition of a Y molecule to the MSA-X dimers and the substitution of Y2 (M and D) for Y1 (A and M) are spontaneous processes from the thermodynamic point of view. It was further confirmed that the synergy between X and Y has a significant influence on the formation of trimers. The enthalpy ΔΔH298 Kθ is also correlated with the stability of a complex.52 The values of ΔΔH298 Kθ of the MSA-based clusters show that synergy can significantly enhance the stability of the MSA–X–Y trimers and plays an important role in atmospheric nucleation.
3.4. The redshift of the O/N–H stretching vibrational frequency
Analysis of the vibrational frequency of O/N–H is helpful to understand the nature of hydrogen bonding and proton transfer as well as the formation mechanism of initial atmospheric clusters. The formation of strong hydrogen bonds in the clusters usually causes a redshift of the stretching vibration of the H–O/N bonds. The synergistic effect significantly affects the H–O/N stretching vibrational frequencies in the MSA–X–Y (X, Y = A, M, and D) trimers. From Tables 2 and 7, the changes in the bond lengths (ΔR) and the redshifts of the stretching frequencies (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) in the H–O/N bonds are closely related. Considering the relationship between the bond lengths and the redshifts of H–O/N in the corresponding trimers, it is clear that the bond length of H–OS (MSA donor) is lengthened by about 0.700 to 0.871 Å and the accompanying stretching frequencies are decreased by 415.5 to 1097.3 cm−1 compared with the corresponding monomers. It should be noted that the remarkable increase of the length of the H–OS bond in the trimers occurs because the proton has been transferred from MSA to the X base molecule. When the basic X donor donates a proton to the Y monomer, the redshifts of H–N in the trimers decrease by 772.2 to 1582.8 cm−1 compared with the corresponding X monomers. The redshifts of the H–N bonds are decreased by 168.0 to 811.9 cm−1 when the Y donor donates a proton to the O atom of the S
) in the H–O/N bonds are closely related. Considering the relationship between the bond lengths and the redshifts of H–O/N in the corresponding trimers, it is clear that the bond length of H–OS (MSA donor) is lengthened by about 0.700 to 0.871 Å and the accompanying stretching frequencies are decreased by 415.5 to 1097.3 cm−1 compared with the corresponding monomers. It should be noted that the remarkable increase of the length of the H–OS bond in the trimers occurs because the proton has been transferred from MSA to the X base molecule. When the basic X donor donates a proton to the Y monomer, the redshifts of H–N in the trimers decrease by 772.2 to 1582.8 cm−1 compared with the corresponding X monomers. The redshifts of the H–N bonds are decreased by 168.0 to 811.9 cm−1 when the Y donor donates a proton to the O atom of the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. It can be concluded from the previous analysis that the influence of the synergy between X and Y on the redshift of the –N⋯H–N bonds is greater than that on the –N···H–OS bonds and the S
O group. It can be concluded from the previous analysis that the influence of the synergy between X and Y on the redshift of the –N⋯H–N bonds is greater than that on the –N···H–OS bonds and the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N bonds in the MSA–X–Y trimers. It was further confirmed that proton transfer from MSA to X is promoted by adding an additional Y molecule to the MSA–X–Y trimers or by the synergy between X and Y molecules. The higher the alkalinity of the X and Y monomers, the more favorable the proton transfer in the trimers. This is consistent with the conclusion in Section 3.3. The synergy is favorable for aerosol particle formation and subsequent growth in the atmosphere. In addition, the stretching vibrational frequencies of the H–O/N bonds further confirmed that the S
O⋯H–N bonds in the MSA–X–Y trimers. It was further confirmed that proton transfer from MSA to X is promoted by adding an additional Y molecule to the MSA–X–Y trimers or by the synergy between X and Y molecules. The higher the alkalinity of the X and Y monomers, the more favorable the proton transfer in the trimers. This is consistent with the conclusion in Section 3.3. The synergy is favorable for aerosol particle formation and subsequent growth in the atmosphere. In addition, the stretching vibrational frequencies of the H–O/N bonds further confirmed that the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–H and S
O–H and S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are superior donors and inferior acceptors of hydrogen bonds in MSA molecules, respectively.
O groups are superior donors and inferior acceptors of hydrogen bonds in MSA molecules, respectively.
| Complex | SO–H⋯N | N–H⋯N | N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
|||
|---|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) |
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) a a |
|
a Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) O(N)–H (monomer) − O(N)–H (monomer) − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) O(N)–H (dimer/trimer). O(N)–H (dimer/trimer). |
||||||
| MSA–A | 2541.4 | 1226.0 | 3572.0 | 16.3 | — | — |
| MSA–MA | 1963.4 | 1804.0 | 3566.6 | 9.0 | — | — |
| MSA–DMA | 1947.6 | 1819.8 | 3492.2 | 35.6 | — | — |
| MSA–A–A | 3118.4 | 649.1 | 2684.5 | 903.8 | 3318.3 | 270.0 |
| MSA–A–MA | 2762.0 | 1005.4 | 2326.9 | 1261.4 | 3363.3 | 212.3 |
| MSA–A–DMA | 2837.1 | 930.3 | 2005.5 | 1582.8 | 3340.8 | 187.1 |
| MSA–MA–A | 3191.2 | 576.2 | 2803.4 | 772.2 | 3321.0 | 267.3 |
| MSA–MA–MA | 2912.6 | 854.8 | 2541.2 | 1034.4 | 3371.8 | 203.8 |
| MSA–MA–DMA | 3351.9 | 415.5 | 2274.6 | 1301.0 | 2715.9 | 811.9 |
| MSA–DMA–A | 2670.2 | 1097.3 | 2670.2 | 857.7 | 3361.2 | 227.1 |
| MSA–DMA–MA | 2756.3 | 1011.1 | 2556.5 | 971.4 | 3358.9 | 216.7 |
| MSA–DMA–DMA | 2783.0 | 984.5 | 2424.8 | 1103.0 | 3359.9 | 168.0 |
3.5. The evaporation rate
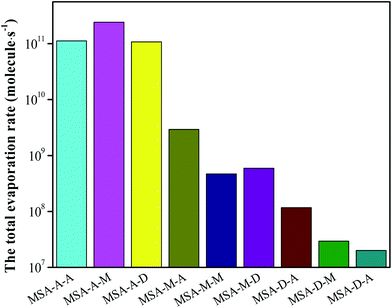
Based on the analyses of AIM, thermodynamics, and the stretching vibrational frequencies of O/N–H, we can easily conclude that the synergy of base molecules can improve the cluster stability, enhance the noncovalent interaction, and facilitate the proton transfer for the MSA–X–Y (X, Y = A, M, and D) trimers. Herein, the total evaporation rate based on ACDC simulations has been determined to increase the in-depth understanding of the formation mechanism of atmospheric MSA–X–Y trimers. One note is that the values of ΔG for the clusters act as an input file for the ACDC simulations (see Section 6 in the ESI†). For the MSA–X–Y trimers, as can be seen from Fig. 3, the total evaporation rate for MSA–D–Y is the lowest; it is orders of magnitude lower than that of MSA–A–Y, followed by the MSA–M–Y and MSA–A–Y trimers. The evaporation rate of the monomers in MSA–X–Y is shown in Table S9.† The conclusions are in agreement with the AIM and NCI analyses above. The difference in evaporation of the MSA–X–Y trimers is due to the difference in alkalinity of X and Y, the synergy between the X and Y monomers, and the steric hindrance within the trimer. Generally, if the alkalinities of X and Y are greater, the synergy between X and Y is more significant, and the formation of trimers is more favorable. Based on the ACDC kinetics simulations, we can easily draw a conclusion that MSA and common nucleation precursors can form very stable clusters, especially with a strong base. Thus, MSA is a strong potential candidate for the formation of atmospheric aerosol particles in coastal areas.3.6. Atmospheric concentration
The stability of a cluster is closely related to its BEs. The BEs are very helpful to understand the formation of MSA–X–Y trimers. However, BEs alone are insufficient to evaluate the effects of the precursor concentration on the atmospheric role of MSA–X–Y trimers. Herein, the ΔG values (298 K and 1 atm) for the trimers combined with the concentrations of the precursors were used to assess their corresponding roles. From station observations, the total concentration of gaseous MSA ranges from 105 to 107 molecules per cm3, i.e. 2.5 × 10−4 to 2.5 × 10−2 ppb,53 which is typically approximately 10% to 100% of the coexisting gaseous SA in the coastal marine boundary layer.54 The typical concentrations of atmospheric ammonia are in the 10 to 100 ppb range.55 The methylamine and dimethylamine concentrations are all in the 0.1 to 1.0 ppb range.55 To evaluate the extreme impacts of MSA-based trimers on NPF, the upper and lower limits of the vapor concentrations of the monomer are used in relevant computations for comparison. Thus, the atmospheric concentrations of MSA–X–Y (X = A, M, and D) trimers have been calculated according to the law of conservation of mass (see Section 6, eqn (5) and (6) in the ESI†). From Table 8, the concentrations of MSA–X dominated by the vapor concentrations of the monomers range from 2 to 6 orders of magnitude. The results show that MSA has a strong capacity to complex with A, M, and D. This has a significant influence on the formation of atmospheric aerosol particles. It is clear that the contribution of MSA to NPF is obviously underestimated in specific areas, especially in coastal areas.56 In addition, the ratios of [MSA–X–Y]/[MSA–X] have been calculated using eqn (6) (see the ESI†). The ratios are 2.5, 0.3, and 5.2 for Y = A, M and D at X = A, respectively. Meanwhile, the ratios for the same sequence are 31.0, 3.4 and 11.0 for X = M and 1.6 × 102, 6.5, and 16.0 for X = D, respectively. From the above, the atmospheric concentrations of the MSA–X–Y trimers except for MSA–A–M are higher than those of the MSA–X dimers, and the concentration of MSA–D–A is the highest of all the trimers. This convincing evidence indicates that synergy in MSA–X–Y trimers plays a significant role in atmospheric NPF.| Complex | Concentrations | Ratio | |
|---|---|---|---|
| Min | Max | [MSA–X–Y]/[MSA–X] | |
| MSA–A | 1.3 × 102 | 1.3 × 105 | — |
| MSA–M | 1.1 × 102 | 1.1 × 106 | — |
| MSA–D | 3.9 × 103 | 3.9 × 105 | — |
| MSA–A–A | 3.4 × 102 | 3.4 × 106 | 2.5 |
| MSA–A–M | 4.1 × 101 | 4.1 × 106 | 0.3 |
| MSA–A–D | 7.0 × 102 | 7.0 × 105 | 5.2 |
| MSA–M–A | 3.4 × 103 | 3.4 × 108 | 31.0 |
| MSA–M–M | 3.7 × 102 | 3.7 × 108 | 3.4 |
| MSA–M–D | 1.3 × 103 | 1.3 × 107 | 11.0 |
| MSA–D–A | 6.4 × 105 | 6.4 × 108 | 160.0 |
| MSA–D–M | 2.5 × 104 | 2.5 × 108 | 6.5 |
| MSA–D–D | 6.3 × 104 | 6.3 × 106 | 16.0 |
3.7. Atmospheric implications
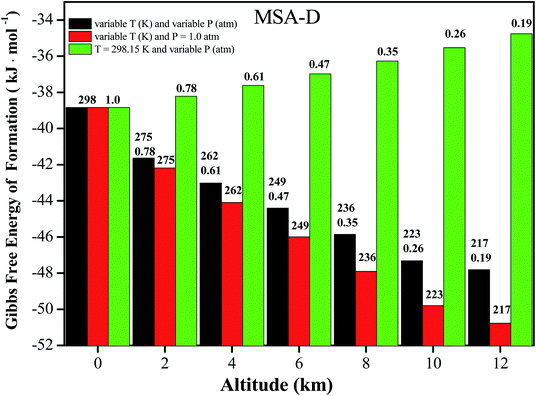
It is well known that NPF events take place in the troposphere (0 to 12 km), where the atmospheric temperature (T) approximately decreases by 6.49 K for every 1 km increase. Ultimately, a constant temperature (T = 216.69 K) is reached 11 km above sea level.57 Therefore, the altitude (from 0 to 11 km above sea level) can be used as a function of T and pressure (P) to investigate the influence on the thermochemical properties of coagulation and evaporation processes in the formation of atmospheric clusters.58 Herein, the values of ΔG for the MSA–D–D trimer at variable T and P, variable T and P = 1.0 atm, and T = 298.15 K and variable T conditions are all presented in Fig. 4 (for the other trimers, the values of ΔG under different conditions are shown in Tables S10–S12†). The value of ΔG decreases by 15.6 to 19.4 kJ mol−1 for the MSA–X–Y (X, Y = A, M, and D) clusters. The results show that the MSA–X–Y trimers are much more stable at 216.69 K and 0.19 atm (12 km) than at 298.15 K and 1 atm (0 km). Low temperature facilitate the formation of hydrogen bonds and the cluster formation of atmospheric precursors, and the opposite is true at low pressure. In general, the effects of temperature on ΔG of the MSA–X–Y trimers are more obvious than the effects of atmospheric pressure. It is essential to assess the influence of temperature and pressure on the formation of the MSA–X–Y atmospheric trimers. However, it is very unrealistic to obtain accurate concentrations of relevant clusters due to the various sources and complicated nucleation processes of their atmospheric precursors. Although the simplified model is only used for qualitative evaluation, it is still helpful to understand the effects of altitude (temperature and pressure) on the formation mechanism of atmospheric aerosol particles.4. Conclusions
In this work, the ternary clusters formed by MSA and common nucleation species (A, M, and D) were investigated using an artificial bee colony algorithm, molecular mechanics, semiempirical, DFT and ACDC methods. Optimization of the atmospheric molecular structures and single-point energy calculations for the stable MSA–X–Y trimers was performed using four DFT methods (B3LYP-D3, M06-2X, PW91PW91, and ωB97X-D). The effects of synergy on the structures, hydrogen bonds, and redshifts of the MSA–X–Y trimers were investigated by the AIM method. The synergy between molecules X and Y in the trimers and the effects of synergy on the volatility of the trimers were evaluated by the average values of ΔG and kinetics simulations, respectively. Six- or eight-membered rings formed by hydrogen bonds are a typical characteristic of trimers. The redshift of the H–OS stretching (MSA donor) is larger than that of the H–N stretching (base donor) in the clusters compared with the monomers. Proton transfer from MSA to X in the MSA–X–Y (X, Y = A, M, and D) trimers is exothermal and barrierless due to the strong synergy between X and Y. The formation of MSA–X–Y is markedly affected by low temperature and high pressure. For MSA–X–Y, the total evaporation rate decreased as the alkalinity of X increased. This work puts forward new points about the role of MSA in the initial stages of NPF at the molecular level and is helpful for understanding the nucleation mechanisms of MSA-based particles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Nature Science Foundation of China (No. 21473107 and 21473108) and the Fundamental Research Supported for the Central Universities Funds (No. 2017TS019). We thank Dr Anand Parkash for his linguistic assistance during the preparation of this manuscript.References
- R. Zhang, G. Wang, S. Guo, M. L. Zamora, Q. Ying, Y. Lin, W. Wang, M. Hu and Y. Wang, Chem. Rev., 2015, 115, 3803–3855 CrossRef CAS PubMed.
- Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, IPCC, 2013. Climate Change 2013: The Physical Science Basis, ed. T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. M. Midgley, Cambridge University Press, Cambridge, 2013 Search PubMed.
- M. O. Andreae, D. Rosenfeld, P. Artaxo, A. A. Costa, G. P. Frank, K. M. Longo and M. A. F. Silvadias, Science, 2015, 303, 1337–1342 CrossRef PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- F. Bianchi, J. Trostl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kurten, H. E. Manninen, S. Munch, O. Perakyla, T. Petaja, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- J. Wang, R. Krejci, S. Giangrande, C. Kuang, H. M. J. Barbosa, J. Brito, S. Carbone, X. Chi, J. Comstock, F. Ditas, J. Lavric, H. E. Manninen, F. Mei, D. Moran-Zuloaga, C. Pöhlker, M. L. Pöhlker, J. Saturno, B. Schmid, R. A. F. Souza, S. R. Springston, J. M. Tomlinson, T. Toto, D. Walter, D. Wimmer, J. N. Smith, M. Kulmala, L. A. T. Machado, P. Artaxo, M. O. Andreae, T. Petäjä and S. T. Martin, Nature, 2016, 539, 416–419 CrossRef CAS PubMed.
- S. Guo, M. Hu, M. L. Zamora, J. Peng, D. Shang, J. Zheng, Z. Du, Z. Wu, M. Shao, L. Zeng, M. J. Molina and R. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17373–17378 CrossRef CAS PubMed.
- J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS.
- D. L. Yue, M. Hu, R. Y. Zhang, Z. B. Wang, J. Zheng, Z. J. Wu, A. Wiedensohler, L. Y. He, X. F. Huang and T. Zhu, Atmos. Chem. Phys., 2010, 10, 4953–4960 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagne, L. Ickes, A. Kurten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkila, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petaja, R. Schnitzhofer, J. H. Seinfeld, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- B. R. Bzdek, D. P. Ridge and M. V. Johnston, J. Geophys. Res.: Atmos., 2011, 116, D03301 CrossRef.
- C.-Y. Wang, S. Jiang, Y.-R. Liu, H. Wen, Z.-Q. Wang, Y.-J. Han, T. Huang and W. Huang, J. Phys. Chem. A, 2018, 122, 3470–3479 CrossRef CAS PubMed.
- H. G. Kjaergaard, T. W. Robinson, D. L. Howard, J. S. Daniel, J. E. Headrick and V. Vaida, J. Phys. Chem. A, 2003, 107, 10680–10686 CrossRef CAS.
- V. Vaida, J. Chem. Phys., 2011, 135, 020901 CrossRef PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin III, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- D. R. Hanson, J. Phys. Chem. A, 2005, 109, 6919–6927 CrossRef CAS PubMed.
- F. L. Eisele and D. J. Tanner, J. Geophys. Res.: Atmos., 1993, 98, 9001–9010 CrossRef CAS.
- H. Zhao, X. Jiang and L. Du, Chemosphere, 2017, 174, 689–699 CrossRef CAS PubMed.
- H. Chen, M. J. Ezell, K. D. Arquero, M. E. Varner, M. L. Dawson, R. B. Gerber and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2015, 17, 13699–13709 RSC.
- H. Chen, M. E. Varner, R. B. Gerber and B. J. Finlayson-Pitts, J. Phys. Chem. B, 2016, 120, 1526–1536 CrossRef CAS PubMed.
- H. Chen and B. J. Finlayson-Pitts, Environ. Sci. Technol., 2017, 51, 243–252 CrossRef CAS PubMed.
- J. Xu, B. J. Finlayson-Pitts and R. B. Gerber, Phys. Chem. Chem. Phys., 2017, 19, 31949–31957 RSC.
- J. Xu, V. Perraud, B. J. Finlayson-Pitts and R. B. Gerber, Phys. Chem. Chem. Phys., 2018, 20, 22249–22259 RSC.
- W. A. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. R. Hanson, P. H. McMurry and C. Jen, J. Geophys. Res.: Atmos., 2015, 120, 1933–1950 CAS.
- S.-K. Miao, S. Jiang, X.-Q. Peng, Y.-R. Liu, Y.-J. Feng, Y.-B. Wang, F. Zhao, T. Huang and W. Huang, RSC Adv., 2018, 8, 3250–3263 RSC.
- X. Sheng, H. Zhao and L. Du, Chemosphere, 2017, 186, 331–340 CrossRef CAS PubMed.
- X. Sheng, B. Wang, X. Song, C. A. Ngwenya, Y. Wang and H. Zhao, J. Phys. Chem. A, 2019, 123, 3876–3886 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- J. Ling, X. Ding, Z. Li and J. Yang, J. Phys. Chem. A, 2017, 121, 661–668 CrossRef CAS PubMed.
- H. R. Leverentz, J. I. Siepmann, D. G. Truhlar, V. Loukonen and H. Vehkamäki, J. Phys. Chem. A, 2013, 117, 3819–3825 CrossRef CAS PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC.
- J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- H. Zhang, W. Wang, S. Pi, L. Liu, H. Li, Y. Chen, Y. Zhang, X. Zhang and Z. Li, Chemosphere, 2018, 212, 504–512 CrossRef CAS PubMed.
- H. J. Zhang, O. Kupiainen-Maatta, X. H. Zhang, V. Molinero, Y. H. Zhang and Z. S. Li, J. Chem. Phys., 2017, 146, 184308–184319 CrossRef.
- A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS.
- I. K. Ortega, O. Kupiainen, T. Kurtén, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 225–235 CrossRef CAS.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurtén, M. Kulmala and H. Vehkamäki, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS.
- L. F. Shampine and M. W. Reichelt, SIAM J. Sci. Comput., 1997, 18, 1–22 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- J. J. P. Stewart, J. Comput.-Aided Mol. Des., 1990, 4, 1–105 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. e. a. Petersson, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- I. S. Bushmarinov, K. A. Lyssenko and M. Y. Antipin, Russ. Chem. Rev., 2009, 78, 283–302 CrossRef CAS.
- P. L. A. Popelier, J. Phys. Chem. A, 1998, 102, 1873–1878 CrossRef CAS.
- B. R. Bzdek, J. W. DePalma and M. V. Johnston, Acc. Chem. Res., 2017, 50, 1965–1975 CrossRef CAS PubMed.
- L. A. Curtiss and M. Blander, Chem. Rev., 1988, 88, 827–841 CrossRef CAS.
- H. Bardouki, H. Berresheim, M. Vrekoussis, J. Sciare, G. Kouvarakis, K. Oikonomou, J. Schneider and N. Mihalopoulos, Atmos. Chem. Phys., 2003, 3, 3869–3906 CrossRef.
- H. Berresheim, J. Geophys. Res., 2002, 107(D19), 8100 CrossRef.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics, John Wiley & Sons, Inc., New Jersey, 2006 Search PubMed.
- M. L. Dawson, M. E. Varner, V. Perraud, M. J. Ezell, R. B. Gerber and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18719–18724 CrossRef CAS PubMed.
- Y. M. Ji, H. H. Wang, Y. P. Gao, G. Y. Li and T. C. An, Atmos. Chem. Phys., 2013, 13, 11277–11286 CrossRef CAS.
- H. Zhao, Q. Zhang and L. Du, RSC Adv., 2016, 6, 71733–71743 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra08760e |
| This journal is © The Royal Society of Chemistry 2020 |