Open Access Article
Open Access ArticleInfluence of 4f filling on electronic and magnetic properties of rare earth-Au surface compounds†
L.
Fernandez
 ad,
M.
Blanco-Rey
ad,
M.
Blanco-Rey
 bc,
R.
Castrillo-Bodero
cd,
M.
Ilyn
cd,
K.
Ali
bc,
R.
Castrillo-Bodero
cd,
M.
Ilyn
cd,
K.
Ali
 cd,
E.
Turco
cd,
E.
Turco
 d,
M.
Corso
d,
M.
Corso
 cd,
M.
Ormaza
cd,
M.
Ormaza
 a,
P.
Gargiani
e,
M. A.
Valbuena
a,
P.
Gargiani
e,
M. A.
Valbuena
 fg,
A.
Mugarza
fg,
A.
Mugarza
 fh,
P.
Moras
fh,
P.
Moras
 i,
P. M.
Sheverdyaeva
i,
P. M.
Sheverdyaeva
 i,
Asish K.
Kundu
i,
Asish K.
Kundu
 i,
M.
Jugovac
i,
M.
Jugovac
 i,
C.
Laubschat
j,
J. E.
Ortega
i,
C.
Laubschat
j,
J. E.
Ortega
 ad and
F.
Schiller
ad and
F.
Schiller
 *cd
*cd
aUniversidad del País Vasco UPV-EHU, Dpto. Física Aplicada I, 20018 San Sebastián, Spain
bUniversidad del País Vasco UPV-EHU, Dpto. de Polímeros y Materiales Avanzados: Física, Química y Tecnología, 20018 San Sebastián, Spain
cDonostia International Physics Center, 20018 Donostia-San Sebastián, Spain. E-mail: frederikmichael.schiller@ehu.es
dCentro de Física de Materiales CSIC/UPV-EHU-Materials Physics Center, 20018 San Sebastián, Spain
eALBA Synchrotron Light Source, Carretera BP 1413 km 3.3, 08290 Cerdanyola del Vallès, Spain
fCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and The Barcelona Institute of Science and Technology, Campus UAB, Bellaterra, 08193 Barcelona, Spain
gIMDEA Nanociencia, 28049 Madrid, Spain
hInstitució Catalana de Recerca i Estudis Avançats (ICREA), 08070 Barcelona, Spain
iIstituto di Struttura della Materia, Consiglio Nazionale delle Ricerche, 34149 Trieste, Italy
jInstitut für Festkörper- und Materialphysik, Technische Universität Dresden, 01062 Dresden, Germany
First published on 21st October 2020
Abstract
One-atom-thick rare-earth/noble metal (RE-NM) compounds are attractive materials to investigate two-dimensional magnetism, since they are easy to synthesize into a common RE-NM2 structure with high crystal perfection. Here we perform a comparative study of the GdAu2, HoAu2, and YbAu2 monolayer compounds grown on Au(111). We find the same atomic lattice quality and moiré superlattice periodicity in the three cases, but different electronic properties and magnetism. The YbAu2 monolayer reveals the characteristic electronic signatures of a mixed-valence configuration in the Yb atom. In contrast, GdAu2 and HoAu2 show the trivalent character of the rare-earth and ferromagnetic transitions below 22 K. Yet, the GdAu2 monolayer has an in-plane magnetic easy-axis, versus the out-of-plane one in HoAu2. The electronic bands of the two trivalent compounds are very similar, while the divalent YbAu2 monolayer exhibits different band features. In the latter, a strong 4f–5d hybridization is manifested in neatly resolved avoided crossings near the Fermi level. First principles theory points to a residual presence of empty 4f states, explaining the fluctuating valence of Yb in the YbAu2 monolayer.
1. Introduction
Rare-earth/noble-metal (RE-NM) monolayer-thick alloys can be readily synthesized by low-temperature vapor epitaxy on the (111) surface of Cu, Ag, and Au single crystals, leading to a rich family of surface compounds.1–6 They all share a common, well-defined structure and excellent crystal quality with a RE-NM2 stoichiometry, as a well as a hexagonal moiré with a nanoscale periodicity that is induced by the lattice mismatch between the RE-NM2 monolayer and the noble metal substrate. This structural homogeneity among the series of lanthanides makes the RE-NM2 monolayer a convenient platform to tune spin textures and magnetic properties of great interest in the field of spintronics,7 while their chemical stability and moiré modulation convert these compounds into suitable magnetic templates to drive self-organized nanostructure growth.8–11 At a more fundamental level, the crystal perfection and identical structure of the RE-NM2 monolayer among the REs appear ideal to investigate the interplay between electronic properties and magnetism, that is, the connection between 4f shell filling, f–d hybridization, RE atom valency and magnetic response in two dimensions. This is of major interest in materials exhibiting competing magnetic and electronic phases around quantum critical points, such as heavy-fermion metals.12 In particular, the Ho case is of recent interest due to its high angular magnetic moment and its unconventional magnetic properties.13–16In the present work we carry out a comparative analysis of GdAu2, HoAu2 and YbAu2 monolayers epitaxially grown on a Au(111) surface. By means of angle resolved photoemission spectroscopy (ARPES) and density functional theory (DFT) we investigate the characteristic signatures of the band structure that define the valence state of the RE atom in the compound, whereas element-sensitive X-ray magnetic circular dichroism (XMCD) is used to probe the magnetic order and determine magnetic anisotropy. For Gd and Ho we find a trivalent electronic configuration in GdAu2 and HoAu2, respectively, and a clear ferromagnetic behavior. However, the magnetization axis is out-of-plane for Ho and in-plane for Gd, reflecting their respective 4f shell filling and orbital moment. YbAu2 behaves notably different. Yb is known to exhibit a variable valence state, ranging from Yb2+, e.g., in bulk Yb metal17 to Yb3+ in oxides,18via a fluctuating (or mixed) valence configuration in metal alloys.19–22 In the YbAu2/Au(111) monolayer system we find a mixed valence for Yb, close to divalency, which we attribute to f–d hybridization around the Fermi level EF.
2. Experimental and computational details
The different RE-Au2 surface compounds were grown in situ under ultra-high vacuum (p < 2 × 10−10 mbar) conditions by evaporation of small amounts of RE atoms on the Au(111) surface which was hold at a fixed temperature. The optimal growth temperature of the substrate varies between 400 and 450 °C for GdAu2, around 420 °C for HoAu2 and at 300 °C for YbAu2. Below these temperatures, the characteristic moiré was not well formed, and above them the RE metals diffuse into the bulk or re-evaporate under vacuum. Several Au(111) samples were used in order to avoid contamination from other RE atoms used in previous experiments.‡Preparation and analysis of the samples were performed in different experimental systems and laboratories. Photoemission data were acquired at two home laboratories (CFM San Sebastian, Universität Zürich) using Helium Iα and IIα excitation lines (hν = 21.2 eV and 40.8 eV, respectively), and at the VUV-Photoemission beamline of the Elettra Synchrotron in Trieste, Italy. In San Sebastian and Trieste a channel plate-based display type hemispherical analyzer was used with angular and energy resolution set to 0.1° and 40 meV, respectively, while in Zürich a hemispherical analyzer with six channeltrons was employed.23 At the synchrotron, p-polarized light was used and the sample temperature during measurements was 17 K. Scanning tunneling microscopy (STM) experiments were carried out at 300 K in San Sebastian using an Omicron VT Setup. XMCD experiments were realized at the BOREAS beamline of ALBA synchrotron, Spain. There, the samples were prepared in situ and their quality was checked with low energy electron diffraction (LEED) prior to the XMCD measurements. Absorption spectra were acquired in total electron yield at two beam-incidence geometries, namely out-of-plane for normal incidence and in-plane for 70° incidence. The applied magnetic field direction was collinear to the light propagation. In all cases 90% circularly polarized light from a helical undulator was used. The measurements were carried out between 2 and 25 K with a variable magnetic field up to ±6 T.
Band structures of free-standing YbAu2 monolayers and YbAu2/Au(111) stacks were obtained from first-principles DFT calculations with the PBE exchange and correlation functional.24 The FLEUR code,25 based on the full-potential linearized augmented plane wave (FLAPW) formalism,26,27 was used. Spin–orbit interactions were included self-consistently in the calculations with spins aligned perpendicular to the surface.28 The FLAPW basis set was constructed with a bidimensional 9 × 9 × 1 Monkhorst–Pack k-point mesh29 and plane wave expansion cutoffs of 109 eV for the wavefunctions, and 272 eV for the density and potential. For the local basis, Yb-6s,4f,5d and Au-6s,5d electrons were included as valence electrons, and Yb-5s,5p and Au-5p as linear orbitals. Muffin tin sphere radii of 1.35 Å were used for Yb and Au, and lmax = 10 in the partial wave expansions. The Fermi energy was determined by the triangular method. Additional calculations were carried out in the GGA+U approximation30–32 (see the ESI†). As in previous works with Gd-based compounds,3 we used the experimentally-determined lattice constant of the compound (5.4 Å) to fix the same in-plane atomic distance for the REAu2 monolayer and the REAu2/Au(111) slab. For YbAu2 on one or several Au substrate layers (supported YbAu2), results presented here correspond to vertical fcc stacking, using 2.25 Å interlayer distance. Yet, we also checked YbAu2/Au(111) with Yb atoms in top stacking, as well as small variations of the geometry parameters, but no significant changes were obtained.
3. Results and discussion
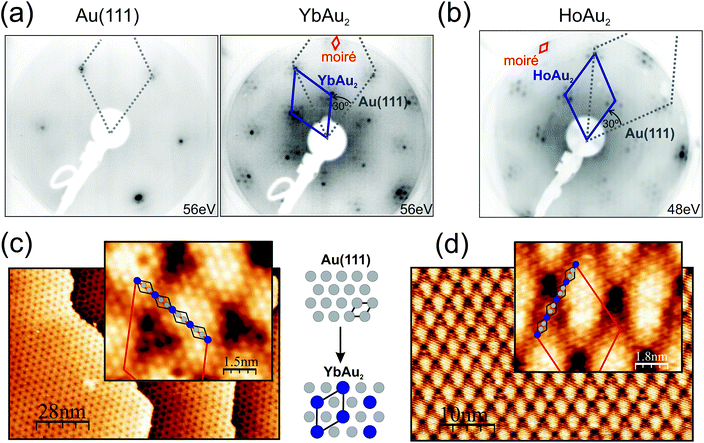
3.1. Structure
Representative low-energy electron diffraction patterns and scanning tunneling microscopy images for structurally-optimal HoAu2 and YbAu2 monolayers are shown in Fig. 1. The LEED images reveal the characteristic (√3 × √3)R30° reconstruction of the 2D RE-Au2 compounds (blue solid line unit-cell) formed on top of the Au(111) surface (grey, dotted) surrounded by hexagonal superstructure spots. Due to the larger ionic radius of the RE atom compared to that of the Au atom, the registry with the Au(111) plane underneath is lost, and a coincidence moiré lattice appears.1 The periodicity of this moiré reconstruction is visible in the LEED pattern through the characteristic satellite spots around the main (√3 × √3)R30° diffraction spots. The atomic misfit is also obvious when comparing the clean and the compound-covered surface patterns, as shown in Fig. 1(a), where the new atomic spacing of the surface is compared to that of Au(111).In STM micrographs two main features are observed, namely the atomically resolved lattice of the surface and the large scale moiré modulation rotated by 30° with respect to the atomic unit cell. Atomically resolved images reveal hexagonal close-packed structures with a = 5.4 Å periodic spacing between neighboring protrusions, which clearly indicates that only the RE sublattice is being probed by the STM tip under the present conditions.33 The same apparent atomic lattice is observed in the previously studied GdAu2, CeAu2, LaAu2, TbAu2, HoAu2 and ErAu2 monolayers.1,2,6,33 The moiré periodicities of YbAu2 and HoAu2 have been determined by averaging over large scale STM images such as those of Fig. 1(c) and (d), rendering (36.5 ± 1.0) Å and (37.6 ± 1.0) Å, respectively. The latter value coincides well with a recent study of HoAu2.6 Taking into account the interatomic distance in the Au(111) surface (aAu = 2.89 Å) one obtains a (12.6 × 12.6) coincidence lattice for YbAu2 and a slightly larger (13.0 × 13.0) lattice for HoAu2, the latter being equal to that found in GdAu2.1 The lattice constant a of the RE-Au2 surface lattice can be extracted from the RE-Au2/Au(111) (n − 1)/n coincidence through (n − 1) × a = n × √3aAu leading to a = 5.4 Å in HoAu2, YbAu2, and GdAu2 monolayers.1 Differences in the moiré periodicity, though, reflect subtle variations in the interatomic distance a of the compound, which cannot be accounted for within the STM accuracy. In this respect, the shorter beating period for the YbAu2 monolayer reveals a 0.3% larger in-plane interatomic spacing. This indeed is the simple expectation for the larger ionic radius of the divalent Yb. However, the effect is very small and may also arise due to other important factors, such as the out-of-plane relaxation of the RE sublattice,34 similar to that observed in Rashba type systems.35
3.2. Electronic properties
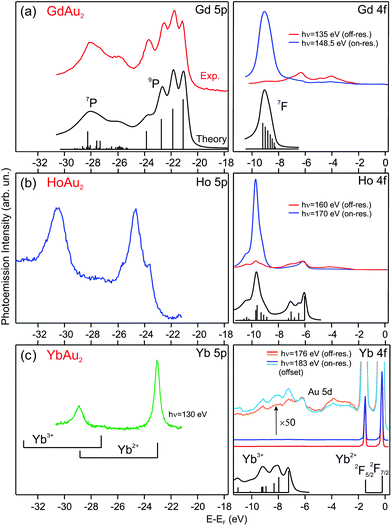 | ||
| Fig. 2 Photoemission spectra taken at T = 17 K of 5p and 4f rare-earth core levels for (a) GdAu2, (b) HoAu2, and (c) YbAu2 monolayers grown on Au(111). The valence state of the rare-earth atom can be determined by comparing with theoretically calculated multiplets, shown under the corresponding spectra (multiplet data reproduced from ref. 20 and 36–39). | ||
In the GdAu2 monolayer, Gd 4f and 5p levels are similar to the calculated and experimentally observed multiplet structures of trivalent Gd metal.38,39 The effect of alloying with Au in the surface compound can be directly assessed by comparison to the surface core level lines in the corresponding RE metal crystals, where RE atoms at the surface have the same atomic coordination (ninefold) but a Au environment within the surface plane. The trivalent Gd 4f and 5p lines of GdAu2 are shifted to higher binding energies by 0.6 eV and 0.7 eV, respectively, with respect to the corresponding surface core levels in metal Gd.43 For HoAu2 the situation is very similar. The Ho 4f multiplet reveals a trivalent character and it is shifted to a higher binding energy by 0.4 eV with respect to the surface component in metallic Ho.44
The valence state for Yb in YbAu2 is deduced by directly comparing the experimental spectrum with the theoretical di- and trivalent configurations of Yb, shown in the lower part of Fig. 2(c). In the surface compound, there is a dominant divalent Yb 4f emission near EF, although a zoom in the spectrum reveals the presence of trivalent Yb emission at a higher binding energy. An accurate determination of the trivalent contribution is difficult, since the trivalent multiplet overlaps with the Au 5d band. The Yb 5p core level, however, is better suited for a quantitative analysis. On- and off-resonant photoemission reveals a small, but well visible, trivalent 5p3/2 emission at 27.24 eV. This binding energy discards emission from bulk Yb impurities,20 and rather indicates a mixed valence scenario, with a dominant divalent state and a minor trivalent contribution (for a detailed discussion see the ESI†). X-ray photoemission is a fast femtosecond-range transition process, particularly when compared to the valence fluctuation time of rare-earth ions in mixed-valence systems.45 Such fluctuation time can be estimated from the valence band dispersion (see the ESI†). Therefore, the relative peak area of the two 5p doublets in Fig. 2(c) directly reflects an intermediate valence value ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 2.059 of the Yb valence in YbAu2.
= 2.059 of the Yb valence in YbAu2.
The Yb 5p and 4f core levels in YbAu2 are shifted to lower binding energies by 1.15 eV and 1.55 eV, respectively, compared with the corresponding surface core levels in metallic Yb.37 The positive shift of the core level in YbAu2 with respect to the corresponding divalent Yb surface contrasts with the negative shift in trivalent Gd and Ho emissions as shown above. The valency-dependent sign of the shift from the pure metal to compound in RE core levels was already observed for a variety of divalent and trivalent bulk RE-metal systems.37 The sign of the shift can be explained by the larger structural stability of the trivalent RE ion, versus divalent or tetravalent states, when forming bulk compounds.37,46 In this way, the trivalent-to-tetravalent core-level photoemission process of Gd and Ho leads to a negative peak shift, while the divalent-to-trivalent excitation in Yb results in a positive shift.
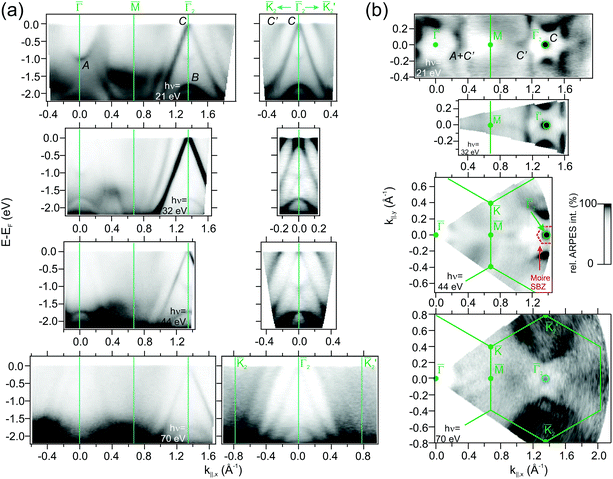
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) , where it strongly resonates at the HoAu2 surface. The GdAu2 valence band exhibits the same features,33 including the intense linearly-dispersing C band. Other RE-Au2 surface compounds such as LaAu2 and CeAu2 possess the same C band with a conic shape centered at
, where it strongly resonates at the HoAu2 surface. The GdAu2 valence band exhibits the same features,33 including the intense linearly-dispersing C band. Other RE-Au2 surface compounds such as LaAu2 and CeAu2 possess the same C band with a conic shape centered at ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) and apex at EF.2 In reality, as indicated in Fig. 4(a) and (b), REAu2 monolayers featuring trivalent RE atoms share an almost identical band structure, including the hole-like B and electron-like A bands, the latter found at −1.0 eV at the center of the Brillouin zone in all cases.2 Even the Fermi surface mappings shown in Fig. 3(b) are similar, showing a bright spot due to the C band apex, and a star-shaped feature around the
and apex at EF.2 In reality, as indicated in Fig. 4(a) and (b), REAu2 monolayers featuring trivalent RE atoms share an almost identical band structure, including the hole-like B and electron-like A bands, the latter found at −1.0 eV at the center of the Brillouin zone in all cases.2 Even the Fermi surface mappings shown in Fig. 3(b) are similar, showing a bright spot due to the C band apex, and a star-shaped feature around the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) points, originating from the A and C′ bands. In a recent study,51 this star-shaped feature was attributed to umklapp bands from the (√3 × √3) R30° surface superstructure replica of the strongly dispersive noble metal s,p band. However, the latter is a bulk band that disperses perpendicular to the surface in kz direction. This would give rise to different Fermi energy features at different photon energies,52–54 but this is not observed here (see Fig. 3 and the ESI†). Our theoretical analysis (see below) reveals that C′ has an intense Au s,p-band nature. We argue that the strong band hybridization with RE d-bands changes not only the band character of C′ but also alters the kz dispersion into a two-dimensional band. Additionally, one can also observe the umklapp bands due to the moiré superstructure. The moiré umklapp bands cause the “X”-like band crossing feature at E − EF = −1.2 eV located at the second
points, originating from the A and C′ bands. In a recent study,51 this star-shaped feature was attributed to umklapp bands from the (√3 × √3) R30° surface superstructure replica of the strongly dispersive noble metal s,p band. However, the latter is a bulk band that disperses perpendicular to the surface in kz direction. This would give rise to different Fermi energy features at different photon energies,52–54 but this is not observed here (see Fig. 3 and the ESI†). Our theoretical analysis (see below) reveals that C′ has an intense Au s,p-band nature. We argue that the strong band hybridization with RE d-bands changes not only the band character of C′ but also alters the kz dispersion into a two-dimensional band. Additionally, one can also observe the umklapp bands due to the moiré superstructure. The moiré umklapp bands cause the “X”-like band crossing feature at E − EF = −1.2 eV located at the second ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) -points of the surface Brillouin zones. A detailed discussion can be found in the ESI.†
-points of the surface Brillouin zones. A detailed discussion can be found in the ESI.†
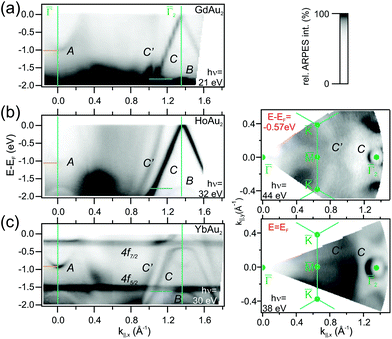
For divalent Yb in YbAu2, the narrow 4f bands shows up right below EF (4f7/2) and at E − EF = −1.5 eV (4f5/2), giving rise to relatively flat bands. Especially the 4f7/2 level strongly hybridizes with the C band, leading to a large disruption of its linear dispersion around the Fermi energy. This additionally affects the Fermi surface around ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) in Fig. 4, which evolves from an intense spot in trivalent HoAu2 [see Fig. 3(b)] to a ring-shaped structure in divalent YbAu2. Also the Au bulk-resonating s,p band (C′) reveals band hybridization and an upward shift. The latter can be nicely observed by comparing the band crossings at the Fermi energy in YbAu2 and the constant energy surface at E − EF = −0.57 eV of HoAu2 featuring similar structures. Valency-dependent differences in the electronic states of REAu2 monolayer systems, from trivalent Gd, La, Ce, and Ho, to divalent Yb, are also found in A and B bands, which exhibit upward shifts of 0.11 and 0.15 eV, respectively, from trivalent compounds to divalent Yb.
in Fig. 4, which evolves from an intense spot in trivalent HoAu2 [see Fig. 3(b)] to a ring-shaped structure in divalent YbAu2. Also the Au bulk-resonating s,p band (C′) reveals band hybridization and an upward shift. The latter can be nicely observed by comparing the band crossings at the Fermi energy in YbAu2 and the constant energy surface at E − EF = −0.57 eV of HoAu2 featuring similar structures. Valency-dependent differences in the electronic states of REAu2 monolayer systems, from trivalent Gd, La, Ce, and Ho, to divalent Yb, are also found in A and B bands, which exhibit upward shifts of 0.11 and 0.15 eV, respectively, from trivalent compounds to divalent Yb.
The hybridization of 4f levels with the s–p–d valence-band many fold has often been observed in three-dimensional bulk Ce, Eu and Yb compounds.55,56 Orbital mixing with 4f levels at the valence band gives rise to an intermediate fluctuating valence in RE materials,45 which in turn is essential to trigger competing magnetic phases around quantum-critical points.57 In Fig. 5 we examine in detail the 4f level hybridization for the two-dimensional YbAu2 compound, comparing ARPES and first principles calculations. In panel (a) we show the YbAu2 ARPES band dispersion along the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif)
![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif)
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) 2 and
2 and ![[K with combining macron]](https://www.rsc.org/images/entities/char_004b_0304.gif) 2
2![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) 2
2![[K with combining macron]](https://www.rsc.org/images/entities/char_004b_0304.gif) 2′ symmetry lines, on top of the corresponding calculations for a YbAu2/3ML-Au(111) slab [(b) panel]. To better determine the surface or bulk nature of the different bands, in panel (c) we show their evolution from the free-standing YbAu2 monolayer, to the YbAu2/1ML-Au(111) and YbAu2/3ML-Au(111) stacks. In the free standing case, one observes the conic C band dispersing from about 0.7 eV above EF at
2′ symmetry lines, on top of the corresponding calculations for a YbAu2/3ML-Au(111) slab [(b) panel]. To better determine the surface or bulk nature of the different bands, in panel (c) we show their evolution from the free-standing YbAu2 monolayer, to the YbAu2/1ML-Au(111) and YbAu2/3ML-Au(111) stacks. In the free standing case, one observes the conic C band dispersing from about 0.7 eV above EF at ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) down to −2 eV at
down to −2 eV at ![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) and
and ![[K with combining macron]](https://www.rsc.org/images/entities/char_004b_0304.gif) . This C band is intercepted by the flat Yb 4f levels. As the number of gold layers in the stack increases, the f levels slightly shift towards EF while the C band shifts downward, spin–orbit splitting sets in, and the more bulk-like C′ band builds up. In fact, the C′ band is significantly contributed by Gd-d electrons, sharing with C a partial s,px,y–dx,y mixed orbital nature, but the occupied part of C lies inside the Au bulk projected band gap and resonates stronger at the YbAu2 surface.§ Additionally, C and C′ mix with the spin–orbit split 4f levels at about −0.25 eV, leading to a clear opening of hybridization gaps (see the discussion on the d and f composition of these hybrid bands in the ESI†). The relative contribution of the 4f levels to the different bands is graphically indicated with a color scale in Fig. 5. The upward shift of the 4f spectral weight leads to a small but relevant 4f spread above EF, thereby explaining the occurrence of mixed valence. It is interesting to note that the DFT approach is enough to properly describe experimental binding energies and anticrossing features,58 even though, at the present theory level, one cannot account for simultaneous divalent and trivalent 4f multiplets in the valence band (for DFT band structures including correlation, which causes renormalization and an increase in bandwidth,59 see the ESI†).
. This C band is intercepted by the flat Yb 4f levels. As the number of gold layers in the stack increases, the f levels slightly shift towards EF while the C band shifts downward, spin–orbit splitting sets in, and the more bulk-like C′ band builds up. In fact, the C′ band is significantly contributed by Gd-d electrons, sharing with C a partial s,px,y–dx,y mixed orbital nature, but the occupied part of C lies inside the Au bulk projected band gap and resonates stronger at the YbAu2 surface.§ Additionally, C and C′ mix with the spin–orbit split 4f levels at about −0.25 eV, leading to a clear opening of hybridization gaps (see the discussion on the d and f composition of these hybrid bands in the ESI†). The relative contribution of the 4f levels to the different bands is graphically indicated with a color scale in Fig. 5. The upward shift of the 4f spectral weight leads to a small but relevant 4f spread above EF, thereby explaining the occurrence of mixed valence. It is interesting to note that the DFT approach is enough to properly describe experimental binding energies and anticrossing features,58 even though, at the present theory level, one cannot account for simultaneous divalent and trivalent 4f multiplets in the valence band (for DFT band structures including correlation, which causes renormalization and an increase in bandwidth,59 see the ESI†).
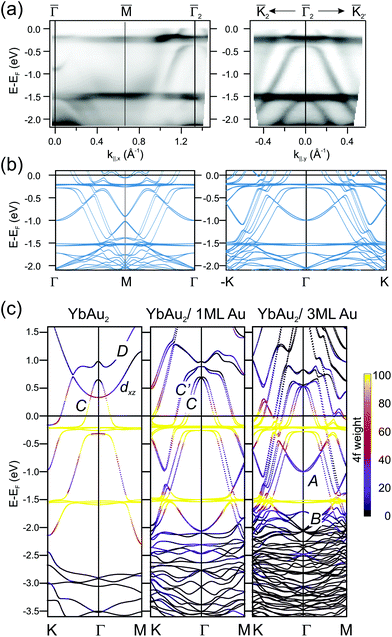 | ||
Fig. 5 (a) ARPES band dispersions for the YbAu2 monolayer compound measured along the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) ![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) 2 and 2 and ![[K with combining macron]](https://www.rsc.org/images/entities/char_004b_0304.gif) 2 2![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/char_e0ba.gif) 2 2![[K with combining macron]](https://www.rsc.org/images/entities/char_004b_0304.gif) 2′ symmetry directions of the surface Brillouin zone (hν = 38 eV, T = 17 K). (b) Corresponding DFT band structure calculated for a YbAu2/3ML-Au(111) slab. Spin–orbit interactions with spins aligned perpendicular to the surface are included. (c) DFT band structure for a free-standing YbAu2 monolayer (left), a YbAu2/1ML-Au(111) bilayer (center), and the YbAu2/3ML-Au(111) stack (right). The 4f composition of each E(k) point is indicated by the violet-to-yellow color scale. Bands are named following ref. 2 and 33. 2′ symmetry directions of the surface Brillouin zone (hν = 38 eV, T = 17 K). (b) Corresponding DFT band structure calculated for a YbAu2/3ML-Au(111) slab. Spin–orbit interactions with spins aligned perpendicular to the surface are included. (c) DFT band structure for a free-standing YbAu2 monolayer (left), a YbAu2/1ML-Au(111) bilayer (center), and the YbAu2/3ML-Au(111) stack (right). The 4f composition of each E(k) point is indicated by the violet-to-yellow color scale. Bands are named following ref. 2 and 33. | ||
On the other hand, bands A and B, which only emerge with the thickest Au slab, also interact with the 4f levels, although such interaction is not clearly resolved in the ARPES experiment. Finally, we must also note the presence of the D and the upward dispersing band of dxz character. The last one crosses C without hybridizing (orthogonal to C) in the free standing case. The D band has mainly dx2−y2 character and hybridizes with the states at the apex of the C band of dxy character forming a gapped region close to the Γ point at around EF + 0.7 eV (details on the orbital character can be found in the ESI†). In terms of orbital character, the aforementioned band crossing features are ubiquitous in RE-Au2 layers and give rise to the magnetic and topological properties of these systems. However, the dispersion details and binding energies differ for different compounds and some of such characteristic features are likely to disappear upon hybridization with substrate bands. For example, in the GdAg2/Ag(111) system the spin–split pair of D bands straddle the Fermi energy, contributing to the ferromagnetic order at high temperature (TC = 85 K),3 and resulting in several degeneracies that have been reported to be Weyl nodal lines.60 We recall that Weyl points are massless Dirac fermions that appear in pairs of opposite parity, protected by the lattice translational symmetry. Additional mirror symmetry can stabilize Weyl points in a two-dimensional system,61 as it has been reported for GdAg2, where band degeneracies of this type appear close to the Fermi level not as discrete points, but forming a line, so-called Weyl nodal line.60 In GdAg2 and ErCu2 the upward-dispersing spin-majority dxz band and the downward-dispersing spin-minority C mutually cross near the Fermi level, defining topologically protected Weyl nodal lines.5,60 Furthermore, the gap formed at the crossing of C and D bands with opposite spin polarization in GdAg2 is stable even against a reorientation of the magnetization from in-plane to out-of-plane.60 Note, however, that the equivalent feature in the YbAu2 layer is strongly distorted by the much larger spin–orbit interaction strength. As mentioned above, the nodal line associated with this C–D crossing in the free-standing YbAu2 case would be a ring near the Γ-point well above the Fermi level EF + 0.7 eV due to the divalent Yb, with a large energy gap of 0.2 eV [see Fig. 5(c)]. ARPES is not suited to probe empty electronic states and we are therefore unable to confirm such theoretical prediction. For the GdAu2 case DFT calculations revealed that the nodal line is at 0.3 eV below the Fermi level.3 The C–D band crossing has a band gap of nearly 0.1 eV with in-plane magnetization, but a marginal one with out-of-plane magnetization, in agreement with the prediction based on the orbital symmetries of these two bands.62 Because of the Fermi level proximity and the small size of the band gap, this feature is not distinguishable by ARPES.
3.3. Magnetic configuration
Rare-earth metals and alloys exhibit diverse magnetic properties across the RE series, explained by the strong effect of the variable 4f shell filling. When combining RE with noble metals long range magnetic ordering was observed for GdAu2,8,64 GdAg2,3 and DyAg2.51 For completely divalent Yb compounds with a filled 4f shell no magnetic moments from that 4f shell can arise, e.g., the pure hcp Yb metal (divalent) is diamagnetic at least down to 1 K.65 We therefore do not expect magnetic ordering in the accessible temperature range (T > 4 K) for YbAu2, although here Yb is in a mixed-valent state.In the following, we will concentrate on the magnetic properties and magnetic anisotropy of HoAu2 measured by X-ray absorption (XAS) and magnetic circular dichroism (XMCD) and compare the results to the magnetic properties observed in GdAu2. To shortly summarize, GdAu2 is a two-dimensional, soft ferromagnetic system with a Curie temperature TC = 19 K, and an in-plane easy magnetization axis.3,8 DFT calculations3,64 and low temperature STM measurements at applied fields64 reveal that the long-range order arises from the polarization of both Gd and Au derived valence electrons by the localized Gd 4f moments via a RKKY-type interaction. The coercive field Hc in GdAu2 is small ranging from 2 mT (ref. 3) to 17.5 mT (ref. 64) depending on the number of defects like dislocation lines at the surface.
For the HoAu2 monolayer case XAS and XMCD spectra are shown in Fig. 6. The XAS line shape in Fig. 6(a) confirms a trivalent Ho 4f10 configuration66 already observed by photoemission. There are remarkable differences between normal and grazing incidence geometries. The dichroism is larger at normal incidence indicating an out-of-plane easy axis, which is corroborated in the XMCD magnetization loops displayed in Fig. 6(b). In the XAS spectra, both, M4 and M5 absorption edges (3d → 4f) display the same sign of the dichroism in the two different geometries with the magnetic field and X-ray incidence perpendicular (θ = 0°) and nearly parallel (θ = 70°) to the surface. Such a situation is expected for late lanthanides (4fn, n > 7). These late lanthanides are characterized by a large magnetic moment arising from the parallel alignment of the orbital L and spin S components leading to the total angular momentum J = L + S. The expectation values of the orbital and spin magnetic moments components on the magnetization axis z, 〈Lz〉 and 〈Sz〉, respectively, can be obtained from sum rules analysis of the integrated XAS and XMCD spectra (see ESI†) and are given in Table 1. For the sake of comparison we also include literature values of single Ho atoms on top of fcc (111) surfaces of noble metals Cu, Ag, and Pt.14,15 The paramagnetic-to-ferromagnetic transition in HoAu2 is tracked from the series of out-of-plane magnetization loops at different temperatures shown in the right panel of Fig. 6(b). An Arrott plot analysis of these magnetization curves3,63 leads to a Curie temperature TC = 22 K (see details in the ESI†).
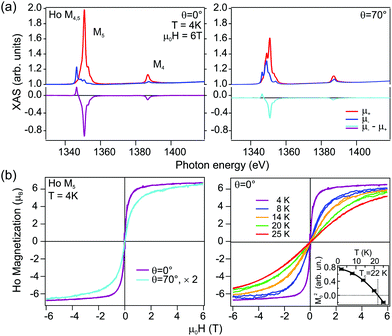 | ||
| Fig. 6 (a) X-ray Magnetic Circular Dichroism (XMCD) in absorption spectra measured at the Ho M4,5 edge in normal (θ = 0°, left) and grazing beam incidence (θ = 70°, right). (b) Magnetization curves acquired at the M5 edge at different incidence geometries (left), and at normal incidence with variable temperature (right). The dependence on the incidence angle reveals ferromagnetic behavior with out-of-plane easy axis. The Arrott plot analysis3,63 of the magnetization curves at different temperatures renders the Curie temperature TC = 22 K (inset). | ||
| System | 〈Lz〉NI | 〈Sz〉NI | 〈Jz〉NI | 〈Lz〉GI | 〈Sz〉GI | 〈Jz〉GI |
|---|---|---|---|---|---|---|
| HoAu2 | (5.26 ± 0.15) | (1.52 ± 0.12) | (6.78 ± 0.19) | (2.62 ± 0.10) | (0.76 ± 0.08) | (3.38 ± 0.13) |
| Ho/Cu(111)14,15 | (5.3 ± 0.2) | (1.7 ± 0.1) | (6.9 ± 0.2) | (3.8 ± 0.1) | (1.1 ± 0.1) | (4.9 ± 0.1) |
| Ho/Ag(111)15 | (5.2 ± 0.1) | (1.2 ± 0.2) | (6.5 ± 0.2) | (4.8 ± 0.1) | (1.2 ± 0.1) | (6.0 ± 0.1) |
| Ho/Pt(111)14,15 | (4.3 ± 0.1) | (1.3 ± 0.1) | (5.5 ± 0.1) | (3.8 ± 0.1) | (1.3 ± 0.1) | (5.1 ± 0.1) |
For the ideal Ho3+ ion with a 4f10 configuration, Hund's rule predicts orbital and spin moments of L = 6 and S = 2, respectively, resulting in a total angular moment J = 8 and oblate form of the 4f charge distribution when the Jz value is maximal.67,68 We observe a normal incidence (NI) ground state value along the field direction z of 〈Jz〉NI = 6.78 for the HoAu2 surface compound (see Table 1), which is very similar to the values measured in Ho single adatoms on Cu(111)14 and Ag(111) surfaces15 but different from the Ho/Pt(111) case.14 For Ho/Cu(111) and Ho/Ag(111) the Ho 4f electron charge density distribution is barely influenced by hybridization with substrate bands formed by delocalized s electrons. Thus, neither the form of the 4f electron charge distribution density, nor the lowest J ground state, is affected. In the case of the HoAu2 monolayer, trivalent Ho atoms embedded in the Au surface have a similar environment as Ho adatoms on Ag(111) and Cu(111) surfaces. As can be observed in Table 1, there is, however, a difference in the grazing incidence (in-plane) value of the surface compound, whose magnetic moments are much lower. This difference is related to the measurement geometry that in the actual HoAu2 case was for more grazing incidence (θ = 70°) than in the adatom cases (θ = 60°).
The out-of-plane easy-axis anisotropy of HoAu2 monolayer contrasts with the in-plane one of GdAu2.8 The main contribution to the magnetic anisotropy in both surface compounds has a different nature that is directly related to the RE 4f occupation and its angular momentum. Trivalent Gd3+ ions have a half-filled 4f7 shell with L = 0 and therefore have a completely isotropic (spherical) 4f electron charge distribution. In this case the main contribution to the magnetocrystalline anisotropy of GdAu2 arises from the hybrid Au–Gd bands and results in a magnetocrystalline anisotropy energy of about 2.7 meV.8 Certainly, in-plane shape anisotropy is also present, but its contribution is minor with an approximate value of 0.05 meV (see the ESI†). In the case of HoAu2, however, the anisotropy originates at the 4f electrons, as suggested by the large L. The observed out-of plane anisotropy may be explained in simple terms by the spatial distribution of the 4f electron cloud. As already mentioned, for a free trivalent Ho3+ ion with a 4f10 configuration the 4f electron density has an oblate shape with the highest Jz level. Additionally, the electrostatic interaction with the Au substrate electron density would favour out-of-plane anisotropy, while the equatorially distributed charge density within the HoAu2 layer would favour in-plane anisotropy.14 All together, the substrate, HoAu2 layer charges and the oblate form of the 4f cloud at high Jz favour out-of-plane anisotropy68–70 as observed by the sum rule result JNIz ≫ JGIz (see Table 1).
4. Conclusions
HoAu2 and YbAu2 monolayer compounds have been synthesized by vapor deposition onto Au(111), and analyzed with surface science techniques and DFT calculations. The resulting structural, electronic and magnetic properties have been compared with those of the GdAu2/Au(111). In all cases we find a (√3 × √3) R30° RE substitution in the topmost Au(111) crystal layer, which triggers analogous nanoscale moiré superstructures, due to mismatch with the underlying substrate. Through X-ray photoemission of valence and core levels we determine a trivalent state for Gd and Ho, and a mixed-valence situation of Yb in YbAu2. Electronic band structures are nearly equivalent for the three surface compounds, with the exception of their characteristic conic C band near EF, which strongly hybridizes with the 4f level in YbAu2. DFT indicates that such f–d hybridization results in a small depletion of the Yb 4f shell in YbAu2, which appears to explain its mixed valence character. Moreover, XMCD experiments reveal a ferromagnetic ordering in HoAu2 with an out-of-plane anisotropy below TC = 22 K. The origin of the out-of-plane anisotropy in HoAu2 is mainly magnetocrystalline due to the strong spin–orbit coupling interaction of the 4f electrons in Ho and their electrostatic interaction with the surrounding charge.Author contributions
L. F. and F. S. conceived and designed the work. L. F., R. C.-B., K. A., E. T., M. C., M. O., P. M., P. M. S., A. K. K., M. J. and F. S. carried out photoemission data collection while the data were analyzed and interpreted by P. M. S., M. O., C. L., E. O. and F. S. X-ray absorption and XMCD data collection were undertaken by L. F., R. C.-B., M. I., P. G., M. A. V., A. M., and F. S. The DFT calculations were performed by M. B.-R. The analysis of these data was carried out by F. S. and the results were interpreted by L. F., M. B.-R., A. M., E. O. and F. S. The article was drafted by L. F., M. B.-R., E. O. and F. S. All authors contributed in the critical revision of the article and its final approval.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the Spanish MINECO (MAT-2017-88374-P, MAT2016-78293-C6, FIS2016-75862-P, PGC2018-098613-B-C21, SEV-2017-0706 and SEV-2016-0686), the Spanish Research Agency (PID2019-107338RB-C65), Basque Government Project IT-1255-19, and University of the Basque Country (UPV/EHU) grant GIU18/138 and the European Regional Development Fund (ERDF) under the program Interreg V-A España-Francia-Andorra (Contract No. EFA 194/16 TNSI). The experiments at Elettra were supported by the EU Calipso project and computational resources were provided by the DIPC computing center. L. F. acknowledges financial support from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement MagicFACE No 797109. A. K. K., M. J., P. M. S. and P. M. acknowledge the project EUROFEL-ROADMAP ESFRI. We furthermore want to thank Prof. T. Greber from the University of Zürich to enable us to use the ARPES spectrometer for the constant energy and Fermi surface measurements.References
- M. Corso, L. Fernández, F. Schiller and J. E. Ortega, ACS Nano, 2010, 4, 1603–1611 CrossRef CAS.
- M. Ormaza, L. Fernández, S. Lafuente, M. Corso, F. Schiller, B. Xu, M. Diakhate, M. J. Verstraete and J. E. Ortega, Phys. Rev. B: Condens. Matter, 2013, 88, 125405 CrossRef.
- M. Ormaza, L. Fernández, M. Ilyn, A. Magaña, B. Xu, M. J. Verstraete, M. Gastaldo, M. A. Valbuena, P. Gargiani, A. Mugarza, A. Ayuela, L. Vitali, M. Blanco-Rey, F. Schiller and J. E. Ortega, Nano Lett., 2016, 16, 4230–4235 CrossRef CAS.
- A. Correa, B. Xu, M. J. Verstraete and L. Vitali, Nanoscale, 2016, 8, 19148–19153 RSC.
- C. Xu, K. Bao, Y. Que, Y. Zhuang, X. Shao, K. Wang, J. Zhu and X. Xiao, Phys. Chem. Chem. Phys., 2020, 22, 1693–1700 RSC.
- Y. Que, Y. Zhuang, Z. Liu, C. Xu, B. Liu, K. Wang, S. Du and X. Xiao, J. Phys. Chem. Lett., 2020, 11, 4107–4112 CrossRef CAS.
- M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502 CrossRef CAS.
- L. Fernández, M. Blanco-Rey, M. Ilyn, L. Vitali, A. Magaña, A. Correa, P. Ohresser, J. E. Ortega, A. Ayuela and F. Schiller, Nano Lett., 2014, 14, 2977–2981 CrossRef.
- L. Fernández, M. Corso, F. Schiller, M. Ilyn, M. Holder and J. E. Ortega, Appl. Phys. Lett., 2010, 96, 013107 CrossRef.
- A. Cavallin, L. Fernández, M. Ilyn, A. Magaña, M. Ormaza, M. Matena, L. Vitali, J. E. Ortega, C. Grazioli, P. Ohresser, S. Rusponi, H. Brune and F. Schiller, Phys. Rev. B: Condens. Matter, 2014, 90, 235419 CrossRef.
- L. Fernández, M. Ilyn, A. Magaña, L. Vitali, J. E. Ortega and F. Schiller, Adv. Sci., 2016, 3, 1600187 CrossRef.
- Q. Si and F. Steglich, Science, 2010, 329, 1161–1166 CrossRef CAS.
- T. Miyamachi, T. Schuh, T. Märkl, C. Bresch, T. Balashov, A. Stöhr, C. Karlewski, S. André, M. Marthaler, M. Hoffmann, M. Geilhufe, S. Ostanin, W. Hergert, I. Mertig, G. Schön, A. Ernst and W. Wulfhekel, Nature, 2013, 503, 1476–4687 CrossRef.
- F. Donati, A. Singha, S. Stepanow, C. Wäckerlin, J. Dreiser, P. Gambardella, S. Rusponi and H. Brune, Phys. Rev. Lett., 2014, 113, 237201 CrossRef CAS.
- A. Singha, R. Baltic, F. Donati, C. Wäckerlin, J. Dreiser, L. Persichetti, S. Stepanow, P. Gambardella, S. Rusponi and H. Brune, Phys. Rev. B, 2017, 96, 224418 CrossRef.
- F. Donati, S. Rusponi, S. Stepanow, L. Persichetti, A. Singha, D. M. Juraschek, C. Wäckerlin, R. Baltic, M. Pivetta, K. Diller, C. Nistor, J. Dreiser, K. Kummer, E. Velez-Fort, N. A. Spaldin, H. Brune and P. Gambardella, Phys. Rev. Lett., 2020, 124, 077204 CrossRef CAS.
- W.-D. Schneider, C. Laubschat and B. Reihl, Phys. Rev. B: Condens. Matter, 1983, 27, 6538–6541 CrossRef CAS.
- G. Kaindl, G. Kalkowski, W. D. Brewer, B. Perscheid and F. Holtzberg, J. Appl. Phys., 1984, 55, 1910–1915 CrossRef CAS.
- R. Pöttgen, D. Johrendt and D. Kußmann, Structure-property relations of ternary equiatomic YbTX intermetallics, Elsevier, 2001, ch. 207, vol. 32, pp. 453–513 Search PubMed.
- G. K. Wertheim, J. H. Wernick and G. Crecelius, Phys. Rev. B: Condens. Matter, 1978, 18, 875–879 CrossRef CAS.
- S. Chatterjee, J. P. Ruf, H. I. Wei, K. D. Finkelstein, D. G. Schlom and K. M. Shen, Nat. Commun., 2017, 8, 2041 CrossRef.
- D. V. Vyalikh, S. Danzenbächer, Y. Kucherenko, C. Krellner, C. Geibel, C. Laubschat, M. Shi, L. Patthey, R. Follath and S. L. Molodtsov, Phys. Rev. Lett., 2009, 103, 137601 CrossRef CAS.
- T. Greber, O. Raetzo, T. J. Kreutz, P. Schwaller, W. Deichmann, E. Wetli and J. Osterwalder, Rev. Sci. Instrum., 1997, 68, 4549–4554 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- FLEUR: http://www.flapw.de.
- H. Krakauer, M. Posternak and A. J. Freeman, Phys. Rev. B: Condens. Matter, 1979, 19, 1706–1719 CrossRef CAS.
- E. Wimmer, H. Krakauer, M. Weinert and A. J. Freeman, Phys. Rev. B: Condens. Matter, 1981, 24, 864 CrossRef CAS.
- C. Li, A. J. Freeman, H. J. F. Jansen and C. L. Fu, Phys. Rev. B: Condens. Matter, 1990, 42, 5433 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter, 1976, 13, 5188 CrossRef.
- V. I. Anisimov, F. Aryasetiawan and A. I. Liechtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef CAS.
- A. B. Shick, A. I. Liechtenstein and W. E. Pickett, Phys. Rev. B: Condens. Matter, 1999, 60, 10763 CrossRef CAS.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyzyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter, 1993, 48, 16929 CrossRef CAS.
- M. Corso, M. J. Verstraete, F. Schiller, M. Ormaza, L. Fernández, T. Greber, M. Torrent, A. Rubio and J. E. Ortega, Phys. Rev. Lett., 2010, 105, 016101 CrossRef CAS.
- A. Correa, M. F. Camellone, A. Barragan, A. Kumar, C. Cepek, M. Pedio, S. Fabris and L. Vitali, Nanoscale, 2017, 9, 17342–17348 RSC.
- I. Gierz, B. Stadtmüller, J. Vuorinen, M. Lindroos, F. Meier, J. H. Dil, K. Kern and C. R. Ast, Phys. Rev. B: Condens. Matter, 2010, 81, 245430 CrossRef.
- F. Gerken, J. Phys. F: Met. Phys., 1983, 13, 703–713 CrossRef CAS.
- C. Laubschat, G. Kaindl, W.-D. Schneider, B. Reihl and N. Mårtensson, Phys. Rev. B: Condens. Matter, 1986, 33, 6675–6683 CrossRef CAS.
- W. J. Lademan, A. K. See, L. E. Klebanoff and G. van der Laan, Phys. Rev. B: Condens. Matter, 1996, 54, 17191–17198 CrossRef CAS.
- G. van der Laan, E. Arenholz, E. Navas, Z. Hu, E. Mentz, A. Bauer and G. Kaindl, Phys. Rev. B: Condens. Matter, 1997, 56, 3244–3250 CrossRef CAS.
- S. R. Mishra, T. R. Cummins, G. D. Waddill, W. J. Gammon, G. van der Laan, K. W. Goodman and J. G. Tobin, Phys. Rev. Lett., 1998, 81, 1306–1309 CrossRef CAS.
- P. A. Cox, J. K. Lang and Y. Baer, J. Phys. F: Met. Phys., 1981, 11, 113–119 CrossRef CAS.
- B. T. Thole, X. D. Wang, B. N. Harmon, D. Li and P. A. Dowben, Phys. Rev. B: Condens. Matter, 1993, 47, 9098–9101 CrossRef CAS.
- G. A. Mulhollan, K. Garrison and J. L. Erskine, Phys. Rev. Lett., 1992, 69, 3240–3243 CrossRef CAS.
- G. Kaindl, A. Höhr, E. Weschke, S. Vandré, C. Schüßler-Langeheine and C. Laubschat, Phys. Rev. B: Condens. Matter, 1995, 51, 7920–7923 CrossRef CAS.
- J. M. Lawrence, P. S. Riseborough and R. D. Parks, Rep. Prog. Phys., 1981, 44, 1–84 CrossRef.
- B. Johansson, Phys. Rev. B: Condens. Matter, 1979, 19, 6615 CrossRef CAS.
- M. Abadía, M. Ilyn, I. Piquero-Zulaica, P. Gargiani, C. Rogero, J. E. Ortega and J. Brede, ACS Nano, 2017, 11, 12392–12401 CrossRef.
- F. Reinert, G. Nicolay, S. Schmidt, D. Ehm and S. Hüfner, Phys. Rev. B: Condens. Matter, 2001, 63, 115415 CrossRef.
- S. A. Lindgren and L. Walldén, Solid State Commun., 1978, 28, 283–286 CrossRef CAS.
- F. Schiller, M. Corso, M. Urdanpilleta, T. Ohta, A. Bostwick, J. L. McChesney, E. Rotenberg and J. E. Ortega, Phys. Rev. B: Condens. Matter, 2008, 77, 153410 CrossRef.
- J. Knippertz, P. M. Buhl, S. Mousavion, B. Dupé, E. S. Walther, K. Medjanik, D. Vasilyev, S. Babenkov, M. Ellguth, M. Maniraj, J. Sinova, G. Schönhense, H.-J. Elmers, M. Aeschlimann and B. Stadtmüller, Exchange Splitting of a Hybrid Surface State and Ferromagnetic Order in a 2D Surface Alloy, 2019, arXiv:1906.03780 Search PubMed.
- P. Aebi, J. Osterwalder, R. Fasel, D. Naumović and L. Schlapbach, Surf. Sci., 1994, 307–309, 917–921 CrossRef CAS.
- A. Stampfl, J. Foo, R. Leckey, J. Riley, R. Denecke and L. Ley, Surf. Sci., 1995, 331–333, 1272–1276 CrossRef CAS.
- J. Osterwalder, Surf. Rev. Lett., 1997, 04, 391–408 CrossRef CAS.
- S. Danzenbächer, D. V. Vyalikh, Y. Kucherenko, A. Kade, C. Laubschat, N. Caroca-Canales, C. Krellner, C. Geibel, A. V. Fedorov, D. S. Dessau, R. Follath, W. Eberhardt and S. L. Molodtsov, Phys. Rev. Lett., 2009, 102, 026403 CrossRef.
- S. Danzenbächer, D. V. Vyalikh, K. Kummer, C. Krellner, M. Holder, M. Höppner, Y. Kucherenko, C. Geibel, M. Shi, L. Patthey, S. L. Molodtsov and C. Laubschat, Phys. Rev. Lett., 2011, 107, 267601 CrossRef.
- Z. Hossain, C. Geibel, N. Senthilkumaran, M. Deppe, M. Baenitz, F. Schiller and S. L. Molodtsov, Phys. Rev. B: Condens. Matter, 2004, 69, 014422 CrossRef.
- M. Matsunami, T. Hajiri, H. Miyazaki, M. Kosaka and S. Kimura, Phys. Rev. B: Condens. Matter, 2013, 87, 165141 CrossRef.
- H. Schweitzer and G. Czycholl, J. Magn. Magn. Mater., 1988, 76–77, 77–79 CrossRef.
- B. Feng, R.-W. Zhang, Y. Feng, B. Fu, S. Wu, K. Miyamoto, S. He, L. Chen, K. Wu, K. Shimada, T. Okuda and Y. Yao, Phys. Rev. Lett., 2019, 123, 116401 CrossRef CAS.
- S. Nie, H. Weng and F. B. Prinz, Phys. Rev. B, 2019, 99, 035125 CrossRef CAS.
- E. Abate and M. Asdente, Phys. Rev., 1965, 140, A1303–A1308 CrossRef.
- A. Arrott, Phys. Rev., 1957, 108, 1394–1396 CrossRef CAS.
- M. Bazarnik, M. Abadia, J. Brede, M. Hermanowicz, E. Sierda, M. Elsebach, T. Hänke and R. Wiesendanger, Phys. Rev. B, 2019, 99, 174419 CrossRef CAS.
- E. Bucher, P. H. Schmidt, A. Jayaraman, K. Andres, J. P. Maita, K. Nassau and P. D. Dernier, Phys. Rev. B: Condens. Matter, 1970, 2, 3911–3917 CrossRef.
- B. T. Thole, G. van der Laan, J. C. Fuggle, G. A. Sawatzky, R. C. Karnatak and J.-M. Esteva, Phys. Rev. B: Condens. Matter, 1985, 32, 5107–5118 CrossRef CAS.
- J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer, Berlin, Heidelberg, 2015 Search PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- D. Givord, Europhys. News, 1987, 18, 93–96 CrossRef CAS.
- R. Skomski and D. Sellmyer, J. Rare Earths, 2009, 27, 675–679 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D0NR04964F |
| ‡ This is especially needed to avoid Gd bulk impurities that reemerge at the Au surface during annealing cycles. |
| § In ref. 3 C′ labels the spin minority branch of C in ferromagnetic GdAg2 and GdAu2. Here, C′ refers to a different bulk resonating band. |
| This journal is © The Royal Society of Chemistry 2020 |