A molecular electron density theory study for [3+2] cycloaddition reactions of N-benzylcyclohexylnitrone with methyl-3-butenoate

Abstract

The [3+2] cycloaddition (32CA) reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 have been studied within molecular electron density theory (MEDT) at the B3LYP/6-311++G(d,p) level of theory. These zwitterionic type 32CA reactions occur through a one-step mechanism. The 32CA reactions undergo two pairs of stereo- and regioisomeric reaction paths to form four different products, 3, 4, 5 and 6. The reaction paths are irreversible due to the exothermic character of −18.5 and −12.4 kcal mol⁻¹. The 32CA reaction leading to the formation of cycloadduct 3 presents the lowest activation enthalpy compared to the other path due to a slight increase in polar character evident from the global electron density transfer (GEDT) at the transition states and along the reaction path. The bonding evolution theory (BET) study suggests that these 32CA reactions occur through the coupling of pseudoradical centers and the formation of new C–C and C–O covalent bonds has not been started in the transition states.

---

Introduction

Recently, computational studies on cycloaddition reactions have been the subject of a number of studies due to their wide applications to synthetic organic compounds.^1–5 Among cycloadditions, [3+2] cycloaddition reactions (32CAs) represent versatile processes for the synthesis of a system with a five membered ring and a large variety of heterocyclic compounds can be synthesized relying on the choice of the three-atom-component (TAC) and the alkene derivative.^6–9 The 32CA reaction of nitrones as a TCA to alkenes has been widely used during the recent two decades as a key step for the construction of various heterocycles that are of great interest in pharmaceutical and medicinal chemistry.^10–13

The advent of computational chemistry in recent years has gradually attracted theoretical chemists to analyze the reactivity and selectivity of organic molecules. A new theoretical outlook for organic reactions was proposed by Domingo in 2016, named molecular electron density theory¹⁴ (MEDT), after interpretation of a vast array of organic reactions, the majority of them Diels–Alder (DA) and 32CA reactions.^15,16 This theory analyzes changes in electron density to study the molecular reactivity and has been successfully applied for several 32CA reactions in the last four years.¹⁵

Numerous DFT studies carried out within MEDT devoted to the TAC reactivity participating in 32CAs have allowed establishing a useful classification of 32CAs relying on the electronic structure and the TAC behavior into pseudodiradical (pdr-type), pseudo(momo)radical (pmr-type), carbenoid (cb-type) and zwitterionic (zw-type).^17–19 The feasibility of zw-type reactions relies on the polar character of the 32CAs, i.e. the electrophilic character of the nitrones and the nucleophilic character of the alkenes, or vice versa. Nitrones, in general, are good nucleophiles that able to react with electron-deficient alkenes.²⁰

Herein, we present an MEDT study at the B3LYP/6-311++G(d,p) level of theory for the synthesis of isoxazolidines from the 32CA reaction of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 (Scheme 1). In this work, we studied the analysis of the reactivity indices derived from conceptual DFT^21,22 (CDFT) for the reagents, the energy profiles of the 32CA of 1 and 2 and electron localization function²³ (ELF) topological analysis for understanding the bonding changes.

Scheme 1 32CA reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2.

Results and discussion

ELF topological analysis of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2

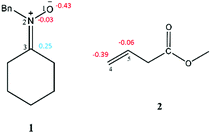
The electron localization function (ELF) establishes a straightforward quantitative connection between the electron density distribution and the chemical structure.^23,24 Herein, the reactivity of N-benzylcyclohexylnitrone 1 in 32CA reactions is studied by ELF topological analysis. Additionally, the ELF of methyl-3-butenoate 2 was also examined. The most significant valence basin populations are listed in Table 1, while the ELF localization domains of the reagents are given in Fig. 1 and calculated natural atomic charges are arranged in Fig. 2.

Table 1 B3LYP/6-311G++(d,p) calculated most significant ELF valence basin populations at N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2. The ELF valence basin populations are given as the average number of electrons, e

	1	2
V(O1)	2.93	—
V′(O1)	3.05	—
V(N2,O1)	1.28	—
V′(N2,C3)	4.15	—
V(C4,C5)	—	1.78
V′(C4,C5)	—	1.77

---

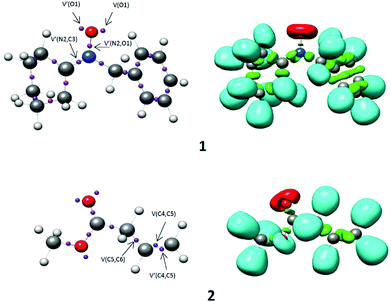Fig. 1 B3LYP/6-311++G(d,p) calculated ELF localisation domains represented at an isosurface value of ELF = 0.80 of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2.

Fig. 2 B3LYP/6-311G++(d,p) calculated natural atomic charges, given as the average number of electrons e, of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2. Positive charges are coloured in blue and negative charges in red.

The ELF topology of N-benzylcyclohexylnitrone 1 shows the presence of two V(O1) and V′(O1) monosynaptic basins having a total population of 5.98 e, associated with the non-bonding electrons of the O1 oxygen lone pairs, and a V(N2,O1) disynaptic basin and a V(N2,C3) disynaptic basin with an integrated population of 1.28 e and 4.15 e, respectively. The V(N2,C3) disynaptic basin can be associated with the under populated N2–C3 double bond, while the V(N2,O1) disynaptic basin is associated with the under populated N2–O1 single bond. Thus, N-benzylcyclohexylnitrone 1 can be classified as a zwitterionic TAC due to the absence of carbenoid or pseudoradical centers.^25–28 This suggests participation of nitrone 1 in zw-type 32CA reactions associated with high activation energies.²⁸

Analysis of the CDFT indices of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2

Analysis of the CDFT indices provides an initial understanding of the reactivity of organic molecules.^14,21,22 The CDFT indices were calculated at the B3LYP/6-31G(d) computational level since this level was used to define the electrophilicity and nucleophilicity scales.^29,30 The electronic chemical potential, μ, chemical hardness, η, electrophilicity, ω, and nucleophilicity, N, in the ground state of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2 are listed in Table 2.

Table 2 The chemical hardness η, electronic chemical potential μ, global nucleophilicity N and global electrophilicity ω, in eV, of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2 at the B3LYP/6-31G(d) level of theory

	μ	η	ω	N
1	−2.90	5.47	0.77	3.85
2	−3.12	9.10	0.54	1.82

---

The electronic chemical potential μ of N-benzylcyclohexylnitrone 1, μ = −2.90 eV, is higher than that of methyl-3-butenoate 2, which is −3.12 eV. The electrophilicity ω and nucleophilicity N indices of N-benzylcyclohexylnitrone 1 are 0.77 and 3.85 eV respectively, being classified as a marginal electrophile and a strong nucleophile within the corresponding scales.^29,30 The electrophilicity ω and nucleophilicity N indices of methyl-3-butenoate 2 are 0.77 and 1.82 eV, respectively, being classified as a marginal electrophile and a marginal nucleophile. In spite of the strong nucleophilic character of nitrone 1, the marginal electrophilic character of 2 indicates that this zw-type 32CA reaction will have non-polar character.

Analysis of the reaction paths associated with the 32CA reactions of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2

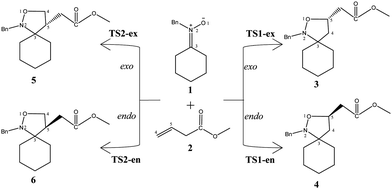
Due to the molecular asymmetry of methyl-3-butenoate 2, four reaction paths are feasible for these 32CA reactions (see Scheme 1). The search for the stationary points involved in the reaction paths associated with these 32CA reactions allowed characterizing the reactants, 1 and 2, four TSs for the 32CA reaction, TS1-ex, TS1-en, TS2-ex and TS2-en, and the corresponding products 3, 4, 5 and 6, respectively (see Scheme 1). The relative energies and thermodynamic data of the TSs and cycloadducts are given in Table 3.

Table 3 B3LYP/6-31G(d) calculated relative energies, enthalpies and Gibbs free energies, in kcal mol⁻¹, computed at 298 K of the stationary points involved in the 32CA reactions of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2

	Gas phase				Toluene
	ΔE	ΔH	ΔG	GEDT	ΔE	ΔH	ΔG	GEDT
TS1-ex	18.1	17.6	31.2	0.008	19.4	18.9	32.3	0.007
3	−17.4	−18.5	−3.2	—	−15.6	−16.6	−1.13	—
TS1-en	19.1	18.6	32.5	0.007	20.5	20.0	34.1	0.007
4	−17.2	−18.2	−2.8	—	−15.5	−16.5	−1.03	—
TS2-ex	21.8	21.3	34.8	0.014	23.2	22.7	84.7	0.014
5	−11.2	−12.4	3.91	—	−9.5	−10.7	5.7	—
TS2-en	22.9	22.4	36.2	0.012	24.3	23.7	37.6	0.012
6	−13.4	−14.3	1.18	—	−11.6	−12.5	2.87	—

---

The activation enthalpies associated with these 32CA reactions are 17.6, 18.6, 21.3 and 22.4 kcal mol⁻¹ for TS1-ex, TS1-en, TS2-ex and TS2-en, respectively, in the gas phase, and 18.9, 20.0, 22.7 and 23.7 kcal mol⁻¹ for TS1-ex, TS1-en, TS2-ex and TS2-en, respectively, in toluene at 298 K; the reactions are exothermic between 12.4 and 18.5 kcal mol⁻¹ in the gas phase, and between 10.7 and 16.6 kcal mol⁻¹ in toluene.

Analysis of the relative enthalpies allows establishing some appealing conclusions: (i) The 32CA reaction between N-benzylcyclohexyl nitrone 1 and methyl-3-butenoate 2 leading the formation of cycloadduct 3 presents the lower activation enthalpy of 17.6 kcal mol⁻¹ in the gas phase and 18.9 kcal mol⁻¹ in toluene. (ii) The activation enthalpy for this 32CA reaction that corresponds to the formation of cycloadduct 3 is lowered by about 1.3 kcal mol⁻¹ in both the gas phase and in toluene. (iii) The reaction enthalpy for cycloadduct 3 obtained from the 32CA reaction between N-benzylcyclohexyl nitrone 1 and methyl-3-butenoate 2 is higher than that of 5 by about 6.1 kcal mol⁻¹ in the gas phase and 5.9 kcal mol⁻¹ in toluene; these values indicate that this reaction is under kinetic and thermodynamic control. (iv) The exothermic character of the 32CA reaction that leads to the formation of cycloadduct 3 makes the reaction irreversible. (v) The inclusion of solvent effects of toluene slightly increases the activation enthalpies and the reaction enthalpies, leading therefore to better solvation of the reagent than the TS.

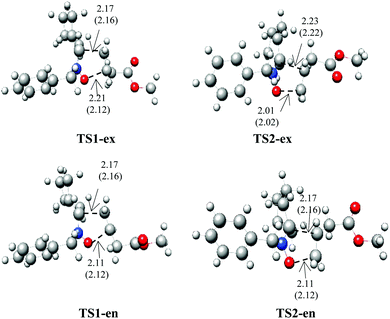
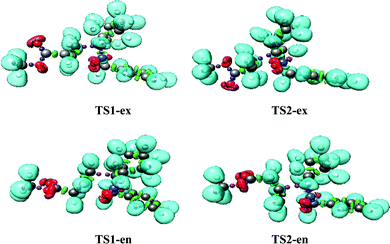
The B3LYP/6-311++G(d,p) optimized geometries of the TSs are given in Fig. 3. In the gas phase, the distances between the C3 and C4, and O1 and C5 interacting centers at the transition states are: 2.17 and 2.11 Å at TS1-ex, 2.17 and 2.11 Å at TS1-en, 2.23 and 2.01 Å at TS2-ex and 2.17 and 2.11 Å at TS2-en, respectively, with Δd (|dC3–C4 − dO1–C5|) values of 0.06 and 0.22 Å. The calculated Δd values in toluene are 0.04 and 0.2 Å.

Fig. 3 B3LYP/6-311++G(d,p) optimized geometries of the transition states involved in the 32CA reaction of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2. Bond lengths are given in Angstroms. The values in parentheses are calculated in toluene.

These geometrical parameters indicate that while TS1-ex is associated with low asynchronicity processes, TS2-ex with the highest activation energy shows the highest asynchronicity. The analysis of the geometrical parameters indicates that at both transition states, the formation of the C–C and C–O single bond has not yet begun.³¹

The polar nature of the 32CA reactions was analyzed by GEDT calculations.³¹ The GEDT values in the gas phase at the TSs are 0.008 e at TS1-ex, 0.007 e at TS1-en, 0.014 e at TS2-ex and 0.012 e at TS2-en (see Table 3). Similar values of GEDT were obtained for both TSs in toluene as a solvent. These values, which are less than 0.05 e, indicate that this 32CA reaction has non-polar character, in clear agreement with the CDFT analysis.

The BET study of the 32CA reactions of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2

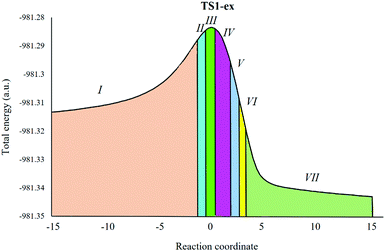
Herein, a study of the BETs for TS1-ex of the 32CA reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 is presented. The 32CA reaction of 1 with 2 takes place along seven different phases (see Table 4).³² Phase I corresponds to the starting phase of the IRCs. S0 (see Table 4) at dO1–C5 = 3.12 Å is the representative IRC point of phase I for the first path of the reaction. The ELF of S0 is similar to that of the separated reagents.

Table 4 ELF valence basin populations and the GEDT values and distances of the forming bonds of the IRC structures S0–S6 and P1 defining the eight phases characterizing the molecular mechanism of the 32CA reaction of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2 yielding product P1. Distances, d(C5–O1) and d(C3–C4), are given in Angstroms, Å

Phases	I	II	III	IV	V	VI	VIII
Structures	S0	S1	S2 = TS1-ex	S3	S4	S5	S6	P1
d(C5–O1)	3.12	2.27	2.11	2.08	1.96	1.68	1.58	1.45
d(C3–C4)	3.41	2.38	2.17	2.11	1.97	1.69	1.63	1.55
GEDT	0.047	0.051	0.008	0.011	0.082	0.221	0.243	0.257
V(O1)	3.05	2.97	2.98	2.97	2.92	2.76	2.66	2.63
V′(O1)	3.93	2.92	2.93	2.92	2.89	2.68	2.62	2.54
V(N2,C3)	4.15	3.26	2.61	2.41	2.03	1.95	1.90	1.89
V(N2,O1)	1.28	1.19	1.14	1.11	1.06	0.95	0.93	0.87
V(N2)		0.99	1.33	1.56	1.83	2.15	2.23	2.33
V(C3)			0.51	1.10	1.41
V(C4,C5)	1.78	1.67	1.62	2.75	2.42	2.06	1.97	1.94
V′(C4,C5)	1.77	1.64	1.58
V(C4)			0.42	1.08	1.39
V(C5)					0.21	0.76
V(C5,O1)							0.96	1.16
V(C3,C4)						1.75	1.82	1.88

---

Phase II starts at S1, d(O1–C5) = 2.27 Å and d(C3–C4) = 2.38 Å. S1 shows the formation of a V(N2) monosynaptic basin with an integrated population of 0.99 e. The electron density for formation of the V(N2) monosynaptic basin in S1 is derived from the V(N2,C3) disynaptic basin, which shows depopulation from 4.15 e in S0 to 3.26 e in S1. Interestingly, S1 shows GEDT values of 0.05. This suggests increased polar character and hence a lower energy requirement to reach S1.

Phase III starts at S2, d(O1–C5) = 2.21 Å and d(C3–C4) = 2.17 Å, and this shows the formation of V(C3) and V(C4) monosynaptic basins with an integrated population of 0.51 e and 0.42 e, respectively. S2 shows a GEDT value of 0.008. Phase IV starts at S3, d(O1–C5) = 2.08 Å and d(C3–C4) = 2.11 Å. S3 shows the formation of a V(C4) monosynaptic basin with an integrated population of 1.08, which is formed by deriving electron density from the V(N2,C3) disynaptic basin, and S3 shows a GEDT value of 0.011. As shown in Fig. 4, TS1-ex belongs to Phase IV. This suggests that the relative energies of the TSs correspond to the energy cost for the formation of pseudoradical centers at the reacting nuclei. This 32CA reaction involves an early TS with no new covalent bond formation.

Fig. 4 ELF topological phases for [3+2] cycloaddition reactions of N-benzylcyclohexylnitrone 1 and methyl-3-butenoate 2. The green line indicates the position of TS1-ex, the phases are shown as colored regions defined by points along the IRC.

Phase V starts at S4, d(O1–C5) = 1.96 Å and d(C3–C4) = 1.97 Å, with the formation of a pseudoradical center at C5 with an integrated population of 0.21 e. Phase VI starts at the structure S5 for the, dO1–C5 = 1.68 Å and dC3–C4 = 1.69 Å. At structure S5, while the V(C4) monosynaptic basin present at S3 is missing in S4. At the beginning of this phase the first more relevant change along the IRCs takes place. A new V(C3,C4) disynaptic basin with an integrated population of 1.75 e is created.

Finally, the last Phase VII starts at S6, d(O1–C5) = 1.58 Å and d(C3–C4) = 1.63 Å, and the second more relevant change along the IRC takes place. In these structures, a new V(O1,C5) disynaptic basin is created with an integrated population of 0.96 e, while the V(C5) monosynaptic basin disappeared. This relevant topological change indicates that the formation of the second O1–C5 single bond has started, through the C− to –O coupling of the electron density of the C5 pseudoradical carbon and part of the non-bonding electron density of the O1 oxygen lone pairs. The molecular electron density, along this phase, is relaxed to reach the structure of product 3 in the 32CA reaction, in which the population of the V(C3,C4) and V(O1,C5) disynaptic basins reaches 1.88 e and 1.16 e, respectively.

ELF topological analysis of TS1-ex, TS1-en, TS2-ex and TS2-en

The ELF topologies of TS1-ex, TS1-en, TS2-ex and TS2-en were analyzed and compared. Table 5 shows the populations of the most significant valence basin at TS1-ex, TS1-en, TS2-ex and TS2-en, whereas Fig. 5 presents the ELF localization domains. The ELF of the four TSs shows the presence of two monosynaptic basins, V(O1) and V′(O1), which are associated with the non-bonding electron densities at the O1 oxygen, already present in N-benzylcyclohexylnitrone 1 (see Tables 1 and 4).

Table 5 B3LYP/6-311++G(d,p) calculated most significant ELF valence basin populations at the TSs

	TS1-ex	TS1-en	TS2-ex	TS2-en
V(O1)	2.98	2.96	2.93	2.92
V′(O1)	2.93	2.91	2.92	2.91
V(N2)	1.33	1.42	1.49	1.48
V(N2,O1)	1.14	1.12	1.11	1.11
V(N2,C3)	2.61	2.52	2.50	2.48
V(C4,C5)	2.92	2.92	2.82	2.83
V(C3)	0.51	0.54	0.58	0.56
V(C4)	0.42	0.42	0.56	0.56

---

Fig. 5 Pictorial representation of the B3LYP/6-311++G(d,p) ELF localization domains of TS1-ex, TS1-en, TS2-ex and TS2-en represented at an isosurface value of ELF = 0.85. Monosynaptic basins are shown in red, disynaptic basins are shown in green and protonated basins are shown in blue. The attractors are shown in violet.

The ELF topological analysis of TS1-ex, TS1-en, TS2-ex and TS2-en also displays the presence of a single V(N2) monosynaptic basin, with an integrated population of 1.33–1.49 e, which comes from the depopulation of the N2–C3 bonding region. The N2–C3 bonding region undergoes a depopulation of the electron density from 4.15 e in 1 to 2.61 e, 2.52 e, 2.50 e and 2.48 e in TS1-ex, TS1-en, TS2-ex and TS2-en, respectively.

In the methyl-3-butenoate framework, a disynaptic basin, V(C4,C5), associated with the C4–C5 bonding region with a total integrated population of 2.92 e (TS1-ex), 2.92 e (TS1-en), 2.82 e (TS2-ex) and 2.83 e (TS2-en) is observed. The ELF of the transition states shows the presence of a single V(C4) monosynaptic basin with an integrated population of 0.42 e, 0.42 e, 0.56 and 0.56 e for TS1-ex, TS1-en, TS2-ex and TS2-en, respectively, and a single V(C3) monosynaptic basin is also observed for TS1-ex, TS1-en, TS2-ex and TS2-en with an integrated population of 0.51 e, 0.54 e, 0.58 e and 0.56 e, respectively. The V(O1,C5) and V(C3,C4) disynaptic basins at TS1-ex, TS1-en, TS2-ex and TS2-en have not appeared, which indicates that the formation of O1–C5 and C3–C4 single bonds has not yet started.

Computational methods

All calculations were done using the Gaussian 16 package under the Linux operating system.³³ The DFT method with the B3LYP functional has been proven to be a suitable method for the study of [2+2] cycloaddition reactions and is employed in this study.^34–36 B3LYP (Becke's three-parameter hybrid exchange functional and the Lee–Yang–Parr correlation functional) is used throughout in combination with the 6-311G++(d,p) basis set.^37,38 We also considered the D3 correction to take into account the role of dispersion energies in the stability of the complexes and intermediates.³⁹ Geometry optimizations were performed with the default settings of geometry convergence, integration grid and electron density (SCF) convergence. Open-shell calculations were done in a spin-restricted formalism.

The computations consist of geometry optimizations followed by frequency calculations to ensure that a transition state has only one imaginary frequency and that a local minimum has no imaginary frequencies (all positive frequencies). Intrinsic reaction coordinate (IRC) computations were carried out to verify that the minimum energy reaction pathway via a transition state connects with the corresponding reactants and products.⁴⁰

All energies and thermodynamic parameters reported in this paper were obtained from frequency calculations at the same level of theory. The enthalpies, Gibbs free energies and entropies in the gas phase were deduced with standard statistical thermodynamics at 298.15 K and 1 atm. The CYLview software was used as a graphical interface.⁴¹

The global electrophilicity index (ω) is calculated using the equation ω = (μ²/2η).⁴² The chemical hardness (η) and the electronic chemical potential (μ) quantities may be approached in terms of the one electron energies of the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO), ε_HOMO and ε_LUMO, as η ≈ ε_LUMO − ε_HOMO and μ ≈ (ε_HOMO + ε_LOMO)/2, respectively.^43,44 The relative nucleophilicity N index⁴⁵ is obtained based on the energies of the HOMO within the scheme of Kohn–Sham.⁴⁶ This quantity can be defined as N = E_HOMO(Nu) − E_HOMO(TCE). As a reference, we chose TCE (tetracyanoethylene) due to its lowest HOMO energy.⁴⁵

The global electron density transfer³¹ (GEDT) was calculated using the sum of the natural atomic charges (q) obtained by a natural population analysis (NPA). Topological analysis of the electron localization function (ELF) and the representation of its basin isosurface were performed by using the Multiwfn package. The topological evaluation of non-covalent interactions (NCI) was also performed using the Multiwfn software by analyzing the gas phase SCF density.

Toluene was used to examine the solvent effects using the conductor like polarizable continuum model⁴⁷ (PCM) in the framework of the self-consistent reaction field⁴⁸ (SCRF). The thermodynamic parameters were calculated in the gas phase and toluene with standard statistical thermodynamics at 298.15 K and 1 atm.

Conclusions

The 32CA reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 have been studied within MEDT at the B3LYP/6-311++G(d,p) level of theory. The ELF topological analysis of N-benzylcyclohexylnitrone 1 clearly indicates that this TAC participates in zw-type cycloaddition reactions. The 32CA reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 take place through a one-step mechanism. The exothermic character of cycloadduct 3 makes the reaction thermodynamically irreversible. The activation enthalpy for the 32CA reaction leading to the formation of 3 is lower than the other path.

Analysis of the geometrical parameters indicates that the TSs are associated with a low asynchronicity process at TS1-ex. A different behaviour at TS2-ex is observed which shows a high asynchronicity with the shortest distance between the O1 and C5 centers in the gas phase and toluene. Analysis of the GEDT at the TSs indicates that the 32CA reaction of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 is non-polar.

The BET analysis of the 32CA reactions of N-benzylcyclohexylnitrone 1 with methyl-3-butenoate 2 leading to the formation of 3 shows the formation of an N2 pseudoradical center at the beginning of the reaction with a GEDT of 0.051 e. Consequently, the increase in the GEDT accounts for the lowering of the energy cost along the reaction paths.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to acknowledge the Department of Chemistry at University of Zakho and Department of Chemistry at Salahaddin University.

References

1. H. A. Mohammad-Salim, H. H. Abdallah, K. R. Maiyelvaganan, M. Prakash and M. Hochlaf, Theor. Chem. Acc., 2020, 139, 19.
2. H. A. Mohammad-Salim and H. H. Abdallah, ARO-The Scientific Journal of Koya University, 2019, 7, 9.
3. H. Mohammad Salim and H. Abdallah, Orient. J. Chem., 2019, 35, 1550–1556.
4. H. A. M. Salim, H. H. Abdallah and P. Ramasami, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 454, 12–49.
5. H. M. Salim, H. H. Abdallah and P. Ramasami, Adv. Mater. Sci. Eng., 2018, 415–419.
6. A. Lauria, R. Delisi, F. Mingoia, A. Terenzi, A. Martorana, G. Barone and A. M. Almerico, Eur. J. Org. Chem., 2014, 3289–3306.
7. Q.-H. Li, L. Wei and C.-J. Wang, J. Am. Chem. Soc., 2014, 136, 8685–8692.
8. S. Shevelev and A. Starosotnikov, Chem. Heterocycl. Compd., 2013, 49, 92–115.
9. H. Mohammad-Salim, R. Hassan, H. H. Abdallah and M. Oftadeh, J. Mex. Chem. Soc., 2020, 64, 147–164.
10. L. L. Anderson, Asian J. Org. Chem., 2016, 5, 9–30.
11. M. Ríos-Gutiérrez, A. Darù, T. Tejero, L. R. Domingo and P. Merino, Org. Biomol. Chem., 2017, 15, 1618–1627.
12. M. Frederickson, Tetrahedron, 1997, 53, 403–425.
13. D. Wanapun, K. V. Gorp, N. Mosey, M. Kerr and T. Woo, Can. J. Chem., 2005, 83, 1752–1767.
14. L. R. Domingo, Molecules, 2016, 21, 1319.
15. M. Rıos-Gutiérrez and L. Domingo, Eur. J. Org. Chem., 2019, 267.
16. L. R. Domingo and J. A. Sáez, Org. Biomol. Chem., 2009, 7, 3576–3583.
17. R. Jasiński, E. Jasińska and E. Dresler, J. Mol. Model., 2016, 23, 1–9.
18. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Org. Biomol. Chem., 2016, 14, 10427–10436.
19. L. R. Domingo, M. J. Aurell and P. Pérez, Tetrahedron, 2015, 71, 1050–1057.
20. L. R. Domingo, M. J. Aurell and P. Pérez, Tetrahedron, 2014, 70, 4519–4525.
21. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 21, 748.
22. P. Geerlings, F. D. Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874.
23. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
24. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
25. M. Ríos-Gutiérrez and L. R. Domingo, Eur. J. Org. Chem., 2019, 267–282.
26. L. R. Domingo and N. Acharjee, ChemistrySelect, 2018, 3, 8373–8380.
27. N. Acharjee and A. Banerji, J. Chem. Sci., 2020, 132, 65.
28. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, J. Org. Chem., 2018, 83, 2182–2197.
29. L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423.
30. L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2011, 9, 7168–7175.
31. L. R. Domingo, RSC Adv., 2014, 4, 32415–32428.
32. X. Krokidis, S. Noury and B. Silvi, J. Phys. Chem. A, 1997, 101, 7277–7282.
33. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Revision A, 2016, 3.
34. R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989.
35. V. N. Khabashesku, K. N. Kudin and J. L. Margrave, Russ. Chem. Bull., 2001, 50, 20–28.
36. D. M. Lemal, J. Org. Chem., 2017, 82, 13012–13019.
37. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys. Lett., 1971, 54, 724–728.
38. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
40. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
41. C. Legault, CYLview 1.0, 2009.
42. R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
43. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
44. R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1994.
45. L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615–4624.
46. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
47. J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094.
48. E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041.

---