Elaeocarpus tectorius derived phosphorus-doped carbon as an electrode material for an asymmetric supercapacitor†
Bose
Nirosha
a,
Rajendran
Selvakumar
a,
Jeyadharmarajan
Jeyanthi
b and
Sundararajan
Vairam
 *ac
*ac
aDepartment of Chemistry, Government College of Technology, Coimbatore-641013, India. E-mail: drsvairam@rediffmail.com; vamshen@yahoo.com
bCentre of Excellence for Environmental Studies (COE-ES), Government College of Technology, Coimbatore-641013, India
cDepartment of Chemistry, KPR Institute of Engineering and Technology, Coimbatore-641407, India
First published on 20th November 2019
Abstract
Phosphorus-doped porous carbon is prepared from a new biomass (Elaeocarpus tectorius) at three different temperatures using a facile H3PO4 activation approach. The physicochemical characterisation of the as-prepared carbons by X-ray diffraction, Raman spectroscopy, thermal analysis, scanning electron microscopy, N2 adsorption–desorption isotherms and X-ray photoelectron spectroscopy indicates that the carbon obtained at 900 °C possesses a high phosphorus content, 2.5% (by mass), and a large interlayer distance of the porous carbon with more expanded channels facilitating the penetration of ions into the interlayers and a rapid adsorption of ions suitable for ultra-high volumetric capacitance. The optimized carbon (900 °C) delivers high gravimetric capacitance (385 F g−1 at 0.2 A g−1) and volumetric capacitance (543 F cm−3 at 0.2 A g−1) in 1 M H2SO4. In 1 M Na2SO4 electrolyte, it still exhibits a gravimetric capacitance of 203 F g−1 at 0.3 A g−1 and a volumetric capacitance of 286 F cm−3 at 0.3 A g−1. Additionally, a coin cell asymmetric device fabricated using this carbon works in a wide potential window from 0 to 1.5 V with 96% capacitance retention in 1 M H2SO4 aqueous electrolyte for 1000 cycles and yields a high energy density of 27 W h kg−1, showing the utility for the development of wearable electronic devices.
1. Introduction
The production of green, renewable and sustainable energy systems for solving global issues (greenhouse gases and global warming) resulting from non-renewable fossil fuels is in demand. Carbon is extensively employed as an advanced functional material in materials science owing to its high specific surface area, high physicochemical stability, superior surface reactivity, and excellent electronic, catalytic and electrochemical properties, specifically in energy conversion and storage.1–4 Supercapacitors are one of the advanced energy storage systems that depend on rapid ion sorption or reversible redox reactions on the surface to store energy.5–7 Carbon-based porous materials including activated carbon,8 graphene,9 carbon nanotubes10 and carbide-derived carbon11 have been comprehensively investigated for electrical double layer capacitors (EDLCs). Graphene and carbon nanotubes possess useful nanostructures for energy applications but are chiefly dependent on fossil fuel-based precursors (CH4, pitch and phenol) and severe synthetic conditions (chemical vapor deposition, laser ablation, and electric arc-discharge methods).12 Some synthetic routes employ toxic chemicals such as KMnO4 and NaNO3 which are environmentally harmful and expensive.13 Therefore, activated carbon materials, derived from renewable biomass, have been the focus of a more meaningful conversion of waste to value-added carbons due to its low cost, tunable pore structure/surface properties and environmentally benign and simple synthesis process. Conventional graphite has an increased interlayer distance (∼0.335 nm) and it can highly promote ion diffusion and storage in the interior of the carbon material. On the other hand, alterations of carbon materials with phosphorus, nitrogen and oxygen functional groups could possibly enrich the electron conductivity and better capacitive performance due to their electron donor properties, causing a shift of electrons from the Fermi level to the valence band in the carbon matrix. Recently a few studies have been reported on the development of functionalized carbon by doping heteroatoms (O, N, S and P) for enhancement of pseudocapacitance. High energy flexible solid state supercapacitors based on O, N, and S-tridoped carbon electrodes were reported by Ziyang Song et al.14 This work demonstrated an improvement in energy production of 90.9 W h kg−1 by using a surface O, N, and S-functionalized carbon (14.85 wt%) and a polymer gel electrolyte with a high operating voltage of 3.5 V. Further, nitrogen and oxygen co-doped porous carbons have also been fabricated based on simple polymerization followed by a carbonization/activation process by Yan et al.15 Carbon obtained using this method consists of interconnected carbon spheres, which facilitate a conductive platform for high performance supercapacitors operating in a wide potential of 2.2 V in a water-in-salt electrolyte with superior cycling stability after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. Activated carbon derived from various biomass precursors, such as corncob residue,16 pistachio nutshell,17 human hair,18 waste coffee beans19 and sugarcane bagasse20 for supercapacitors, have been reported. There are many reports on nitrogen rich carbon from biomass for supercapacitors. Only a few reports are available for phosphorus-doped carbon electrodes for supercapacitors. Wang Yang et al. prepared a 3D-phosphorus-doped porous carbon with 367 F g−1 at 0.2 A g−1 in 6 M KOH.21 A hierarchically porous N/P co-doped carbon with high level heteroatom doping and a moderate surface area of 414 m2 g−1 exhibiting a specific capacitance of 212 F g−1 at 0.5 A g−1 was reported by Ying Zhang et al.22 All the above works indicate the necessity of a high surface area of carbon and an additional pseudocapacitive effect by heteroatoms for high performance supercapacitors. Feili Lai et al. proved dual doping of heteroatoms into carbon with an expanded interlayer distance for efficient energy storage.23 In this work, with the purpose of selecting a new carbon source through which the above required properties could be easily achieved, a waste biosource possessing a large number of compounds having heteroatoms was chosen, namely, Elaeocarpus tectorius. Elaeocarpus tectorius (common name: bikki fruit) grown in the tropical and subtropical regions of Tamil Nadu (The Nilgiris) are generally thrown away as waste, and are accumulating continuously, creating environmental problems. Moreover, no reports on the use of these shells have been so far made in any of the research areas such as adsorption, catalysis, energy related fields, etc.
000 cycles. Activated carbon derived from various biomass precursors, such as corncob residue,16 pistachio nutshell,17 human hair,18 waste coffee beans19 and sugarcane bagasse20 for supercapacitors, have been reported. There are many reports on nitrogen rich carbon from biomass for supercapacitors. Only a few reports are available for phosphorus-doped carbon electrodes for supercapacitors. Wang Yang et al. prepared a 3D-phosphorus-doped porous carbon with 367 F g−1 at 0.2 A g−1 in 6 M KOH.21 A hierarchically porous N/P co-doped carbon with high level heteroatom doping and a moderate surface area of 414 m2 g−1 exhibiting a specific capacitance of 212 F g−1 at 0.5 A g−1 was reported by Ying Zhang et al.22 All the above works indicate the necessity of a high surface area of carbon and an additional pseudocapacitive effect by heteroatoms for high performance supercapacitors. Feili Lai et al. proved dual doping of heteroatoms into carbon with an expanded interlayer distance for efficient energy storage.23 In this work, with the purpose of selecting a new carbon source through which the above required properties could be easily achieved, a waste biosource possessing a large number of compounds having heteroatoms was chosen, namely, Elaeocarpus tectorius. Elaeocarpus tectorius (common name: bikki fruit) grown in the tropical and subtropical regions of Tamil Nadu (The Nilgiris) are generally thrown away as waste, and are accumulating continuously, creating environmental problems. Moreover, no reports on the use of these shells have been so far made in any of the research areas such as adsorption, catalysis, energy related fields, etc.
In order to achieve a high capacitance by doping phosphorus atoms into a carbon matrix, the shells were carbonized with H3PO4 at different temperatures of 700, 800 and 900 °C, the carbons were electrochemically characterized and the results are discussed in this work.
2. Experimental
2.1. Preparation of samples
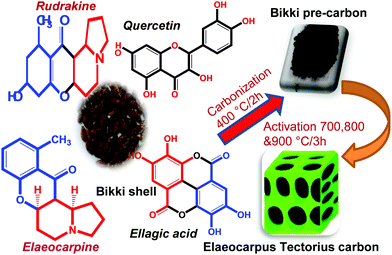
The shells were washed well with deionized water to remove impurities, dried in an air oven for 24 h at 110 °C and then crushed into a fine powder. The powder was subjected to carbonization for 400 °C for 2 h in a muffle furnace and then cooled to room temperature.To synthesize carbon, 50 g of the shell precursor powder was mixed with 200 g H3PO4 (specific gravity: 1.68 kg L−1) and stirred at 80 °C for 3 h using a magnetic stirrer. The slurry obtained was kept at 110 °C in an air oven for 24 h. A solid mass was obtained, which was pyrolysed at 700, 800 and 900 °C for 3 h in a muffle furnace, cooled to room temperature, washed several times with deionized water until neutral, and then dried in an oven at 60 °C. The activated carbon thus obtained was specified as Elaeocarpus tectorius carbon (ETC-700, 800 and 900), respectively.
The steps for ETC preparation are shown in Fig. 1. The bikki shell consists of aromatic indolizidine alkaloids and polyphenols such as rudrakine, elaeocarpine, quercetin and ellagic acid. The molecules enriched with hydroxyl and carbonyl groups in conjugation with the aromatic system are the efficient sources, which could modify the functionality of carbon and enhance the capacitive behaviour as an electrode for supercapacitors.
2.2. Characterization techniques
The crystallinity and phase-purity of the synthesized carbons were assessed by X-ray diffraction studies using a diffractometer (X’-Pert Pro PAnalytic) equipped with CuKα (λ = 1.5184 Å) radiation. The diffraction data were collected in the 2θ range of 10–75° at a scan rate of 10° min−1. Fourier transform infrared (FT-IR) spectra were recorded using a PerkinElmer system using the KBr pellet technique. Raman spectra were measured using a Witec, confocal Raman instrument with Ar ion laser 750 nm CRM200. The surface morphology and structures of the carbon were analysed using field emission scanning electron microscopy (FE-SEM, Carl Zeiss SUPRA55VP) and high-resolution transmission electron Microscopy (HRTEM, JEOL JEM2100). The elemental composition analysis was carried out using X-ray photo-electron spectroscopy (PES-AIPES beamline of Indus). The surface area and pore diameter of the carbon was characterized using N2 sorption isotherms (BET; Belsorb Mini-II, Belmaster Software-Japan).2.3. Electrochemical characterization
Cyclic voltammetry (CV), galvanostatic charge–discharge (CD) and electrochemical impedance spectroscopy (EIS) were carried out using a Biologic SP-200 system. The electrochemical evaluation of the electrode was executed using a three-electrode cell in 1 M H2SO4 aqueous solution. The working electrode was prepared by mixing 80% of ETC, 15% of super-P-carbon black and 5% of PVDF binder, by weight in N-methyl pyrrolidone to form a paste and then coated on a carbon cloth (CC) of 1 cm2 area. The ETC coated electrode was dried at 80 °C for 12 h. Prior to the coating, the CC was treated with conc. HNO3 to make it a hydrophilic surface. The areal mass loading of the ETC in 1 M H2SO4 is 4 mg cm−2. A three-electrode setup, comprising ETC, a standard calomel electrode (SCE) and a platinum rod as the working, reference and counter electrodes, respectively, was used to examine the electrochemical performance of the materials. The CV and CD experiments were carried out in the potential range of 0–1 V (vs. SCE) at various scan rates ranging from 10 to 100 mV s−1 and diverse current densities ranging from 0.2 to 10 A g−1.The specific and volumetric capacitance for the three-electrode system were calculated by using eqn (1)–(3),
| Cs = IΔt/mΔV | (1) |
| Cvol = Cs × ρ | (2) |
| ρ = m × V−1 | (3) |
In a two-electrode setup, a CR2032 type coin cell was fabricated using ETC-900 and reduced graphene oxide (RGO) as the positive and negative electrode materials with Whatman filter paper as a separator and a carbon cloth as the current collector in 1 M H2SO4 electrolyte. The mass ratio of the positive and negative electrodes was calculated from the formula,
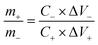 | (4) |
In order to compare the electrochemical performance of ETC-900 the electrochemical analysis was carried out in 1 M Na2SO4 aqueous medium in the three electrode configuration. The areal mass loading of the working electrode is 1.6 mg cm−2.
3. Results and discussion
3.1. Structural characterization of ETC
IR spectra of the ETCs are displayed in Fig. 2a. Though there are many common peaks in their spectra, a slight shifting and vanishing of some peaks could be observed. All ETCs show multiplet peaks centred at 3600 cm−1 corresponding to νOH attached to an aromatic carbon in the surface. However, a broad peak near 3500 cm−1 seen in the case of ETC-700 is found to be absent in the case of the other two carbons. This means that, during activation, OH groups linked to other groups by hydrogen bonding are eliminated. Furthermore, all the carbons have peaks at 1687 cm−1 indicating that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group is present.24–26 Furthermore, the presence of sharp peaks at 1524 cm−1 corresponding to C–C stretching in all carbons indicate that they are all of more graphitic nature. A medium broad band observed at 1100–1200 cm−1 in ETC-700 is found to be changed to a single sharp band at 1084 cm−1 in the other two carbons, (in particular ETC-900 shows a clear peak) leading to the understanding that P–C–P is formed strongly in the carbon matrix. Another interesting observation is that a small band observed at 675 cm−1 for ETC-800 and ETC-700 becomes very clear in ETC-900 and corresponds to νP–C.27 All the above observations substantiate the presence of stable functional groups such as, –C
O group is present.24–26 Furthermore, the presence of sharp peaks at 1524 cm−1 corresponding to C–C stretching in all carbons indicate that they are all of more graphitic nature. A medium broad band observed at 1100–1200 cm−1 in ETC-700 is found to be changed to a single sharp band at 1084 cm−1 in the other two carbons, (in particular ETC-900 shows a clear peak) leading to the understanding that P–C–P is formed strongly in the carbon matrix. Another interesting observation is that a small band observed at 675 cm−1 for ETC-800 and ETC-700 becomes very clear in ETC-900 and corresponds to νP–C.27 All the above observations substantiate the presence of stable functional groups such as, –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–, –P–C–, –P–O–C– and –P
C–, –P–C–, –P–O–C– and –P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O– groups on the surface of ETC-900.
O– groups on the surface of ETC-900.
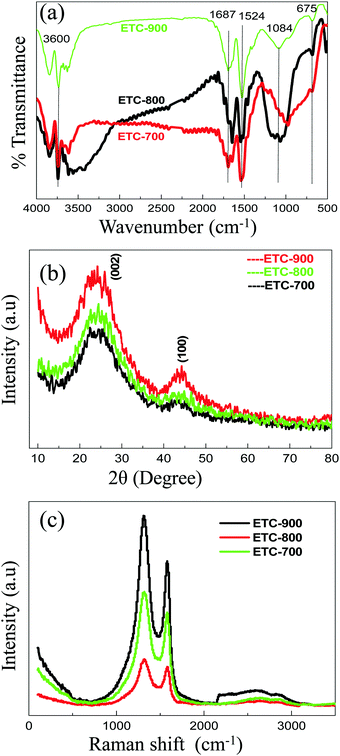 | ||
| Fig. 2 (a) FT-IR spectra, (b) XRD patterns and (c) Raman spectra of ETC at an excitation wavelength of 750 nm. | ||
XRD patterns of ETC-700, 800 & 900 were plotted and are shown in Fig. 2b. Two broad peaks at 23° and 43° can be indexed to the (002) and (100) crystal planes exhibiting the amorphous graphitic structure of the sample. Interestingly, all the samples show shifting of the (002) plane from 26.4° of graphite to lower values of 23.3–24°, which suggests the expansion of the interlayer spacing. Furthermore, from Bragg's law the calculated interlayer distance of 3.87 Å was observed for ETC-900 which is greater than graphite (∼3.36 Å) and is almost equal to the nitrogen-sulphur dual doped carbon reported by Feili Lai et al.23 It has been reported that P is likely to be assimilated on the edges of the graphene, which may augment the interlayer spacing. This may be ascribed to the distortion of the graphitic planes caused by phosphorus doping.
Fig. 2c shows the Raman spectra of ETC-700, ETC-800 and ETC-900 samples. Two discrete broad peaks assigned as D and G bands are observed in all the samples. The occurrence of defects in the carbon lattice was denoted by the D band around 1320 cm−1 corresponding to A1g symmetry, whereas, the G band appearing at 1520 cm−1 is attributed to the E2g, due to the stretching vibration of the C–C bonds.28 The level of disorder in the carbon samples is measured using the intensity ratio of the D and G bands. The incorporation of heteroatoms into the carbon scaffold prompts the edge defects on the carbon surface which is responsible for increased D band intensity. Hence, the ETC-900 sample shows more defects with increased defect intensity representing the disorderliness produced by P-functional groups.
To find the thermal stability of ETC-900 simultaneous TG-DTA was carried out and the thermogram is given in Fig. S1 (ESI†). The curves indicate that carbon undergoes dehydration at about 90 °C. This is due to the occluded water in the carbon. This dehydration is accompanied by a weight loss of about 25%. The second weight loss is observed with an exothermic decomposition at about 650 °C leaving no residue. From the results it may be inferred that the carbon is stable up to 550 °C.
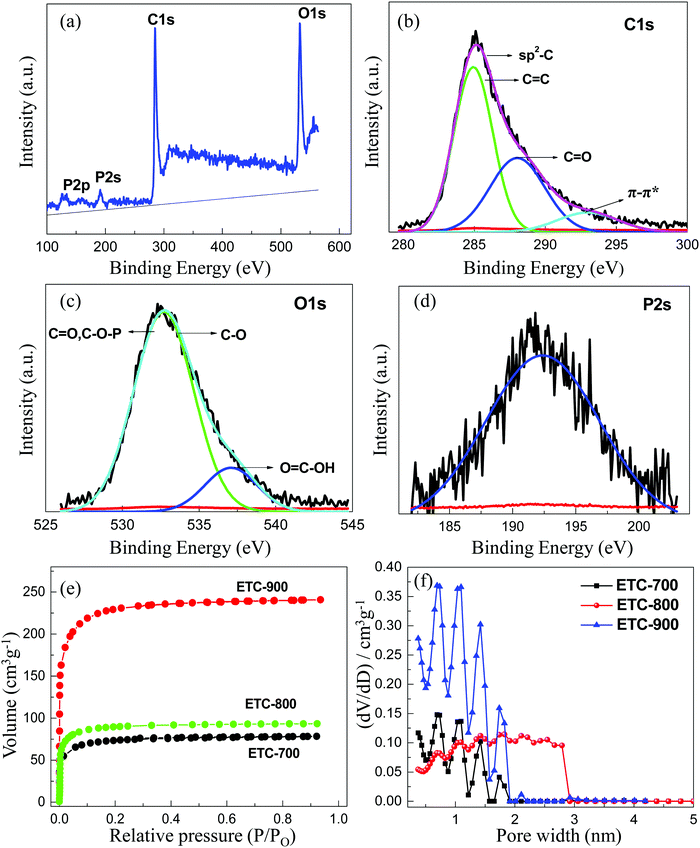
X-ray photoelectron spectroscopy (XPS) is a surface probe technique which further attests the elemental composition and bonding state of carbon with surface functional groups. Fig. 3a shows the survey spectrum of ETC-900 with a peak at the binding energy of 285 (70.74%), 532.6 (21.16%), 133.3 (8.1%) and 192.2 eV representing C1s, O1s, P2p and P2s, respectively. The de-convoluted spectrum of C1s shown in Fig. 3b with four types of peaks at 284.8 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), and 285 (C–C) eV in aromatic rings and at 288.1 eV (C
C), and 285 (C–C) eV in aromatic rings and at 288.1 eV (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). The satellite peak at 292 eV (π–π*) in the higher binding energy region, is attributed to the presence of a graphene-like microstructure carbon, which enhances the conductivity.29 The O1s spectrum (Fig. 3c) has three peaks at the binding energy of 531.5 eV (C
O). The satellite peak at 292 eV (π–π*) in the higher binding energy region, is attributed to the presence of a graphene-like microstructure carbon, which enhances the conductivity.29 The O1s spectrum (Fig. 3c) has three peaks at the binding energy of 531.5 eV (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) carbonyl and C–O–P groups; 532.6 eV (C–O) and (C–O–C) ether functional group; 536 eV (O
O) carbonyl and C–O–P groups; 532.6 eV (C–O) and (C–O–C) ether functional group; 536 eV (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–OH) carboxyl group, all of which favor the electrochemical redox activity and wettability. Phosphorus is present in the form of P–O (pyrophosphate [P2O7]4− and metaphosphate [PO3]−) and it is covalently bonded to the carbon in the form of C–PO3 at the binding energy of 133.3 eV
C–OH) carboxyl group, all of which favor the electrochemical redox activity and wettability. Phosphorus is present in the form of P–O (pyrophosphate [P2O7]4− and metaphosphate [PO3]−) and it is covalently bonded to the carbon in the form of C–PO3 at the binding energy of 133.3 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 as indicated in the survey spectrum (Fig. 3a). This implies that P functional groups may be positioned on the edges of the graphitic planes by bonding to more oxygens with the result of increased interlayer spacing, which is consistent with the XRD results. The distinct peak at 192.2 eV for P2s (Fig. 3d) implies the formation of phosphorous pentoxide as an intermediate.31 The effective doping of P atoms into the carbon lattice is corroborated with the presence of P–C bonds, which are in agreement with FT-IR spectra. This result substantiates that ETC-900 has more oxygen and phosphorus functional groups which may produce pseudocapacitance. The higher oxygen content was mostly due to a dehydration reaction which converts the cellulose to carboxyl/ketone groups at a high temperature.
30 as indicated in the survey spectrum (Fig. 3a). This implies that P functional groups may be positioned on the edges of the graphitic planes by bonding to more oxygens with the result of increased interlayer spacing, which is consistent with the XRD results. The distinct peak at 192.2 eV for P2s (Fig. 3d) implies the formation of phosphorous pentoxide as an intermediate.31 The effective doping of P atoms into the carbon lattice is corroborated with the presence of P–C bonds, which are in agreement with FT-IR spectra. This result substantiates that ETC-900 has more oxygen and phosphorus functional groups which may produce pseudocapacitance. The higher oxygen content was mostly due to a dehydration reaction which converts the cellulose to carboxyl/ketone groups at a high temperature.
N2-Sorption analysis was employed to determine the surface area, pore size distribution (PSD) and textural properties of the ETC (Fig. 3e and f). N2 adsorption–desorption isotherms display a steep rise in the adsorbed volume at P/Po < 0.05, which indicates the type I isotherms of microporous materials.32 The specific surface area (SSA) of P-doped carbons escalated as the temperature is increased. ETC-900 has a high BET-SSA of 858 m2 g−1 with an average pore diameter of 1.8 nm and pore volume of 0.43 cm3 g−1, respectively. Pore characteristics play a crucial effect on the electrochemical performance of carbon in supercapacitors. At a high temperature phosphoric acid forms its corresponding anions that can act as catalysts for the reduction of tar formation by producing polyphosphate bridges via crosslinking reactions.30 Therefore, it may develop the micropores during pyrolysis. It is observed that the phosphorus-rich carbons have narrow micropores with little mesopores as tabulated in Table 1. In comparison with ETC-900, both ETC-800 and 700 have low BET-SSA and pore volumes of 0.22 and 0.24 cm3 g−1 which are not very effective for ion transportation. Fig. 3f exhibits the pore distributions calculated from the non-local density functional theory (NLDFT) model. The pores for ETC samples are mainly composed of micropores (<2 nm), particularly sub-nanopores (<1 nm). The predominant sub-nanopores ranging from 0.5–1 nm provide accessible sites for penetration of aqueous electrolyte ions leading to capacitance enhancement.15 All the ETCs have the pore width centred at 0.4 to 1.8 nm with a high adsorption volume for ETC-900. The above result denotes that the increase in surface area at a higher temperature is owing to the gases resulting from decomposition and volatilization, which can generate new pores in the carbon surface.
| Sample | S BET (m2 g−1) | Micro surface area (m2 g−1) | Meso surface area (m2 g−1) | Total pore volume (cm3 g−1) | Micropore volume (cm3 g−1) | Average pore size (nm) |
|---|---|---|---|---|---|---|
| ETC-700 | 267 | 235 | 33 | 0.24 | 0.12 | 1.72 |
| ETC-800 | 339 | 320 | 19 | 0.15 | 0.22 | 1.76 |
| ETC-900 | 858 | 781 | 77 | 0.43 | 0.38 | 1.80 |
The microstructure of ETC was elucidated by field-emission scanning electron microscopy (FE-SEM) and high-resolution transmission electron microscopy (HRTEM) observations. The FE-SEM image of ETC-900 is depicted in Fig. 4a. The images display an ordered porous network structure for ETC-900 at higher magnification. The decomposition of cellulose and hemicellulose at a temperature higher than 700 °C results in uniform pores for the facilitation of ion transport and offers more accessible active sites in the carbon matrix of ETC-900. Moreover, the doping of phosphorus leads to the existence of numerous micropores in the carbon matrix. The amount of phosphorus, oxygen and carbon content were found to be 2.5%, 13.8% and 84% (by mass), respectively, from SEM-EDAX analysis given in Fig. S2 (ESI†). The HRTEM image (Fig. 4b) of ETC-900 clearly reveals the porous wrinkled structure with numerous pores on the carbon matrix. This implies that phosphorus has triggered a greater structural effect on the morphologies of the carbon matrix with the elevation in the temperature. As reported earlier, by Jens Peter et al., the greater percentage of phosphorus content transfers the morphology to a tube-like structure or crumbled carbon lumps that are also wrinkled.33 The creation of enormous mixed micro and mesopores in the carbon matrix by H3PO4, owing to the escaped gas from partial decomposition of H3PO4, (4H3PO4 + 10C → P4 + 10CO + 6H2O) above 750 °C, with the formation of P2O5 as an intermediate. The transformation of bulk particles to uniform pores with wrinkles takes place as the temperature increased from 700° to 900 °C which is well attained at 900 °C. Hence, this kind of carbon surface provides an ion buffering pool to enrich the electrolyte transport kinetics during the electrochemical process. The SAED pattern exhibits a polycrystalline nature with a hexagonal lattice representing the reflections of the graphene plane given in Fig. 4c. Fig. 4(d–f) shows the elemental composition of ETC-900, substantiating the presence of phosphorus in the carbon matrix. This investigation concludes that the formation of uniform pores and a graphitic nature was successful with H3PO4 activation at a higher temperature.
 | ||
| Fig. 4 (a and b) FE-SEM images of ETC-900, (c–f) HRTEM images (inset of (f): SAED pattern) and elemental mappings of ETC-900 (g) carbon, (h) oxygen and (i) phosphorus. | ||
3.2. Electrochemical assessment of ETCs
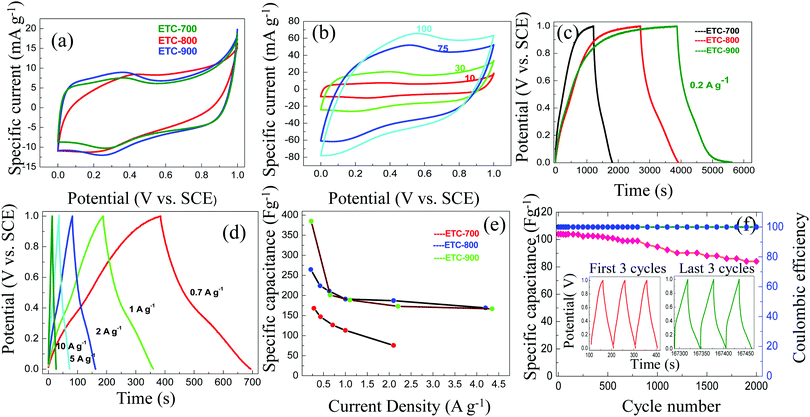
The electrochemical performances of ETC were investigated in a three-electrode configuration in both 1 M H2SO4 and 1 M Na2SO4. Fig. 5a illustrates the cyclic voltammetry (CV) profile of ETC at a lower scan rate of 10 mV s−1. It is observed that all the CV profiles are characterized by a quasi-rectangular shape with a pair of small humps indicating the predominant electrical double layer formation (EDLC). The reversible redox peaks approximately at 0.2 V imply the pseudocapacitance contribution, which becomes an added mechanism of energy storage besides the double layer mechanism. The CV curves recorded at the scan rates 10 to 100 mV s−1 show a trend of enlargement of area for the carbons when heated from 700 to 900 °C. However, ETC-900 maintains the shape of the curve comparatively in a better manner (Fig. 5b). The redox peaks observed at 0.2 V is due to the reaction given below presumably PO43− + 2H++ 2e− →PO33− + H2O. According to the Pourbaix diagram of the phosphorus–water system, the conversion of PO43− ↔ PO33− occurs at pH 1, which is accompanied by the electrode potential of 0.2 V.34 The same is observed in the present case also, where small amounts of PO43− in the carbon surface undergo reduction at a potential of 0.2 V in the CV profile. It is inferred from the largest area that ETC-900 has superior charge storage abilities, which may be attributed to the combination of more microporous and mesoporous volumes. In addition, the increased phosphorus content acts as an electron donor for carbon causing a shift of the conduction band from the Fermi level, which enables the adsorption of electrolyte ions.35Galvanostatic charge–discharge (CD) profiles of ETCs in three electrode cells and within the optimized potential window of 0–1 V at 0.2 A g−1 are displayed in Fig. 5c. The CD profiles (Fig. 5d) at diverse current densities from 0.7–10 A g−1 for ETC-900 shows isosceles triangular shape, signifying the EDLC with better electrochemical stability and charge–discharge reversibility. The discharge curves of ETC-900 without an apparent voltage drop reveal the minor internal resistance and excellent electrical conductivity. The capacitive characteristics of ETC-700 and 800 (CV and CD profiles) are listed in Fig. S3 (ESI†).
It is clear that the performances of the carbons vary with different temperatures, which is also interrelated with BET-SSA and porosity. Micropores (<2 nm) are necessary for double layer formation of charge storage at lower current density (<100 mA g−1) and mesopores aid as an ion buffering source at higher scan rates (>100 mA g−1). The specific capacitance of the prepared carbon decreases in the following order: ETC-900 > ETC-800 > ETC-700 as shown in Fig. 5e. The poor capacitance behaviour of ETC-800 and ETC-700 may be ascribed to reduced total pore volumes and BET-SSA. ETC-900 provides the highest gravimetric capacitance of 385, 250, 201, 189, 173 and 132 F g−1 at the current densities of 0.2, 0.7, 1, 2, 5 and 10 A g−1, respectively. The ETC-900 also displays a high volumetric capacitance of 543 F cm−3 at a current density of 0.2 A g−1 and 186 F cm−3 at 10 A g−1 as shown in Table S1 (ESI†). The high volumetric capacitance was due to the high packing density (1.41 g cm−3) of the ETC-900. The high packing density of the material is also due to the low mesopore/macropore content in the ETC-900 sample. Jiangying et al., reported the specific capacitance of 260 F g−1 at 0.05 A g−1 and 169 F g−1 at 1 A g−1 for nitrogen/oxygen/phosphorus decorated carbons from shrimp cells.36 The highest capacitance witnessed for ETC-900 as compared to ETC-700 and ETC-800 was ascribed to the effect of the contribution of the p-electron of the P-functional groups which improve the wettability of the electrode and also induce direct pseudocapacitance through a redox reaction. The reaction is proposed below.37
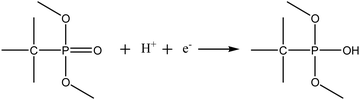 | (1) |
Another accepted reason is that pores considerably larger than electrolyte ion size and its solvation shells are necessary for higher capacitance values. The micropore with a pore size ranging between 0.77 and 1.8 nm could be completely accessible to the hydronium ions (0.36–0.42 nm)38 and hydrated bisulphate ions (0.53 nm),39 which agrees well in our case. The unstable oxygen functional group declines the capacitance which is suppressed by P2O5 formation as seen in the XPS results. However, ETC-900 could hold a specific capacitance of 132 F g−1 and volumetric capacitance of 186 F cm−3 even at the higher current density of 10 A g−1 showing outstanding rate capability. Compared to nano-sized carbons, micro-sized carbons are suitable for practical energy storage applications, as they empower a higher tap density.40 The electrochemical performances of activated carbons derived from various biowaste sources are compared in Table 2. The long term cycle stability and coulombic efficiency of ETC-900 were reviewed at a high current density of 2 A g−1, implying 71% of capacitance retention and 100% efficiency was perceived after 2000 charge–discharge cycles (Fig. 5f).
| Biomass precursor | Activation method | S BET (m2 g−1) | C sp (F g−1) | Electrolyte | Ref. |
|---|---|---|---|---|---|
| Beer lees | KOH | 3560 | 188 | 0.1 M H2SO4 | 41 |
| Natural wood | KOH | 2925 | 200 | 6 M KOH | 42 |
| Wood saw dust | KOH | 2960 | 236 | 1 M TEABF4 | 43 |
| Willow catkin | KOH | 645 | 279 | 6 M KOH | 44 |
| Corn grains | KOH | 3199 | 257 | 6 M KOH | 45 |
| Tea leaves | KOH | 2841 | 330 | 2 M KOH | 40 |
| Coconut shell | ZnCl2 | 1874 | 268 | 6 M KOH | 46 |
| Borassus flabellifer flower | H3PO4 | 633 | 234 | 1 M KOH | 47 |
| Pine cone | KOH | 1515 | 137 | 1 M Na2SO4 | 48 |
| Elaeocarpus tectorius shell | H3PO4 | 860 | 385 | 1 M H2SO4 | Present work |
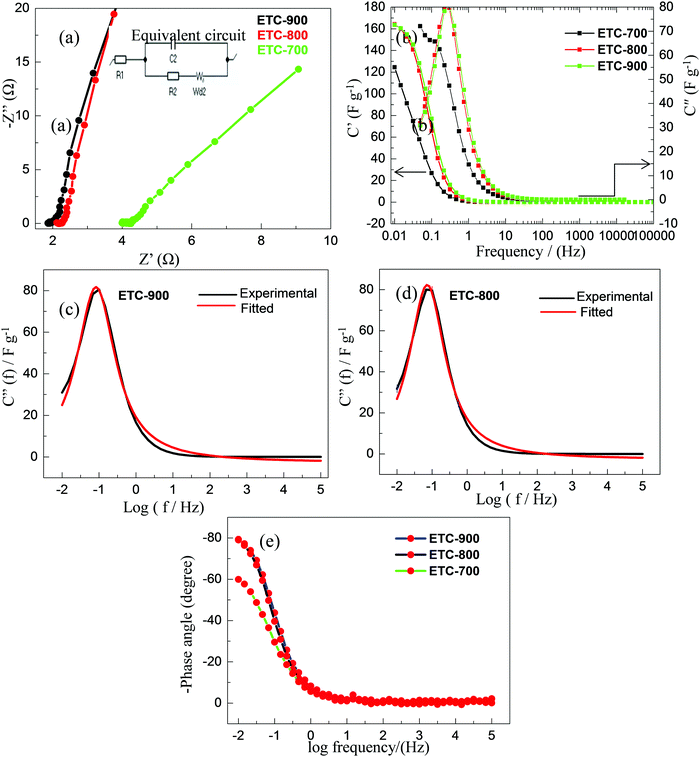
Electrochemical impedance spectroscopic analysis was conducted to evaluate the electrode kinetics of the activated carbons. The total impedance can be classified into three components in Nyquist plots: (1) bulk electrolyte resistance (intercept of real axis at a high frequency region), (2) interfacial impedance has been assigned between the electrode and electrolyte solution (the diameter of the semicircle at the middle frequency region) and (3) diffuse layer resistance (i.e. impedance that is related to the intra-particle pores which occur at intermediate frequency regions).49 The Nyquist plots for all the carbons (Fig. 6a) display a real axis with a short intercept at a high frequency region which is the indication of bulk electrolyte resistance (Rs) and it is estimated to be 1.8 Ω (ETC-900), 2.1 Ω (ETC-800) and 4 Ω (ETC-700), respectively. The equivalent circuit fitting was performed by a Randles circuit fitting and is represented in Fig. 6a. The circuit is composed of intrinsic resistance Rs, charge transfer resistance Rct and Warburg diffusion element W. The impedance of the circuit is Resr − j/ωCutil, where j is the imaginary unit and ω is the angular frequency (=2πf); the Resr (equivalent series resistance) and Cutil (utilizable capacitance) were calculated from the perpendicular region of real and imaginary parts in the Nyquist impedance. The rate capability of the porous carbons can be deduced from a smaller relaxation time constant using a simple relation τ = R × C.50 The calculated relaxation time signifies the required time needed to discharge the efficient energy stored from the device, which are 2.7, 3.8 and 5.5 s for ETC-900, 800 and 700, respectively. For more detailed information regarding rate capability and capacitive characteristics, complex capacitance analysis was performed. The transformation of measured impedance to complex capacitance was carried out using the relationship 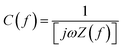 .51 The real (C′(f)) and imaginary (C′′(f)) capacitance as a function of frequency are shown in Fig. 6b.
.51 The real (C′(f)) and imaginary (C′′(f)) capacitance as a function of frequency are shown in Fig. 6b.
The capacitance as a function of frequency can be calculated using the following equations.
| C′(f) = −Z′′(f)/ω|Z(f)|2 | (5) |
| C′′(f) = −Z′(f)/ω|Z(f)|2 | (6) |
The real part of complex capacitance denotes the capacitance value as a function of frequency, whereas the imaginary part (C′′(f)) is correlated with the Kronig–Kramers (K–K) relationship. The appearance of peak shaped curves is noticed for ETC-900 and ETC-800 in the imaginary capacitance plots as a function of frequency in semi log scale as shown in Fig. 6c and d. As implied by the K–K relationship, the total capacitance (Ctot) can be calculated from the peak area (Ap) as Ctot = 1.466Ap.52 Furthermore, the peak frequency (fp) at the maximum of (C′′(f)) corresponds to the representative frequency which is inversely proportional to the time constant (τ) of the system. The Ctot values and fp are 71 F g−1/45 mHz (ETC-900) and 65 F g−1/20 mHz (ETC-800) with the FWHM values of 0.91 and 0.88 for ETC-900 and 800, respectively. The peak shaped curve was not observed for ETC-700 indicating the very low rate capability. The results indicate that capacitance and rate capability of the porous electrode can be evaluated well by C′′(f) vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f plot. The Bode plot in the low-frequency region (Fig. 6e) with a phase shift of −80° is close to −90° indicating the nature of the ideal capacitive charge storage behaviour. Among the three samples, ETC-900 has the rapid and better capacitive response as a superior electrode for a supercapacitor.
f plot. The Bode plot in the low-frequency region (Fig. 6e) with a phase shift of −80° is close to −90° indicating the nature of the ideal capacitive charge storage behaviour. Among the three samples, ETC-900 has the rapid and better capacitive response as a superior electrode for a supercapacitor.
The electrochemical analysis for the ETC-900 sample in a 1 M Na2SO4 aqueous solution was also studied. The CV curves (Fig. 7a) are in a rectangular shape indicating the EDLC behaviour. From the GCD profiles shown in Fig. 7b and the Table S2 (ESI†), low gravimetric and volumetric capacitance was observed compared to that of an acidic electrolyte. This can be imputed to the smaller cationic radius, higher ionic mobility and larger molar ionic conductivity of H+ ions. The Na+ ions possess a large hydrated radius and the faradaic capacitance contribution is also insignificant which leads to low capacitance values.53 The cycle stability of the electrode was executed at a constant current of 3 A g−1 for 1000 cycles as shown in Fig. 7c. Electrochemical impedance spectroscopy (EIS) was used to reveal the ionic and electronic transport processes. As displayed in Fig. 7d, the Nyquist plot has a small ohmic resistance Rs = 2.6 Ω but is higher compared with that of an acidic electrolyte. The lower ohmic resistance is associated with the highest Pmax values. As shown in the Bode plot, the phase angle is 80°, confirming that the capacitance was contributed by an EDLC behaviour.
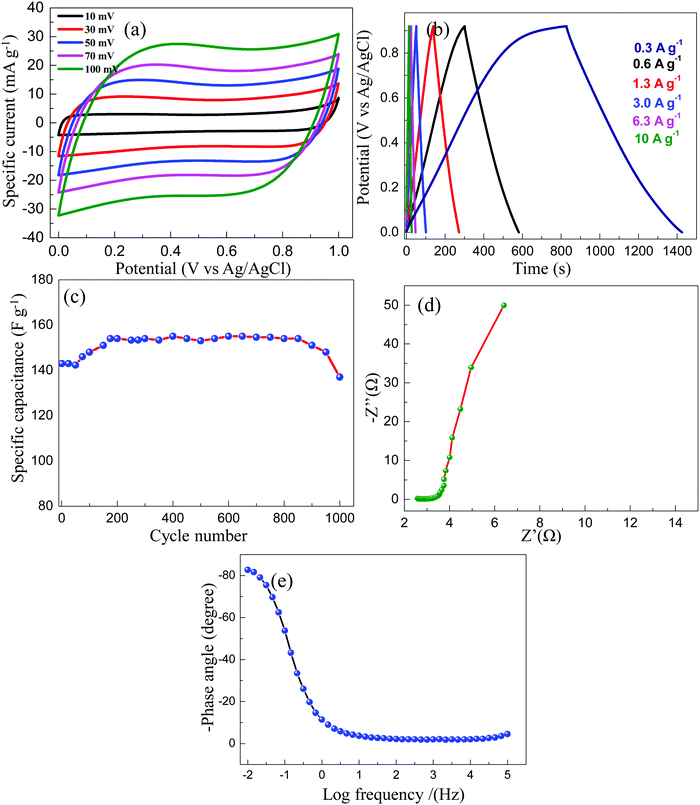 | ||
| Fig. 7 (a) CV profile of ETC-900 at 1 M Na2SO4, (b) GCD profile of ETC-900, (c) specific capacitance as a function of cycle number, (d) Nyquist plot of ETC-900, and (e) Bode plot of ETC-900. | ||
3.3. Performance of asymmetric supercapacitor device
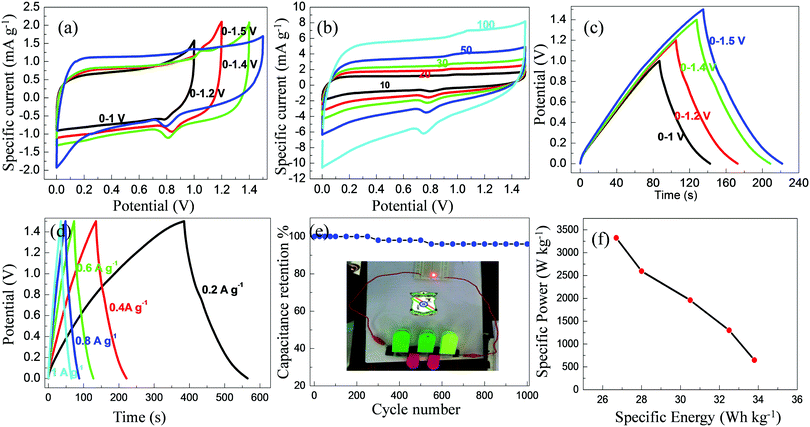
From the electrochemical and charge/discharge studies, it is ascertained that the ETC-900 electrode showed better capacitance compared to the other two samples. Therefore, ETC-900 was further subjected to its practical application in the two-electrode asymmetric cell. The asymmetric device was fabricated in the form of a coin cell bearing ETC-900 as the positive electrode and reduced graphene oxide (RGO) as the negative electrode in 1 M H2SO4 using a Whatman filter paper as the separator. The electrochemical property of the fabricated asymmetric device was investigated in a wide potential range of 0–1.5 V. The improvement of energy density is mutually related to the operating window. The P-doped carbon is able to achieve a high electrochemical window beyond the decomposition potential of water in an aqueous electrolyte. Hence, the assembled cell was tested at a higher operating voltage range 0–1.5 V by a gradual increase in potential above 1 V at 10 mV s−1 (Fig. 8a). Fig. 8b depicts the CV profiles of the asymmetric device at different scan rates ranging from 10 to 100 mV s−1. It is apparent that the CV profiles of the asymmetric device displayed a quasi-rectangular shaped curve with an operating cell voltage of 1.5 V. It should be noticed that with the increase of the scan rate, the areas under the CV curves showed a significant increase, which is usually observed for an ideal EDLC-based supercapacitor. Fig. 8c. illustrates the galvanostatic charge–discharge curves obtained for the fabricated asymmetric device at a current density of 0.4 A g−1 by varying the voltage range. The charge–discharge profiles at various current densities are shown in Fig. 8d. Obviously, the presence of nearly symmetrical charge–discharge curves of the device within the investigated voltage range of 0–1.5 V was in good agreement with the three-electrode CV data.The specific capacitance, energy density and power density for the two-electrode cell were calculated using the following equations:
| Csp (F g−1) = 4it/(m1 + m2)V | (7) |
| E = 1/2Csp(ΔV)2 | (8) |
| P = E/Δt, | (9) |
From the above calculations, the high specific capacitance is 100 F g−1 at a current density of 0.2 A g−1 and it still retains 79 F g−1 at 1 A g−1 with 79% capacitance retention signifying its excellent rate capability. The energy density has a direct relationship with the operating potential window. The operating potential window of phosphorus functionalized carbons is extended up to 1.3 V beyond the decomposition of water (1.23 V) as reported by Densia-Hulicova et al.54 The result indicates that storage of energy depends mainly on the quantity of phosphorus content which could stabilize the carbon surface and ultramicropores (0.65–0.83 nm) which are responsible for double layer formation. As reported by Huang et al., the wide electrochemical window of 1.5 V in sulfuric acid for phosphorus rich carbons is due to the positive effect of phosphorus functional groups for the stabilization of carbon surface and some redox reactions for the overall improvement of energy storage.55 The wide potential window of 0–1.5 V may be ascribed to the electrochemical reversible hydrogen storage in carbon materials. It is worth mentioning here that P-doped graphene can operate stably in aq. H2SO4 at 1.7 V with an excellent cycling performance and high energy densities.56 In accordance with this result, it is observed that this system also works in a wide window up to 1.5 V. The sufficient polyphosphate functional groups in carbon materials could enrich the strength of hydrogen adsorption on the carbon surface for the electrochemically stable potential window (ESPW) in the aqueous supercapacitor. Hence, the fabricated asymmetric device delivered a maximum specific energy of 33.8 W h kg−1 at a specific power of 648 W kg−1. The specific power achieved the highest value of 3323 W kg−1 at the specific energy of 27 W h kg−1 as shown in Fig. 8f. The obtained results suggest that the ETC-900-based asymmetric device holds great promise for potential applications in energy storage devices. The long-term cycling stability of the fabricated asymmetric device was studied over 1000 cycles at 1 A g−1 (shown in Fig. 8e). It is apparent that at the 1000th cycle, the asymmetric device exhibits almost 96% capacitance retention. The practical usability of the ETC-900-based asymmetric device electrode was examined by charging the device to a potential up to 1.5 V and then discharging it to light a commercial LED for more than 2 minutes.
From the overall results and discussion above, we have demonstrated that the ETC-900 has all the desirable features given below, and could act as a promising electrode for an advanced supercapacitor:
(i) enhancement of electrode wettability: the huge quantity of phosphorus and oxygen functional groups on the carbon surface favor the impregnation of the electrolyte into the inner core of the electrode material,
(ii) involvement of pseudocapacitance: redox-active functional groups such as P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O can furnish electroactive sites for capacitance enhancement,
O can furnish electroactive sites for capacitance enhancement,
(iii) generation of structural defects: the least electronegative phosphorus forms a C–P bond with carbon which increases the charge delocalization on the carbon atom directly to influence the surface morphology forming more open edged sites and the electron donor property of phosphorus increased the electrical conductivity of the ETC-900.
4. Conclusions
In summary, naturally abundant and unexplored bikki shells are utilized as carbon precursors for the preparation of porous P-doped carbon through a simple H3PO4 activation process, for use as an electrode in high performance supercapacitors. The resultant carbon at 900 °C has a reasonable specific surface area (858 m2 g−1), suitable PSD (1.2 nm), with huge quantity (2.5% P and 13.81% O by weight) of surface functional groups and high electrical conductivity, with ensuing excellent electrochemical properties. Furthermore, it has been witnessed that phosphorus with a dual nature such as a doping and gas expanding agent plays a crucial role in the creation of uniform micropores and increase in interlayer distance of the carbon leading to the formation of EDLCs. The pseudocapacitance contribution was observed owing to the electron-donor properties of phosphorus on a carbon material, which also enhances the supercapacitive performance. More captivatingly, P-doped porous carbon-900 can withstand a wide operating potential window in 1 M H2SO4 aqueous electrolyte at 1.5 V with an excellent cycle stability and a high energy density. The formation of P–O and P–C bonds is cogitated as the main factor for supercapacitive improvement. This analysis paves a way for probing and adoption of renewable resources, such as bikki shells, in the field of energy storage.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the Centre of Excellence for Environmental Studies (CoE-ES), TEQIP-II, Government College of Technology, Coimbatore, India by providing instrumentation facilities. We thank Lenin Elumalai, Metrohm Private Ltd, Chennai for providing NLDFT analysis.Notes and references
- X. Tan, S. Liu, Y. Liu, Y. Gu, G. Zeng, X. Hu, X. Wang, S. Liu and L. Jiang, Bioresour. Technol., 2017, 227, 359–372 CrossRef CAS PubMed.
- L. J. Brennan, M. T. Byrne, M. Bari and Y. K. Gun’ko, Adv. Energy Mater., 2011, 1, 472–485 CrossRef CAS.
- L. Yu, L. Hu, B. Anasori, Y. T. Liu, Q. Zhu, P. Zhang, Y. Gogotsi and B. Xu, ACS Energy Lett., 2018, 3, 1597–1603 CrossRef CAS.
- R. Zhong, Y. Liao, R. Shu, L. Ma and B. F. Sels, Green Chem., 2018, 20, 1345–1353 RSC.
- P. Simon and Y. Gogotsi, Acc. Chem. Res., 2013, 46, 1094–1103 CrossRef CAS PubMed.
- M. Beidaghi and Y. Gogotsi, Energy Environ. Sci., 2014, 7, 867 RSC.
- P. Simon and Y. Gogotsi, Nanoscience and Technology, Co-Published with Macmillan Publishers Ltd, UK, 2009, pp. 320–329 Search PubMed.
- M. Wahid, D. Puthusseri, D. Phase and S. Ogale, Energy Fuels, 2014, 28, 4233–4240 CrossRef CAS.
- L. L. Zhang, R. Zhou and X. S. Zhao, J. Mater. Chem., 2010, 20, 5983 RSC.
- G. Lota, K. Fic and E. Frackowiak, Energy Environ. Sci., 2011, 4, 1592 RSC.
- J. Chmiola, C. Largeot, P.-L. Taberna, P. Simon and Y. Gogotsi, Science, 2010, 328, 480–483 CrossRef CAS PubMed.
- H. Dai, Acc. Chem. Res., 2002, 35, 1035–1044 CrossRef CAS PubMed.
- W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339 CrossRef CAS.
- Z. Song, H. Duan, L. Li, D. Zhu, T. Cao and Y. Lv, Chem. Eng. J., 2019, 372, 1216–1225 CrossRef CAS.
- A. J. Yan, D. Zhu, Y. Lv and W. Xiong, Chin. Chem. Lett. DOI:10.1016/j.cclet.2019.05.035.
- A.-H. Lu, W.-C. Li, Y.-Y. Xu, W.-H. Qu and X.-Q. Zhang, Bioresour. Technol., 2015, 189, 285–291 CrossRef PubMed.
- J. Xu, Q. Gao, Y. Zhang, Y. Tan, W. Tian, L. Zhu and L. Jiang, Sci. Rep., 2015, 4, 5545 CrossRef PubMed.
- W. Qian, F. Sun, Y. Xu, L. Qiu, C. Liu, S. Wang and F. Yan, Energy Environ. Sci., 2014, 7, 379–386 RSC.
- C. Huang, T. Sun and D. Hulicova-Jurcakova, ChemSusChem, 2013, 6, 2330–2339 CrossRef CAS PubMed.
- K. Zou, Y. Deng, J. Chen, Y. Qian, Y. Yang, Y. Li and G. Chen, J. Power Sources, 2018, 378, 579–588 CrossRef CAS.
- G. Shao, X. Qin, W. Yang, A. Song, L. Kong and W. Yang, Carbon, 2017, 127, 557–567 Search PubMed.
- Y. Zhang, Q. Sun, K. Xia, B. Han, C. Zhou, Q. Gao, H. Wang, S. Pu and J. Wu, ACS Sustainable Chem. Eng., 2019, 7, 5717–5726 CrossRef CAS.
- F. Lai, G. Zhou, F. Li, Z. He, D. Yong and W. Bai, ACS Sustainable Chem. Eng., 2018, 6(3), 3143–3153 CrossRef CAS.
- Y. Guo and D. A. Rockstraw, Microporous Mesoporous Mater., 2007, 100, 12–19 CrossRef CAS.
- X. Li, E. Xin and J. Zhang, Electron. Mater. Lett., 2015, 11, 143–148 CrossRef CAS.
- Z. Lei, J. Zhang and X. S. Zhao, J. Mater. Chem., 2012, 22, 153–160 RSC.
- L. W. Daasch and D. C. Smith, Anal. Chem., 1951, 23, 853–868 CrossRef CAS.
- T. Panja, D. Bhattacharjya and J. S. Yu, J. Mater. Chem. A, 2015, 3, 18001–18009 RSC.
- C. Shi, K. Guo, T. Zhai, L. Hu and H. Li, Adv. Sustainable Syst., 2017, 1, 1600011 CrossRef.
- X. Ma, G. Ning, C. Qi, C. Xu and J. Gao, ACS Appl. Mater. Interfaces, 2014, 6, 14415–14422 CrossRef CAS PubMed.
- Y. Wang and P. M. A. Sherwood, Surf. Sci. Spectra, 2002, 9, 159–165 CrossRef CAS.
- L. Miao, X. Qian, D. Zhu, T. Chen, G. Ping, Y. Lv, W. Xiong, Y. Liu, L. Gan and M. Liu, Chin. Chem. Lett., 2019, 30, 1445–1449 CrossRef CAS.
- J. P. Paraknowitsch and A. Thomas, Energy Environ. Sci., 2013, 6, 2839–2855 RSC.
- H. H. Huang, Metals, 2016, 6, 23 CrossRef.
- M. Guo, J. Huang, X. Kong, H. Peng, H. Shui, F. Qian, L. Zhu, W. Zhu and Q. Zhang, New Carbon Mater., 2016, 31, 352–362 CrossRef.
- J. Qu, C. Geng, S. Lv, G. Shao, S. Ma and M. Wu, Electrochim. Acta, 2015, 176, 982–988 CrossRef CAS.
- Y. Wang, M. Zhang, Y. Dai, H.-Q. Wang, H. Zhang, Q. Wang, W. Hou, H. Yan, W. Li and J.-C. Zheng, J. Power Sources, 2019, 438, 227045 CrossRef CAS.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887 CrossRef CAS.
- M. Endo, T. Maeda, T. Takeda, Y. J. Kim, K. Koshiba, H. Hara and M. S. Dresselhaus, J. Electrochem. Soc., 2001, 148, A910 CrossRef CAS.
- Z. Li, L. Zhang, B. S. Amirkhiz, X. Tan, Z. Xu, H. Wang, B. C. Olsen, C. M. B. Holt and D. Mitlin, Adv. Energy Mater., 2012, 2, 431–437 CrossRef CAS.
- S. G. Lee, K. H. Park, W. G. Shim, M. S. Balathanigaimani and H. Moon, J. Ind. Eng. Chem., 2011, 17, 450 CrossRef CAS.
- L. Chen, T. Ji, L. Brisbin and J. Zhu, ACS Appl. Mater. Interfaces, 2015, 7, 12230–12237 CrossRef CAS PubMed.
- L. Wei, M. Sevilla, A. B. Fuertes, R. Mokaya and G. Yushin, Adv. Energy Mater., 2011, 1, 356–361 CrossRef CAS.
- K. Wang, N. Zhao, S. Lei, R. Yan, X. Tian, J. Wang, Y. Song, D. Xu, Q. Guo and L. Liu, Electrochim. Acta, 2015, 166, 1–11 CrossRef CAS.
- M. S. Balathanigaimani, W.-G. Shim, M.-J. Lee, C. Kim, J.-W. Lee and H. Moon, Electrochem. Commun., 2008, 10, 868–871 CrossRef CAS.
- L. Sun, C. Tian, M. Li, X. Meng, L. Wang, R. Wang, J. Yin and H. Fu, J. Mater. Chem. A, 2013, 1, 6462 RSC.
- M. Sivachidambaram, J. J. Vijaya, L. J. Kennedy, R. Jothiramalingam, H. A. Al-Lohedan, M. A. Munusamy, E. Elanthamilan and J. P. Merlin, New J. Chem., 2017, 41, 3939–3949 RSC.
- A. Bello, N. Manyala, F. Barzegar, A. A. Khaleed, D. Y. Momodu and J. K. Dangbegnon, RSC Adv., 2016, 6, 1800–1809 RSC.
- B. A. Mei, O. Munteshari, J. Lau, B. Dunn and L. Pilon, J. Phys. Chem. C, 2018, 122, 194–206 CrossRef CAS.
- H. D. Yoo, J. H. Jang, J. H. Ryu, Y. Park and S. M. Oh, J. Power Sources, 2014, 267, 411–420 CrossRef CAS.
- J. Lee, M. A. Abbas and J. H. Bang, ACS Appl. Mater. Interfaces, 2019, 11, 14126–14135 CrossRef CAS PubMed.
- J. H. Jang and S. M. Oh, J. Electrochem. Soc., 2004, 151, 571–577 CrossRef.
- B. Liu, M. Yang, H. Chen, Y. Liu, D. Yang and H. Li, J. Power Sources, 2018, 397, 1–10 CrossRef CAS.
- D. Hulicova-Jurcakova, A. M. Puziy, O. I. Poddubnaya, F. Suárez-García, J. M. D. Tascón and G. Q. Lu, J. Am. Chem. Soc., 2009, 131, 5026–5027 CrossRef CAS PubMed.
- C. Huang, T. Sun and D. Hulicova-Jurcakova, ChemSusChem, 2013, 6, 2330–2339 CrossRef CAS PubMed.
- B. Wang, D. Hulicova-Jurcakova, C. Huang, Y. Wen and L. Wang, Chem. – Eur. J., 2014, 21, 80–85 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nj04813h |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2020 |