 Open Access Article
Open Access ArticleThe non-stationary case of the Maxwell-Garnett theory: growth of nanomaterials (2D gold flakes) in solution†
Prakash
Natarajan‡
 a,
Awad
Shalabny‡
a,
Awad
Shalabny‡
 a,
Sumesh
Sadhujan
a,
Ahmad
Idilbi
a and
Muhammad Y.
Bashouti
a,
Sumesh
Sadhujan
a,
Ahmad
Idilbi
a and
Muhammad Y.
Bashouti
 *ab
*ab
aDepartment of Solar Energy and Environmental Physics, Swiss Institute for Dryland Environmental and Energy Research, J. Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Midreshet Ben-Gurion 8499000, Israel. E-mail: bashouti@bgu.ac.il
bThe IlSe-Katz Institute for Nanoscale Science & Technology, Ben-Gurion University of the Negev, Beersheba, 8410501, Israel
First published on 4th December 2019
Abstract
The solution-based growth mechanism is a common process for nanomaterials. The Maxwell-Garnett theory (for light–matter interactions) describes the solution growth in an effective medium, homogenized by a mean electromagnetic field, which applies when materials are in a stationary phase. However, the charge transitions (inter- and intra-transitions) during the growth of nanomaterials lead to a non-stationary phase and are associated with time-dependent permittivity constant transitions (for nanomaterials). Therefore, time-independence in the standard Maxwell-Garnett theory is lost, resulting in time dependence, εi(t). This becomes important when the optical spectrum of a solution needs to be deconvoluted at different reaction times since each peak represents a specific charge/energy transfer with a specific permittivity constant. Based on this, we developed a time-resolved deconvolution approach, f(t) ∝ εi(t), which led us to identify the transitions (inter- and intra-transitions) with their dominated growth regimes. Two gold ion peaks were precisely measured (322 nm and 367 nm) for the inter-transition, and three different polyaniline oxidation states (PAOS) for the intra-transition, including A (372 nm), B (680 nm), and C (530 nm). In the initial reaction time regime (0–90 min), the permittivity constant of gold was found to be highly dependent on time, i.e. fE ∝ εi(t), since charge transfer takes place from the PAOS to gold ions (i.e. inter-transition leads to a reduction reaction). In the second time regime (90–180 min), the permittivity constant of gold changes as the material deforms from 3D to 2D (fS ∝ ε3D–2D), i.e. intra-transition (combined with thermal reduction). Our approach provides a new framework for the time-dependent modelling of (an)isotropic solutions of other nanomaterials and their syntheses.
Introduction
The solution-based chemical process has been established decades ago as a successful strategy for the bottom-up growth of nanomaterials (nano-plasmonics and semiconductors).1–8 Today, it is the main synthetic route for fabricating almost all types of nanomaterials with well-controlled shapes, sizes, compositions and disparity.9–16 The solution mechanism has been discussed and described in detail, basically using the LaMer diagram (for the growth of nanomaterials) and Maxwell-Garnett theory (for light–matter interactions), thereby gaining a lot of insight into the processes involved regarding the nucleation, aggregation, growth state and absorbance.17–19 However, all of the abovementioned factors describe the solution growth in an effective medium, homogenized by a mean electromagnetic field, which applies in the Maxwell-Garnett theory when materials are in a stationary phase.19,20 Surprisingly, non-stationary cases, where the supplied charges (inter-transitions) or material deformation (intra-transitions) allow for substantial deviations from the effective permittivity constant, for example, in the initial and final regimes of the growth procedure, have scarcely been discussed before. In this work, we aim to initialize a more fundamental discussion of how to utilize the effective mean theory approach in non-stationary phases of light–matter interactions.In our case, we are interested in the time period for gold nucleation towards 2D gold formation, which is a dynamically changing process, during which the permittivity of the different elements of the mixture changes with time as the charge transfer (i.e. inter-transition for nucleation) and energy (i.e. intra-transition for 2D formation) continue. Thus, light as an external probe, was illuminated during the formation time to measure the transitions.21,22 Accordingly, we unraveled the inter- and intra-transitions by introducing the time-dependent Maxwell-Garnett permittivity (MGt) effective parameter, which to the best of our knowledge has never been done before. Based on this, we performed deconvolution based on the time-dependence model (MGt) at the different stages of the chemical reaction until the formation of the final state. Two main regimes were identified: (i) the first time regime (0–90 min), where the permittivity constant of gold was found to be highly dependent on time, i.e., fE ∝ εi(t) as charge transfer from the polyaniline oxidation states (PAOS) to gold ions (i.e. inter-transitions leads to a reduction reaction) takes place, and (ii) the second time regime (90–180 min), where the permittivity constant of gold changes as the material deforms from 3D to 2D (fS ∝ ε3D–2D), i.e. intra-transition.
After performing the deconvolution, we correlated the data analysis with the material, chemical kinetics and electronic properties of the 2D gold flakes. The data was cross-checked with data from SEM and AFM to follow the morphology, EBSD and XRD to follow the material crystallinity, KPFM to follow the electronic properties, and absorbance to follow the transitions and kinetics. Materially, we showed the formation of high-quality 2D gold flakes (monocrystalline) with ultra-sharpness (roughness below 1 nm) and a low level of residual impurities, regardless of the time, temperature and concentration. The formation of 2D monocrystalline gold flakes is particularly appealing as a basis for precise plasmonic nanostructures for the transport of both optical signals without grain boundaries or defects and for associated strongly enhanced local fields with marginal ohmic losses.23 Thus, these 2D structures combine the superior technical advantages of both photonics and electronics on the same chip.24 Chemically, we tuned the lateral area dimension of the flake from the nanoscale (250 nm2) to sub-millimetre area size, 0.006 mm2, while keeping the thickness always at the nanoscale (below 60 nm). Electronically, the KPFM studies revealed the electronic grade surface quality of the 2D flake (with work-function of 5.17 eV) as in a bulk. Optically, we identified three states with intra-transitions for the PAOS, A (372 nm),25 B (680 nm),26 and C (530 nm),27 and two states for the gold (322 nm and 367 nm) for inter-transitions.28 The presented model, i.e. MG (t), is simple and allows a time-resolved deconvolution and follows the evolution of the nanomaterial growth with its permittivity constant in the solution process. The model can be justified based on experimental data that already has been published by other researchers as well as by our group for different materials.
Experimental
Synthesis
A series of gold plates with different edge lengths were prepared via an improved wet chemical synthesis procedure based on our pervious publication.5 In a typical procedure, hydrogen tetrachloroaurate trihydrate (HAuCl4·3H2O, 0.18 mmol) was dissolved in 50 mL ethylene glycol at 80 °C with continuous stirring for 15 min in a 100 mL conical flask. Subsequently, 0.072 mmol aniline solution (0.73 mL from 1 M stock aniline solution) was added to the hot gold precursor solution. The resulting solution was stirred for 5 min and then stopped. The redox reaction continued for 3 h at 100 °C without stirring for the complete reduction and microplate growth of gold. After 3 h, the product was collected from the bottom and walls of the conical flask by mild sonication. The product was washed several times with absolute ethanol to clean and purify the gold microplates. The edge length of the gold plates was varied by modifying the reaction parameters such as [gold precursor], [aniline] and reaction temperature.Electron back scattering diffraction (EBSD)
The electron beam inside a Tescan Lyra 3 SEM was scanned over the sample in an angle of 70° to the sample normal. The backscattered primary electrons, which were partly diffracted by the crystal lattice, were collected by a phosphorous screen. The screen was imaged by a high-speed camera that collected the resulting, characteristic Kikuchi patterns. A software analyzed these patterns for crystal orientation and created maps of orientation, phase, grains and misorientation (=stresses). Since the silicon substrate was also crystalline and the EBSD software was not able to distinguish between Si and Au, the scanning parameters had to be chosen in a way that the EBSD camera recognized the Kikuchi pattern from Au, but not able to resolve the Si patterns.KPFM
The KPFM measurement showed a homogeneous contact potential difference (CPD) with a value of 170 meV lower than that of the SiO2 substrate. From here, the work function was determined, which was equal to 5.17 eV and fit the pure gold work function at room temperature.Model
Herein, we present an extension to the stationary situations and homogeneity approach of the MG model. This was mainly motivated by whether the commonly discussed permittivity time-independent approach is permissible or reliable to describe the solution growth of nanomaterials. One of the main questions we tried to address is how to deal with the inter and intra charge transfer at all stages of the reaction, i.e., how to deconvolute the optical absorbance spectra when the solution electromagnetic constants are not constant in time. The importance of this continuous-time deconvolution procedure arises from the two extreme boundary conditions present: at t = 0 min, we have only gold ions and at the end of the reaction (t = 180 min), we have 2D gold flakes. As mentioned above, the effective mean theory is supposed to give a very good approximation for solving the Maxwell equation when light interacts with matter.18 However, there are two main premises of the MG theory: (i) stationary medium, i.e., the permittivity parameter is constant in time, and (ii) inhomogeneous mixtures of two or more phases with different permittivity constants (εi) (e.g., solvents, colloidal solutions of metal nanoparticles) can be replaced with εeff ∝ f(εi,σi).29,30 The function (f) depends on all the εi, and σi represents the relative weights (concentrations) of the different composites. εi can be expressed as: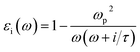 | (1) |
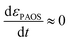 | (2) |
This is supported by the marginal shift in the absorbance spectrum of the different states. For example, state A shows a shift of 3 nm, while that of states B and C is about 10 nm. This holds even in the non-stationary phase when the total mass reserved. However, we distinguished between the two transitions, (i) inter charge transition, where the charges are transferred between PAOS (from state A to gold ions, as will be explained later); and (ii) when the gold nuclei are transferred from 3D to 2D gold flakes (shown later). Therefore, the time independence in the standard MG is lost and we have a time dependent εi(t), and in turn, εMG also becomes time dependent: εMG = εMG(t). Since dεPAOS/dt = 0, we propose the following:
| εMG(t) = fE[1 − θ(t − t1)] + fS[1 + θ(t1 − t)] | (3) |
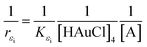 | (4) |
| εMG(t) = εMG × [[e−rtθ(t1 − t) + e−rt1[θ(t − t1) − θ(t − t2)]] + [e−rt1 + fS,2D(t − t2)]θ(t − t2)] | (5) |
The theoretical foundations on which the construction of the last equation are based on are as follows. The polymer will definitely have certain PAOS. In general, some of these states will start transferring charges and energy to the host medium and to other PAOS, as will be shown in the chemistry and kinetics parts. In the initial period, (t < t1), and the host medium will not undergo major changes in its structure other than starting to form gold nuclei. Thus, we assumed that until a certain time t1, the main change in the permittivity comes solely from the inter transitions (from ions), while some of the PAOS may transform between their own states. Thus, we get a contribution to εMG(t) only from the first term (in our case t1 = 60 min), i.e. after this time no charge will be supported to the gold ions. The first term in eqn (5) results from a solution of a first order differential equation with the initial condition: εMG(t = 0) = εMG. This gives an exponential decay, as discussed above and as will be shown later. Subsequently, it is expected to have a short period of time, which can be considered as a semi-relaxation time, where the remaining PAOS organize themselves energetically while the gold nuclei aggregate. At this intermediate stage, the shape of the gold nuclei is still unchanged (basically spherical) and the permittivity is constant (60 min < t < t2). This is depicted in the second term in eqn (5). At a later time, 2D gold flakes will form (thus creating the nano gold flakes) and all the decay rates will become constant with time, and thus the total effect on the time changing εMG(t) comes from the shape deformation of the 3D to 2D transition and described by fS,2D. This is the contribution of the third and last term in our formula, where we assumed a linear time-dependence while considering the shape deformation through the parameter fS,2D. In our case, we t2 = 90 min. The above formula is valid until the reaction has stopped at tfinal = 180 min. It should be mentioned that our formula for εMG(t) is a continuous function of time (t), while not differentiable at t1 and t2. The second term describes the shape deformation at the second stage of the reaction, where we averaged the initial dielectric constant εMG (t = t1) and the final value (t1 ≪ t).
Chemistry
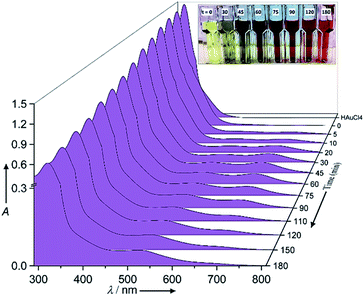
The chemical reaction details were fully described in the Experimental section. Fig. 1 shows the normalized raw data of the UV/Vis spectra with reaction time as function of wavelength ranging from 280 nm to 820 nm. In the corresponding UV/Vis spectra, and prior to the redox reaction, two peaks are apparent at 322 ± 3 nm and 367 ± 1 nm, which represent the ligand to metal charge transfer and the metal ion–EG interaction, respectively (see ESI-1†).28 After the redox reaction began and upon the addition of aniline, the UV/Vis spectra showed three additional peaks at 372 ± 1 nm, 680 ± 10 nm and 530 ± 10 nm, which represent the oligo/poly(semiquinone) radical cation (oxidation state A), pernigraniline (poly(quinoneimine) cation (oxidation state B), and pernigraniline base (poly(quinoneimine) (oxidation state C) of the polyaniline (PA), respectively.26,27,31 Over time, the intensity of the gold ions at 322 ± 3 nm and 367 ± 1 nm decreased monotonously but with different rates, while the PAOS showed an inverse tendency. With further oxidation, the intensity of the B and C peaks at 680 ± 5 nm and 530 ± 10 nm, respectively, increased, a change that was accompanied by a gradual decrease in the intensity of the A (at 372 ± 1 nm) peak. These changes correspond to the different inter and intra transitions occurring between the PAOS and the gold ions, respectively. Since all three states (A, B and C) have a similar chemical structure, we can assume that they have similar permittivity parameters.26,32However, the as the charge transferred from the PAOS to gold ions and formed gold nuclei, the permittivity parameter of the gold ions/nanoparticle was not constant and is time dependent (see the Model section, eqn (5)). Visually, the charge transfer can be followed by the color of the reaction (see Fig. 1). For example, at t = 0 min, and before aniline was added, the solution color was yellow. When the solution was heated to 80 °C, it remained green (#8A8871) for less than 30 min, after which its color slowly changed to “blue” dove gray (#696363) (t = 45–75 min). As the reaction proceeded, the solution color again changed, becoming a “red” Chico color (#A0645C) at time exceeding 90 min and until the end of the reaction (t = 180 min, see Fig. 1).
Structure
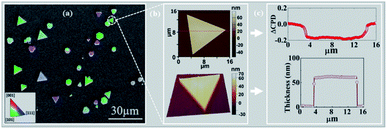
2D gold flakes started to be obtained at the second regime, i.e. t > 90 min, when all the inter charge transfer occurred. The structure of the synthesized 2D gold flakes was investigated via EBSD in more detail to reveal the interplay between the chemical process with the underlying crystal structure of the 2D flakes. Fig. 2a shows the secondary electron (SE) micrograph of the 2D flakes on the Si substrate. The overlap of the EBSD image with the SEM image gives two-dimensional information on the crystal orientations of the probed spot. The different colors indicate grains of different orientations (Fig. 2a). Relatively large grains (e.g., the green areas) can be observed with an area of up to several tens of μm2. Thus, the EBSD measurements together with the SEM image (area of 100 × 100 μm2) show the perfect monocrystalline quality of the single flakes, consistent with the [111] zone axis of the face-centered cubic (fcc) Au and consistent with ICSD 44362. The inset is the color that codes the orientation in the IPF-Y (inverse pole figure Y) direction. This is in good agreement with our previous study and TEM measurements.5 The X-ray pattern of the gold flakes shows a perfect diffraction from the [111] zone (see ESI-2†). To demonstrate further the quality of a single flake, AFM images were obtained and shown in Fig. 2b. As is clearly shown, we obtained a very smooth surface (2D image), which was supported by 3D image for the single flake and confirms the high quality and homogeneity. This was further supported by measuring the work function and roughness along the red line, as shown in Fig. 2c. Fig. 2c shows a uniform work function of 5.17 ± 0.02 eV (ΔCPD = −0.2 eV relative to the reference sample SiO2) with a homogenous thickness of 55 nm and roughness of ±1 nm. The work function value (measured by KPFM) coincides with that in the literature for pure gold, which is the basis for plasmonic and optical nano-circuitry and quantum computation applications.The kinetic case
To follow the kinetics of the PAOS and gold nanostructures, we applied our model to the UV-Vis spectra. We could in situ resolve the inter-charge transfer to the gold ions and the intra-transitions of PAOS (Fig. 3). As already mentioned, the different PAOS show similar structures, thus we can assume that they have a similar permittivity constant and the intra-transitions are constant in time. This is a crucial observation since by implementing the formula for performing the subtracted deconvolution, the pre-factor, εMG, has to be calculated based on the different permittivities of all species.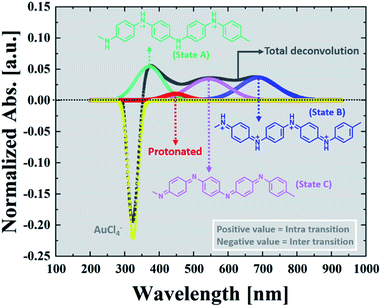 | ||
| Fig. 3 Subtracted deconvolution of the UV/Vis spectra, showing an example of the deconvoluted spectra for t = 20 min. | ||
Since all the PAOS have the same permittivities then a great simplification in calculating εMG is obtained. Therefore, we posited the full width at half-maximum (fwhm) to be similar for all the PAOS and constant over the reaction course (57 ± 8 nm).25 In contrast, the Au spectra showed a varying fwhm, which become larger (∼50%) with the reaction time (from 12.4 nm to 21.6 nm). The observed differences in the fwhm values of the components of the Au spectra are attributed to the charge transfer and to the gradual permittivity constant transition (from ions to metal). Note that we subtracted the “ground absorbance” values of the Au particles and of the solvent (ethylene glycol) to obtain the absorbance of only the PAOS and gold ions. Accordingly, we deconvoluted the optical spectra at different reaction times in Fig. 1. Thus, all the positive spectra represent the PAOS (intra transitions), while the negative spectra represent the Au ions (inter transition). When combining the two sets of spectra, we obtained excellent agreement between our model-based theoretical spectra with that recorded in the experiments (Fig. 3–6). Consequently, our subtracted deconvolution model based on the time-dependent permittivity constant works sufficiently well.
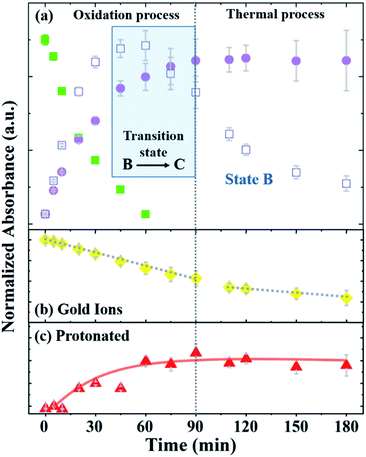
Fig. 4 depicts the normalized intensity values of the PAOS peaks (IPAOS) and the Au peaks (IAu) versus the reaction time, as determined by the fitted data. The rates of the three PAOS states A, B and C [KPAOS = ΔIPAOS/Δt], and the gold ions, [KAu = ΔIAu/Δt] show two main reaction time regimes: (i) 0–90 min, and (ii) 90–180 min (Fig. 4). For the PAOS, in the first regime, we can define two phases (0–60 min and 60–90 min). In first phase, an inter-transition is observed, where state A is transferred equally to B and C, i.e.: −[KA]0–60min = [KB]0–60min + [KC]0–60min, with the rate of [KA]0–60min = −2.0 × 10−3 min−1, where [KB]0–60min = 1.1 × 10−3 min−1 and [KC]0–60min = 0.9 × 10−3 min−1. Based on the model, the kinetics of A, [KA], follows the first pseudo-order reaction. This experimental observation is depicted in our model by the existence of only one decay rate parameter, r, rather than a multiple of decay rates and represents the decay rate of state A (Fig. 4a). This is also a result of solving the first order differential equation, resulting in the exponential factor in the model. In the second phase, the inter-transition stops (no more oxidation of gold ions), and an intra-transition starts, where state B oxidizes to state C, but at an inversed rate, −[KB]60–90min > [KC]60–90min. However, in the second regime (90–180 min), state C is constant with time, i.e., [KC]90–180min = 0, while state B continues to lose its weight, but decomposes thermally by the rate of [KB]90–180min = −0.8 × 10−3 min−1 (Fig. 4a).
Thus, we can define the two regimes based the PAOS kinetic analysis where the first regime (0–90 min) is controlled by the oxidation process of PA (i.e. inter-transition), while the second regime (90–180 min) is controlled by the thermal decomposition process (no more inter-transition). It is worth pausing and clarifying the agreement of the above kinetic analysis with the third term in our master formula (eqn (5)). At the period of time: 90 < t < 180 min, all the intra-transitions have stopped, states A and B become irrelevant and state C becomes constant. The only remaining dynamic factor is the formation of 2-D gold flakes. This shape deformation is exactly the origin of the linear third term in eqn (5). The difference between the intra-transition rates in the two regimes indicates further the existence of two different mechanisms, protonation in the first regime (oxidation of PA) and thermal decomposition in the second regime. Similar kinetic behavior was observed in the inter-transition rates in the case of gold ions, i.e., KAu = ΔIAu/Δt, which shows the same two regimes. In the first regime, [KAu]0–90min = 6 × 10−3 min−1 was higher by three times relative to the second regime of [KAu]90–180min = 2 × 10−3 min−1 (Fig. 4b). The different rates (triple rate factor) indicate that [KAu] is affected by the two mechanisms in the first regime and only by the thermal reduction in the second regime via the ethylene glycol solvent (since there is no more state A in the second regime).33
Considering these results, we suggest the following scenario for the inter- and intra-transitions: state A undergoes rapid oxidation (factor of 2) to produce states B and C until it is completely eliminated (t = 60 min). The oxidation process consists of consuming protons by converting the benzoid groups to quinoid groups.25 This is followed by the appearance of a peak at 440 nm (Fig. 4c), which represents the protonated quinoid groups. Subsequently, there is a short interval, from 60 min to 90 min, as a transition state, during which we observed a rapid intermediate transition from state B to state C via the deprotonation of B. During this short period of time, the effective MG is constant since the B and C states are almost identical in structure and the transition of gold from 3-D to 2-D flakes has marginally started. This is depicted in our master formula (eqn (5)) by the second term in the square brackets. However, after 90 min, the deprotonation stopped and state B began to decompose thermally (Fig. 4a), and therefore, the concentration of state C became constant (the suggested reaction pathway is schematically drawn in ESI-3†). This scenario is supported not only by the fact that no further deprotonation was possible (after 90 min), but also by the mass conservation law. The total mass (Mtot = A + B + C) remains constant until B starts to decompose, where the mass becomes lower than Mtot in the second regime, and therefore, dεPAOS/dt will be ≈ 0 (see ESI-4†). In the second regime along the time axis, state C reached a saturation level, i.e., [KC]90–180min = 0, and therefore, the oxidation ceased (Fig. 4a). Additional support for the intra-transition is apparent in the reduction mechanism of the gold ions (inter transition). Accordingly, we followed the concentration of the gold ions, as explained earlier (Fig. 4b). After 90 min, the protonated quinoid became constant, indicating the termination of the polyaniline-driven reduction of AuCl4−. Therefore, the reduction rate of the gold ions became thermal only in the second regime. This is also found to be in good agreement with the non-constant ratio between the gold peaks (322 nm and 367 nm) in the two regimes since the permittivity constant became different in the two regimes and fE ≠ fS. The last inequality is obvious since the two functions have two completely different physical origins. The above experimental observations and the physical insight behind the existence of the two distinct regimes were the basis for constructing our master formula for εMG(t), in which the two theta functions distinguish between regime (i) and regime (ii), where two different mechanisms (charge transfer in the first part with mass conservation) intact and shape deformation in the second part, and the mass lost due to thermal decomposition of state B affects the effective time-changing permittivity parameter.
Correlation between the PAOS and gold shape
To correlate the different PAOS states with the growth of the anisotropic 2D gold flakes, we sampled the solution (sample volume = 100 μL) in the two regimes and in the transition state and measured the structure with SEM. SEM enabled us to rapidly determine the Au particle sizes and shapes, as shown in Fig. 5a–c.Additional information based on AFM can be found in ESI-5.†Fig. 5a represents the first phase (0–60 min) in regime (i) and shows faceted nuclei with sizes ranging from 50 nm to 300 nm. Note that the growth of Au nuclei can be minimized by adding additional surfactant (CTAB) and by replacing ethylene glycol with water as the solvent (shown in ESI-6†). Since state A was completely converted to states B and C, the oxidizing capability of polyaniline reached the minimum and the Au reduction decreased (second phase in regime (i)), and hence the Au seeds aggregated to reduce the energy of the system (three examples are marked in blue in Fig. 5b). This tendency can also be understood in terms of Le Chatelier's principle. As the seeds are formed, the Gibbs energy of the system increases. The seeds are brought closer together to reduce this increase in energy (state B rate of oxidation induces aggregation), and therefore acts to counteract the perturbation. In this phase (60–90 min), the seeds undergo aggregation and begin to form nano-flakes in regime (ii). Therefore, the permittivity constant is not time dependent in this regime, as supported by eqn (5). This indicates that the internal migration to produce 2D flakes with uniform thickness in regime (ii) is cause due to state C. The anisotropic growth in the second regime starts to generate gold flakes with lateral edge lengths of several microns. However, the horizontal lengths remain in the nanoscale due to the capping effect of state C on the (111) plane direction, which emphasizes the role of state C in this regime.34,35 After 90 min of reaction, the aggregated structures are replaced with more regular Au microplates, indicating that the Au seeds coalesce into 2D flakes (Fig. 5c). According to the comparison of the different stages of the reaction (Fig. 3 and 5), it can be concluded that the 2D flakes grow at the expense of the 3D particles, which is known as the “crystal nucleation and growth” model. Therefore, we can explain the transformation of 3D aggregates to 2D flakes by the differences in the growth rates of the various crystallographic facets. Briefly, once the nucleation starts, the seeds coalesce to reduce the surface energy. Since the {111} facet has a lower surface energy compared to the other facets such as {110} and {100}, the oxidized aniline adsorbs on the {111} plane and acts as a capping agent. This process facilitates the addition of the gold atoms to the high energy facets ({110} and {100}) to release the maximum energy. The Au seeds fuse through the {110} and {100} facets to form thin 2D flakes (Fig. 5b). After the formation of the 2D flakes, the growth continues very fast at the edges, i.e. lateral direction due to the high surface energy of {110} and {100} facets and slow growth taking place in the vertical {111} direction. Therefore, the converted 2D flakes can expand to micrometre flakes but with nanometre thickness.35–39 Actually, the differences in the growth rates of the different facets are the main source for the changes in the permittivity constant in the second regime.
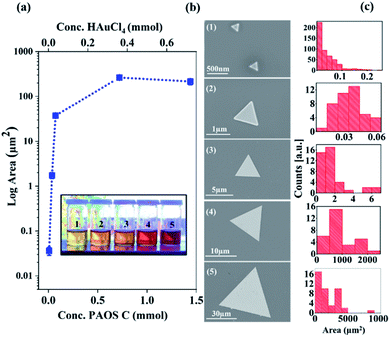
Accordingly, we conclude that controlling the concentration of state C in the second regime enables control of the generated 2-D Au flakes. Indeed, as shown in Fig. 6, the 2-D flakes can be tuned from the nanoscale to the microscale by adjusting the concentration of state C (factor scale, Fig. 6a).
We found that by increasing the state concentration by a factor of 10, it resulted in an increase in flake area by 106 orders of magnitude (from an area of nanometer size, 250 nm2, to one of millimeter area size, 0.006 mm2, Fig. 6a and b). These results are based on the SEM analysis of 106 particles, as shown in Fig. 6c. The solution color darkened as a function of the factor scale (see inset in Fig. 6). The differences in color are due to the higher concentration of state C that was produced over the course of the reaction.
Conclusions
Herein, we presented a time-resolved deconvolution model for the solution growth of nanomaterials (2D monocrystalline gold flakes). For the first time, we calculated a time-resolved permittivity constant with the related inter- and intra-charge and energy transitions. In each regime, a permittivity function was applied (fE in the first regime and fS in the second regime). The model proposed here can accurately describe the different regimes, nucleation and growth with a transition state of the agglomeration, which fits with the LaMer model. The function fE is related to the inter-charge transfer, and thus, this function will be equal to zero when the oxidation of PANI is completed. This was identified in the present work by following the PAOS peaks in the UV-Vis spectra. At t = 60 min, the base form of PANI is finished (no more inter-charges). After this time, the transition state from 3D to 2D starts, mainly by aggregation of the gold nuclei. t1 = 60 min is a critical time that has been defined to follow the kinetics of the PANI oxidation and relate it to the crystallization mechanism. At t2 = 90 min no more oxidation occurs, and deformation starts. We successfully showed that our proposed model of the time-dependent MG effective approach is relevant for a transient and non-stationary phase of light–matter interactions, and can be used to describe the change with time of the effective permittivity parameter in solutions. This model allowed us to perform a (subtracted) deconvolution, from which we extracted valuable insight regarding the charge and energy transfers between a polymer and a host medium. Consequently, we managed to identify and correlate the different PASO with the gold flake growth starting from the ion form to the end of the reaction. Our approach also opens the window for establishing time-continuous monitoring of nanoscale layer formation by applying the MGt theory presented above. Accordingly, we can also examine the time-dependent electromagnetic properties of a growing nanomaterial. These properties are crucial to determine the usefulness and the technological applicability of nano monolayers in actual devices. Finally, the plasmonic nanostructures that we can fabricate based on the 2D monocrystalline gold are able to perform logical operations with photons only.25,40 The use of gold over other materials is promising due to its plasmon resonance in the visible regime and its stability against oxidation in ambient air, contrary to other metals such as silver.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a MAOF Grant from the Council for Higher Education in Israel for new faculty members. Dr P. Natarajan is thankful for the SEEDER scholarship for post-doctoral students. Awad Shalabny and Sumesh Sadhujan are appreciative of the institutional scholarships for PhD students they received from Ben-Gurion University of the Negev. MYB gratefully acknowledges A. M. Salaheldin for his help to understand the growth mechanism of the gold flakes.References
- E. Krauss, R. Kullock, X. Wu, P. Geisler, N. Lundt, M. Kamp and B. Hecht, Cryst. Growth Des., 2018, 18, 1297–1302 CrossRef CAS.
- N. Li, P. Zhao and D. Astruc, Angew. Chem., Int. Ed., 2014, 53, 1756–1789 CrossRef CAS PubMed.
- F. Wang and X. Wang, Nanoscale, 2014, 6, 6398–6414 RSC.
- K. Bazaka, I. Levchenko, J. W. M. Lim, O. Baranov, C. Corbella, S. Xu and M. Keidar, J. Phys. D: Appl. Phys., 2019, 52, 183001 CrossRef CAS.
- B. Hoffmann, M. Y. Bashouti, T. Feichtner, M. Mačković, C. Dieker, A. M. Salaheldin, P. Richter, O. D. Gordan, D. R. T. Zahn, E. Spiecker and S. Christiansen, Nanoscale, 2016, 8, 4529–4536 RSC.
- S. Girish Kumar and K. S. R. Koteswara Rao, Nanoscale, 2014, 6, 11574–11632 RSC.
- T. K. Sau and C. J. Murphy, J. Am. Chem. Soc., 2004, 126, 8648–8649 CrossRef CAS PubMed.
- B. Weintraub, Z. Zhou, Y. Li and Y. Deng, Nanoscale, 2010, 2, 1573–1587 RSC.
- M. Bashouti and E. Lifshitz, Inorg. Chem., 2008, 47, 678–682 CrossRef CAS PubMed.
- X. Wu, R. Kullock, E. Krauss and B. Hecht, Cryst. Res. Technol., 2015, 50, 595–602 CrossRef CAS.
- W. Van Der Stam, Q. A. Akkerman, X. Ke, M. A. Van Huis, S. Bals and C. De Mello Donega, Chem. Mater., 2015, 27, 283–291 CrossRef CAS.
- L. Manna, E. C. Scher and A. P. Alivisatos, J. Am. Chem. Soc., 2000, 122, 12700–12706 CrossRef CAS.
- L. Qu and X. Peng, J. Am. Chem. Soc., 2002, 124, 2049–2055 CrossRef CAS PubMed.
- J. D. Holmes, K. P. Johnston, R. C. Doty and B. A. Korgel, Science, 2000, 287, 1471–1474 CrossRef CAS PubMed.
- X. Peng, L. Manna, W. Yang, J. Wickham, E. Scher, A. Kadavanich and A. Alivisatos, Nature, 2000, 404, 59–61 CrossRef CAS PubMed.
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325 CrossRef CAS.
- R. G. Barrera, G. Monsivais and W. L. Mochan, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 5371–5379 CrossRef PubMed.
- J. C. Maxwell Garnett, Philos. Trans.: Math., Phys. Eng. Sci., 1904, 203, 359–371 Search PubMed.
- V. K. Lamer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- A. Sihvola, Subsurf. Sens. Technol. Appl., 2000, 1, 393–415 CrossRef.
- I. Y. Sapurina and J. Stejskal, Russ. Chem. Rev., 2010, 79, 1123–1143 CrossRef CAS.
- W. S. Huang and A. G. MacDiarmid, Polymer, 1993, 34, 1833–1845 CrossRef CAS.
- J. S. Huang, V. Callegari, P. Geisler, C. Brüning, J. Kern, J. C. Prangsma, X. Wu, T. Feichtner, J. Ziegler, P. Weinmann, M. Kamp, A. Forchel, P. Biagioni, U. Sennhauser and B. Hecht, Nat. Commun., 2010, 1, 150 CrossRef PubMed.
- Y. Li, Z. Li, C. Chi, H. Shan, L. Zheng and Z. Fang, Adv. Sci., 2017, 4, 1600430 CrossRef PubMed.
- H. Jun, H. Lihong, Z. Xiuli, C. Xuesi, W. Yen and J. Xiabin, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 1124–1135 CrossRef.
- I. Sapurina and J. Stejskal, Polym. Int., 2008, 57, 1295–1325 CrossRef CAS.
- F. F. C. Bazito, L. T. Silveira, R. M. Torresi and S. I. Córdoba de Torresi, Phys. Chem. Chem. Phys., 2008, 10, 1457–1462 RSC.
- M. E. Aguirre, G. Perelstein, A. Feldhoff, A. Condó, A. J. Tolley and M. A. Grela, New J. Chem., 2015, 39, 909–914 RSC.
- V. A. Markel, J. Opt. Soc. Am. A, 2016, 33, 2237–2255 CrossRef PubMed.
- V. A. Markel, J. Opt. Soc. Am. A, 2016, 33, 1244–1256 CrossRef PubMed.
- T. M. Kabomo and M. S. Scurrell, Polym. Adv. Technol., 2016, 27, 1195–1203 CrossRef CAS.
- Z. Ding, T. Sanchez, A. Labouriau, S. Iyer, T. Larson, R. Currier, Y. Zhao and D. Yang, J. Phys. Chem. B, 2010, 114, 10337–10346 CrossRef CAS PubMed.
- Z. Guo, Y. Zhang, Y. DuanMu, L. Xu, S. Xie and N. Gu, Colloids Surf., A, 2006, 278, 33–38 CrossRef CAS.
- G. Lin, W. Lu, W. Cui and L. Jiang, Cryst. Growth Des., 2010, 10, 1118–1123 CrossRef CAS.
- X. Bai, L. Zheng, N. Li, B. Dong and H. Liu, Cryst. Growth Des., 2008, 8, 3840–3846 CrossRef CAS.
- G. Kaune, M. A. Ruderer, E. Metwalli, W. Wang, S. Couet, K. Schlage, R. Röhlsberger, S. V. Roth and P. Müller-Buschbaum, ACS Appl. Mater. Interfaces, 2009, 1, 353–360 CrossRef CAS PubMed.
- Z. Guo, Y. Zhang, A. Xu, M. Wang, L. Huang, K. Xu and N. Gu, J. Phys. Chem. C, 2008, 112, 12638–12645 CrossRef CAS.
- B. Radha and G. U. Kulkarni, Cryst. Growth Des., 2011, 11, 320–327 CrossRef CAS.
- W. L. Huang, C. H. Chen and M. H. Huang, J. Phys. Chem. C, 2007, 111, 2533–2538 CrossRef CAS.
- M. Hoffmann, T. Feichtner and S. Christiansen, Mater. Today, 2016, 19, 240–241 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00636b |
| ‡ PN and AS are equally contributed. |
| This journal is © The Royal Society of Chemistry 2020 |


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: