Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High performance photocatalytic and thermoelectric two-dimensional asymmetrically ordered Janus-like MXene alloys†
Zicong Marvin
Wong
 ,
Tianqi
Deng
,
Tianqi
Deng
 ,
Wen
Shi
,
Wen
Shi
 ,
Gang
Wu
,
Gang
Wu
 ,
Teck Leong
Tan
,
Teck Leong
Tan
 * and
Shuo-Wang
Yang
* and
Shuo-Wang
Yang
 *
*
Institute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, 138632, Singapore. E-mail: yangsw@ihpc.a-star.edu.sg; tantl@ihpc.a-star.edu.sg
First published on 25th June 2020
Abstract
MXenes are two-dimensional transition metal carbides, nitrides, and/or carbonitrides which display extensive versatility in their elemental composition for tuning and optimization of their functional properties. In this work, by using a multiscale approach of density functional theory calculations, cluster expansion method, and Monte Carlo simulations, we systematically investigate the Ti2(1−x)Mo2xCO2 alloy system of two-dimensional Ti2CO2 and Mo2CO2 MXenes with 0 < x < 1. From the alloy formation energies, we identify the stable ground-state and report the possible existence of an asymmetrically ordered Janus-like MXene alloy TiMoCO2. This alloy is theoretically validated to be stable thermodynamically, mechanically, and thermally, with a high order–disorder phase transition temperature of ∼640 K. Importantly, TiMoCO2 is a semiconductor with a band gap of 0.60 eV and its valence band maximum and conduction band minimum are located on opposite sides of the MXene monolayer. As such, the asymmetric configuration generates an intrinsic dipole moment, which realigns the conduction and valence band edges, permitting photocatalytic redox water-splitting to favorably occur with a higher solar absorption efficiency in the visible-infrared region due to the smaller band gap. From the transport calculations, we propose the TiMoCO2 MXene alloy to exhibit high room temperature n- and p-type power factors of 49.8 μW cm−1 K−2 and 15 μW cm−1 K−2, respectively, outperforming other related experimentally synthesized Ti–Mo based MXene alloys and even similar to that of p-doped SnSe which is one of the best performing thermoelectric materials. All these indicate the stable asymmetrically ordered Janus-like TiMoCO2 MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material, paving the way for more stable Janus-like MXenes with interesting and outstanding functional properties to be discovered.
1. Introduction
MXenes are a large family of two-dimensional (2D) layered transition metal carbides, nitrides, and/or carbonitrides discovered in 2011, with the structural formula Mn+1Xn (where M is transition metal, and X is C and/or N, with n = 1, 2, 3, or 4).1–3 They are typically derived from their MAX phase precursors by the selective chemical etching of the A-group elements such as Al or Ge,4 although other synthesis approaches are feasible as well.5,6 Although post-chemical etching results in MXenes to be mostly terminated with a mixture of functional groups, e.g., O, OH, and F, a recent study has shown that exclusively O-terminated MXenes, i.e., Mn+1XnO2, can be attainable via post-treatment under vacuum and subsequent exposure to O2 gas at slightly elevated temperatures.7 Owing to the compositional tunability, elemental flexibility, 2D crystallinity, excellent electrical conductivity, and hydrophilicity, MXenes have been under the spotlight for a wide spectrum of research spanning from energy,3 environment,8 and even biomedical applications.9 This rich chemistry exhibits the versatility of MXenes in the design of materials.As the world becomes increasingly conscious towards climate change and sustainability, alternative green energy sources such as hydrogen production from photocatalytic water-splitting have become heavily sought for as a clean fuel. As such, MXenes have been garnering intense research interest in photocatalytic water-splitting.10–12 Typically, a practical water-splitting photocatalyst has to fulfill 3 main requirements: (1) band gap > 1.23 eV such that the band edges straddle water redox potentials; (2) high solar photon absorption; and (3) a low electron–hole recombination rate.13,14 Moreover, 2D materials like MXenes display high specific reaction surface and the low dimensionality minimizes the distances that photogenerated electrons and holes have to migrate to the reaction interface, reducing the possibility of electron–hole recombination and enhancing the photocatalytic performance. Currently, only a handful of MXenes are theoretically identified to exhibit semiconducting behaviors, e.g., Ti2CO2, Zr2CO2, Hf2CO2, and Sc2CT2 (where T = O, F, OH).15 Unfortunately, these MXenes possess either insufficient band gaps, misaligned band edges, or weak solar absorption, which compromise their photocatalytic performance.16 Our previous work has suggested stoichiometric engineering of the disordered alloy of Ti2CO2 and Zr2CO2, i.e., Ti2(1−x)Zr2xCO2 where x = 0.2778, to show enhanced photocatalytic capabilities.17 However, it is possible that the random distribution of Ti and Zr in the M-sites could lead to disorder-based scatterings which may impede the mobility of the photogenerated electrons and holes.18 Therefore, ordered semiconductor MXene alloys with reduced disorder-based scatterings would be desirable.
Likewise, another abundant but inefficiently utilized energy source is waste thermal energy, for which, thermoelectric (TE) materials can be exploited for conversion into useful electrical energy. The efficiency of thermoelectric materials can be evaluated using a dimensionless figure-of-merit, defined as 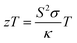 , where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity, and T is the temperature. As such, a good performing thermoelectric material should possess a high power factor S2σ and low κ, although these two parameters are usually negatively correlated.19 Recently, a few Mo-based MXene flexible thin films, e.g., Mo2C, Mo2TiC2, and Mo2Ti2C3, have been experimentally investigated for their thermoelectric performance.20 The Mo2TiC2 film displays the highest S2σ of ∼3.09 μW cm−1 K−2 at 800 K (and ∼0.5 μW cm−1 K−2 at 300 K) among these thin films. While these values are not exceptional, one can exploit the compositional versatility of MXenes to further optimize, tune, and create a better thermoelectric material.
, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity, and T is the temperature. As such, a good performing thermoelectric material should possess a high power factor S2σ and low κ, although these two parameters are usually negatively correlated.19 Recently, a few Mo-based MXene flexible thin films, e.g., Mo2C, Mo2TiC2, and Mo2Ti2C3, have been experimentally investigated for their thermoelectric performance.20 The Mo2TiC2 film displays the highest S2σ of ∼3.09 μW cm−1 K−2 at 800 K (and ∼0.5 μW cm−1 K−2 at 300 K) among these thin films. While these values are not exceptional, one can exploit the compositional versatility of MXenes to further optimize, tune, and create a better thermoelectric material.
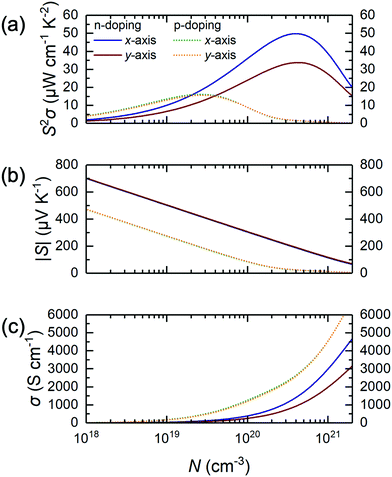
As such, we wonder whether it is possible to surpass these limitations to discover a novel alloying approach to make MXene photocatalysis and thermoelectric properties better for sustainability applications. Herein, we investigate the substitutional alloy MXene Ti2(1−x)Mo2xCO2 and attempt to predict its synthesizability, noting that its thicker counterparts, Mo2TiC2 and Mo2Ti2C3, have been successfully synthesized and are well-studied.20–22 Using a multiscale approach of density functional theory (DFT) calculations, cluster expansion (CE) method, and Monte Carlo (MC) simulations,23–27 we screened through a total of more than 9 million different Ti2(1−x)Mo2xCO2 MXene alloy configurations with the 3 different types of O-termination. We then systematically map out their structure–stability relationship by validating the thermodynamically stable alloy ground-state(s), followed by the assessment of their suitability as water-splitting photocatalysts and thermoelectric materials, using their respective figure-of-merit derived from electronic, optical, and thermal calculations. Thus, for the first time, we report the possible existence of an asymmetrically ordered Janus-like (or 2-faced) MXene alloy TiMoCO2. This alloy is thermodynamically, mechanically, and thermally stable with a high order–disorder phase transition temperature of ∼640 K. In essence, the TiMoCO2 MXene alloy is a semiconductor with a band gap of 0.60 eV. The asymmetric structure gives rise to an intrinsic dipole moment leading to band edge realignment due to the valence band maximum (VBM) and conduction band minimum (CBM) situating on the opposite surfaces of the MXene monolayer, which in turn straddles water redox potentials. Photocatalytic redox water-splitting can therefore occur with a much higher solar absorption efficiency, reaching above 104–105 cm−1 in the visible-infrared region. Its room temperature intrinsic hole and electron mobilities are evaluated to be 133.61–142.39 cm2 V−1 s−1 and 19.65–29.99 cm2 V−1 s−1, respectively, surpassing some 2D monolayer transition metal dichalcogenides (TMDs). Moreover, we determine the TiMoCO2 MXene alloy to exhibit high room temperature n- and p-type power factors of 33.7–49.8 μW cm−1 K−2 and ∼15 μW cm−1 K−2, respectively, which outperform other related experimentally synthesized Ti–Mo based MXene alloys and are even comparable to that of p-doped SnSe, which is one of the best performing thermoelectric materials. All these indicate the stable asymmetrically ordered Janus-like TiMoCO2 MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material. Our work paves the way for more Janus-like MXenes with interesting and outstanding properties to be discovered.
2. Methodology
2.1 Cluster expansion (CE) method and Monte Carlo (MC) simulations
According to the CE formalism,28–30 a particular alloy configuration, ϱ, on a fixed lattice, can be described using a set of occupational variables. For this work, a pseudo-binary Ti2(1−x)Mo2xCO2 substitutional MXene alloy is generated on the metallic sublattice with Ti and Mo, while ensuring the composition of C and O on the anion sublattice to remain unvaried. As such, for a given ϱ, its respective formation energy Ef corresponds its stability at 0 K to its most stable O-terminated MXene constituents, fcc-Ti2CO2 and hcp-Mo2CO2:| Ef(Ti2(1−x)Mo2xCO2,ϱ) = E(Ti2(1−x)Mo2xCO2,ϱ) − (1 − x)E(Ti2CO2) − xE(Mo2CO2) | (1) |
Utilizing the properly truncated CE, we perform MC simulations via the TTK code to survey the equilibrium Ti–Mo distribution in the alloys at the ground-state hull composition across different temperatures. A simulation cell of 24 × 24 × 1 times the size of the primitive unit cell of Ti2CO2 and Mo2CO2 is used. As such, a series of canonical (fixed chemical potential and temperature) MC runs with 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sampling steps per run is conducted to assess the Ti–Mo distribution, and to predict the order–disorder phase transition temperature of the alloy at ground-state hull composition.
000 sampling steps per run is conducted to assess the Ti–Mo distribution, and to predict the order–disorder phase transition temperature of the alloy at ground-state hull composition.
2.2 First-principles calculations
Density functional theory (DFT) calculations42 are performed using the Perdew–Burke–Ernzerhof (PBE) exchange correlation based on the generalized gradient approximation (GGA)43,44 as implemented in the Vienna ab initio Simulation Package (VASP).45,46 Electron-ion interactions are described via the projector augmented-wave (PAW) method.47 The plane-wave cut-off energy is set to 500 eV. During structural relaxation, the volume of the unit cell is fixed while the cell shape is allowed to change. A vacuum spacing of ∼15 Å is ensured in the out-of-plane direction to minimize spurious interactions between periodic images. All atomic coordinates are therefore fully relaxed until the Hellmann–Feynman forces on each atom are <0.001 eV Å−1. A dipole correction in the direction normal to the MXene plane is included for all the calculations.48 Monkhorst–Pack k-point meshes49 with a density of ∼40 k-points per Å−1 inclusive of the Γ-point are used during structural optimizations, whereas finer meshes of ∼160 k-points per Å−1 are utilized for detailed electronic density-of-states (DOS) and electronic band structure calculations. To achieve an accurate description of the band gaps, the band-edge positions, and the dielectric functions of the ground-state alloy, the Heyd–Scuseria–Ernzerhof (HSE06)50,51 hybrid functional is utilized. The effective electron and hole masses are determined by the parabolic fitting of the conduction band minimum (CBM) and valence band maximum (VBM), respectively, along selected k-point paths in the in-plane directions.52To investigate the elastic properties, the elastic tensor is determined using the stress–strain relationship via six finite distortions of the lattice to derive the elastic constants.53 The ionic contributions are determined from the inversion of the ionic Hessian matrix which is evaluated from finite differences and multiplied with the internal strain tensor.54
Ab initio molecular dynamics (AIMD) simulations are employed to evaluate the stability of the ground-state MXene alloy at finite temperatures; the simulations are carried out with a 5 × 5 × 1 supercell at 300 K and 600 K with the Nosé–Hoover thermostat55,56 for 20 ps with a time step of 1 fs.
The elucidation of the phonon dispersions and the electron–phonon couplings is performed using density functional perturbation theory (DFPT)57,58 under PBE-GGA as implemented in the PHONON package of QUANTUM ESPRESSO.59,60 Here, a set of optimized norm-conserving Vanderbilt (ONCV) pseudopotentials from PseudoDojo61 are used to replace core electrons, along with a plane-wave cut-off energy of 100 Ry and a well-converged and uniform 12 × 12 × 1 k-point mesh for the Brillouin zone sampling, followed by the interpolation of the phonon dispersion and electron–phonon matrix elements into well-converged ultrafine 240 × 240 × 1 k-point and 400 × 400 × 1 q-point meshes with maximally localized Wannier functions62,63 as implemented in Electron–Phonon coupling using the Wannier function (EPW)64 code for the evaluation of the transport properties for an accurate description of the carrier mobilities and thermoelectric performance via the self-energy relaxation time approximation (SERTA)65 within the framework of the Boltzmann transport equation (BTE). On the basis of the BTE, we evaluate the electron velocity matrix using first-order k-derivatives of the Hamiltonian via EPW, followed by the subsequent determination of the electrical conductivity σ and Seebeck coefficient S as elaborated according to published works.66,67
3. Results and discussion
3.1 Alloy screening and formation stability
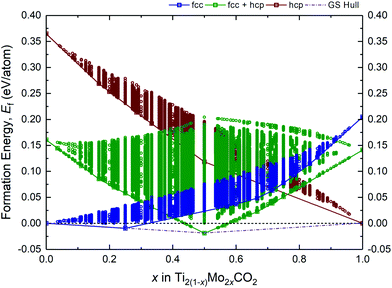
A fully O-terminated MXene M2CO2 can adopt 1 of the 3 possible geometries of O atoms, i.e., fcc, hcp, or fcc + hcp (fcc on one surface, and hcp on the other) (Fig. S1, ESI†). While our previous and other published works have shown Ti2CO2 and Mo2CO2 to preferentially adopt the fcc and hcp geometry, respectively,15,17,41 we have considered all 3 geometries in our screening of alloys lest there are thermodynamically MXene alloys with any of these 3 possible geometries. As such, Fig. 1 illustrates the formation energies Ef of more than 9 million different alloy configurations derived from eqn (1) for the fcc, hcp, and fcc + hcp O-termination geometries, using the constructed ECIs by the CE method. The most stable configurations (at 0 K) are known as ground-states, which form a ground-state hull (dashed–dotted line) across compositions, implying the theoretical lower bound of Ef for the Ti2(1−x)Mo2xCO2 alloy. On the other hand, states or configurations above the ground-state hull are accessible only at finite temperatures. Accordingly, from Fig. 1, only 2 stable alloy ground-states at x = 0.25 (Ti1.5Mo0.5CO2) and x = 0.5 (TiMoCO2) can be observed, of which Ti1.5Mo0.5CO2 and TiMoCO2 occur as fcc and fcc + hcp O-terminated MXenes, respectively. On the grounds that only TiMoCO2 displays semiconducting character which is crucial for photocatalytic water-splitting and will be revealed later, whereas Ti1.5Mo0.5CO2 is metallic, we focus on the in-depth investigations of the TiMoCO2 MXene alloy in the following sections.3.2 Asymmetrically ordered Janus-like TiMoCO2 MXene alloy
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 164) like most other M2CO2 MXenes) and possesses no inversion symmetry. The configuration of the M-sites (M–C–M′) in this MXene alloy is rather intriguing because from our previous works on other Ti-based MXene alloy systems (Ti2(1−x)M2xCO2, where M = Zr, Hf, V, Nb, and Ta),17,41 alloys with such a Janus-like configuration typically possess the most positive Ef and if ground-states with x = 0.5 exist, it would likely occur with in-plane ordering. Analogously, even experimentally synthesized 2D TMD MoSSe alloys with a Janus-like configuration (S–Mo–Se)68,69 have been theoretically evaluated to be energetically less favorable than the disordered counterpart.70–72 The origin of this stability in TiMoCO2 can be attributed to the appropriate O-termination geometries for the respective Ti (fcc) and Mo (hcp) sides resulting in Bader charges to be similar to those of O, Ti, and Mo in their thermodynamically stable constituent MXenes Ti2CO2 (fcc) and Mo2CO2 (hcp) (Table S1, ESI†). Moreover, we have further verified that even the bare TiMoC MXene alloy without O-terminations is stable by 81.8 meV per atom with respect to the constituent Ti2C and Mo2C MXenes (Table S2, ESI†). Accordingly, our TiMoCO2 MXene alloy with its favorable Ef and thermodynamic stability would have enhanced synthesizability.
m1 (no. 164) like most other M2CO2 MXenes) and possesses no inversion symmetry. The configuration of the M-sites (M–C–M′) in this MXene alloy is rather intriguing because from our previous works on other Ti-based MXene alloy systems (Ti2(1−x)M2xCO2, where M = Zr, Hf, V, Nb, and Ta),17,41 alloys with such a Janus-like configuration typically possess the most positive Ef and if ground-states with x = 0.5 exist, it would likely occur with in-plane ordering. Analogously, even experimentally synthesized 2D TMD MoSSe alloys with a Janus-like configuration (S–Mo–Se)68,69 have been theoretically evaluated to be energetically less favorable than the disordered counterpart.70–72 The origin of this stability in TiMoCO2 can be attributed to the appropriate O-termination geometries for the respective Ti (fcc) and Mo (hcp) sides resulting in Bader charges to be similar to those of O, Ti, and Mo in their thermodynamically stable constituent MXenes Ti2CO2 (fcc) and Mo2CO2 (hcp) (Table S1, ESI†). Moreover, we have further verified that even the bare TiMoC MXene alloy without O-terminations is stable by 81.8 meV per atom with respect to the constituent Ti2C and Mo2C MXenes (Table S2, ESI†). Accordingly, our TiMoCO2 MXene alloy with its favorable Ef and thermodynamic stability would have enhanced synthesizability.
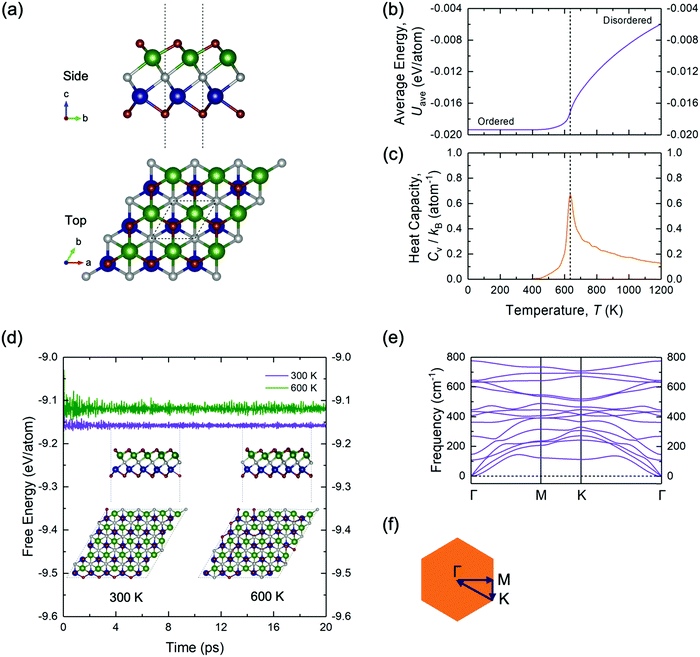
To further validate the stability of the ground-state configuration of TiMoCO2, a series of canonical MC runs, AIMD simulations, and phonon calculations are performed. Fig. 2b and c show, respectively, a plot of average energy Uavg (of the MC simulation cell) and another plot of heat capacity Cv, both versus temperature T. The ordered configuration at the end of the MC runs corresponds exactly to the configuration of the DFT- and CE-determined ground-state TiMoCO2 MXene alloy (Fig. 2a). Moreover, the order–disorder phase transition temperature, which is the peak in the plot of Cvversus T, is determined to be ∼640 K, implying that the ordered configuration is thermodynamically stable under room conditions (∼300 K). Besides, AIMD simulations in Fig. 2d carried out at 300 K and 600 K (below its order–disorder phase transition temperature) show the energies to fluctuate about constant values, with negligible structural deviations and no structural reconstructions after annealing for 20 ps. In addition, the phonon dispersion in Fig. 2e along the high-symmetry path of the Brillouin zone exhibits no negative (imaginary) frequencies, suggesting the dynamic stability of the TiMoCO2 ground-state configuration.
Likewise, the mechanical stability of the TiMoCO2 MXene alloy is also examined. A (hexagonal) 2D MXene possesses 3 independent non-zero elastic constants which are calculated to be: C11 = 322.22 N m−1, C12 = 103.06 N m−1, and C66 = 109.58 N m−1. These elastic constants fulfill the Born stability criteria according to Born–Huang's lattice dynamical theory for hexagonal 2D structures,73,74i.e., C11 > 0, C11 − C12 > 0, and 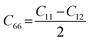 , indicating that the TiMoCO2 MXene alloy is mechanically stable. Using these elastic constants, we evaluate the in-plane Young's modulus Ys and the Poisson's ratio ν according to the following expressions:75,76
, indicating that the TiMoCO2 MXene alloy is mechanically stable. Using these elastic constants, we evaluate the in-plane Young's modulus Ys and the Poisson's ratio ν according to the following expressions:75,76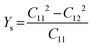 and
and 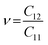 , which give 289.26 N m−1 and 0.32, respectively. We note that using the same approach, we obtain Ys values of 243.02 N m−1 and 241.04 N m−1 for the constituent MXenes Ti2CO2 and Mo2CO2, indicating that the alloying would produce a mechanically stronger material. Moreover, this value of Ys is much higher than those of 2D TMDs such as monolayer MoS2 (171 ± 11 N m−1)77 and WS2 (177 ± 12 N m−1),77 and slightly lower than that of graphene (324 ± 13 N m−1)78 which is the strongest 2D material. This implies the TiMoCO2 MXene alloy to overall possess high mechanical strength as well. With the thermodynamically favorable Ef, dynamically stable phonon dispersion, thermally stable MC and AIMD simulations, and favorable elastic constants, we believe that the experimental realization of this material is highly feasible.
, which give 289.26 N m−1 and 0.32, respectively. We note that using the same approach, we obtain Ys values of 243.02 N m−1 and 241.04 N m−1 for the constituent MXenes Ti2CO2 and Mo2CO2, indicating that the alloying would produce a mechanically stronger material. Moreover, this value of Ys is much higher than those of 2D TMDs such as monolayer MoS2 (171 ± 11 N m−1)77 and WS2 (177 ± 12 N m−1),77 and slightly lower than that of graphene (324 ± 13 N m−1)78 which is the strongest 2D material. This implies the TiMoCO2 MXene alloy to overall possess high mechanical strength as well. With the thermodynamically favorable Ef, dynamically stable phonon dispersion, thermally stable MC and AIMD simulations, and favorable elastic constants, we believe that the experimental realization of this material is highly feasible.
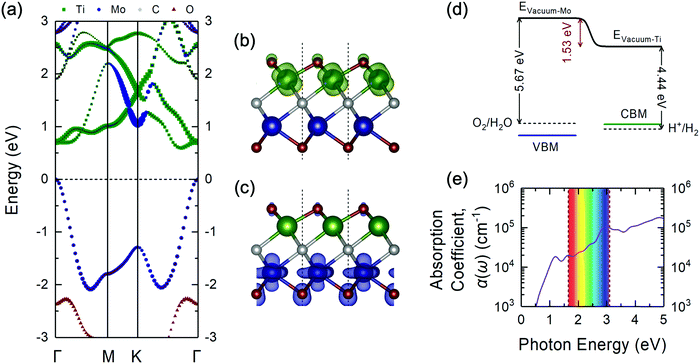 | ||
| Fig. 3 (a) Projected electronic band structure of the Janus-like ground-state TiMoCO2 MXene alloy via the HSE06 functional plotted along the high-symmetry path of the hexagonal Brillouin zone (see Fig. 2f). The size of each point corresponds to the relative magnitude of the respective elemental contribution to the band. The Fermi level is set to 0 eV at the VBM. The side view of the partial charge density of the (b) CBM (in green) and (c) VBM (in blue) of the TiMoCO2 MXene alloy. The value of the isosurfaces is 0.02 e Å−3. The red, green, blue, and grey spheres correspond to O, Ti, Mo, and C, respectively. (d) Band edge alignments of the VBM and CBM in blue and green solid lines, respectively, with regard to the water redox potentials in dashed lines, and their corresponding vacuum levels. The potential difference between the two sides of the TiMoCO2 MXene alloy induced by the intrinsic dipole moment is denoted in red. For the actual electrostatic potential profile, please refer to Fig. S2 (ESI†). (e) Plot of the in-plane optical absorption coefficient α(ω) versus photon energy for the TiMoCO2 MXene alloy. The visible wavelength region (1.65 to 3.10 eV) is shown as an iridescent rectangle for guide. | ||
From the atomic projections of the electronic band structure and the charge density isosurface distributions (Fig. 3a–c), it can be observed that the VBM state is mainly composed of Mo-dz2 and O-pz (at Mo side) orbitals, whereas the CBM state mainly originated from Ti-dxz orbitals. This distinction in the orbital contributions for both sides of TiMoCO2 is the key factor for allowing photocatalytic redox water-splitting to be thermodynamically feasible even with a small band gap. Due to the difference in the electronegativity between Ti (1.54) and Mo (2.16),80 and consequent Bader charge of Ti (+1.92e), Mo (+1.60e), and the fcc-terminated and hcp-terminated O (−1.08e and −0.93e, respectively), an intrinsic dipole moment of 0.232 D is generated with the electric field pointing from the Ti to Mo side. This dipole moment-induced electric field promotes photogenerated electron–hole separation and localizes the electrons and holes on Ti and Mo sides, respectively. As such, there exists an electrostatic potential difference of 1.53 eV as shown in Fig. S2 (ESI†) and Fig. 3d. Moreover, by aligning the band edge positions relative to the respective water redox potentials, i.e., the VBM to water oxidation potential (5.67 eV) w.r.t. the Mo side's vacuum level and the CBM to water reduction potential (4.44 eV) w.r.t. the Ti side's vacuum level, we observe in Fig. 3d that both the VBM and CBM straddle the water redox potentials, indicating that redox water-splitting photocatalysis is thermodynamically feasible albeit there is a band gap of 0.60 eV. The bending of the vacuum level along the direction of the internal electric field permits the reduction of the band gap requirement, i.e., difference between oxidation and reduction potentials of water, from 1.23 eV to 1.23 eV minus the value of the electrostatic potential difference between the two surfaces.81 Intriguingly, for our TiMoCO2 MXene alloy with an electrostatic potential difference of 1.53 eV, the band gap requirement would therefore be 0 eV, indicating that so long as the VBM and CBM are located on the opposite sides of the MXene, the size of its band gap would not affect the thermodynamic feasibility of photocatalytic redox water-splitting.
With the omission of the band gap prerequisite, the absorption properties of the TiMoCO2 MXene alloy is investigated to elucidate its efficiency in solar conversion. Fig. 3e shows the absorption coefficient α(ω) derived from the calculated frequency-dependent complex dielectric function ε(ω) = ε1(ω) + iε2(ω) according to the relation:82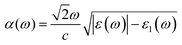 , with c being the speed of light in vacuum. It can be observed that the TiMoCO2 MXene alloy exhibits strong absorption of a wide wavelength range from ultraviolet to visible to infrared with α(ω) reaching above 104–105 cm−1 in the visible-infrared region. Since this region accounts for majority of the incident solar energy, by implementation of the metric which integrates the product of the incident solar photon flux according to the AM1.5G solar spectrum with the absorbance of the material up to its band gap's equivalent wavelength, as elaborated comprehensively in our previous work as well as other literature,17,36,83 we obtain its maximum short-circuit current of 4.2 mA cm−2. This value is much larger than those of conventional photovoltaic materials such as Si, and also those of 2D materials like MoS2 and WS2, with maximum short-circuit currents ranging from 0.1 to 3.6 mA cm−2 (Table 1), which suggests TiMoCO2 to be a potential photovoltaic material, in addition to its desirable visible-infrared absorbance for efficient photocatalysis.
, with c being the speed of light in vacuum. It can be observed that the TiMoCO2 MXene alloy exhibits strong absorption of a wide wavelength range from ultraviolet to visible to infrared with α(ω) reaching above 104–105 cm−1 in the visible-infrared region. Since this region accounts for majority of the incident solar energy, by implementation of the metric which integrates the product of the incident solar photon flux according to the AM1.5G solar spectrum with the absorbance of the material up to its band gap's equivalent wavelength, as elaborated comprehensively in our previous work as well as other literature,17,36,83 we obtain its maximum short-circuit current of 4.2 mA cm−2. This value is much larger than those of conventional photovoltaic materials such as Si, and also those of 2D materials like MoS2 and WS2, with maximum short-circuit currents ranging from 0.1 to 3.6 mA cm−2 (Table 1), which suggests TiMoCO2 to be a potential photovoltaic material, in addition to its desirable visible-infrared absorbance for efficient photocatalysis.
Other than the appropriate band and promising absorption characteristics, the electron and hole mobilities of the TiMoCO2 MXene alloy are also investigated to elucidate its efficacy in photocatalytic water-splitting. Herein, using the SERTA approach and accounting for electron–phonon scattering of all the phonon modes,65 we obtain the room temperature intrinsic hole mobility μp to be 142.39 and 133.61 cm2 V−1 s−1 along the x- and y-direction, respectively. These values show high isotropy in both x- and y-directions, which are consistent with the VBM being comprised of Mo-dz2 and O-pz orbitals, and the consequent isotropic effective hole mass of 0.23m0 along both x- and y-directions, indicating in-plane orientation-independent hole transport in either direction of TiMoCO2. In contrast, the room temperature intrinsic electron mobility μn is anisotropic with 29.99 and 19.65 cm2 V−1 s−1 along the corresponding x- and y-directions, in accord with the contribution of the in-plane anisotropic Ti-dxz orbitals to the CBM with anisotropic effective electron masses of 0.81m0 and 1.31m0 along the respective x- and y-directions. It is evident that μp is larger than μn as a result of lighter effective mass. Besides, the ∼1 order of magnitude difference between μp and μn promotes the effective spatial separation of the holes and electrons, which decreases the probability of photogenerated electron–hole recombination.35,38 To estimate the reliability of the calculated carrier mobilities with our approach, μp and μn values of widely investigated 2D MoS2 are analogously calculated to be 29.22 and 121.58 cm2 V−1 s−1, respectively, which are close to their corresponding experimental measurements of ∼40–76 and ∼60–150 cm2 V−1 s−1.84–86 Evidently, TiMoCO2 possesses a higher μp than that of MoS2, suggesting its potential application as a hole transport material. Accordingly, the indirect band gap, dipole-induced electric field, appropriate band edge positions, high absorbance, and decent mobilities would favor photogeneration of the electrons and holes while bolstering effective spatial and charge separation of these photoelectrons and holes for effective water redox reactions, establishing the TiMoCO2 MXene alloy to be an efficient water-splitting photocatalyst.
4. Conclusions
In summary, through a systematic first-principles multiscale approach using DFT calculations, CE method, and MC simulations, we are able to identify a novel asymmetrical ordered Janus-like TiMoCO2 MXene alloy ground-state by screening through the formation energies of more than 9 million different configurations of Ti2(1−x)Mo2xCO2 substitutional alloy system with consideration of all 3 possible types of O-termination. This alloy is thermodynamically, mechanically, and thermally stable with a high order–disorder phase transition temperature of ∼640 K. Importantly, TiMoCO2 is semiconducting with a band gap of 0.60 eV. It possesses an intrinsic dipole moment as a consequence of the asymmetric structure which realigns the conduction and valence band edges located on opposite sides of the MXene, permitting photocatalytic redox water-splitting to be thermodynamically favorable with enhanced solar absorption efficiency above 104–105 cm−1 in the visible-infrared region. As a thermoelectric material, it is found that TiMoCO2 exhibits high room temperature n- and p-type power factors of 33.7–49.8 μW cm−1 K−2 and ∼15 μW cm−1 K−2, respectively, surpassing other related experimentally synthesized Ti–Mo based MXene alloys and are even similar to that of p-doped SnSe which is one of the best performing thermoelectric materials. All these demonstrate the asymmetrically ordered Janus-like TiMoCO2 MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material, paving the way for more stable Janus-like MXenes with interesting and outstanding properties awaiting to be discovered.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the Agency for Science, Technology and Research (A*STAR) of Singapore (1527200024). TLT acknowledges the Advanced Manufacturing and Engineering Young Individual Research Grant (AME YIRG) of Agency for Science, Technology and Research (A*STAR) of Singapore (A1884c0016) for support in furthering the development of the cluster expansion code (TTK) used in this work. Computational resources are provided by the National Supercomputing Centre Singapore (NSCC) and A*STAR Computational Resource Centre (A*CRC).References
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- M. Naguib, N. Mochalin Vadym, W. Barsoum Michel and Y. Gogotsi, Adv. Mater., 2013, 26, 992–1005 CrossRef PubMed.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS.
- O. Mashtalir, M. Naguib, V. N. Mochalin, Y. Dall’Agnese, M. Heon, M. W. Barsoum and Y. Gogotsi, Nat. Commun., 2013, 4, 1716 CrossRef PubMed.
- Y. Gogotsi, Nat. Mater., 2015, 14, 1079 CrossRef CAS PubMed.
- J. Zhou, X. Zha, Y. Chen Fan, Q. Ye, P. Eklund, S. Du and Q. Huang, Angew. Chem., Int. Ed., 2016, 55, 5008–5013 CrossRef CAS.
- I. Persson, J. Halim, T. W. Hansen, J. B. Wagner, V. Darakchieva, J. Palisaitis, J. Rosen and P. O. Å. Persson, Adv. Funct. Mater., 2020, 1909005 CrossRef.
- K. Rasool, R. P. Pandey, P. A. Rasheed, G. R. Berdiyorov and K. A. Mahmoud, in 2D Metal Carbides and Nitrides (MXenes): Structure, Properties and Applications, ed. B. Anasori and Y. Gogotsi, Springer International Publishing, Cham, 2019, pp. 417–444, DOI:10.1007/978-3-030-19026-2_22.
- H. Lin, Y. Chen and J. Shi, Adv. Sci., 2018, 5, 1800518 CrossRef PubMed.
- Y. Sun, X. Meng, Y. Dall’Agnese, C. Dall’Agnese, S. Duan, Y. Gao, G. Chen and X.-F. Wang, Nano-Micro Lett., 2019, 11, 79 CrossRef.
- Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452 RSC.
- L. Cheng, X. Li, H. Zhang and Q. Xiang, J. Phys. Chem. Lett., 2019, 10, 3488–3494 CrossRef CAS PubMed.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098 CrossRef CAS PubMed.
- X. Zhang, Z. Zhang, D. Wu, X. Zhang, X. Zhao and Z. Zhou, Small Methods, 2018, 2, 1700359 CrossRef.
- M. Khazaei, M. Arai, T. Sasaki, C. Y. Chung, S. Venkataramanan Natarajan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2012, 23, 2185–2192 CrossRef.
- H. Zhang, G. Yang, X. Zuo, H. Tang, Q. Yang and G. Li, J. Mater. Chem. A, 2016, 4, 12913–12920 RSC.
- Z. M. Wong, T. L. Tan, S.-W. Yang and G. Q. Xu, ACS Appl. Mater. Interfaces, 2018, 10, 39879–39889 CrossRef CAS PubMed.
- V. K. Sangwan and M. C. Hersam, Annu. Rev. Phys. Chem., 2018, 69, 299–325 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- H. Kim, B. Anasori, Y. Gogotsi and H. N. Alshareef, Chem. Mater., 2017, 29, 6472–6479 CrossRef CAS.
- B. Anasori, Y. Xie, M. Beidaghi, J. Lu, B. C. Hosler, L. Hultman, P. R. C. Kent, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2015, 9, 9507–9516 CrossRef CAS PubMed.
- T. L. Tan, H. M. Jin, M. B. Sullivan, B. Anasori and Y. Gogotsi, ACS Nano, 2017, 11, 4407–4418 CrossRef CAS PubMed.
- N. A. Zarkevich, T. L. Tan, L. L. Wang and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144208 CrossRef.
- G. Ceder, A. V. d. Ven, C. Marianetti and D. Morgan, Modell. Simul. Mater. Sci. Eng., 2000, 8, 311 CrossRef CAS.
- W. Chen, D. Schmidt, W. F. Schneider and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075415 CrossRef.
- V. Ozoliņš, C. Wolverton and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6427–6443 CrossRef.
- L. Cao, C. Li and T. Mueller, J. Chem. Inf. Model., 2018, 58, 2401–2413 CrossRef CAS PubMed.
- J. W. D. Connolly and A. R. Williams, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5169–5172 CrossRef CAS.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Phys. A, 1984, 128, 334–350 CrossRef.
- N. A. Zarkevich and D. D. Johnson, Phys. Rev. Lett., 2004, 92, 255702 CrossRef PubMed.
- A. van de Walle, Nat. Mater., 2008, 7, 455 CrossRef CAS PubMed.
- T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, Nano Lett., 2012, 12, 4875–4880 CrossRef CAS PubMed.
- T. L. Tan, L.-L. Wang, J. Zhang, D. D. Johnson and K. Bai, ACS Catal., 2015, 5, 2376–2383 CrossRef CAS.
- N. A. Zarkevich, T. L. Tan and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104203 CrossRef.
- M.-F. Ng and T. L. Tan, Nano Lett., 2013, 13, 4951–4956 CrossRef CAS PubMed.
- T. L. Tan, M.-F. Ng and G. Eda, J. Phys. Chem. C, 2016, 120, 2501–2508 CrossRef CAS.
- Z. M. Wong, H. Cheng, S.-W. Yang, T. L. Tan and G. Q. Xu, J. Phys. Chem. C, 2017, 121, 26446–26456 CrossRef.
- T. L. Tan and M.-F. Ng, Phys. Chem. Chem. Phys., 2015, 17, 20391–20397 RSC.
- T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, J. Phys. Chem. C, 2013, 117, 22696–22704 CrossRef CAS.
- Z. M. Wong, T. L. Tan, S.-W. Yang and G. Q. Xu, J. Phys.: Condens. Matter, 2018, 30, 485402 CrossRef PubMed.
- Z. M. Wong, T. L. Tan, A. J. K. Tieu, S.-W. Yang and G. Q. Xu, Chem. Mater., 2019, 31, 4124–4132 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- C. Hamaguchi, in Basic Semiconductor Physics, ed. C. Hamaguchi, Springer International Publishing, Cham, 2017, pp. 125–151, DOI:10.1007/978-3-319-66860-4_3.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- X. Gonze, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 1096–1114 CrossRef CAS PubMed.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54 CrossRef CAS.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133 CrossRef.
- S. Poncé, E. R. Margine and F. Giustino, Phys. Rev. B, 2018, 97, 121201 CrossRef.
- G. D. Mahan and J. O. Sofo, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7436 CrossRef CAS PubMed.
- T. Deng, X. Yong, W. Shi, Z. M. Wong, G. Wu, H. Pan, J.-S. Wang and S.-W. Yang, J. Mater. Chem. A, 2020, 8, 4257–4262 RSC.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed.
- H.-P. Komsa and A. V. Krasheninnikov, J. Phys. Chem. Lett., 2012, 3, 3652–3656 CrossRef CAS PubMed.
- J. Kang, S. Tongay, J. Li and J. Wu, J. Appl. Phys., 2013, 113, 143703 CrossRef.
- J. Wang, H. Shu, T. Zhao, P. Liang, N. Wang, D. Cao and X. Chen, Phys. Chem. Chem. Phys., 2018, 20, 18571–18578 RSC.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press, 1954 Search PubMed.
- R. John and B. Merlin, Crystal Structure Theory and Applications, 2016, vol. 05, No. 03, 13 Search PubMed.
- X. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407 CrossRef.
- J. Zhou and R. Huang, J. Mech. Phys. Solids, 2008, 56, 1609–1623 CrossRef CAS.
- K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Nano Lett., 2014, 14, 5097–5103 CrossRef CAS PubMed.
- G.-H. Lee, R. C. Cooper, S. J. An, S. Lee, A. van der Zande, N. Petrone, A. G. Hammerberg, C. Lee, B. Crawford, W. Oliver, J. W. Kysar and J. Hone, Science, 2013, 340, 1073 CrossRef CAS PubMed.
- T. Luttrell, S. Halpegamage, J. Tao, A. Kramer, E. Sutter and M. Batzill, Sci. Rep., 2014, 4, 4043 CrossRef PubMed.
- A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221 CrossRef CAS.
- X. Li, Z. Li and J. Yang, Phys. Rev. Lett., 2014, 112, 018301 CrossRef PubMed.
- G. Dresselhaus and M. S. Dresselhaus, Proceedings of the International School of Physics, ed. E. Fermi and J. Tauc, Academic Press, NY, 1966 Search PubMed.
- M. Bernardi, M. Palummo and J. C. Grossman, Nano Lett., 2013, 13, 3664–3670 CrossRef CAS PubMed.
- D. Lembke, A. Allain and A. Kis, Nanoscale, 2015, 7, 6255–6260 RSC.
- M.-W. Lin, L. Liu, Q. Lan, X. Tan, K. S. Dhindsa, P. Zeng, V. M. Naik, M. M.-C. Cheng and Z. Zhou, J. Phys. D: Appl. Phys., 2012, 45, 345102 CrossRef.
- T. Momose, A. Nakamura, M. Daniel and M. Shimomura, AIP Adv., 2018, 8, 025009 CrossRef.
- S. Sarikurt, D. Çakır, M. Keçeli and C. Sevik, Nanoscale, 2018, 10, 8859–8868 RSC.
- K. Hippalgaonkar, Y. Wang, Y. Ye, D. Y. Qiu, H. Zhu, Y. Wang, J. Moore, S. G. Louie and X. Zhang, Phys. Rev. B, 2017, 95, 115407 CrossRef.
- G. E. Yakovleva, A. I. Romanenko, A. S. Berdinsky, V. A. Kuznetsov, A. Y. Ledneva, S. B. Artemkina and V. E. Fedorov, Semiconductors, 2017, 51, 725–728 CrossRef CAS.
- L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structures of the 3 different fully O-terminated MXenes; electrostatic potential profile for the Janus-like ground-state TiMoCO2 MXene alloy; projected electronic band structures of the Janus-like ground-state TiMoCO2, and its analogous conjectural ZrMoCO2, HfMoCO2, TiCrCO2, and TiWCO2 MXene alloys; table of structures of various TiMoCO2 MXene alloys with different O-sites and their constituent MXenes Ti2CO2 and Mo2CO2, their relative energies with respect to the constituents obtained via density functional theory, and the Bader charges of the respective elements; table of calculated DFT and alloy formation energies of bare TiMoC MXene with respect to its constituent Ti2C and Mo2C MXenes; and table of band gap and the respective contributions and directional effective hole and electron masses of the valence band maximum and conduction band minimum for Janus-like ground-state TiMoCO2, and its analogous conjectural ZrMoCO2, HfMoCO2, TiCrCO2, and TiWCO2 MXene alloys. See DOI: 10.1039/d0ma00391c |
| This journal is © The Royal Society of Chemistry 2020 |