Real structure micromodels based on reservoir rocks for enhanced oil recovery (EOR) applications

Abstract

Although the application of microfluidics is not new in the petroleum industry, the upscaling of fluid flow behavior from micromodels to reservoir rocks is still challenging. In this work, an attempt to close the gaps between micromodels and reservoir rocks was performed by constructing micromodels based on the X-ray micro-computed tomography (μCT) images of a Bentheimer core plug. The goal of this work was to build a digital 3D model of reservoir rocks and transfer its rock properties and morphological features such as porosity, permeability, pore and grain size distribution into a 2D microfluidics chip. The workflow consists of several steps which are (1) rock property extraction from a μCT image stack of the core plug, (2) micromodel pore structure design, (3) lithographic mask construction and (4) fabrication. Flooding experiments, including single- and two-phase flow experiments, were performed to confirm the micromodel design. As a result, the real structure micromodels show similar rock properties, as well as a comparable fluid flow behavior, to those of the Bentheimer core plug during typical water flooding and EOR polymer application. This framework demonstrates the potential for the general applicability of micromodels to support EOR studies on a larger scale, such as those on sandpacks or core plugs before field implementation.

---

1 Introduction

The application of microfluidics in the oil and gas industry started in the early 1950s when Chatenever and Calhoun¹ inserted glass spheres in between two glass plates to observe fluid flow behavior in porous media. Since then, microfluidics has been used for several applications such as in EOR studies, for example polymer flooding,^2–5 surfactant flooding^6,7 or a combination of them with an alkali (ASP),^8,9 miscible gas injection,¹⁰ and other EOR methods such as microbial,^11,12 foam^13–16 and nanoparticle flooding.^17,18 With all the advantages offered, microfluidics applications could be used to support well-established technologies such as sandpack and core flooding experiments for EOR screening processes before field implementation. However, until now, the acceptance of microfluidics in the oil and gas industry is still relatively low.¹⁹ One reason for this could be the difficulty in upscaling fluid flow behavior from microfluidics to reservoir rocks.

The pore structure and surface characteristics of microfluidic chips or micromodels need to be analogous to those of real rocks so that a relationship between them can be established. Reservoir rocks typically contain various minerals, and until now, micromodels have been generally fabricated with homogeneous materials (i.e., silicon, glass, or polymers). Several studies have investigated surface modification techniques for micromodels to mimic the surface characteristics of reservoir rocks.^20,21 Wang et al. (2017) and Yun et al. (2020) developed a nanofabrication process to homogeneously cover the original surface (silica) of micromodels with calcium carbonate (CaCO₃). Their result showed that the modified chips could be used to investigate EOR methods for carbonate reservoirs. Moreover, the pore structure is one main factor that governs fluid flow behavior in reservoir rocks. The pore structure is generally quantified with several properties such as porosity and permeability as well as pore and grain size distribution. It is crucial to design micromodels that have the same rock properties as reservoir rocks. Therefore, this paper focuses on constructing a digital 3D image of reservoir rocks and transferring its properties/morphology into micromodels. However, modifications of the surface characteristics of the micromodels are not covered in this work.

Karadimitriou and Hassanizadeh (2012)²² classified micromodel pore structures into regular models (entirely and partially), irregular patterns and fractal patterns. Regular micromodels are generally constructed with identical grains where they can be distributed randomly or in specific patterns.⁵ Gunda et al. (2011)²³ and Wu et al. (2012)²⁴ used Delaunay triangulation and Voronoi tessellations, respectively, to generate an irregular network for the micromodels. Additionally, Cheng et al. (2004)²⁵ and Nolte et al. (1989)²⁶ designed and constructed micromodels based on flow area fractions (fractal geometry) of SEM micrographs. All of these patterns can be designed to reproduce the basic properties of reservoir rocks, such as porosity and permeability. However, little attention has been paid to the direct comparison between all rock properties of micromodels and reservoir rocks. Therefore, in this work, the pore structure of micromodels was designed based on μCT images of a Bentheimer core plug; thus, their rock properties can be compared before the fabrication process.

Conventionally, the properties of reservoir rocks can be measured directly in laboratories. Nowadays, with the availability of high-resolution imaging techniques such as microscale X-ray computed tomography (μCT), focused ion beam scanning electron microscopy (FIB-SEM) or nuclear magnetic resonance (NMR), the rock properties can be computed by using the digital rock physics (DRP) methodology.²⁷ In this work, the DRP approach was used to extract rock property information from μCT images of a Bentheimer core plug; subsequently, these properties were used to design the pore structure of micromodels. This pore structure was then etched on a silicon material sealed with glass layers to enable direct optical visualization during experiments. Several studies have reported the advantages of glass–silicon–glass micromodels for enhanced oil recovery (EOR) experimental studies.^5,28,29

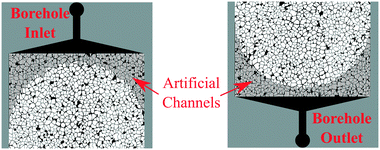
It is generally accepted that a high degree of heterogeneity in reservoirs can cause poor oil displacement efficiency. When the permeability of the rocks is significantly different, the displacing fluid only flows through the high-permeability zone while the low permeability zone remains unswept. To mimic this condition, we constructed heterogeneous micromodels with two different permeability zones (low and high permeability). Afterward, we performed single- and two-phase flooding experiments to confirm the capability of the micromodels. Furthermore, one example of EOR application (polymer flooding) was performed to investigate the oil sweep efficiency improvement in heterogeneous porous media.

2 Materials and methods

2.1 Design and construction of micromodels

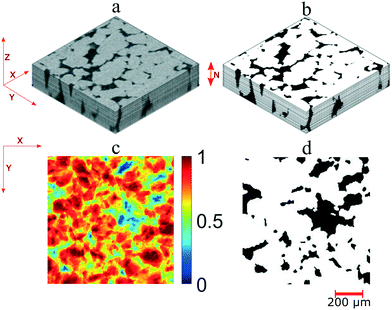
Here, we describe a novel workflow to produce micromodels which have similar flow characteristics to those of porous media. The workflow is described in the following steps: (i) rock property extraction from a μCT image stack of a core plug, (ii) micromodel pore structure design, (iii) lithographic mask design and (iv) micromodel fabrication. These steps are described in the subsequent sections.

2.1.1 Rock property extraction from a μCT image stack of a core plug. The DRP methodology consists of three main steps, which are the acquisition of high-resolution images of the core plug, image processing and computation of the rock properties.³⁰ In this study, a Bentheimer core plug (length = 50 mm and diameter = 10 mm) was scanned to obtain more than one thousand two-dimensional (2D) high-resolution (1 pixel = 5 μm) μCT images with dimensions of 1850 × 10 000 pixels (Fig. 1a and b). The raw μCT images were converted into binary images using Otsu's thresholding method to differentiate pore and grain pixels. Several of the 2D binary images (N) were then used to reconstruct a 3D image stack. Fig. 1c illustrates the image stack of a Bentheimer core plug with dimensions of 1850 × 10 000 × 100 pixels. The number of images used to reconstruct the image stack should be sufficient enough to exceed the representative elementary volume (REV). The REV is the minimum volume needed for rock property computation so that the results can be representative of a larger domain (macroscopic scale).³¹ In this work, the REV value was obtained based on porosity values. Then, by using this image stack, rock properties such as pore and grain size distribution and permeability were calculated.

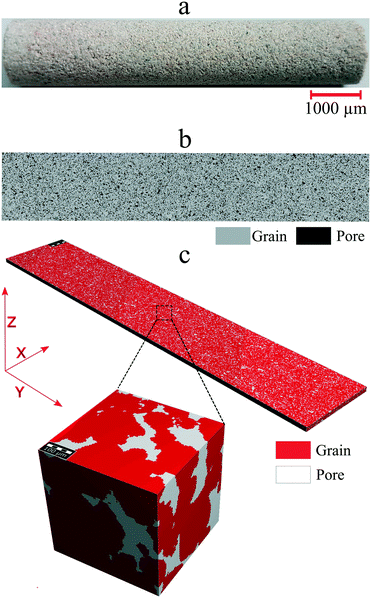Fig. 1 (a) An image of the Bentheimer sandstone core plug; (b) a 2D cross-section μCT image of the same sample with a resolution of 5 μm (c) a 3D μCT image stack after binary segmentation.

Pore and grain size distributions are critical parameters that affect fluid flow in porous media. A maximal ball algorithm was used to estimate the pore and grain size distribution of the image stack. This approach was performed by assigning virtual spheres to all voxels and calculating the maximum radii of the spheres. The radii of the spheres were estimated based on the distance from the sphere's center to the closest grain points.³²

Another main rock property that also influences the fluid flow behavior in porous media is tortuosity. This property describes the ratio of the shortest geometric flow path to the actual straight-line length of the porous media.³³ In this study, a percolation path algorithm was used (Math2Market GmbH) to estimate the tortuosity of the image stack. By defining a sphere with a specific diameter, the shortest path length for the sphere to pass through the porous media can be estimated. Furthermore, pore-network modeling also enables the calculation of fluid transport properties such as permeability. Since the fluid flow in oil reservoirs is typically in the laminar regime, therefore, the Stokes–Brinkman approach was used (eqn (1)). A constant pressure drop and no-slip boundary applied on the grain surface of the porous media were used as boundary conditions.

−μΔu + μK⁻¹u + ∇p = f (1)

here K⁻¹ is the inverse of the permeability tensor, μ is the fluid viscosity, p is the pressure drop between the inlet and outlet boundaries, u is the velocity and f is the force density.

2.1.2 Micromodel pore structure design.
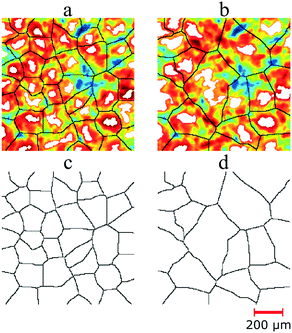
Pore body extraction. Micromodels are porous media that have a two-dimensional pore structure. Therefore, to construct a pore structure based on real rocks, the pore morphology information from a 3D domain (image stack) needs to be transformed into a 2D field. By using the same image stack in the previous step (Fig. 2a), a grain density topographic map (Fig. 2c) was calculated. This map was generated by adding the binary values (Fig. 2b) from all the images and then dividing with the total number of images (N). The grain density distribution is an m × n matrix (image), where m and n are the numbers of pixels in the two principal coordinate directions. Matrix entries range from zero to one, where zero means all the voxels in the image stack are pores and one means the other way around. The pore body map was generated by applying a single-threshold value that subdivides the grain density matrix into pores and grains (Fig. 2d). As can be seen in the image, most of the pore bodies are not connected. This appearance occurs because some morphology information disappeared during the matrix transformation from the 3D to the 2D domain. Therefore, pore throat information was needed to connect all of these pore bodies.

Fig. 2 Schematic overview of pore space characterization for generating the pore body map. (a) Exemplary gray-scale μCT image stack (1000 × 1000 × 500 μm). (b) The binary image stack of the same domain. (c) A grain density map generated based on the binary image stack. (d) A pore body map calculated from the grain density map by using a single-threshold value.

Pore throat extraction. A pore throat map was extracted based on the medial axis algorithm applied to the grain density topographic map. One of the earliest studies regarding this was reported by Lindquist et al.,³⁴ where the medial axis algorithm was used to detect the centrally located pore-skeleton of real rocks based on 3D tomographic images.³⁵ In this work, before the medial axis extraction, a morphological operation called “opening–closing reconstruction” was performed to generate a flatter grain density map. This operation was executed by eroding and dilating the topological map using a radial structure element with a specific size. The purpose of this approach was to reveal all the possibilities of the medial axis on the map. Then, grain distribution was generated by calculating the local maxima of the “new” topological map. By applying the Euclidean distance transform on the grain distribution map, the distance between pore pixels to the nearest grain pixels was calculated. The medial axis (skeleton) of the pore space was then obtained by using a “watershed” approach on the distance matrix. In the 2D grain distribution map, the medial axes are the watershed ridgelines between two neighboring grains.

The number and size of pore throats are primary factors that govern the pore size distribution of micromodels. Fig. 3 shows the medial axis extraction from the grain density map with two different structure elements, which resulted in two different amounts of pore throats. As illustrated in this figure, the white areas indicate the local maxima of the grain density map and the medial axis is the watershed ridge-line between them. The number of local maxima depends on the size of structural elements used in the morphology operations. By using a smaller structural element (size = 5 pixels), more maxima were detected (Fig. 3a and c); thus, more pore throats could be extracted compared to the larger structural element (size = 7 pixels, Fig. 3b and d). Furthermore, as indicated in this image, the extracted medial axis has the same dimensions (uniform) at each position in the matrix. This medial axis does not reflect real reservoir rocks where the pore throat size is non-uniform. Therefore, in the next step, the width of the medial axis was adjusted based on the actual distance between the center of the medial axis to the nearest grain pixels.

Fig. 3 A schematic overview of pore throat extraction from the grain density map. The pore throats are watershed ridgelines (black lines) between two local maxima (white). The grain density map overlaid with pore throats extracted with structural elements of 5 pixels (a) and 7 pixels (b). The pore throat maps (c and d), respectively.

Rock on a chip. After the pore body (Fig. 2d) and pore throat (Fig. 3d) maps were extracted, the pore structure of micromodels can be constructed by superimposing these two matrices (Fig. 4a). This new structure, in this work, referred to as “rock on a chip (ROC),” was then used for the rock property calculation. In this work, the pore throat matrix based on a structural element of 7 pixels was selected for the ROC construction. The reason for this selection was because this ROC showed more similar rock properties (e.g., pore size distribution) to those of the Bentheimer core plug. Then, the same algorithms used for computing the rock properties of the Bentheimer image stack were also used for the ROC; thus, comparison between them could be performed. The rock properties of ROCs are mainly dependent on the number and size of pore bodies and pore throats. To match the rock properties of the image stack, three previously described parameters were thoroughly adjusted. These parameters were (1) the single-threshold value for defining the size and number of pore bodies from the grain density map, (2) the size of the structural element to adjust the number of pore throats and (3) the ratio of the pore throat width to the actual distance of the medial-axis center to the nearest grain pixels. Fig. 4b shows the image of the ROC that matched the rock properties (porosity, pore size distribution, and permeability) of the Bentheimer image stack. In this paper, this ROC will be referred to as “Micromodel Structure-1”.

Fig. 4 (a) An image of the rock on a chip (ROC) obtained by superimposing the pore body and pore throat maps. The pore throats of the ROC initially have a uniform size (one voxel or 5 μm). (b to d) The images of ROCs which have non-uniform pore throats. The size of pore throats was defined based on the actual distance of the medial axis to the nearest grain pixel. The permeability of the ROCs are 3.5, 2.0 and 0.8 Darcy, respectively.

The algorithm developed in this work enables the design of several micromodel realizations while still accommodating the pore morphology of real rocks. With this algorithm, pore structures with different permeabilities can be easily generated by adjusting the pore throat size. In this work, a total of five ROC realizations were generated, which consist of three homogeneous and two heterogeneous pore structures. The three homogeneous structures, namely “Structure-1, Structure-2 and Structure-3,” have an average permeability of 3.5, 2.0 and 0.8 Darcy, respectively (Fig. 4b–d). Additionally, to facilitate the investigation of oil displacement efficiency, two heterogeneous structures, namely “Structure-A and Structure-B,” were designed with two different zones: low permeability zones at the sides of the micromodels and a high permeability zone in the middle. The difference between these two structures was the permeability in the high-permeability zone. The high-permeability zone of Structure-A and Structure-B was designed to be 2 Darcy and 3.5 Darcy, respectively. For both structures, the low-permeability zones have a permeability of 0.8 Darcy.

2.1.3 Lithographic mask. After finalizing the pore structure design, a “flooding flow approach” was introduced to make connections for fluids freely entering the micromodel during experiments. In this approach, an inlet and outlet of the micromodel, as well as artificial channels, were implemented on the ROC, which can be seen in Fig. 5. The inlet and outlet boreholes (diameter = 1.2 mm) were connected to the pore structure with a trapezoid shape to provide a homogeneous fluid flux across the micromodel. Previous experimental results showed that in linear micromodels with centrally located boreholes (without artificial channels), the displacing fluid velocity was faster in the middle of the micromodels inlet rather than on the sidewalls.³⁶ This phenomenon could be explained by the friction on the sidewalls of the micromodels. To minimize this effect, artificial channels (width = 25 μm) were added around the inlet and outlet to connect the trapezoid base and the pore structure. The design of these artificial channels follows a convex shape to provide a linear shock-front of injected fluid when entering the micromodel system. The length of the channels was designed longer on the edges of the micromodels than in the middle. Therefore, the length of the artificial channels varies from 1 to 6 mm. The result, as presented in the next section, is promising where the fluid front around the inlet of the micromodel is relatively linear. However, it is clear that much additional work, such as pore-scale simulation and particle image velocimetry (PIV), is required to estimate the precise size of the artificial channels. Thus, a uniform fluid velocity along the micromodel width can be reached before entering the pore structure. Furthermore, after the flooding flow approach has been added, the final design of the micromodel, namely “lithographic mask,” was delivered to the manufacturing process.

Fig. 5 Design of the flooding flow approach for the micromodels. Inlet/outlet boreholes and artificial channels were introduced to enable fluid flow through the micromodel.

2.1.4 Micromodel fabrication. Several materials such as quartz, glass, polymethylmethacrylate (PMMA), polydimethylsiloxane (PDMS) and silicon can be used for micromodel fabrication.²² Each of these materials has advantages and disadvantages and also requires different fabrication techniques. Details of material and technique selection are described by Wegner (2015).⁵ In this work, a silicon material was selected as a substrate sealed with two glass layers. The fabrication of micromodels consists of several major steps from photo-lithography until the bonding process. The process started with transferring the lithographic mask to the substrate, which is a UV light-sensitive layer, then followed by removing the photo-resist material which was affected by UV-light. As the next step, an etching process was performed to project the pattern of the pore network onto the silicon material. A dry etching method was selected instead of wet etching to avoid slopping effects on the silicon walls. The etching depth in this process was 50 ± 1 μm. With this technique, the ratio between the depth and the width of the pore channels obtained was 6 : 1, and the angle of the vertical walls was 82–90°. The minimum pore size of the fabricated micromodels was about 8 μm. This value was considered to be acceptable since, as previously described, the resolution of the μCT images is 5 μm. It is generally recognized that the pore size of reservoir rocks, particularly in unconventional tight reservoirs, can be on the nanoscale (5–900 nm).^37,38 The approach presented in this study could also be applied to design pore structures and morphology features at the nanoscale level, especially with finer-resolution images (e.g., FIB-SEM images). However, it is evident that considerable additional work is required to manufacture micromodels containing nanoscale pores.

After the etching process was finished, the remaining photo-resist material was removed. Afterward, an anodic bonding process was performed to seal the silicon substrate with two transparent glass layers that enable visual access to the porous structure. In this work, Borofloat 33, with a thickness of 0.5 mm and a high degree of flatness, was used. The anodic bonding was performed separately; the first glass was bonded on the top side of the silicon, followed by the second glass, in which two boreholes were powder blasted. Since the grain size of the micromodels was relatively small, there was not enough bonding surface between the silicon and glass materials. Therefore to avoid the contact problem between the materials, the micromodels were baked in an oven at 400 °C and an electric field of 400 V was applied for 9 hours.

2.2 Experimental setup and procedure

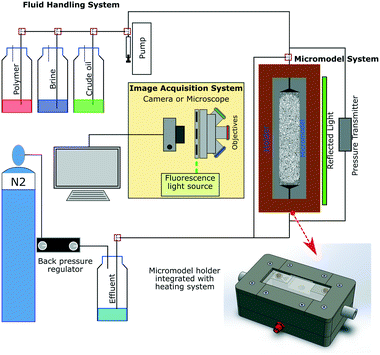
The experimental microfluidics setup used in this study is depicted in Fig. 6. This setup mainly consists of three systems: first is the fluid handling system, including influent bottles with HPLC caps, tubing, microfluidic valves, a pump and effluent bottles. During the flooding experiments, a low-flow syringe pump (Harvard Pump 11 Elite Series, Harvard Apparatus Ltd.) was used to provide high-accuracy injection rates. The differential pressure across the micromodel was measured by using a PD-33X differential pressure transmitter (Keller GmbH). The image acquisition system was used in microfluidic applications for obtaining images or videos during the flooding process. An inverted epi-fluorescence microscope (Axio Imager.Z2m, Carl Zeiss GmbH), which is equipped with a CCD camera, was used to obtain high-resolution images during the flooding process, particularly at the small pore size. A fluorescent light source (Visitron Systems HXP 120) was used to differentiate the aqueous phase from crude oil. However, by using this configuration, only a limited area of the micromodel can be observed at the same time, because the optical window of the microscope only covers a small area. Therefore, to investigate the displacement process on the macroscopic scale (whole area of the micromodel), an integrated microfluidic flooding device equipped with a high-resolution camera was used (InspIOR, HOT Microfluidics GmbH). The last system is the micromodel system, which consists of the micromodel and a holder integrated with a heating system. The holder includes borosilicate glass coated with an indium tin oxide (ITO) layer as a heating source. This ITO glass received an electrical current from a power supply through four spring pins mounted below it. Moreover, the temperature of the micromodel was measured by using a temperature sensor (SA1-RTD-80, Omega Engineering GmbH). An algorithm developed in the LabVIEW framework was used to maintain the working temperature of the micromodel during the experiments.

Fig. 6 Schematic of the experimental microfluidics setup used for flooding experiments.

The wetting fluid phase used in this study is scientific-subsea-water (SSW) brine, which has a salinity of 35 g l⁻¹ TDS. The oil (non-wetting) is original crude oil from a Romanian oil field which has a viscosity of 14 mPa s at a shear rate of 10 s⁻¹. The interfacial tension (IFT) of the oil and brine is 14.3 mN m⁻¹, which was measured in the laboratory using the Du Noüy ring method. For the EOR application, a commercial polymer (Flopaam 3530) with a molecular weight of 8 million Daltons was used. The concentration of the polymer of 1500 ppm was designed to obtain a mobility ratio close to one. The details of the fluid properties can be seen in Table 1.

Table 1 Fluid properties used in the micromodel flooding experiments

Properties at room temperature	Fluids
	Crude oil	Brine	Polymer solution
Density (kg m^−3)	869	1013	—
Viscosity at 10 s^−1 (mpa s)	13.82	1.1	14.02
IFT between oil and brine (mN m^−1)	14.29		—
Salinity (ppm)	—	35 000	—
Polymer concentration (ppm)	—	—	1500

---

Before the experiments started, the micromodel was saturated with N₂ or CO₂ to avoid gas bubble formation during the experiments. Injection of distilled water was performed to displace all the gas bubbles, followed by the injection of brine. During this injection, the pressure drop across the micromodel was measured to estimate the absolute permeability. This value will be used to validate the computed permeability of the micromodels. Then, the crude oil was injected into the brine-saturated micromodel at an injection rate of 0.1 μl min⁻¹ equivalent to 1 ft per day Darcy velocity. The oil initialization was conducted until the differential pressure across the micromodel stabilized, followed by higher injection rates (bump rates, e.g., 10–50 ft per day). As the initial oil saturation (Soi) condition was reached, a standard secondary mode of brine flooding was performed to investigate the oil displacement efficiency in the micromodels. The brine was injected at an injection rate of 0.1 μl min⁻¹ into the micromodel. During the brine injection, images of the micromodel were obtained using a camera. The images were then used to estimate fluid saturations inside the chip by using an image processing tool developed in MATLAB. Furthermore, 5 PV of the polymer solution was then injected into the micromodel (tertiary mode) at a similar injection rate (0.1 μl min⁻¹) to investigate the sweep efficiency improvement.

Additionally, all flooding experiments were performed at room temperature and 1 bar(g) backpressure. This backpressure was established to avoid gas bubble formation in the micromodel during the experiments. Based on the pressure test, the fabricated micromodels could operate at a maximum of 25–30 bar differential pressure under atmospheric conditions.

3 Results

Fig. 7 shows an example of the design of a micromodel and image of heterogeneous Structure-A with two different permeability zones after the fabrication. As previously described, this micromodel has two different permeability zones, which is low (k = ∼800 mD) at the edges and high (k = ∼2000 mD) at the middle. In this section, the rock properties of the micromodels and core plug and the result of the flooding experiments are presented.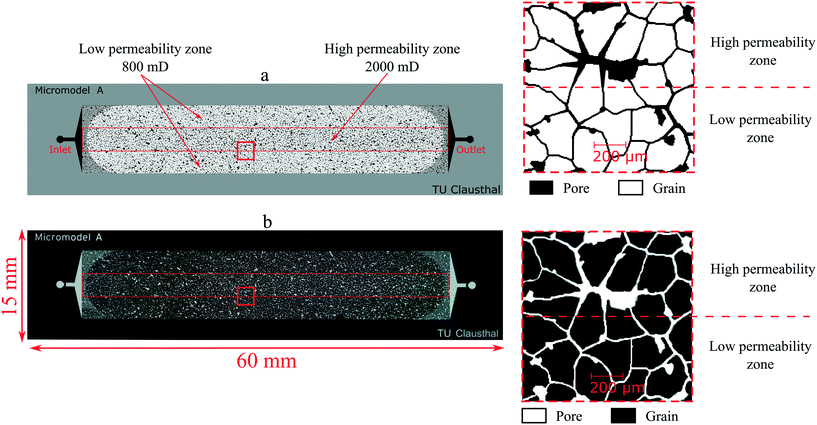

Fig. 7 (a) Lithographic mask of the heterogenous micromodel Structure-A. (b) Image of the micromodel acquired using a high-resolution camera after fabrication.

3.1 Rock properties of the Bentheimer core plug

The total elementary volume of the Bentheimer core plug based on image acquisition was ∼2.3 × 10³ mm³. This value was calculated based on the one thousand two-dimensional (2D) μCT images with dimensions of 1850 × 10 000 pixels (1 pixel = 5 μm). The calculated REV of the Bentheimer image stack was ∼200 mm³ or 10% of the total elementary volume. The porosity of the image stack started to converge towards a porosity level of 0.238. This value was in very good agreement with our measurement data using a gas pycnometer, which showed the porosity of the Bentheimer core plug in the range of 0.24 to 0.26. The REV value estimated in this study was slightly higher than the value calculated by Halisch (2013), which showed a REV of Bentheimer μCT images of 8% (REV domain with an edge length of 500 voxels from a maximum of 1750 voxels).³⁹ This difference might be due to the variation in the μCT image resolution.

The results of the rock property computations of the Bentheimer core plug are summarized in Table 2. As can be observed in this table, the calculated median pore size of the 3D μCT image stack was about 46.42 μm, with 10% of all the pores having a diameter less than 18.55 μm (D10) while 90% were below 94.46 μm (D90). This result was comparable to the pore size distribution of Bentheimer sandstone that was found in the literature.^39–41 Maloney et al. (1990) reported that Bentheimer sandstone might have a broad range of pore size values ranging from 1–140 μm.⁴¹ Their results showed that using a visual microscopy technique and an image analysis technique, the median pore diameter of Bentheimer sandstone was in the range of 60 to 140 μm while smaller pore diameter values were obtained based on the mercury intrusion method, which were in the range of 1–60 μm.

Table 2 Rock properties of the Bentheimer core plug based on computations using the μCT image stack

Properties	Value	Unit
D10/50/90 mean that 10%/50%/90% of all pores have a diameter smaller than the values shown.
Porosity	0.2341	[—]
Pore size
D10	18.55	μm
D50	46.42	μm
D90	94.46	μm
Grain size
D10	68.46	μm
D50	124.10	μm
D90	180.01	μm
Tortuosity in the X direction	1.11	[—]
Tortuosity in the Y direction	1.12	[—]
Permeability, X direction	3106	mD
Permeability, Y direction	3491	mD

---

Based on the computation, 90% of the grains of the Bentheimer image stack have a diameter less than 180 μm (D90) while the median value was approximately 124 μm (D50). These values were slightly lower than the results reported by Peksa et al. (2015).⁴⁰ Their results, based on the analysis of 20 thin sections, showed that the median grain size of Bentheimer sandstone was 235 μm while it was 320 μm based on μCT scans.⁴⁰ Moreover, the calculated tortuosity of the image stack was about 1.11 and 1.12 in the X and Y directions, respectively. These values were comparable with those from the study reported by Kahl et al. (2013) that investigated the pathways of elastic waves through Bentheimer sandstone for the tortuosity estimation. Their result showed a tortuosity of 1.05 both in the X and Y directions.⁴²

As outlined in the methodology, the absolute water permeability of the Bentheimer image stack was calculated based on the Stokes–Brinkman approach. The permeability values of the image stack were 3.1 and 3.5 Darcy in the X and Y directions, respectively. These values were similar to data from the literature.^40,43 According to Peksa et al. (2015), the absolute permeability of Bentheimer sandstone can be in the range of 1.4 to 3.09 Darcy based on laboratory measurement techniques such as measurements using a Ruska gas and liquid permeameter or core flooding experiments.⁴⁰ However, some literature studies also reported variations of Bentheimer sandstone permeability.⁴³ The permeability of Bentheimer sandstone could vary, depending on the environmental conditions during the deposition of the rocks. An extensive study of Bentheimer sandstone with different sedimentation environments was reported by Traska et al. (2013), which showed that the permeability of Bentheimer sandstone could vary in the range of 0.1 to 4.1 Darcy.⁴³

3.2 Rock properties of the micromodels and comparison to the Bentheimer core plug

As mentioned previously, a total of five realizations of the micromodel pore structure were evaluated. Table 3 shows the results of the rock property computation of these structures. As listed in this table, the homogeneous Structure-1, which was generated based on the image stack, matched the rock properties of the Bentheimer core plug. To obtain this ROC, the single threshold value used for defining the pore body map was 0.55, the structural element size was seven pixels and the ratio of pore throat diameters to the actual distance was about 32%. The porosity, pore size distribution, tortuosity and permeability of this structure, as expected, were in line with the properties of the image stack. However, the grain size distribution of this structure, which was in the range of 98.9–240.3 μm was slightly higher than that of the image stack. This deviation was related to the number of pore throats extracted, which intentionally was reduced to match the pore size distribution during the pore structure design. Consequently, few “large” grains appeared in the pore structure matrix.

Table 3 Rock properties of the micromodel for all realized structures

Rock properties	Homogeneous			Heterogeneous
	1	2	3	A	B
D10/50/90 mean that 10%/50%/90% of all pores have a diameter smaller than the values shown.
Porosity (—)	0.245	0.212	0.177	0.192	0.202
Pore size (μm)
D10	16.97	14.32	11.52	12.21	12.66
D50	40.86	34.98	28.08	31.50	35.12
D90	107.91	108.85	105.12	112.52	112.39
Grain size (μm)
D10	98.93	98.47	97.28	99.34	99.44
D50	174.13	176.48	176.86	178.15	177.39
D90	240.30	244.31	249.67	254.78	253.64
Tortuosity in the X-dir. [—]	1.11	1.12	1.13	1.13	1.12
Tortuosity in the Y-dir. [—]	1.09	1.09	1.11	1.10	1.10
Permeability in the X-dir. (mD)	3200	1762	803	1123	1605
Permeability in the Y-dir. (mD)	3563	1974	869	1237	1767

---

Table 3 also shows the properties of heterogeneous Structure-A and Structure-B. As predicted, the rock properties of these structures lie between the properties of the low and high permeability zones. For example, the calculated average permeability of the micromodel Structure-A was ∼1.2 Darcy (Y-direction), where the permeability of the low and high-permeability zones was ∼0.86 and 1.9 Darcy, respectively.

The rock properties of the micromodels show a better relationship with the Bentheimer core plug than other methods from the literature.^2,24,44,45 The approach presented in this study allows the construction of pore structures with realistic porosity while still maintaining the connections between pore bodies. Buchgraber et al. (2011) and Gauteplass et al. (2014) reported micromodels based on a thin section of sandstone with porosities close to 50%.^2,44 The reason for these high porosity values was to provide flow connections across micromodels. A similar result was also described by Karadimitriou (2013), where the porosities of micromodels generated based on Delaunay triangulation were ∼50%.⁴⁵

An irregular network micromodel based on Voronoi tessellations constructed by Wu et al. (2012) showed a porosity of 0.11–0.20 and a permeability of 0.42 to 0.55 Darcy.²⁴ However, these micromodels were constructed with uniform pore throats, which were ∼10 μm to connect all the pore bodies. As described previously, this situation most likely does not occur in reservoir rocks; therefore, in this work, the size of pore throats in the micromodels was designed to be non-uniform. Fig. 8 shows the pore size comparison between the Bentheimer image stack and micromodels with uniform and non-uniform pore throats. As can be seen in this figure, the pore size distribution of the non-uniform micromodel Structure-1 was comparable to that of the image stack. The difference between their mean pore diameters was only ∼5 μm. As for the uniform pore throats, the difference from the image stack was noticeable, because the uniform pore throats dominated the distribution. Furthermore, the relationship between the local porosity and permeability of the micromodel was also compared to that of the Bentheimer image stack. As illustrated in Fig. 9, the local porosity–permeability relationship of the micromodel was in agreement with that of the Bentheimer core plug.

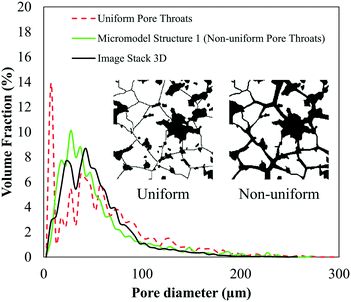Fig. 8 Comparison between the pore size distribution of the Bentheimer 3D image stack and micromodel structures with uniform and non-uniform pore throats.

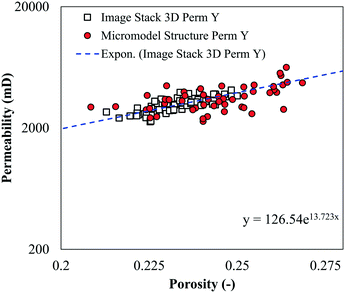Fig. 9 Porosity–permeability relationship of the Bentheimer image stack and the micromodel Structure-1.

3.3 Micromodel flooding experiments

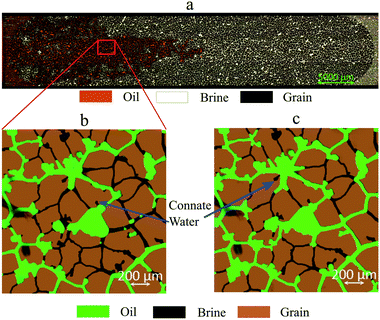
As previously described, during the injection of water and brine, the differential pressure across the micromodel was measured. This pressure data were then used to estimate the absolute permeability based on Darcy's law. The measurement results were then compared to the computed values based on the pore-scale simulation. The results show that the permeability values based on simulation and measurement were in good agreement with a deviation of ±5%. As a continuation, the crude oil was injected into the brine-saturated micromodel at an injection rate of 0.1 μl min⁻¹ equivalent to 1 ft per day Darcy velocity. This oil initialization was conducted until the differential pressure across the micromodel had stabilized, followed by higher injection rates (bump rates, e.g., 10–50 ft per day). Fig. 10 shows the micromodel image during oil initialization obtained using a camera connected to the microscope's objective at 5× magnification.

Fig. 10 Images of the micromodel during oil initialization obtained using a microscope with a 5× magnification objective. Fluorescent light was used to differentiate between the aqueous and oil phases. (a) An image covering the micromodel which contains 100 image tiles. (b) A section of the micromodel after oil injection at an injection rate of 0.2 μl min⁻¹ equivalent to 2 ft per day Darcy velocity. (c) The same section of the micromodel after oil injection at an injection rate of 0.5 μl min⁻¹.

As can be observed in Fig. 10a, 100 images were stitched and synchronized to obtain the whole area of the micromodel. Fig. 10b and c show a section of the micromodel during the oil initialization at two different injection rates. As indicated in these images, not all the pores were filled with the oil since there was the presence of connate water (S_wc) in the micromodel. Oil injection at a higher rate (0.5 μl min⁻¹ equivalent to 5 ft per day Darcy velocity) was performed to minimize the connate water saturation (S_wc). With this procedure, the typical initial oil saturation (S_wc) was 79.0 ± 2%.

A standard secondary mode of brine flooding was performed to investigate the oil displacement efficiency in the micromodels. The brine was injected with an injection rate equivalent to 1 ft per day after the oil initialization. Fig. 11 shows a series of micromodel images during the brine flooding experiment. The images presented here were obtained by processing the raw images taken during the flooding experiment. Fig. 11a and b show the state after the oil initialization and at the brine breakthrough time. As illustrated in this image, the water-front in the high permeability zone, as predicted, was significantly ahead than that in the low permeability zones. The results show that the oil recovery factor at the breakthrough time was relatively low at 19.6 ± 4%. At this stage, most of the oil was produced from the high permeability zone and only small fractions were from the low permeability zones. However, even after breakthrough was already reached, oil displacement still can be observed in the low permeability zones (Fig. 11c). Typically, after a two pore-volume (PV) injection of the brine, no significant oil movement was observed anymore. In this study, the injection was performed until 10 PV to reduce the remaining oil saturation (ROS) to the smallest possible amount or close to residual oil saturation (Sor). The oil recovery factor measured after injection of 10 PV was 31.3 ± 2%.

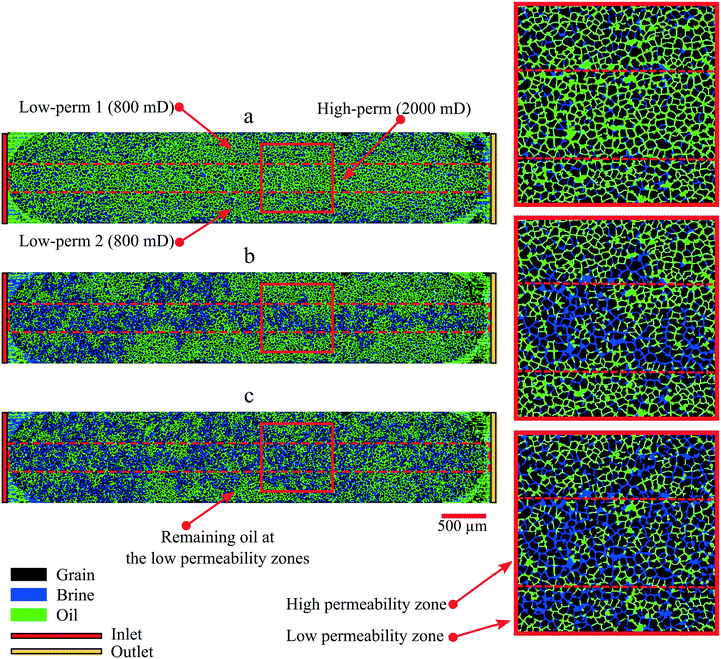Fig. 11 Images of the micromodel during brine flooding. Images of the micromodel (a) under initial conditions, (b) at water breakthrough and (c) after ten pore volume injection of brine.

As a continuation, three polymer flooding experiments were performed after brine flooding (tertiary mode). The oil recovery factor obtained from these experiments is depicted in Table 4. As indicated in this table, after the injection of a 5 PV polymer solution, an additional oil recovery of 4.7% was observed in the whole micromodel. The incremental oil was mainly produced from the low permeability zones (3% to 8%), with only 3% from the high permeability zone. This result indicated that the macroscopic conformance of the flooding process was improved during the polymer flooding.

Table 4 Two-phase flooding experiments using the micromodels

Parameters	Micromodel area
	Whole chip	Low perm 1	High perm	Low perm 2
Initial oil saturation [—]	0.79	0.78	0.83	0.75
RF at breakthrough (%)	19.65	9.02	41.78	3.56
RF after 10 PV brine flooding (%)	31.34	25.60	44.48	20.87
RF after polymer flooding (%)	36.01	29.08	47.38	28.92
ΔRF after polymer flooding (%)	4.67	3.48	2.90	8.05

---

Fig. 12 shows the oil recovery factor and the differential pressure during brine (secondary mode) and polymer (tertiary mode) flooding experiments in the micromodels. From this figure, it can be seen that the trend of the oil recovery factor during polymer flooding is aligned with the increase in differential pressure. The differential pressure recorded across the micromodel was increased by 300%. This pressure increase was due to a change in the viscosity of the displacing fluid. Since the viscosity of the displacing fluids increased by 15 times (change from brine to polymer), the capillary number of the displacement process increased by only one order of magnitude. Based on the capillary desaturation curve (CDC) analysis, the increment of the capillary number should be higher than two orders of magnitude to mobilize the trapped oil significantly.

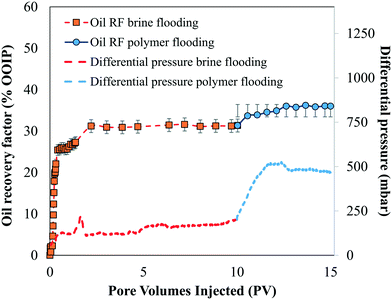Fig. 12 The oil recovery factor and the differential pressure during brine (secondary mode) and polymer (tertiary mode) flooding experiments in the micromodels.

4 Conclusions

In this work, a novel approach for generating micromodels based on real reservoir rocks has been presented. The digital rock physics (DRP) approach was used to extract the rock properties of Bentheimer sandstone based on microscale X-ray computed tomography (μCT) images. By using this approach, the information about the pore bodies and pore throats of reservoir rocks was obtained and then transferred to a 2D pore structure of micromodels. The algorithm presented offers the flexibility to adjust the number and size of the pore bodies and pore throats. Therefore, the porosity, pore and grain size distribution and tortuosity, as well as permeability, of the micromodels can be very similar to the properties of real rocks. Furthermore, the algorithm also enables us to construct heterogeneous micromodels with different permeabilities.

The results of flooding experiments show that the absolute permeability of the micromodel matched the simulated values. It was also found that during typical brine flooding experiments (secondary mode), most of the oil was produced from the high permeability zone and only small fractions were from the low permeability zones. This result suggested that the areal sweep efficiency of this micromodel during brine flooding was relatively low; therefore, it is excellent for an investigation of conformance improvement by using polymer, gel or microbial injection. An increase of the oil recovery factor was observed during polymer flooding (tertiary mode), where extra oil was mainly produced from the low permeability zones. This result indicates that an improvement of macroscopic conformance could be obtained in the heterogeneous micromodels.

Furthermore, the results demonstrate the benefits gained from the digital rock physics method for the construction of micromodels and could be used to support EOR studies on a larger scale, for example, sandpacks or core plugs or even for quick EOR screening before field application. Therefore, future work should focus on the direct comparison between the oil displacement efficiency of micromodels and the corresponding core plug to validate the construction workflow. By comparing these two approaches (core plug and micromodel), the differences between them could be quantitatively estimated and beneficial for improving the construction of micromodels.

An important question for future studies is to integrate the presented approach with surface modification techniques to mimic the surface heterogeneity of reservoir rocks. As previously described, several studies have investigated coating processes to cover the silicon materials of micromodels.^20,21,46 Extensive research was reported by Saefken et al. (2019), where the surface wettability of silicon and glass micromodels could be altered by coating the silicon and glass materials with trichlorosilane.⁴⁶ Furthermore, an in situ growing process of a calcium carbonate layer suggested by Wang et al. (2017) and Yun et al. (2020) could be beneficial to obtain micromodels that mimic carbonate reservoir rocks.^20,21

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors of this paper would like to thank DGMK-746 and the participating companies for financing this research project. The conclusions and opinions stated in this paper are those of the authors and do not necessarily represent those of the partner companies. We acknowledge support by Open Access Publishing Fund of Clausthal University of Technology.

Notes and references

1. A. Chatenever and J. C. Calhoun, J. Pet. Technol., 1952, 4, 149–156.
2. M. Buchgraber, T. Clemens, L. M. Castanier and A. Kovscek, SPE Reservoir Eval. Eng., 2011, 14, 269–280.
3. A. Dupas, I. Hénaut, J.-F. Argillier and T. Aubry, Oil Gas Sci. Technol., 2012, 67, 931–940.
4. A. M. Howe, A. Clarke and D. Giernalczyk, Soft Matter, 2015, 11, 6419–6431.
5. J. Wegner, Investigation of Polymer Enhanced Oil Recovery (EOR) in Microfluidic Devices that Resemble Porous Media: An Experimental and Numerical Approach, Shaker, 2015.
6. K. He, L. Xu, Y. Gao, K. B. Neeves, X. Yin, B. Bai, Y. Ma and J. Smith, SPE Improved Oil Recovery Symposium, 2014.
7. D. K. N. Sinz, M. Hanyak and A. A. Darhuber, J. Phys. Chem. Lett., 2013, 4, 1039–1043.
8. Z. Tong, C. Yang, G. Wu, H. Yuan, L. Yu and G. Tian, SPE/DOE Improved Oil Recovery Symposium, 1998.
9. B. Schumi, T. Clemens, J. Wegner, L. Ganzer, A. Kaiser, R. E. Hincapie and V. Leitenmüller, SPE Europec featured at 81st EAGE Conference and Exhibition, 2019.
10. A. Danesh, J. Peden, D. Krinis and G. Henderson, SPE Annual Technical Conference and Exhibition, 1987.
11. R. T. Armstrong and D. Wildenschild, J. Pet. Sci. Eng., 2012, 94–95, 155–164.
12. C. Gaol, J. Wegner, L. Ganzer, N. Dopffel, F. Koegler, A. Borovina and H. Alkan, SPE Europec featured at 81st EAGE Conference and Exhibition, 2019.
13. D. J. Manlowe and C. J. Radke, SPE Reservoir Eng., 1990, 5, 495–502.
14. K. Ma, R. Liontas, C. A. Conn, G. J. Hirasaki and S. L. Biswal, Soft Matter, 2012, 8, 10669.
15. C. A. Conn, K. Ma, G. J. Hirasaki and S. L. Biswal, Lab Chip, 2014, 14, 3968–3977.
16. N. Quennouz, M. Ryba, J.-F. Argillier, B. Herzhaft, Y. Peysson and N. Pannacci, Oil Gas Sci. Technol., 2014, 69, 457–466.
17. K. Xu, P. Zhu, C. Huh and M. T. Balhoff, Langmuir, 2015, 31, 13673–13679.
18. M. A. Nilsson, R. Kulkarni, L. Gerberich, R. Hammond, R. Singh, E. Baumhoff and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2013, 202, 112–119.
19. V. A. Lifton, Lab Chip, 2016, 16, 1777–1796.
20. W. Yun, S. Chang, D. A. Cogswell, S. L. Eichmann, A. Gizzatov, G. Thomas, N. Al-Hazza, A. Abdel-Fattah and W. Wang, Sci. Rep., 2020, 10, 1–12.
21. W. Wang, S. Chang and A. Gizzatov, ACS Appl. Mater. Interfaces, 2017, 9, 29380–29386.
22. N. K. Karadimitriou and S. M. Hassanizadeh, Vadose Zone J., 2012, 11(3), vzj2011.0072.
23. N. S. K. Gunda, B. Bera, N. K. Karadimitriou, S. K. Mitra and S. M. Hassanizadeh, Lab Chip, 2011, 11, 3785.
24. M. Wu, F. Xiao, R. M. Johnson-Paben, S. T. Retterer, X. Yin and K. B. Neeves, Lab Chip, 2012, 12, 253–261.
25. J.-T. Cheng, L. J. Pyrak-Nolte, D. D. Nolte and N. J. Giordano, Geophys. Res. Lett., 2004, 31, 111–138.
26. D. D. Nolte, L. J. Pyrak-Nolte and N. G. W. Cook, Pure Appl. Geophys., 1989, 131, 111–138.
27. H. Andrä, N. Combaret, J. Dvorkin, E. Glatt, J. Han, M. Kabel, Y. Keehm, F. Krzikalla, M. Lee, C. Madonna, M. Marsh, T. Mukerji, E. H. Saenger, R. Sain, N. Saxena, S. Ricker, A. Wiegmann and X. Zhan, Comput. Geosci., 2013, 50, 25–32.
28. H. Födisch, J. Wegner, R. Hincapie and L. Ganzer, SPE Latin American and Caribbean Petroleum Engineering Conference, 2015.
29. A. Rock, R. E. Hincapie, J. Wegner and L. Ganzer, SPE Europec featured at 79th EAGE Conference and Exhibition, 2017.
30. J. Dvorkin, N. Derzhi, E. Diaz and Q. Fang, Geophysics, 2011, 76, E141–E153.
31. M. Yio, H. Wong and N. Buenfeld, Cem. Concr. Res., 2017, 102, 187–202.
32. D. Silin and T. Patzek, Phys. A, 2006, 371, 336–360.
33. P. Adler, Porous media: geometry and transports, Butterworth-Heinemann, Boston, 1992.
34. W. B. Lindquist, S.-M. Lee, D. A. Coker, K. W. Jones and P. Spanne, J. Geophys. Res.: Solid Earth, 1996, 101, 8297–8310.
35. M. Prodanović, W. Lindquist and R. Seright, J. Colloid Interface Sci., 2006, 298, 282–297.
36. C. Gaol, J. Wegner and L. Ganzer, DGMK-Tagungsbericht 2017, 2017.
37. Z. Yang, C. Zou, S. Wu, S. Tao, L. Hou, R. Zhu and X. Yuan, Shenzhen Daxue Xuebao, Ligongban, 2015, 32, 257.
38. J. Lai, G. Wang, Z. Wang, J. Chen, X. Pang, S. Wang, Z. Zhou, Z. He, Z. Qin and X. Fan, Earth-Sci. Rev., 2018, 177, 436–457.
39. M. Halisch, Application and Assessment of the Lattice Boltzmann Method for Fluid Flow Modeling in Porous Rocks, Technische Universität Berlin, 2013.
40. A. E. Peksa, K.-H. A. Wolf and P. L. Zitha, Mar. Pet. Geol., 2015, 67, 701–719.
41. D. R. Maloney, M. M. Honarpour and A. D. Brinkmeyer, The effects of rock characteristics on relative permeability, United States: N. p., 1990,  DOI:10.2172/5086900.
42. W.-A. Kahl, R. Hinkes, V. Feeser and A. Holzheid, J. Struct. Geol., 2013, 49, 35–49.
43. M. Traska and V. Cnudde, Water Transport Properties In Building Materials: Traditional Methods Versus Ct-Based Pore Network Analysis, Master of Science in Geology, Faculty of Sciences, Ghent University, 2014.
44. J. Gauteplass, K. Chaudhary, A. R. Kovscek and M. A. Fernø, Colloids Surf., A, 2015, 468, 184–192.
45. N. K. Karadimitriou, Two-phase flow experimental studies in micro-models, UU Department of Earth Science, 2013.
46. S. Saefken, J. Wegner and L. Ganzer, DGMK-Tagungsbericht 2019-1, 2019.

---