Open Access Article
Open Access ArticleDroplet encapsulation of electrokinetically-focused analytes without loss of resolution†
Vasileios A.
Papadimitriou
 *,
Stella A.
Kruit
,
Loes I.
Segerink
*,
Stella A.
Kruit
,
Loes I.
Segerink
 and
Jan C. T.
Eijkel
and
Jan C. T.
Eijkel
BIOS-Lab on a Chip Group, MESA+ Institute of Nanotechnology, Technical Medical Centre, Max Planck Center for Complex Fluid Dynamics, University of Twente, The Netherlands. E-mail: v.papadimitriou@utwente.nl
First published on 15th May 2020
Abstract
Lab-on-chip electrokinetic focusing and separation techniques are widely used in several scientific fields. In a number of cases, these techniques have been combined with a selective analyte extraction for off-chip analysis. Nevertheless, the usability of the extracts is limited by diffusion which reduces the separation resolution. In this paper we propose the integration of a droplet generator capable of continuous or on-demand generation and extraction of electrokinetically separated and focused analytes. We demonstrate the selective droplet extraction of model analytes separated and concentrated via ion concentration polarization focusing (ICPF). We report extracted droplets with 1000-fold increased concentration. Importantly, the droplet generator does not interrupt the ICPF process making it suitable for integration with the majority of electrokinetic separation techniques.
1 Introduction
In microfluidic systems electrokinetic focusing techniques can be used to separate, purify and increase the effective concentration of analytes, finding applications in various research and industry sectors. However, in almost all of the presently available systems the focused analytes are trapped in the microchannel, making the integration of a detection system in a lab-on-chip device mandatory. This integration requirement significantly limits the detection methods and processes, namely to those that can be integrated on chip and that are compatible with the electrokinetic method. Powerful tools such as mass spectrometry cannot be used as they are impossible to be implemented on chip.The extraction of analytes electrokinetically focused via ion concentration polarization focusing (ICPF) has been reported before by our group1,2 and a number of other researchers.3–8 Continuous extraction methods such as our previous work and the work2 of Kwak et al.5 suffer from low preconcentration rates. On the other hand in non-continuous methods, after extraction a significant decrease in concentration and separation resolution inevitably occurs due to diffusion. A typical method for avoiding the effects of diffusion during transport of analytes is the use of droplet microfluidics to compartmentalize reactants into picolitre volumes9 while allowing control over transport in space and time. Droplet microfluidics has been investigated over the years and due to its versatility has seen many applications in research and industry such as for material science and biological/chemical platforms.10 The surface to volume ratio is high at the microdroplet scale, facilitating short heat and mass transfer times, short diffusion distances, and fast reaction times, making the droplets highly efficient microreactors. Moreover, droplet microfluidics tools allow the production of size-controlled and reproducible droplets, generated at high frequency, with the ability to independently control each droplet. Also, droplets can be transported, sorted, merged and split.11–13 These characteristics make droplet microfluidics a versatile technique and countless examples can be found in literature.9,10,12–15
The integration of a droplet generator with an electrokinetic separation technique has been demonstrated before, allowing the encapsulation of separated analytes while maintaining their spatial concentration profile. An example of this is given by Edgar et al.16 where capillary electrophoresis was used to separate the analytes in bands and propagated these towards a flow focusing droplet generator. In another paper, Chen et al.17 coupled ICPF to a droplet generator. First, they used ICPF to concentrate biomolecules into a plug. Once a sufficient concentration factor was reached, the ICPF process was stopped and the plug was pushed towards the droplet generator where the analytes were encapsulated in droplets. Though the sample was concentrated by a 100-fold, an increase in concentration of only 20-fold was measured in the droplets due to diffusion of the analytes before they were encapsulated in the droplets.17 While the first example mainly concerns separating the analytes, and the second example concentrating the sample, Van Kooten et al.18 used isotachophoresis (ITP) to separate and concentrate analytes, and selectively extract them by droplet microfluidics. However, the droplet generator in that work disrupted the electrokinetic separation, not allowing continuous extraction. In this article we propose a droplet generator suitable for both continuous and on-demand droplet generation that does not disrupt the electrokinetic separation and concentration process. We demonstrate the droplet generator functionality when integrated with an ICPF chip.
2 Theory
2.1 Ion concentration polarization focusing
Electrokinetic focusing techniques are a powerful tool in analytical chemistry. ICPF is such a focusing technique and it was chosen for integration with the droplet generator because of its ease of use compared to other focusing techniques such as isoelectric focusing or ITP that require application of specific electrolytes. ICPF was introduced by Wang et al.19 who demonstrated concentration of biomolecules by a factor of 106. Later Quist et al.20 in addition showed simultaneous separation of anionic analytes using ICPF. Since then a vast amount of research has been performed in ion concentration polarization (ICP) and ICPF.5,17,21–30 We refer the reader to a short theoretical background of ICPF in the ESI† in order to define the requirements of the droplet generator. For a deeper theoretical background of ICPF the reader is referred to our previous work1 or the work of Ouyang et al.31 and the more recent work of Gong et al.6,7There are two operating modes in ICPF namely peak and plateau mode. In peak mode analytes that are in low concentration compared to the bulk electrolyte will form a Gaussian peak when they concentrate by ICPF. In our previous work1 we derived the variance σi2 [m2] of this Gaussian distribution as
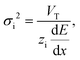 | (1) |
Once the concentration of analytes is increased due to ICPF to approximately match the concentration of the bulk electrolyte then the Gaussian concentration peaks will not increase in height and start widening forming plateaus (plateau mode). The longer the concentration time in plateau mode the wider the plateaus.
2.2 Droplet generator
We formulated the set of requirements for the droplet generator as follows:i. The continuous phase (oil) should not cross/fill the separation channel, as the goal is to package the focused analytes (dispersed phase) without interrupting the ICPF process. ICPF and all electrokinetic separations require an electric field (and hence a current) running through the whole separation channel. If the non-conductive oil protrudes in the separation channel, the electric current would be interrupted causing the focusing process to stop.
ii. The pressure of the dispersed phase (applied to the separation channel reservoirs) should not be directly controlled. The separation and focusing of analytes are strongly affected by the convective flow. The addition of pressure in the separation channel can easily affect the convective flow with undesired results. Pressure control of the dispersed phase is feasible but not trivial and hence it needs to be avoided.
iii. The droplet generator should allow both continuous and droplet-on-demand (DoD) operation. In the DoD operation of the generator, it is desired that it is able to form a predetermined number of droplets (one or more).
iv. The droplet size should be smaller than the size of a concentrated analyte peak, as otherwise the analyte will be diluted in the volume of the droplet. Assuming the aforementioned peak size and considering the height (30 μm) and the width (50 μm) of our channel, we arrive at a focused analyte volume ranging from 42.8 pL to 105.8 pL for a 2σ width of the Gaussian peak. Thus, the droplets should be smaller than 42.8 pL.
In droplet microfluidic systems, five device geometries can be distinguished: i) cross flow (e.g. T-junction), ii) co-flow, iii) flow focusing, iv) step emulsification, and v) microchannel emulsification.32 To satisfy our first requirement (the continuous phase not crossing into the separation channel) we are limited to a T-junction geometry. T-Junction droplet generators are extensively used in microfluidics and the droplet formation and break-up mechanisms have been investigated in numerous review papers.11,32–34 The T-junction is characterized by two immiscible flows meeting at an angle to produce monodispersed droplets in the carrier phase.
Generally, three break-up modes are distinguished for T-junctions: squeezing, dripping, and jetting,32 of which the latter two are dominantly shear-driven. The first T-junction was reported by Thorsen et al.35 who used pressure-induced flow to form droplets by shearing one phase by a second immiscible one. They stated that the droplet formation in this case is the result of the competition between interfacial tension and shear forces. For a precise control over droplet formation in DoD systems (our third requirement) the break-up should be in the squeezing regime.36 The pressure balance between the dispersed and continuous phase interface at the junction dominates the droplet formation in the squeezing regime.
The capillary number can be used to determine in which mode the device operates. The capillary number (Ca) is defined as
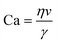 | (2) |
The droplet formation mechanism in the squeezing regime can be described in short as follows. At the orifice, the two immiscible phases form an interface. As the dispersed phase penetrates into the continuous phase channel, the shear stress exerted by the continuous phase is not sufficient to break off the droplet and the dispersed phase penetrates deeper into the continuous channel until it fills its cross section. This leaves only a thin wetting film of continuous phase on the walls, giving rise to an increased pressure at the interface. The resulting pressure exerts a force on the droplet in the downstream direction and a neck is formed connecting the emerging droplet with the bulk dispersed phase. The neck thins as the droplet elongates in the downstream direction. As the neck approaches the downstream edge of the orifice, it breaks off and a droplet is formed inside the continuous channel. The droplet is transported downstream by the continuous phase, while the dispersed phase stream retracts into the orifice.
Presently, not many examples are known in literature in which a passive (i.e. without any on chip active elements such as valves) DoD is used, and even less in combination with a T-junction geometry. Vanapalli et al.,37 and in a similar setup Hamidović et al.,36 used simple pressure actuation to form a single water droplet in oil in a T-junction. In this case, the oil phase was driven by hydrostatic heads. A droplet was created by using short pressure pulses on the dispersed phase to squeeze a small volume of water into the oil channel. In another approach Churski et al.38 used external valves coupled to the dispersed and continuous phase to demonstrate DoD in a T-junction setup. In both cases the pressure of the dispersed phase was actively controlled. Teo et al.39 used negative pressure to produce DoD in a flow-focusing configuration. The water pressure and oil pressure were first balanced to form a stable interface. By applying a negative pressure on the continuous phase at the outlet, a droplet was formed.
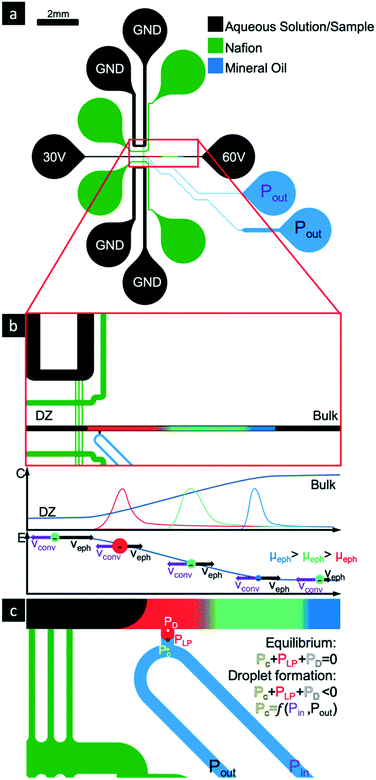
Our proposed passive droplet generator (capable of both DoD and continuous actuation) is shown in Fig. 1c. A continuous phase (oil) channel intercepts a dispersed phase via a small sampling channel. The sampling channel is connected perpendicularly to the separation channel. An oil–water interface is established at the orifice of the sampling channel with the continuous phase channel. Three pressures act on this oil–water interface, namely Laplace pressure (PLP), continuous phase pressure (Pc) and dispersed phase pressure (Pd).
Several factors contribute to the Pd at the water–oil interface. The reservoirs of the dispersed (aqueous) phase channel (the separation channel) are open to the atmospheric pressure and the pressure is not actively controlled. Based on the height of the liquid in the reservoirs there will thus be a small hydrostatic pressure contribution in addition to the Laplace pressure due to the curvature of the meniscus in the reservoirs. Furthermore, there is also small negative pressure created due to the ICPF process, caused by the non-uniform EOF along the separation channel.1,31
The two reservoirs of the continuous (oil) phase channel are connected to two pressure controllers. A positive pressure is applied to the Pin reservoir and a negative pressure to the Pout reservoir, resulting in a net pressure driven flow from Pin to Pout. The hydraulic resistance in the oil channel causes a pressure drop along this channel. The pressure at the oil–water interface will range between Pin and Pout (Pin > Pc > Pout), depending on the hydraulic resistance of channel from the inlet (where Pin is applied) to the droplet generator and the resistance from the droplet generator to the outlet (where Pout is applied).
The Laplace pressure difference at the oil–water interface (i.e. oil pressure with respect to water pressure):40
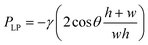 | (3) |
If the sum of all the pressures at the interface is zero then the system is at an equilibrium state, the meniscus remains stagnant at the site of the droplet generator and no droplets are created.
| PLP + Pd + Pc = 0 | (4) |
| PLP + Pd + Pc < 0 | (5) |
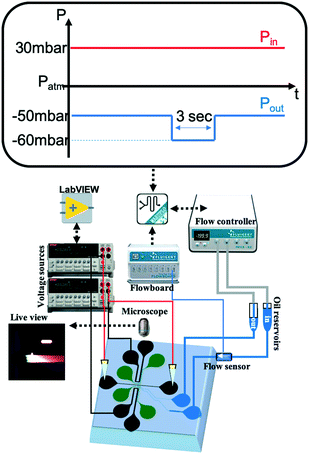 | ||
| Fig. 2 Schematic of the setup and a typical pressure actuation scheme for a single droplet generation (DoD). | ||
3 Experimental
A 30 μm layer of Microchem SU-82050 photoresist was spin-coated on a silicon wafer and the instructions of the manufacturer were followed for exposure and development. Polydimethylsiloxane (PDMS, DOWSIL™ 184 silicone elastomer kit) and curing agent (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) were mixed and PDMS chips were fabricated using standard soft lithography41 with the prepared silicon wafer as a mold. The chips were bonded to standard microscopy glass slides after O2 plasma treatment. The sample and the Nafion channels have a width of 50 μm while the buffer channels have a width of 150 μm. The channels of the droplet generator vary in width and their dimensions are discussed in the ESI.†
1 ratio) were mixed and PDMS chips were fabricated using standard soft lithography41 with the prepared silicon wafer as a mold. The chips were bonded to standard microscopy glass slides after O2 plasma treatment. The sample and the Nafion channels have a width of 50 μm while the buffer channels have a width of 150 μm. The channels of the droplet generator vary in width and their dimensions are discussed in the ESI.†
A droplet of Nafion perfluorinated resin solution (20 wt%) (Sigma-Aldrich) was introduced at the designated reservoirs (Fig. 1a) and the solution was patterned via capillary forces42 followed by a drying step of 30 min at 60 °C. During the drying process the Nafion solution loses a considerable fraction of its volume, occasionally creating microchannels/-gaps between the separation and buffer channels. To prevent any convective flow from the separation channel into the buffer channels by these gaps, while still maintaining electric contact, a solution of 2 wt% UltraPure™ Agarose (Invitrogen) in 1x phosphate buffered saline (PBS, Sigma-Aldrich) was later introduced in the buffer channels (Fig. 1a) to seal the gaps. The warm agarose solution (>60 °C) was introduced in the buffer reservoir and filled the channels via capillary flow. It was then allowed to cool down for 5 min and the devices were tested immediately afterwards to prevent the drying of the agarose gel.
The aqueous sample used is 1xPBS spiked with the fluorescent markers Bodipy 492/515 Disulfonate (BDP, Invitrogen), Cascade Blue (CB, Invitrogen) and Alexa Fluor 647 (AF647, Invitrogen). This aqueous sample was added in the separation channel followed by filling the continuous phase, mineral oil (GE Healthcare Life Sciences) into the designated channels. To prevent coalescence of the droplets, surfactant Span80 (Sigma-Aldrich) was added to the oil in 3 wt% percent.
The continuous phase inlet and outlet were connected to a Fluigent MFCS-EZ pressure controller which was operated via the MAESFLO software. Platinum wires (Alfa Aesar 0.01 in ∅) were introduced in the other six reservoirs (buffer channels and separation channel) and were connected to two Keithley 2410 SourceMeters (Fig. 2). The power supplies were operated and the current recorded via in-house built LabVIEW software. The formation of droplets and focusing of analytes was optically captured via an Olympus IX51 microscope and a FLIR Grasshopper3 color camera. The droplet size and frequency were analyzed with Droplet morphometry and velocimetry (DMV) software provided by Basu.43 The fluorescent image analysis was performed via ImageJ and MATLAB (R2016a).
4 Results and discussion
4.1 Droplet generator characterization
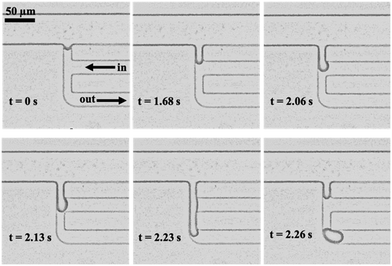
Several designs of the droplet generator were evaluated in initial experiments without the use of ICPF. The main design variations occurred at the channel widths of the dispersed and continuous (small sampling channel) phase (all the tested designs can be found in the ESI†). The initial aim was to determine the equilibrium pressures Pin and Pout (i.e. a stable meniscus and no visible droplet formation) for each design, starting from the expected values based on the dimensions shown in the ESI.† For all designs, we noticed a difference between the theoretical and experimental equilibrium pressures of −2.8 ± 5.1 mBar. We ascribe this difference to inaccuracies in the calculation of the hydrostatic pressure at the reservoirs of the separation channel (Pd) and in the measurement of the contact angle for the calculation of the Laplace pressure (PLP). In addition, the pressure applied by the pressure controller (Pin and Pout) was fluctuating by ±1 mBar. In view of these error sources we believe that our model reasonably predicted the system behavior.Once the equilibrium state was achieved a small negative pressure pulse was applied to Pin or a negative pressure pulse on both Pin and Pout. Note that Pout is a negative (suction) pressure hence a negative pulse will result in a higher flow towards Pout. Pin on the other hand is a positive pressure hence a negative pulse results in a lower pressure and lower flow towards Pout. A negative pressure pulse at Pin and/or Pout in both cases tilts the pressure balance in the same direction (eqn (5)). For the formation of a single droplet, the duration and magnitude of the pulse was found to be dependent on the design. Typically, the pulse duration ranged between 3 and 5 s for a step size of between 5 and 20 mbar (Fig. 3).
We furthermore investigated the success rate of the DoD generators. Either a single or five droplets were requested for each design and the success rate was determined. If the generator created more, or less, droplets than the requested number, the attempt was counted as a fail. In case of single droplet generation, on average in 77% of the cases a successful single droplet was produced. For 12% of the cases, no droplet was created and in 11% of the cases two droplets were created. Taking into account also the multiple (5) droplets requests out of the total 213 requests (for all the designs), on average 74% of cases were successful. A detailed look on success rate per design is shown in the ESI.†
As previously mentioned, a critical requirement for the droplet generator is that the droplet volume is smaller than the volume of the focused analyte plug, which is 42.8 pL for 2σ of the smallest Gaussian of a focused analyte in ICPF in the present structures. For all designs, 80% of the droplets were found to be smaller than 20 pL with the largest droplet being 27 pL, which is well below this required volume. Although we did not find a significant correlation between flow rate and droplet size, in all cases the capillary number is below 0.001 which indicates that the device operates in the desired squeezing regime. The droplet size is thereby mainly determined by the geometry of the T-junction and more specifically the dimension (width) of the continuous phase channel (see ESI†).
4.2 Integration of DoD and ICPF
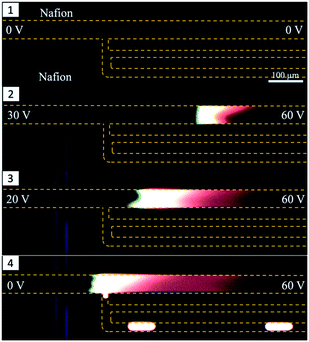
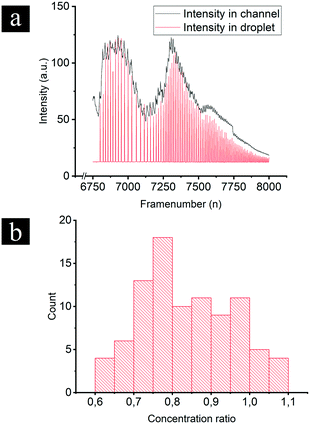
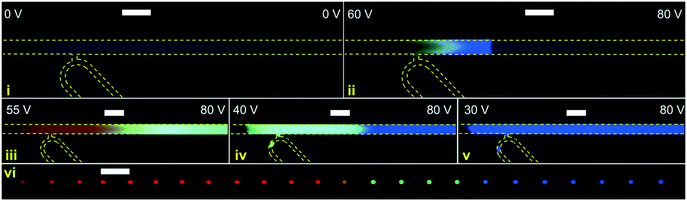
Experiments were performed with integrated DoD generation and ICPF process. An example of the experimental procedure followed is shown in Fig. 4. First the aqueous sample (dispersed phase – 2 μM BDP and 8 μM AF647 in 1xPBS) was introduced in the separation channel. This was followed by filling the continuous phase channels with mineral oil. The equilibrium state was established by tuning Pin and Pout (Fig. 4-1). The ICPF process started by applying suitable potentials to the two reservoirs of the separation channel to have the analytes focusing at a location that did not overlap with the droplet generator (Fig. 4-2). By allowing sufficient time for the ICPF, the desired concentration of analyte was reached. By subsequently tuning the actuation potentials to control the focusing location,1,20,29 the focusing location could be moved to the site of the droplet generator (Fig. 4-3). Once the analytes properly overlapped the droplet generator, the pressure scheme was applied and droplets with highly concentrated analyte were formed and extracted. Importantly, we found that the droplet formation did not affect the ICPF process, which continued concentrating the analytes.In order to investigate the concentration ratio (i.e. the ratio of the analyte concentration in the droplet with respect to the concentration in the focused plug) of the droplet generator setup working in the continuous mode, the analyte (1 μM BDP in 1xPBS) was focused in a location that did not intercept with the droplet generator. In contrast to the previous DoD approach, now the droplet generator was set to continuous droplet generation. Then the focused analyte plug by voltage tuning was moved to the location of the droplet generator, and subsequently pressures were changed such that the analyte plug became continuously “packaged” and extracted in a stream of droplets. A video of this process was recorded, and the concentration of the newly formed droplet was compared to the concentration in the separation channel (at the intercept with the droplet generator averaged over the separation channel width) of the same video frame. We report an average concentration ratio droplet/channel of 0.84 with a minimum of 0.62 and a maximum of 1.1 (Fig. 5b) compared to 0.2 (ref. 17) and 0.6 (ref. 18) reported in similar works. A value higher than 1 can be reached because the droplet and focused concentration are compared in the same frame (time moment) while in reality the droplet contents were sampled from the separation channel at an earlier moment. It should be noted that a relatively high exposure time was required for the microscopy images which results in slightly blurred images of the fast-moving droplets which may cause underestimation of their fluorescence intensity. We nevertheless believe this method gives a reasonable estimate of the recovery. In the future a downstream processing method can be used for a more accurate droplet concentration quantification.
In this demonstration we used a lower salinity background electrolyte (0.1xPBS), which favors the preconcentration rate in ICPF. Nevertheless, ICPF can achieve similar and higher preconcentration factors if it is allowed sufficient time in higher salinities, if needed. Preconcentration factors in the order of millions have been reported in similar setups.19 Once highly concentrated droplets of the relevant analytes (e.g. proteins) are formed, downstream processing can take place using droplet microfluidics, e.g. by merging droplets containing reactants to achieve similar results as reported in the work of Chen et al.17
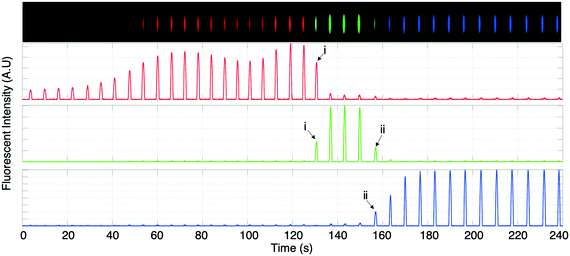
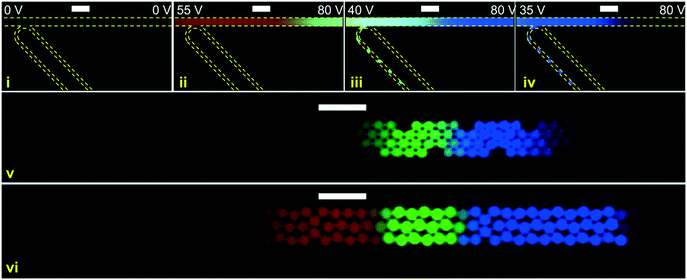
In Fig. 7 another instance of multiple DoD droplets is shown and the purity of each droplet is investigated. Depending on the placement of the plateaus with respect to the droplet generator orifice either pure droplets or a mixture between adjacent plateaus is extracted. For example, the droplet (i) in Fig. 7 contains a mixture of AF647 and BDP and droplet (ii) contains a mixture of BDP and CB. In Fig. 6 and 7 the diameter of the extracted droplets was measured and for all droplets ranged between 20 μm (9.4 pL) and 22 μm (11.4 pL). Since the analytes are present in high concentration there is no longer a linear relation between concentration and fluorescent intensity due to self-quenching. For a precise quantitative purity investigation, a downstream analysis process of the droplet content would thus be needed, such as by mass spectrometry.
In addition to the DoD operation, the same device could also be used for continuous droplet generation. Two examples of continuous droplet extraction are shown in Fig. 8 (a video in real time can be found in the ESI† – (Fig. S8-contiuous.avi)). As shown in the two examples of Fig. 7 and 8 pure and variously mixed droplets can be extracted. Since in ICPF analytes sort themselves based on their mobility, a possible application of continuous droplet extraction could be as follows: the analytes of a complex sample (e.g. proteins in human serum) are separated and allowed sufficient time to concentrate via ICPF. The longer the focusing time, the higher the concentration of low abundance analytes, while the concentration of the highly abundant analytes is limited by their plateau concentration. After the desired focusing time, a continuous droplet generation process is started while the actuation potentials are tuned so the sample is “swept” across the droplet generator orifice. The resulting droplets then contain highly concentrated analytes and are sorted based on their electrophoretic mobility, creating in a sense a spatially separated electrophoretic mobility “memory” of the sample.
5 Conclusion and outlook
We demonstrated a versatile droplet generator that can be successfully integrated with ICPF. The droplet generator is capable of either DoD (an average success rate of 0.77) operation or continuous droplet generation without the need of any on-chip active elements or external valves. The droplet generator does not affect the ICPF process, which was able to continuously concentrate analytes while highly concentrated analyte droplets were extracted on demand or in continuous fashion. We report droplets with analyte concentrations of up to 1003 times the original sample concentration. In case the ICPF duration for concentrating analytes is prolonged, we expect that a much higher concentration factor would still be possible. The concentration ratio of our system (0.84) improved the results earlier reported by Chen et al.17 (0.2) and Van Kooten et al.18 (0.6). In addition to the improved ratio, our device does not interrupt or affect the ICPF process compared to the aforementioned works, making it suitable for integration with a plethora of electrokinetic separation techniques.We demonstrated separation and selective droplet extraction from a simple sample with three analytes. We furthermore showed selective droplet extraction either in DoD or continuous droplet generation. A possible application of the continuous droplet generation mode can make use of the fact that focused analyte bands appear in order of electrophoretic mobility. The analytes of a complex sample such as human serum could be focused by ICPF followed by sequential extraction of all analytes in concentrated form. This procedure would create in a sense a concentrated electrophoretic mobility “memory” of the sample, with the analytes spatially sorted in the droplets in order of electrophoretic mobility.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported and funded by the Horizon 2020 Framework Programme of the European Union under the project H2020-PHC-634013 (PHOCNOSIS).References
- V. A. Papadimitriou, L. I. Segerink and J. C. T. Eijkel, Lab Chip, 2019, 19, 3238–3248 RSC.
- V. A. Papadimitriou, L. I. Segerink and J. C. T. Eijkel, Anal. Chem., 2020, 92, 4866–4874 CrossRef CAS.
- Y. Y. Chen, P. H. Chiu, C. H. Weng and R. J. Yang, Biomicrofluidics, 2016, 10(1), 014119 CrossRef PubMed.
- J. Choi, K. Huh, D. J. Moon, H. Lee, S. Y. Son, K. Kim, H. C. Kim, J. H. Chae, G. Y. Sung, H. Y. Kim, J. W. Hong and S. J. Kim, RSC Adv., 2015, 5, 66178–66184 RSC.
- R. Kwak, S. J. Kim and J. Han, Anal. Chem., 2011, 83(19), 7348–7355 CrossRef CAS PubMed.
- L. Gong, Z. Li and J. Han, Sep. Purif. Technol., 2019, 217, 174–182 CrossRef CAS.
- L. Gong, W. Ouyang, Z. Li and J. Han, J. Membr. Sci., 2018, 556, 34–41 CrossRef CAS PubMed.
- D. T. Phan, L. Jin, S. Wustoni and C. H. Chen, Lab Chip, 2018, 18, 574–584 RSC.
- T. S. Kaminski, O. Scheler and P. Garstecki, Lab Chip, 2016, 16, 2168–2187 RSC.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- A. M. Pit, M. H. G. Duits and F. Mugele, Micromachines, 2015, 6(11), 1768–1793 CrossRef.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- F. T. G. Van Den Brink, T. Phisonkunkasem, A. Asthana, J. G. Bomer, A. M. J. M. Van Den Maagdenberg, E. A. Tolner and M. Odijk, Lab Chip, 2019, 19, 1332–1343 RSC.
- L. Shang, Y. Cheng and Y. Zhao, Chem. Rev., 2017, 117(12), 7964–8040 CrossRef CAS PubMed.
- B. J. Hindson, K. D. Ness, D. A. Masquelier, P. Belgrader, N. J. Heredia, A. J. Makarewicz, I. J. Bright, M. Y. Lucero, A. L. Hiddessen, T. C. Legler, T. K. Kitano, M. R. Hodel, J. F. Petersen, P. W. Wyatt, E. R. Steenblock, P. H. Shah, L. J. Bousse, C. B. Troup, J. C. Mellen, D. K. Wittmann, N. G. Erndt, T. H. Cauley, R. T. Koehler, A. P. So, S. Dube, K. A. Rose, L. Montesclaros, S. Wang, D. P. Stumbo, S. P. Hodges, S. Romine, F. P. Milanovich, H. E. White, J. F. Regan, G. A. Karlin-Neumann, C. M. Hindson, S. Saxonov and B. W. Colston, Anal. Chem., 2011, 83(22), 8604–8610 CrossRef CAS PubMed.
- J. S. Edgar, G. Milne, Y. Zhao, C. P. Pahbati, D. S. W. Lim and D. T. Chiu, Angew. Chem., Int. Ed., 2009, 48(15), 2719–2722 CrossRef CAS.
- C. H. Chen, A. Sarkar, Y. A. Song, M. A. Miller, S. J. Kim, L. G. Griffith, D. A. Lauffenburger and J. Han, J. Am. Chem. Soc., 2011, 133(27), 10368–10371 CrossRef CAS.
- X. F. Van Kooten, M. Bercovici and G. V. Kaigala, Lab Chip, 2018, 18, 3588–3597 RSC.
- Y. C. Wang, A. L. Stevens and J. Han, Anal. Chem., 2005, 77(14), 4293–4299 CrossRef CAS PubMed.
- J. Quist, K. G. H. Janssen, P. Vulto, T. Hankemeier and H. J. Van Der Linden, Anal. Chem., 2011, 83, 7910–7915 CrossRef CAS PubMed.
- S. J. Kim, S. H. Ko, K. H. Kang and J. Han, Nat. Nanotechnol., 2010, 5, 297–301 CrossRef CAS PubMed.
- J. K. Sung and J. Han, Anal. Chem., 2008, 80, 3507–3511 CrossRef PubMed.
- L. F. Cheow, A. Sarkar, S. Kolitz, D. Lauffenburger and J. Han, Anal. Chem., 2014, 86(15), 7455–7462 CrossRef CAS PubMed.
- H. L. Jeong, S. Chung, J. K. Sung and J. Han, Anal. Chem., 2007, 79(17), 6868–6873 CrossRef PubMed.
- V. Liu, Y.-A. Song and J. Han, Lab Chip, 2010, 10, 1485 RSC.
- S. H. Ko, Y.-A. Song, S. J. Kim, M. Kim, J. Han and K. H. Kang, Lab Chip, 2012, 12, 4472 RSC.
- J. H. Lee, Y. A. Song and J. Han, Lab Chip, 2008, 8, 596–601 RSC.
- S. J. Kim, Y. C. Wang, J. H. Lee, H. Jang and J. Han, Phys. Rev. Lett., 2007, 99(4), 044501 CrossRef PubMed.
- J. Quist, P. Vulto, H. Van Der Linden and T. Hankemeier, Anal. Chem., 2012, 84, 9065–9071 CrossRef CAS PubMed.
- Y. C. Wang and J. Han, Lab Chip, 2008, 8, 392–394 RSC.
- W. Ouyang, X. Ye, Z. Li and J. Han, Nanoscale, 2018, 10, 15187–15194 RSC.
- P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75 RSC.
- C.-X. Zhao and A. P. J. Middelberg, Chem. Eng. Sci., 2011, 66(7), 1394–1411 CrossRef CAS.
- M. De Menech, P. Garstecki, F. Jousse and H. A. Stone, J. Fluid Mech., 2008, 595, 141–161 CrossRef.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86(18), 4163 CrossRef CAS PubMed.
- M. Hamidović, W. Haselmayr, A. Grimmer, R. Wille and A. Springer, Nano Commun. Netw., 2019, 19, 33–46 CrossRef.
- S. A. Vanapalli, A. G. Banpurkar, D. Van Den Ende, M. H. G. Duits and F. Mugele, Lab Chip, 2009, 9, 982–990 RSC.
- K. Churski, P. Korczyk and P. Garstecki, Lab Chip, 2010, 10, 816–818 RSC.
- A. J. T. Teo, K. H. H. Li, N. T. Nguyen, W. Guo, N. Heere, H. D. Xi, C. W. Tsao, W. Li and S. H. Tan, Anal. Chem., 2017, 89(8), 4387–4391 CrossRef CAS PubMed.
- V. A. Papadimitriou, L. I. Segerink, A. van den Berg and J. C. T. Eijkel, Anal. Chim. Acta, 2018, 1000, 232–238 CrossRef CAS PubMed.
- D. B. Weibel, W. R. DiLuzio and G. M. Whitesides, Nat. Rev. Microbiol., 2007, 5, 209–218 CrossRef CAS PubMed.
- V. Liu, Y. A. Song and J. Han, Lab Chip, 2010, 10, 1485–1490 RSC.
- A. S. Basu, Lab Chip, 2013, 13, 1892–1901 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0lc00191k |
| This journal is © The Royal Society of Chemistry 2020 |