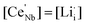X-ray pair distribution function analysis and electrical and electrochemical properties of cerium doped Li₅La₃Nb₂O₁₂ garnet solid-state electrolyte

Abstract

Garnet solid state electrolytes have been considered as potential candidates to enable next generation all solid state batteries (ASSBs). To facilitate the practical application of ASSBs, a high room temperature ionic conductivity and a low interfacial resistance between solid state electrolyte and electrodes are essential. In this work, we report a study of cerium doped Li₅La₃Nb₂O₁₂ through X-ray pair distribution function analysis, impedance spectroscopy and electrochemical testing. The successful cerium incorporation was confirmed by both X-ray diffraction refinement and X-ray pair distribution function analysis, showing the formation of an extensive solid solution. The local bond distances for Ce and Nb on the octahedral site were determined using X-ray pair distribution function analysis, illustrating the longer bond distances around Ce. This Ce doping strategy was shown to give a significant enhancement in conductivity (1.4 × 10⁻⁴ S cm⁻¹ for Li_5.75La₃Nb_1.25Ce_0.75O₁₂, which represents one of the highest conductivities for a garnet with less than 6 Li) as well as a dramatically decreased interfacial resistance (488 Ω cm² for Li_5.75La₃Nb_1.25Ce_0.75O₁₂). In order to demonstrate the potential of this doped system for use in ASSBs, the long term cycling of a Li//garnet//Li symmetric cell over 380 h has been demonstrated.

---

Introduction

State-of-the-art lithium ion batteries (LIBs) have dominated the energy storage market for more than 2 decades because of their long cycle life and high energy and power densities over other battery systems.^1–3 Nowadays, the increasing demand in developing electrical vehicles (EVs) not only needs higher energy density, but more importantly, requires improved safety properties.⁴ The flammable organic solvent in LIBs can trigger safety issues, and so makes it a non-ideal system for EVs. Instead, all-solid-state batteries (ASSBs) using a non-flammable inorganic solid-state electrolyte are considered to be a promising candidate to address the safety issues for future EVs.⁵

Garnet lithium ion conductors have attracted increasing interest in the last decade due to their relatively good electrochemical stability against Li metal/cathode materials, and high room temperature lithium ionic conductivity compared to other solid state electrolyte materials.^6–8 The ideal garnet framework has the chemical formula A₃B₂C₃O₁₂, where A, B and C ions are located at eight, six and four oxygen coordinated sites, respectively. La₃M₂Li₅O₁₂ (M = Nb, Ta), was the first fast Li⁺ ion conducting garnet reported by Thangadurai et al. in 2003.⁹ Detailed studies have revealed that the lithium content and the distribution of lithium in the structure are key to the diffusion pathway and resulting lithium ion conductivity in garnet materials.^10,11 Li⁺ ions occupy both 24d tetragonal and 96h/48g octahedral Wyckoff sites in cubic Li₅La₃Nb₂O₁₂, with lithium ions shifting from 24d tetragonal sites to 96h/48g octahedral sites as a function of increasing lithium content, thus enabling a reduction in the lithium–lithium interaction strain.^6,7 The maximum lithium content in the structure has been found to be 7, leading to compositions such as Li₇La₃Zr₂O₁₂, which adopts tetragonal symmetry with lithium ions ordering in three fully occupied tetrahedral 8a and octahedral 16f and 32g sites; this Li ordering reduces its ionic conductivity.^12–14 The highly conductive cubic phase can be stabilised through the creation of lithium vacancies, and the optimum conductivity is found for lithium contents of 6.4–6.6 per garnet formula unit.^15–25

In addition, to facilitate the practical application of ASSBs, issues such as high interfacial resistances between the electrode and electrolyte, and the lithium dendrite penetration problem within solid state electrolytes have attracted much attention in recent years.^26–29 The interfacial impedance between the garnet and electrode mainly arises from the poor contact in association with microscopic voids and grain boundaries of garnet, as well as an insulating Li₂CO₃ surface layer formed in air initiated by the proton/lithium exchange at the surface.^30–33 The ionic transport was reported to be limited by the grain boundaries, which are heavily affected by the segregation of dopants and Li.³⁴ Mechanical polishing, carbon annealing or acid treatment were reported to remove this unwanted surface layer.^35,36 Metal or non-metal coatings on garnet pellets, which consequently enables lithium alloying, have also been used to minimise the interfacial resistance between lithium metal and garnet, and to reduce the dendrite growth.^37–40 Despite the potential for short-circuiting from electronic conduction, a mixed ion/electron-conductive interface was demonstrated to beneficial for Li dendrite suppression.^41,42 Another common strategy in this field is to utilise polymer–ceramic composite electrolytes, which combine good wetting properties of polymer electrolytes with the high ionic conductivity of ceramic electrolytes, forming a uniform interfacial contact with decreased interfacial resistance.^43–45

Ce³⁺ or Ce⁴⁺ incorporation on La³⁺ site in Li₇La₃Zr(Hf)₂O₁₂ has been previously studied albeit showing a limited solid solution range for this site substitution, before the detection of impurity phases.^46,47 In contrast, we showed in a previous study, that there was a greater degree of Ce⁴⁺ substitution possible on the Zr⁴⁺ site in Li₇La₃Zr₂O₁₂ leading to a reduction in the tetragonal distortion, which consequently increased the ionic conductivity, although due to the stoichiometric Li content in this system, the room temperature conductivity was just below the value of 10⁻⁴ S cm⁻¹, which is considered the minimum for applications.⁴⁸ In this paper, the possibility to replace Ce⁴⁺ on the Nb⁵⁺ site in Li₅La₃Nb₂O₁₂ with the creation of excess Li⁺ as the charge compensation mechanism has been examined for the first time, aiming to enhance the overall conductivity for these Ce doped garnets, in addition to providing the beneficial decrease in the interfacial impedance previously reported for Ce-doped Li₇La₃Zr₂O₁₂. We investigate effects on the local structure, electrical and electrochemical properties of Ce-doped Li₅La₃Nb₂O₁₂ through combined X-ray pair distribution function analysis, impedance spectroscopy and electrochemical testing.

Experimental

Synthesis

Li₂CO₃ (99.9%, Alfa Aesar), CeO₂ (99.9%, Acros), La₂O₃ (99.9%, Sigma Aldrich) and Nb₂O₅ (99%, Sigma Aldrich) were used as starting materials. Li₂CO₃ was dried at 180 °C while La₂O₃ and Nb₂O₅ were dried at 900 °C before use. Samples of Li_5+xLa₃Nb_2−xCe_xO₁₂ with x = 0, 0.25, 0.5, 0.75 and 1 were prepared from intimately ground stoichiometric amounts of starting reagents which were heated initially to 650 °C for 12 hours at a rate of 5 °C min⁻¹. 10–15% excess Li₂CO₃ was then added to the precursor and the powder milled for 30 minutes using a Pulverisette 5 planetary ball mill. The mixture was pressed into a pellet and heated to 950–1000 °C for 12 hours at a rate of 5 °C min⁻¹ to form the final product.

Characterisation

A Bruker D8 X-ray diffractometer (XRD) with a CuKα radiation and a linear position sensitive detector was used to collect X-ray diffraction data. Patterns were recorded over the 2θ range 15° to 80° with a 0.02° step size. Structural refinement was carried out with the GSAS suite of Rietveld refinement software using the XRD data.⁴⁹

Scanning electron microscopy (SEM, HITACHI TM4000plus) was employed to assess the microstructure. Bulk samples were polished and thermally etched at 90% of the sintering temperature for 0.5 h. The distribution of elements was probed with an energy dispersive X-ray spectroscopy (EDX) detector.

Pellets (9.8 mm diameter) were pressed and sintered at 1000–1050 °C for 4 hours (ramp rate of 5 °C min⁻¹) in a dry room to limit H⁺/Li⁺ exchange and prevent the decomposition of samples for impedance measurements. Mother powder was used to cover the pellets to prevent the Li loss and reduce reaction with the Al₂O₃ crucible. Au paste was painted on both sides of the pellet and heated at 850 °C for 1 hour in air. Impedance data were collected with a HP 4192 analyser over the frequency range of 1 to 10⁷ Hz with 100 mV ac amplitude.

Cell assembly and electrochemical test

For the cell tests, a Li_5.75La₃Zr_1.25Ce_0.75O₁₂ pellet (2 mm thickness) was sintered at 1000 °C for 12 h in a dry room. The Li//Li_5.75La₃Zr_1.25Ce_0.75O₁₂//Li symmetric cell was hot pressed at 175 °C for 1 hour and assembled using a Swagelok cell in an Argon filled glove box. Electrochemical impedance spectroscopy (EIS) was performed over the frequency range from 0.1 to 10⁷ Hz (100 mV ac applied potential) with a Solatron 1260 analyser. The Li plating/stripping performance was evaluated using a Bio-logic SP50 cell tester.

Pair distribution function data collection

Total scattering data were collected at the I15-1 XPDF beamline at Diamond Light Source, UK. Powdered samples were loaded into borosilicate capillaries (1.5 mm OD, 1.17 mm ID) and spun perpendicular to the beam during data collection to improve powder averaging. Scattering data were collected at an X-ray energy of 76.69 keV using a PerkinElmer XRD 4343 CT area detector placed ∼200 mm from the sample. The 2-D data were corrected for polarization and flat-field, then integrated to 1-D using the DAWN package prior to processed the scattering range 0.7 Å⁻¹ ≤ Q ≤ 25 Å⁻¹ into PDFs using the GudrunX package.^50,51 A modified Lorch Function (Δ₁ = 0.05 Å) was applied to suppress spurious low-r features.⁵²

Results and discussion

Phase formation

Stoichiometric Li₅La₃Nb₂O₁₂ (LLNO) can be indexed with an Ia3̄d cubic cell. In Kroger–Vink notation, the relationship for substitution of Nb⁵⁺ by Ce⁴⁺ is as follows:

As shown in Fig. 1a, XRD patterns of Ce-doped Li₅La₃Nb₂O₁₂ with formulae Li_5+xLa₃Nb_2−xCe_xO₁₂ show peak shifts to lower 2θ angle with increasing Ce content, without the detection of any impurity phases up to x = 0.75. The cell parameter was shown to obey Vegard's law, increasing linearly as a function of x (Fig. 1b), which further confirms the successful incorporation of Ce into the structure due to the larger radius of Ce⁴⁺ to that of Nb⁵⁺ (0.87 and 0.64 ionic radius for Ce⁴⁺ and Nb⁵⁺ respectively in 6 oxygen coordinated octahedral sites). Li₂La₂CeO₆ and CeO₂ impurity phases were detected for compositions with x = 1, which is consistent with the leveling off of the cell parameter increase; from these data, a solid solution limitation around x = 0.85 is estimated. As shown in Fig. 2, EDX mapping of Li_5.75La₃Nb_1.25Ce_0.75O₁₂ shows a homogeneous distribution of La, Nb, Ce and O within the sample.

Fig. 1 (a) XRD patterns of Li_5+xLa₃Nb_2−xCe_xO₁₂: x = 0, 0.25, 0.5, 0.75, 1. Triangle and rectangle labels represent CeO₂ and La₂CeLi₂O₆ respectively. (b) Variation of lattice parameter, a, and volume, V, of Li_5+xLa₃Nb_2−xCe_xO₁₂ with composition x.

Fig. 2 EDX elemental mapping of Li_5.75La₃Nb_1.25Ce_0.75O₁₂.

XRD data of Li₅La₃Nb₂O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ were used to carry out structure refinement in order to confirm the incorporation of Ce on the Nb site. The U_iso parameters of all atoms were initially set to a typical value of 0.01 Å. It was not possible to refine the Li positions and occupancies due to the poor sensitivity of Li with X-rays in the presence of heavier elements; Li positions were not refined and Li occupancies for the doped samples were scaled up from published occupancies of the undoped phase to ensure the charge-neutrality of the resulting structure. First the scale factor, background (6 terms of shifted Chebyshev function) and lattice parameters were refined. Then, peak profile parameters and 2θ zero error were refined before fixing them at the converged value. Finally, the atomic coordinates of O1, U_isos of La1, Nb1 were refined in sequence followed by refining together in the last step. Final refined parameters for Li₅La₃Nb₂O₁₂ are summarised in Table 1.

Table 1 Refined structural parameters for Li₅La₃Nb₂O₁₂ using XRD data

Atom	x	y	z	Mult.	Occupancy	u iso × 100 (Å^2)
a = 12.7949(1) Å, V = 2094.67(4) Å^3, χ^2 = 5.266, Rwp = 11.49%, Rp = 9.13%.
La1	0.125	0	0.25	24	1	0.6(1)
Nb1	0	0	0	16	1	0.2(1)
O1	0.2844(5)	0.1044(6)	0.1996(6)	96	1	0.7(3)
Li1	0.25	0.875	0	24	0.836	1
Li2	0.125	0.6798	0.5702	48	0.110	1
Li3	0.095	0.6818	0.5778	96	0.152	1

---

A similar structure refinement for Li_5.75La₃Nb_1.25Ce_0.75O₁₂ was performed. In this case, a constraint of the same atomic coordinates, the same U_isos and full occupancy between Nb1 and Ce1 was made initially. This refinement gave site occupancies of 0.61(1) for Nb1 and 0.39(1) for Ce1 which is consistent with the expected composition within 2 esds. Final refined parameters for Li_5.75La₃Nb_1.25Ce_0.75O₁₂ are shown in Table 2. Observed, calculated and difference profiles from Rietveld refinement for Li₅La₃Nb₂O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ are shown in Fig. 3. Selected bond lengths for both Li₅La₃Nb₂O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ are shown in Table 3. The data show that all Nb1/Ce1–O1 bonds expand in the Ce doped sample (bond distance = 2.138 Å) compared to undoped LLNO (bond distance = 2.020 Å), consistent with the larger size of Ce⁴⁺versus Nb⁵⁺.

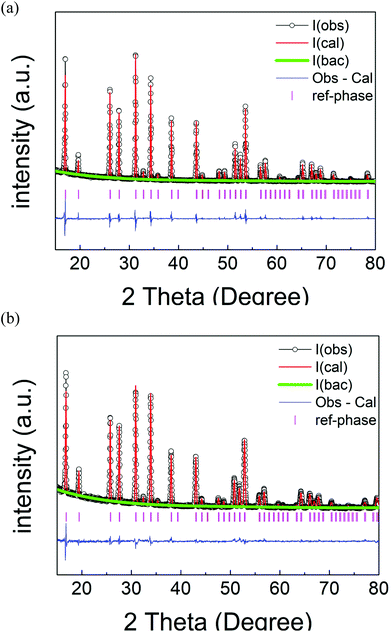Fig. 3 Observed, calculated and difference profiles from Rietveld refinement for (a) Li₅La₃Nb₂O₁₂ and (b) Li_5.75La₃Nb_1.25Ce_0.75O₁₂ using XRD data.

Table 2 Refined structural parameters for Li_5.75La₃Nb_1.25Ce_0.75O₁₂ using XRD data

Atom	x	y	z	Mult.	Occupancy	u iso × 100 (Å^2)
a = 12.9761(1) Å, V = 2184.90(7) Å^3, χ^2 = 2.823, Rwp = 8.18, Rp = 6.69%.
La1	0.125	0	0.25	24	1	1
Nb1	0	0	0	16	0.61(1)	1
Ce1	0	0	0	16	0.39(1)	1
O1	0.2874(4)	0.0980(5)	0.1984(5)	96	1	1.2(3)
Li1	0.25	0.875	0	24	0.961	1
Li2	0.125	0.6798	0.5702	48	0.127	1
Li3	0.095	0.6818	0.5778	96	0.175	1

---

Table 3 Bond lengths for Nb1(Ce1)–O of Li₅La₃Nb₂O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ from refinement results

Composition	Bond	Length (Å)
Li5La3Nb2O12	Nb1–O1 (×6)	2.020(8)
Li5.75La3Nb1.25Ce0.75O12	Nb1/Ce1–O1 (×6)	2.138(6)

---

Pair distribution function (PDF)

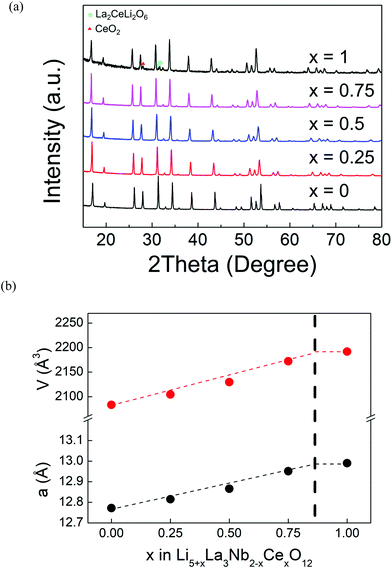
X-ray PDF data for undoped Li₅La₃Nb₂O₁₂ and Ce-doped Li_5.5La₃Nb_1.5Ce_0.5O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ are shown in Fig. 4. The peaks in the low-r region of the PDF were assigned based on simulations of the partial PDFs of the undoped structure using the computer program PDFgui (Fig. S1†).⁵³ The single Nb–O peak at ∼1.94 Å in undoped LLNO develops a shoulder at high-r with doping, which increases in intensity concurrent with Ce content. Gaussian peaks were fit to the observed PDF data using the computer program TOPAS (Fig. S2†) allowing for the extraction of the local structure bond lengths given in Table 4.⁵⁴ In contrast to the long-range average bond length from Rietveld refinement which calculates a single average Nb,Ce–O bond length which increases from 2.020(8) Å to 2.138(6) Å on doping, the local structure information provided by the PDF allows us to separate the contributions of the individual bond distances. These results show that the Nb–O bond remains constant at ∼1.94 Å, while the Ce–O bond length of 2.16 Å can be extracted for the doped samples, which is consistent with the increase expected on moving to the larger Ce⁴⁺ ion on simple ionic radii arguments.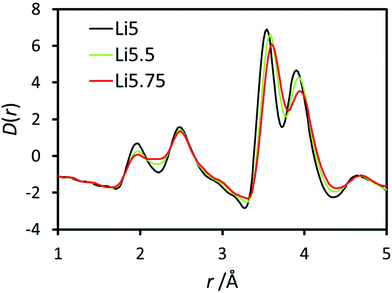

Fig. 4 Pair distribution function data for Li₅La₃Nb₂O₁₂ (black), Li_5.5La₃Nb_1.5Ce_0.5O₁₂ (green) and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ (red) focusing in the low-r region.

Table 4 Bond lengths for Nb–O, Ce–O, La–O, La–Nb,Ce, La–La of Li₅La₃Nb₂O₁₂, Li_5.5La₃Nb_1.5Ce_0.5O₁₂ and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ from X-ray PDF data

Bond	Li5La3Nb2O12	Li5.5La3Nb1.5Ce0.5O12	Li5.75La3Nb1.25Ce0.75O12
Nb–O	1.93(3) Å	1.95(2) Å	1.94(2) Å
Ce–O	—	2.16(4) Å	2.16(2) Å
La–O	2.474(5) Å	2.475(7) Å	2.476(7) Å
La–Nb,Ce	3.531(1) Å	3.572(1) Å	3.591(1) Å
La–La	3.904(1) Å	3.929(1) Å	3.942(2) Å

---

Fig. 5 shows the PDF data with the r axis for the doped samples normalised to the lattice parameter of the undoped LLNO; this normalisation highlights changes upon doping beyond simple expansion of the lattice. At low-r (Fig. 5a), peaks around 5.9 Å due to the second La–La and Nb,Ce–Nb,Ce coordination shell contract relative to the normalised lattice parameter, but the rest of the features remain unchanged. Neutron PDF data would be required to determine the full impact of doping on the Li and O environments (previous neutron PDF study shows lithium atoms within either tetrahedral or octahedral sites prefer to stay at the off-center positions in the undoped Li₅La₃Nb₂O₁₂ ⁵⁵). However, it is clear that doping introduces more disorder into the system, evidenced by broader peaks at high r (Fig. 5b); this additional disorder is expected due to the significantly different sizes of Nb and Ce, and the additional lithium which requires occupation of more varied coordination environments.

Fig. 5 Pair distribution function data for Li₅La₃Nb₂O₁₂ (black), Li_5.5La₃Nb_1.5Ce_0.5O₁₂ (green) and Li_5.75La₃Nb_1.25Ce_0.75O₁₂ (red), with the r axis normalized to the lattice parameter of Li₅La₃Nb₂O₁₂ at (a) low r (b) high r.

Conductivity measurement

The morphology of undoped and cerium doped Li₅La₃Nb₂O₁₂ are shown in Fig. 6. The relative density of garnet pellets increased as a function of Ce content (51.2% for Li₅La₃Nb₂O₁₂ and 75.1% for Li_5.75La₃Nb_1.25Ce_0.75O₁₂). A typical dataset of Li_5.75La₃Nb_1.25Ce_0.75O₁₂ impedance spectroscopy is shown in Fig. 7. From the Z* complex plane (Fig. 7a), a non-ideal semicircle was observed at higher frequency while a sharp spike is seen at lower frequency. To fit the circuit, a resistor R1 and a constant phase element (CPE) CPE1 in parallel were used to simulate the high frequency semicircle. Another CPE2 which is in series with the R1/CPE1 in the circuit was utilised to interpret the low frequency spike.

Fig. 6 SEM images of (a) Li₅La₃Nb₂O₁₂, (b) Li_5.5La₃Nb_1.5Ce_0.5O₁₂ and (c) Li_5.75La₃Nb_1.25Ce_0.75O₁₂ pellets.

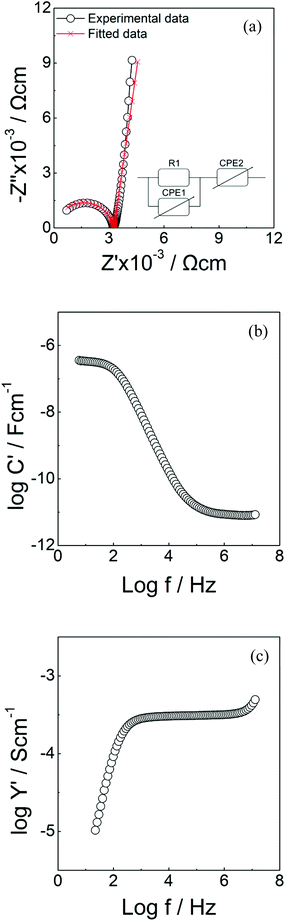Fig. 7 Impedance data of Li_5.75La₃Nb_1.25Ce_0.75O₁₂. (a) Complex Z* plot (b) spectroscopic plot of C′ (c) spectroscopic plot of Y′.

The corresponding spectroscopic C′ plot (Fig. 7b) shows a higher frequency plateau with a capacitance of 8.2 pF cm⁻¹ with an associated permittivity of 91 (calculated from ε′_∞ = C/ε₀, where ε₀ is the permittivity of free space with a value of 8.854 × 10⁻¹⁴ F cm⁻¹), which is a typical value for the bulk response.⁵⁶ In addition, a low frequency plateau with a capacitance of 3 μF cm⁻¹ was observed, which is due to the double layer effect at the sample–electrode interface; hence consistent with Li⁺ ion conduction.

The spectroscopic Y′ plot (Fig. 7c) shows a frequency-independent plateau at intermediate frequency, which is associated with the bulk conductivity. A dispersion at lower frequency was seen due to the blockage of lithium ions at the sample–electrode interface. At higher frequency, a curvature was detected related to the Jonscher's power law.⁵⁷

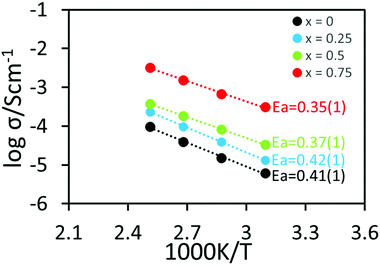
The Arrhenius plot (Fig. 8) shows the bulk conductivities of undoped and Ce-doped LLNO. Conductivities increased with increasing cerium content in agreement with more excess lithium in the structure. The maximum conductivity was found in Li_5.75La₃Nb_1.25Ce_0.75O₁₂ sample, which reached a value of 1.4 × 10⁻⁴ S cm⁻¹ at 25 °C, which is ∼two orders more than that of LLNO, and represents one of the highest conductivities for a garnet with less than 6 Li. The activation energy also decreased from 0.41(1) eV for Li₅La₃Nb₂O₁₂ to 0.35(1) eV for Li_5.75La₃Nb_1.25Ce_0.75O₁₂. This decrease in activation energy may be indicative of an opening of the bottleneck for Li migration between sites, due to the increase in cell size through Ce doping.

Fig. 8 Arrhenius conductivity plot for Ce-doped Li₅La₃Nb₂O₁₂.

Electrochemical properties

The electrochemical impedance spectroscopy of the Li//Li_5.75La₃Nb_1.25Ce_0.75O₁₂//Li cell is shown in Fig. 9a. For circuit fitting, a parallel R1 and CPE1 representing a bulk semicircle in series with another parallel R2 and CPE2 related to the interfacial semicircle were used. A significant interfacial resistance decrease from 3802 Ω cm² for Li₅La₃Nb₂O₁₂ to 488 Ω cm² for Li_5.75La₃Nb_1.25Ce_0.75O₁₂ was observed (Fig. S3†), which is consistent with our previous work on Ce doped Li₇La₃Zr₂O₁₂, and represents a reduced interfacial resistance attributed to the formation of a mixed valence Ce⁴⁺/Ce³⁺ product at the electrode/lithium interface.⁴⁸ Long-term cycling properties of the Li//Li_5.75La₃Nb_1.25Ce_0.75O₁₂//Li cell at 55 °C are shown in Fig. 9b. A voltage plateau with a voltage overpotential of 251 mV at 50 μA cm⁻² current density was observed; the long-term cycling stability over 380 h was shown.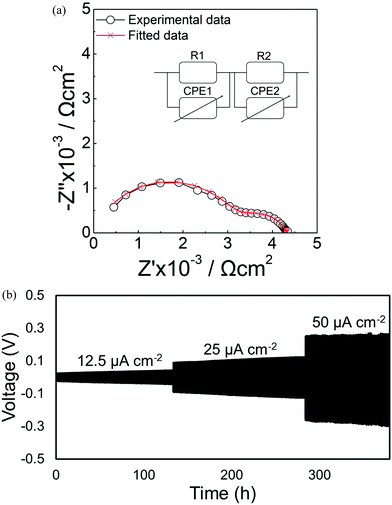

Fig. 9 (a) Electrochemical impedance spectroscopy of Li//Li_5.75La₃Nb_1.25Ce_0.75O₁₂//Li cell. (b) Stripping/plating properties of Li//Li_5.75La₃Nb_1.25Ce_0.75O₁₂//Li cell at 55 °C.

Conclusion

Cerium was successfully doped into the Li₅La₃Nb₂O₁₂ garnet structure through a conventional solid-state method. The lattice parameter increased linearly as a function of composition to x ∼ 0.85, indicating the formation of an extensive solid solution range. XRD PDF analysis confirmed the incorporation of cerium, allowing the separate Nb/Ce–O bond distances to be determined, and thus illustrating the longer bond distances for Ce on the octahedral site to those of Nb. The conductivity increased by two orders of magnitude of Li_5.75La₃Nb_1.25Ce_0.75O₁₂ compared to that of Li₅La₃Nb₂O₁₂ with a notable reduction in the activation energies for Ce-doped samples. The interfacial resistance also dramatically decreased to 488 Ω cm² for Li_5.75La₃Nb_1.25Ce_0.75O₁₂, demonstrating that cerium doping benefits the interfacial issue. The long-term cycling stability of a Li//garnet//Li symmetric cell over 380 h was demonstrated, thus illustrating the potential of this Ce doped garnet system. Further studies are required to characterise the formation and possible change of the interlayer between garnet and lithium metal.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

We acknowledge the support of Engineering and Physical Sciences Research Council grant EP/R024006/1: ICSF Wave 1: GENESIS: Garnet Electrolytes for New Energy Storage Integrated Solutions, and the APC (GEM: Garnet Electrolyte Manufacture 56065). The University of Birmingham (Studentship for MPS) for the financial support. This work was carried out with the support of the Diamond Light Source, instrument I15-1 XPDF (proposal EE20877).

References

1. J.-M. Tarascon and M. Armand, Issues and Challenges Facing Rechargeable Lithium Batteries, Nature, 2001, 414(6861), 359–367.
2. P. G. Bruce, B. Scrosati and J. M. Tarascon, Nanomaterials for Rechargeable Lithium Batteries, Angew. Chem., Int. Ed., 2008, 47(16), 2930–2946.
3. J. B. Goodenough and K. S. Park, The Li-Ion Rechargeable Battery: a Perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176.
4. D. Larcher and J. M. Tarascon, Towards Greener and More Sustainable Batteries for Electrical Energy Storage, Nat. Chem., 2015, 7(1), 19–29.
5. N. Zhao, W. Khokhar, Z. Bi, C. Shi, X. Guo, L.-Z. Fan and C.-W. Nan, Solid Garnet Batteries, Joule, 2019, 3(5), 1190–1199.
6. V. Thangadurai, S. Narayanan and D. Pinzaru, Garnet-Type Solid-State Fast Li Ion Conductors for Li Batteries: Critical Review, Chem. Soc. Rev., 2014, 43(13), 4714–4727.
7. S. Ramakumar, C. Deviannapoorani, L. Dhivya, L. S. Shankar and R. Murugan, Lithium Garnets: Synthesis, Structure, Li⁺ Conductivity, Li⁺ Dynamics and Applications, Prog. Mater. Sci., 2017, 88, 325–411.
8. A. J. Samson, K. Hofstetter, S. Bag and V. Thangadurai, A Bird's-Eye View of Li-Stuffed Garnet-Type Li₇La₃Zr₂O₁₂ Ceramic Electrolytes for Advanced All-Solid-State Li Batteries, Energy Environ. Sci., 2019, 12(10), 2957–2975.
9. V. Thangadurai, H. Kaack and W. Weppner, Novel Fast Lithium Ion Conduction in Garnet-Type Li₅La₃M₂O₁₂ (M = Nb, Ta), J. Am. Ceram. Soc., 2003, 86(3), 437–440.
10. E. J. Cussen, The Structure of Lithium Garnets: Cation Disorder and Clustering in a New Family of Fast Li⁺ Conductors, Chem. Commun., 2006,(4), 412–413.
11. E. J. Cussen, Structure and Ionic Conductivity in Lithium Garnets, J. Mater. Chem., 2010, 20(25), 5167–5173.
12. J. Percival, E. Kendrick, R. I. Smith and P. R. Slater, Cation Ordering in Li Containing Garnets: Synthesis and Structural Characterisation of the Tetragonal System, Li₇La₃Sn₂O₁₂, Dalton Trans., 2009,(26), 5177–5181.
13. J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, Synthesis and Structure Analysis of Tetragonal Li₇La₃Zr₂O₁₂ with the Garnet-Related Type Structure, J. Solid State Chem., 2009, 182(8), 2046–2052.
14. J. Awaka, N. Kijima, K. Kataoka, H. Hayakawa, K.-I. Ohshima and J. Akimoto, Neutron Powder Diffraction Study of Tetragonal Li₇La₃Hf₂O₁₂ with the Garnet-related Type Structure, J. Solid State Chem., 2010, 183(1), 180–185.
15. V. Thangadurai and W. Weppner, Li₆ALa₂Ta₂O₁₂ (A = Sr, Ba): Novel Garnet-Like Oxides for Fast Lithium Ion Conduction, Adv. Funct. Mater., 2005, 15(1), 107–112.
16. R. Murugan, V. Thangadurai and W. Weppner, Fast Lithium Ion Conduction in Garnet-Type Li₇La₃Zr₂O₁₂, Angew. Chem., Int. Ed., 2007, 46(41), 7778–7781.
17. S. Ohta, T. Kobayashi and T. Asaoka, High Lithium Ionic Conductivity in the Garnet-Type Oxide Li_7−xLa₃(Zr_2−x, Nb_x)O₁₂ (x = 0–2), J. Power Sources, 2011, 196(6), 3342–3345.
18. M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Effect of Ga Incorporation on the Structure and Li Ion Conductivity of La₃Zr₂Li₇O₁₂, Dalton Trans., 2012, 41(39), 12048–12053.
19. M. A. Howard, O. Clemens, K. S. Knight, P. A. Anderson, S. Hafiz, P. M. Panchmatia and P. R. Slater, Synthesis, Conductivity and Structural Aspects of Nd₃Zr₂Li_7–3xAl_xO₁₂, J. Mater. Chem. A, 2013, 1(44), 14013–14022.
20. H. El Shinawi and J. Janek, Stabilization of Cubic Lithium-Stuffed Garnets of the Type “Li₇La₃Zr₂O₁₂” by Addition of Gallium, J. Power Sources, 2013, 225, 13–19.
21. L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, First-Principles Studies on Cation Dopants and Electrolyte/Cathode Interphases for Lithium Garnets, Chem. Mater., 2015, 27(11), 4040–4047.
22. S. R. Yeandel, B. J. Chapman, P. R. Slater and P. Goddard, Structure and Lithium-Ion Dynamics in Fluoride-Doped Cubic Li₇La₃Zr₂O₁₂ (LLZO) Garnet for Li Solid-State Battery Applications, J. Phys. Chem. C, 2018, 122(49), 27811–27819.
23. A. G. Squires, D. O. Scanlon and B. J. Morgan, Native Defects and Their Doping Response in the Lithium Solid Electrolyte Li₇La₃Zr₂O₁₂, Chem. Mater., 2019, 32(5), 1876–1886.
24. B. Dong, L. L. Driscoll, M. P. Stockham, E. Kendrick and P. R. Slater, Low Temperature Synthesis of Garnet Solid State Electrolytes: Implications on Aluminium Incorporation in Li₇La₃Zr₂O₁₂, Solid State Ionics, 2020, 350, 115317.
25. M. P. Stockham, B. Dong, Y. Ding, Y. Li and P. R. Slater, Evaluation of the effect of site substitution of Pr doping in the lithium garnet system Li₅La₃Nb₂O₁₂, Dalton Trans., 2020, 49(30), 10349–10359.
26. K. Park, B.-C. Yu, J.-W. Jung, Y. Li, W. Zhou, H. Gao, S. Son and J. B. Goodenough, Electrochemical Nature of the Cathode Interface for a Solid-State Lithium-Ion Battery: Interface between LiCoO₂ and Garnet- Li₇La₃Zr₂O₁₂, Chem. Mater., 2016, 28(21), 8051–8059.
27. F. M. Pesci, R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, R. J. Chater and A. Aguadero, Elucidating the Role of Dopants in the Critical Current Density for Dendrite Formation in Garnet Electrolytes, J. Mater. Chem. A, 2018, 6(40), 19817–19827.
28. P. Canepa, J. A. Dawson, G. Sai Gautam, J. M. Statham, S. C. Parker and M. S. Islam, Particle Morphology and Lithium Segregation to Surfaces of the Li₇La₃Zr₂O₁₂ Solid Electrolyte, Chem. Mater., 2018, 30(9), 3019–3027.
29. M. Philipp, B. Gadermaier, P. Posch, I. Hanzu, S. Ganschow, M. Meven, D. Rettenwander, G. J. Redhammer and H. M. R. Wilkening, The Electronic Conductivity of Single Crystalline Ga–Stabilized Cubic Li₇La₃Zr₂O₁₂: A Technologically Relevant Parameter for All–Solid–State Batteries, Adv. Mater. Interfaces, 2020, 2000450.
30. C. Galven, J.-L. Fourquet, M.-P. Crosnier-Lopez and F. O. Le Berre, Instability of the Lithium Garnet Li₇La₃Sn₂O₁₂: Li⁺/H⁺ Exchange and Structural Study, Chem. Mater., 2011, 23(7), 1892–1900.
31. G. Larraz, A. Orera and M. L. Sanjuán, Cubic Phases of Garnet-Type Li₇La₃Zr₂O₁₂: the Role of Hydration, J. Mater. Chem. A, 2013, 1(37), 11419–11428.
32. L. Truong, M. Howard, O. Clemens, K. S. Knight, P. R. Slater and V. Thangadurai, Facile Proton Conduction in H⁺/Li⁺ Ion-Exchanged Garnet-Type Fast Li-Ion Conducting Li₅La₃Nb₂O₁₂, J. Mater. Chem. A, 2013, 1(43), 13469–13475.
33. R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, F. M. Pesci, R. J. Chater, J. A. Kilner and A. Aguadero, Garnet Electrolytes for Solid State Batteries: Visualization of Moisture-Induced Chemical Degradation and Revealing Its Impact on the Li-Ion Dynamics, Chem. Mater., 2018, 30(11), 3704–3713.
34. F. M. Pesci, A. Bertei, R. H. Brugge, S. P. Emge, A. K. O. Hekselman, L. E. Marbella, C. P. Grey and A. Aguadero, Establishing Ultralow Activation Energies for Lithium Transport in Garnet Electrolytes, ACS Appl. Mater. Interfaces, 2020, 12(29), 32806–32816.
35. Y. Li, X. Chen, A. Dolocan, Z. Cui, S. Xin, L. Xue, H. Xu, K. Park and J. B. Goodenough, Garnet Electrolyte with an Ultralow Interfacial Resistance for Li-Metal Batteries, J. Am. Chem. Soc., 2018, 140(20), 6448–6455.
36. Y. Ruan, Y. Lu, X. Huang, J. Su, C. Sun, J. Jin and Z. Wen, Acid Induced Conversion Towards a Robust and Lithiophilic Interface for Li–Li₇La₃Zr₂O₁₂ Solid-State Batteries, J. Mater. Chem. A, 2019, 7(24), 14565–14574.
37. X. Han, Y. Gong, K. K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H. Wang, G. Rubloff, Y. Mo, V. Thangadurai, E. D. Wachsman and L. Hu, Negating Interfacial Impedance in Garnet-Based Solid-State Li Metal Batteries, Nat. Mater., 2017, 16(5), 572–579.
38. K. Fu, Y. Gong, G. T. Hitz, D. W. McOwen, Y. Li, S. Xu, Y. Wen, L. Zhang, C. Wang, G. Pastel, J. Dai, B. Liu, H. Xie, Y. Yao, E. D. Wachsman and L. Hu, Three-Dimensional Bilayer Garnet Solid Electrolyte Based High Energy Density Lithium Metal–Sulfur Batteries, Energy Environ. Sci., 2017, 10(7), 1568–1575.
39. J. Dai, C. Yang, C. Wang, G. Pastel and L. Hu, Interface Engineering for Garnet-Based Solid-State Lithium-Metal Batteries: Materials, Structures, and Characterization, Adv. Mater., 2018, 30(48), 1802068.
40. J. Fu, P. Yu, N. Zhang, G. Ren, S. Zheng, W. Huang, X. Long, H. Li and X. Liu, In situ Formation of a Bifunctional Interlayer Enabled by a Conversion Reaction to Initiatively Prevent Lithium Dendrites in a Garnet Solid Electrolyte, Energy Environ. Sci., 2019, 12(4), 1404–1412.
41. Y. Song, L. Yang, L. Tao, Q. Zhao, Z. Wang, Y. Cui, H. Liu, Y. Lin and F. Pan, Probing into the Origin of an Electronic Conductivity Surge in a Garnet Solid-State Electrolyte, J. Mater. Chem. A, 2019, 7(40), 22898–22902.
42. J. Gao, J. X. Zhu, X. L. Li, J. P. Li, X. X. Guo, H. Li and W. D. Zhou, Rational Design of Mixed Electronic-Ionic ConductingTi-Doping Li₇La₃Zr₂O₁₂ for Lithium Dendrites Suppression, Adv. Funct. Mater., 2020, 11(1), 2001918.
43. W. Zhou, Z. Wang, Y. Pu, Y. Li, S. Xin, X. Li, J. Chen and J. B. Goodenough, Double-Layer Polymer Electrolyte for High-Voltage All-Solid-State Rechargeable Batteries, Adv. Mater., 2019, 31(4), 1805574.
44. Z. Huang, W. Pang, P. Liang, Z. Jin, N. Grundish, Y. Li and C.-A. Wang, A Dopamine Modified Li_6.4La₃Zr_1.4Ta_0.6O₁₂/PEO Solid-state Electrolyte: Enhanced Thermal and Electrochemical Properties, J. Mater. Chem. A, 2019, 7(27), 16425–16436.
45. S.-S. Chi, Y. Liu, N. Zhao, X. Guo, C.-W. Nan and L.-Z. Fan, Solid Polymer Electrolyte Soft Interface Layer with 3D Lithium Anode for All-Solid-State Lithium Batteries, Energy Storage Mater., 2019, 17, 309–316.
46. E. Rangasamy, J. Wolfenstine, J. Allen and J. Sakamoto, The Effect of 24c-Site (A) Cation Substitution on the Tetragonal–Cubic Phase Transition in Li_7−xLa_3−xA_xZr₂O₁₂ Garnet-Based Ceramic Electrolyte, J. Power Sources, 2013, 230, 261–266.
47. A. A. Trofimov, C. Li, K. S. Brinkman and L. G. Jacobsohn, Luminescence Investigation of Ce Incorporation in Garnet-Type Li₇La₃Zr₂O₁₂, Opt. Mater., 2017, 68, 7–10.
48. B. Dong, S. R. Yeandel, P. Goddard and P. R. Slater, Combined Experimental and Computational Study of Ce-Doped La₃Zr₂Li₇O₁₂ Garnet Solid-State Electrolyte, Chem. Mater., 2019, 32(1), 215–223.
49. B. H. Toby, EXPGUI, a Graphical User Interface for GSAS, J. Appl. Crystallogr., 2001, 34(2), 210–213.
50. A. K. Soper, Programs for Correcting Raw Neutron and X-Ray Diffraction Data to Differential Scattering Cross Section, Technical Report RAL-TR-2011-013, Rutherford Appleton Laboratory, 2011.
51. J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day, M. Drakopoulos, M. W. Gerring, M. L. Hart, O. V. Magdysyuk, S. Michalik, A. Smith, C. C. Tang, N. J. Terrill, M. T. Wharmby and H. Wilhelm, Processing Two-Dimensional X-Ray Diffraction and Small-Angle Scattering Data in DAWN 2, J. Appl. Crystallogr., 2017, 50(Pt 3), 959–966.
52. A. K. Soper and E. R. Barney, On the Use of Modification Functions When Fourier Transforming Total Scattering Data, J. Appl. Crystallogr., 2012, 45(6), 1314–1317.
53. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. Billinge, PDFfit2 and PDFgui: Computer Programs for Studying Nanostructure in Crystals, J. Phys.: Condens. Matter, 2007, 19(33), 335219.
54. A. A. Coelho, TOPAS and TOPAS-Academic: an Optimization Program Integrating Computer Algebra and Crystallographic Objects Written in C⁺⁺, J. Appl. Crystallogr., 2018, 51(1), 210–218.
55. Y. Wang, M. Klenk, K. Page and W. Lai, Local Structure and Dynamics of Lithium Garnet Ionic Conductors: A Model Material Li₅La₃Ta₂O₁₂, Chem. Mater., 2014, 26(19), 5613–5624.
56. J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2(3), 132–138.
57. B. Dong, J. Yan, B. Walkley, K. K. Inglis, F. Blanc, S. Hull and A. R. West, Synthesis and Characterisation of the New Oxyfluoride Li⁺ Ion Conductor, Li₅SiO₄F, Solid State Ionics, 2018, 327, 64–70.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0dt02112a

---