Appraisal of calcium ferrites as cathodes for calcium rechargeable batteries: DFT, synthesis, characterization and electrochemistry of Ca₄Fe₉O₁₇

Abstract

Sustainability combined with high energy density prospects makes Fe-based oxides attractive as cathodes for calcium rechargeable batteries. This work presents a DFT evaluation of the CaFe_2+nO_4+n (0 < n < 3) family, for which both the average intercalation voltage and the theoretical specific capacity decrease with the increasing n value. The term n = 1/4, Ca₄Fe₉O₁₇, meets the most appealing characteristics: a calculated average voltage of 4.16 V, a theoretical specific capacity of 230 mA h g⁻¹ and the lowest energy barrier for Ca migration so far predicted for an existing oxide (0.72 eV). To overcome the previously reported synthesis difficulties, we employed a novel synthesis procedure in sealed quartz tubes followed by quenching in water. The XRD and SAED patterns of the prepared Ca₄Fe₉O₁₇ powder reveal a certain degree of stacking defects along the c axis. Attempts to deinsert Ca ions from Ca₄Fe₉O₁₇ by chemical means (NO₂BF₄ in ACN) and in electrochemical Ca cells were unsuccessful, although some hints of oxidation are observed in Li cells with the LP30 electrolyte. The suitability of Ca₄Fe₉O₁₇ as a Ca cathode is pending further studies utilizing Ca-electrolytes with high anodic stability.

---

Introduction

The Li-ion technology currently dominates the rechargeable battery market for portable electronics and appears to be a possible near term solution for applications such as electric vehicles and grid storage, in parallel with the storage of energy from renewable and intermittent sources – solar, wind, waves, etc. However, Li-ion batteries are currently approaching their fundamental limits in terms of energy density, which in addition to the limited supply of Li instigate the race for the development of alternative technologies exhibiting advantages in terms of energy density, safety and cost. Rechargeable batteries based on a Ca-metal anode are attractive given the abundance of calcium in the Earth's crust, the high capacity of calcium anodes (1340 mA h g⁻¹) and its negative reduction potential (only 170 mV above that of lithium metal).^1,2 Advances in the development of such batteries are intricate due to the lack of competitive cathode materials and electrolytes.^3,4 While recent findings demonstrate the feasibility of Ca anode operation using different electrolytes,^5–8 the identification of suitable cathode materials has been facing several roadblocks.^4,9,10 Limited reversible electrochemical Ca intercalation has been reported for a handful of compounds⁴ (V₂O₅,¹¹ TiS₂,¹² MoO₃,¹³ Ca_0.5CoO₂,¹⁴ and manganese hexacyanoferrate¹), all of them showing poor cycling, if any. Parallel experimental and computational investigations establish a link between the lack of reversible electrochemical activity (experimentally observed) and hampered Ca diffusion (computationally estimated).^15–20 In this regard, the poor diffusion of Ca²⁺ in inorganic structures is the major challenge for cathode discovery.²¹ Compared to Li⁺ diffusion, the hindrance to Ca mobility resides in the larger size of Ca²⁺ ions on one hand and its divalent charge on the other that increases the electrostatic repulsion/attraction with the neighbouring cations/anions in the structure.

Sustainable cathode materials should include abundant and non-toxic elements, and at the same time, comply with the high energy density requirements. These criteria prompted the investigation of light and abundant oxidizing 3d-transition metal oxides as cathodes for Ca batteries. So far several Mn oxides and polyoxoanionic compounds have been reported, going from the virtual spinel CaMn₂O₄²² to the CaMnO₃ perovskite,¹⁶ its reduced derivative -Ca₂Mn₂O₅,²³ the known CaMn₂O₄ polymorphs (marokite and its high pressure form),¹⁵ a related oxidized phase, CaMn₄O₈,²³ and the minerals K_0.31MnO₂ 0.25H₂O (birnessite),²⁴ Mg_0.19Na_0.07MnO₂ 0.37H₂O (todorokite),²⁵ CaMn(CO₃)₂ (kutnahorite)²⁶ and CaMnSi₂O₆ (johannsenite).²⁶ In contrast, research on Fe oxides has been scarce; the perovskite CaFeO₃ and the related brownmillerite Ca₂Fe₂O₅ compounds have been only evaluated by computational means.^16,23 It was found that Ca-perovskites are not competitive materials due to hindered Ca mobility (a calculated energy barrier of 2 V).¹⁶ In the brownmillerite structure the oxygen vacancies respective to the perovskite create a new pathway with much lower energy barrier (1 eV).²³ The present investigation turns to other known oxides in the Ca–Fe–O system with general formulae CaFe_2+nO_4+n that might be worthy candidates (Fig. 1).

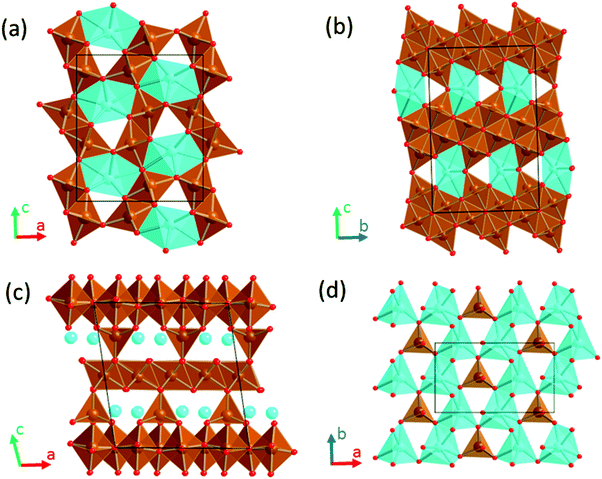Fig. 1 Crystal structures of CaFe_2+nO_4+n oxides. (a) n = 0, CaFe₂O₄ (b) n = 2, CaFe₄O₆ (c) n = 1/4, CaFe₉O₁₇ showing the [CaO₆]–[FeO₄] plane in (d). Color code: Ca in blue, Fe in brown and O in red.

The crystal structure of CaFe₂O₄ (S.G. Pmna, no. 53)^27,28 consists of edge-sharing chains of MnO₆ octahedra, forming double rutile chains (see Fig. 1a). Each double-rutile chain is connected to two adjacent chains through edge-sharing oxygen. As a result, tunnels appear along the b axis where Ca ions reside in eight-fold coordination. The calcium ferrite CaFe_2+nO_4+n family is formed by stacking along the c axis (S.G. Cmcm, no. 63) of blocks with the CaFe₂O₄ composition and blocks with the FeO composition (see Fig. 1b). Within this family, the compounds with n = 0, 1, 3/2, 2, 5/2, and 3 have been reported.^29,30 Interestingly, for n = 1/4, the compound Ca₄Fe₉O₁₇ crystallizes in a different structure (S.G. C2, no. 5), built up by layers of Fe atoms in edge-sharing FeO₆ octahedra and vertex-sharing Fe in trigonal-based bipyramid coordination (see Fig. 1c and d).³¹ These hexagonal layers stack along the c-axis direction, being cross-linked by iron atoms in tetrahedral coordination. The [FeO₄]-tetrahedra are connected in the ab plane of the structure by hexa-coordinated Ca–O polyhedra (Fig. 1d). The CaO₆ distorted octahedra share edges forming rings around the FeO₄-tetrahedra. Unsurprisingly, this structure with Fe in three different coordination environments, and in an average oxidation state of 2.888, is thermodynamically quite unstable.^32–34 The oxygen partial pressure is critical in the stability of Ca₄Fe₉O₁₇, and therefore the complex synthesis of the material usually results in a mixture of a low crystalline Ca₄Fe₉O₁₇ and more stable oxides (CaFe₂O₄, FeO, and Ca₂Fe₂O₅). Indeed, the crystal structure determination was accomplished using single crystals grown under very specific conditions.³¹

To evaluate the performance of CaFe_2+nO_4+n compounds as cathode materials for Ca batteries, we have selected the compounds with n = 0, 1/4, 1 and 2 for computational investigations. Density Functional Theory (DFT) calculations are used to anticipate the average intercalation voltage so as to estimate their theoretical energy density, assuming the full Ca extraction from the structures. Ca diffusion is a key parameter, for which the migration energy barriers provide an approximate indication.^3,35 Following vast literature in the field,^18,21,22,35 in this work the energy barriers for Ca migration are extracted from DFT calculations. The results found for Ca₄Fe₉O₁₇ motivated an experimental investigation comprising the synthesis, characterization and electrochemical testing of the material. We present a novel synthesis method to produce highly crystalline powder.

Materials and methods

Computational

The calculations have been carried out using the ab initio total-energy and molecular dynamics program VASP (Vienna ab initio simulation program) developed at the Universität Wien.³⁶ Total energy calculations based on Density Functional Theory (DFT) were performed within the General Gradient Approximation (GGA), with the exchange and correlation functional form developed by Perdew, Burke and Ernzerhof (PBE).³⁷ The interaction of core electrons with the nuclei is described by the Projector Augmented Wave (PAW) method.³⁸ The energy cut off for the plane wave basis set is fixed at a constant value of 600 eV throughout the calculations. The integration in the Brillouin zone is done on an appropriate set of k-points determined using the Monkhors–Pack scheme. A convergence of the total energy close to 10 meV per formula unit is achieved with such parameters. Spin polarization calculations were performed in all cases. All crystal structures were fully relaxed (atomic positions, cell parameters and volume). The final energies of the optimized geometries were recalculated to correct the changes in the basis set of wave functions during relaxation. Average voltages for Ca deinsertion from CaFe_2+nO_4+n were calculated within the GGA+U method, following the methodology described by Aydinol et al.³⁹. For consistency with the literature on this topic,^16,21,22,40 the effective U value for the Fe-d orbitals was set to 5 eV (J = 1 eV).

Calcium mobility is investigated using the Nudged Elastic Band method (NEB) as implemented in VASP. To study diffusion, a vacancy is created in the structural model of the stoichiometric oxides and a simple jumping mechanism from an occupied position to the vacant site is considered. Supercells 1 × 2 × 1 (Ca₈Fe₁₈O₃₄) and 1 × 4 × 1 (Ca₄Fe₈O₁₆) for the n = 1/4 and n = 0 compounds, respectively, were used for the calculations. Constant volume calculations were performed within the GGA approximation for three or five intermediate images initialized by linear interpolation between the two fully relaxed end-points. To calculate the energy at the saddle point, cubic splines were fit through the relaxed images along each hop.

Experimental

Synthesis. Polycrystalline Ca₄Fe₉O₁₇ powder samples were prepared by the conventional solid state synthesis method. Stoichiometric mixtures of Ca₂Fe₂O₅, Fe₂O₃ and Fe₃O₄ in a molar ratio of 2 : 1 : 1 were thoroughly mixed in an agate mortar, pressed into a pellet and vacuum sealed in a quartz tube. First the samples were thermally treated at 1000° C for 24 h and quenched in water. Then, the purest sample was obtained after four consecutive regrinding and annealing processes of 24 h each at 1150 °C in evacuated quartz tubes. Ca₂Fe₂O₅ was previously synthesized following the Pechini method. Ca(NO₃)₂·4H₂O (Aldrich 99%), Fe(NO₃)₃·9H₂O (Aldrich 99.95%), C₆H₈O₇ (citric acid, Aldrich 99.5%) and C₂H₆O₂ (ethylene glycol) were subsequently dissolved in water in a molar ratio of Ca : Fe : C₆H₈O₇ : C₂H₆O₂ = 1 : 1 : 3 : 1. The solution was kept under continuous stirring at 80 °C until complete evaporation. The obtained citrate complexes were decomposed in air at 500 °C for 8 h. The decomposition process was carried out at a rate of 100 °C h⁻¹. Finally, polycrystalline Ca₂Fe₂O₅ was obtained by calcination of the amorphous carbonates at 1000° C for 24 h.

Structural, morphological and compositional characterization. X-Ray powder diffraction patterns were acquired on a Bruker D8 Advance A25 diffractometer in a Debye Scherrer configuration equipped with an Mo K_α1 radiation source. High resolution synchrotron X-ray diffraction (SXRD) patterns were collected in the MSPD beamline (ALBA synchrotron Light Source, Cerdanyola del Vallès, Spain)⁴¹ using a Mythen detector and λ = 0.8260 Å. In both cases, 0.5 mm diameter borosilicate glass capillaries were used as sample holders and rotated during data collection.

Scanning Electron Microscopy (SEM) and Energy Dispersive X-ray Spectroscopy (EDS) analyses were performed by using a FEI Quanta 200 FEG microscope equipped with an EDAX detector (resolution: 132 eV). Selected Area Electron Diffraction (SAED) studies were performed using a JEOL 1210 transmission electron microscope operating at 120 kV and equipped with a Gathan sample holder. The specimens for electron microscopy were prepared by dispersing the powders in dimethyl carbonate and depositing a droplet of this suspension on a carbon coated film supported on a copper grid.

Electrochemical tests. Electrode tapes were prepared by dispersing a powder mixture of the active material (80 wt%), Super P carbon (10 wt%) and a polyvinylidene difluoride (PVdF, Kynar) binder (10 wt%) in N-methyl pyrrolidinone solvent (NMP, Sigma-Aldrich). The obtained dispersion was ball milled for 1 hour at 500 Hz with a RETSCH PM100 instrument before being doctor-blade cast on Al foil (Goodfellow, 99%). Once cast, the tapes were dried under vacuum and cut into discs of 11 mm diameter, with an average active material load of about 2 mg. The electrodes were pressed at 5 Tons before being used.

The electrochemical tests were run in two and three electrode Swagelok cells assembled in an Ar-filled dry box, employing Al and stainless steel current collectors for the working and reference (RE)/counter (CE) electrodes, respectively, and a Whatman separator soaked in 0.6 ml of electrolyte solution. Mechanically polished Ca metal discs (obtained by pressing Ca pieces under an inert atmosphere) or Li metal were used as the counter/reference or counter electrodes, respectively.

Lithium hexafluorophosphate solutions in ethylene carbonate (EC) and dimethyl carbonate (DMC) (LP30, 1.0 M LiPF6 in EC/DMC = 50/50 (v/v), Solvionic) and the lithium bis(oxalato)borate salt (LiBoB, Chemetal, Battery grade) in a 1 : 1 v/v mixture of ethylene carbonate (EC) and propylene carbonate (PC) solvents (Solvionic, 99.9%) were used as electrolytes for the electrochemical tests in Li cells. The electrolyte used in Ca cells was a dry (<40 ppm H₂O, Karl-Fischer titration) 0.45 M calcium tetrafluoroborate hydrate (Alfa Aesar) solution in EC/PC = 50/50 (v/v).

The electrochemical tests were performed on a Bio-Logic VMP3 potentiostat. Electrochemical deintercalation/intercalation tests were carried out in galvanostatic mode (i.e. Galvanostatic Cycling with Potential Limitation–GCPL). In order to avoid kinetic limitations the rate was set to C/100. A stabilization time of 5 hours at the OCV was applied before each measurement was carried out at 100 °C. Once tested, the cells were disassembled in an Ar-filled dry box and the electrodes were washed with dimethyl carbonate solvent (DMC, Sigma-Aldrich, ≥99%) and further collected in borosilicate glass capillaries of 0.5 mm diameter for ex situ XRD measurements.

Chemical oxidation tests. Chemical oxidation tests were performed by dispersing the active material in an NO₂BF₄ solution in acetonitrile (ACN) in a molar ratio of 1 : 8. The dispersion was kept under reflux at 80 °C for 6 hours. Uninterrupted Ar bubbling served to maintain the reaction atmosphere inert and to eliminate the NO₂ gas formed as the byproduct. Once the reactions were completed, the samples were washed with dry ACN, vacuum filtered, dried and collected for XRD analysis.

Results and discussion

DFT evaluation of basic electrode characteristics

The GGA+U method correctly reproduces the cell lattice parameters of CaFe_2+nO_4+n compounds (see Table S1†). The deinsertion of Ca can be expressed by the reaction:

CaFe_2+nO_4+n → Fe_2+nO_4+n + Ca (1)

The higher the n term, the lower the theoretical specific capacity is. These values are listed in Table 1, together with the average voltage predicted for n = 0, 1/4, 1 and 2. As n increases the Fe ions are in a lower oxidation state, and accordingly Ca deinsertion is predicted at lower voltages. Note that the average voltage depends primarily on the redox couple, but it is also influenced by the crystal structure.³⁹ For instance, the voltages predicted for the Fe³⁺/Fe⁴⁺ couple are 4.16 V in brownmillerite-Ca₂Fe₂O₅ (ref. 23) and 3.87 V in CaFe₂O₄. Taking the calculated voltage and the theoretical specific capacities into account, theoretical energy densities exceeding 600 mA h g⁻¹ (the state of the art in the Li-ion technology) could be viable for n = 0, 1/4 and 1.

Table 1 Electrode characteristics of CaFe_2+nO_4+n assuming full Ca deinsertion (reaction 1)

CaFe2+nO4+n composition	n	Fe redox couple	Theoretical specific capacity (mA h g^−1)	Calculated average voltage (V)	Theoretical specific energy (mW h g^−1)
CaFe2O4	0	+3/+4	249	3.87	964
Ca4Fe9O17	1/4	+2.88/3.77	230	4.16	957
CaFe3O5	1	+2.66/+3.33	186	3.66	680
CaFe4O6	2	+2.5/+3	149	2.37	353

---

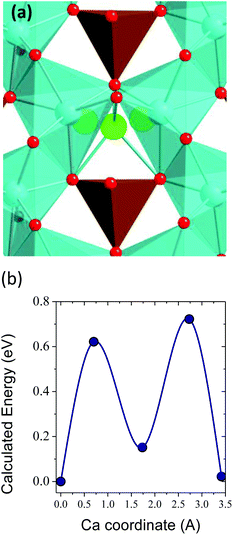
One of the major concerns in cathode material design for the Ca battery technology is the mobility of Ca²⁺ ions in inorganic structures. Although other factors can certainly limit the success of Ca battery cathodes, a good cation diffusion, that is to say a low migration energy barrier, is a necessary prerequisite. It has been estimated that for a reasonable cell power rate (discharging time 2 hours) the energy barriers for cation diffusion should be below 0.525 eV in micrometer particles and 0.65 eV in nanosized-particles.³ The calculated energy barrier for CaFe₂O₄ (1.2 eV, see Fig. 1 in the ESI†) greatly surpasses this tolerable value, and therefore, the ferrites CaFe_2+nO_4+n built up from CaFe₂O₄ blocks will also suffer from poor Ca mobility. However, the n = 1/4 term might be a viable option. Fig. 2 shows the pathway for Ca diffusion in Ca₄Fe₉O₁₇ and the calculated energy barrier. In the two-dimensional diffusion pathway in the [CaO₆]–[FeO₄] plane (shown in Fig. 1d) the diffusing Ca ions exit from their polyhedra across a triangular face to occupy the intermediate tetrahedral site (see Fig. 2a). The associated energy barrier for in-plane Ca diffusion is 0.72 eV (Fig. 2b), the lower energy ever reported for an existing transition metal oxide. The tetrahedral site represents a local energy minimum in the energy landscape. The similarity in Ca–Fe distances at this intermediate site and at the equilibrium sites (3.22 Å and 3.29 Å, respectively) suggests that the diffusing Ca ion does not experience large electrostatic repulsions with the neighbouring Fe^+2.88 cations. Compared to other oxides, the lower repulsive forces between the diffusing Ca²⁺ and other cations in the structure reduce the migration energy.⁴ Although the barrier is relatively low for Ca diffusion, it is still too high for fast rate performance. Note that the barriers for Li diffusion in layered, olivine and spinel cathodes are below 0.3 eV.^3,35,42,43

Fig. 2 (a) View of the Ca diffusion pathway in Ca₄Fe₉O₁₇, showing the tetrahedral site at the transition state. (b) Calculated energy barrier. Color code: Ca sites in blue, diffusing Ca in green, Fe in brown, O in red.

Interestingly, a related compound, K₂Fe₄O₇, has been recently reported and suggested as a K-superionic conductor.⁴⁴ The framework of K₂Fe₄O₇ consists of planes of edge-sharing FeO₆ octahedra sandwiched between planes of FeO₄ tetrahedra and octahedrally coordinated K ions. The K octahedra form rings around FeO₄ tetrahedra, thus providing a 2D conduction plane similar to that in Ca₄Fe₉O₁₇ (Fig. 1d and 2a). When tested in the K/K₂Fe₄O₇/Pt cell no significant current due to the solid electrolyte decomposition was observed up to 5.0 V. Despite the presence of Fe³⁺, the authors found that the material is also stable upon reduction down to 0 V.

Synthesis

Ca₄Fe₉O₁₇ was first reported by B. Malaman et al. in the 80's³¹ and its crystal structure was elucidated from a single crystal. Despite a few articles mentioning its existence (a summary of those is provided in Table S2†), no reliable bulk powder synthesis method is available in the literature. In all cases, this phase is reported to form, mixed with CaFe₂O₄ and Ca₂Fe₂O₅ phases that are stable in the same region of the FeO–Fe₃O₄–CaO phase diagram.

In view of the discrepancies present in the literature, in this work different synthesis methods were attempted at temperatures ranging from 800 to 1200 °C, including conventional solid state synthesis using CaCO₃ or CaO as Ca sources and Fe₂O₃, Fe₃O₄ or FeO as iron precursors. The Pechini method was also attempted.⁴⁵ Most reaction products consisted of a mixture of Fe₂O₃ and CaFe₂O₄ in all cases, whatever the reaction times (from 6 to 64 hours), except for the samples treated at 1200 °C for which melting and thermal reduction of iron oxide was observed. Further synthesis attempts were carried out in a tube sealed under vacuum, and the phase Ca₄Fe₉O₁₇ was observed in small amounts after synthesis at 1000° C for 48 h followed by quenching. Optimization of this reaction protocol, modifying precursors, temperature and time, enabled the synthesis of pure Ca₄Fe₉O₁₇ using a stoichiometric mixture of Ca₂Fe₂O₅, Fe₂O₃ and Fe₃O₄ as precursors, targeting to control the iron oxidation state by tuning the amount of oxygen available in the precursors. However, a pure phase was achieved only after several treatments at 1150 °C for 24 h each in a sealed quartz tube followed by quenching in water (a summary of synthesis results is provided in Fig. S2†).

Structure and morphology

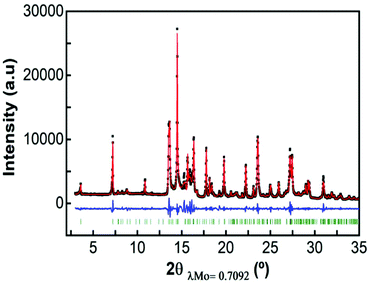
Fig. 3 shows a full pattern matching of X-ray diffraction patterns of the as prepared Ca₄Fe₉O₁₇ sample in the monoclinic system, space group C2 using the Fullprof program. The cell parameters obtained by the Le Bail method were a = 10.44177(24) Å, b = 6.02422(21) Å, c = 11.36840(36) Å and β = 98.7853(16) which are in good agreement with those previously reported from the single crystal structural determination.³¹

Fig. 3 Pattern matching of Ca₄Fe₉O₁₇ in the monoclinic system, space group C2.

Attempts to perform a Rietveld refinement of this X-ray diffraction pattern using the structural model reported by B. Malaman et al.³¹ resulted in unsatisfactory fitting of the model to the experimental pattern, despite all efforts to modify cell parameters, occupation factors, etc. The differences in the observed and calculated integrated intensities of several reflections suggest that the prepared material might present some structural differences with respect to the single crystal studied by B. Malaman (see Fig. S3†).

In order to further characterize the structure of the as prepared Ca₄Fe₉O₁₇ phase, SAED was performed and micrometric particles were observed, as shown in Fig. 4. The cell parameters obtained by electron diffraction were a = 10.4 Å, b = 6.02 Å and c = 11.4 Å. The ED image along the c zone axis presents the characteristic scattered lines indicative of the presence of stacking defects along the c axis. The occurrence of stacking faults could explain the differences between observed and calculated intensities in Rietveld refinement. The stacking faults are not expected to perturb the in-plane Ca conductivity, unless they imply inter-layer cation mixing or phase transformations.^42,46

Fig. 4 SAED images of the Ca₄Fe₉O₁₇ sample.

Chemical and electrochemical tests on Ca₄Fe₉O₁₇ and Ca₂Fe₂O₅

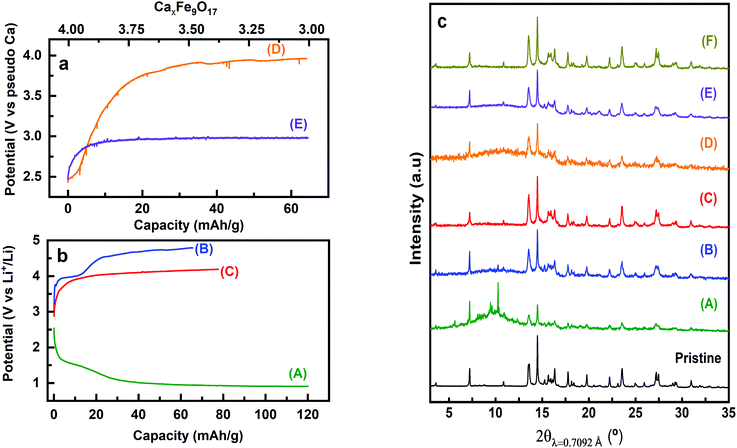
Attempts to extract Ca²⁺ from Ca₄Fe₉O₁₇ were carried out both by chemical oxidation with NO₂BF₄ (ref. 47) and by electrochemical methods at room temperature and 100 °C. Tape electrodes were prepared and cycled according to the electrochemical protocol described in the experimental section. The characteristic potential vs. capacity profiles of these electrodes upon galvanostatic cycling at RT and 100 °C in Li or Ca cells and in several Li or Ca electrolytes at C/100 are shown in Fig. 5(a and b) for Ca₄Fe₉O₁₇ and in Fig. S4† (left panel) for Ca₂Fe₂O₅. The utilization of a low rate (C/100) is in line with the calculated energy barrier of 0.72 eV, which as commented before is too high for fast-rate performance. Indeed, Ca intercalation in TiS₂ (calculated energy barrier 0.75 eV) requires similarly slow rates.¹² Upon oxidation, a short plateau-like region centered between 2.9 V and 4.8 V vs. Mⁿ⁺/M (M = Li or Ca) is observed, with the potential at which the plateau appears depending on the nature of the electrolyte, the temperature and the counter electrode used. The ex situ X-ray powder diffraction patterns of the Ca₄Fe₉O₁₇ samples collected after the electrochemical and chemical oxidation tests are shown in Fig. 5(c) and Fig. S4† (right panel), respectively. Compared with the pristine phase, neither peak shifts nor formation of extra phases is observed in any spectra except for the one corresponding to electrochemical measurement performed on Ca₄Fe₉O₁₇ in the lithium cell with the LP30 electrolyte. Thus, except for that case, the electrochemical capacity observed is ascribed to side reactions most likely involving electrolyte decomposition, which are enhanced at high temperature. In contrast, the synchrotron X-ray diffraction patterns of the pristine sample and the sample electrochemically oxidized in a lithium/LP30 cell exhibit minor differences (see Fig. 6). Indeed, the pattern full width at half maximum for peaks situated at Q values of 2.09 Å⁻¹, 2.24 Å⁻¹ and 2.53 Å⁻¹ is different.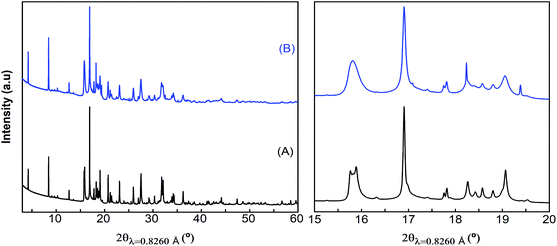

Fig. 5 Characteristic voltage profiles versus specific capacity (bottom) and versus moles of virtually de-inserted Ca²⁺ (Δx, estimated that calcium deintercalation is the only reaction taking place) (top) for Ca₄Fe₉O₁₇ in Ca cells (a), with 0.45 M Ca(BF₄)₂, EC/PC (1 : 1 vol) electrolyte at RT (D) and 100 °C (E) and in Li cells (b), with LP30 electrolyte at RT (A and B), 1 m LiBOB, EC/PC (1 : 1 vol) electrolyte at 100 °C (C). Corresponding ex situ XRD patterns in (c). XRD patterns of the pristine and chemically oxidized samples (F) are also displayed in (c).

Fig. 6 Synchrotron X-ray powder diffraction patterns of pristine (A) and electrochemically oxidized (in the LP30 electrolyte) (B) Ca₄Fe₉O₁₇ samples.

While the origin of these subtle changes has been unclear to date, one may speculate that they could be related to de-insertion of a small amount of calcium from Ca₄Fe₉O₁₇ at the 4.0 V plateau (capacity 12 mA h g⁻¹, curve B in Fig. 5b) concomitant with the oxidation of iron. In fact, hypothetical oxidation to yield Ca_3.5Fe₉O₁₇ could be related to the Fe²⁺/Fe³⁺ redox pair, with an expected voltage considerably smaller than 4.16 V, and thus within the voltage window of the LP30 electrolyte stability. Further oxidation should involve the Fe³⁺/Fe⁴⁺ couple, with a higher voltage (ca. 4.2 V), which may be out of the voltage window of the electrolyte stability, especially if polarization is significant. Yet, in light of the low value of the capacity and the disorder present in the crystals, this phenomenon has not been further studied.

Regardless of the partial oxidation of Fe detected in Li cells (likely the Fe²⁺/Fe³⁺ couple), further oxidation has not been achieved either electrochemically or chemically. Noteworthily, the calculated average voltage for the full Ca deinsertion, the Fe^+2.88/Fe^+3.77 couple (4.16 V, see Table 1), is probably beyond the anodic stability of available Ca electrolytes⁵ and in the limit of Li electrolytes if cell polarization is significant. In this regard, we attempted the electrochemical and chemical oxidation of Ca₂Fe₂O₅, for which DFT investigations found an average voltage of 4.16 V for the Fe³⁺/Fe⁴⁺ couple, although with a sluggish kinetics (calculated energy migration barrier 1 eV).²³ The combination of electrochemical and XRD characterization (see Fig. 3 in the ESI†) reflects the inactivity of Ca₂Fe₂O₅ in both Ca and Li electrolytes. A plausible explanation is that Ca deintercalation from these materials requires electrolytes operating in the 5 V range, so as to allow the oxidation of Fe to the +4 oxidation state.

To test the electrochemical stability window of Ca₄Fe₉O₁₇, Li/LP30/Ca₄Fe₉O₁₇ cells were discharged down to 1 V. Upon reduction, the potential vs. capacity profiles for Ca₄Fe₉O₁₇ displayed in Fig. 5b(A) present a long plateau-like region centered at 1 V vs. Li⁺/Li and additional diffraction peaks are observed in the 2θ = 10° region of the corresponding ex situ X-ray powder diffraction pattern shown in Fig. 5c(A). This large capacity can be regarded as the combination of two competing processes: the low-voltage decomposition of the electrolyte and the reduction of Fe³⁺ to Fe²⁺ upon Li uptake. Noteworthily, a similar potential vs. capacity profile is observed for the reduction of Fe₂O₃ electrodes in Li cells;⁴⁸ the electrochemical conversion reactions of Fe³⁺ compounds with lithium are known to evolve until the eventual formation of small Li₂O and metallic iron domains.^48,49 In the present case, the identification of the phases formed during the reduction remains undetermined due to the complex nature of the starting material. However, these results highlight the instability of Ca₄Fe₉O₁₇ upon reduction, contrary to the reported stability of the related K-phase down to 0 V vs. K⁺/K.⁴⁴

Conclusions

Sustainability combined with high energy density prospects makes Fe-based oxides appealing cathodes for calcium rechargeable batteries. The present DFT investigation reveals that among the CaFe_2+nO_4+n materials, Ca₄Fe₉O₁₇ combines the most appealing characteristics. The favorable local topology for Ca diffusion in Ca₄Fe₉O₁₇ bestows the lowest energy barrier so far reported for an existing oxide (0.72 eV). However, the predicted average deintercalation voltage (4.16 V for full Ca deinsertion) is beyond the stability range of current Ca electrolytes and, accordingly, electrochemical attempts to deintercalate Ca ions from Ca₄Fe₉O₁₇ in Ca cells were unsuccessful. However, a small charge capacity probably associated with the oxidation of Fe²⁺ to Fe³⁺ is observed in Li cells using the LP30 electrolyte. The suitability of Ca₄Fe₉O₁₇ as a Ca cathode is pending further studies utilizing electrolytes with higher anodic stability. Electrochemical and any other property investigations will no doubt benefit from the novel synthesis route reported here which, contrary to previous strategies, allows synthesizing pure and crystalline Ca₄Fe₉O₁₇ powders.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the European Union's Horizon 2020 research and innovation programme H2020 FETOPEN-1-2016-2017 (CARBAT, grant agreement no. 766617). The authors are grateful for access to the computational facilities from Universidad de Oviedo (MALTA-Consolider cluster), to ALBA synchrotron for the provision of beam time and to Dr F. Fauth for his help during data collection and also acknowledge Dr. J. Oró-Solé for assistance with electron diffraction and Dr. Clemens Ritter for helpful discussions. ICMAB authors are also grateful to the Spanish Ministry for Economy, Industry and Competitiveness Severo Ochoa Programme for Centres of Excellence in R&D (SEV-2015-0496).

Notes and references

1. A. L. Lipson, B. Pan, S. H. Lapidus, C. Liao, J. Y. Vaughey and B. J. Ingram, Chem. Mater., 2015, 27, 8442–8447.
2. J. Muldoon, C. B. Bucur and T. Gregory, Chem. Rev., 2014, 114, 11683–11720.
3. P. Canepa, G. S. Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341.
4. M. E. Arroyo-de Dompablo, A. Ponrouch, P. Johansson and M. R. Palacin, Chem. Rev., 2019 DOI:10.1021/acs.chemrev.9b00339.
5. A. Ponrouch, C. Frontera, F. Barde and M. R. Palacin, Nat. Mater., 2015, 15, 169–172.
6. D. Wang, X. Gao, Y. Chen, L. Jin, C. Kuss and P. G. Bruce, Nat. Mater., 2018, 17, 16–20.
7. A. Shyamsunder, L. E. Blanc, A. Assoud and L. F. Nazar, ACS Energy Lett., 2019, 49, 2271–2276.
8. Z. Li, O. Fuhr, M. Fichtner and Z. Zhao-Karger, Energy Environ. Sci., 2019, 12, 3496–3501.
9. A. Ponrouch and M. R. Palacin, Curr. Opin. Electrochem., 2018, 9, 1–7.
10. R. J. Gummow, G. Vamvounis, M. B. Kannan and Y. He, Adv. Mater., 2018, 30, e1801702.
11. G. G. Amatucci, F. Badway, A. Singhal, B. Beaudoin, G. Skandan, T. Bowmer, I. Plitza, N. Pereira, T. Chapman and R. Jaworski, J. Electrochem. Soc., 2001, 148, A940–A950.
12. D. S. Tchitchekova, A. Ponrouch, R. Verrelli, T. Broux, C. Frontera, A. Sorrentino, F. Barde, N. Biskup, M. E. Arroyo-de Dompablo and M. R. Palacin, Chem. Mater., 2018, 30, 847–856.
13. M. Cabello, F. Nacimiento, R. Alcantara, P. Lavela, C. Pérez-Vicente and J. L. Tirado, Chem. Mater., 2018, 30, 5853–5861.
14. M. Cabello, F. Nacimiento, J. R. González, G. Ortiz, R. Alcántara, P. Lavela, C. Pérez-Vicente and J. L. Tirado, Electrochem. Commun., 2016, 67, 59–64.
15. M. E. Arroyo-de Dompablo, C. Krich, J. Nava-Avendano, N. Biskup, M. R. Palacin and F. Barde, Chem. Mater., 2016, 28, 6886–6893.
16. M. E. Arroyo-de Dompablo, C. Krich, J. Nava-Avendaño, M. R. Palacín and F. Bardé, Phys. Chem. Chem. Phys., 2016, 18, 19966–19972.
17. R. Verrelli, A. P. Black, C. Pattanathummasid, D. S. Tchitchekova, A. Ponrouch, J. Oro-Sole, C. Frontera, F. Barde, P. Rozier and M. R. Palacin, J. Power Sources, 2018, 407, 162–172.
18. G. S. Gautam, P. Canepa, R. Malik, M. Liu, K. Perssonb and G. Ceder, Chem. Commun., 2015, 51, 13619–13622.
19. D. S. Tchitchekova, C. Frontera, A. Ponrouch, C. Krich, F. Barde and M. R. Palacin, Dalton Trans., 2018, 47, 11298–11302.
20. A. Torres, F. Bardé and M. E. Arroyo-de Dompablo, Solid State Ionics, 2019, 340, 115004.
21. Z. Rong, R. Malik, P. Canepa, G. S. Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Chem. Mater., 2015, 27, 6016–6021.
22. M. Liu, Z. Rong, R. Malik, P. Canepa, A. Jain, G. Ceder and K. A. Persson, Energy Environ. Sci., 2015, 8, 964–974.
23. A. Torres, F. J. Luque, J. Tortajada and M. E. Arroyo-de Dompablo, Energy Storage Mater., 2019, 21, 354–360.
24. J. Hyoung, J. W. Heo and S.-T. Hong, J. Power Sources, 2018, 390, 127–133.
25. S. Suzuki, T. Kato, H. Kawabata and M. Miyayama, J. New Mater. Electrochem. Syst., 2016, 19, 51–55.
26. A. Torres, F. J. Luque, J. Tortajada and M. E. Arroyo-de Dompablo, Sci. Rep., 2019, 9, 9644.
27. E. F. Bertaut, P. Blum and G. Magnano, Acta Crystallogr., 1957, 10, 238–238.
28. B. F. Decker and J. S. Kasper, Acta Crystallogr., 1957, 10, 332–337.
29. B. Malaman, H. Alebouyeh, F. Jeannot, A. Courtois, R. Gerardin and O. Evrard, Mater. Res. Bull., 1981, 16, 1139–1148.
30. O. Evrard, B. Malaman, F. Jeannot, A. Courtois, H. Alebouyeh and R. Gerardin, J. Solid State Chem., 1980, 35, 112–119.
31. B. Malaman, H. Alebouyeh, A. Courtois, R. Gerardin and O. Evrard, Mater. Res. Bull., 1982, 17, 795–800.
32. M. Aspiala, T. Hidayat, P. Taskinen and E. Jak, J. Alloys Compd., 2016, 658, 939–945.
33. H.-Y. Li and X.-M. Guo, Metall. Mater. Trans. B, 2015, 46, 278–285.
34. E. Rosen and B. Saitton, Scand. J. Metall., 1995, 24, 176–179.
35. D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30–A32.
36. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. P. E. Bloch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365.
40. A. Torres and M. E. Arroyo-de Dompablo, J. Phys. Chem. C, 2018, 122, 9356–9362.
41. F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, 360–370.
42. C. R. Fell, D. H. Lee, Y. S. Meng, J. M. Gallardo-Amores, E. Moran and M. E. Arroyo-de Dompablo, Energy Environ. Sci., 2012, 5, 6214–6224.
43. Y. S. Meng and M. E. Arroyo-de Dompablo, Energy Environ. Sci., 2009, 2, 589–609.
44. H. Yuan, H. Li, T. Zhang, G. Li, T. He, F. Du and S. Feng, J. Mater. Chem. A, 2018, 6, 8413–8418.
45. M. P. Pechini, US Pat, 3330697, 1967.
46. B. Mortemard de Boisse, M. Reynaud, J. Ma, J. Kikkawa, S.-i. Nishimura, M. Casas-Cabanas, C. Delmas, M. Okubo and A. Yamada, Nat. Commun., 2019, 10, 2185.
47. A. R. Wizansky, P. E. Rauch and F. J. Disalvo, J. Solid State Chem., 1989, 81, 203–207.
48. D. Larcher, D. Bonnin, R. Cortes, I. Rivals, L. Personnaz and J.-M. Tarascon, J. Electrochem. Soc., 2003, 150, A1643–A1650.
49. J. M. Tarascon, S. Grugeon, S. Laruelle, D. Larcher and P. Poizot, in Lithium Batteries: Science and Technology, ed. G. Nazri and G. Pistoia, Kluwer Academic Publishers, 2004.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1: DFT and lattice parameters, Fig. S1: calculated energy migration barrier for CaFe₂O₄, Table S2 and Fig. S2: summary of synthesis methods, Fig. S3: Rietveld refinement, and Fig. S4: electrochemistry and XRD of Ca₂Fe₂O₅. See DOI: 10.1039/C9DT04688G

---