 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High pressure ammonia decomposition on Ru–K/CaO catalysts†
Salvador
Sayas
a,
Natalia
Morlanés
a,
Sai P.
Katikaneni
b,
Aadesh
Harale
b,
Bandar
Solami
b and
Jorge
Gascon
 *a
*a
aKAUST Catalysis Center (KCC), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia. E-mail: Jorge.Gascon@kaust.edu.sa
bCarbon Management R&D Division, Research and Development Center, Saudi Aramco, Dhahran, 31311, Saudi Arabia
First published on 29th June 2020
Abstract
Potassium-promoted ruthenium supported on CaO is a very efficient catalyst for ammonia decomposition, surpassing the performance of other Ru-supported solids. At an optimum Ru loading of 3% wt, catalysts with a K/Ru atomic ratio of 0.9 showed the best catalytic performance under a wide range of operating conditions, P = 1–40 bar, T = 250–550 °C and WHSV = 9000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mL g−1 h−1. Although NH3 conversion levels decrease considerably upon increasing the reaction pressure (X550 °C, 40 bar = 0.8), high pressure ammonia decomposition offers the possibility of COx-free compressed hydrogen and hydrogen productivities and TOFs 40 times bigger than when applying atmospheric pressure. Extensive characterization by CO chemisorption and HR-TEM demonstrates that potassium promotion increases metal dispersion by decreasing the Ru particle size. Electronic effects derived from the close proximity between K and Ru result in a decrease in the reaction apparent activation energy, as shown by a detailed kinetic analysis.
000 mL g−1 h−1. Although NH3 conversion levels decrease considerably upon increasing the reaction pressure (X550 °C, 40 bar = 0.8), high pressure ammonia decomposition offers the possibility of COx-free compressed hydrogen and hydrogen productivities and TOFs 40 times bigger than when applying atmospheric pressure. Extensive characterization by CO chemisorption and HR-TEM demonstrates that potassium promotion increases metal dispersion by decreasing the Ru particle size. Electronic effects derived from the close proximity between K and Ru result in a decrease in the reaction apparent activation energy, as shown by a detailed kinetic analysis.
Introduction
The use of hydrocarbons as energy carriers has facilitated human development over the last century. However, the derived environmental consequences and scarcity issues are a strong driving force to look for cleaner and more sustainable alternatives.1–3 Among the different possibilities, the use of hydrogen offers great advantages4–7 especially if its production8–12 is accompanied by CO2 capture or if it is directly produced from water.Hydrogen storage, however, is still an issue for which several alternatives are being proposed: metal hydrides, such as NaAlH4 and LiAlH4,13,14 or methanol15,16 are among the most studied, but there is also growing interest in the use of ammonia. NH3 offers several advantages: high volumetric (108 kg H2 per m3 NH3 at 20 °C and 8.6 bar) and gravimetric energy density (17.8 wt%), ease of storage and transport, and the fact that NH3 production is a very well established technology (global production of 176 million metric tons in 2014 (ref. 17–21)); these all point to ammonia as a very promising energy carrier readily compatible with the current distribution network. Moreover, ammonia decomposition is economically more viable than reforming processes, including methanol reforming,22,23 and hydrogen and N2 are the only decomposition products, in contrast to the co-production of CO, CO2, and CH4 from other liquid H2 carriers.24,25 Last but not least, this reaction can be carried out at lower temperatures (450 °C or below) than reforming processes (above 800 °C).17,26,27
Ammonia decomposition proceeds through stepwise dehydrogenation followed by recombination of two N and two H adatoms to form N2 and H2 followed by desorption, and it is thought that NH cleavage is the rate limiting step. Ru is at the top of the volcano-type relationship observed for the classical ammonia decomposition rate vs. nitrogen binding enthalpy plot.28–30 Consequently, the best ammonia decomposition catalysts known to date are based on Ru. K-promoted catalysts supported on either MgO or carbon nanotubes (CNTs) are among the most active catalysts for this reaction.31–37 The nature of the support has been shown to strongly influence the catalytic performance of Ru-based catalysts. Widely reported is the use of basic supports like MgO and La2O3,33,38,39 neutral supports, such as CNTs,40,41 and acidic supports, like Al2O3.31,32,35,42 In general, the use of basic and neutral supports results in better catalytic properties.43 In addition, the use of alkali promoters has been shown to further decrease the nanoparticle size and the associative desorption of nitrogen, decreasing the activation energy of the reaction.44,45
As can be derived from the previous paragraphs, ammonia decomposition is a relatively well-known process. However, for most potential applications of ammonia derived H2 (i.e. fuel cells), hydrogen should be supplied at elevated pressures, or separated from nitrogen or stored at high pressure. Therefore, in order to avoid additional compression costs46–48 and derived emissions (estimates are about 6.0 kW h kg−1 for compression of H2 to 70 MPa, which leads to approximately 1.3 kg of CO2 per kg of hydrogen),49 high pressure ammonia decomposition would be preferred, in spite of the obvious thermodynamic limitations.50,51 Surprisingly, to the best of our knowledge, this is among the first publications on this topic.
Here we demonstrate the potential and limitations of Ru-based catalysts for the high-pressure decomposition of ammonia. In a first step, by performing experiments at atmospheric pressure, CaO is found to be the most adequate support for Ru. Successive promotion with K results in further improvements in the catalytic performance. Finally, the optimized catalyst is studied at different pressures. Extensive characterization by CO chemisorption and HR-TEM demonstrates that potassium promotion increases metal dispersion by decreasing the Ru particle size. Electronic effects derived from the close proximity between K and Ru result in a decrease in the reaction apparent activation energy, as shown by a detailed kinetic analysis.
Experimental
Catalyst synthesis
Commercial multiwall carbon nanotubes (MWCNTs, Aldrich), magnesium oxide (Sigma-Aldrich), natural sepiolite (NS) (Aldrich) and calcium oxide (Sigma-Aldrich) were used as supports.Rehydrated ruthenium(III) chloride (Aldrich) was selected as the Ru precursor, and it was incorporated onto the different supports by incipient wetness impregnation using acetone, in order to achieve different Ru loadings (from 1 to 7 wt%). After drying at 60 °C for 3 hours and a subsequent thermal treatment under argon at 500 °C for 3 hours, a potassium promoter was introduced by incipient wetness impregnation using KOH in ethanol, to reach the desired K loading (0 to 15 wt%). Finally, a second thermal treatment under Ar at 500 °C for 3 h was performed.
Catalyst characterization
Nitrogen adsorption and desorption isotherms were recorded on a Micromeritics ASAP 2040 system at 77 K. The samples were previously evacuated at 373 K for 16 h. The Brunauer–Emmett–Teller (BET) method was used to calculate the specific surface area. The P/P0 range for the BET analysis was 0.067 < P/P0 < 0.249.X-ray diffraction (XRD) patterns were obtained using a Bruker D8 instrument in the Bragg–Brentano configuration using Cu Kα radiation. The diffractograms were scanned with a step size of 0.02° in the 2θ range of 10–90°. The crystalline phase was identified by comparison with the Joint Committee on Powder Diffraction Standards (JCPDS).
CO pulse chemisorption studies were carried out on a Micromeritics ASAP 2920 analyzer. The samples were previously reduced with a 50%H2/50%Ar gas mixture from room temperature to 500 °C, and this temperature was kept for two hours. After the reduction, the samples were cooled down to 35 °C, and treated with several CO pulses (10%CO/90%He). For further calculations, a stoichiometric factor Ru/CO = 1 and a spherical geometry for the ruthenium metal particles were assumed.
Inductively coupled plasma-optical emission spectrometry (ICP-OES) was used to analyze the composition and metal loadings of the catalysts on a Thermo-Electron 3580 instrument. Complete digestion of the powders was achieved at 240 °C and 35 bar using an UltraWAVE apparatus (Milestone) and aqua regia in a ratio of 1 mg of catalyst![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mL of aqua regia.
1 mL of aqua regia.
Transmission electron microscopy (TEM) of the samples was performed with a Titan Themis-Z microscope from Thermo-Fisher Scientific operated at an accelerating voltage of 300 kV and a beam current of 0.5 mA. Dark-field imaging was performed on a scanning TEM (STEM) coupled to a high-angle annular dark-field (HAADF) detector. Furthermore, a high throughput X-ray energy dispersive spectrometer (EDS) was also utilized in conjunction with DF-STEM imaging to acquire STEM-EDS spectrum-imaging datasets. During the acquisition of these datasets, at every image pixel, a corresponding EDS spectrum was also acquired to simultaneously generate the elemental maps of Ru, O, K, and Ca atoms. It is also pertinent to note herein that the spectrum-imaging datasets were acquired in the so-called frame mode, in which the electron beam was allowed to dwell at each pixel for only a few microseconds in order to keep the total frame time to 6 s or less. Both imaging and spectroscopy datasets for each sample were acquired as well as analyzed with a newly developed software package called Velox from Thermo-Fisher Scientific. The elemental maps for Ru, O, K and Ca atoms were computed using the extracted intensities of their respective Kα lines after background subtraction. The generated maps were slightly post-filtered by applying a Gaussian filter (σ = 0.5).
Catalytic testing
Ammonia decomposition catalytic tests were carried out in a PID Microactivity Reference system, using a continuous fixed bed stainless steel reactor coated with alumina to avoid any activity of the reactor. Prior to the activity measurement, the catalysts (200 mg pelletized between 300 μm and 500 μm and diluted with 1 g of SiC) were reduced/activated in situ with hydrogen (25 mL min−1) at 500 °C for 3 h. The catalytic performance was evaluated at different temperatures in the range of 150–550 °C, achieving 7 h of total reaction time. For the experiments at atmospheric pressure, ammonia in the gas phase (30–100 mL min−1, WHSV = 9000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mL gcat−1 h−1) was flowed, using a mass flow controller, over the catalytic bed. For the experiments at high pressure (10–40 bar), a liquefied feeding system was used pumping liquid ammonia with an HPLC Gilson pump (30 N mL min−1, WHSV = 9000 mL gcat−1 h−1) through a preheater at 100 °C, in order to expand the liquid ammonia into gas before reaching the catalytic bed, where the operating pressure was automatically controlled using a back pressure regulator.
000 mL gcat−1 h−1) was flowed, using a mass flow controller, over the catalytic bed. For the experiments at high pressure (10–40 bar), a liquefied feeding system was used pumping liquid ammonia with an HPLC Gilson pump (30 N mL min−1, WHSV = 9000 mL gcat−1 h−1) through a preheater at 100 °C, in order to expand the liquid ammonia into gas before reaching the catalytic bed, where the operating pressure was automatically controlled using a back pressure regulator.
Reaction products (nitrogen, hydrogen and ammonia) were analyzed under isothermal conditions with an online gas chromatograph (3000A Micro-GC gas analyzer, Agilent) using helium (1 ml min−1) as the internal standard for quantitative analysis. The Micro-GC is equipped with two columns: a PLOTU precolumn/Molsieve column using argon as the carrier gas for nitrogen and hydrogen and a PLOTU column with helium carrier gas for ammonia. Both columns are equipped with thermal conductivity detectors.
Results and discussion
Catalyst characterization
The BET area and ICP results are shown in Table 1. Very small specific surface areas were observed for all the catalysts based on CaO (in the range of 4–10 m2 g−1), independent of Ru and K loadings while moderate to very high surface areas were obtained using other support materials (see MWCNTs or natural sepiolite). The ICP results are in good agreement with the nominal composition for all the samples, corroborating the successful incorporation of the active species (Ru) and promoter (K).| Sample | S BET | Rua | K a |
|---|---|---|---|
| (m2 g−1) | (wt%) | (wt%) | |
| a Calculated by ICP-OES measurements. | |||
| 5%Ru10%K/MWCNT | 758 | 4.7 | 9.7 |
| 5%Ru10%K/MgO | 32 | 4.8 | 9.7 |
| 5%Ru10%K/NS | 138 | 4.9 | 9.4 |
| 1%Ru10%K/CaO | 6 | 0.9 | 9.6 |
| 2%Ru10%K/CaO | 7 | 1.8 | 9.7 |
| 3%Ru10%K/CaO | 5 | 2.8 | 9.6 |
| 5%Ru10%K/CaO | 4 | 4.7 | 9.5 |
| 7%Ru10%K/CaO | 8 | 6.6 | 9.4 |
| 3%Ru/CaO | 10 | 2.9 | — |
| 3%Ru5%K/CaO | 5 | 2.8 | 4.9 |
| 3%Ru15%K/CaO | 5 | 2.7 | 13.8 |
The Ru–K/CaO catalysts with different Ru and K loadings were characterized by XRD at different stages: after thermal decomposition at 500 °C under an Ar atmosphere, after activation under H2 at 500 °C for 3 h, and after being exposed to ammonia under reaction conditions for 7 h. The XRD patterns are shown in Fig. 1. It is important to note that the CaO support tends to carbonate upon exposure to the atmosphere. Nevertheless, this phenomenon does not alter the properties of the catalysts since it does not occur during the catalytic testing under the activation or reaction conditions.
 | ||
| Fig. 1 XRD patterns of the Ru–K/CaO samples. A) Calcined samples, B) reduced samples and C) after catalytic testing. | ||
The XRD patterns recorded after thermal treatment under Ar, Fig. 1A, show CaO, K2O and RuO2 phases. As expected, the most intense reflections are assigned to CaO (JCPDS 00-37-1497) with 2θ angles of 32.2°, 37.4°, 53.9°, 64.2°, and 67.4°. K2O with a small diffraction peak (JCPDS 00-47-1701) at a 2θ angle of 45.3° is formed under Ar thermal treatment after the incorporation of the promoter by impregnation. Additionally, diffraction peaks corresponding to RuO2 are also detected, due to the incorporation of Ru by impregnation (JCPDS 00-43-1027) with 2θ angles of 31.7 and 44.1°; the intensity of these reflections increases when increasing the Ru loading. After H2 treatment, Fig. 1B, apart from the reflections assigned to CaO and K2O, full reduction of Ru is observed: see the disappearance of RuO2 associated with diffraction and the appearance of metallic Ru (JCPDS 00-06-0663) at 2θ angles of 38.4° and 44°. In the samples with different loadings of K, a well-defined Ru pattern was also observed (Fig. 1B). After the catalytic test, CaO, K2O and Ru are still visible in the XRD patterns (Fig. 1C).
The ruthenium dispersion and particle size were evaluated by CO pulse chemisorption in the samples after the activation under H2 treatment. Table 2 summarizes the obtained results for the metal dispersion, active metal surface area (AMSA), Ru particle size and number of surface active sites. It is interesting to observe that, in spite of the low surface area of the support, the metal dispersion and particle size remain constant for Ru loadings up to 3 wt%. Addition of Ru further results in bigger nanoparticles and therefore lower dispersions. Addition of K further contributes to enhancing dispersion, most probably by inhibiting Ru sintering as previously observed.52–54
| Sample | Dispersiona | AMSAb | d p | N AS × 10−3 |
|---|---|---|---|---|
| (%) | (m2 gmetal−1) | (nm) | (mol g−1) | |
| a Metal dispersion (%): weight of exposed metal atoms/weight of total metal atoms. b Active metal surface area (AMSA). c Active particle size; (spherical geometry). d p (nm) = 6/(AMSA)·ρRu (where ρRu = 12.2 g cm−3).Number of surface active sites: NAS (mol g−1) = Ru loading (wt) × dispersion/Ru mass (g mol−1). | ||||
| 1%Ru10%K/CaO | 16.2 | 87 | 6 | 1.6 |
| 2%Ru10%K/CaO | 15.2 | 81 | 6 | 3.0 |
| 3%Ru10%K/CaO | 15.5 | 83 | 6 | 4.6 |
| 5%Ru10%K/CaO | 8.5 | 45 | 11 | 4.2 |
| 7%Ru10%K/CaO | 5.2 | 28 | 17 | 3.6 |
| 3%Ru/CaO | 9.8 | 52 | 9 | 2.9 |
| 3%Ru5%K/CaO | 11.2 | 60 | 8 | 3.3 |
| 3%Ru15%K/CaO | 14.8 | 79 | 6 | 4.4 |
The comparison of the obtained results reveals 3%Ru10%K/CaO as the composition with the highest active surface area.
The local structures of the Ru–K/CaO catalysts were evaluated using high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) and energy-dispersive X-ray spectroscopy (EDX). Representative TEM images are shown in Fig. 2 for 3%Ru10%K/CaO and 3%Ru/CaO catalysts after activation treatment under H2 at 500 °C for 3 h. In the TEM images of the sample without K (3%Ru/CaO), Ru nanoparticles are dispersed on the CaO support with a quite broad particle size distribution in the range of 2.5 to 22.5 nm. The mean particle size, 9 nm, is in agreement with that calculated by CO chemisorption (Tables 2 and S4†). Elemental mapping shows that the Ru dispersion is not completely regular in these samples, with Ru localized preferably in certain regions. In the TEM images for the sample containing K (3%Ru10%K/CaO), significant differences are observed compared to the sample without potassium. Ru nanoparticles are better dispersed, with a narrower particle size distribution, from 2 to 15 nm, and a smaller mean particle size, 7 nm, that matches with the particle size calculated by CO chemisorption (6 nm). Mapping shows that K, although is dispersed throughout the catalyst surface, it is preferably located on top of the Ru nanoparticles.
Catalytic activity
In a preliminary stage, the catalytic performance of potassium-promoted Ru catalysts on different supports was evaluated. Table 3 shows the ammonia conversion levels and hydrogen production rates at 400 °C for the Ru–K catalysts on different supports. The Ru–K catalysts supported on CaO and NS were found to be more efficient catalysts compared to those on other supports reported for this process, such as MWCNTs or MgO, with Ru–K/CaO showing the highest ammonia conversion (54%) and hydrogen productivity (574.3 mol H2 per mol Ru h−1) at 400 °C. It is worth highlighting that these results are not correlated with the measured surface areas of the different catalysts. Considering that both Ru loadings and Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K ratios are similar for all the catalysts, this suggests that the chemical nature of the support has an important influence on the catalytic performance. For instance, the use of basic supports resulted in better catalytic performance, in line with this fact, CaO is a more basic support with a larger number and strength of basic sites.55,56
K ratios are similar for all the catalysts, this suggests that the chemical nature of the support has an important influence on the catalytic performance. For instance, the use of basic supports resulted in better catalytic performance, in line with this fact, CaO is a more basic support with a larger number and strength of basic sites.55,56
| Catalyst | X NH3 (%) | H2 production (mol H2 per mol Ru h−1) |
|---|---|---|
| 5%Ru10%K/MWCNT | 30.8 | 322.7 |
| 5%Ru10%K/MgO | 39.4 | 407.8 |
| 5%Ru10%K/NS | 46.6 | 474.4 |
| 5%Ru10%K/CaO | 53.7 | 574.3 |
In view of these results, the optimal metal and promoter loadings were subsequently investigated using CaO as the support. Fig. 3 shows the ammonia conversion versus reaction temperature, while the insets compare the activity at 400 °C for different Ru and K loadings. The conversions are not affected by heat or mass transport limitation (Fig. S1–S3†).
 | ||
| Fig. 3 Ammonia conversion versus temperature of Ru–K/CaO catalysts; effect of Ru and K loadings. P = 1 atm; T = 250–550 °C; NH3 flow rate 30 N ml min−1; Wcat = 200 mg; WHSV: 9000 mL g−1 h−1. | ||
First, the samples with Ru loadings in the range of 1–7 wt% and constant K loading (10 wt%) were evaluated. The positive effect of Ru is clearly observed up to 3 wt% loading. After that, the activity decreases significantly. Secondly, the samples with the optimum Ru loading (3 wt%) and K loadings in the range of 0–15 wt% were also analyzed. For K promotion, also an optimum loading is observed, in this case 10 wt%. For CaO-supported samples, the catalytic performance is very well in line with the obtained characterization results, especially in terms of Ru dispersion, active metal surface area and TEM characterization, according to the beneficial effect of K preventing Ru agglomeration under activation and reaction conditions.52–54 The best catalytic results are obtained for Ru nanoparticles of 6–7 nm. Ammonia decomposition on Ru has been shown to be a highly structure-sensitive reaction, with terrace sites being the main active sites57 and with particles below 6 nm being hardly active. Our experimental results further confirm this earlier observation.
Once the catalyst composition was optimized, we studied the high-pressure (10–40 bar) decomposition performance of the 3%Ru10%K/CaO sample. Fig. 4A shows the impact of operating pressure on the catalytic performance. The ammonia conversion is greatly decreased when the pressure increases from 1 to 40 bar. Meanwhile a high conversion, around 80%, is still observed at 550 °C and 40 bar. This is further analysed in Fig. 4B. Interestingly, although a drastic decrease is observed in the conversion level, the hydrogen productivity increases with pressure (Fig. 4C), already anticipating a positive reaction order for NH3 (vide infra) (Fig. 4C and D).
Finally, turnover frequencies (TOFs) were calculated (Fig. 4D and 5) considering the number of active surface sites evaluated by CO chemisorption studies (see above in section 3.1, Table 2). Rates far from equilibrium were considered to compare the TOF calculated for both samples. The promotion effect of potassium on the catalytic activity of the Ru catalysts is clearly observed in Fig. 5.
 | ||
| Fig. 5 Calculated turnover frequencies (TOFs) for K-promoted and unpromoted Ru/CaO catalysts. P =1 atm; T = 150–500 °C; NH3 flow rate 30 ml min−1; WHSV = 9000 mL h−1 g−1. | ||
Kinetic analysis
Kinetic studies at atmospheric pressure were performed for the optimized 3%Ru10%K/CaO catalyst, as well as for the unpromoted catalyst in order to elucidate the effect of potassium from a kinetic point of view. Reaction orders for NH3 and H2 were calculated from differential experiments varying the NH3 and H2 partial pressures and the temperature (details of the kinetic study in the ESI† and Fig. S4–S6). The results are summarized in Table 4. The apparent activation energy was calculated from the Arrhenius plots for both catalysts. Incorporation of K results in a decrease in the activation energy from 96 to 75 kJ mol−1. Promotion with alkali metals is well known to decrease the hydrogenation ability of Ru via electronic promotion.27| Sample | E a (kJ mol−1) | a | b |
|---|---|---|---|
| 3%Ru/CaO | 96 | 0.8 | −1.9 |
| 3%Ru10%K/CaO | 75 | 0.5 | −1.2 |
Inhibition of the ammonia decomposition rate by the hydrogen produced is observed. The negative orders observed for hydrogen for both catalysts can be explained, considering that chemisorbed hydrogen blocks surface sites that are necessary for ammonia decomposition, or reacts chemically and hydrogenates NHx intermediates generated during the ammonia decomposition.58 As shown in Table 4, potassium promotion results in a decrease of both the reaction order on NH3 (from 0.8 to 0.5) and the negative reaction order on H2 (from −1.9 to −1.2), highlighting the positive electronic promotion of the alkali metal.
For Ru-based catalysts, it is generally agreed that the limiting reaction step is the dissociation of ammonia59,60 and the observed negative order on hydrogen is related to the re-hydrogenation of partially dehydrogenated species (NHx intermediates, x = 1, 2). The kinetic data clearly show the ability of K to decrease the hydrogenation capability of Ru. In this way, inhibition of ammonia decomposition by hydrogen becomes less important and this is translated into an enhancement of the catalytic activity.
The observed kinetics for the Ru–K/CaO catalysts at atmospheric pressure are well described using the power law given by eqn (1).
| (−rNH3) = k × PNH3aPH2b | (1) |
 | (2) |
Considering the inhibition of the decomposition rate by the hydrogen produced, and taking into account that the gas composition is very different along the reactor with the increasing conversion level, an integral reactor must be considered for the kinetic analysis in this case, to account for the increasing hydrogen concentrations at the different conversion levels along the catalytic bed.61 The integration of eqn (3) allows the calculation of the ammonia conversion in a plug-flow reactor, where the ammonia conversion rate (−rNH3) is given by the expression in eqn (2), and can be compared with the experimental values. See details of the kinetic study in an integral reactor in the ESI.†
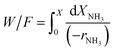 | (3) |
 | ||
| Fig. 6 Experimental vs. modeled ammonia conversion using the proposed power-law model (eqn (2)) for ammonia decomposition over the 3%Ru10%K/CaO catalyst. Red: ammonia conversion at high pressure. Black: conversion at atmospheric pressure. | ||
Furthermore, other kinetic models taking into account different mechanistic considerations and assuming different rate determining steps (given by eqn (S5)–(S8) in the ESI†) were explored here to fit the experimental data, as well as to predict the catalytic performance at high pressure. Fittings obtained with all the kinetic models selected are shown in Fig. S7 and S8 in the ESI.† Considering the parity plots that compare the experimental and calculated values of ammonia conversion, it is difficult to draw conclusions related to the limiting step, since almost identical fittings are obtained with the mechanistic models that consider different rate determining steps, such as those assuming the ammonia dissociation (eqn (S7)†) or nitrogen desorption as the rate limiting step (eqn (S5)†). This is the main reason why, in spite of the research over the past decades in this reaction, there is no agreement about the limiting step or the kinetically relevant surface species. In fact, the results in Fig. S7 and S8† clearly corroborate that all the species present at the catalyst surface must be considered as kinetically relevant. The fitting of the experimental data with the models that consider a few adsorbed species as the most abundant ones (such as kinetic eqn (S6) and (S8)†) provides worse matching. This aspect becomes more significant when the process is conducted at high pressure (Fig. S8†).
Interestingly, from Fig. 6 and S7 and S8 in the ESI,† with the parity plots for different kinetic models, it is concluded that the power law given by eqn (2) is as good as the mechanistic models that take into account different rate limiting steps, while offering, by far, the simplest equation for a kinetic model. Furthermore, this model is the most robust to predict the catalytic performance for ammonia decomposition at high pressure (Fig. S8†).
Conclusions
In summary, our work further demonstrates that Ru-based catalysts are very efficient for the decomposition of ammonia. Considering the relatively low Ru loadings desired and the strong structure sensitivity of this reaction, with an optimal Ru particle size in the order of 7 nm, the chemical nature of the support, especially its basicity, plays a much bigger role than other physical properties such as surface area. Considering these facts, among the studied supports, CaO has been identified as a very promising one.The reaction proceeds with inhibition of the decomposition reaction rate by the hydrogen produced, suggesting that competitive adsorption of H2 and/or re-hydrogenation of NHx intermediates occur, and pointing to the ammonia dissociation as the limiting step of the reaction rate. By promoting Ru with K, the competitive adsorption of H2 is reduced and the hydrogenation capability of Ru is decreased, as shown by the strong decrease in the H2 negative reaction order. This effect translates into higher intrinsic catalytic activity.
Last but not least, our modelling results demonstrate that kinetic analysis in the low-pressure regime using the power law-derived equation can be used to accurately predict catalytic performance at higher decomposition pressures, which, from an application perspective, are much more attractive but may be difficult to measure in many laboratories.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Saudi Aramco is gratefully acknowledged for financial support.References
- A. J. Chapman, B. C. McLellan and T. Tezuka, Appl. Energy, 2018, 219, 187–198 CrossRef.
- V. Ş. Ediger, Energy Procedia, 2019, 156, 2–6 CrossRef.
- R. York and S. E. Bell, Energy Res. Soc. Sci., 2019, 51, 40–43 CrossRef.
- A. Singh, P. Baredar and B. Gupta, Energy Convers. Manage., 2017, 145, 398–414 CrossRef.
- E. Abokyi, P. Appiah-Konadu, F. Abokyi and E. F. Oteng-Abayie, Energy Rep., 2019, 5, 1339–1353 CrossRef.
- H. A. D. Hdom, Renewable Energy, 2019, 139, 186–197 CrossRef.
- N. M. Jalal, A. R. Jabur, M. S. Hamza and S. Allami, Energy Procedia, 2019, 157, 1494–1505 CrossRef CAS.
- A. Chica and S. Sayas, Catal. Today, 2009, 146(1), 37–43 CrossRef CAS.
- S. Sayas and A. Chica, Int. J. Hydrogen Energy, 2014, 39(10), 5234–5241 CrossRef CAS.
- M. Menor, S. Sayas and A. Chica, Fuel, 2017, 193, 351–358 CrossRef CAS.
- D. Guban, I. K. Muritala, M. Roeb and C. Sattler, Int. J. Hydrogen Energy, 2019 DOI:10.1016/j.ijhydene.2019.08.145.
- D. Xu, W. Li, X. Ren, W. Shen and L. Dong, Int. J. Hydrogen Energy, 2019 DOI:10.1016/j.ijhydene.2019.09.030.
- C. Weidenthaler, J. Energy Chem., 2020, 42, 133–143 CrossRef.
- M. Lototskyy, I. Tolj, Y. Klochko, M. W. Davids, D. Swanepoel and V. Linkov, Int. J. Hydrogen Energy, 2019, 45(14), 7958–7967 CrossRef.
- P. T. Aakko-Saksa, C. Cook, J. Kiviaho and T. Repo, J. Power Sources, 2018, 396, 803–823 CrossRef CAS.
- H. Jorschick, M. Vogl, P. Preuster, A. Bösmann and P. Wasserscheid, Int. J. Hydrogen Energy, 2019, 44(59), 31172–31182 CrossRef CAS.
- S. Mukherjee, S. V. Devaguptapu, A. Sviripa, C. R. F. Lund and G. Wu, Appl. Catal., B, 2018, 226, 162–181 CrossRef CAS.
- N. Itoh, A. Oshima, E. Suga and T. Sato, Catal. Today, 2014, 236, 70–76 CrossRef CAS.
- A. Kantürk Figen, M. B. Pişkin, B. Coşkuner and V. İmamoğlu, Int. J. Hydrogen Energy, 2013, 38(36), 16215–16228 CrossRef.
- Y. Kojima, Int. J. Hydrogen Energy, 2019, 44(33), 18179–18192 CrossRef CAS.
- J. W. Makepeace, T. He, C. Weidenthaler, T. R. Jensen, F. Chang, T. Vegge, P. Ngene, Y. Kojima, P. E. de Jongh, P. Chen and W. I. F. David, Int. J. Hydrogen Energy, 2019, 44(15), 7746–7767 CrossRef CAS.
- R. Metkemeijer and P. Achard, Int. J. Hydrogen Energy, 1994, 19(6), 535–542 CrossRef CAS.
- C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111(1), 140–144 CrossRef CAS.
- Y. W. Cheng, M. R. Khan, K. H. Ng, S. Wongsakulphasatch and C. K. Cheng, Renewable Energy, 2019, 138, 1114–1126 CrossRef CAS.
- L. P. Didenko, L. A. Sementsova, P. E. Chizhov and T. V. Dorofeeva, Int. J. Hydrogen Energy, 2019, 44(48), 26396–26404 CrossRef CAS.
- F. R. García-García, Y. H. Ma, I. Rodríguez-Ramos and A. Guerrero-Ruiz, Catal. Commun., 2008, 9(3), 482–486 CrossRef.
- A. K. Hill and L. Torrente-Murciano, Int. J. Hydrogen Energy, 2014, 39(15), 7646–7654 CrossRef CAS.
- J. C. Ganley, F. S. Thomas, E. G. Seebauer and R. I. Masel, Catal. Lett., 2004, 96(3–4), 117–122 CrossRef CAS.
- A. Boisen, S. Dahl, J. K. Nørskov and C. H. Christensen, J. Catal., 2005, 230(2), 309–312 CrossRef CAS.
- C. J. H. Jacobsen, S. Dahl, B. S. Clausen, S. Bahn, A. Logadottir and J. K. Nørskov, J. Am. Chem. Soc., 2001, 123(34), 8404–8405 CrossRef CAS PubMed.
- S. Bajus, F. Agel, M. Kusche, N. Ní Bhriain and P. Wasserscheid, Appl. Catal., A, 2016, 510, 189–195 CrossRef CAS.
- A. Di Carlo, L. Vecchione and Z. Del Prete, Int. J. Hydrogen Energy, 2014, 39(2), 808–814 CrossRef CAS.
- C. Huang, Y. Yu, J. Yang, Y. Yan, D. Wang, F. Hu, X. Wang, R. Zhang and G. Feng, Appl. Surf. Sci., 2019, 476, 928–936 CrossRef CAS.
- D.-C. Huang, C.-H. Jiang, F.-J. Liu, Y.-C. Cheng, Y.-C. Chen and K.-L. Hsueh, Int. J. Hydrogen Energy, 2013, 38(8), 3233–3240 CrossRef CAS.
- K. Lamb, S. S. Hla and M. Dolan, Int. J. Hydrogen Energy, 2019, 44(7), 3726–3736 CrossRef CAS.
- L. Li, Y. Wang, Z. P. Xu and Z. Zhu, Appl. Catal., A, 2013, 467, 246–252 CrossRef CAS.
- L. Li, Z. H. Zhu, Z. F. Yan, G. Q. Lu and L. Rintoul, Appl. Catal., A, 2007, 320, 166–172 CrossRef CAS.
- X.-C. Hu, W.-W. Wang, Z. Jin, X. Wang, R. Si and C.-J. Jia, J. Energy Chem., 2019, 38, 41–49 CrossRef.
- X. Ju, L. Liu, P. Yu, J. Guo, X. Zhang, T. He, G. Wu and P. Chen, Appl. Catal., B, 2017, 211, 167–175 CrossRef CAS.
- J. Chen, Z. H. Zhu, S. Wang, Q. Ma, V. Rudolph and G. Q. Lu, Chem. Eng. J., 2010, 156(2), 404–410 CrossRef CAS.
- S.-F. Yin, B.-Q. Xu, C.-F. Ng and C.-T. Au, Appl. Catal., B, 2004, 48(4), 237–241 CrossRef CAS.
- S. Chiuta, R. C. Everson, H. W. J. P. Neomagus and D. G. Bessarabov, Int. J. Hydrogen Energy, 2016, 41(6), 3774–3785 CrossRef CAS.
- I. Lucentini, A. Casanovas and J. Llorca, Int. J. Hydrogen Energy, 2019, 44(25), 12693–12707 CrossRef CAS.
- S. J. Wang, S. F. Yin, L. Li, B. Q. Xu, C. F. Ng and C. T. Au, Appl. Catal., B, 2004, 52(4), 287–299 CrossRef CAS.
- P. Chen, X. Ju, L. Liu, X. Zhang, J. Feng and T. He, ChemCatChem, 2019, 11, 4161–4170 CrossRef.
- J. Bellosta von Colbe, J.-R. Ares, J. Barale, M. Baricco, C. Buckley, G. Capurso, N. Gallandat, D. M. Grant, M. N. Guzik, I. Jacob, E. H. Jensen, T. Jensen, J. Jepsen, T. Klassen, M. V. Lototskyy, K. Manickam, A. Montone, J. Puszkiel, S. Sartori, D. A. Sheppard, A. Stuart, G. Walker, C. J. Webb, H. Yang, V. Yartys, A. Züttel and M. Dornheim, Int. J. Hydrogen Energy, 2019, 44(15), 7780–7808 CrossRef CAS.
- C. Deng, M. Zhu, Y. Zhou and X. Feng, Energy, 2018, 159, 203–215 CrossRef.
- G. Sdanghi, G. Maranzana, A. Celzard and V. Fierro, Renewable Sustainable Energy Rev., 2019, 102, 150–170 CrossRef CAS.
- P. Di Profio, S. Arca, F. Rossi and M. Filipponi, Int. J. Hydrogen Energy, 2009, 34, 9173–9180 CrossRef CAS.
- M. Al-Zareer, I. Dincer and M. A. Rosen, Int. J. Hydrogen Energy, 2019, 44(33), 18214–18224 CrossRef CAS.
- B. Wang, H. Kong, H. Wang, Y. Wang and X. Hu, Int. J. Hydrogen Energy, 2019, 44(49), 26874–26887 CrossRef CAS.
- K. Aika, K. Shimazaki, Y. Hattori, A. Ohya, S. Ohshima, K. Shirota and A. Ozaki, J. Catal., 1985, 92(2), 296–304 CrossRef CAS.
- G. Ertl, Catal. Rev.: Sci. Eng., 1980, 21(2), 201–223 CrossRef CAS.
- F. F. Gadallah, R. M. Elofson, P. Mohammed and T. Painter, Stud. Surf. Sci. Catal., ed. G. Poncelet, P. Grange and P. A. Jacobs, Elsevier, 1983, vol. 16, pp. 409–420 Search PubMed.
- H. Hattori and Y. Ono, Catalysts and catalysis for acid–base reactions, in Metal Oxides in Heterogeneous Catalysis, ed. J. C. Védrine, Elsevier, 2018, ch. 4, pp. 133–209 Search PubMed.
- Y. Ono and H. Hattori, Preparation and Catalytic Properties of Solid Base Catalysts - I. Metal Oxides, in Solid Base Catalysis, Springer, Berlin, Heidelberg, 2011, pp. 69–156 Search PubMed.
- A. M. Karim, V. Prasad, G. Mpourmpakis, W. W. Lonergan, A. I. Frenkel, J. G. Chen and D. G. Vlachos, J. Am. Chem. Soc., 2009, 131(34), 12230–12239 CrossRef CAS PubMed.
- W. Tsai, J. J. Vajo and W. H. Weinberg, J. Am. Chem. Soc., 1985, 89, 4926 CAS.
- T. E. Bell and L. Torrente-Murciano, Top. Catal., 2016, 59(15–16), 1438–1457 CrossRef CAS.
- F. Schüth, R. Palkovits, R. Schlögl and D. S. Su, Energy Environ. Sci., 2012, 5, 6278–6289 RSC.
- S. Armenise, E. García-Bordejé, J. L. Valverde, E. Romeo and A. Monzón, Phys. Chem. Chem. Phys., 2013, 15(29), 12104–12117 RSC.
- A. Di Carlo, A. Dell'Era and Z. Del Prete, Int. J. Hydrogen Energy, 2011, 36, 11815–11824 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy00686f |
| This journal is © The Royal Society of Chemistry 2020 |


